1. Introduction
The takeoff and landing phases are key to the entire flight phase of a fixed-wing UAV (UAV). Currently, the launching methods of fixed-wing UAVs include hand-launching, skid-launching, vertical-launching, landing gear skid-launching, rocket-launching, and air-launching. There are also various recovery methods, which can be summarized as parachute recovery, landing gear taxi recovery, interceptor net recovery, and disposal landing recovery [
1].
Correction control during landing taxiing is an important aspect of UAV wheeled takeoff and landing. The existence of asymmetry in the aircraft structure as well as in the wing auxiliary support, the existence of various wind disturbances at airports, the existence of convexity and concavity in the runway, the existence of slipstream influence in the propellers, the existence of yaw angle and lateral offset relative to the runway when the aircraft is grounded for landing, etc., all of which will lead to the occurrence of a lateral deviation of the aircraft relative to the runway during takeoff or landing taxi. If the lateral deviation is not corrected in time, the aircraft may veer off the runway, resulting in a serious accident. In the takeoff and landing taxiing phase, the large UAV mainly realizes the corrective control by controlling the front wheel turn, rudder, and differential brake. At low speeds, the rudder is less efficient, and it mainly relies on the front wheel and differential brake to correct the heading. At high speeds, the rudder is used to realize the correction control.
To address the taxiing problem of UAVs, Yong Wang [
2] designed a correction control law based on active braking and rudder deflection using a model-referenced control architecture based on the establishment of a mathematical model of the landing gear and braking device of a UAV with a front-three-point layout. J-M. Biannic [
3] established a nonlinear model of a ground plane, replacing the strong nonlinearity of the initial model with time-varying uncertainty and saturation. Ejagen Sadien [
4] developed a three-degree-of-freedom ground aircraft model considering aerodynamics, thrust, and tire ground interactions for several runway states, controlling the aircraft by engine thrust, rudder deflection, front wheel steering, and differential braking. Edouard Sadien [
5] built a UAV ground model and added the control assignment to the control end to realize the accurate tracking of the aircraft to the runway centerline. Yaqi Dai [
6] et al. solved the problem of automatic lateral control of an aircraft during ground deceleration. J. Duprez [
7] et al. used feedback linearization for the nonlinearities of the aircraft model during the ground taxi phase and designed the yaw control law for aircraft in the landing phase. Chen Bihua [
8] designed an adaptive back-stepping control law for the path tracking control problem of a ground aircraft. Zheng Wu [
9] studied the sliding mode control problem of a ground aircraft in the deceleration phase. Clement Roos [
10] improved the ground taxi control of a civil aircraft by proposing a non-standard anti-saturation control strategy instead of dynamic inverse control. Jiguang Li [
11] designed a rhombic wing UAV ground takeoff skid run controller based on the back-stepping control method, which effectively controls the heading of the UAV takeoff skid run. Chengfu Wu [
12] and others established a nonlinear mathematical model of ground taxiing for a three-point landing gear UAV and adopted a control structure with a combination of lateral deviation and lateral speed to realize taxiing takeoff control by linking the front wheel and rudder. Yinping Deng [
13] modeled a UAV with a four-wheel landing gear layout and designed a corrective deviation control law based on the PID method. Yanxiong Wang [
14] proposed a nonlinear taxiing correction control method for UAVs based on self-impedance control theory to address the taxiing disturbance problem of UAVs with flying wing layout. Tran Ngoc Son [
15] et al. designed taxiing correction controllers by using a predictive control method to address the nonlinear model of UAVs taxiing on the ground. Caijuan Jia [
16] proposed a multiple fuzzy control correction scheme applying a combination of primary and secondary fuzzy controllers. Qingyang Chen [
17] and others designed a taxiing trajectory controller using an improved L1 nonlinear guidance algorithm and introduced a second-order linear expansion state observer to improve the control accuracy for gusts of wind and other random perturbations.
Summarizing the above research results, most of them adopt the simplified ground taxiing model to construct the aircraft dynamics equations, and at the same time adopt the control mode of the rudder and front wheel differential to complete the control of UAV ground taxiing, and adopt the control method with adaptive or robust control method to design the control law in the control method. Although these methods have solved the takeoff taxiing control problems of some airplanes, the use of rudders and nose wheels for heading control is not feasible for large-scale UAVs, at the same time, solar-powered drones are more susceptible to environmental disturbances. It is still necessary to establish accurate ground taxiing models and construct effective control modes to realize the accurate control of ground taxiing.
The research object of this paper is a large-scale long-endurance solar UAV, which is not equipped with front wheel turning and brake control devices in order to simplify the structure and reduce the weight. The taxiing corrective function relies on the rudder joint engine differential realization. In this paper, a detailed aircraft ground motion model is established by analyzing the dynamics process. And the ground motion characteristics of this UAV are analyzed. In terms of control, due to the presence of nonlinear factors such as environmental perturbation and slipstream influence, this paper adopts the adaptive back-stepping control method and designs a slip run correction control structure based on the combined engine differential and rudder. Among various methods of dealing with nonlinear problems, the adaptive back-stepping control method has a good ability to deal with nonlinear problems and a rigorous mathematical proof process, which has been paid attention to by a large number of researchers and gained applications in various fields. Finally, the rationality of the proposed control scheme and control structure and the efficiency of the control law design method are verified through the medium-speed and high-speed taxiing tests.
2. Unmanned Aerial Vehicle (UAV) Skid Running Motion Model
The large-scale long-endurance solar UAV studied in this paper has a takeoff weight of about 500 kg, a wingspan of more than 35 m, and adopts taxiing takeoff and landing mode. A main wheel is installed on the front landing gear, and auxiliary support wheels are set on both wings and the tail. Two high-power motors are installed on both sides of the wing to drive the propellers to generate power, as shown in
Figure 1.
During taxiing, the aircraft is subjected to aerodynamic forces, engine pull, ground support, rolling friction, and wheel lateral forces. Since the landing gear system of the solar UAV is relatively simple, it does not have the functions of cushioning strut, turning, braking, and retracting. Only its rigid body characteristics are considered when analyzing the landing gear force characteristics. In order to make the dynamic analysis universal, the landing gear layout in
Figure 1 is simplified to a front three-point model.
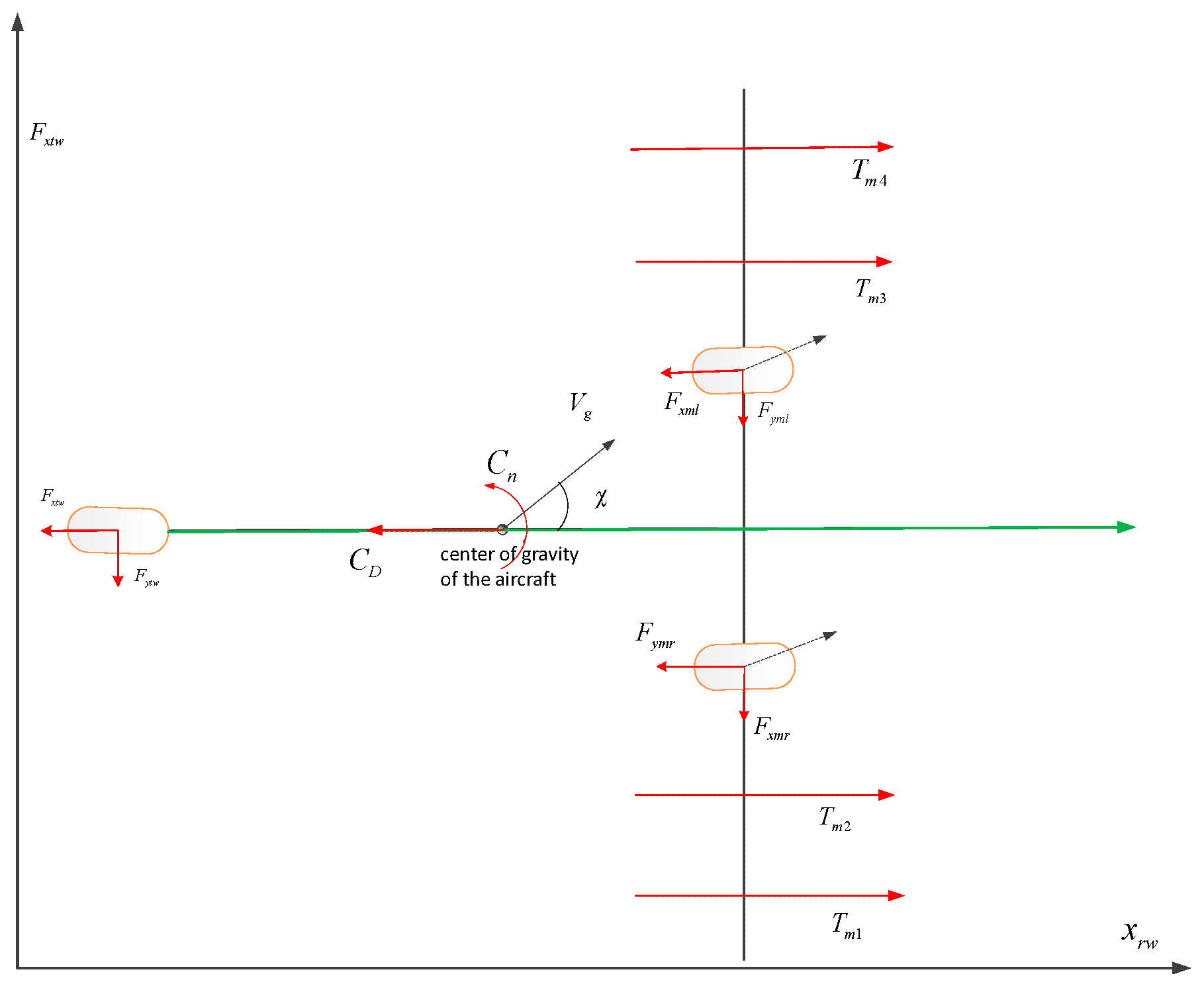
Figure 2 shows the external forces on the airplane when taxiing on the runway at speed
, including ground support force
,
,
, ground friction force
,
,
, ground lateral force
,
,
, engine tension force
,
,
,
, and aerodynamic drag force
, aerodynamic yaw moment
. The subscripts
,
, and
denote the left main wheel, the right main wheel, and the tail wheel, respectively.
The wheel support force
is calculated from the compression of the landing gear tires
and the coefficient of elasticity of the tires
as follows:
Tire compression was solved using the following equation:
where:
,
, and
are the positions of the wheel axes relative to the airplane’s center of mass;
and
denote the airplane’s pitch and roll attitudes;
is the radius of the wheel;
is the airplane’s center of mass altitude; and the subscript is
.
Rolling friction of the wheels is calculated from the support force and the coefficient of friction
:
Lateral wheel forces
are related to the angle
between the wheel’s plane of symmetry and its velocity vector
, and to the number of lateral friction coefficients
. Lateral wheel slip is defined as the presence of a velocity component in the
direction in the wheel coordinate system. The angle between the plane of symmetry of the wheel and the direction of forward speed is defined as the wheel sideslip angle.
where:
is the distance between the main wheel axis line and the center of gravity of the aircraft, and
is the distance between the tail wheel and the center of gravity of the aircraft.
Comprehensive aircraft ground motion by the ground, motor tension, and aerodynamic and other forces will be converted to the fuselage coordinate system to establish a dynamic model.
where:
is the left motor pull,
is the right motor pull.
Combining the ground-acting moment, the aerodynamic moment, and the differential engine moment, the airplane is subjected to a combined moment of:
In the ground taxiing corrective motion analysis, the aircraft pitch and roll direction motion is constrained by the ground, and the aircraft only has the degree of freedom around the axis, so the moment equation can be further simplified as follows:
is the generation of heading maneuvering moment by engine differential as well as rudder deflection.
In order to facilitate the analysis of the ground taxiing corrective motion, the aircraft motion is analyzed based on the ground coordinate system. The runway direction is defined as the
x-axis direction of the ground coordinate system, and the
y-axis points to the left perpendicular to the axis in the horizontal plane. According to the kinematic equations, there are:
Derivation of the above equation gives:
Based on the equations of inertial system dynamics, and also integrating the forces and moments generated by the ground, motor pull, and aerodynamic forces, the equations of aircraft ground dynamics can be written as:
where:
is the ground speed,
is the trajectory angle,
is the heading angle, and
,
is the combined force of ground, engine, and aerodynamic forces.
When taxiing on the ground, the motion of the airplane in the pitch and roll directions is constrained by the ground, and assuming that there is no rotational motion of the airplane in the pitch as well as the roll directions and that the airplane has only degrees of freedom around the
z-axis, the equation of rotation of the airplane is:
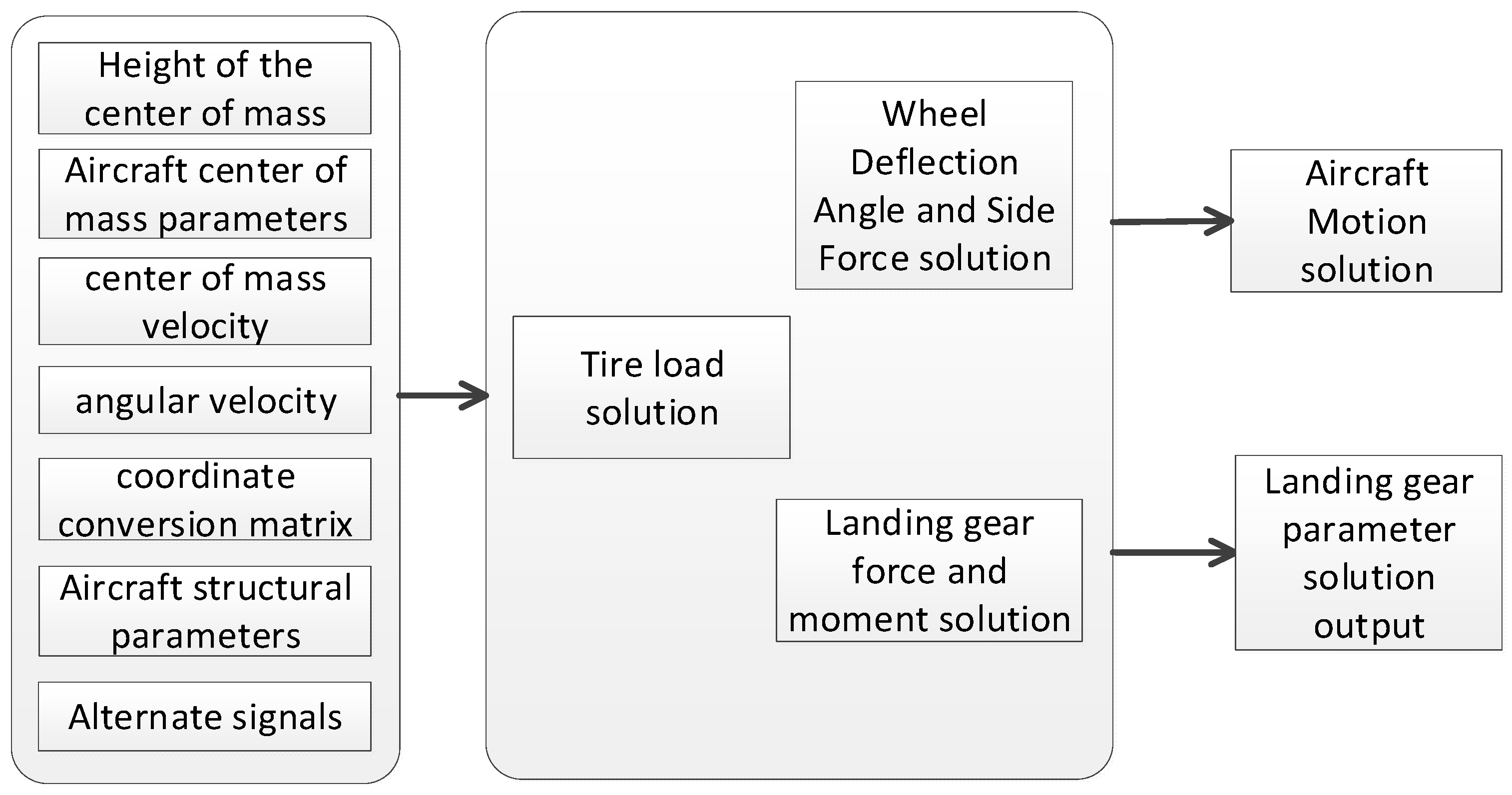
Reference [
2] solves the tire compression based on parameters such as aircraft center of mass height, center of mass position, aircraft angular rate, aircraft speed, and Euler angle, which are used for the force solution of each landing gear strut. Then it is linearly superimposed to obtain the force of the whole landing gear system on the airplane. After coordinate transformation, the landing gear force is decomposed into the airframe axis system, integrated with the aerodynamic force and the motor pull force, and then input into the aircraft motion solution module to realize the whole aircraft dynamics solution. The solution code is written in C language and connected to the airplane model in the form of the MATLAB S function, and its flow is shown in
Figure 3.
3. Adaptive Back-Stepping Based Correction Control
3.1. Trajectory Correction Control Law Design
In order to simplify the structure and reduce the weight, the large-scale long-endurance solar UAV does not use a front wheel turning and braking control device, and the ground taxiing correction uses the rudder and the engine differential to correct the lateral deviation
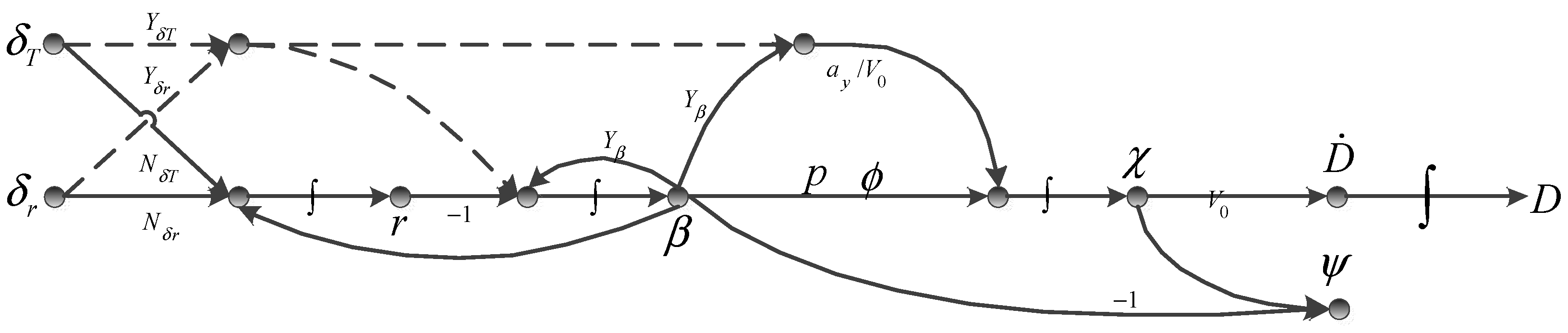
of the aircraft center of gravity so that the aircraft skids along the runway centerline. According to the kinetic equation of the inertial system, the signal flow process of heading control using engine differential and rudder jointly is shown in
Figure 4 below. From the figure, it can be seen that the ground trajectory correction process is affected by the yaw moment as well as the lateral force generated by the sideslip. The engine differential and rudder deflection generate yaw moment, which in turn generates the heading deflection rate to form the trajectory deflection angle after integration. The trajectory deflection angle changes the velocity vector of the airplane, which generates a displacement rate
in the lateral direction that is integrated to form the lateral displacement
. The lateral force generated by the side slip angle is small compared to the ground friction force. Therefore, the whole deflection correction process is dominated by the moment maneuver.
According to the dynamics process shown in
Figure 4, the control law for correcting the lateral deviation
of the airplane’s center of gravity for slip running correction can be designed by using the inverse process. According to the lateral deviation
, the desired lateral velocity
is formed. According to Equation (11), there exists a fixed kinematic relationship between a and b. The kinematic relationship between a and b is the same as that between
and
. A proportional-integral controller based on the
objective can be designed, and an angular rate controller based on
is used for the inner loop. The correction of lateral deviation is realized by controlling
. In practical engineering, the angular rate of trajectory deflection
cannot be measured directly. During the ground motion, the rate of change of yaw angle
is equal to the yaw angle rate
by the ground constraint. Since
can be directly measured by the angular rate gyro, yaw angle
and yaw angular rate
are considered to replace
and
, respectively.
Further analyzing Equation (12), the lateral acceleration rate of the aircraft
is affected by
when accelerating or decelerating the taxi. In order to improve the accuracy of the correction control and reduce the overshoot, the acceleration compensation term
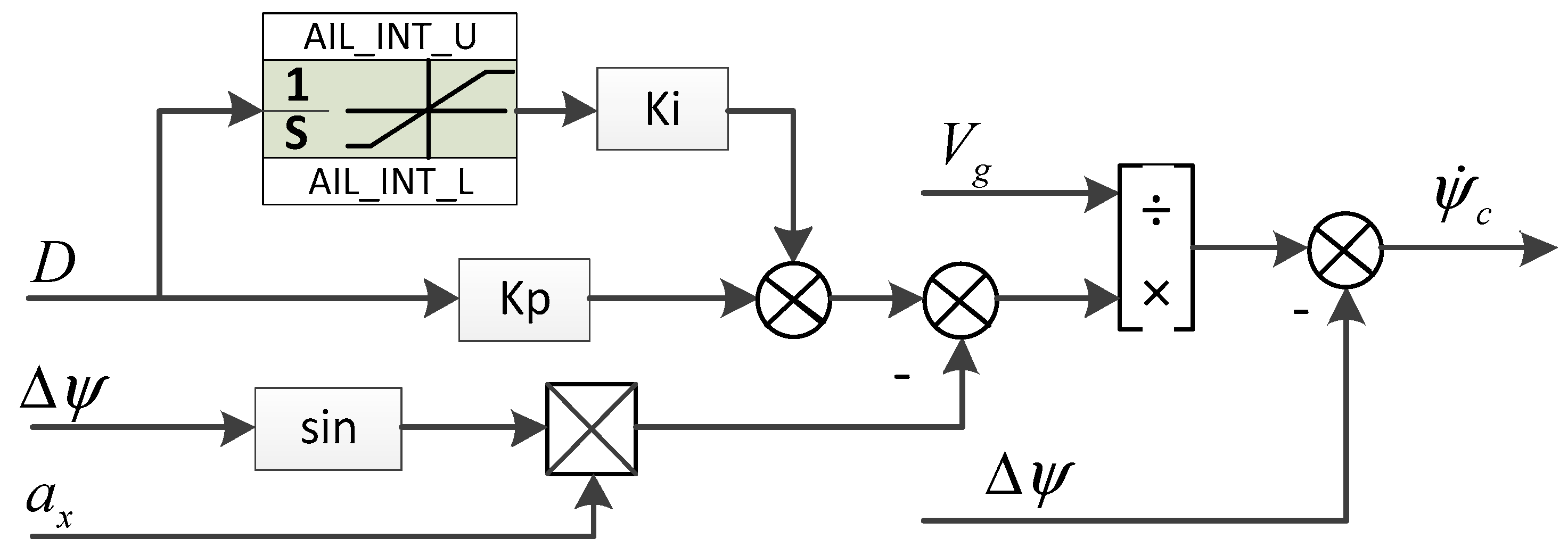
is introduced in the control architecture, and this part is subtracted from the desired command. The control law of taxi correction is shown in
Figure 5 below. The basic controller is a PI controller based on lateral deviation gap
for accurate precise trajectory tracking. Further based on the dynamics in
Figure 4, the control output of the lateral yaw gap is converted into the target yaw angular rate
. The yaw angular rate
is used as the inner-loop control target because it is a fast variable compared to the trajectory motion, and its frequency is about 1~1.2 rad/s, while the design bandwidth of the trajectory controller is 0.3 rad/s. The direct response to the moment perturbation generated by the ambient wind and ground misalignment friction is the change in yaw angular rate, and the use of angular rate-based inner-loop control law makes it easier to carry out rapid compensation of the perturbation.
3.2. Adaptive Back-Stepping Control Law Design
Referring to
Figure 5, the corrective command
is formed by the lateral offset, lateral velocity, and acceleration, and its control precision and response speed directly affect the corrective effect. Due to the large structural deformation of the solar airplane, there is a large aerodynamic data deviation, and the wing auxiliary support adopts the non-precision installation. Inevitably, there exists asymmetry. There are all kinds of wind disturbances in the airport, there are bumps and concavity in the runway, and there is the influence of slipstream in the propellers, etc., and all of these unfavorable factors will affect the controlling effect of the heading.
According to the analysis of Equations (9) and (14), it can be found that the response of heading angular rate
to the rudder and engine differentials during the ground taxiing process presents a second-order characteristic. The airplane dynamics equations are solved jointly with the kinematics relation (15).
The system frequency of the heading second-order system can be derived as:
Analyzing the system frequency damping:
The stability of the ground skid is related to the difference between the main wheel moments and the tail wheel moments and the heading stabilizing moment .
The system damping decreases gradually with increasing velocity.
Therefore, in order to improve the heading damping characteristics, as well as to overcome the influence of various uncertainties, the inner loop adopts the adaptive back-stepping method to realize accurate tracking control of the angular rate. The design process of adaptive back-stepping control law is as follows:
First, the kinetic Equations (13) and (14) are rewritten in affine nonlinear form:
where:
;
and
are the coefficients of the nonlinear equation;
is the modeling errors generated by external perturbations as well as inaccurate aerodynamic data.
Define the Lyapunov function as:
Derivation is obtained on both sides:
Let , then satisfies Lyapunov stabilization.
Derive the back-stepping control law from
:
where
is the estimation of the modeling and perturbation error
, and let
denote the estimation error, i.e., the deviation between the estimated value and the true value. Equation (20) is guaranteed to be less than or equal to 0 only when
. When the estimation error is large, it will lead to Equation (20) less than or equal to 0 no longer holds, affecting the stability of the system, so the Lyapunov function needs to be redefined as:
Derive the above equation:
The back-stepping control law Equation (21) solved above is brought into the new Lyapunov function:
For
to hold, the adaptive law needs to satisfy the following equation:
i.e.:
The specific structure of the adaptive back-stepping control law is shown in
Figure 6.
is the heading virtual maneuver volume, which is composed of rudder and engine differential maneuver volume linearly superimposed, as in Equation (27). At low speeds, the engine differential control is the main control, and at high speeds, the engine and rudder work together. The gain
adopted in this paper is shown in
Figure 7.
In order to ensure that the speed control accuracy is not affected during the motor differential control process, the design uses only the outer motor for correction control, and the authority is 30% of the maximum speed, while the speed control can drive all four motors.
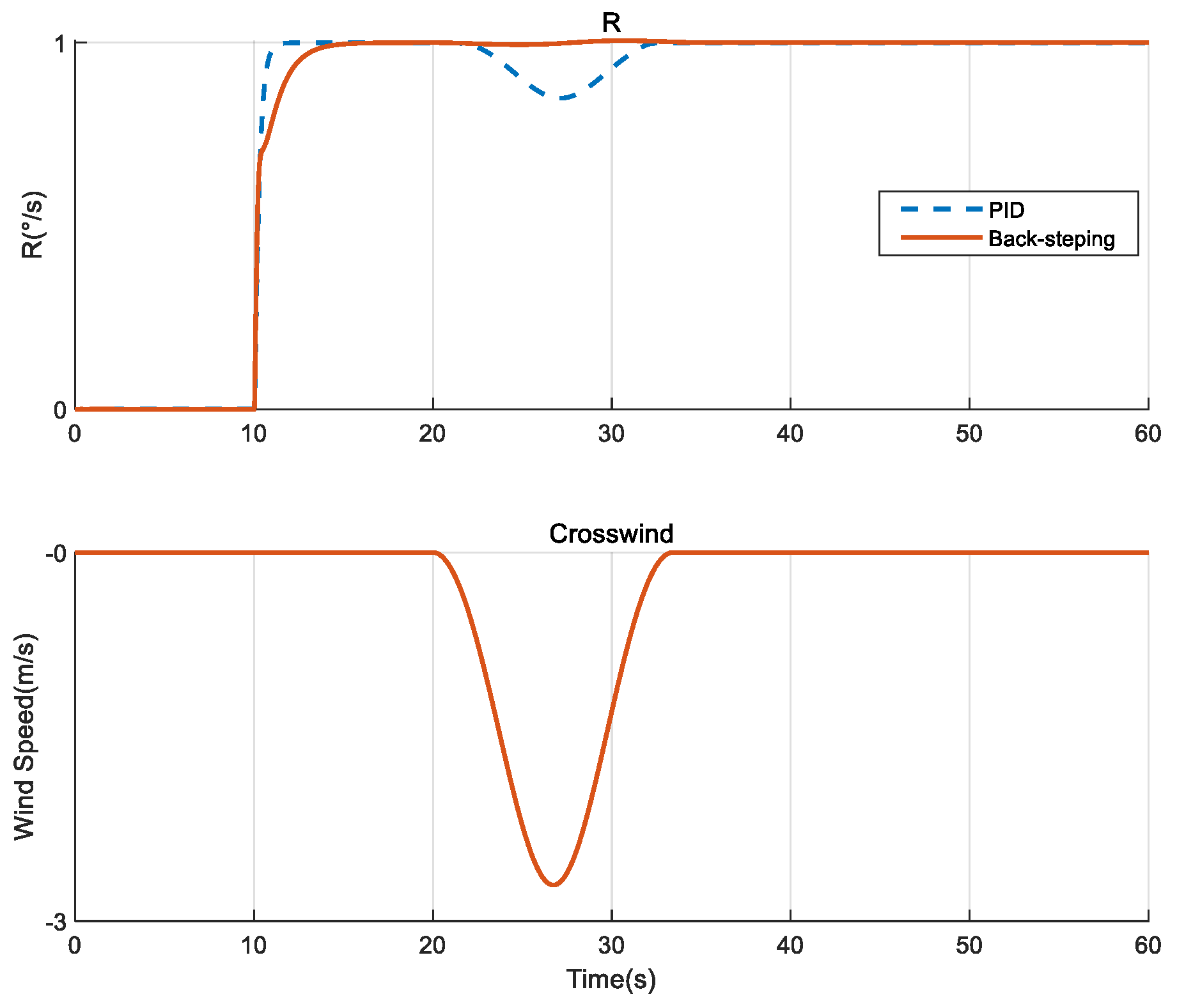
In order to verify the robustness of the back-stepping controller, this paper conducts simulation tests for the crosswind disturbance by applying a yaw angle rate command of 1°/s at 10 s. The simulation results are shown in
Figure 8. When the aircraft was perturbed by a 3 m/s crosswind, the tracking of the R command by the PID control system was significantly perturbed, while the back-stepping maintained good immunity characteristics. Crosswinds are in the form of 1-cos, with a wind size of 3 m/s and a spatial scale of 25 m.
4. Verification of Slide Running Correction Test
A certain solar UAV adopts a similar front three-point landing gear layout, with two high-power motor-driven propellers installed on the left and right sides, the weight of the aircraft is about 500 kg, and the theoretical takeoff speed is 16 m/s. In order to verify the effectiveness of the combined engine differential and rudder correction control, low-speed, medium-speed, and high-speed autonomous taxiing tests were carried out at Yulin Jingbian Airport. The tests required that the response transition of the taxiing correction control is smooth, the speed control error is no more than 0.5 m/s, and the steady state error of the lateral deviation distance is no more than 2 m in the case of no more than 3 m/s side wind, no more than 5 m/s headwind, and the existence of the initial course angle deviation. The taxiing tests were conducted at Yulin Jingbian Hazetan Airport. This airport belongs to an A1 class runway type general aviation airport, with a runway length of 2400 m and a width of 45 m. Through the actual measurement, it is found that there is a height difference of about 20 m between the southeast end and the northwest end of the runway, the width direction is high in the middle and low on both sides, and there is a slope of about 0.5 degrees. Due to the local environment, there is always a side wind as well as a crosswind effect during the whole taxiing test. During low-speed taxiing, due to the inefficiency of the rudder, it relies solely on the engine differential to realize the heading control. In order to illustrate the joint correction control effect of rudder and engine differential, this paper only analyzes and illustrates the results of the medium and high-speed tests.
The autonomous medium-speed taxiing test requires the airplane to be placed at the taxiing point, the initial heading angle deviation is set to 5° or 10°, and the taxiing test under different speed limits is carried out according to the ground speed 6.0 m/s, 7.0 m/s, and 8 m/s commands.
Four autonomous taxiing tests and four manual taxiing tests were performed for the medium-speed test. As shown in
Figure 9, mode No. 14 is the autonomous skid mode, and mode No. 8 is the artificial mode. The target ground speed of the 1st and 2nd autonomous gliding tests is 3 m/s, the initial deviation of heading is 10°, the maximum side deviation in gliding is 2.7 m, and the steady-state side deviation is better than 1 m. The target ground speed of the 3rd and 4th autonomous gliding tests is 6 m/s, the initial deviation of heading is 5°, the maximum side deviation in gliding is 0.9 m, and the steady-state side deviation is better than 1 m. The target ground speed of the 5th and 7th autonomous gliding tests is 8 m/s, the initial deviation of heading is 5°, and the maximum side deviation in gliding is 0.9 m. The 5th and 7th autonomous gliding tests are 8 m/s, the initial deviation of heading is 5°, and the maximum side deviation in gliding is 1 m. The initial deviation of the 5th and 7th autonomous taxiing test target ground speed is 8 m/s, the initial deviation of the heading is 5°, the maximum side deviation of taxiing is 1.1 m, and the steady-state side deviation is better than 1 m. The 6th and 8th autonomous taxiing test target ground speed is 7 m/s, the initial deviation of the heading is 5°, the maximum side deviation of taxiing is 1.0 m, and the steady state side deviation is better than 1 m. Speed tracking control of different targets responds normally, the steady-state accuracy is better than 0.5 m/s, and the speed tracking delay is small. The amount of throttle control is within the range of 20~30%.
Six autonomous taxiing tests and one manual taxiing test were performed for the high-speed test, as shown in
Figure 10. The autonomous high-speed taxiing test requires the airplane to be placed at the slip run point, the initial heading angle deviation is set to ±2 deg, and the taxiing test under different speed limitations is carried out according to the instruction of ground speed 10.0 m/s and 11.5 m/s.
The target ground speed of the 1st autonomous taxiing test is 4 m/s, the initial deviation of heading is 0.8°, and the maximum side deviation in taxiing is 0.25 m. The target ground speed of the 2nd autonomous taxiing test is 6 m/s, the initial deviation of heading is 1.6°, and the maximum side deviation in taxiing is 0.3 m. The target ground speed of the 3rd autonomous taxiing test is 6 m/s, the initial deviation of heading is 0.7°, and the maximum side deviation in taxiing is 0.4 m. The target ground speed of the 4th autonomous taxiing test is 10.0 m/s, 11.5 m/s, and the target ground speed is 10.0 m/s, 11.5 m/s, and the target ground speed is 10.0 m/s, 11.5 m/s. The autonomous taxiing test target ground speed is 10 m/s, the initial deviation of heading is 0.9°, and the maximum side deviation of taxiing is 0.9 m. The 5th autonomous taxiing test target ground speed is 11 m/s, the initial deviation of heading is 1.4°, the maximum side deviation of taxiing is 1.2 m, and the steady state side deviation is better than 1 m. The 6th autonomous taxiing test target ground speed is 12 m/s, the initial deviation of heading is 1.5°, and the maximum side deviation of taxiing is 1.1 m. The speed tracking control of different targets responds normally, the steady state accuracy is better than 0.5 m/s, and the speed tracking delay is small. The amount of throttle control is within the range of 19~34%.
In summary, under the presence of runway slope and ambient wind disturbance, in the medium and high-speed taxiing (6~12 m/s) tests, the taxiing speed control is normal, and the airplane can quickly turn the nose to correct the initial heading deviation, and the maximal steady-state side deviation error is better than 1 m, so the side deviation correction ability is strong.
5. Conclusions
For the correction control of solar UAV, the ground taxiing force characteristics of the aircraft are analyzed, and the ground dynamics equations are established by considering the geometric constraints of the ground. Based on the ground taxiing model, the modal characteristics of the solar UAV are deduced and the damping control law is designed. Based on the signal flow diagram of the ground taxiing dynamics, a bias correction strategy based on the combined control of the engine differential and rudder is proposed. The adaptive back-stepping method is adopted to overcome the deviation caused by environmental perturbation and aerodynamic uncertainty and realize fast and accurate control of the inner loop. The effectiveness of the corrective control law is effectively verified by setting the initial heading deviation in medium-speed and high-speed taxiing tests.
Author Contributions
Conceptualization, B.W. and W.W.; methodology, B.W.; software, B.W.; validation, B.W.; formal analysis, B.W.; investigation, B.W. and W.W.; resources, B.W. and X.C.; data curation, B.W.; writing—original draft preparation, B.W., X.C. and X.L.; writing—review and editing, B.W.; visualization, B.W.; supervision, B.W., W.W. and X.L.; project administration, B.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data presented in this study are available on request from the corresponding author due to privacy.
Acknowledgments
This research is supported by the Key Laboratory of Flight Control Simulation Technology of China.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Hao, H. UAV Approach and Landing/Ground Rolling Control and Simulation. Master’s Thesis, Nanjing University of Aeronautics and Astronautics, Nanjing, China, 2011. [Google Scholar] [CrossRef]
- Wang, Y. Lateral Deviation Correction Control for UAV Taxiing. Acta Aeronaut. Astronaut. Sin. 2008, 143, 145. [Google Scholar]
- Biannic, J.M.; Marcos, A.; Jeanneau, M.; Roos, C. Nonlinear simplified LFT modelling of an aircraft on ground. In Proceedings of the 2006 IEEE Conference on Computer Aided Control System Design, 2006 IEEE International Conference on Control Applications, 2006 IEEE International Symposium on Intelligent Control, Munich, Germany, 4–6 October 2006; IEEE: Piscataway, NJ, USA, 2006; pp. 2213–2218. [Google Scholar]
- Sadien, E.; Roos, C.; Birouche, A.; Grimault, C.; Romana, L.E.; Boada-Bauxell, J. Control design oriented modeling of an on-ground aircraft. In Proceedings of the 2018 European Control Conference (ECC), Limassol, Cyprus, 12–15 June 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 2757–2762. [Google Scholar]
- Sadien, E.; Roos, C.; Birouche, A.; Carton, M.; Grimault, C.; Romana, L.E.; Basset, M. A simple and efficient control allocation scheme for on-ground aircraft runway centerline tracking. Control Eng. Pract. 2020, 95, 104228. [Google Scholar] [CrossRef]
- Dai, Y.; Song, J.; Yu, L.; Lu, Z.; Sheng, Z.; Li, F. The lateral control during aircraft-on-ground deceleration phases. Aerosp. Sci. Technol. 2019, 95, 105482. [Google Scholar] [CrossRef]
- Duprez, J.; Mora-Camino, F.; Villaume, F. Control of the aircraft-on-ground lateral motion during low speed roll and manoeuvers. In Proceedings of the 2004 IEEE Aerospace Conference Proceedings (IEEE Cat. No. 04TH8720), Big Sky, MT, USA, 6–13 March 2004; IEEE: Piscataway, NJ, USA, 2004; Volume 4, pp. 2656–2666. [Google Scholar]
- Chen, B.; Jiao, Z.; Ge, S.S. Aircraft-on-ground path following control by dynamical adaptive back-stepping. Chin. J. Aeronaut. 2013, 26, 668–675. [Google Scholar] [CrossRef][Green Version]
- Wu, Z.; Peng, H.; Li, F.; Huang, T.; Yang, C.; Gui, W. Extended dissipative analysis and taxiing control of fuzzy model based aircraft-on-ground systems via sliding mode approach. J. Frankl. Inst. 2022, 359, 4623–4641. [Google Scholar] [CrossRef]
- Roos, C.; Biannic, J.M.; Tarbouriech, S.; Prieur, C.; Jeanneau, M. On-ground aircraft control design using a parameter-varying anti-windup approach. Aerosp. Sci. Technol. 2010, 14, 459–471. [Google Scholar] [CrossRef]
- Li, J.; Dong, Y.; Yang, F.; Shen, Y. Take-off and run control of rhomboid wing UAV based on backstep control method. J. Beijing Univ. Aeronaut. Astronaut. 2020, 46, 496–504. [Google Scholar]
- Wu, C.; Yan, B.; Shao, P. Research on Unmanned Aerial Vehicle (UAV) Taxi-run and Take-off Control Method Based on Fuzzy Control. J. Northwestern Polytech. Univ. 2015, 33, 33–39. [Google Scholar]
- Deng, Y.; Fan, Y. Design and Simulation of Ground Taxiing System for UAV with Four Wheels. J. Syst. Simul. 2008, 20, 5929–5935. [Google Scholar]
- Wang, Y.; Zhou, Z.; Shao, Z.; Zhu, X. Lateral Deviation Correction Control for Flying—Wing UAV Taxiing. J. Northwestern Polytech. Univ. 2016, 34, 593–601. (In Chinese) [Google Scholar]
- Sont, N.; Datn, T. Preview control of aircraft in ground operation. In Proceedings of the 2018 5th International Conference on Control, Decision and Information Technologies (CoDIT), Thessaloniki, Greece, 10–13 April 2018; pp. 550–554. [Google Scholar]
- Jia, C. Design and Simulation of the Lateral Deviation Correction Control System for Flying-Wing UAV Taxiing. Autom. Appl. 2018, 7, 59–60. (In Chinese) [Google Scholar]
- Chen, Q.; Xin, H.; Lu, Y.; Wang, P.; Wang, Y.; Zheng, J. Ground Taxiing Lateral Deviation Correction Control for High Subsonic UAVs. J. Beijing Univ. Aeronaut. Astronautics. 2024. [Google Scholar] [CrossRef]
| Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).