A Deep Reinforcement Learning Approach to Injection Speed Control in Injection Molding Machines with Servomotor-Driven Constant Pump Hydraulic System
Abstract
1. Introduction
- A nonlinear hydraulic servo control system in a typical IMM is formulated and the optimal tracking control of the injection speed throughout the filling phase of the molding process is studied.
- An efficient MDP model is established for injection molding speed control, encompassing the definition and design of the state space, action space, and the specific formulation of the reward function. Subsequently, an efficient optimal controller based on the DDPG is devised to achieve swift and precise tracking control of the injection speed within a predefined time frame.
- Extensive numerical experiments are performed to comprehensively confirm the feasible and efficient properties of the proposed method. Furthermore, a comparative analysis with the traditional PID algorithm is carried out, offering additional evidence to underscore the superiority of the proposed algorithm.
2. Problem Formulation
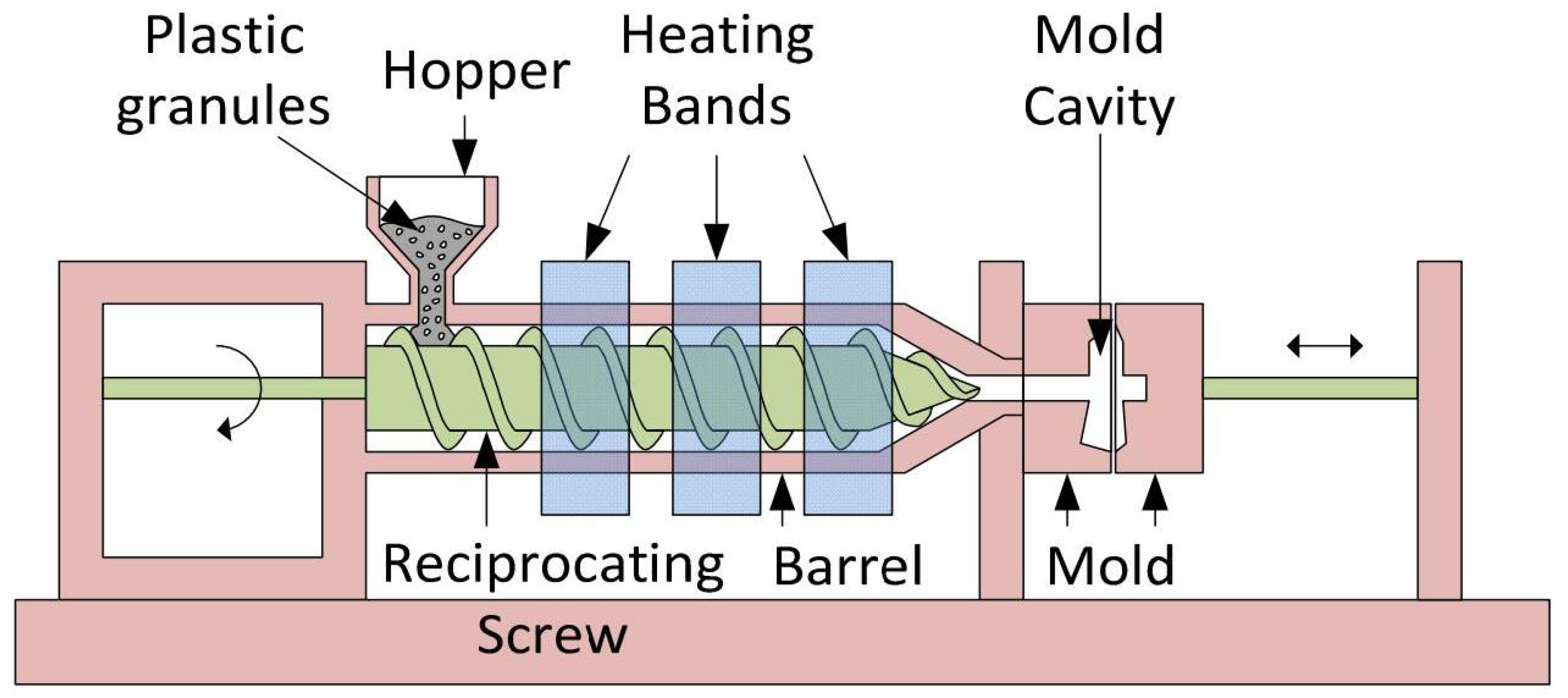
2.1. Dynamic Model of the Hydraulic Servo Speed System
2.2. Initialization of Initial Conditions in Process Control Systems
2.3. Control Objective
3. Construction of the Markov Decision Process (MDP) Model
3.1. Definition of the State Space
3.2. Definition of the Action Space
3.3. Definition of the Reward Function
4. Optimal Velocity Tracking Strategy Based on the DDPG Algorithm
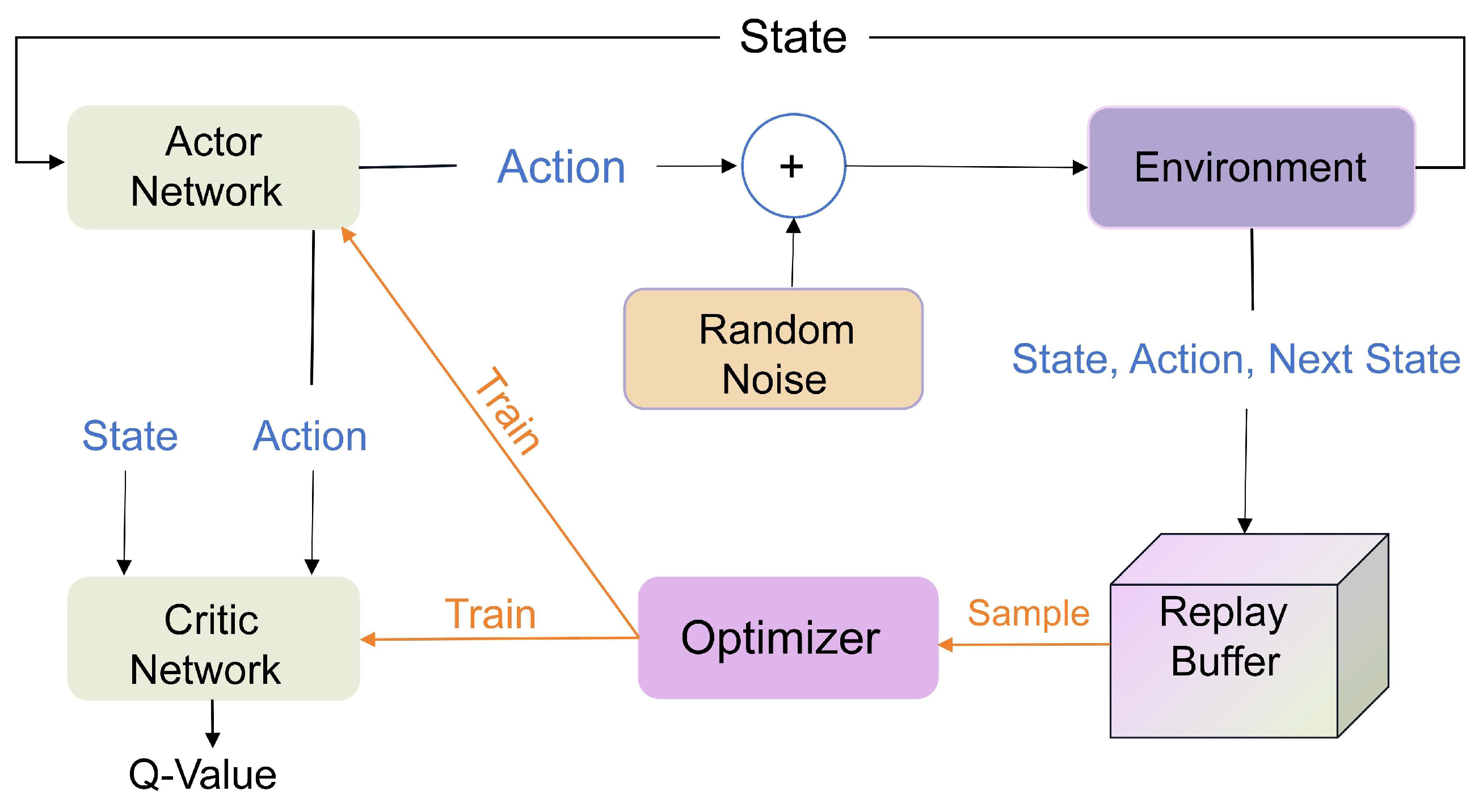
4.1. Deep Deterministic Policy Gradient (DDPG) Algorithm
4.2. Training Procedure of DDPG
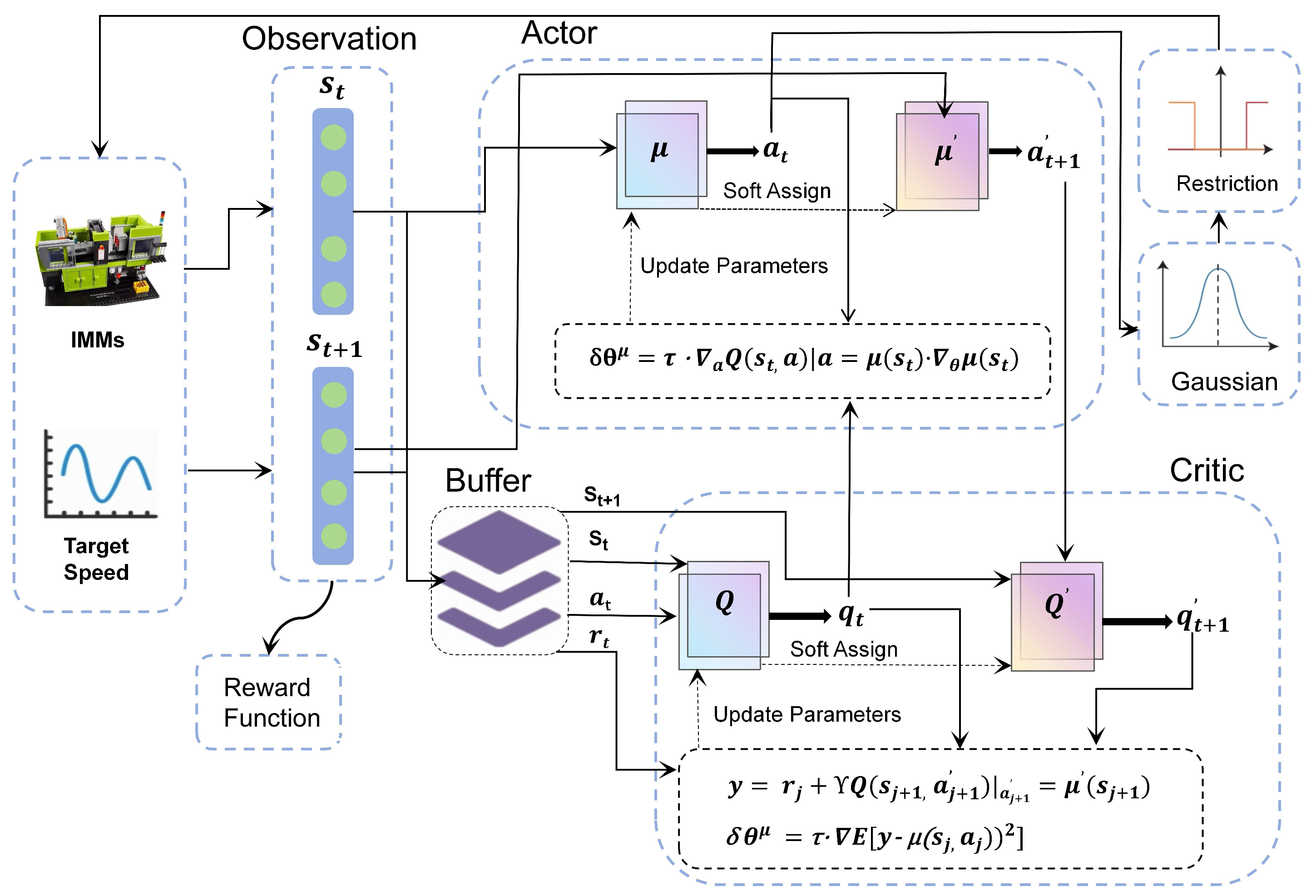
4.3. Velocity Tracking Control Strategy Based on DDPG
| Algorithm 1 Training process of injection speed tracking control strategy via DDPG. |
|
5. Experimental Results
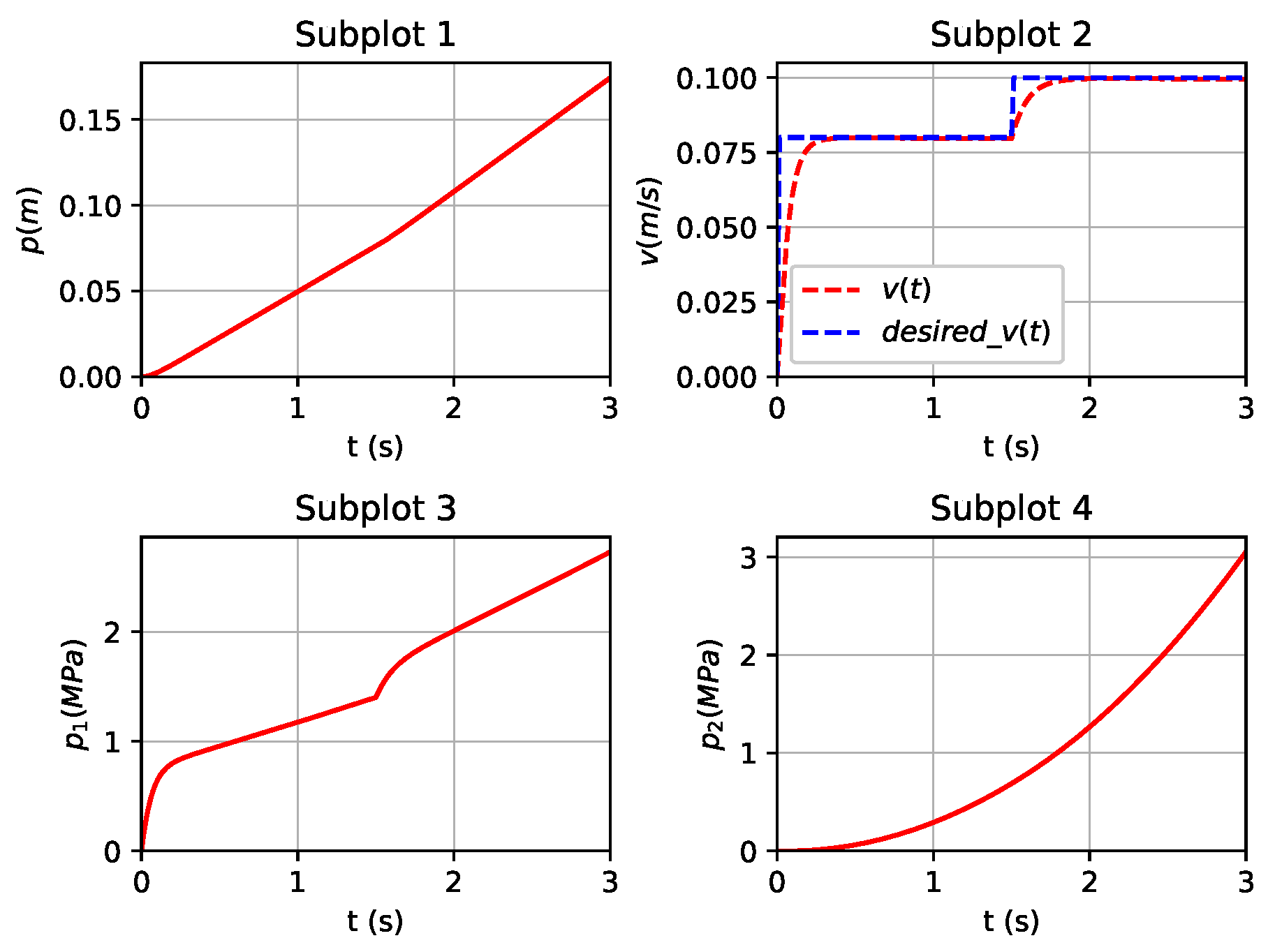
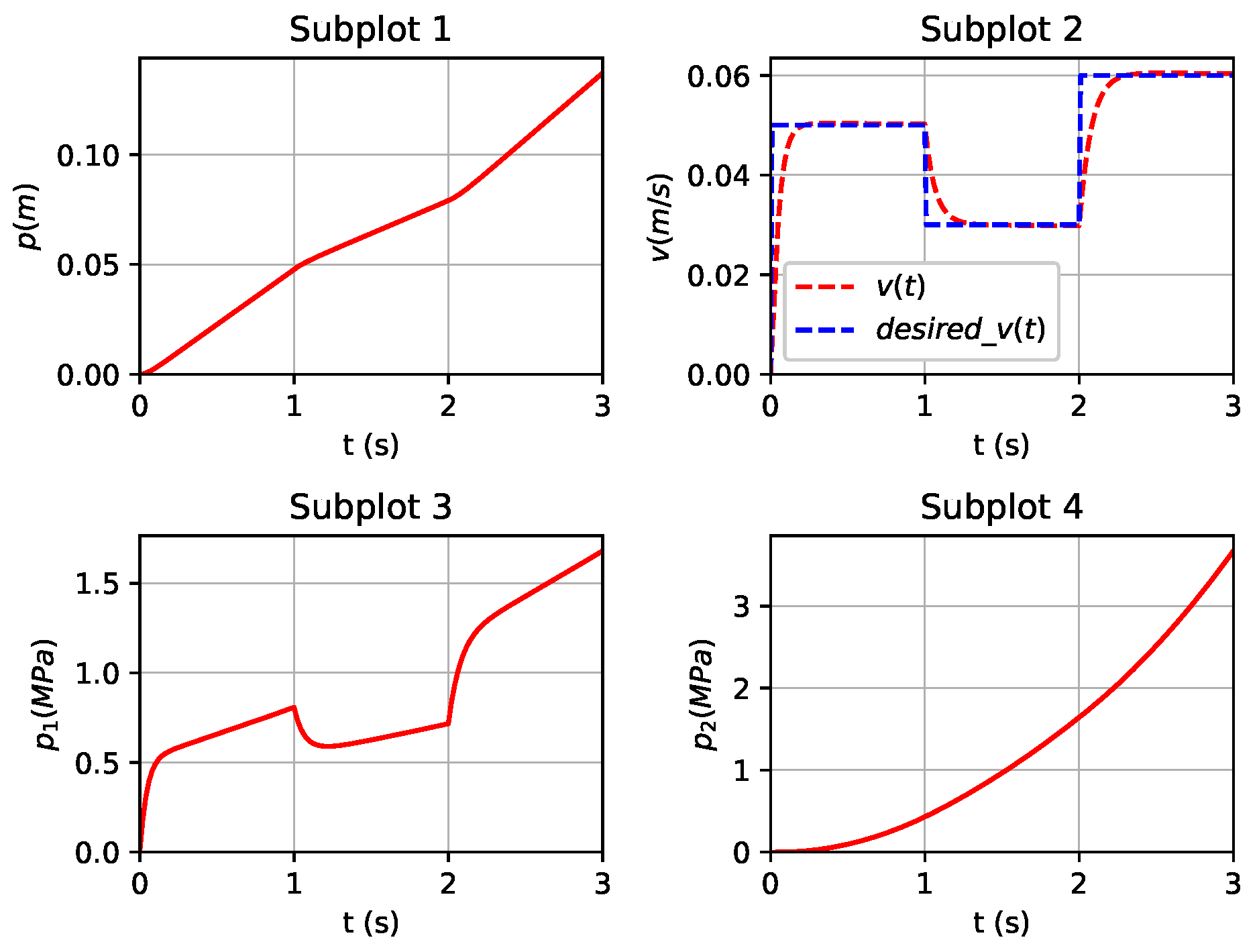
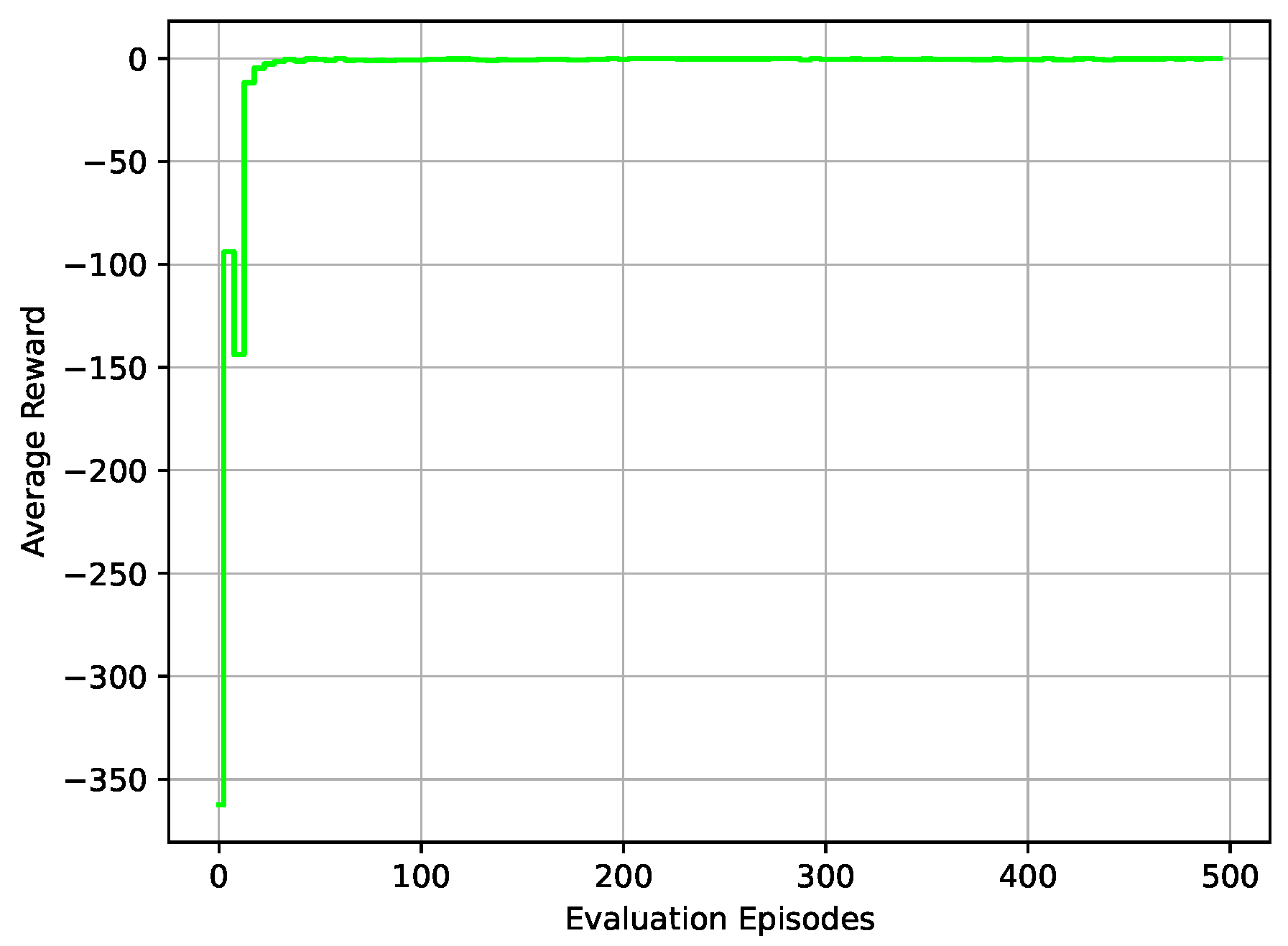
5.1. Validation of DDPG-Based Controller
5.2. Hyperparameter Tuning
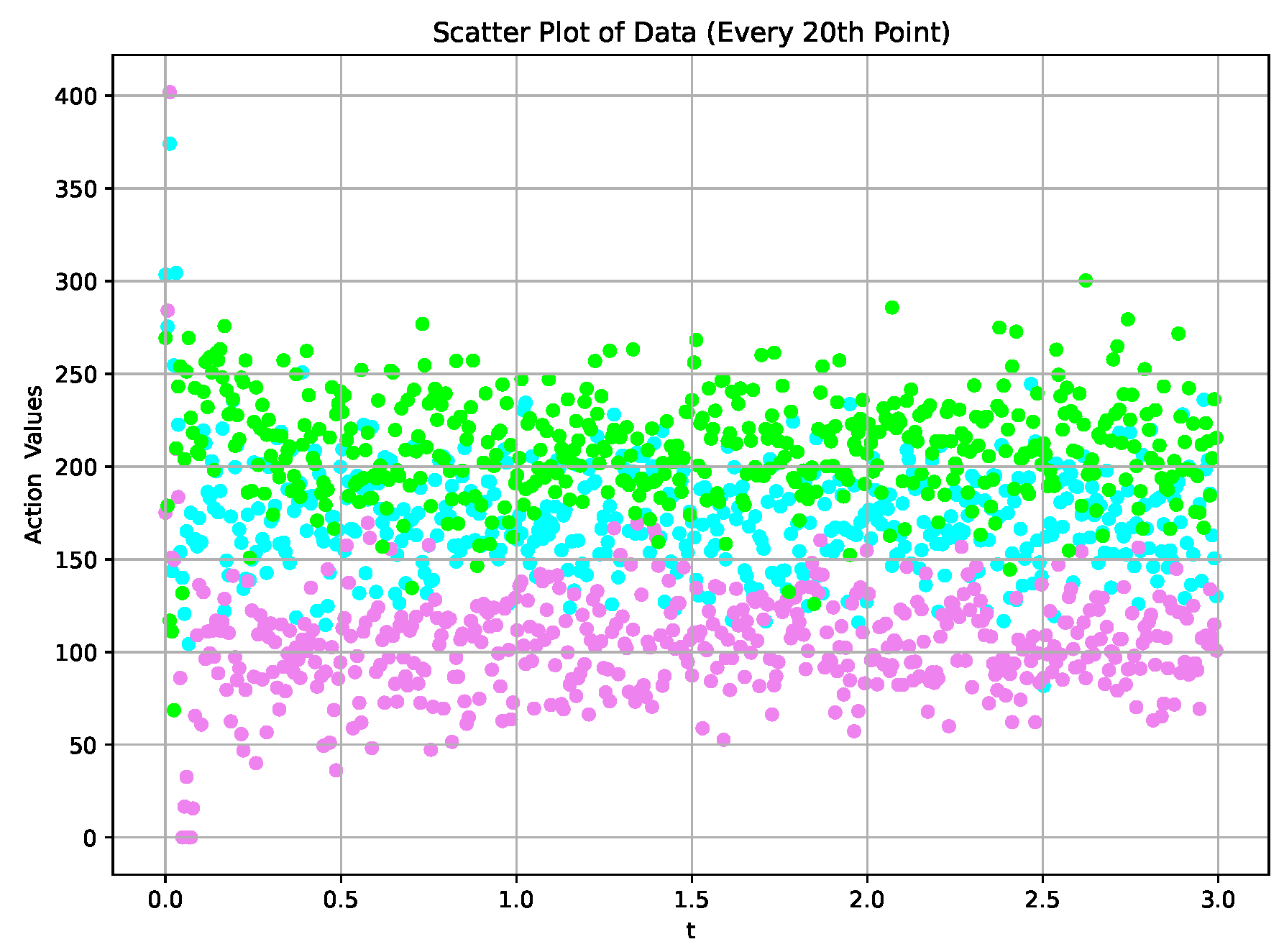
5.2.1. Gaussian Noise in Action Space
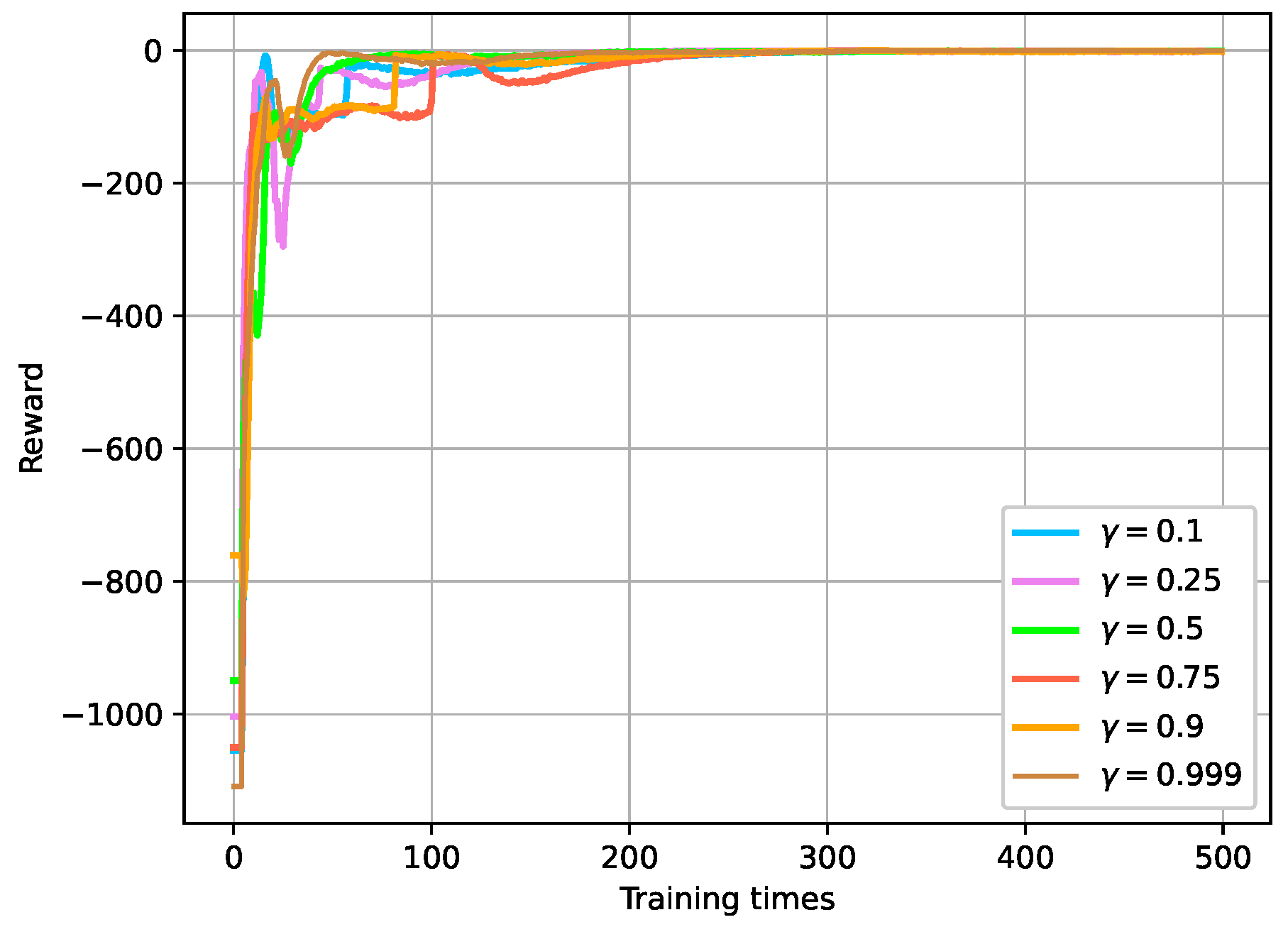
5.2.2. Discount Factor in the Reward Function
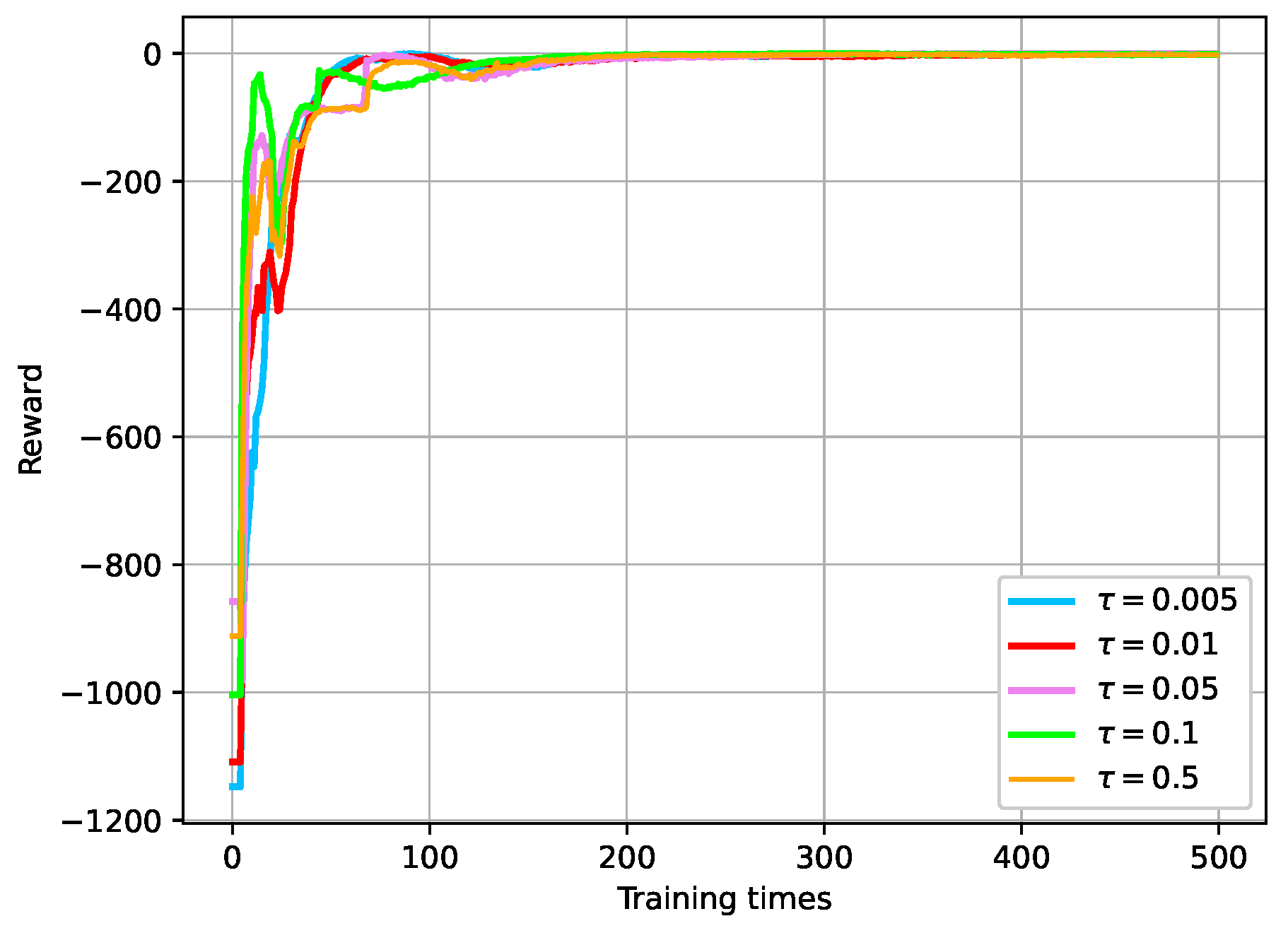
5.2.3. Soft Update Parameter for Updating Target Network
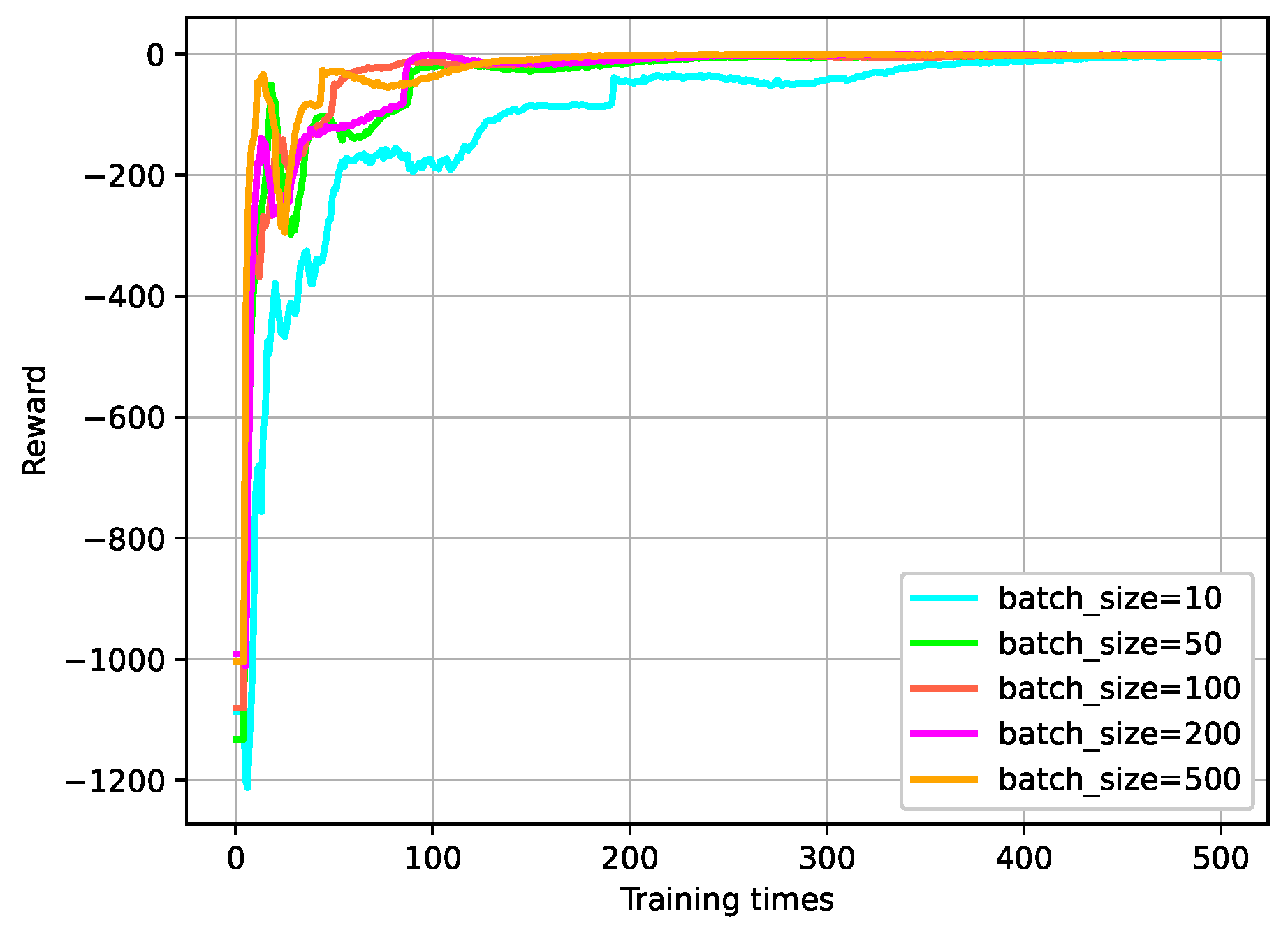
5.2.4. Batch Size for Training
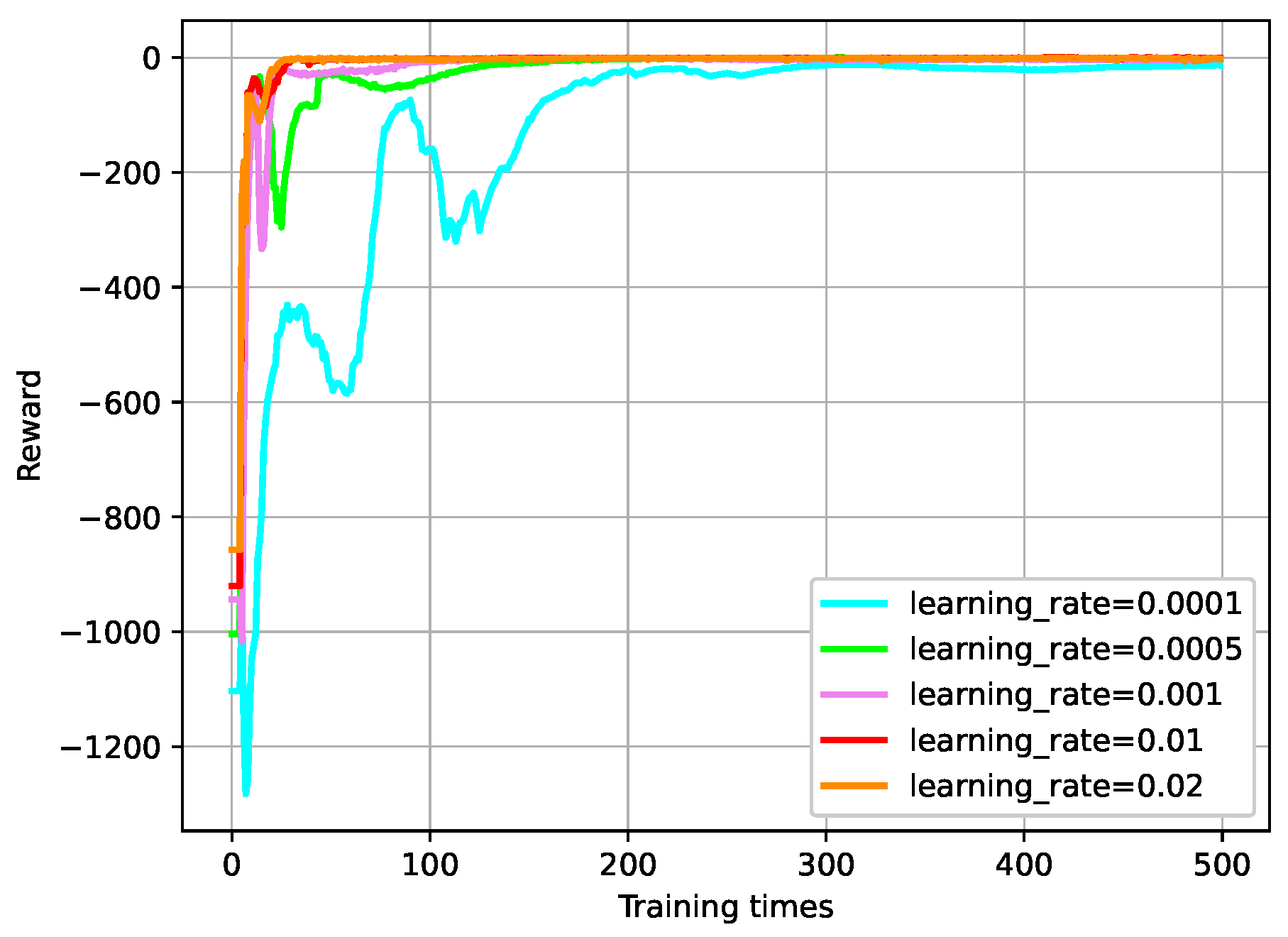
5.2.5. Learning Rate
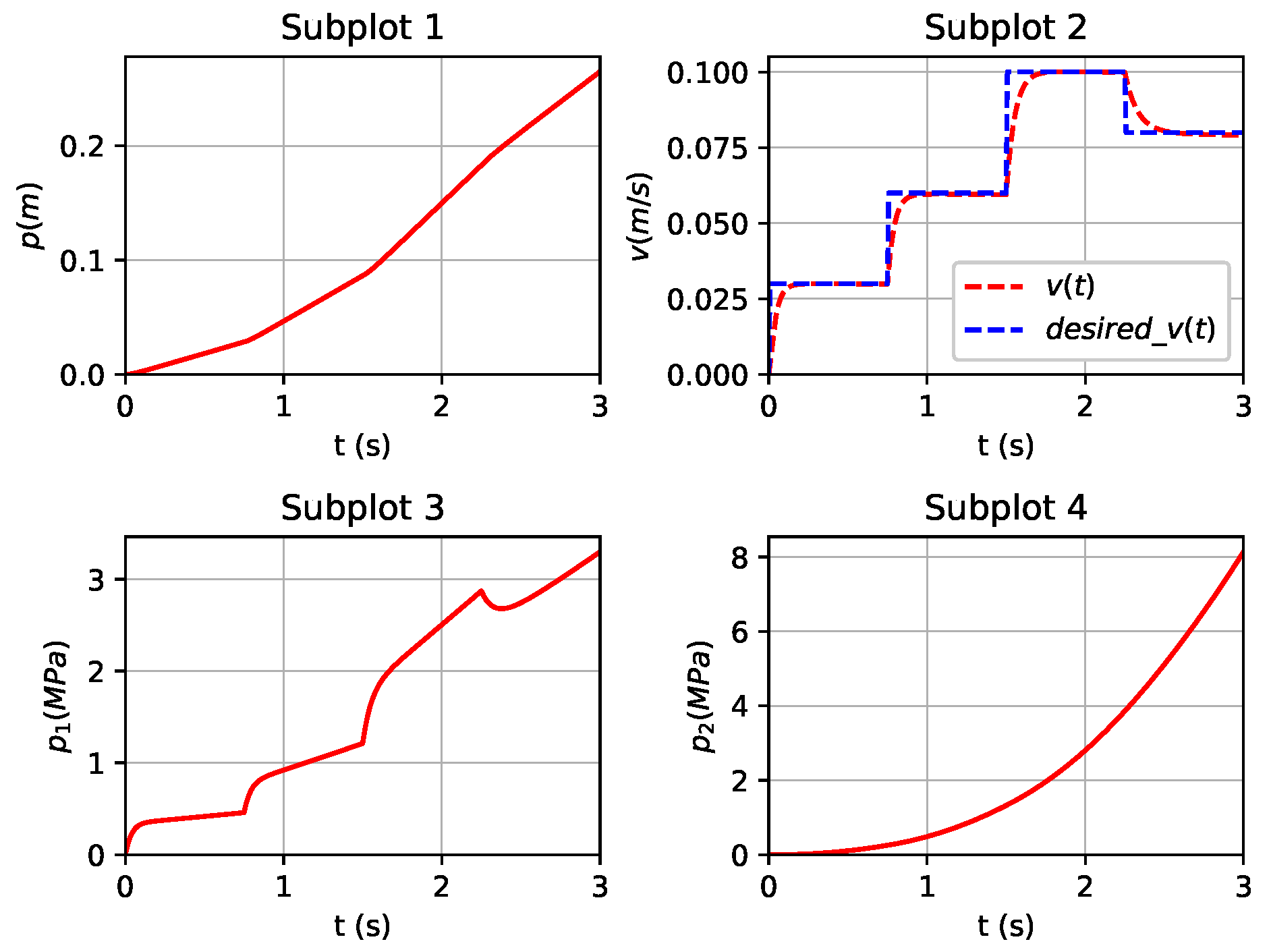
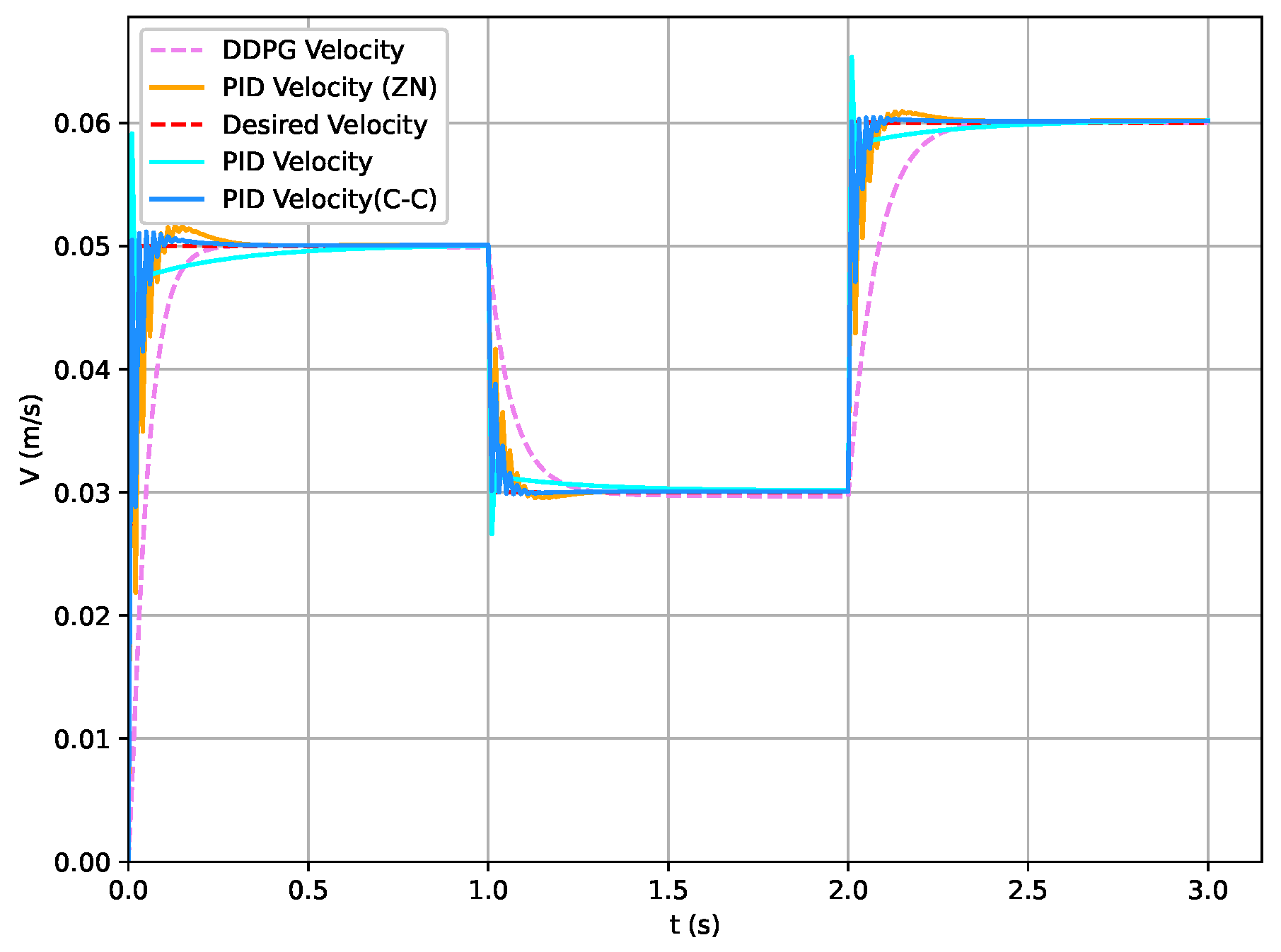
5.3. Compared with PID Method
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fernandes, C.; Pontes, A.J.; Viana, J.C.; Gaspar-Cunha, A. Modeling and Optimization of the Injection-Molding Process: A Review. Adv. Polym. Technol. 2018, 37, 429–449. [Google Scholar] [CrossRef]
- Gao, H.; Zhang, Y.; Zhou, X.; Li, D. Intelligent methods for the process parameter determination of plastic injection molding. Front. Mech. Eng. 2018, 13, 85–95. [Google Scholar] [CrossRef]
- Fu, H.; Xu, H.; Liu, Y.; Yang, Z.; Kormakov, S.; Wu, D.; Sun, J. Overview of injection molding technology for processing polymers and their composites. ES Mater. Manuf. 2020, 8, 3–23. [Google Scholar] [CrossRef]
- Cho, Y.; Cho, H.; Lee, C.O. Optimal open-loop control of the mould filling process for injection moulding machines. Optim. Control Appl. Methods 1983, 4, 1–12. [Google Scholar] [CrossRef]
- Havlicsek, H.; Alleyne, A. Nonlinear control of an electrohydraulic injection molding machine via iterative adaptive learning. IEEE/ASME Trans. Mechatron. 1999, 4, 312–323. [Google Scholar] [CrossRef]
- Dubay, R. Self-optimizing MPC of melt temperature in injection moulding. ISA Trans. 2002, 41, 81–94. [Google Scholar] [CrossRef]
- Huang, S.; Tan, K.K.; Lee, T.H. Neural-network-based predictive learning control of ram velocity in injection molding. IEEE Trans. Syst. Man Cybern. Part C (Appl. Rev.) 2004, 34, 363–368. [Google Scholar] [CrossRef]
- Yao, K.; Gao, F. Optimal start-up control of injection molding barrel temperature. Polym. Eng. Sci. 2007, 47, 254–261. [Google Scholar] [CrossRef]
- Chen, W.C.; Tai, P.H.; Wang, M.W.; Deng, W.J.; Chen, C.T. A neural network-based approach for dynamic quality prediction in a plastic injection molding process. Expert Syst. Appl. 2008, 35, 843–849. [Google Scholar] [CrossRef]
- Xia, W.; Luo, B.; Liao, X. An enhanced optimization approach based on Gaussian process surrogate model for process control in injection molding. Int. J. Adv. Manuf. Technol. 2011, 56, 929–942. [Google Scholar] [CrossRef]
- Wang, Y.; Jin, Q.; Zhang, R. Improved fuzzy PID controller design using predictive functional control structure. ISA Trans. 2017, 71, 354–363. [Google Scholar] [CrossRef] [PubMed]
- Yang, A.; Guo, W.; Han, T.; Zhao, C.; Zhou, H.; Cai, J. Feedback Control of Injection Rate of the Injection Molding Machine Based on PID Improved by Unsaturated Integral. Shock Vib. 2021, 2021, 9960021. [Google Scholar] [CrossRef]
- Farahani, S.; Khade, V.; Basu, S.; Pilla, S. A data-driven predictive maintenance framework for injection molding process. J. Manuf. Process. 2022, 80, 887–897. [Google Scholar] [CrossRef]
- Xiao, H.; Meng, Q.X.; Lai, X.Z.; Yan, Z.; Zhao, S.Y.; Wu, M. Design and trajectory tracking control of a novel pneumatic bellows actuator. Nonlinear Dyn. 2023, 111, 3173–3190. [Google Scholar] [CrossRef]
- Ruan, Y.; Gao, H.; Li, D. Improving the Consistency of Injection Molding Products by Intelligent Temperature Compensation Control. Adv. Polym. Technol. 2019, 2019, 1591204. [Google Scholar] [CrossRef]
- Stemmler, S.; Vukovic, M.; Ay, M.; Heinisch, J.; Lockner, Y.; Abel, D.; Hopmann, C. Quality Control in Injection Molding based on Norm-optimal Iterative Learning Cavity Pressure Control. IFAC-PapersOnLine 2020, 53, 10380–10387. [Google Scholar] [CrossRef]
- Xu, J.; Ren, Z.; Xie, S.; Wang, Y.; Wang, J. Deep learning-based optimal tracking control of flow front position in an injection molding machine. Optim. Control Appl. Methods 2023, 44, 1376–1393. [Google Scholar] [CrossRef]
- Ren, Z.; Wu, G.; Wu, Z.; Xie, S. Hybrid dynamic optimal tracking control of hydraulic cylinder speed in injection molding industry process. J. Ind. Manag. Optim. 2023, 19, 5209–5229. [Google Scholar] [CrossRef]
- Wu, G.; Ren, Z.; Li, J.; Wu, Z. Optimal Robust Tracking Control of Injection Velocity in an Injection Molding Machine. Mathematics 2023, 11, 2619. [Google Scholar] [CrossRef]
- Ren, Z.; Lin, J.; Wu, Z.; Xie, S. Dynamic optimal control of flow front position in injection molding process: A control parameterization-based method. J. Process Control 2023, 132, 103125. [Google Scholar] [CrossRef]
- Tan, K.; Tang, J. Learning-enhanced PI control of ram velocity in injection molding machines. Eng. Appl. Artif. Intell. 2002, 15, 65–72. [Google Scholar] [CrossRef]
- Tian, Y.C.; Gao, F. Injection velocity control of thermoplastic injection molding via a double controller scheme. Ind. Eng. Chem. Res. 1999, 38, 3396–3406. [Google Scholar] [CrossRef][Green Version]
- Lillicrap, T.P.; Hunt, J.J.; Pritzel, A.; Heess, N.; Erez, T.; Tassa, Y.; Silver, D.; Wierstra, D. Continuous control with deep reinforcement learning. arXiv 2015, arXiv:1509.02971. [Google Scholar]
- Zamfirache, I.A.; Precup, R.E.; Roman, R.C.; Petriu, E.M. Reinforcement Learning-based control using Q-learning and gravitational search algorithm with experimental validation on a nonlinear servo system. Inf. Sci. 2022, 583, 99–120. [Google Scholar] [CrossRef]
- Zamfirache, I.A.; Precup, R.E.; Roman, R.C.; Petriu, E.M. Policy iteration reinforcement learning-based control using a grey wolf optimizer algorithm. Inf. Sci. 2022, 585, 162–175. [Google Scholar] [CrossRef]
- Wang, N.; Gao, Y.; Zhao, H.; Ahn, C.K. Reinforcement learning-based optimal tracking control of an unknown unmanned surface vehicle. IEEE Trans. Neural Netw. Learn. Syst. 2020, 32, 3034–3045. [Google Scholar] [CrossRef]
- Shuprajhaa, T.; Sujit, S.K.; Srinivasan, K. Reinforcement learning based adaptive PID controller design for control of linear/nonlinear unstable processes. Appl. Soft Comput. 2022, 128, 109450. [Google Scholar] [CrossRef]
- Sun, Y.; Ran, X.; Zhang, G.; Wang, X.; Xu, H. AUV path following controlled by modified Deep Deterministic Policy Gradient. Ocean Eng. 2020, 210, 107360. [Google Scholar] [CrossRef]
- Bilal, H.; Yin, B.; Aslam, M.S.; Anjum, Z.; Rohra, A.; Wang, Y. A practical study of active disturbance rejection control for rotary flexible joint robot manipulator. Soft Comput. 2023, 27, 4987–5001. [Google Scholar] [CrossRef]
- Xu, L.; Yuehui, J.; Yu, S.; Junjie, L.; Qiang, G. Modified deep deterministic policy gradient based on active disturbance rejection control for hypersonic vehicles. Neural Comput. Appl. 2024, 36, 4071–4081. [Google Scholar] [CrossRef]
- Ning, L.; Zhou, M.; Hou, Z.; Goverde, R.M.; Wang, F.Y.; Dong, H. Deep deterministic policy gradient for high-speed train trajectory optimization. IEEE Trans. Intell. Transp. Syst. 2021, 23, 11562–11574. [Google Scholar] [CrossRef]
- Yan, R.; Jiang, R.; Jia, B.; Huang, J.; Yang, D. Hybrid car-following strategy based on deep deterministic policy gradient and cooperative adaptive cruise control. IEEE Trans. Autom. Sci. Eng. 2021, 19, 2816–2824. [Google Scholar] [CrossRef]
- Wang, N.; Gao, Y.; Yang, C.; Zhang, X. Reinforcement learning-based finite-time tracking control of an unknown unmanned surface vehicle with input constraints. Neurocomputing 2022, 484, 26–37. [Google Scholar] [CrossRef]
- Hao, G.; Fu, Z.; Feng, X.; Gong, Z.; Chen, P.; Wang, D.; Wang, W.; Si, Y. A deep deterministic policy gradient approach for vehicle speed tracking control with a robotic driver. IEEE Trans. Autom. Sci. Eng. 2021, 19, 2514–2525. [Google Scholar] [CrossRef]
- Guo, H.; Ren, Z.; Lai, J.; Wu, Z.; Xie, S. Optimal navigation forAGVs: A soft actor–critic-based reinforcement learning approach with composite auxiliary rewards. Eng. Appl. Artif. Intell. 2023, 124, 106613. [Google Scholar] [CrossRef]
- Ma, Y.; Zhu, W.; Benton, M.G.; Romagnoli, J. Continuous control of a polymerization system with deep reinforcement learning. J. Process Control 2019, 75, 40–47. [Google Scholar] [CrossRef]
- Qiu, C.; Hu, Y.; Chen, Y.; Zeng, B. Deep deterministic policy gradient (DDPG)-based energy harvesting wireless communications. IEEE Internet Things J. 2019, 6, 8577–8588. [Google Scholar] [CrossRef]
- Joshi, T.; Makker, S.; Kodamana, H.; Kandath, H. Twin actor twin delayed deep deterministic policy gradient (TATD3) learning for batch process control. Comput. Chem. Eng. 2021, 155, 107527. [Google Scholar] [CrossRef]
- Wei, Z.; Quan, Z.; Wu, J.; Li, Y.; Pou, J.; Zhong, H. Deep deterministic policy gradient-DRL enabled multiphysics-constrained fast charging of lithium-ion battery. IEEE Trans. Ind. Electron. 2021, 69, 2588–2598. [Google Scholar] [CrossRef]
- Yoo, H.; Kim, B.; Kim, J.W.; Lee, J.H. Reinforcement learning based optimal control of batch processes using Monte-Carlo deep deterministic policy gradient with phase segmentation. Comput. Chem. Eng. 2021, 144, 107133. [Google Scholar] [CrossRef]
- Watkins, C.J.; Dayan, P. Q-learning. Mach. Learn. 1992, 8, 279–292. [Google Scholar] [CrossRef]





| Variable | Variable Name | Value |
|---|---|---|
| Weight of Actuator-Screw Assembly | M | 8.663 kg |
| Cross-sectional Area of Cylinder | 3342 mm2 | |
| Cross-sectional Area of Barrel | 201 mm2 | |
| Polymer Viscosity | 4600 Pa·s | |
| Nozzle Radius | R | 2 m |
| Initial Length of Screw | L | 0.1 m |
| Ratio of Unit Radius to Nozzle Radius | 0.9 | |
| Bulk Modulus of Hydraulic Fluid | 1020 MPa | |
| Nozzle Bulk Modulus | 1100 MPa | |
| Oil Volume on Jet Side | 17,045 mm3 | |
| Polymer Volume in Barrel | 11,678 mm3 | |
| Polymer Flow Velocity | 0.0011/min |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ren, Z.; Tang, P.; Zheng, W.; Zhang, B. A Deep Reinforcement Learning Approach to Injection Speed Control in Injection Molding Machines with Servomotor-Driven Constant Pump Hydraulic System. Actuators 2024, 13, 376. https://doi.org/10.3390/act13090376
Ren Z, Tang P, Zheng W, Zhang B. A Deep Reinforcement Learning Approach to Injection Speed Control in Injection Molding Machines with Servomotor-Driven Constant Pump Hydraulic System. Actuators. 2024; 13(9):376. https://doi.org/10.3390/act13090376
Chicago/Turabian StyleRen, Zhigang, Peng Tang, Wen Zheng, and Bo Zhang. 2024. "A Deep Reinforcement Learning Approach to Injection Speed Control in Injection Molding Machines with Servomotor-Driven Constant Pump Hydraulic System" Actuators 13, no. 9: 376. https://doi.org/10.3390/act13090376
APA StyleRen, Z., Tang, P., Zheng, W., & Zhang, B. (2024). A Deep Reinforcement Learning Approach to Injection Speed Control in Injection Molding Machines with Servomotor-Driven Constant Pump Hydraulic System. Actuators, 13(9), 376. https://doi.org/10.3390/act13090376







