A Hinge Moment Alleviation Control Strategy for Morphing Tail Aircraft Based on a Data-Driven Method
Abstract
1. Introduction
2. Flight Mechanics Model Formulation
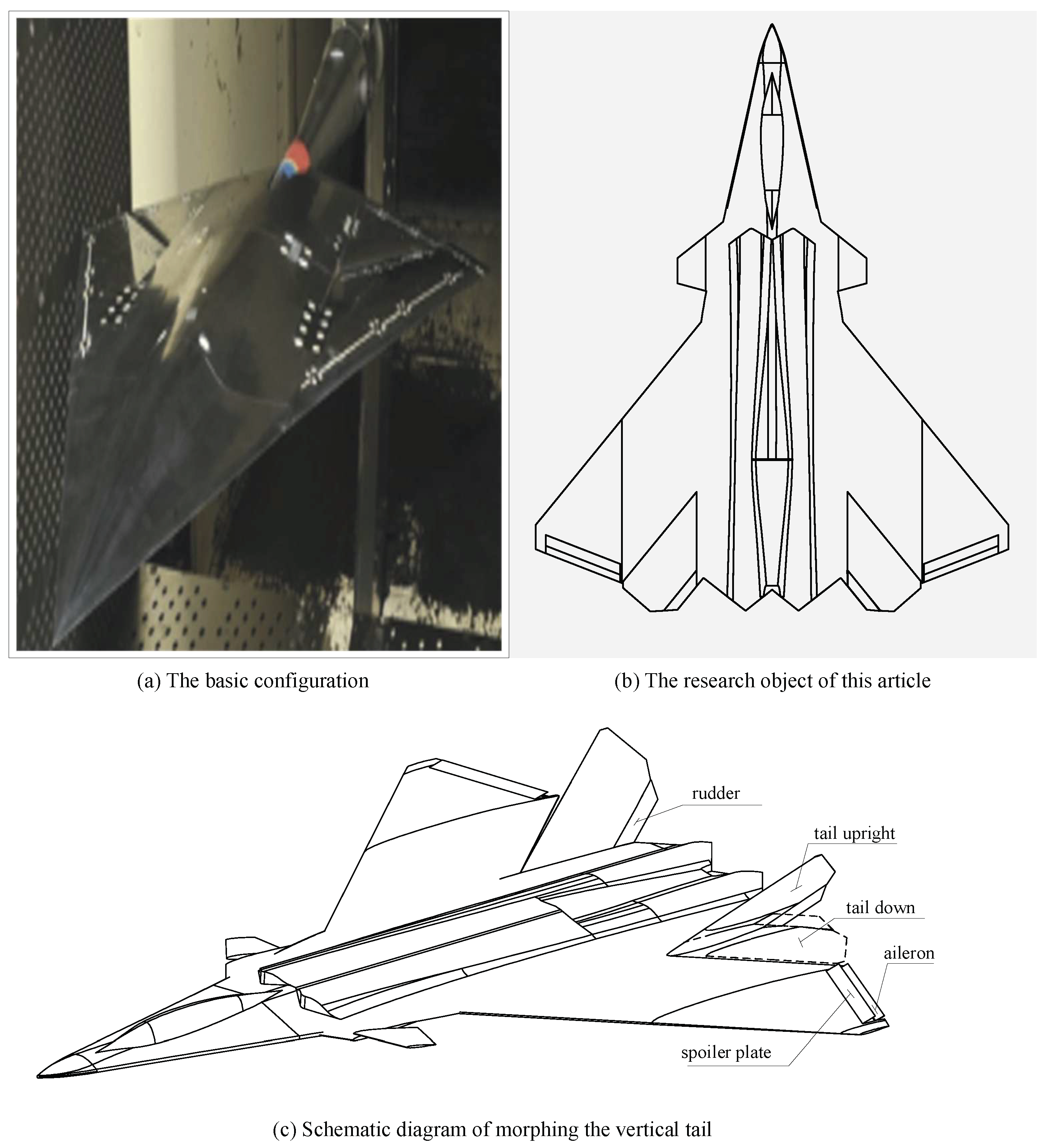
2.1. Aircraft Model
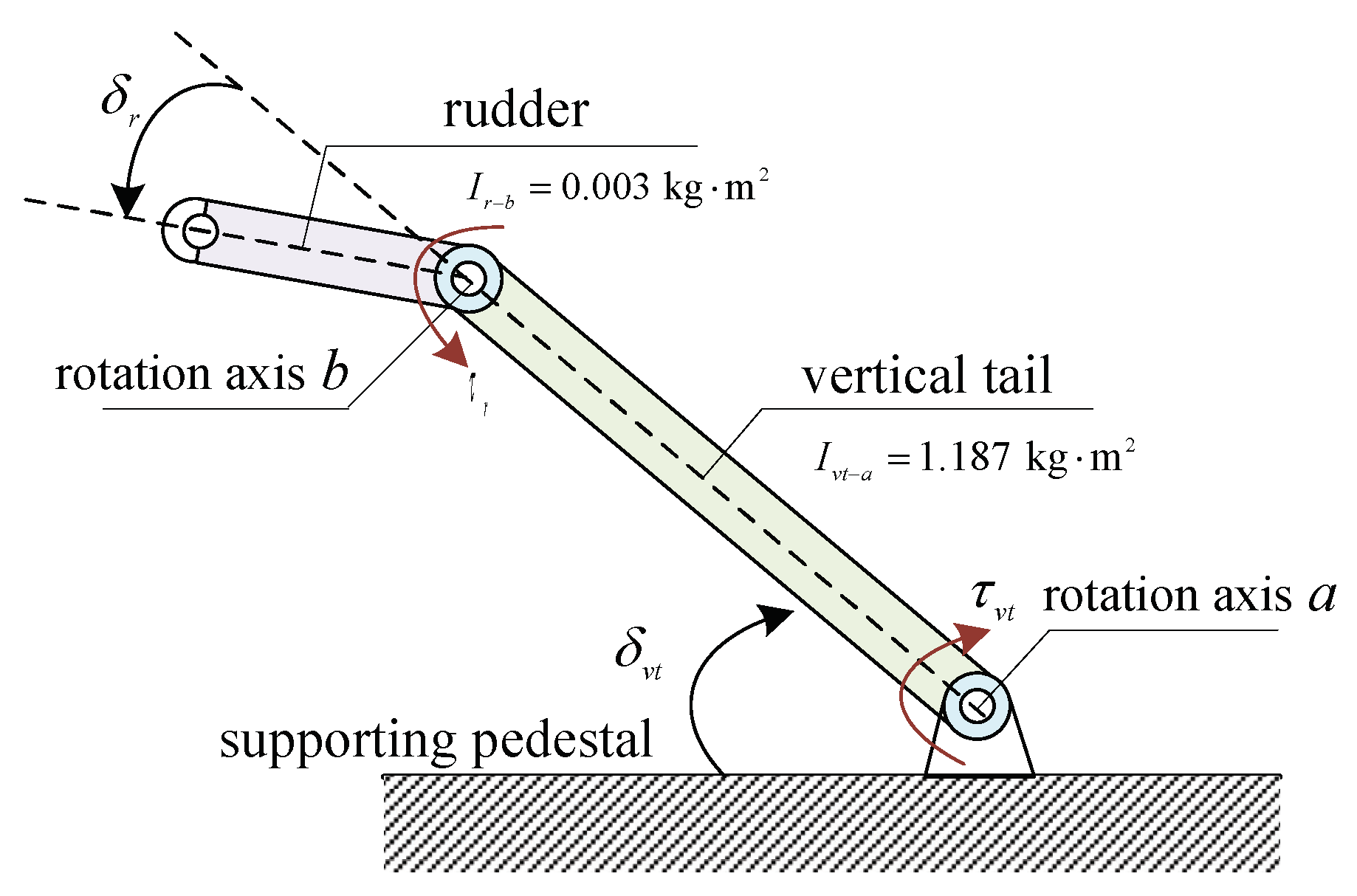
2.2. Tail Deformation Setting
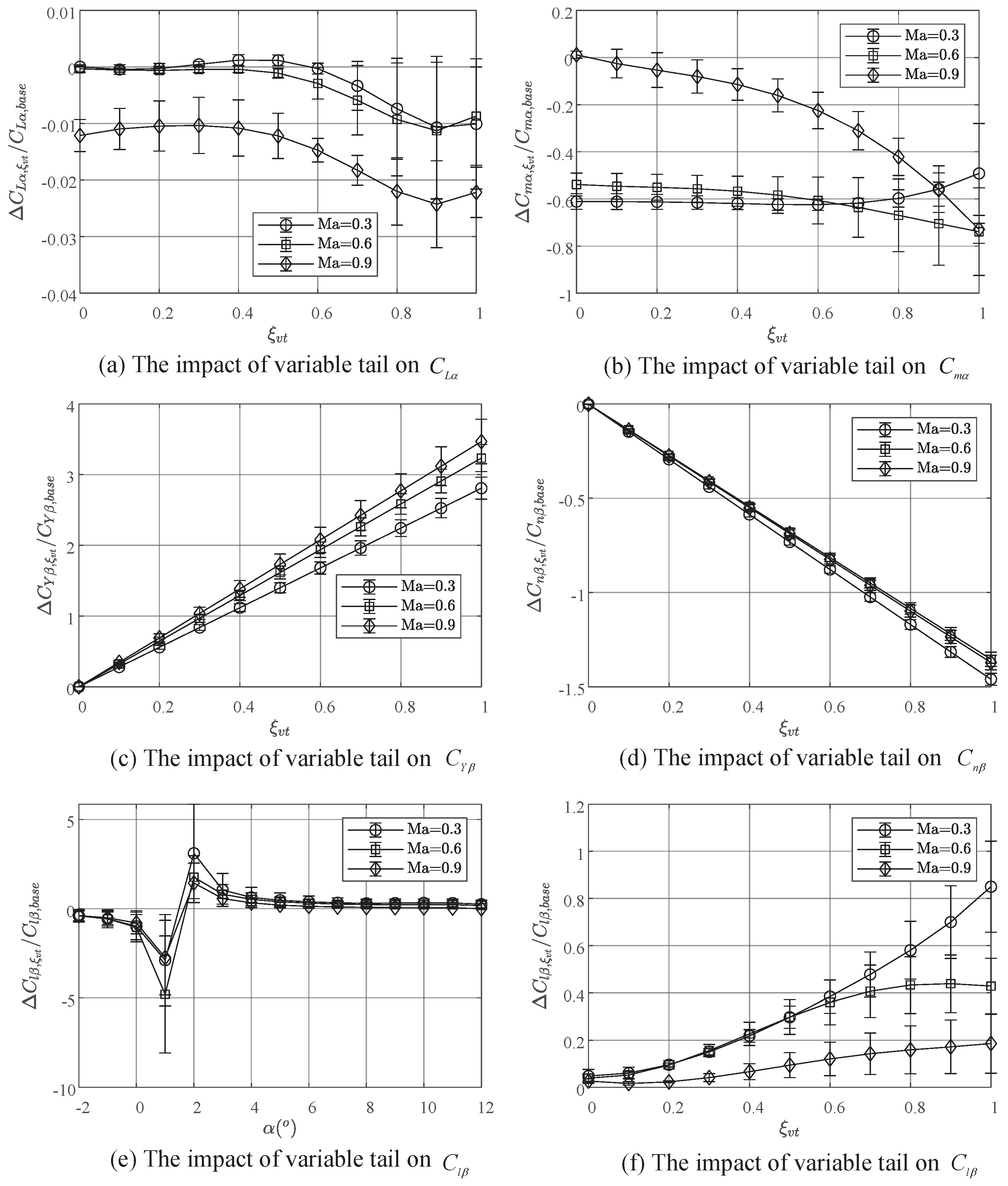
2.3. Analysis of Tail Hinge Moment Characteristics
3. Adaptive Morphing Tail Hinge Moment Reduction
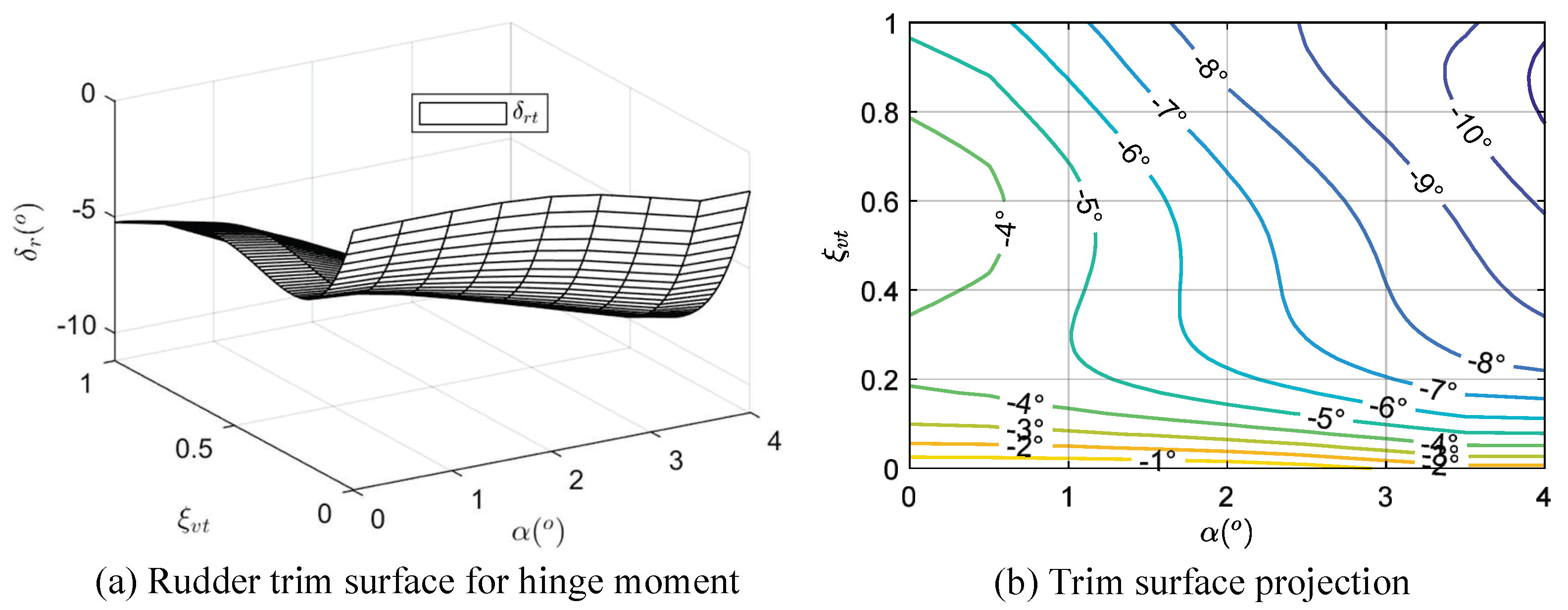
3.1. Analysis of Tail Hinge Moment Reduction
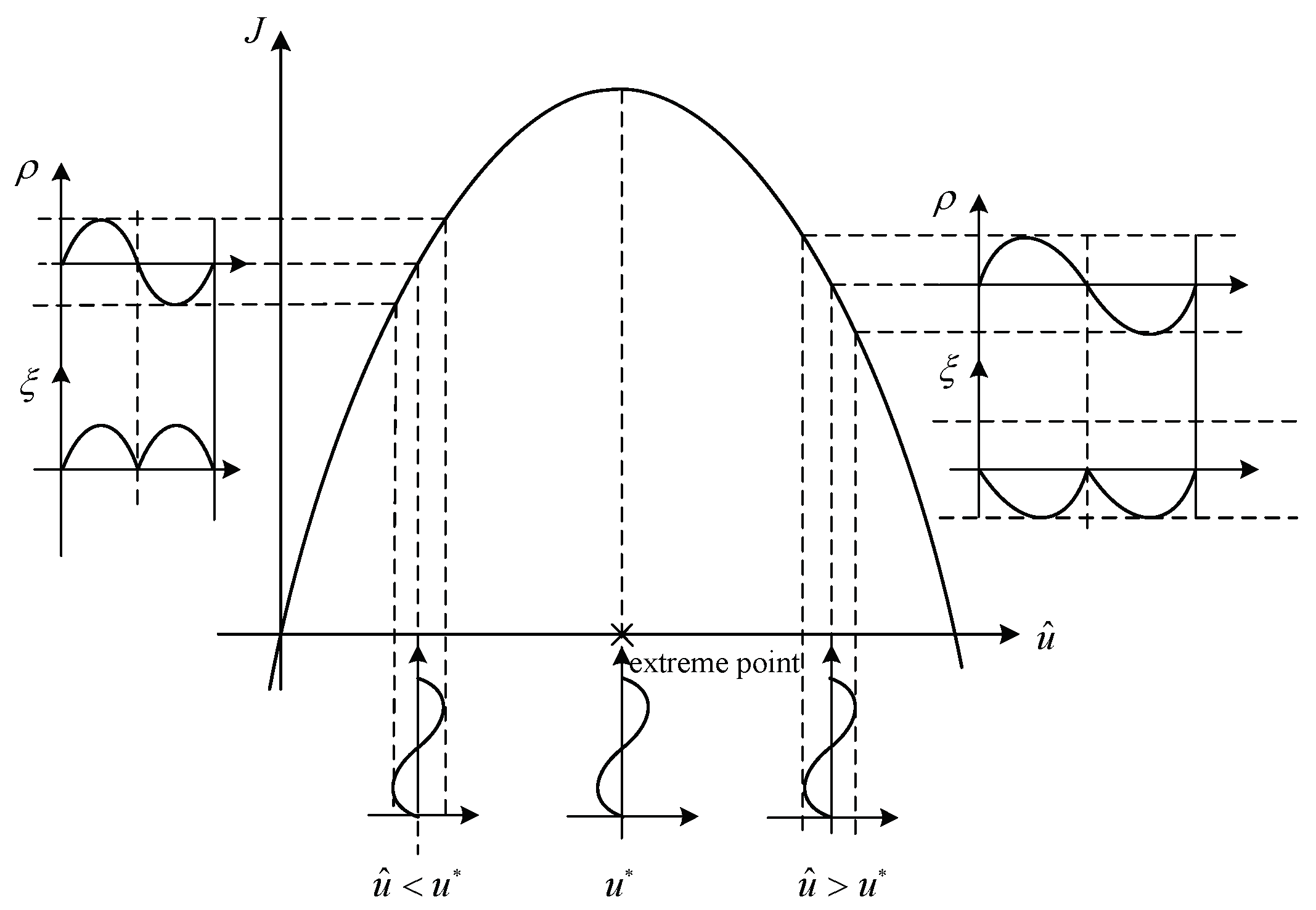
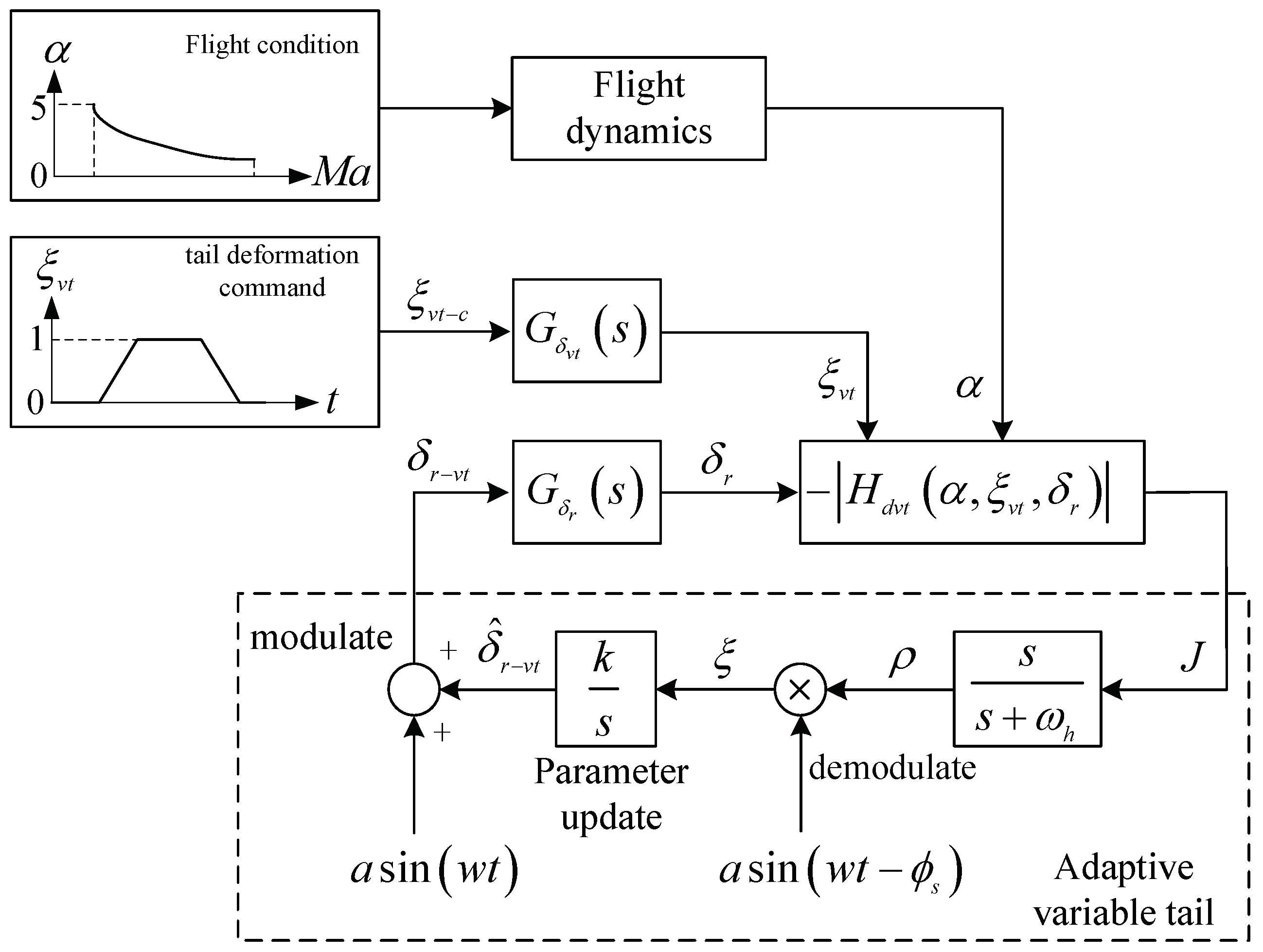
3.2. AMTHR Based on ESC
3.3. AMTHR Scheme
- (1)
- A sinusoidal perturbation with amplitude a and frequency w is injected into the control input signal to modulate ;
- (2)
- A high-pass filter with a cutoff frequency of is utilized to compute the gradient of the cost function J, and then it is multiplied by the signal after phase shifting for demodulation;
- (3)
- The demodulated signal is integrated and multiplied by the learning rate k to obtain an estimated value of the optimal rudder angle after parameter update.
4. Numerical Simulation
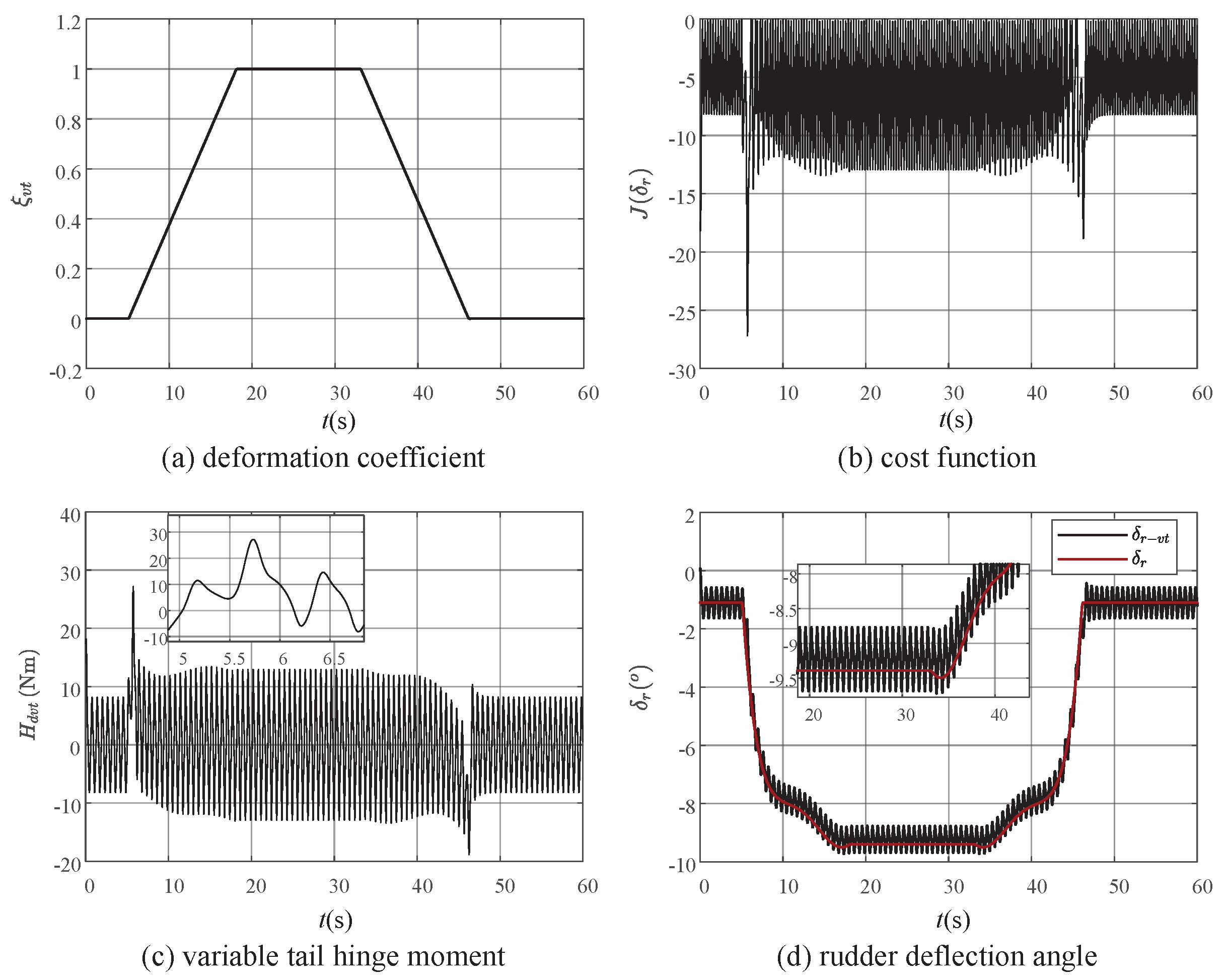
4.1. Load Reduction of Vertical Tail Hinge Moment
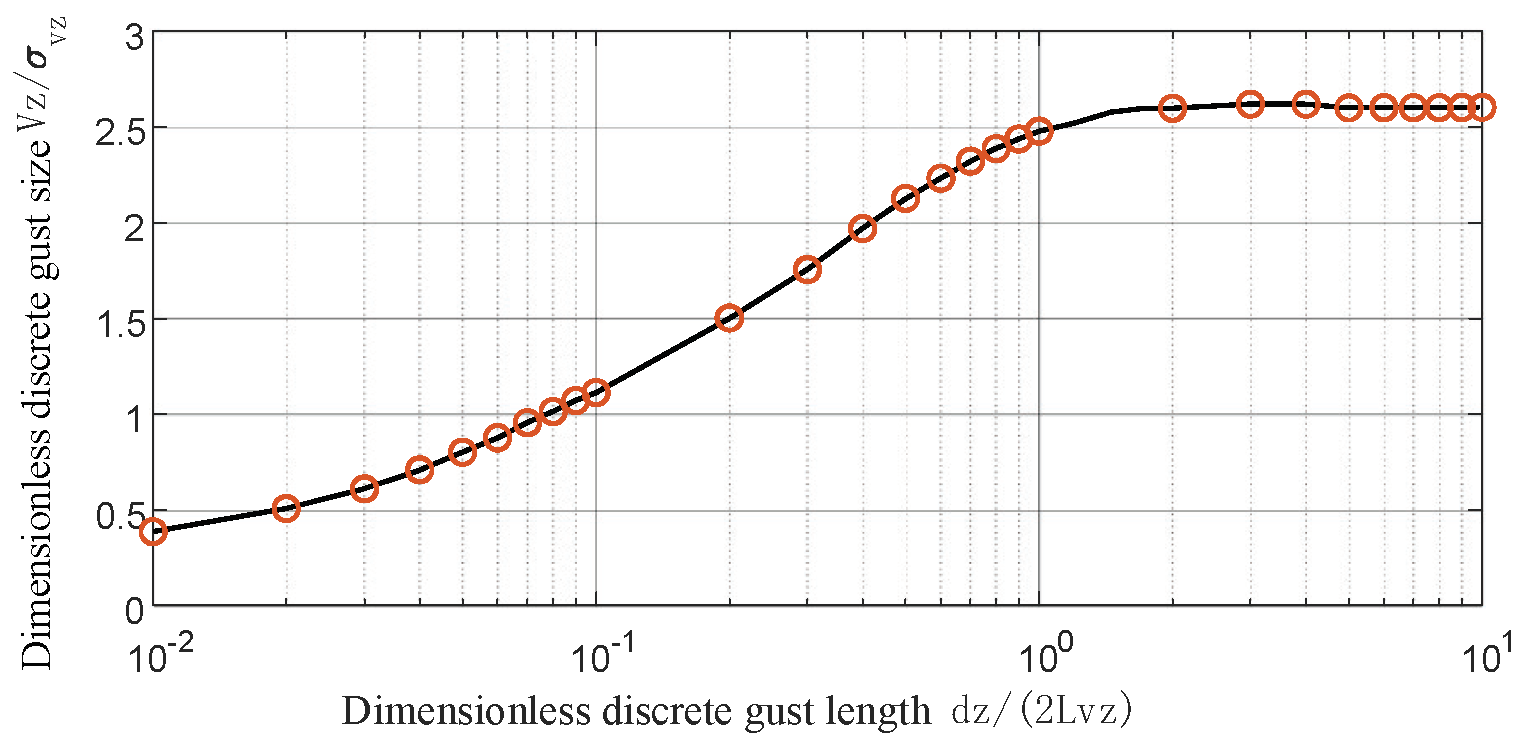
4.2. Simulation under Gust Disturbance
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AMTHR | adaptive morphing tail hinge moment reduction |
| NGAD | Next-Generation Air Dominance |
| ESC | Extreme-seeking control |
| Vertical tail angle | |
| Deformation coefficient | |
| Hinge moment of single tail | |
| Rudder angle | |
| Angle of attack | |
| Oscillation excitation signal | |
| J | Objective function of ESC |
References
- Bolander, C.R.; Kohler, A.J.; Hunsaker, D.F.; Myszka, D.; Joo, J. Development of smart structures for aircraft vibration and noise control. In Proceedings of the AIAA SCITECH 2023 Forum, National Harbor, ML, USA, 23–27 January 2023; pp. 1–6. [Google Scholar]
- Grellmann, H. B-2 aerodynamic design. In Proceedings of the Aerospace Engineering Conference and Show, Los Angeles, CA, USA, 3–15 February 1990; p. 1802. [Google Scholar]
- Brinker, J. Autonomous steering of the joint unmanned combat air system (J-UCAS) X-45A. In Proceedings of the AIAA 3rd “Unmanned Unlimited” Technical Conference, Chicago, IL, USA, 20–23 September 2004; p. 6575. [Google Scholar]
- Sepulveda, E.; Smith, H. Technology challenges of stealth unmanned combat aerial vehicles. Aeronaut. J. 2017, 121, 1261–1295. [Google Scholar] [CrossRef]
- Dean, S.E. USAF’s Next Generation Air Dominance Programme Status Report and Impact. Eur. Secur. Def. 2021, 10, 1–3. [Google Scholar]
- Wang, H.; Du, X.; Hu, Y. Investigation on the reduced-order model for the hydrofoil of the blended-wing-body underwater glider flow control with steady-stream suction and jets based on the POD method. Actuators 2024, 13, 194. [Google Scholar] [CrossRef]
- Zhang, B.; Li, Q.; Wang, T.; Wang, Z. Development of a bionic dolphin flexible tail experimental device driven by a steering gear. Actuators 2021, 10, 167. [Google Scholar] [CrossRef]
- Goetzendorf-Grabowski, T.; Kwiek, A. Study of the impact of aerodynamic model fidelity on the flight characteristics of unconventional aircraft. Appl. Sci. 2023, 13, 12522. [Google Scholar] [CrossRef]
- Ryseck, P.; Yeo, D.; Hrishikeshavan, V.; Chopra, I. Expanding the mission capabilities of a quadrotor biplane tail-sitter with morphing winglets. In Proceedings of the AIAA Scitech 2020 Forum, Orlando, FL, USA, 6–10 January 2020; pp. 1–8. [Google Scholar]
- Ma, X.Y.; Su, J.C.; Zhong, S.D.; Huang, Y.; Zhang, Y. Study of aerodynamic and stealthy performance for a multifunctional morphing tail. ACTA Aerodyn. Sin. 2020, 5, 896–900. [Google Scholar]
- Nieto, C.; Sobel, K. Eigen-structure assignment for a tailless aircraft. In Proceedings of the AIAA Guidance, Navigation and Control Conference and Exhibit, San Francisco, CA, USA, 20–23 August 2007; pp. 1–6. [Google Scholar]
- Ansell, P.J.; Kerho, M.F.; Bragg, M.B. Application of a hinge-moment-based envelope protection system on a wing. J. Aircr. 2014, 51, 2038–2042. [Google Scholar] [CrossRef]
- Gu, H.; Cheung, R.; Healy, F.; Rezgui, D.; Lowenberg, M.; Cooper, J. Experimental study of the impact of folding wingtip devices on aircraft flight mechanics and handling qualities. In Proceedings of the AIAA SCITECH 2023 Forum, National Harbor, ML, USA, 23–27 January 2023; pp. 1–6. [Google Scholar]
- Concilio, A.; Galasso, B.; Ameduri, S. Scaling effects on morphing structures: Preliminary guidelines for managing the effects on a case study. Actuators 2023, 12, 366. [Google Scholar] [CrossRef]
- Ameduri, S.; Dimino, I.; Pellone, L.; Concilio, A.; Mercurio, U.; Gallorini, F.; Pispola, G.; D’Andrea, M. Kinematic chain of a morphing winglet: Specifications, Conceptual and Advanced Design. Actuators 2023, 12, 194. [Google Scholar] [CrossRef]
- Huang, R.; Yu, X.; Zhou, X. Efficient nonlinear aeroservoelastic modeling for morphing wing with bilinear stiffness. AIAA J. 2021, 60, 3135–3146. [Google Scholar] [CrossRef]
- Lv, B.; Wang, Y.; Lei, P. Effects of trailing edge deflections driven by shape memory alloy actuators on the transonic aerodynamic characteristics of a super critical airfoil. Actuators 2021, 10, 160. [Google Scholar] [CrossRef]
- Mkhoyan, T.; Ruland, O.; Breuker, R.D.; Wang, X. On-line black-box aerodynamic performance optimization for a morphing wing with distributed sensing and control. IEEE Trans. Control Syst. Technol. 2023, 31, 1063–1077. [Google Scholar] [CrossRef]
- Zhang, B.; Guo, J.; Wang, H.; Tang, S. Autonomous morphing strategy for a long-range aircraft using reinforcement learning. Aerosp. Sci. Technol. 2024, 148, 109087. [Google Scholar] [CrossRef]
- Grigorie, T.L.; Botez, R.M. A self–tuning intelligent controller for a smart actuation mechanism of a morphing wing based on shape memory alloys. Actuators 2023, 12, 350. [Google Scholar] [CrossRef]
- Wu, Y.; Dai, Y.; Yang, C. Time-delayed active control of stall flutter for an airfoil via camber morphing. AIAA J. 2022, 60, 5723–5734. [Google Scholar] [CrossRef]
- Feng, L.; Guo, T.; Zhu, C.; Chen, H. Control design and flight test of aerodynamics-driven monoplane–biplane morphing aircraft. J. Guid. Control Dyn. 2023, 46, 2373–2387. [Google Scholar] [CrossRef]
- Ariyur, K.B.; Krstic, M. Real-Time Optimization by Extremum-Seeking Control; John Wiley and Sons: New York, NY, USA, 2003; pp. 154–196. [Google Scholar]
- Brunton, S.L.; Kutz, J.N. Data-Driven Science and Engineering: Machine Learning, Dynamical Systems, and Control; Cambridge University Press: Britain, UK, 2022; pp. 261–267. [Google Scholar]
- Krstic, M.; Wang, H. Stability of extremum seeking feedback for general nonlinear dynamic systems. Automatica 2000, 36, 595–602. [Google Scholar] [CrossRef]
- Scaramal, M.; Horn, J.F. Load alleviation on compound rotorcraft using load feedback and extremum seeking control. J. Guid. Control Dyn. 2023, 46, 2399–2409. [Google Scholar] [CrossRef]
- Bratcu, A.; Munteanu, I.; Bacha, S.; Raison, B. Maximum power point tracking of grid-connected photovoltaic arrays by using extremum seeking control. J. Control Eng. Appl. Inform. 2008, 10, 3–12. [Google Scholar]
- Brunton, S.L.; Rowley, C.W.; Kulkarni, S.R.; Clarkson, C. Maximum power point tracking for photovoltaic optimization using ripple-based extremum seeking control. IEEE Trans. Power Electron. 2010, 25, 2531–2540. [Google Scholar] [CrossRef]
- Tanelli, M.; Astolfi, A.; Savaresi, S. Non-local extremum seeking control for active braking control systems. In Proceedings of the 2006 IEEE Conference on Computer Aided Control System Design, Munich, Germany, 4–6 October 2006; pp. 891–896. [Google Scholar]
- Binetti, P.; Ariyur, K.B.; Krstic, M.; Bernelli, F. Formation flight optimization using extremum seeking feedback. J. Guid. Control Dyn. 2003, 26, 132–142. [Google Scholar] [CrossRef]
- Krieger, J.P.; Krstic, M. Extremum seeking based on atmospheric turbulence for aircraft endurance. J. Guid. Control Dyn. 2011, 36, 1876–1885. [Google Scholar] [CrossRef][Green Version]
- Shtessel, Y.; Buffington, J.; Banda, S. Tailless aircraft flight control using multiple time scale reconfigurable sliding modes. IEEE Trans. Control Syst. Technol. 2002, 10, 288–296. [Google Scholar] [CrossRef]
- Stankovic, M.S.; Stipanovic, D.M. Extremum seeking under stochastic noise and applications to mobile sensors. Automatica 2010, 46, 1243–1251. [Google Scholar] [CrossRef]
- Moorhouse, D.J.; Woodcock, R.J. Background Information and User Guide for MIL-F-8785C, Military Specification: Flying Qualities of Piloted Airplanes; AFWAL-TR-81-3109; Air Force Flight Dynamics Laboratory: Dayton, OH, USA, 1982. [Google Scholar]






| Parameters | Symbol | Values | Unit |
|---|---|---|---|
| Take off mass | 575 | kg | |
| Center of gravity | 2.66 | m | |
| Span | b | 3.4 | m |
| Average aerodynamic chord length | 0.9 | m | |
| Reference area | S | 3.2 | m2 |
| Sweep angle | 55 | ° | |
| Maximum vertical tail angle | 65 | ° | |
| Minimum vertical tail angle | 0 | ° | |
| Rolling inertia | 104 | ||
| Pitch inertia | 465 | ||
| Yaw inertia | 612 | ||
| Cross inertia product | |||
| Maximum ground thrust (single) | 1750 | N |
| (kg) | (kg · m2) | (kg · m2) | (kg · m2) | (kg · m2) | ||
|---|---|---|---|---|---|---|
| 476 | 0 | 0 | 101 | 452 | 586 | −9 |
| 476 | 65 | 1 | 96 | 452 | 581 | −15 |
| 565 | 0 | 0 | 104 | 475 | 632 | −11 |
| 565 | 65 | 1 | 99 | 476 | 630 | −17 |
| Parameters | Value | Unit | Meaning |
|---|---|---|---|
| k | 2 | / | learning rate |
| w | 10 | rad/s | input excitation frequency |
| a | 0.5 | ° | input excitation amplitude |
| 2 | rad/s | cutoff frequency of high-pass filter | |
| 0.0061 | rad | phase shift angle |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, R.; Lyu, H. A Hinge Moment Alleviation Control Strategy for Morphing Tail Aircraft Based on a Data-Driven Method. Actuators 2024, 13, 369. https://doi.org/10.3390/act13090369
Cao R, Lyu H. A Hinge Moment Alleviation Control Strategy for Morphing Tail Aircraft Based on a Data-Driven Method. Actuators. 2024; 13(9):369. https://doi.org/10.3390/act13090369
Chicago/Turabian StyleCao, Rui, and Huitao Lyu. 2024. "A Hinge Moment Alleviation Control Strategy for Morphing Tail Aircraft Based on a Data-Driven Method" Actuators 13, no. 9: 369. https://doi.org/10.3390/act13090369
APA StyleCao, R., & Lyu, H. (2024). A Hinge Moment Alleviation Control Strategy for Morphing Tail Aircraft Based on a Data-Driven Method. Actuators, 13(9), 369. https://doi.org/10.3390/act13090369






