Abstract
The study proposes an active trailer steering control method for tractor semitrailers to promote the path tracking effect of the trailer portion as well as lateral stability during lane changing. Firstly, a simplified model of a tractor semitrailer is constructed, and the MAP map is formed based on the genetic algorithm for the identification of the key parameters, which improves the model’s accuracy. Then the tractor and trailer’s yaw rate and sideslip angle at CG are tracked as the control objective and the trailer angle distribution strategy is given. Then the LQR-based corner controller is designed to control the steering actuators of each axle of the trailer. Finally, the effectiveness of the designed control strategy is verified based on the Trucksim/Simulink joint simulation platform and the semi-physical HiL test platform. The simulation results show that the designed controller can effectively improve the path tracking effect of the tractor and the trailer, and at the same time, the lateral stability parameters of the tractor and the trailer are also significantly improved, which improves the driving stability of the tractor semitrailer.
1. Introduction
With the rise of the courier industry and the high-speed development of the highway, the modern logistics and transport industry has entered the fast lane of vigorous development, and is slowly moving towards large-scale, heavy-duty and professional transport, in which the tractor semitrailer plays a very important role and is the mainstay of road transport [1]. The tractor semitrailer offers advantages such as a large load capacity, low transport costs, easy maintenance, and high transport efficiency [2]. Therefore, it is widely used in the road freight and logistics industry. Meanwhile, in recent years, the demand for coal, steel, and other raw materials has remained strong, further driving the growth of the tractor semitrailer industry [3].
However, there are also many problems with the tractor semitrailer; due to the existence of the connecting device, the structure of the tractor semitrailer is relatively complex, which also brings about the phenomenon of the amplification of the rear end of the tractor semitrailer. This is unique, specifically, as when the is tractor steering, the rear of the trailer will produce a kind of centrifugal force, which makes the rear of the trailer deviate from the original driving trajectory, and makes it prone to collisions between the rear of the trailer and the surrounding obstacles or other vehicles [4]. Meanwhile, since the manipulation of the driver of the tractor semitrailer is mainly based on the state of the tractor and it is difficult to perceive the state of the trailer [5], if the driver does not operate properly or the road conditions are poor, it is easy to cause accidents, such as the common rollover accidents and folding accidents. In addition to this, the tractor semitrailer also has problems such as a high centre of cargo mass and high load capacity [6].
In order to improve these problems, more and more scholars have studied the active trailer steering control strategy; by applying control to the steering actuators of each axle of the trailer, the trailer path tracking effect and lateral stability of the tractor semitrailer can be improved. Wang [7] et al. elaborated the effect of rear-end amplification on the stability of tractor semitrailers, and used it as a control target to improve the stability of tractor semitrailers at medium and high speeds by using an active trailer steering system. Jujnovich [8] et al. used an active trailer steering system and targeted the rear end of the trailer to follow the trajectory of the articulation point, and applied the linear quadratic regulator (LQR) control algorithm in the control strategy to improve the lateral stability of the tractor semitrailer and trailer tracking effect. Nie Zhigen [9] et al. identified the parameters of the three-degree-of-freedom (DOF) yaw model and the five-DOF yaw–roll model, and controlled the active trailer steering system by using proportional integral derivative (PID) and LQR algorithms for the low-speed and high-speed scenarios, respectively, and the simulation experiments and the verification of the hardware-in-the-loop platform under different test conditions showed the effectiveness of the control strategy. Kural K [10] et al. designed an active trailer steering control system which is regulated by a single PID controller over all speed ranges and the gain scheduling method was used to obtain the best results to improve the low-speed manoeuvrability as well as the high-speed stability of the tractor semitrailer. Kim K [11] et al. established a simplified three-DOF model of a tractor semitrailer, identified the key parameters of the model under the specified speed and corners by an annealed particle swarm optimization algorithm, and then designed an active trailer steering controller based on the LQR algorithm, which tracked the desired yaw rate so as to improve the tracking effect and stability. Ding X [12] et al. used fuzzy control and the LQR algorithm to study the active trailer steering system; the study showed that both methods can improve the tracking effect and stability of the tractor semitrailer, and the LQR algorithm is better than the fuzzy control algorithm.
The trailer part of tractor semitrailer usually has three axles and is located in the rear of the vehicle; the above studies are the equivalent of the trailer part as an axle for the study, the output of the controller is the equivalent axle angle of the trailer, and there is no detailed control of each axle angle of the trailer. In addition, when the tractor semitrailer undertakes the task of logistics and freight transport, the mass of the loaded cargo often changes [13], and the changing mass of the cargo will lead to changes in the key parameters required in the controller, such as the cornering stiffness of each axle [14], thus affecting the effectiveness of the controller, and the above studies have not been carried out in this regard.
Therefore, the innovations of this paper are mainly in two aspects: firstly, for the uncertainty of the vehicle’s key parameter of the cornering stiffness of each axle, a parameter identification strategy is designed, which improves the accuracy of the model by getting the parameter mean arterial pressure (MAP) diagram and obtaining the real-time accurate value of the parameter by looking up the table. Secondly, considering that the current research on active trailer steering control usually combines three axles of the trailer section into one for research, this paper provides more detailed control of the trailer’s cornering angle of each axle based on the allocation strategy, which helps to further improve the stability of the vehicle.
Based on the above analysis, an active trailer steering control strategy will be proposed in this paper, and the main research contents are as follows: Firstly, the three-DOF simplified model is derived based on the force analysis. Then, the parameter identification strategy based on a genetic algorithm is designed to identify the key parameter, i.e., the cornering stiffness of each axle under different cargo mass and lateral acceleration, and form the MAP diagram of the key parameter. Next, the trailer angle allocation strategy for each axle is designed and the active trailer steering controller is built based on the LQR algorithm. Finally, we verify the effectiveness of the control strategy under a double lane change condition using the Trucksim/Simulink joint simulation platform and the semi-physical hardware-in-loop (HiL) test platform.
2. Model Establishment for Tractor Semitrailers
The tractor semitrailer studied in this paper consists of two parts, namely, the tractor and the trailer, which are connected by a coupling device. The tractor is a two-axle vehicle; the front axle is responsible for steering and the rear axle is responsible for driving, while the trailer is a three-axle vehicle, with all three axles located at the rear of the vehicle.
2.1. Differential Equations of Motion
In this paper, mainly the yaw motion of the tractor semitrailer is investigated, so a simplified model can be used to meet the needs of this study. In order to facilitate the analysis, the structural dimensions of the tractor semitrailer are given and the required dimensions are marked, as shown in Figure 1.

Figure 1.
Structural dimensions of a tractor semitrailer.
In this paper, the simplified three-DOF yaw model of tractor semitrailers will be used, and the yaw model of tractor semitrailers is shown in Figure 2. Meanwhile, the differential equations of tractor and trailer dynamics can be obtained according to Newton’s laws of motion [15].
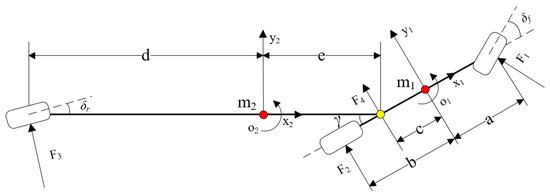
Figure 2.
Yaw model of tractor semitrailer.
The tractor dynamics equations are as follows:
The trailer dynamics equations are as follows:
The constraint equation at the articulation point of the tractor and trailer is as follows:
In order to facilitate the description of the object, the tractor-related parameters are denoted by the subscript 1, and the trailer-related parameters are denoted by the subscript 2, and the symbolic meaning of each parameter is shown in Table 1.

Table 1.
Symbolic meaning of each parameter.
2.2. Tyre Model
The tyre model used in this paper is a linear tyre model, and in the case of a tyre sideslip angle less than 5°, the relationship between the sideslip angle and the lateral force is linear, so the lateral force of each axle is equal to the product of the tyre cornering stiffness and the sideslip angle of each axle, as shown below:
Among them, α1, α2, and α3 are the front axle sideslip angle of the tractor, rear axle sideslip angle of the tractor, and equivalent axle sideslip angle of the trailer, and k1, k2, and k3 are the front axle cornering stiffness of the tractor, rear axle cornering stiffness of the tractor, and equivalent axle cornering stiffness of the trailer, respectively.
2.3. Equation of State
The state space of the three-DOF tractor semitrailer can be obtained by taking β1, 1 and β2, 2 as state variables, and combining Equations (1) and (9) to eliminate the interaction force at the connecting device. The expression is as follows:
In this equation
3. Parameter Identification for the Tractor Semitrailer Model
In Trucksim software, we can read some basic parameters of the vehicle, such as dimensional parameters, suspension stiffness and damping, vehicle moment of inertia, etc., but there are still a lot of key parameters that cannot be read directly, such as tyre cornering stiffness, etc. In order to provide accurate parameters for the model in Matlab, the parameter identification of the tractor semitrailer model will be investigated in this section, and the main focus is on the identification of the tyre cornering stiffness of each axle. In order to provide accurate parameters for the model in Matlab, this section will investigate the identification of the model parameters of the tractor semitrailer, mainly focusing on the identification of the cornering stiffness of each axle tyre.
3.1. Parameter Acquisition Based on the Genetic Algorithm
The genetic algorithm is an optimisation algorithm based on natural selection and a genetic mechanism, which is widely used in optimisation and search problems of complex systems. Genetic algorithms search for optimal solutions in the solution space by simulating the operations of selection, crossover, and mutation in the natural evolutionary process [16].
The genetic algorithm used in this paper adopts binary coding, roulette selection for the selection method, uniform crossover for the crossover method, basic bit mutation for the mutation method, and the search space limitation method for constraint processing. For the simplified three-DOF yaw model of the tractor semitrailer, the sideslip angle at the CG of the tractor and trailer as well as the yaw rate data are used to identify the cornering stiffness of the front axle of the tractor, the rear axle of the tractor, and the equivalent axle of the trailer, and the fitness function is shown in Equation (11).
where β1s(i), 1s(i) and β2s(i), 2s(i) are the sideslip angle at the CG and yaw rate for the tractor and trailer in the simplified model, respectively. β1t (i), 1t(i) and β2t(i), 2t(i) are the sideslip angle at the CG and the yaw rate of the tractor and trailer output from the Trucksim model, respectively.
By selecting a set of step conditions with no load 0.3 g lateral acceleration for testing, the front axle cornering stiffness of the tractor was identified as −274543 N/rad, the rear axle cornering stiffness of the tractor was identified as −413562 N/rad, and the equivalent axle cornering stiffness of the trailer was identified as −245674 N/rad.
However, in the actual operation of the tractor semitrailer, the mass of the loaded cargo often changes, and then the cornering stiffness of each axle tyre will also change accordingly. Therefore, genetic algorithms are used to identify the cornering stiffness of each axle for different masses of cargo and form the MAP map of cornering stiffness to obtain an accurate value for each axle’s cornering stiffness under different test conditions, which can improve the accuracy of the model, and the identification process is shown in Figure 3.
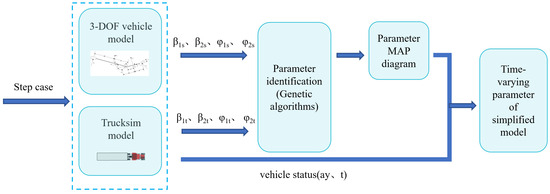
Figure 3.
Parameter identification flowchart.
The simplified three-DOF yaw model of the tractor semitrailer was firstly established, and then the offline identification of the cornering stiffness of each axle of the tractor semitrailer was carried out by the genetic algorithm; these axles were the front axle of the tractor, the rear axle of the tractor, and the equivalent axle of the trailer, respectively. After identifying the parameters under different test conditions, the parameter MAP diagrams can be obtained, in which the independent variables are lateral acceleration and cargo mass, and finally, the time-varying parameter values can be obtained by using the look-up table method according to the real-time state of the vehicle, which can significantly improve the accuracy of the simplified model.
In this study, step conditions were used to identify the parameters of the simplified three-DOF model, covering different conditions from small lateral acceleration to large lateral acceleration, and from unloaded to fully loaded (the load is taken at every 1/8 times of the fully loaded mass), and the MAP diagrams were obtained after identifying the points of the conditions, as shown in Figure 4, Figure 5 and Figure 6, and the values of cornering stiffness in the diagrams are the absolute values for the sake of the convenience of presentation.
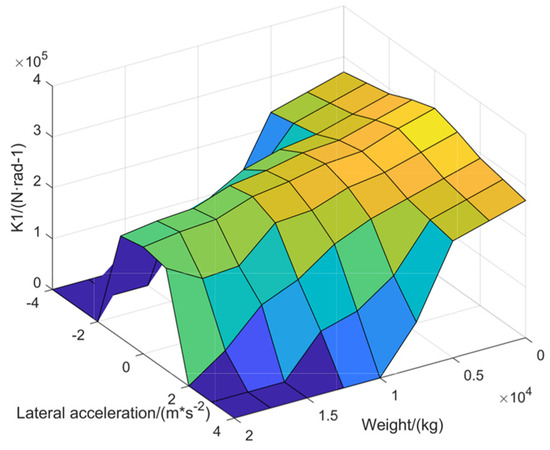
Figure 4.
MAP diagram of the cornering stiffness of the tractor front axle.

Figure 5.
MAP diagram of the cornering stiffness of the tractor rear axle.
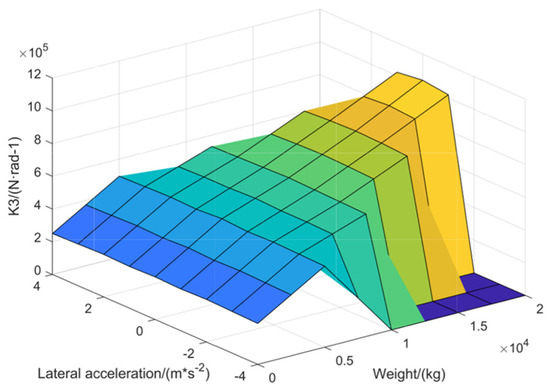
Figure 6.
MAP diagram of the cornering stiffness of the trailer axle.
From Figure 4, it can be seen that, for the same cargo mass, the tractor front axle cornering stiffness decreases with the increase in lateral acceleration, and the change is obvious when the cargo mass is large, while the change is small when the cargo mass is small. Under the same lateral acceleration, the tractor front axle cornering stiffness decreases with the increase in cargo mass, and the change is obvious when the lateral acceleration is large, while the change is small when the lateral acceleration is small. The variation in the tractor front axle cornering stiffness is in accordance with the knowledge of automobile theory, that is, with the increase in lateral acceleration, the load transfer rate will increase accordingly, which leads to the decrease in the cornering stiffness [17].
Figure 5 and Figure 6 have the same trend, in the case of the same cargo mass, and the tractor rear axle cornering stiffness and the trailer equivalent axle side deflection stiffness have the tendency of decreasing slowly with the increase in lateral acceleration. In the case of the same lateral acceleration, the tractor rear axle cornering stiffness and the trailer equivalent axle side deflection stiffness have a more obvious tendency to increase with the increase in cargo mass.
Combined with Figure 4, Figure 5 and Figure 6, it can be concluded that the values of the cornering stiffness of the three axles of the tractor semitrailer under different test conditions are relatively obvious, so it is necessary to carry out the research of parameter identification, which can significantly improve the accuracy of the model under different test conditions.
3.2. Validation of Simplified Models
In order to verify the accuracy of the model after parameter identification, the double lane change test condition is chosen to compare the simplified model and Trucksim model, where the double lane change condition refers to the test condition with an initial speed of 50 km/h and a road adhesion coefficient of 0.85, and the mass of the cargo loaded in the test condition is 5000 kg, which can be a better comparison for the accuracy of the model after parameter identification. The results are shown in the figure below. The validation results are shown in the following figures, in which Figure 7 shows the steering wheel angle, and Figure 8 shows the comparison of the responses of the tractor and trailer under the simplified model and Trucksim model.
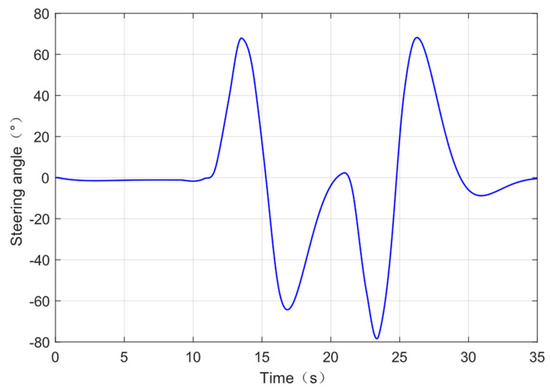
Figure 7.
Steering angle.
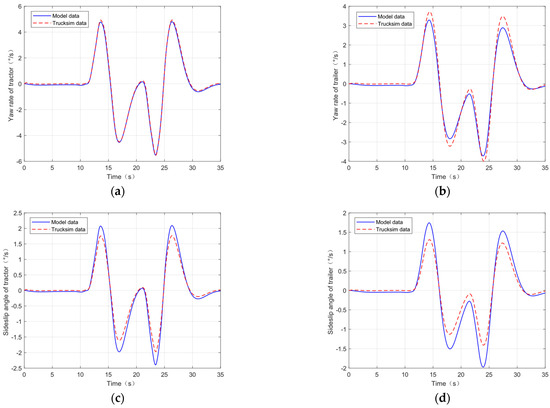
Figure 8.
Response comparison under the double lane condition of the simplified model and Trucksim model. (a) Yaw rate of the tractor; (b) yaw rate of the trailer; (c) sideslip angle at the CG of the tractor; and (d) sideslip angle at the CG of the trailer.
Figure 8 shows that the vehicle characteristics of the simplified model are in good agreement with those of Trucksim, i.e., the simplified three-DOF model with parameter identification can respond well to the dynamics of the tractor semitrailer, and the mean square errors of the response comparison curves of the state quantities are shown in Table 2. The meaning of the mean square error shows that the simplified three-DOF model after parameter identification has a better response, so the model meets the requirements of this study and can be used in the stability control study.

Table 2.
Mean square error of the response comparison curve of each state quantity.
4. Active Trailer Steering Control Strategy
In this section, the active trailer steering control strategy under medium- and high-speed conditions is investigated, and the main purpose is to solve the path-following and lateral stability problems of trailers. Firstly, we discuss the corner allocation strategy under medium- and high-speed conditions and establish the active trailer steering controller based on the linear quadratic regulator (LQR) to control the steering actuator of trailer, then the effectiveness of the controller is verified and analysed based on the Trucksim/Simulink joint simulation platform, and finally, the effectiveness of the proposed control strategy is verified when running on a real controller based on the semi-physical HiL test platform.
4.1. Active Trailer Steering Corner Allocation Strategy
When the tractor semitrailer is travelling at medium and high speeds, the yaw motion of the tractor semitrailer after increasing the active trailer steering system is shown in Figure 9.
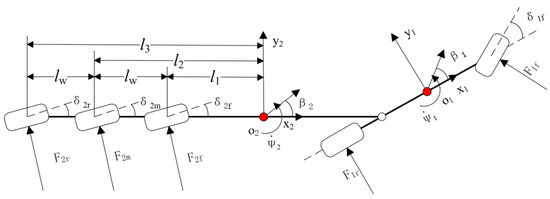
Figure 9.
Diagram of yaw motion for the tractor semitrailer with ATS.
When the active trailer steering system is added, the force on the trailer during steering is not the same as that of passive steering, the difference lies in the change of lateral force on the tyres during steering, which leads to the change in the sideslip angle of each of the trailer’s axles. The cornering angles of each of the trailer’s axles are named as δ2f, δ2m, and δ2r, and the sideslip angles of each axle of the tyres are α2f, α2m, and α2r, respectively, and the calculation method is shown in Equation (12).
where l1, l2, and l3 are the distances from the first, second, and third axles of the trailer to the centre of mass, respectively, as shown in Figure 9.
Due to the inclusion of the trailer corner, the state space equations of the simplified three-DOF yaw model of the tractor semitrailer in the previous section need to be slightly changed and written in the following form:
In this equation
The rest of the parameters are the same as those in the state space equations in the previous chapters. The three axles of the trailer are equivalent to one axle in the above equations, and the equation represents the response of the state of the tractor semitrailer at the time of steering the wheels on the front axle of the tractor and the equivalent axle of the trailer.
In order to further improve the control effect, it is necessary to allocate the three cornering angles of the trailer axle. The first thing to consider is the stability of the trailer when allocating the cornering angle of the tractor semitrailer in the state of medium- and high-speed driving. Therefore, in order to prevent a large gap between the lateral forces of each axle, which will have a negative effect on the lateral stability of the trailer, the axle cornering angles are allocated on the principle of equal lateral forces in each axle. Since the tyres used in each axle are of the same type, the condition of equal lateral force in each axle can be obtained by meeting the equal sideslip angle of each axle, i.e., as in the following:
In the simplified model of the tractor semitrailer, the three axles of the trailer part are simplified to one axle, and the equivalent axle is the middle axle of the trailer, so the cornering angle of the middle axle of the trailer is used as the reference to calculate the cornering angles of the front and rear axles of the trailer, as follows:
where lw is the wheelbase between the axles of the trailer.
4.2. Design of LQR-Based Cornering Controller
In this paper, the yaw rate and sideslip angle at the CG of the tractor and trailer are used as the indicators in the control strategy, and the yaw rate and sideslip angle at the CG have a very important influence on the path tracking effect and stability of the vehicles, so most of the previous studies chose them as the main control quantities. By incorporating both the tractor and trailer indicators into the control volume, more accurate tractor semitrailer vehicle status information can be provided than using only the two indicators of the tractor. The control strategy is to make the actual yaw rate reach the theoretical yaw rate, while minimising the difference in the sideslip angle at the CG. Usually the reference value is obtained from the theoretical vehicle model according to the steering wheel angle, and the specific strategy is shown in Figure 10. The tractor cornering angle can be obtained from the pre-scan control and used as an input to the system, the trailer cornering angle is then manipulated by the designed LQR controller, and enables the yaw rate and sideslip angle at the CG of the tractor and trailer to track the desired values.
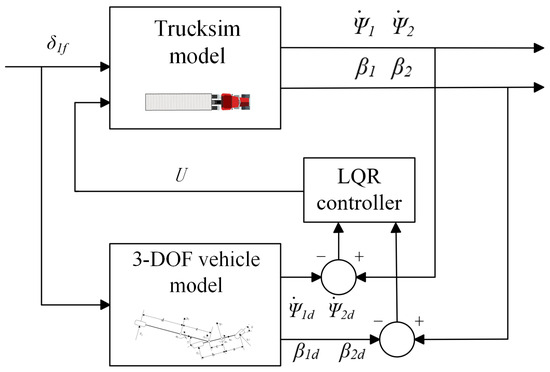
Figure 10.
Block diagram of control strategy.
The active trailer steering controller is designed based on a Linear Quadratic Regulator (LQR), according to the state equation described in the previous section as follows:
Thus, the desired state vector can be expressed as follows:
Assuming that the system behaves consistently with the desired state, in that case d = 0, and thus, the desired state can be obtained as follows:
The error vector can be obtained by combining the above equations as follows:
where e = X − Xd, u = δ2m.
The tractor and trailer yaw rate and sideslip angle at the CG are taken as the control objectives in the case of high-speed driving, and the following optimisation objective function is constructed:
In the formula, 1, β1, 2, β2 are the yaw rate and sideslip angle at the CG of the tractor and trailer, respectively; δ2m is the control input for the middle axle cornering angle of the trailer; and W1, W2, W3, W4, and W5 are the weighting factors corresponding to these metrics, respectively.
The above controller design was implemented in Matlab/Simulink, where the required optimal gain vector K was calculated by calling the function lqr in Matlab, so that the expression for the middle axle cornering angle of the trailer was obtained as follows:
where K is the optimal gain matrix, which is obtained from the Riccati equation, and the objective function can be written in the following form:
where Q = diag(W1, W2, W3, W4), R = W5
4.3. Construction of Joint Simulation Platform
In order to verify the designed control strategy and controller effect, it is necessary to build a joint Trucksim/Simulink simulation platform for the active trailer steering control of a tractor semitrailer, so that the corner controllers designed in Simulink can be applied to a five-axle tractor semitrailer in the Trucksim platform, and thus further simulation verification can be carried out.
Firstly, the 2A Cab-over/3A Trailer five-axle tractor semitrailer model constructed in Trucksim was imported into Simulink to generate the Trucksim S-Function file, which completes the output of the vehicle model required in the controller, including vehicle speed, vehicle location information, road information, and vehicle status parameters. These outputs are then processed and connected with the controller model to obtain the trailer axle cornering angles according to the designed control strategy. Finally, the obtained cornering angles of each axle of the trailer are inputted into the Trucksim vehicle model to complete the joint simulation study of the active trailer steering control of tractor semitrailer.
4.4. Simulation Results and Analysis
In order to verify the effectiveness of the proposed active trailer steering control strategy based on LQR, this was tested under a double lane change condition and compared with the traditional tractor semitrailer without active trailer steering control, where the test conditions of the traditional tractor semitrailer without active trailer steering control are called the baseline case, shown by dashed lines, and the test conditions of the tractor semitrailer with active trailer steering are called the ATS case, shown by solid lines. The double lane change condition refers to the condition with an initial speed of 60 km/h, a lateral offset of 3.5 m, and a pavement adhesion coefficient of 0.85.
The simulation results are shown in Figure 11, Figure 12, Figure 13, Figure 14, Figure 15, Figure 16, Figure 17 and Figure 18, and the specific parameter comparisons are shown in Table 3 and Table 4.
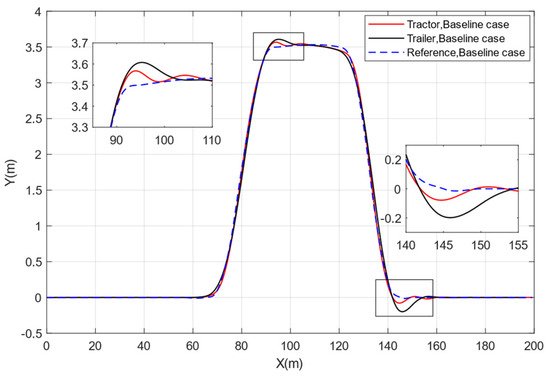
Figure 11.
The trajectories of the tractor and trailer in the baseline case.
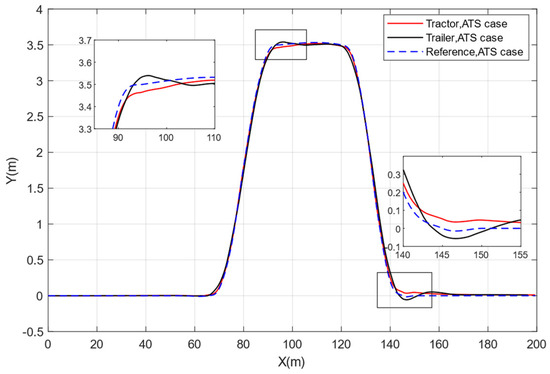
Figure 12.
The trajectories of the tractor and trailer in the ATS case.
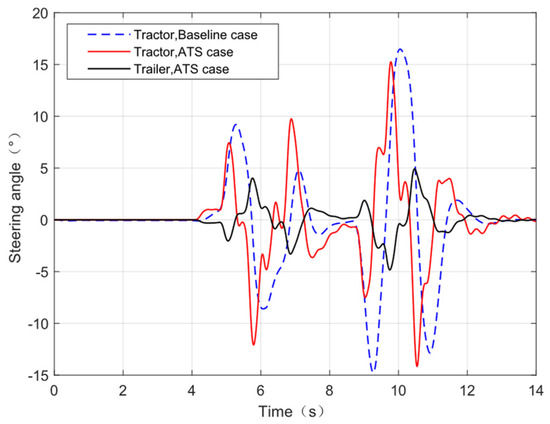
Figure 13.
Steering angle of tractor and trailer wheels.
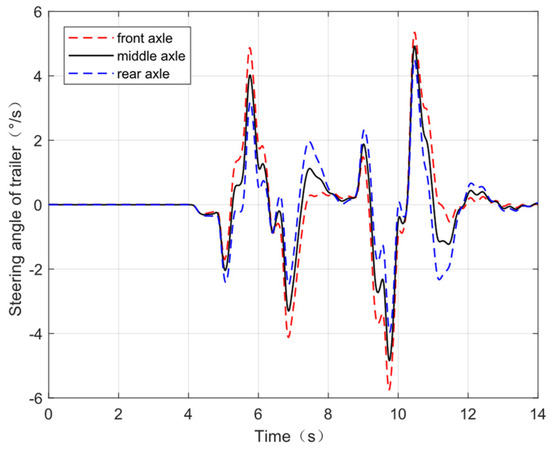
Figure 14.
Angle distribution of the trailer.
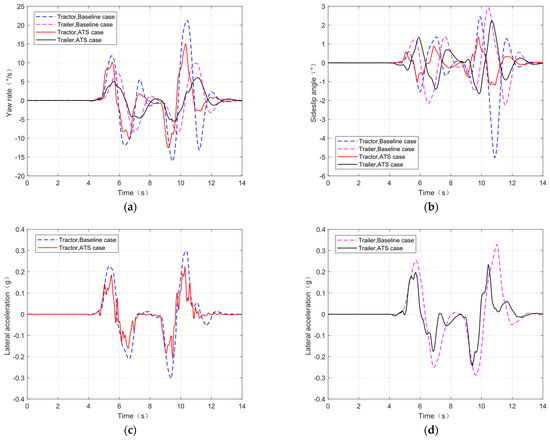
Figure 15.
Comparison of lateral stability indicators. (a) Yaw rate of tractor and trailer; (b) sideslip angle at the CG of the tractor and trailer; (c) lateral acceleration of the tractor; and (d) lateral acceleration of the trailer.
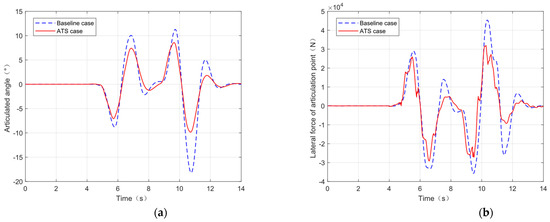
Figure 16.
Comparison of parameters related to the articulation point. (a) Articulated angle and (b) lateral force of articulation point.
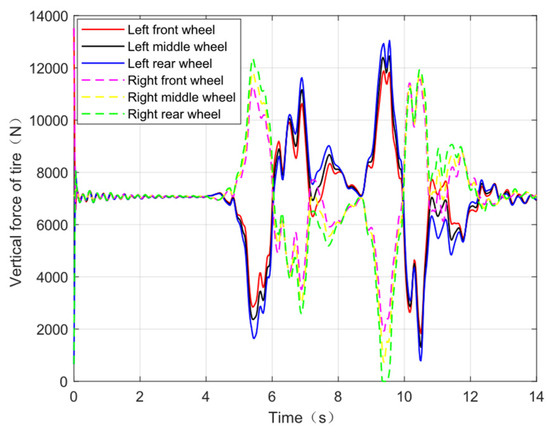
Figure 17.
Vertical force of trailer wheels in the baseline case.
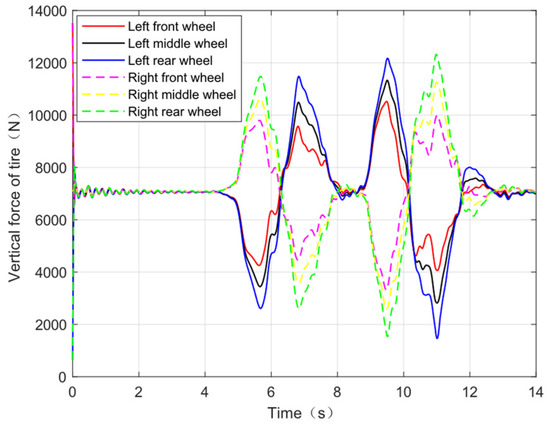
Figure 18.
Vertical force of trailer wheels in the ATS case.

Table 3.
Comparison of trailer trajectory deviation.

Table 4.
Comparison of simulation result.
Figure 11 shows the tractor and trailer trajectories of a traditional tractor semitrailer without active trailer steering control, and Figure 12 shows the tractor and trailer trajectories of a tractor semitrailer with active trailer steering. As can be seen from the figure, compared with the traditional tractor semitrailer, both the tractor and trailer sections of the tractor semitrailer with active trailer steering control can track the reference trajectory better. Compared to the uncontrolled results, the tractor part does not show any overshooting of the trajectory, while the overshooting of the trailer’s trajectory is significantly optimized, which means that the trailer part will have less encroachment on the lateral space of the roadway during lane change process. Combining Figure 11 and Figure 12 with Table 3, it can be seen that the maximum tracking deviation of the trailer was improved by 53.49% and 71.55%, respectively, at the two obvious overshooting phenomena.
Figure 13 shows a comparison between the tractor cornering angle of a traditional tractor semitrailer without active trailer steering and the trailer cornering angle and equivalent tractor cornering angle of a tractor semitrailer with active trailer steering. The tractor cornering angle of the tractor semitrailer with active trailer steering is relatively smaller, which is consistent with the travelling trajectory diagram, while the equivalent trailer cornering angle is smaller compared with the tractor cornering angle, and there is a certain time delay.
Figure 14 shows the distribution of trailer axle cornering angles for the tractor semitrailer with active trailer steering. The equivalent cornering angle is the trailer middle axle cornering angle, with the front axle cornering angle of the trailer being larger than the middle axle, and the rear axle cornering angle of the trailer being smaller than the middle axle.
Figure 15a shows the comparison between the tractor and trailer yaw rates for the two cases. The extreme values of the tractor and trailer yaw rates are improved by 29.05% and 34.04%, respectively. Figure 15b shows the comparison between the tractor and trailer sideslip angle at the CG for the two cases. The extreme values of the sideslip angle at CG for the tractor and trailer are improved by 72.29% and 19.32%, respectively. Figure 15c,d show the comparison of the lateral acceleration of the tractor and trailer for the two cases, and the extreme values of the lateral acceleration of the tractor and trailer are improved by 25.81%and 29.41%, respectively. Yaw rate, sideslip angle at the CG, and lateral acceleration have a significant effect on the stability of the vehicle; by carefully observing the pictures it can be seen that these parameters are well suppressed at each peak compared to the uncontrolled results, which indicate that the stability of the tractor and trailer of the tractor semitrailer with active trailer steering control was significantly improved.
Figure 16a shows the comparison of the variation in the articulated angle between the tractor and trailer in the two cases. From the figure, it can be seen that, compared with the traditional tractor semitrailer without active trailer steering, the articulated angle of the tractor semitrailer with active trailer steering is obviously smaller, and the maximal articulated angle is reduced by 45.56%, and the larger change of the articulated angle means that it is easier for accidents such as collapsing to occur [18]. Figure 16b shows the comparison of the lateral force at the articulation point between the tractor and the trailer in the two cases, the maximum lateral force is reduced by 30.66%, and the lateral force at the articulation point is significantly reduced, which means that in the process of changing lanes, the trailer will interfere less with the lateral force on the tractor, which is very important for the improvement of the lateral stability of the tractor semitrailer [19]. Meanwhile not only at the maximum values, but also at each peak, both parameters are significantly improved, meaning that stability problems caused by the articulation can be significantly optimized during lane change.
In addition, Figure 17 and Figure 18 show the distribution of vertical wheel forces on each axle of the trailer without active trailer steering and with active trailer steering, respectively. Load transfer LTR is often used to measure the stability of tractor semitrailers [20], and this is the ratio of the difference between the vertical load on the wheels on both sides to the sum of the vertical loads, as shown in Equation (23):
where Fli is the vertical load of the left wheel of the vehicle, Fri is the vertical load of the right wheel of the vehicle, and i and n are the relative positions of the axles and the total number of axles, respectively.
When the vehicle is travelling straight on a good road surface, the LTR is zero. When a rollover occurs, the LTR value is one because one side of the wheels is off the ground and loses the vertical load; therefore, the higher the LTR value is, the worse the lateral stability of the vehicle is [21], and it is easier to have a rollover accident. The maximum LTR value of the trailer section without active trailer steering is 0.86, while the maximum LTR value of the trailer section with active trailer steering is 0.62. The maximum LTR value of the trailer section with active trailer steering is significantly reduced, which indicates that the stability of the trailer section is significantly improved [22]. Meanwhile, in Figure 17, the right rear axle wheel of the trailer without active trailer steering showed a vertical load of zero from 9.3 s to 9.5 s, which means that the wheel was already off the ground at that time, indicating that the lateral stability of the vehicle was poor. Also, a comparison of the two figures on a macroscopic scale shows that the range of variation in the trailer wheel vertical force is smaller in the ATS case, which means that the average load transfer is also smaller, and therefore, the stability of the vehicle is better.
4.5. Semi-Physical HiL Testbed-Based Validation
In order to verify the feasibility and effectiveness of the proposed active trailer steering control strategy under medium-/high-speed conditions when running on a real controller, a semi-physical hardware-in-loop testbed for a tractor semitrailer was constructed based on the HiL test system, and then the proposed control strategy was verified based on the constructed testbed.
Figure 19 shows the architecture of the semi-physical HiL testbed, which mainly contains the host computer, D2P rapid prototype, HiL cabinet, and actuator parts.
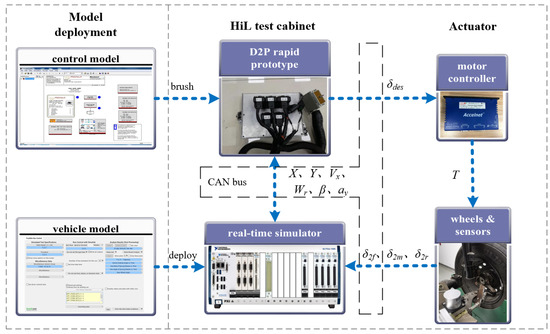
Figure 19.
Structure of the semi-physical HiL test platform.
The construction of the semi-physical HiL test platform follows the following process: firstly, build the vehicle model and the active trailer steering control strategy, respectively; then use VeriStand software to deploy the vehicle model into the real-time simulator, and at the same time, use MotoTune software to brush the control strategy model into the D2P rapid prototype; and finally, use VeriStand software to configure CAN communication and analogue inputs and outputs between the modules to complete the closed-loop communication within the test system.
In order to verify the effectiveness of the proposed active trailer steering control strategy, the double lane change condition was selected for testing, in which the initial speed was 60 km/h, the lateral offset was 3.5 m, and the roadway adhesion coefficient was 0.85. The test results are shown in Figure 20, and the detailed result comparisons are shown in Table 5.
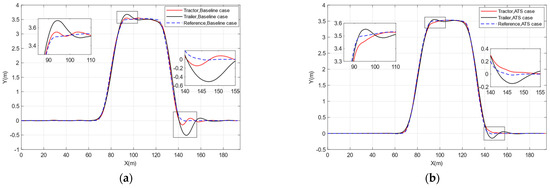

Figure 20.
Test result of active trailer steering control under semi-physical HiL platform. (a) The trajectories of the tractor and trailer in the baseline case. (b) The trajectories of the tractor and trailer in the ATS case. (c) Angle distribution of the trailer. (d) Yaw rate of tractor and trailer. (e) Sideslip angle at the CG of the tractor and trailer. (f) Lateral acceleration of the tractor and trailer.

Table 5.
Comparison of test results.
As shown in the figure, in the semi-physical hardware-in-loop test, although there are fluctuations in some parameters, the trailer part of the tractor semitrailer with active trailer steering control is still able to have better tracking accuracy, and at the same time, the lateral stability of the tractor semitrailer is also improved. Combined with the table data, it can be seen that the maximum tracking deviation of the trailer is improved by 70.58%, the maximum yaw rate of the tractor and trailer are reduced by 22.13% and 10.84%, respectively, the maximum sideslip angle at CG of the tractor and trailer are reduced by 65.56% and 35.03%, respectively, and the maximum lateral acceleration of the tractor and trailer are reduced by 22.22% and 22.85%, respectively. In summary, the active trailer steering control strategy under the medium-/high-speed conditions in this paper has an obvious effect on the improvement of vehicle stability, and at the same time, the tracking effect of the trailer part is also optimized.
5. Conclusions
In this paper, an active trailer steering control strategy under medium- and high-speed test conditions is proposed. Firstly, a simplified model of a tractor semitrailer was constructed and a MAP diagram was formed based on a genetic algorithm to identify the key parameters, which improves the accuracy of the model, and then an active trailer steering control strategy was given and a cornering controller based on LQR was designed in order to control the steering actuator of the trailer. Finally, the effectiveness of the designed controller was verified by a double lane change simulation based on the Trucksim/Simulink joint simulation platform. The simulation results show that the designed controller can effectively improve the path tracking effect of the tractor and trailer of a tractor semitrailer, especially the trailer, whose maximum tracking deviation was improved by 70.58%. Meanwhile, the lateral stability parameters of the tractor and trailer were also significantly improved; for example, the maximum values of the tractor and trailer sideslip angle were improved by 65.56% and 35.03%, thus improving the driving stability of the tractor semitrailer. In addition, due to the limitations of time and conditions, there are still many aspects in this paper that can be improved and studied in depth; for example, the weight coefficients of the controller in this paper are manually adjusted through repeated simulation, which is a large amount of work and may not be able to obtain the best control effect, and the optimization algorithms can be considered to be applied to the selection of weight coefficients in future research, in order to obtain a better control effect.
Author Contributions
Conceptualization, Y.T. and Y.C.; methodology, Y.T.; software, Y.T.; validation, Y.T.; formal analysis, Y.T.; investigation, Y.T.; resources, Y.T. and Y.C.; data curation, Y.T.; writing—original draft preparation, Y.T.; writing—review and editing, Y.T.; visualization, Y.T.; supervision, Y.C., Z.L., X.S., L.C., H.W. and Z.D.; project administration, Y.C.; funding acquisition, Y.C. All authors have read and agreed to the published version of the manuscript.
Funding
This work has been supported by the National Natural Science Foundation of China (52225212, 52272418, U22A20100), the National Key Research and Development Program of China (2022YFB2503302).
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wei, C.; Liang, Q.; Chen, Z.; Xue, G. Study On High Speed Driving Stability of Tractor-Semitrailer. In Proceedings of the 5th International Conference on Advanced Design and Manufacturing Engineering, Shenzhen, China, 19–20 September 2015; pp. 1681–1685. [Google Scholar]
- Xu, X.; Chen, D.; Zhang, L.; Chen, N. Hopf bifurcation characteristics of the vehicle with rear axle compliance steering. Shock Vib. 2019, 2019, 3402084. [Google Scholar] [CrossRef]
- Zhang, H.; Ren, Z.-K.; Zhang, H.-W.; Ou, C.-J. Research on lateral stability of double semitrailer road train. In Proceedings of the International Symposium for Intelligent Transportation and Smart City (ITASC) 2017 Proceedings: Branch of ISADS (The International Symposium on Autonomous Decentralized Systems) 3; Springer: Singapore, 2017; pp. 83–89. [Google Scholar]
- Kamnik, R.; Boettiger, F.; Hunt, K. Roll dynamics and lateral load transfer estimation in articulated heavy freight vehicles. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2003, 217, 985–997. [Google Scholar] [CrossRef]
- Dal Poggetto, V.F.; Serpa, A.L. Vehicle rollover avoidance by application of gain-scheduled LQR controllers using state observers. Veh. Syst. Dyn. 2016, 54, 191–209. [Google Scholar] [CrossRef]
- Kati, M.S.; Fredriksson, J.; Jacobson, B.; Laine, L. Design of a robust load-dependent steering controller for improved high capacity vehicle safety. In Proceedings of the 2021 IEEE International Intelligent Transportation Systems Conference (ITSC), Indianapolis, IN, USA, 19–22 September 2021; pp. 298–303. [Google Scholar]
- Wang, Q.; He, Y. A study on single lane-change manoeuvres for determining rearward amplification of multi-trailer articulated heavy vehicles with active trailer steering systems. Veh. Syst. Dyn. 2016, 54, 102–123. [Google Scholar] [CrossRef]
- Jujnovich, B.; Cebon, D. Comparative performance of semi-trailer steering systems. In Proceedings of the 7th International Symposium on Heavy Vehicle Weights and Dimensions, Delft, The Netherlands, 16–20 June 2002; pp. 195–214. [Google Scholar]
- Nie, Z.-G.; Wang, W.Q.; Wang, C.; Zong, Z.-F. Integrated control strategy of articulated heavy vehicle based on timely mode switching under medium/high speed conditions. Jiao Tong Yun Shu Gong Cheng Xue Bao 2017, 17, 135–149. [Google Scholar]
- Kural, K.; Hatzidimitris, P.; van de Wouw, N.; Besselink, I.; Nijmeijer, H. Active trailer steering control for high-capacity vehicle combinations. IEEE Trans. Intell. Veh. 2017, 2, 251–265. [Google Scholar] [CrossRef]
- Kim, K.-I.; Guan, H.; Wang, B.; Guo, R.; Liang, F. Active steering control strategy for articulated vehicles. Front. Inf. Technol. Electron. Eng. 2016, 17, 576–586. [Google Scholar] [CrossRef]
- Ding, X.; He, Y.; Ren, J.; Sun, T. A comparative study of control algorithms for active trailer steering systems of articulated heavy vehicles. In Proceedings of the 2012 American Control Conference (ACC), Montreal, QC, Canada, 27–29 June 2012; pp. 3617–3622. [Google Scholar]
- Nie, Z.; Zong, C.; Wan, Y. Mass Estimation and Axle Load Distribution Algorithm for EBS of Large Bus; 0148-7191; SAE Technical Paper; SAE: Warrendale, PA, USA, 2013. [Google Scholar] [CrossRef]
- Zhang, P.; He, L.; Liu, X.T.; Xia, Q.S. Study on the Dynamic Characteristics of Automobile Tire. Adv. Mater. Res. 2013, 655, 558–561. [Google Scholar] [CrossRef]
- Qureshi, K.; Liscano, R.; He, Y. Optimization of Gain Scheduled Controller for an Active Trailer Steering System Using an Evolutionary Algorithm. Machines 2022, 10, 1019. [Google Scholar] [CrossRef]
- Li, J.; Li, L. An improvement proposal of genetic algorithms based on information entropy and game theory. In Proceedings of the 2019 Sixth International Conference on Social Networks Analysis, Management and Security (SNAMS), Granada, Spain, 22–25 October 2019; pp. 36–43. [Google Scholar]
- Bai, F.; Guo, K.H.; Zhang, B.J.; Lu, D. Analysis of tire cornering stiffness property under slight driving or braking condition. Appl. Mech. Mater. 2013, 271, 767–772. [Google Scholar] [CrossRef]
- Lee, S.-H.; Park, T.-W.; Moon, K.-H.; Choi, S.-H.; Jun, K.-J. The articulated vehicle dynamic analysis using the AWS (All Wheel Steering) ECU (Electronic Control Unit) test. J. Mech. Sci. Technol. 2009, 23, 923–926. [Google Scholar] [CrossRef]
- Salati, L.; Cheli, F.; Schito, P. Heavy truck drag reduction obtained from devices installed on the trailer. SAE Int. J. Commer. Veh. 2015, 8, 747–760. [Google Scholar] [CrossRef]
- Fu, Z.-C.; Gong, A.-H.; Liao, Z.-W.; Hu, M.-M.; Yu, H.-D. Anti-rollover control of heavy-duty dump truck with distributed model predictive control. Int. J. Heavy Veh. Syst. 2023, 30, 139–166. [Google Scholar] [CrossRef]
- Liu, Q.; Gao, C.; Wang, H.; Cai, Y.; Chen, L.; Lv, C. Learning from Trajectories: How Heterogeneous CACC Platoons Affect the Traffic Flow in Highway Merging Area. IEEE Trans. Veh. Technol. 2024, 1–13. [Google Scholar] [CrossRef]
- Liu, Q.; Gao, F.; Zhao, J.; Cai, Y.; Chen, L.; Lv, C. Real-Time LNG Buses Emissions Prediction Based on a Temporal Fusion Trans-Formers Model. J. Environ. Inform. 2024, 44, 17. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).