Abstract
This study explores the integration of dynamic vehicle trajectories, vehicle safety factors, static traffic environments, and actuator constraints to improve cooperative intent modeling for autonomous vehicles (AVs) navigating uncertain traffic scenarios. Existing models often focus solely on interactions between dynamic trajectories, limiting their ability to fully interpret the intentions of surrounding vehicles. To address this limitation, we present a more comprehensive approach using the Cooperative Intent Multi-Layer Graph Neural Network (CMGNN) model. The CMGNN analyzes not only the dynamic trajectories but also the lane position relationships, vehicle angle changes, and actuator constraints and performs group interaction analysis. This richer information allows the CMGNN to more accurately capture the cooperative intent and better understand the surrounding vehicle behavior. This study investigated the impact of the CMGNN in the Carla simulator on surrounding vehicle trajectory prediction and AV safe trajectory planning. An innovative mechanism for dynamic trajectory risk assessment is introduced, which takes into account the constraints of the actuators when evaluating trajectory planning metrics. The results show that incorporating cooperative intent and considering the actuator limitations enhanced the CMGNN’s safety and driving efficiency in uncertain scenarios, significantly reducing the probability of AVs colliding. This is achieved as the model dynamically adapts its driving strategy based on the real-time traffic conditions, the perceived intentions of the surrounding vehicles, and the physical constraints of the vehicle actuators.
1. Introduction
The recent advances in autonomous vehicle technology hold great promise in terms of improving traffic safety and efficiency [1]. By integrating predicted behavior and understanding intent [2,3,4], autonomous vehicles can prevent collisions, optimize lane changes, and maintain a smooth traffic flow [5]. This approach not only mitigates the risk of accidents but also enhances the overall traffic flow [6,7,8,9]. While rule-based trajectory planning excels in controlled environments with minimal variation, it struggles to respond to the complexities and uncertainties of real-world traffic [10,11]. Data-driven methods offer a more robust solution [12]. By learning from historical data on vehicle interactions and dynamic trajectories, these methods achieve impressive results in predicting the behavior of surrounding vehicles and planning safe paths for the autonomous car itself [13,14]. Researchers are further enhancing these models by incorporating information about the static elements of the traffic scene [15], such as lane markings and traffic signs, to improve their overall situational awareness [16]. This combined approach holds great promise for the future of autonomous vehicles, navigating the intricate domain of traffic with ever-increasing accuracy and safety [17,18].
The existing autonomous vehicle models frequently treat trajectory interaction and static map information as distinct components, integrating them at a later stage [19]. This approach overlooks the crucial element of dynamic changes in cooperative intent due to varying traffic conditions and safety factors [20]. Recent works have also emphasized the importance of controlling the motion duration in trajectory planning to enhance the precision and safety of autonomous vehicles. A new trajectory planning approach with motion duration control has been proposed to address these issues [21]. Additionally, time-optimal trajectories for car-like vehicles have been explored to improve their efficiency and safety in dynamic environments [22].
To address the above limitations, we propose a novel approach that incorporates driving intentions, represented by vehicle angle changes and lane position relationships, into the analysis of dynamic vehicle trajectories. This enables a greater understanding of the cooperative intent between the surrounding vehicles and the self-driving car. Our contributions are threefold.
- (1)
- Multi-Level Cooperative Intent Modeling
The Cooperative Intent Multi-Layer Graph Neural Network (CMGNN) captures the dynamic intentions of the surrounding vehicles by conducting a thorough analysis of their behavior. It moves beyond mere trajectories by examining both lane position relationships and angle changes. This allows the CMGNN to segment vehicles into sub-groups based on their interactions, providing a richer context for intention recognition. Additionally, the network leverages an attention mechanism alongside the trajectory-based relationships between vehicles to effectively share information across different levels. This multi-layered approach enables the CMGNN to capture cooperative intent with greater nuance and accuracy.
- (2)
- Actuator-Feasible Dynamic Trajectory Risk Assessment
This study introduces a novel mechanism for dynamic trajectory risk assessment in autonomous vehicles that considers the constraints imposed by the actuators. Traditional approaches often overlook these real-world limitations, potentially leading to unsafe or infeasible trajectories. By integrating the actuator dynamics into the risk assessment process, the model generates trajectories that are not only low risk but also achievable considering the vehicle’s physical capabilities. The proposed approach dynamically assigns weights to safety indicators while accounting for the response time; maximum force/torque output; and nonlinear behaviors of the steering, throttle, and braking systems. This enables a more comprehensive and realistic evaluation of the potential trajectories. The model dynamically adjusts these weights based on the current state of the actuators and the prevailing traffic conditions. Consequently, it can identify and prioritize trajectories that strike a balance between safety and feasibility, guiding the vehicle towards paths that are both low risk and executable.
- (3)
- Improved Trajectory Planning and Reduced Collisions
The experimental results reveal that the incorporation of cooperative intent through the CMGNN leads to a significant improvement in the accuracy of surrounding vehicles’ trajectory prediction. This improved prediction capability translates into a reduced likelihood of collision during the autonomous vehicle’s own trajectory planning. This advantage is especially apparent in complex scenarios, such as turns and intersections, where precise interaction with other vehicles is of the utmost importance. By dynamically adapting its driving strategy based on the real-time traffic conditions and the perceived intentions of surrounding vehicles, the CMGNN navigates these situations with enhanced safety and efficiency.
2. Autonomous Vehicle Trajectory Planning Model Considering Cooperative Intent
This section explores the challenges associated with trajectory planning for autonomous vehicles (AVs) operating in dynamic traffic environments populated by surrounding vehicles. A crucial aspect of this challenge is determining how to better model vehicle interactions. To address these challenges, this section proposes a novel AV trajectory planning approach that captures the cooperative intent of surrounding vehicles by considering vehicle angle changes and lane position relationships.
2.1. Autonomous Vehicle (AV) Trajectory Planning Problem Description
Under the predefined mission objectives, the trajectory planning model of the AV needs to consider both its own motion state and the surrounding driving environment to generate an executable path. The environment can be divided into static elements, such as traffic lights, road boundaries, and lane markings, and dynamic elements, consisting of surrounding vehicles. Comprehending the dynamic environment, particularly the behavior of surrounding drivers, presents the greatest challenge. Therefore, the traffic scenario consisting of AVs and surrounding vehicles is modeled as a discrete-time system operating in a continuous space [23].
The trajectory of the autonomous vehicle at time is expressed as , and the trajectory of social vehicle at time is expressed as . The goal of the trajectory planning model is to learn a function that can generate the future trajectory of the autonomous vehicle and plan the trajectory of the autonomous vehicle at time according to the historical dynamic environment , composed of the historical trajectory of the autonomous vehicle at the previous time step and the historical trajectory of the surrounding social vehicle:
2.2. Model Framework
This section introduces a novel model for safe trajectory planning in autonomous vehicles (AVs), as depicted in Figure 1. The model tackles the challenge of navigating uncertain traffic environments by taking into account several crucial factors. First, it categorizes the surrounding vehicles based on their lane positions relative to the AV. Then, it utilizes a multi-layer graph neural network (GNN) to analyze the historical trajectories and angle changes for these vehicle groups. By constructing multi-level node relationships and employing a multi-head attention mechanism, the GNN aggregates node information to create comprehensive features. These features are then used to predict the future trajectories of the surrounding vehicles, which are subsequently encoded as “future trajectory features”. Next, the model incorporates a dynamic risk representation mechanism that is combined with the future trajectory features. This combined information is then decoded into a representation of the future traffic environment. Finally, the dynamic risk characterization mechanism guides the future traffic environment’s characterization to ensure safe trajectory planning for the AV.
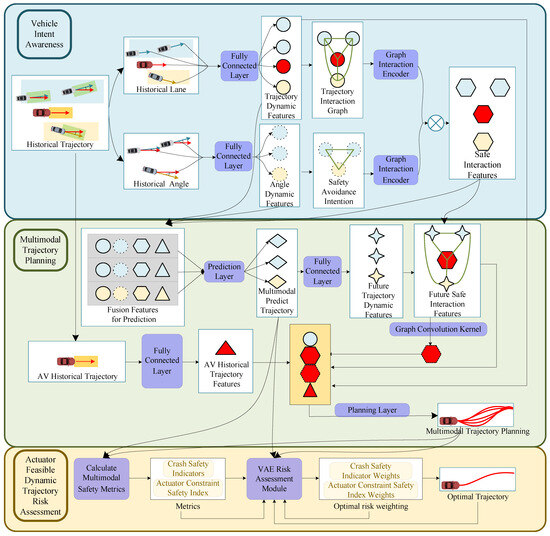
Figure 1.
A trajectory planning model for autonomous vehicles based on the cooperative intent of surrounding vehicles.
The dynamic risk representation mechanism plays a crucial role in the trajectory planning model. It is designed to capture the potential risks associated with the predicted future trajectories of the surrounding vehicles. The mechanism takes into account various factors, such as the relative distances between the vehicles, their velocities, and the likelihood of collisions. By incorporating these risk factors, the model can generate a comprehensive risk representation that encodes the inherent uncertainties and potential dangers in the future traffic environment. This risk representation is then integrated with the future trajectory features obtained from the GNN. The integration process involves concatenating the risk representation with the trajectory features and passing them through a series of fully connected layers. This allows the model to learn the complex interactions between the predicted trajectories and their associated risks. The resulting combined representation provides a rich and informative input for the subsequent decoding stage, where the model performs the characterization of the future traffic environment, which includes both the predicted trajectories and their corresponding risk levels. This integrated approach enables the model to make more informed decisions during the trajectory planning process, as it can explicitly consider the potential risks associated with different future scenarios.
2.2.1. Cooperative Intent Reasoning and Cooperation Area Interaction
Comprehending the surrounding traffic environment is essential for the safe and efficient navigation of autonomous vehicles (AVs). This research proposes a novel two-layer network that addresses the limitations of traditional global modeling approaches [24]. The first layer prioritizes pertinent vehicles for analysis by grouping the surrounding vehicles based on their lane positions and historical trajectories. Vehicles in closer proximity to the AV’s lane or directly influencing its trajectory are given greater attention. This approach is based on the premise that vehicles in different lanes have diverse purposes and adhere to different traffic rules. The network then models the “interaction features” by grouping the vehicles based on these factors. The second layer focuses on deciphering a vehicle’s intention to cooperate or maneuver by examining its angle changes (i.e., whether it increases, decreases, or remains stable). This layer predicts the vehicle’s potential actions, such as turning, changing lanes, or merging. Furthermore, it interprets its cooperative intent based on abrupt or rapid angle changes. For example, a sharp increase might indicate that the vehicle is actively avoiding a collision. Subsequently, a multi-head attention mechanism integrates the “interaction features” from the first layer with the “intention features” from the second layer. This integrated analysis enables the model to capture the underlying cooperative intent of surrounding vehicles. This two-tier approach offers significant advantages. In contrast to global models, this approach develops a more nuanced understanding by taking into account cooperative intent and regional interactions. Moreover, focusing on relevant vehicles enhances its efficiency. Essentially, this innovative network structure empowers AVs to perceive their surroundings more effectively, resulting in safer navigation.
Traditional self-driving car approaches depend on “global modeling” to perceive their surroundings. This method examines the interactions between all traffic participants, assigning equal importance to each vehicle. However, in practice, not all vehicles significantly impact the self-driving car. Factors such as the relative safety between vehicles and the lane positioning influence their interactions. Vehicles form dynamic groups based on these factors, resulting in intra-group and inter-group interactions that reflect varying levels of cooperation. Traditional global modeling struggles to capture the dynamic nature of cooperative intent. The following sections investigate alternative approaches to address this limitation.
To address the limitations of the current collaborative intent modeling, in this work, autonomous vehicles (AVs) employed a regional interaction network constructed using graph neural networks. This network analyzes the cooperative intent of the surrounding vehicles within specific zones relative to the AV’s lane position (left, right, and front). By combining the left and right zones with the front, the model simplifies the cooperative areas as “left” and “right”. These zones, depicted by a regional interaction diagram, become the focus of interaction. Vehicles are represented as nodes connected by edges, enabling the AV to learn “social norms” for collision avoidance within these zones, while still considering broader cooperative goals. This regional approach, coupled with the understanding of the interactions facilitated by the graph, enhances the model’s sensitivity to the AV’s location, ultimately leading to more flexible collaboration between the AV and the surrounding vehicles. The surrounding vehicles can anticipate the AV’s movements and adjust their behavior accordingly, promoting safer navigation in unpredictable traffic scenarios.
As shown in the cooperative intent interaction diagram in Figure 2, the cooperative intent caused by the existence of autonomous vehicles produces a nonequal global interaction, and the original global modeling method has difficulty in modeling this new interaction mode. As the driving angles of the surrounding vehicles are significantly changed at times of cooperation, considering the difference in the movement angle of autonomous vehicle and the surrounding vehicles , the historical trajectory of the autonomous vehicle, the historical trajectories of the surrounding vehicles , and the output are taken as the characteristics of cooperative intent in the time period .
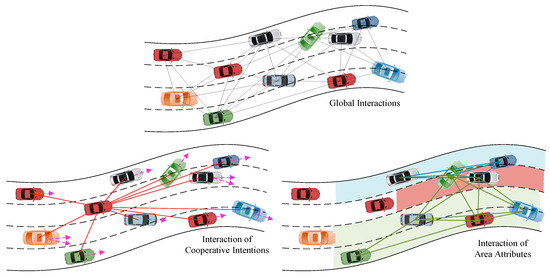
Figure 2.
Interactions between different categories.
The area interaction diagram is defined, which is composed of the vehicle node and the edge between the nodes in a cooperation area.
2.2.2. Cooperative Intent Inference and Cooperative Area Interaction
Deep graph neural networks (GNNs), employed in autonomous vehicles (AVs), encounter a challenge known as over-smoothing. While adding layers increases an AV’s “awareness” of the surrounding vehicles, it can cause all vehicles to appear highly similar, hindering their differentiation.
This approach offers a two-part solution. Drawing inspiration from PairNorm, the model promotes similar representations for directly connected vehicles within the traffic graph, effectively capturing local relationships. To mitigate the over-smoothing caused by distant vehicles, the graph is partitioned into “cooperative regions” based on traffic rules (e.g., left/right lanes). This approach directs the GNN’s attention to the immediate neighborhood during information gathering, thereby diminishing the influence of distant vehicles. Within each region, a “cooperative intention” feature is employed to enhance the information density for each vehicle. This captures the one-to-one cooperative intent between the surrounding vehicles and the AV. Essentially, this approach promotes differentiation between non-adjacent vehicles based on their willingness to cooperate with the AV. This allows the GNN to capture the nuances of the traffic flow involving AVs while avoiding the problem of over-smoothing in deep networks.
The Cooperative Intent Multi-Layer Graph Neural Network (CMGNN) utilizes a two-layer architecture. The first layer consists of a graph convolutional network (GCN) with 64 neurons, which processes the historical trajectories and lane position relationships of the vehicles. The second layer employs a gated recurrent unit (GRU) with 128 hidden units to capture the temporal dependencies in the vehicle angle changes. The outputs from both layers are then fused using a multi-head attention mechanism with four attention heads, each with a dimensionality of 32. This allows the model to weigh the importance of different features and interactions.
The CMGNN model is trained using the Adam optimizer with a learning rate of 0.001 and a batch size of 64. We employed the cross-entropy loss function for the trajectory prediction task and an additional regularization term to encourage the model to learn meaningful information about the cooperative intent. The model was trained for 100 epochs on a dataset collected from real-world traffic scenarios, with 80% used for training and 20% for validation. Early stopping is applied to prevent overfitting.
2.3. Feasible Dynamic Trajectory Risk Characterization Mechanism for Actuator
Conventional self-driving car systems depend on a two-step process involving traffic prediction, route generation, and subsequent risk assessment. However, this approach can suffer from the accumulation of errors and limitations imposed by pre-defined risk criteria that do not account for the physical constraints of the vehicle’s actuators. The proposed mechanism tackles these limitations by directly incorporating the actuator dynamics into the risk assessment process through the use of unsupervised learning techniques, such as variational autoencoders (VAEs).
As shown in Figure 3, the VAE-based approach allows the system to learn directly from the data, eliminating the need to explicitly define target weights. The network learns to compress and reconstruct the input data, revealing the underlying relationships between the vehicle’s state, its surroundings, and the actuator constraints. This empowers the system to adapt to diverse situations and generate more robust and efficient routes that are both safe and feasible. By considering factors such as the proximity to other vehicles, their relative speeds, and the limitations of the vehicle’s actuators, the risk assessment becomes more dynamic and comprehensive. Instead of relying on rigid rules, the model identifies inherent risk factors and uses them to generate safe and efficient routes that respect the physical capabilities of the vehicle. This integrated approach to risk assessment and trajectory planning enables the autonomous vehicle to navigate complex traffic scenarios with greater safety and efficiency.
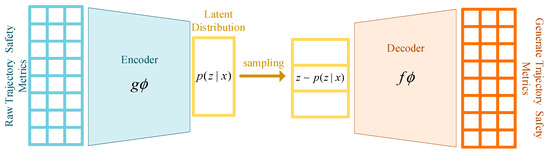
Figure 3.
Diagram of the adaptive VAE encoder model.
Therefore, according to the vehicle ’s operating state and the actuator constraint at a certain time , the actuator’s feasible risk at the current time is calculated.
where represents the maximum steering angle, maximum acceleration (throttle), and maximum curvature among the actuator constraints of vehicle . represents the actual steering angle, acceleration, and curvature of vehicle at time .
Then, considering the speed, acceleration, risk value, actuator constraints, and hysteresis of the autonomous vehicle, the interaction between the group trajectory and the risk is constructed. The risk characteristics of each trajectory are summarized into the same feature space through the safety filter layer. The risk value time series composed of the trajectory time series of a vehicle at time and the time step, the speed time series , the acceleration time series , and the actuator’s feasible risk are input into the model and characterized as the risk interaction characteristics of the current time ,
represents the graph attention neural network layer, which obtains the final risk feature through the security filter layer of the risk interaction relationship feature ,
where is a cumulative distribution function of the standard normal distribution. By modeling the interactive relationship between the trajectory and risk while considering the actuator constraints, the static risk value at a certain point in time is transformed into a dynamic risk representation with time series characteristics. The model captures not only the risk but also the relationship between the risk, trajectory, and actuator constraints. It considers how a vehicle’s changing risk value, based on its actuator dynamics, can impact the trajectory planning of the surrounding vehicles. The proposed approach assigns dynamic weights to safety indicators while taking into account the response time, maximum force/torque output, and nonlinear behaviors of the steering, throttle, and braking systems. This allows for a more comprehensive and realistic analysis of the potential trajectories. The model adjusts these weights in real time based on the current state of the actuators and the surrounding traffic conditions. The benefits are threefold. First, the model provides a holistic view by considering the interplay between the risk, trajectory, and actuator constraints. Second, it enables the AV to anticipate how its own actuator-constrained risk will impact others’ trajectory planning. Third, by incorporating feasible actuator dynamics, the model generates trajectories that are not only low risk but also executable given the vehicle’s physical capabilities. In essence, this method creates a dynamic, interconnected understanding of risk and trajectory planning that respects the AV’s actuator limitations. The static risk value is transformed into an actuator-aware, dynamic risk representation. This leads to safer, more adaptable, and physically realistic navigation for AVs in complex traffic scenarios, with the risk and actuator information continuously integrated into the trajectory planning process.
This system takes a smarter approach to planning a car’s path by combining risk assessment and route selection. It considers factors such as safety, comfort, and efficiency to select the best option from the start. Unlike traditional systems that plan a route and then check its safety, this approach optimizes all aspects together. The system also takes into account real-time conditions such as traffic, the weather, and the car’s handling, including the constraints and lags of the actuators. This allows it to make informed decisions for each situation, leading to safer and more suitable paths that respect the vehicle’s physical limitations. If the initial plan does not meet the safety standards or efficiency goals, the system can refine it based on the risk assessment feedback, ensuring that the final route is both safe and optimized within the capabilities of the vehicle’s actuators.
3. Experimental Setup
3.1. Data Set
Evaluating the self-driving capabilities of vehicles (AVs) in real-world traffic is challenging and expensive due to data collection difficulties. To address this issue, this study utilized a simulated traffic environment built using the OpenCDA platform (v 0.1), which combines the Carla (v0.9.12) and SUMO software (v1.11.0). As shown in Figure 4, this simulated environment allows the performance of the AV agent to be tested in diverse urban traffic scenarios, including both three-lane and four-lane roads. Driving in traffic congestion, performing unprotected turns at intersections, and navigating forked or merged roads are some of the preset route navigation tasks designed to challenge the agents. The simulation leverages the OpenCDA base algorithm while adding hierarchical avoidance logic for the surrounding vehicles. This logic considers factors such as the distance, speed, and relative position on the road. The traffic flow is controlled by SUMO and visualized in Carla for testing, and the data are synchronized between the platforms for a comprehensive evaluation. This well-designed simulation environment allows researchers to assess the self-driving capabilities of AVs in various challenging scenarios, without the limitations of real-world data collection.
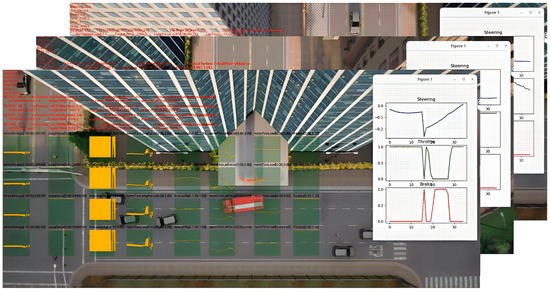
Figure 4.
Uncertain traffic scenarios for building of autonomous vehicles.
3.2. Trajectory Prediction Evaluation Metrics
The performance of trajectory prediction systems for autonomous vehicles, especially when designed to mimic human driving behavior, is evaluated using two key metrics: the final displacement error (FDE) and the average displacement error (ADE). The FDE captures the average difference between the planned and actual end points of a vehicle’s journey, reflecting the accuracy in reaching the destination. Finally, the ADE measures the average distance between the planned trajectory and the actual path throughout the trip, indicating how closely the vehicle follows the planned route. By considering these metrics, researchers can evaluate the system’s ability to be situationally aware of the traffic and predict the trajectories of surrounding vehicles. In this study, the model not only responds to the predictions of the surrounding vehicle trajectories with high confidence and accuracy but also considers predictions with low confidence and accuracy.
3.3. Trajectory Planning Evaluation Metrics
In trajectory planning with regard to autonomous vehicles, various evaluation indicators are used to assess the safety, comfort, and smoothness of the generated trajectories.
3.3.1. Safety Indicators of Ego Vehicle and Surrounding Vehicles
- Collision Time (TTC)
This metric measures the remaining time before a potential collision between the ego vehicle and another object, assuming constant speeds and positions. A higher TTC signifies a safer situation.
- Minimum Distance
This metric quantifies the closest proximity between the ego vehicle and surrounding objects during the planned path’s execution. A larger minimum distance indicates a safer trajectory with a greater buffer zone.
3.3.2. Feasible Risk of Ego Vehicle Actuator
- Curvature
This metric measures how quickly the trajectory’s direction changes relative to the distance traveled. Lower curvature indicates a smoother path, which is desirable for passenger comfort and vehicle stability.
- Acceleration
This metric evaluates the magnitude and rate of change in acceleration along the planned trajectory. Rapid changes can cause passenger discomfort.
- Lateral Agitation (LA)
This metric measures the acceleration perpendicular to the direction of travel, which is especially relevant during turns and lane changes. Excessive values can lead to discomfort or instability.
3.4. Comparison with Baseline Model
Several recent trajectory planning methods exist, each with their own strengths.
- IR-STP [25]
Pre-sets interaction relationship rules and utilizes a prediction-based framework to explicitly simulate interactions between vehicles.
- LAM [26]
Utilizes transformer-based models to encode driving scenarios and considers the planned trajectories of autonomous vehicles during prediction.
The Collaborative Multi-Layer Graph Neural Network (CMGNN) model proposed in this study excels by continuously integrating dynamic risk representation throughout the planning process. This focus on dynamic risks enables the model to achieve safer and more adaptable navigation for autonomous vehicles in complex traffic situations [27].
3.5. Experimental Details
To plan safe trajectories in uncertain traffic scenarios, the simulation environment employs a specific prediction framework. This framework divides the next 1.2 s into 12 times steps and performs updates every 0.1 s. To predict surrounding vehicles’ movements, the model analyzes historical data from the autonomous vehicle (AV) and nearby vehicles over the past 0.8 s.
Leveraging the OpenCDA algorithm on the Carla simulator platform, the environment generates surrounding vehicles with layered avoidance logic. This ensures reactive planning by focusing only on the trajectories of nearby vehicles relevant to the AV. For efficient calculation, these future trajectories are further segmented into smaller time steps.
4. Analysis of Experimental Results
This study implemented a rigorous three-part evaluation process to assess the performance of our proposed autonomous vehicle (AV) trajectory planning system, with a particular focus on critical scenarios such as turns and intersections. Baseline Comparison: A benchmark model was established for comparison against our proposed system. This comparison demonstrates our model’s enhanced capabilities in both predicting surrounding vehicles’ trajectories and planning safe and efficient paths for the ego vehicle. Ablation Study: To understand the relative importance of each component within our framework, we conducted an ablation study. Here, specific parts were systematically removed, and the resulting impact on the overall performance was analyzed. This highlighted the key components that significantly contributed to the model’s success. Analysis of Turns and Intersections: Finally, a more in-depth analysis was conducted by examining how each model performed when planning trajectories in turning and intersection scenarios. This meticulous examination provided valuable insights into the model’s behavior in these crucial situations. By combining these methods, this study provides a comprehensive understanding of the proposed model’s effectiveness. Specifically, it highlights the system’s advantages over existing models in handling turns and intersections and clarifies how the individual components contribute to this superior performance.
4.1. Baseline Comparison of Trajectory Prediction and Planning
This study evaluated the performance of the comparison models for surrounding vehicles’ trajectory prediction and self-vehicle trajectory planning over different time frames (0.4, 0.8, and 1.2 s).
4.1.1. Baseline Comparison of Trajectory Prediction
Across both the turning lane (Table 1) and intersection scenarios (Table 2), a consistent trend emerged: as the prediction horizon (Th) increased from 0.4 s to 1.2 s, all three models (IR-STP, LAM, CMGNN) exhibited a statistically significant increase in both the final displacement error (FDE) and average displacement error (ADE). This finding aligns with the established knowledge that medium-term trajectory prediction becomes inherently more challenging due to increased uncertainty, particularly in complex traffic environments such as intersections.

Table 1.
Baseline model trajectory prediction comparison (turning lane scenario).

Table 2.
Baseline model trajectory prediction comparison (intersection scenario).
The CMGNN consistently achieved the lowest FDE and ADE across all prediction horizons and both traffic scenarios, demonstrating its superior predictive performance. The LAM maintained good performance with an increasing Th, indicating its capability to handle moderate prediction ranges. While statistically less accurate than the CMGNN, the difference was minimal at the shortest prediction horizon (Th = 0.4 s). The IR-STP exhibited the most significant increase in errors compared to the other two models as the Th increased. This suggests limitations in the IR-STP’s ability to handle medium-term predictions in both turning lane situations and intersections, potentially due to its rule-based nature. The CMGNN offered the most accurate trajectory predictions across both scenarios, making it a suitable choice for applications requiring high-fidelity medium-term predictions. The LAM provided a favorable balance between accuracy and potential stability across different prediction windows, making it well suited for scenarios in which both precision and computational efficiency are crucial. The IR-STP might be suitable for real-time applications with lower computational costs due to its potentially simpler rule-based approach. However, its effectiveness diminished for medium-term predictions and in complex traffic environments.
4.1.2. Baseline Comparison of Trajectory Planning
Table 3 presents the performance of the three trajectory planning models (IR-STP, LAM, CMGNN) during turning maneuvers. We evaluated its effectiveness in three key aspects that are crucial for safe and comfortable navigation: minimizing the risk of collision (TTC), maintaining a smooth trajectory (curvature, acceleration), and ensuring passenger comfort (lateral acceleration).

Table 3.
Baseline model trajectory planning comparison (turning lane scenario).
In all models, the time to collision (TTC) decreased significantly as the prediction horizon (Th) increased. This suggests that medium-term planning strategies around corners may result in a higher risk of collision compared to shorter horizons. The CMGNN prioritized safety by maintaining the highest TTC throughout the Th, suggesting a conservative approach to maximizing the traffic safety gap. In contrast, the IR-STP exhibited the lowest TTC values, possibly leading to a greater likelihood of collision during turns, especially when the prediction range is long. While all vehicle models generally maintained a safe distance from the surrounding vehicles (high minimum distance—MD), the LAM’s MD increased most significantly as the Th increased. This suggests that the LAM’s ability to maintain safety buffers for medium-term planning exercises around corners may be diminished.
Curvature, acceleration, and lateral acceleration (LA) are key factors affecting the trajectory smoothness and passenger comfort during cornering maneuvers. The CMGNN exhibited the most consistent and smallest curvature profile and the smoothest acceleration pattern with minimal variation, and it consistently maintained the lowest LA values across all Th ranges. This means smoother cornering maneuvers with minimal acceleration and lateral forces, resulting in the most comfortable passenger experience. In contrast, the LAM exhibited greater variability in all three metrics, potentially resulting in more abrupt turns, jerky motion, and increased passenger discomfort during turns. The IR-STP is an intermediate option, with moderate curvature and acceleration changes but greater LA changes compared to the CMGNN.
By prioritizing safety with a high TTC and maintaining a safe maneuvering buffer (MD), the CMGNN can generate smoother trajectories with minimal acceleration and lateral forces, providing the most comfortable passenger experience when cornering. The LAM strikes a balance between security and smoothness, and the TTC value was generally between those of the CMGNN and IR-STP. Although the curvature changes were moderate, the LAM’s acceleration pattern showed some fluctuations that may affect the smoothness. The IR-STP focuses on efficiency but may compromise the safety due to its lower TTC values. Despite initially maintaining the minimum acceptable distance, the MD showed the largest increase as the prediction horizon was lengthened. Furthermore, its larger curvature changed and acceleration fluctuations resulted in less comfortable cornering maneuvers.
Table 4 presents the performance of the three trajectory planning models (IR-STP, LAM, CMGNN) at intersections, considering various prediction horizons (Th) of 0.4, 0.8, and 1.2 s. It focuses on three key aspects associated with navigating safely and comfortably through intersections: minimizing the risk of collision (TTC), maintaining a smooth trajectory (curvature, acceleration), and ensuring passenger comfort (lateral acceleration).

Table 4.
Baseline model trajectory planning comparison (intersection scenario).
The same trend is seen for the IR-STP and LAM as the planning horizon increased. Their time to collision (TTC) decreased significantly, indicating a higher risk of collision at intersections with a medium-term planning strategy (Th = 1.2 s) compared to a shorter planning strategy (Th = 0.4 s). Instead, the CMGNN prioritized collision avoidance, maintaining consistently high TTC values across all fields of view, thereby reducing the risk of accidents at intersections.
Furthermore, the medium-term planning of the IR-STP and LAM resulted in increased fluctuations in curvature and acceleration. This means that more sudden turns and less smooth maneuvers are possible during intersection navigation. The LAM had the most significant increase in curvature, indicating the steepest turning among the three models. Likewise, its high acceleration variation indicated that it has the least smooth motion at the intersection point. In contrast, the CMGNN maintained consistently low curvature and minimal fluctuations over all prediction ranges, meaning that it performed the smoothest turns when navigating intersections. Furthermore, the minimal changes in the CMGNN’s acceleration curve indicate its smooth vehicle motion during intersection maneuvers.
Passenger comfort is also a key factor at intersections. The lateral acceleration (LA) of the IR-STP and LAM showed a similar trend to their acceleration, with increasing variability as the prediction horizon was extended. This suggests that passengers may experience discomfort when turning, especially when medium-term planning strategies are adopted at intersections. On the other hand, the CMGNN maintained the lowest LA value and the smallest change among all Th ranges. This means that minimal lateral forces were exerted on the passengers, resulting in the most comfortable experience when turning at intersections.
4.2. Ablation Experiment Analysis
Ablation studies confirmed the importance of the two modules in the CMGNN. Removing either module will have a negative impact on the prediction accuracy. As shown in Figure 5, the maximum final displacement error (FDE) increased after ablation. Likewise, the minimal FDE also worsened with ablation. These findings indicate that both modules help to reduce errors and improve the endpoint accuracy. The ablation studies also reveal potential trade-offs. While the time-to-contact (TTC) heatmap showed a broader distribution of values after ablation (indicating potential instability), the overall model accuracy improved. An analysis of the average error per 60 trajectory points shows that the ablation model fell below the average error line. This shows that the model achieved better overall accuracy despite potential outliers in specific metrics such as the TTC.
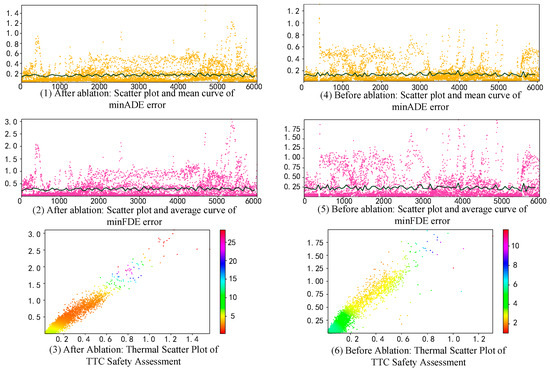
Figure 5.
Ablation cooperative intent module and dynamic risk characterization module.
The dynamic risk signature module further strengthens these findings. Its inclusion resulted in a significant increase in the average TTC score, indicating improved time-to-collision prediction, especially for less accurate trajectory points. However, the greater the distance between the vehicle and its surroundings, the higher the TTC score. Further investigation is required to clearly confirm this hypothesis.
4.3. Actuator-Feasible Dynamic Trajectory Risk Assessment and Visualization
An experiment was performed to investigate the effectiveness of the actuator-feasible dynamic trajectory risk assessment model in improving the safety of multimodal trajectory planning for autonomous vehicles, especially around turns and intersections. The trajectory planning algorithm generates and visualizes various candidate paths for the vehicle. These trajectories are then evaluated based on five safety metrics: the time to collision (TTC), minimum distance (MD), curvature, acceleration, and lateral disturbance (LA). The orange trajectory is the best trajectory selected by the actuator-feasible dynamic trajectory risk assessment module, which dynamically weighs different safety metrics. The blue trajectory is the best trajectory selected for the safety metric using a fixed set of weights [3, 2, 2, 1, 2]. The green trajectory is the best trajectory selected using a different set of fixed weights [2, 2, 2, 2, 2]. The results show that the actuator-feasible dynamic trajectory risk assessment module has the ability to identify and select safer trajectories compared to fixed weights and the baseline methods, balancing the safety metrics, trajectory smoothness, and comfort through dynamic weighting.
4.3.1. Research on Dynamic Trajectory Safety Assessment in Turning Lane Scenarios Considering Actuator Constraints
The actuator-feasible dynamic trajectory risk assessment approach consistently enables the autonomous vehicle to maintain a longer time-to-collision (TTC) buffer and greater separation from the surrounding vehicles, thereby enhancing its safety during turns. This innovative mechanism dynamically adjusts the weightings of the safety indicators based on the real-time traffic conditions, actuator constraints, and vehicle dynamics. By considering factors such as the response time, maximum force/torque output, and nonlinear behaviors of the steering, throttle, and braking systems, the approach generates trajectories that are not only low risk but also feasible given the vehicle’s physical capabilities. This not only increases the safety margin against potential collisions but also mitigates the likelihood of sideslips, which is particularly advantageous in cornering scenarios.
As illustrated by the curvature plot in Figure 6, the orange trajectory, representing the actuator-feasible dynamic trajectory risk assessment, follows a smoother curve, resulting in lower lateral acceleration. This contributes to improved vehicle stability and enhanced passenger comfort, especially when executing sharp turns in close proximity to other vehicles. In the acceleration plot in Figure 6, the orange trajectory exhibits a more consistent acceleration profile, particularly evident between frames 2 and 4 and frames 10 and 12. This steady modulation minimizes the jerk, which is the rate of change in acceleration, leading to a smoother overall riding experience. Furthermore, in the lateral acceleration (LA) plot in the same figure, the orange trajectory demonstrates fewer lateral fluctuations compared to the blue and green trajectories. Consequently, this results in fewer abrupt lateral movements, contributing to a stabler trajectory and increased passenger comfort during cornering maneuvers.
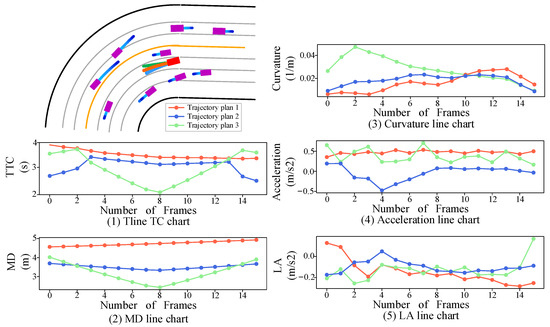
Figure 6.
Research on dynamic trajectory safety assessment in turning lane scenarios.
The actuator-feasible dynamic trajectory risk assessment mechanism has the capability to dynamically adjust the weightings of the safety indicators while considering the actuator limitations; thus, it offers a comprehensive approach that balances safety, trajectory smoothness, and comfort. In contrast, a fixed-weight approach that neglects the actuator constraints may compromise these factors by reducing the TTC, decreasing the minimum distance to the surrounding vehicles, and potentially heightening the risk of collision or skidding during turns. Additionally, higher curvature and lateral acceleration could adversely impact the vehicle stability and passenger comfort. The lack of flexibility in adapting to dynamic traffic conditions and actuator constraints may also result in suboptimal or infeasible trajectory choices.
4.3.2. Research on Dynamic Safety Assessment of Intersection Scenario Trajectories Considering Actuator Feasibility
As shown in Figure 7, the orange trajectory planned by the actuator-feasible dynamic trajectory risk assessment shows significant advantages in managing complex intersections with multiple vehicles. By consistently maintaining a high time to collision (TTC) and a significant minimum distance (MD) to adjacent vehicles, the trajectory expands the safety buffer and significantly reduces the risk of collision—key factors in managing the unpredictable dynamic changes of the intersection environment.
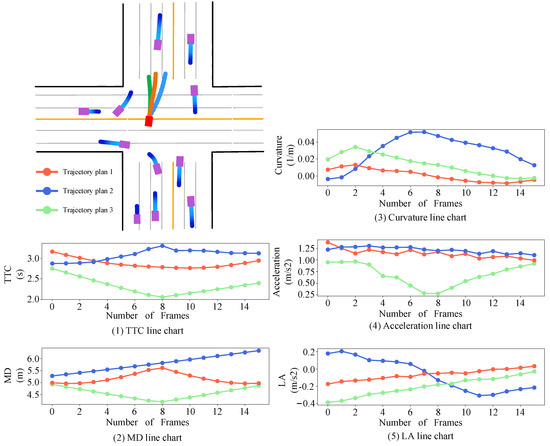
Figure 7.
Research on dynamic safety assessment of intersection scenario trajectories.
The curvature analysis shows that the orange trajectory planned by the actuator-feasible dynamic trajectory risk assessment follows a smoother route compared to the other trajectories. This reduces the lateral acceleration, improving the vehicle stability and passenger comfort at the intersection by minimizing sudden lateral movements. The actuator-feasible dynamic trajectory risk assessment strategically prioritizes the safety and the improvement of the TTC and MD, while ensuring comfort, through moderate curvature and acceleration and enhanced stability, achieved through consistent lateral acceleration (LA). These characteristics highlight the module’s ability to skillfully and dynamically adapt to different safety indicators, thereby producing safer and more comfortable driving strategies. In contrast, the blue trajectory, based on the fixed weight approach, exhibits a moderate level of safety but may compromise the comfort due to the increased curvature and acceleration. Similarly, the green trajectory tends to choose the most direct route, which may reduce the safety (as shown by the lower TTC and MD values) and may increase the discomfort due to the elevated lateral acceleration.
Compared with the fixed-weight approach used for the blue and green trajectories, the actuator-feasible dynamic trajectory risk assessment, represented by the orange trajectory, clearly excels in identifying and selecting trajectories that enhance the safety and comfort. This innovative module demonstrates its ability to dynamically adjust to complex traffic scenarios and achieve a harmonious balance between safety and passenger comfort at intersections. By combining the actuator constraints and dynamically optimizing the risk weights, this approach generates trajectories that are not only safer but also feasible given the physical limitations of the vehicle. This breakthrough in risk assessment enables autonomous vehicles to navigate intersections with unprecedented safety and efficiency.
4.4. Comparative Study: Three Planning Models for Turns and Intersections
This research compares the trajectory planning performance of three models: our proposed CMGNN model, the LAM, and the IR-STP. We evaluated their performance in two common traffic scenarios: corners and intersections. We first visually analyzed the planning environments of these scenarios to understand the models’ planning motivations. We then evaluated the quality of the generated trajectories using the curvature and acceleration metrics to determine which model generates smoother and safer paths for autonomous vehicles (AVs).
4.4.1. Verification of Different Vehicle Densities in Turning Lane Scenario
This study compares the CMGNN’s trajectory planning with that of the LAM and IR-STP in simulated turning scenarios with dynamic obstacles (slower vehicles) in order to evaluate their ability to handle uncertain traffic environments. Here, we focus on the model’s ability to understand the intentions of surrounding vehicles and optimize the trajectories for safety and efficiency.
As shown in Figure 8, the CMGNN model generated a trajectory that prioritizes safety by maintaining a consistent minimum distance (MD) from the surrounding vehicles. This behavior translates into a statistically significant increase in the safety buffer zone, demonstrably reducing the probability of collision events (p(collision)) in the dynamic traffic environment. Additionally, the CMGNN’s trajectory adheres to a smooth curvature profile, as evidenced by the lack of sharp turns. This translates into minimized lateral acceleration, which not only enhances the vehicle stability but also contributes to improved passenger comfort during the lane change maneuver by mitigating abrupt lateral movements (jerks).
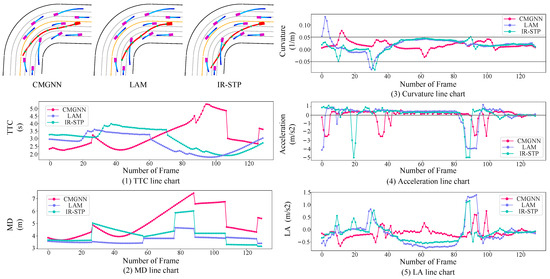
Figure 8.
Turning lane scenario: trajectory planning visualization and trajectory planning safety indicator line charts for the three models.
A key innovation of the CMGNN model is its actuator-feasible dynamic trajectory risk assessment mechanism. By considering the physical constraints and response times of the vehicle’s steering, throttle, and braking systems, the CMGNN generates trajectories that are not only low risk but also executable given the vehicle’s capabilities. The model dynamically adjusts the weights of safety indicators such as the TTC and MD based on the real-time actuator states and traffic conditions. This allows it to identify paths that balance safety and feasibility, as seen in the consistent minimum distance maintained from other vehicles. In contrast, the LAM model’s trajectory exhibited a shorter distance to the preceding vehicle within the same lane. This might indicate its prioritization of the travel efficiency, potentially minimizing the travel time by maintaining its momentum. However, this approach could lead to reduced safety margins, particularly when considering the close following distance regarding the surrounding vehicles. While the LAM model’s trajectory might be efficient in terms of the travel time, it could compromise the passenger comfort due to the potentially increased lateral acceleration during the maneuver; more importantly, it could elevate the risk of collision events. The assertion that rule-based approaches such as the IR-STP could facilitate smoother lane transitions is verified in the observed trajectories. This implies that the application of deterministic algorithms may offer a balance between adherence to traffic regulations and the execution of lane-changing maneuvers with reduced vehicular jerk, thereby potentially improving the ride smoothness and passenger comfort.
Figure 8 provides a comparative evaluation of the CMGNN, LAM, and IR-STP models across various metrics, showcasing their performance in vehicle trajectory planning. In the time-to-collision (TTC) plot, the CMGNN model consistently showed higher TTC values than the LAM and IR-STP models, indicating better collision avoidance capabilities. This suggests the CMGNN’s superior ability to anticipate and manage potential traffic conflicts during turns. The minimum distance (MD) graph reveals that the CMGNN model maintained a larger MD from nearby vehicles throughout the turn, reducing the collision risk and indicating its more accurate prediction of the vehicle trajectories for safer path planning. In terms of curvature, the CMGNN model’s trajectory showed a more consistent curvature profile compared to the LAM and IR-STP models, implying reduced lateral acceleration and increased vehicular stability and comfort, especially during turns near other vehicles. This smooth curvature was achieved through the CMGNN’s consideration of the steering system’s constraints and nonlinear behaviors in its risk assessment. The acceleration profile of the CMGNN model was more stable, with fewer abrupt changes than those seen in the LAM and IR-STP models, leading to smoother turns and potentially enhancing the safety and efficiency in response to the surrounding traffic. This was enabled by the CMGNN’s capacity to dynamically adjust the acceleration based on the throttle and braking actuators’ limitations. Furthermore, the lateral acceleration (LA) plot shows that the CMGNN model experienced lower variability in its lateral acceleration, indicating a smoother and more stable trajectory, which may improve passenger comfort during maneuvers. The CMGNN achieved this by incorporating the maximum force/torque output of the actuators into its trajectory risk evaluation.
The CMGNN model effectively integrates safety and efficiency, maintaining stable TTC and MD values while ensuring smoother curvature and acceleration profiles, thanks to its innovative actuator-aware risk assessment tool. The LAM model appears to focus on efficiency, possibly at the cost of safety margins, as evidenced by the greater variability in its TTC, MD, and lateral acceleration. The IR-STP model clearly prioritizes safety, showing minimal variations in the TTC and MD along with stable acceleration and curvature, suggesting good predictive capabilities and smooth driving dynamics.
4.4.2. Verification of Different Vehicle Densities in Turning Lane Scenario
This study further evaluated the trajectory planning capabilities of the three models in complex intersection scenarios with a particular focus on the innovative actuator-feasible dynamic trajectory risk assessment mechanism employed by the CMGNN. Here, the key factors influencing trajectory planning were the two left-turning vehicles ahead. The models needed to predict the timing and potential avoidance intentions of these vehicles, along with their future trajectories, while considering the physical constraints and dynamics of the vehicle’s actuators.
In Figure 9, a visual representation of the intersection scene depicts the vehicle trajectories computed by the CMGNN, LAM, and IR-STP algorithms. These trajectories illustrate each model’s predictive ability to drive an autonomous vehicle through complex traffic intersections while taking into account the dynamic positioning of the surrounding vehicles and the feasibility of the planned trajectory given the vehicle’s actuator limitations. The trajectory quality exhibited by the CMGNN appears to be superior to that of both the LAM and IR-STP. Specifically, the LAM’s trajectory is characterized by significant inefficiencies; it depicts a route that merges into the original lane after bypassing a nearby left-turning vehicle, in a manner that increases the risk of interacting with the other left-turning vehicle. Additionally, the significant changes in the apparent curvature and acceleration associated with the LAM’s trajectories may compromise the vehicle safety and passenger comfort, as they may exceed the capabilities of the vehicle’s actuators. The IR-STP, while generating a smoother trajectory than the LAM, still exhibits higher curvature and lateral acceleration values compared to the CMGNN, suggesting potential issues with actuator feasibility and passenger comfort. In contrast, the CMGNN succeeds in computing a safe, smooth, and actuator-feasible trajectory. By dynamically adjusting the weights of safety indicators such as the TTC and MD based on the current state of the actuators and the traffic conditions, the CMGNN ensures that the planned trajectory is not only low risk but also executable by the vehicle. This innovative approach allows the CMGNN to navigate the intersection more efficiently and safely than the other models.
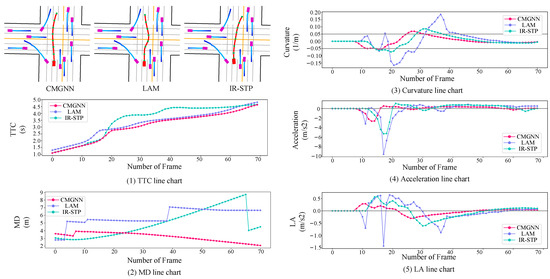
Figure 9.
Intersection scenario: trajectory planning visualization and trajectory planning safety indicator line charts for the three models.
In the data shown in Figure 9, the CMGNN exhibited consistently low and stable curvature, acceleration, and lateral acceleration values, indicating its ability to plan smooth, comfortable, and actuator-feasible trajectories. The lower TTC and MD values observed for the CMGNN suggest that it can maintain a safe distance from the surrounding vehicles while still navigating the intersection efficiently. This is made possible by the CMGNN’s superior predictive accuracy regarding the surrounding vehicles’ behavior, which allows it to mitigate the risks associated with closer vehicle interactions. The LAM and IR-STP models, on the other hand, exhibited higher curvature, acceleration, and lateral acceleration values, which may result in less stable, less comfortable, and potentially actuator-infeasible trajectories. The significant decrease in the acceleration profile of the IR-STP model, in particular, indicates the presence of abrupt deceleration events, which could lead to passenger discomfort and exceed the capabilities of the vehicle’s braking system.
In summary, the CMGNN model’s actuator-feasible dynamic trajectory risk assessment mechanism enables it to plan safe, smooth, and executable trajectories in complex intersection scenarios. By considering the physical constraints and dynamics of the vehicle’s actuators, while assessing the risk of potential trajectories, the CMGNN ensures that the planned path is not only low risk but also feasible for the vehicle to execute. This innovative approach, combined with the CMGNN’s superior predictive accuracy regarding the surrounding vehicles’ behavior, results in improved safety, efficiency, and passenger comfort compared to the LAM and IR-STP models.
4.4.3. Discussion
While the proposed Cooperative Intent Multi-Layer Graph Neural Network (CMGNN) model demonstrates impressive performance in navigating uncertain traffic scenarios, there are a few potential limitations that are worth considering. First, the model’s reliance on historical data to learn vehicle interactions and dynamic trajectories may prevent it from fully capturing the breadth of possible real-world scenarios. Rare or unexpected events, such as sudden road obstacles or extreme weather conditions, might pose challenges to the model’s adaptability. Moreover, the computational complexity of the multi-layered approach and the integration of various data sources might impact the real-time performance of the system, especially in resource-constrained environments. Balancing the trade-off between model sophistication and computational efficiency is an ongoing challenge in the field of autonomous driving.
Traditional methods such as rule-based approaches, including the IR-STP, offer advantages in terms of computational simplicity and predictability. These methods can be more easily implemented in real-time systems due to their lower computational demands. Additionally, rule-based models are typically easier to understand and debug, providing clear and interpretable decision-making processes.
In contrast, while the CMGNN excels in capturing complex interactions and performing dynamic risk assessments, it may suffer from overfitting to historical data and struggles with real-time processing due to its computational intensity. The need for extensive training data and large amounts of computational resources may limit its practicality in some scenarios, particularly where rapid deployment and low-cost solutions are required. Therefore, while the CMGNN offers significant advancements in terms of predictive accuracy and safety, the traditional methods retain their relevance in scenarios where simplicity, transparency, and computational efficiency are prioritized.
5. Conclusions
This study introduces the Cooperative Intent Multi-Layer Graph Neural Network (CMGNN), an innovative approach to safe trajectory planning in autonomous vehicles operating in uncertain traffic scenarios. The CMGNN captures cooperative intent by analyzing dynamic trajectories, lane positions, and angle changes, and it incorporates actuator constraints for a realistic risk assessment. The experiments in the Carla simulator show that the CMGNN significantly enhanced the accuracy in surrounding vehicles’ trajectory prediction and reduced the collision risks during autonomous vehicles’ trajectory planning. The model dynamically adapts its driving strategies based on the real-time traffic conditions, perceived intentions, and actuator constraints, leading to safer and more efficient navigation, especially in complex scenarios such as turns and intersections.
Future research could explore the integration of the CMGNN with reinforcement learning to improve its adaptability and performance in diverse driving environments. Additionally, incorporating vehicle-to-vehicle communication could further enhance cooperative intent modeling and the overall safety in mixed traffic scenarios.
Author Contributions
Conceptualization, J.L., Y.Z. and Q.L.; methodology, J.L. and Q.L.; software, Q.L.; validation, Y.Z. and Q.L.; formal analysis, J.L., Y.Z. and Q.L.; investigation, J.L., Y.Z. and Q.L.; resources, J.L.; data curation, Y.Z. and Q.L.; writing—original draft preparation, J.L. and Q.L.; writing—review and editing, J.L., Y.Z. and Q.L.; visualization, J.L. and Q.L.; supervision J.L.; project administration, J.L.; funding acquisition, J.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Key R&D Program of the Ministry of Science and Technology of the People’s Republic of China under grant no. 2023YFB2504400, the National Natural Science Foundation of China (52372413, U20A20333, U20A20331, 52225212), the Overseas Training Plan for Outstanding Young and Middle-Aged Teachers and Principals in Colleges and Universities in Jiangsu Province, and the Young Talent Cultivation Project of Jiangsu University.
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Mahajan, N.; Zhang, Q. Intent-aware autonomous driving: A case study on highway merging scenarios. arXiv 2023, arXiv:2309.13206. [Google Scholar]
- Lim, W.; Lee, S.; Sunwoo, M.; Jo, K. Hybrid trajectory planning for autonomous driving in on-road dynamic scenarios. IEEE Trans. Intell. Transp. Syst. 2019, 22, 341–355. [Google Scholar] [CrossRef]
- Ma, C.; Yu, C.; Yang, X. Trajectory planning for connected and automated vehicles at isolated signalized intersections under mixed traffic environment. Transp. Res. Part C Emerg. Technol. 2021, 130, 103309. [Google Scholar] [CrossRef]
- Luo, W.; Park, C.; Cornman, A.; Sapp, B.; Anguelov, D. Jfp: Joint future prediction with interactive multi-agent modeling for autonomous driving. In Proceedings of the Conference on Robot Learning, Atlanta, GA, USA, 6–9 November 2023; pp. 1457–1467. [Google Scholar]
- Liu, Y.; Zhang, J.; Fang, L.; Jiang, Q.; Zhou, B. Multimodal motion prediction with stacked transformers. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 7577–7586. [Google Scholar]
- Lee, D.; Gu, Y.; Hoang, J.; Marchetti-Bowick, M. Joint interaction and trajectory prediction for autonomous driving using graph neural networks. arXiv 2019, arXiv:1912.07882. [Google Scholar]
- Liu, Z.; Chen, J.; Xia, H.; Lan, F. Human-like trajectory planning for autonomous vehicles based on spatiotemporal geometric transformation. IEEE Trans. Intell. Transp. Syst. 2022, 23, 20160–20176. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, J.; Zhang, J.; Wang, J.; Lu, K.; Hong, J. Integrating algorithmic sampling-based motion planning with learning in autonomous driving. ACM Trans. Intell. Syst. Technol. (TIST) 2022, 13, 1–27. [Google Scholar] [CrossRef]
- Jia, H.; Zhang, L.; Wang, Z. A dynamic lane-changing trajectory planning scheme for autonomous vehicles on structured road. In Proceedings of the 2020 IEEE 9th International Power Electronics and Motion Control Conference (IPEMC2020-ECCE Asia), Nanjing, China, 29 November–2 December 2020; pp. 2222–2227. [Google Scholar]
- Yu, C.; Velu, A.; Vinitsky, E.; Wang, Y.; Bayen, A.; Wu, Y. The surprising effectiveness of MAPPO in cooperative, multi-agent games. CoRR. arXiv 2021, arXiv:2103.01955. [Google Scholar]
- Lefkopoulos, V.; Menner, M.; Domahidi, A.; Zeilinger, M.N. Interaction-aware motion prediction for autonomous driving: A multiple model kalman filtering scheme. IEEE Robot. Autom. Lett. 2020, 6, 80–87. [Google Scholar] [CrossRef]
- Hubmann, C.; Becker, M.; Althoff, D.; Lenz, D.; Stiller, C. Decision making for autonomous driving considering interaction and uncertain prediction of surrounding vehicles. In Proceedings of the 2017 IEEE intelligent vehicles symposium (IV), Los Angeles, CA, USA, 11–14 June 2017; pp. 1671–1678. [Google Scholar]
- Gupta, P.; Isele, D.; Lee, D.; Bae, S. Interaction-aware trajectory planning for autonomous vehicles with analytic integration of neural networks into model predictive control. In Proceedings of the 2023 IEEE International Conference on Robotics and Automation (ICRA), London, UK, 29 May–2 June 2023; pp. 7794–7800. [Google Scholar]
- Liu, Q.; Gao, C.; Wang, H.; Cai, Y.; Chen, L.; Lv, C. Learning from Trajectories: How Heterogeneous CACC Platoons Affect the Traffic Flow in Highway Merging Area. IEEE Trans. Veh. Technol. 2024, 1–13. [Google Scholar] [CrossRef]
- Ming, Z.; Jun, L. Smarts: Scalable multi-agent reinforcement learning training school for autonomous driving. arXiv 2020, arXiv:2010.09776. [Google Scholar]
- Li, H.; Wu, C.; Chu, D.; Lu, L.; Cheng, K. Combined trajectory planning and tracking for autonomous vehicle considering driving styles. IEEE Access 2021, 9, 9453–9463. [Google Scholar] [CrossRef]
- He, X.; Lv, C. Toward personalized decision making for autonomous vehicles: A constrained multi-objective reinforcement learning technique. Transp. Res. Part C Emerg. Technol. 2023, 156, 104352. [Google Scholar] [CrossRef]
- Yang, B.; Yan, S.; Wang, Z.; Nakano, K. Prediction Based Trajectory Planning for Safe Interactions between Autonomous Vehicles and Moving Pedestrians in Shared Spaces. IEEE Trans. Intell. Transp. Syst. 2023, 24, 10513–10524. [Google Scholar] [CrossRef]
- Xu, D.; Ding, Z.; He, X.; Zhao, H.; Moze, M.; Aioun, F.; Guillemard, F. Learning from naturalistic driving data for human-like autonomous highway driving. IEEE Trans. Intell. Transp. Syst. 2020, 22, 7341–7354. [Google Scholar] [CrossRef]
- Fang, J.; Wang, F.; Xue, J.; Chua, T.-S. Behavioral intention prediction in driving scenes: A survey. IEEE Trans. Intell. Transp. Syst. 2024, 1–13. [Google Scholar] [CrossRef]
- de Andrade Both, L.; Lange, F. A New Trajectory Planning Approach With Motion Duration Control for Kinematic Constrained Systems. IEEE Robot. Autom. Lett. 2023, 9, 467–474. [Google Scholar] [CrossRef]
- Ben-Asher, J.Z.; Rimon, E.D. Time optimal trajectories for a car-like mobile robot. IEEE Trans. Robot. 2021, 38, 421–432. [Google Scholar] [CrossRef]
- Huang, Z.; Liu, H.; Wu, J.; Lv, C. Differentiable integrated motion prediction and planning with learnable cost function for autonomous driving. IEEE Trans. Neural Netw. Learn. Syst. 2023. [Google Scholar] [CrossRef] [PubMed]
- Xin, L.; Wang, P.; Chan, C.-Y.; Chen, J.; Li, S.E.; Cheng, B. Intention-aware long horizon trajectory prediction of surrounding vehicles using dual LSTM networks. In Proceedings of the 2018 21st International Conference on Intelligent Transportation Systems (ITSC), Maui, HI, USA, 4–7 November 2018; pp. 1441–1446. [Google Scholar]
- Chen, Y.; Cheng, J.; Gan, L.; Wang, S.; Liu, H.; Mei, X.; Liu, M. IR-STP: Enhancing Autonomous Driving with Interaction Reasoning in Spatio-Temporal Planning. IEEE Trans. Intell. Transp. Syst. 2024. [Google Scholar] [CrossRef]
- Huang, Z.; Liu, H.; Wu, J.; Huang, W.; Lv, C. Learning interaction-aware motion prediction model for decision-making in autonomous driving. In Proceedings of the 2023 IEEE 26th International Conference on Intelligent Transportation Systems (ITSC), Bilbao, Spain, 24–28 September 2023; pp. 4820–4826. [Google Scholar]
- Naveed, K.B.; Qiao, Z.; Dolan, J.M. Trajectory planning for autonomous vehicles using hierarchical reinforcement learning. In Proceedings of the 2021 IEEE International Intelligent Transportation Systems Conference (ITSC), Indianapolis, IN, USA, 19–22 September 2021; pp. 601–606. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).