Abstract
In this paper, serial elastic actuators (SEAs) in conjunction with an accelerometer are proposed as force sensors to detect the intention of movement, and the SEA is proposed as a gentle actuator of a patient’s upper-limb exoskeleton. A smooth trajectory is proposed to provide comfortable performance. There is an offset trajectory between the link and the motor, which increases safety by preventing sudden movements, and the offset is equivalent to the torsional elastic spring constant. The proposed control law is based on a backstepping approach tested in real-time experiments with robust results in a 2-DoF upper-limb rehabilitation exoskeleton. The experimental results showed a sensitivity of 100% and a positive predictive value of 97.5% for movement intention detection.
1. Introduction
Loss of mobility is a condition that renders a person unable to perform body movements in a coordinated manner and without pain. Diverse factors can cause this condition, for example, stroke, musculoskeletal disorders, neuromuscular disorders, or physical trauma like broken bones or spinal cord injury. When motor functions are lost, the affected individual becomes unable to perform daily living tasks such as walking, standing up, eating, or even manipulating objects easily. This means that not only is the individual’s independence affected, but their mental health is also altered. However, through rehabilitation therapy, it is possible to recover mobility and functionality, which also leads to restoring confidence in the individual.
Rehabilitation therapy is a medical treatment focused on recovering as much of the motor capabilities of the affected individual as possible by using different methods, including traditional methods (assisted exercises, massages, electrostimulation, etc.) as well as modern treatments that may include the use of robotic devices such as exoskeletons, which can improve the effectiveness of the therapy [1,2].
The objective of the exoskeleton is to aid the patient in performing repetitive movement exercises that are focused on increasing muscular strength, improving coordination, and relearning movement patterns. This means that the rehabilitation process involves a complex human–robot interaction (HRI) since physical coupling is needed between the exoskeleton and the patient´s limbs [3]. So, to ensure correct rehabilitation, it is essential that the actions of the exoskeleton be coordinated and adapted to the user’s capabilities, since unexpected behavior during the interaction can result in serious damage. In Ref. [4], the authors claim that one way to improve the HRI is by using exoskeletons driven by series elastic actuators (SEAs). The basic mechanical configuration of an SEA consists of a spring coupled between the shaft of the motor and the link. This configuration offers a wide range of advantages over rigid exoskeletons. The elastic element serves as a compliant interface between the human and the exoskeleton, allowing better adaptation to the natural movements of the user and protecting them from sudden shocks while also adding backdrivability properties, which, in exoskeletons, are useful, especially in force-sensing applications. With this configuration, safety and comfort during the rehabilitation process are ensured. Another way to increase the HRI is by incorporating a system capable of detecting human motion intentions into the exoskeleton so that the exoskeleton will offer assistance only when the patient requires it. This gives a better sense of control to the patient over the exoskeleton.
The detection of voluntary motion intention involves the use of electronic devices and algorithms to analyze biological and biomechanical signals related to the body motion process [5,6,7]. At the brain level, the intention to move originates in the form of electrical impulses in the motor cortex [8]. Brain–computer interfaces (BCIs) can be used to analyze the electrical signals related to the movement intention [9]. A common method to acquire and analyze the brain’s electrical activity is electroencephalography (EEG) [10]. At the muscle level, techniques to analyze electrical activity in the muscle fibers, like electromyography (EMG), can be used to detect motion intention [11]. At the body level, small changes in the movement state can be detected by encoders, inertial measurement units (IMUs), and force sensors [12,13]; these changes can be used to identify the voluntary motion intention. In the case of SEAs, the deformation of the spring can be exploited to detect the movement intention. This can be achieved by measuring the angular difference between the rotor and the spring [14,15].
In recent times, several researchers have developed human–robot interfaces to detect human movement intentions. These interfaces enable the exoskeletons to adapt their assistance dynamically to fulfill the requirements of each patient. For instance, Refs. [16,17,18,19] used EEG to detect the motion intention signals generated by the user’s brain and convert them into commands for the exoskeleton. In Refs. [20,21,22], EMG was utilized to develop diverse control methods with the objective of assisting the user in the rehabilitation process according to the patient’s movement intention. The main issue when using bioelectrical signals to detect human motion intentions is that these signals are prone to noise and are also hard to analyze [23]. In the specific case of EMG, these signals are susceptible to changes due to muscle fatigue and electrode location. On the other hand, EEG requires high concentration on the body movement task, which can be complicated in an uncontrolled environment due to the presence of distractors.
Some researchers have used biomechanical signals to detect human motion intentions. In Ref. [24], a human–machine interface for an upper-limb exoskeleton that integrates a force sensor was developed; in another study [25], IMUs in conjunction with encoders were used to detect the gait state and recognize the patient’s gait intentions; meanwhile, in Refs. [26,27], IMUs and neural networks were employed for human motion intention detection. Other prototypes take advantage of the mechanical properties of exoskeletons driven by SEAs and include algorithms for movement intention detection based on signals obtained through EMG or IMUs [28,29,30,31].
The accuracy of motion detection is an important characteristic to ensure a correct HRI [32,33]. In Ref. [34], the authors used EEG signals to evaluate seven classifiers in order to choose the best one to detect the movement intention of the arm. Experimental tests were performed by six health subjects, obtaining a detection accuracy of 70%. In Ref. [35], nine IMUs and a pressure sensor were used to measure the angles of human body parts. Neural networks were employed for the detection of gait movement identification, obtaining a recognition accuracy of 98.5%. The authors in [36] used an IMU to detect foot contact and potentiometers to measure the angle of the left and right hip joints to develop an online gait recognition algorithm based on a Fuzzy Inference System. The algorithm was evaluated using three subjects, obtaining a recognition accuracy of 98%. The motion detection algorithm proposed in [37] fuses EMG and accelerometer signals to recognize the motion patterns of the lower limbs, showing that the fused feature-based recognition algorithm can achieve 95% or higher accuracy than recognition with only EMG or an accelerometer. In Ref. [38], the movement intention detection algorithm fuses data obtained from EMG and force sensors located in various muscles. The experimental results showed an accuracy of 90% in detecting the movement intention. Finally, in Ref. [39], the authors proposed a movement intention detection algorithm based on logistic regression and multiple data fusion (force sensor, joint angle measurement, air pressure sensor, and EMG). This algorithm reached an accuracy of 98%.
The present study proposes a new method for the detection of human movement intention by data fusion of the signal provided by SEAs in conjunction with an IMU. The performance of the proposed detection method is analyzed through experimental tests using an exoskeleton for the glenohumeral joint. The objective is to detect the human intention of the movements related to flexion–extension, as well as the abduction–adduction of the glenohumeral joint. The experimental results showed a sensitivity of 100% and a positive predictive value of 97.5% for the movement intention detection.
The main contribution of this work is the proposition and implementation of a new method to detect human movement intention that takes advantage of the mechanical configuration of the series elastic actuator to operate as a force sensor. This approach is capable of accurately detecting small changes in the angular positions of each joint, which can be directly related to the movement intention.
The paper is organized as follows. Materials and methods are presented in Section 2, including the mechanical description of the exoskeleton, its instrumentation, its dynamic model, the design of its control, the motion intention detection algorithm, and the experimental protocol. The experimental results are presented in Section 3. Finally, the conclusions are presented in Section 4.
2. Materials and Methods
2.1. Upper-Limb Rehabilitation Exoskeleton
2.1.1. Mechanical Design
This section provides a study on a glenohumeral joint rehabilitation exoskeleton, which is a robot with rotational joints and two moving links with two degrees of freedom. As shown in Figure 1, each rehabilitation exoskeleton joint corresponds to a specific human shoulder movement: the first joint corresponds to the abduction–adduction movement, while the second joint corresponds to the flexion–extension movement. The exoskeleton design includes an adjustable structure, so that it can be used by adult patients of different sizes, and it has mechanical stops to prevent hyperextension of the glenohumeral joint. The exoskeleton was manufactured in 6061-T6 aluminum alloy using rapid prototyping.
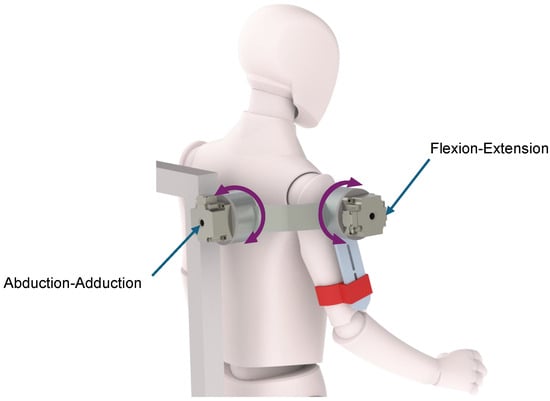
Figure 1.
Glenohumeral joint rehabilitation exoskeleton showing the two degrees of freedom that allow the flexion–extension and abduction–adduction movements.
2.1.2. Sensors and Actuators
In order to obtain a direct measurement of the patient’s intention to move a particular joint, serial elastic actuators (SEAs) were added to each of the exoskeleton joints, as shown in Figure 2. SEAs act as both actuators and force sensors, giving the patient a small range of joint displacement to generate movements that can be interpreted as motion intention.
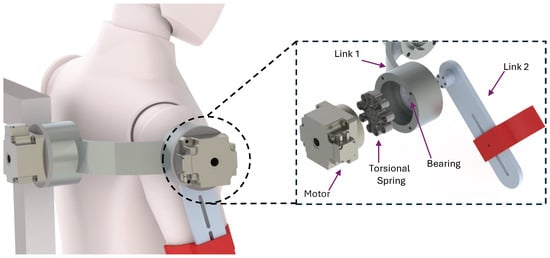
Figure 2.
Configuration scheme of the serial elastic actuator used in the two joints of the exoskeleton.
The elastic element of the SEAs is formed by a torsional spring located between the power element, in this case a motor harmonic drive FHA-14C-100 (from HARMONIC DRIVE), and the link to be moved, supported by a double row ball bearing, which prevents the spring from suffering from unwanted deformations (Figure 2). The spring has a stiffness of 138.65 Nm/rad and a symmetrical configuration which exerts the same torque both clockwise and counterclockwise.
The reading of the angular positions of the motor (before the torsional spring) and the link (after the torsional spring) is carried out through a coaxial configuration using two AMT203-V (from CUI Devices) absolute rotary magnetic encoders, with a resolution of 12 bits.
Finally, a low-cost inertial measurement unit based on a MPU-6050 chip was included at the distal end of the exoskeleton to obtain direct measurements of the angular velocity of the joint and linear end-link accelerations. These inertial signals are acquired using a 6-DOF (three angular speeds and three linear accelerations) IMU GY-521 module connected to PC target through an I2C communication interface.
The angular speeds for X, Y, and Z axes are given by a triaxial angular speed sensor (gyroscope) with a sensitivity of up to 131 LSBs / dps and a full range of , , , and dps, while linear accelerations are given by a triaxial accelerometer with a full scale programmable range of g, g, g, and g.
2.1.3. Dynamical Model of the Exoskeleton
Figure 3 shows the simplified free-body diagram of the exoskeleton shoulder. The mass of each link is specified by for link 1 and for link 2; and represent the distances from the center of mass of link 1 to the proximal articulation (origin); represents the length of link 1 and corresponds to the distance from center of mass of link 2 to its proximal articulation. The inertia of each link is denoted by and . and are the elastic joint stiffness; and are the inertia of each of the rotors, respectively. The angular positions of links 1 and 2 are denoted by and , while and are the angular positions of motors 1 and 2, respectively. The dynamical model expressed in compact form obtained through the Euler–Lagrange approach is as follows.
with
and
where represents the angular position vector of the exoskeleton links, and their derivatives and represent the vector of the velocity and acceleration of the links, while represents the angular position vector of the exoskeleton motors, and and represent the vector of the velocity and acceleration of the motors. denotes the inertia matrix, is the Coriolis and centripetal force matrix, corresponds to the vector of gravitational forces and torques, B is a positive definite diagonal matrix and its values are the viscous friction parameters of each motor , denotes the external movements of the user, and represents the control input.
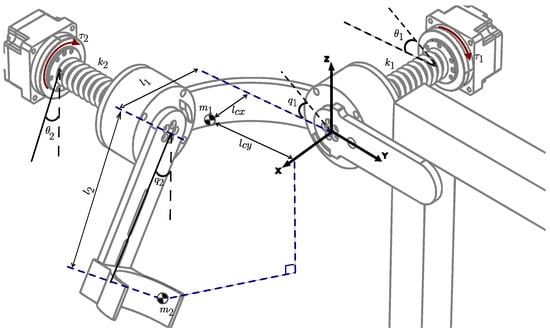
Figure 3.
Schematic diagram of the exoskeleton’s shoulder with elastic joints.
The first equation in (1) represents the dynamics of the robot links, while the second equation is the dynamics of the actuators.
The dynamic parameters of the exoskeleton are shown in Table 1:

Table 1.
Exoskeleton dynamic parameters.
2.2. Control Strategy
The control law applied in this work is based on the model proposed by [38], which adopts a backstepping methodology as follows: By rewriting (1), we obtain a cascaded form:
Solving for from the definition of , and substituting in the first equation of (2), we have
with .
The following Lyapunov candidate function is proposed:
In order to study the stability of the system (5), the derivative of (6) along the trajectories of the system is calculated as follows:
where the matrix is skew-symmetric and implies that . Then:
If , then and tends to zero when . Moreover, since and its transfer function is stable and minimum phase, it follows that and converge to zero when .
The motor torque is calculated with the purpose of ensuring the global asymptotic stability of the system. In this case, we considered as the input of the second equation of (2). To calculate the control law , the time derivative of is computed as and , and substituting the above into the second equation of (2), it follows that
The proposed control law is:
where and are positive diagonal matrices.
Then, introducing (10) into (9), we obtain:
and therefore
which is a linear second-order differential equation.
Choosing the following variable change:
(12) can be rewritten in the form as follows:
where , and recalling that , and , it follows that
It can be easily demonstrated that A is a Hurwitz matrix; therefore, (12) is globally exponentially stable, and then , and from (8), it follows that if , then .
is a variable that serves as the virtual control input of the first equation of (1), and depends on the dynamics of the links and their desired path (). In addition, this variable compensates the exoskeleton gravity vector.
On the other hand, is the desired trajectory of the exoskeleton links. remains at zero until the user’s motion intention is detected, and then generates a single cycle of motion in the joint that detected the movement intention.
The control parameters for the backstepping controller are shown in Table 2.

Table 2.
Backstepping control parameters.
2.3. Movement Intent Detection
In order to detect the human intention movement, data fusion is used by appropriately combining the force sensed by the SEA () and the derivative of the accelerometers measurement signals (), where:
The force signal is passed through a filter , while the derivative of the accelerometer measurement signals is passed through a filter . These filters were designed as second-order lowpass filters, with a cut-off frequency of 10 Hz. In this way, the movement intent signal () is given as . The complementary filters are such that , where , while .
For , and , and the movement intent signal is equal to the full force signal. On the other hand, for , and , the force signal is completely suppressed, and the movement intent signal is only the derivative of the accelerometer measurement signals. In practice, the filter parameter has been selected experimentally so that the amplitude of the motion intention signal is as large as possible. Figure 4 shows the diagram of the complementary filter to obtain the movement intent signal.
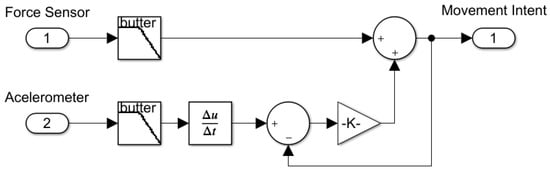
Figure 4.
Movement intent signal diagram.
2.4. Exoskeleton Motion Start Algorithm
Once the intention to move has been detected, the exoskeleton must be able to start the rehabilitation routine corresponding to the movement that has been detected. The task of the exoskeleton motion start algorithm is to decide when the patient wishes to move and to start a rehabilitation routine depending on the input signals.
The motion start algorithm consists, first of all, of a comparison of the movement intent signal with a variable threshold to determine the start of the exoskeleton movement. The variable threshold is given by an average of plus an offset; i.e.,
where the average of () is obtained from the last 50 samples of , while the offset is obtained experimentally. For these experiments, the offset was set to 1.
As a result of the comparison of the movement intent signal with the variable threshold , the flag is obtained. Once the flag is activated (), the trajectory control stage begins. During this phase, the reading of the movement intention signal is ignored, and the rehabilitation process is initiated. This process involves a movement routine where the patient performs a flexion–extension or abduction–adduction cycle, depending on the input signal. In this phase, the range of movement and duration can be modified according to the capabilities of the patient. The adaptability of the movement routine is crucial for a personalized rehabilitation. By adjusting the parameters of the trajectory, the system can fit each patient’s unique progress and needs. For instance, in the early stages of rehabilitation, when the patient’s muscles are still weak, the system will set a lower amplitude and frequency to prevent overexertion and potential injury. As the patient gradually builds strength and flexibility, these parameters can be increased progressively to provide a more challenging workout that promotes further improvement. To assist the patient in correctly executing the movement routine, trajectory control by the backstepping approach, as defined in (10), is implemented.
Upon completion of the movement cycle, the rest stage commences. In this phase, the exoskeleton returns to the rest position () for a predefined time (). This stage is designed to delay the reading of the movement intention signals, allowing the patient to rest between rehabilitation cycles. It is important to note that the resting time can be adjusted according to the needs of each patient. This rest period is essential for preventing fatigue and allowing muscles to recover, thereby reducing the risk of strain or injury.
The rest time can be tailored based on the patient’s endurance and overall health, minimizing risks. At the end of the rest stage, the algorithm resumes measuring movement intention signals, awaiting the activation of the flag once again. This cyclical process of activity and rest ensures a structured and effective rehabilitation regimen that adapts dynamically to the patient’s progress. Figure 5 shows the exoskeleton motion start algorithm flow chart, which illustrates each of the stages previously explained.
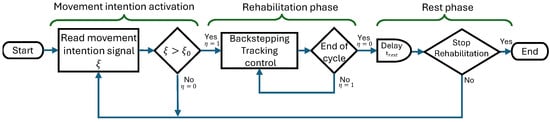
Figure 5.
Exoskeleton motion start algorithm flow chart.
Meanwhile, Figure 6 graphically depicts an example of how the exoskeleton motion start algorithm process is carried out. Initially, the system waits for the activation of the flag by reading the movement intention signal , shown in blue. Once the threshold () is surpassed, the backstepping trajectory control stage starts, with the desired and actual trajectories shown in green and red, respectively. After the movement cycle is completed, the rest stage begins, which in this case lasts s. Finally, the system restarts the process of detecting movement intention, waiting for the flag to be activated again.
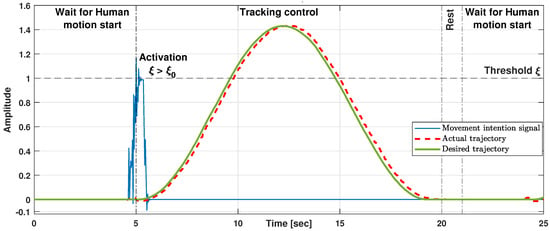
Figure 6.
Example of exoskeleton motion start algorithm.
2.5. Experimental Protocol
To test the efficiency of our approach, we conducted a concept test experiment with four healthy voluntary subjects (4 males, 31/31/30/24 years old, height 164/166/168/168 cm, weight 74/62/60/66 kg). The experimental procedures were approved by the Ethics and Safety Committee for Research in Human Beings of the National Laboratory in Autonomous Vehicles and Exoskeletons of the Center for Research and Advanced Studies of the National Polytechnic Institute, CDMX, México. Participants signed an informed written consent to participate in the study after being presented with the objectives of the study and experimental protocol.
The experimental protocol consisted of two stages, a training stage and a movement intent detection stage, which are detailed below:
- In the first stage, each of the subjects was asked to wear the glenohumeral joint rehabilitation exoskeleton to perform a series of passive rehabilitation routines so they could become familiar with the exercise. This stage helped determine the amplitude and duration of the movements which were comfortable for each subject. The passive rehabilitation routine consisted of 5 flexion–extension movements followed by 5 shoulder abduction–adduction movements, with a resting time of 5 s between each of them. The final amplitude of the movements ranged from 0.6 to 0.9 rad for flexion–extension and from 0.6 to 0.7 rad for abduction–adduction, while the duration of each movement varied between 8.3 and 15.5 s.
- Later, in the second stage, the mode of the exoskeleton was changed to that of “movement intent detection” (Figure 7). In this mode, the subjects were asked to try to perform the same movements they performed in the previous stage. Although it was suggested to the subjects to rest 5 s between each exercise, the subjects had complete freedom to choose when to start each movement, as long as the rest was longer than 2 s. This series of exercises was repeated twice. For each attempt, the movement began from the natural anatomical position (the relaxed arms at the sides of the torso) which was called the “initial position”; in case of detecting the movement intent, the exoskeleton performs a movement cycle with the parameters captured in the training stage and ends again in the initial position pending another attempt of movement by the subject. Throughout this phase, subjects were asked to indicate the robot’s correct or incorrect detections; that is, if the robot executed a rehabilitation routine, the subject was asked to indicate whether or not he attempted to do so, or to indicate the case in which the robot did not detect a movement that the user did attempt to make. In order to reduce incorrect detections, before carrying out the two series of previously mentioned exercises, a manual adjustment of the parameter was executed for each participant through 3 offline detection tests. The parameter had an adjustment range between 0.3 and 1.
 Figure 7. Movement intent detection experimental tests.
Figure 7. Movement intent detection experimental tests.
3. Experimental Results
3.1. Movement Intent Detection Experimental Results
From the experiments performed, the data shown in Table 3 for flexion–extension movements and in Table 4 for abduction–adduction movements were obtained, where true positive (TP) indicates the number of cases that the test detected the subject’s motion intention and the subject actually attempted to move. False positive (FP) indicates the number of cases that the test detected an intent to move but that actually the subject did not intend to move, and false negative (FN) indicates the number of cases that the test did not detect the intention of movement of the subject but actually the subject intended to move.

Table 3.
Movement intent detections for flexion–extension.

Table 4.
Movement intent detections for abduction–adduction.
To analyze these data, the Sensitivity and Specificity Method was used, from which the following indexes were obtained:
- Sensitivity: The proportion of positive cases that are well detected by the experiment.
- Positive predictive value (PPV): The proportion of truly positive cases among positive cases detected by the experiment.
3.2. Control Law Performance
Figure 8 shows graphically the signals obtained during a flexion–extension motion detection experiment. The upper graph shows the desired trajectory, the actual trajectory, and the motion intention signal, while the lower graph shows the control signal input during the experiment. Figure 9 shows similar graphs, but for an abduction–adduction motion detection experiment.
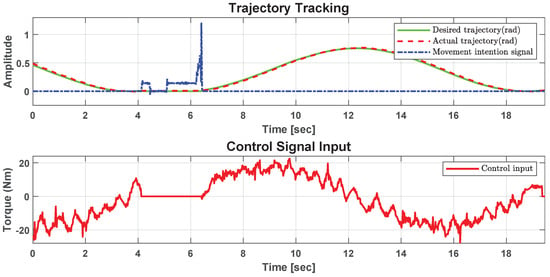
Figure 8.
Trajectory tracking and control signal input for extension detection.
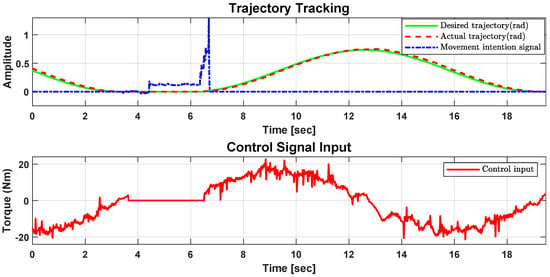
Figure 9.
Trajectory tracking and control signal input for abduction detection.
Figure 10 shows in detail the articular behavior of the robot for an abduction exercise when the subject is opposed to tracking the trajectory.
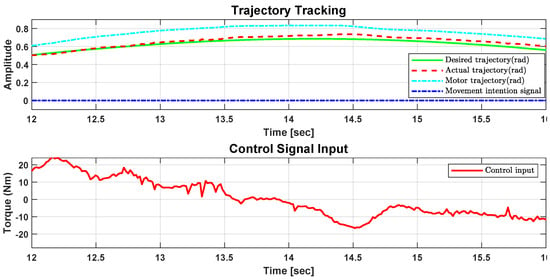
Figure 10.
Detail of trajectory tracking and control signal input for abduction exercise.
4. Conclusions
The experimental results presented in this work showed a good performance based on the proposed backstepping control strategy even though the perturbations are not considered in the stability analysis; robustness is proved in a real-time experiment. Stiffness compliance between the human body and the exoskeleton is a priority issue, and the SEA elastic element provided human comfort. The flexion–extension control allowed the human to move in the desired trajectories. In the case of abduction–adduction trajectory tracking, the weight of the links 1 and 2 were compensated for by the control law. This behavior was observed in the experimental results without tradeoff between comfort and performance.
Following a smooth exoskeleton trajectory avoids sudden movements. If the user tries to oppose the trajectory, the elastic joint acts to avoid a rude trajectory. The motor actuator has a positive offset trajectory with respect to the exoskeleton link, this offset is equivalent to . In the case when the user exerts enough effort not to follow the desired trajectory, the exoskeleton link only reduces the offset due to the elastic actuator. This offset could also be changed by K. When K is large enough the offset is almost zero, which means a direct connection between the motor and the exoskeleton link. In the 14.5 s (Figure 10) the user pushed up to avoid following the trajectory, which means the offset trajectory was reduced but the link followed gently the desired trajectory.
From the data shown in Table 3 and Table 4, and the results obtained from the sensitivity analysis, it can be observed that our movement intent detection approach has a sensitivity of , which means that all of the subjects’ attempts to move have been detected correctly. On the other hand, a positive predictive value of can also be observed, which indicates that of cases detected as attempts to move but which were not actually real. These cases can be attributed to small involuntary movements of the subject.
In contrast to other motion intention detection techniques, described in the introduction section, our approach has better sensitivity and the parameters are easier to adjust. On the other hand, this proposed algorithm requires a passive training stage as well as a threshold adjustment for each subject to start the movement stage.
Author Contributions
Conceptualization, Y.R.-L.; Data curation, Y.R.-L.; Formal analysis, Y.R.-L., S.S., J.F. and D.C.-B.; Funding acquisition, S.S. and R.L.; Investigation, Y.R.-L., J.F. and D.C.-B.; Methodology, Y.R.-L.; Project administration, S.S. and R.L.; Resources, R.L.; Software, Y.R.-L. and D.C.-B.; Supervision, Y.R.-L. and R.L.; Validation, Y.R.-L. and D.C.-B.; Visualization, Y.R.-L. and S.S.; Writing—original draft, Y.R.-L.; Writing—review and editing, Y.R.-L., R.L. and S.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
The study was conducted according to the guidelines of the Declaration of Helsinki, and approved by the Ethics and Safety Committee for Research in Human Beings of the National Laboratory in Autonomous Vehicles and Exoskeletons of the Center for Research and Advanced Studies of the National Polytechnic Institute, CDMX, México.
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
Data are contained within the article.
Acknowledgments
The authors are grateful to National Council of Science, Humanities and Technology (CONAHCYT) for its support.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Calafiore, D.; Negrini, F.; Tottoli, N.; Ferraro, F.; Ozyemisci-Taskiran, O.; de Sire, A. Efficacy of robotic exoskeleton for gait rehabilitation in patients with subacute stroke: A systematic review. Eur. J. Phys. Rehabil. Med. 2022, 58, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Chien, W.T.; Chong, Y.Y.; Tse, M.K.; Chien, C.W.; Cheng, H.Y. Robot-assisted therapy for upper-limb rehabilitation in subacute stroke patients: A systematic review and meta-analysis. Brain Behav. 2020, 10, e01742. [Google Scholar] [CrossRef] [PubMed]
- De Santis, A.; Siciliano, B.; De Luca, A.; Bicchi, A. An atlas of physical human–robot interaction. Mech. Mach. Theory 2008, 43, 253–270. [Google Scholar] [CrossRef]
- Lagoda, C.; Schouten, A.C.; Stienen, A.H.; Hekman, E.E.; van der Kooij, H. Design of an electric series elastic actuated joint for robotic gait rehabilitation training. In Proceedings of the 2010 3rd IEEE RAS & EMBS International Conference on Biomedical Robotics and Biomechatronics, Tokyo, Japan, 26–29 September 2010; pp. 21–26. [Google Scholar]
- Shakeel, A.; Navid, M.S.; Anwar, M.N.; Mazhar, S.; Jochumsen, M.; Niazi, I.K. A review of techniques for detection of movement intention using movement-related cortical potentials. Comput. Math. Methods Med. 2015, 2015, 346217. [Google Scholar] [CrossRef] [PubMed]
- Losey, D.P.; McDonald, C.G.; Battaglia, E.; O’Malley, M.K. A review of intent detection, arbitration, and communication aspects of shared control for physical human–robot interaction. Appl. Mech. Rev. 2018, 70, 010804. [Google Scholar] [CrossRef]
- Wang, D.; Gu, X.; Yu, H. Sensors and algorithms for locomotion intention detection of lower limb exoskeletons. Med. Eng. Phys. 2023, 113, 103960. [Google Scholar] [CrossRef] [PubMed]
- Pons, J.L.; Moreno, J.C.; Torricelli, D.; Taylor, J. Principles of human locomotion: A review. In Proceedings of the 2013 35th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Osaka, Japan, 3–7 July 2013; pp. 6941–6944. [Google Scholar]
- Bandara, D.; Kiguchi, K. Brain signal acquisition methods in BCIs to estimate human motion intention—A survey. In Proceedings of the 2018 International Symposium on Micro-NanoMechatronics and Human Science (MHS), Nagoya, Japan, 9–12 December 2018; pp. 1–7. [Google Scholar]
- Lana, E.P.; Adorno, B.V.; Tierra-Criollo, C.J. Detection of movement intention using EEG in a human-robot interaction environment. Res. Biomed. Eng. 2015, 31, 285–294. [Google Scholar] [CrossRef]
- Zheng, Y.; Zheng, G.; Zhang, H.; Zhao, B.; Sun, P. Mapping Method of Human Arm Motion Based on Surface Electromyography Signals. Sensors 2024, 24, 2827. [Google Scholar] [CrossRef]
- Xiang, Q.; Wang, J.; Liu, Y.; Guo, S.; Liu, L. Gait recognition and assistance parameter prediction determination based on kinematic information measured by inertial measurement units. Bioengineering 2024, 11, 275. [Google Scholar] [CrossRef]
- Net’uková, S.; Bejtic, M.; Malá, C.; Horáková, L.; Kutílek, P.; Kauler, J.; Krupička, R. Lower limb exoskeleton sensors: State-of-the-art. Sensors 2022, 22, 9091. [Google Scholar] [CrossRef]
- Sanchez-Villamañan, M.d.C.; Gonzalez-Vargas, J.; Torricelli, D.; Moreno, J.C.; Pons, J.L. Compliant lower limb exoskeletons: A comprehensive review on mechanical design principles. J. Neuroeng. Rehabil. 2019, 16, 55. [Google Scholar] [CrossRef] [PubMed]
- Penna, M.F.; Trigili, E.; Amato, L.; Eken, H.; Dell’Agnello, F.; Lanotte, F.; Gruppioni, E.; Vitiello, N.; Crea, S. Decoding Upper-Limb Movement Intention Through Adaptive Dynamic Movement Primitives: A Proof-of-Concept Study with a Shoulder-Elbow Exoskeleton. In Proceedings of the 2023 International Conference on Rehabilitation Robotics (ICORR), Singapore, 24–28 September 2023; pp. 1–6. [Google Scholar]
- Bi, L.; Xia, S.; Fei, W. Hierarchical decoding model of upper limb movement intention from EEG signals based on attention state estimation. IEEE Trans. Neural Syst. Rehabil. Eng. 2016, 29, 2008–2016. [Google Scholar] [CrossRef] [PubMed]
- Ferrero, L.; Quiles, V.; Ortiz, M.; Iáñez, E.; Azorín, J.M. A BMI based on motor imagery and attention for commanding a lower-limb robotic exoskeleton: A case study. Appl. Sci. 2021, 11, 4106. [Google Scholar] [CrossRef]
- Tang, Z.; Sun, S.; Zhang, S.; Chen, Y.; Li, C.; Chen, S. A brain-machine interface based on ERD/ERS for an upper-limb exoskeleton control. Sensors 2016, 16, 2050. [Google Scholar] [CrossRef] [PubMed]
- Saga, N.; Tanaka, Y.; Doi, A.; Oda, T.; Kudoh, S.N.; Fujie, H. Prototype of an ankle neurorehabilitation system with heuristic BCI using simplified fuzzy reasoning. Appl. Sci. 2019, 9, 2429. [Google Scholar] [CrossRef]
- Wang, Q.; Chen, C.; Mu, X.; Wang, H.; Wang, Z.; Xu, S.; Guo, W.; Wu, X.; Li, W. A Wearable Upper Limb Exoskeleton System and Intelligent Control Strategy. Biomimetics 2024, 9, 129. [Google Scholar] [CrossRef] [PubMed]
- Kong, D.; Wang, W.; Guo, D.; Shi, Y. RBF sliding mode control method for an upper limb rehabilitation exoskeleton based on intent recognition. Appl. Sci. 2022, 12, 4993. [Google Scholar] [CrossRef]
- Li, S.; Zhang, L.; Meng, Q.; Yu, H. A Real-Time Control Method for Upper Limb Exoskeleton Based on Active Torque Prediction Model. Bioengineering 2023, 10, 1441. [Google Scholar] [CrossRef]
- Wang, F.; Wei, X.; Guo, J.; Zheng, Y.; Li, J.; Du, S. Research progress of rehabilitation exoskeletal robot and evaluation methodologies based on bioelectrical signals. In Proceedings of the 2019 IEEE 9th Annual International Conference on CYBER Technology in Automation, Control, and Intelligent Systems (CYBER), Suzhou, China, 29 July–2 August 2019; pp. 826–831. [Google Scholar]
- Gandolla, M.; Luciani, B.; Pirovano, D.; Pedrocchi, A.; Braghin, F. A force-based human machine interface to drive a motorized upper limb exoskeleton. A pilot study. In Proceedings of the 2022 International Conference on Rehabilitation Robotics (ICORR), Rotterdam, The Netherlands, 25–29 July 2022; pp. 1–6. [Google Scholar]
- Sun, L.; An, H.; Ma, H.; Wei, Q.; Gao, J. Adaptive Prosthetic Trajectory Estimation Based on Key Points Constraints. Appl. Sci. 2024, 14, 3063. [Google Scholar] [CrossRef]
- Kuo, C.T.; Lin, J.J.; Jen, K.K.; Hsu, W.L.; Wang, F.C.; Tsao, T.C.; Yen, J.Y. Human posture transition-time detection based upon inertial measurement unit and long short-term memory neural networks. Biomimetics 2023, 8, 471. [Google Scholar] [CrossRef]
- Lin, J.J.; Hsu, C.K.; Hsu, W.L.; Tsao, T.C.; Wang, F.C.; Yen, J.Y. Machine Learning for Human Motion Intention Detection. Sensors 2023, 23, 7203. [Google Scholar] [CrossRef] [PubMed]
- Chen, B.; Grazi, L.; Lanotte, F.; Vitiello, N.; Crea, S. A real-time lift detection strategy for a hip exoskeleton. Front. Neurorobot. 2018, 12, 17. [Google Scholar] [CrossRef] [PubMed]
- Dos Santos, L.F.; Escalante, F.M.; Siqueira, A.A.; Boaventura, T. IMU-based Transparency Control of Exoskeletons Driven by Series Elastic Actuator. In Proceedings of the 2022 IEEE 61st Conference on Decision and Control (CDC), Cancun, Mexico, 6–9 December 2022; pp. 2594–2599. [Google Scholar]
- Hu, B.; Zhang, F.; Lu, H.; Zou, H.; Yang, J.; Yu, H. Design and assist-as-needed control of flexible elbow exoskeleton actuated by nonlinear series elastic cable driven mechanism. Actuators 2021, 10, 290. [Google Scholar] [CrossRef]
- Zhu, L.; Wang, Z.; Ning, Z.; Zhang, Y.; Liu, Y.; Cao, W.; Wu, X.; Chen, C. A novel motion intention recognition approach for soft exoskeleton via IMU. Electronics 2020, 9, 2176. [Google Scholar] [CrossRef]
- Li, L.L.; Cao, G.Z.; Liang, H.J.; Zhang, Y.P.; Cui, F. Human lower limb motion intention recognition for exoskeletons: A review. IEEE Sens. J. 2023, 23, 30007–30036. [Google Scholar] [CrossRef]
- Zhang, L.; Liu, G.; Han, B.; Wang, Z.; Zhang, T. sEMG based human motion intention recognition. J. Robot. 2019, 2019, 3679174. [Google Scholar] [CrossRef]
- Planelles, D.; Hortal, E.; Costa, Á.; Úbeda, A.; Iáñez, E.; Azorín, J.M. Evaluating classifiers to detect arm movement intention from EEG signals. Sensors 2014, 14, 18172–18186. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, H.; Hu, J.; Zheng, J.; Wang, X.; Deng, J.; Wan, Z.; Wang, H.; Wang, Y. Gait pattern identification and phase estimation in continuous multilocomotion mode based on inertial measurement units. IEEE Sens. J. 2022, 22, 16952–16962. [Google Scholar] [CrossRef]
- Jang, J.; Kim, K.; Lee, J.; Lim, B.; Shim, Y. Online gait task recognition algorithm for hip exoskeleton. In Proceedings of the 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–2 October 2015; pp. 5327–5332. [Google Scholar]
- Ai, Q.; Zhang, Y.; Qi, W.; Liu, Q.; Chen, K. Research on lower limb motion recognition based on fusion of sEMG and accelerometer signals. Symmetry 2017, 9, 147. [Google Scholar] [CrossRef]
- Rosales-Luengas, Y.; Espinosa-Espejel, K.I.; Lopéz-Gutiérrez, R.; Salazar, S.; Lozano, R. Lower Limb Exoskeleton for Rehabilitation with Flexible Joints and Movement Routines Commanded by Electromyography and Baropodometry Sensors. Sensors 2023, 23, 5252. [Google Scholar] [CrossRef]
- Zhang, Y.; Han, P.; Liu, H.; Chen, J. Human motion intention recognition method based on gasbag human-machine interactive force detection and multi-source information fusion. In Proceedings of the 2022 International Conference on Service Robotics (ICoSR), Chengdu, China, 10–12 June 2022; pp. 198–204. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).