Abstract
In recent years, robot manipulator arms have become increasingly prevalent and are playing pivotal roles across various industries. Their ability to replace human labor in arduous and hazardous tasks has positioned them as indispensable assets. Consequently, there has been a surge in research efforts aimed at enhancing their operational performance. The imperative to improve their efficiency and effectiveness has garnered significant attention within the research community. In this study, a novel fault-tolerant control (FTC) scheme for robot manipulators to handle the effects of the unknown input is proposed to aid robots in achieving good tracking performance. In the first step, an extended state observer (ESO) is constructed to approximate both velocities and the unknown input in the robot system. The observer offers estimation information with good accuracy and quick convergence. The estimated signals are then combined with computed torque control (CTC), which is a useful control technique for trajectory tracking of robot manipulator systems, to construct an active FTC to decrease the influences of the unknown input. The proposed algorithm does not require velocity measurement in the design process. In addition, with a novel design approach, the combination of controller and observer provides a novel control signal that delivers higher tracking performance compared to the traditional design approach. The global and asymptotic stability of the suggested technique is proved through the Lyapunov theory. Finally, simulations are implemented on a 2-degree-of-freedom (DOF) robot manipulator to validate the efficiency of the proposed controller–observer method.
1. Introduction
In today’s industrial landscape, robot manipulator arms are commonly used in industry and play vast special roles because of their capability to replace laborers in hard and dangerous activities. They also assist in increasing both the quality and quantity of products; therefore, they help to save the cost for manufacturers and to reduce the price of products. Along with their applications, a lot of researchers have paid attention to controlling robot manipulator systems, which try to help robots track preferred trajectories with the highest tracking precision [1,2]. Practically, the robot dynamics is highly nonlinear and complex due to the coupling effect. In addition, it is impossible to precisely identify the robot dynamics due to dynamics uncertainties, including payload oscillations, frictions, external disturbances, etc. In unusual cases, with long-term working, unknown faults can appear in the system, including actuator faults, process faults, or sensor faults. They are huge challenges for researchers in this field. In this paper, faults affecting the robot are considered as extra uncertainties; thus, the total influence of unknown input in the robot system is evaluated.
In response to the challenge posed by unknown inputs, researchers have embarked on a comprehensive exploration of fault-tolerant control (FTC) techniques [3,4]. These methodologies, aimed at mitigating the disruptive effects of unknown inputs, can generally be classified into two distinct categories: passive FTC (PFTC) [5,6] and active FTC (AFTC) [7,8,9]. In the PFTC paradigm, a robust control strategy is devised to effectively manage the impact of unknown inputs without relying on feedback information from fault diagnosis methods. Given that the control mechanisms employed in PFTC are subject to greater influence from unknown inputs compared to those utilized in AFTC, PFTC strategies necessitate a higher degree of resilience to effectively counteract these effects. On the other hand, AFTC techniques incorporate online fault diagnosis methods into their design framework. By accurately approximating the unknown inputs, AFTC strategies offer significantly improved control performance compared to their PFTC counterparts. Consequently, AFTC methodologies are considered more suitable for practical applications where precise control and robust fault tolerance are essential. Through the integration of advanced fault diagnosis techniques, AFTC approaches provide a robust framework for maintaining system stability and performance in the existence of unforeseen disturbances and faults.
Numerous researchers have been concentrating their attempts on developing efficient observers to estimate the unknown input. Neural network (NN) observer is often utilized because of its learning ability and high estimation accuracy [10,11,12]. Qi et al. [13] employed a radial basis function NN (RBFNN) as an estimator to rebuild the change rate of the fault and mitigate its impact on nonlinear systems. Cho et al. [14] introduced a fault detection algorithm based on neural networks (NN), leveraging a hyperbolic tangent function as the activation function. By harnessing the capabilities of NNs, this proposed algorithm enables the estimation of fault torque, facilitating effective fault detection and diagnosis in systems. However, learning capability leads to the system being more complex; therefore, it needs higher system configuration, especially when using online training methods. The time delay estimation (TDE) method [15,16,17] is a simpler approach with good estimation performance. Kim et al. [18] introduced a TDE designed to handle the challenges posed by variations in mechanical structure, disturbances, and coupled nonlinear dynamics encountered in hydraulic excavators. The primary objective of this method is to achieve satisfactory motion-tracking regulation by accurately estimating the target trajectory and compensating for deviations caused by system uncertainties and external disturbances. In reference [19], Zhang et al. presented a control strategy termed super-twisting control, which integrates TDE to deal with nonlinear terms, including friction, external disturbances, and dynamics model uncertainties for a satellite manipulator. However, this technique requires velocity measurement, which is commonly unavailable in real robot systems. A sliding mode observer (SMO) has the ability to estimate both unknown input and system velocity with high precision and less chattering [20,21,22,23]. However, the SMO is limited in real applications because of its drawbacks, including the chattering phenomenon and the requirement of the knowledge of the unknown input bounded in choosing parameters. Another popular method for estimating system states is the high-gain observer [24]. Although the high-gain observer offers quite good estimation results, it is unable to estimate unknown input in the system. Extended state observer (ESO) is developed to overcome the drawback of the high-gain observer [25,26]. This technique is a regular method for online observation where simply changing the observer’s parameter values makes implementation simpler in realistic robot systems. Additionally, the upper bound of unknown input is not necessarily precisely known when designing ESO. Further, the ESO has the linear feature that strongly handles the perturbations, which are especially far away from the origin; therefore, the convergence rate of this observer is expeditious and provides quite good approximation accuracy. Hence, ESO can effortlessly employ it in real systems.
After faults estimation, the unknown input information is compensated for using numerous control strategies [27]. In research, many attempts have been made to address the FTC problems of robot manipulators. Proportional–integral–derivative (PID) control is famous as an elementary and monotonic control where the requirement of a dynamics model is not necessary [28,29]. Song et al. [28] introduced an adaptive fault-tolerant PID control methodology tailored for multi-input multi-output (MIMO) nonlinear systems. The approach involves the application of an adaptive algorithm for the tuning of PID gains. Naji et al. [29] proposed a modification of the PID-type control method augmented with a distributed delay term to Euler–Lagrange systems characterized by an unidentified coefficient input delay. This modification aims to increase the control performance by accounting for the delayed feedback information, which is crucial for stabilizing and regulating the dynamics of the system effectively. However, the PID control cannot provide high-ranking tracking accuracy. Adaptive control is a valuable algorithm for handling structured uncertainties [30,31,32,33]; however, it is not suitable for handling unstructured uncertainties. Neural network (NN) control with learning capability and good quality in an approximation of nonlinear function is a useful selection for modeling complicated processes and compensating for unstructured uncertainties [34,35,36]. Wu et al. [37] presented a tracking control method leveraging RBFNN with the aim of minimizing the tracking error in nonlinear systems. Qiu et al. [38] introduced an adaptive NN control algorithm tailored for MIMO nonlinear systems to tackle unknown dynamical behaviors. Nonetheless, its transient performance in the presence of disturbances may suffer due to the necessity of employing online learning techniques. On the other hand, the fuzzy logic control (FLC) technique is established on the basis of the expert’s knowledge and experience [39,40], making them appealing for addressing complex control challenges. However, despite their effectiveness in handling complex systems, FLC approaches face significant challenges in stability analysis and require a comprehensive understanding of system requirements. Sliding mode control (SMC) is a great, robust controller that has been broadly employed for FTC due to its efficiency in eliminating the impacts of unknown input [41,42,43]. It can also resolve the two major challenging problems in controlling them, which are system stability and robustness. However, the biggest disadvantage of the SMC is the chattering phenomenon, which reduces its practical, applicable ability. Computed torque control (CTC) [44,45,46] is a popular control method that has demonstrated its effectiveness in trajectory tracking of robot manipulator systems. It can perform the decoupling control of robot dynamics and obtain a good result based on feedback linearization. Nevertheless, the traditional CTC only performs appropriately under the hypothesis that an accurate and complete dynamics model of a system is provided, which is not practical.
From the motivation above, it is important to investigate an AFTC with the principal objective of enabling the robot manipulators to operate with high precision of position-tracking performance in the presence of unknown inputs. In this study, the ESO is employed to estimate both the system velocities and the unknown input. The acquired velocities are applied to the system to replace the real velocities, and the approximated unknown input is employed to eliminate their effects. To reach a superior position tracking correctness and the stability of the system under the influences of the unknown input, an AFTC method in which the CTC is combined with the ESO is proposed. Especially with a novel control design approach, the combination of the CTC and the ESO provides a novel control signal that delivers higher tracking performance compared to the traditional design approach. The proposed controller–observer algorithm delivers superior tracking precision, speedy convergence, and no chattering effect. The following are the study’s main contributions:
(1) Proposing an AFTC technique to enhance the robot systems control performance under the impacts of the unknown input;
(2) Proposing a novel control signal by using a distinctive design approach in combining controller and observer;
(3) Demonstrating the stability of the robot manipulator system through the Lyapunov theory;
(4) Removing the requirement of real velocity measurements of the robot in the design process.
This study is structured as follows. After the introduction, the problem statement and the dynamics equation of a 2-degree-of-freedom (DOF) robot manipulator are presented in Section 2. Then, the design for the robot manipulator systems of ESO is presented in Section 3. Section 4 illustrates the design of the AFTC approach using the CTC and the ESO. To demonstrate the effectiveness of the suggested tactic, numerous simulations on a serial 2-DOF robot manipulator are presented in Section 5. Ultimately, several conclusions are expressed in Section 6.
2. Problem Statement
The dynamics equation of a serial robot manipulator in Lagrangian form is typically represented as follows:
where represent the vector of the robot’s joint angular positions, velocities, and accelerations, respectively; and symbolize the inertia matrix and the Coriolis and centripetal forces, respectively; is the vector of the control input torques; denotes the gravitational forces; is the friction vector, and represents external disturbances.
The dynamics system in (1) is converted toward the following:
where represents uncertainty terms, and the function is defined as .
With long-term work, faults can occur in the system; therefore, this paper assumes that the robot manipulator system works under the influence of an unknown fault function . As a result, the dynamics system in (2) is modified as follows:
where is the time of occurrence; the element denotes the time function of the unknown faults that is defined as where ; and is the growth rate.
Remark 1.
In robot manipulator systems, there are some types of faults including actuator faults, process faults, or sensor faults. In this article, it is supposed that the system is subjected to the impacts of actuator faults .
The robotic system in (3) is transferred into the following form:
where , , and represents the unknown input.
The principal objective of this paper is to propose an AFTC tactic for the robot manipulator, enabling precise tracking of designated trajectories in the presence of unknown inputs. This novel method is crafted based on a set of underlying assumptions, which are delineated as follows.
Assumption 1.
The position measurements of the robot’s joints are available and bounded at all times.
Assumption 2.
The velocity measurements of the robot’s joints are unavailable due to the absence of tachometers in the robot system.
Assumption 3.
The derivative with respect to the time of the unknown input is limited by a positive coefficient as .
3. Design of Extended State Observer
In this part, with the assumption that the velocities are unreachable due to the lack of tachometers in the robot system, the ESO is utilized to estimate this information. Additionally, the unknown input will be rebuilt from the obtained information and afterward utilized to construct the AFTC in the later part.
For the robot system in (4), the ESO is designed as follows:
where is the estimation value of the real state , represent positive constants, the polynomial is Hurwitz, and .
According to [24], the function is a known function, and we can take . Subtracting (5) from (4) yields,
where denotes estimation error.
Theorem 1.
Consider the robot manipulator system presented in (4); if the ESO is constructed as (5) and satisfying and , then the system is stable and , , and as .
Proof of Theorem 1.
Defining an error variable as where , and . According to assumption 3, there exists a constant satisfying . The value of does not require to be precisely known.
A suitable Lyapunov function is chosen:
where P denotes a unique, positive, and symmetric matrix.
Taking the time derivative of the Lyapunov function, V yields
where
where
As we can see, the matrix A is Hurwitz; thus, there is a Q matrix that is symmetric and positive definite sufficient for the Lyapunov function.
Substituting (9) and (10) into (8), we can obtain
Therefore,
To guarantee the robot system stability, we enforce ; thus, the error variable convergence is provided as follows:
□
Remark 2.
It is important to highlight that the integration of state estimation within the closed-loop system necessitates a period of convergence for achieving accurate approximation of the system states. This convergence time signifies a transient phase during which the system’s states gradually align with their true values. However, it is imperative to acknowledge that throughout this convergence period, additional errors may persist within the system. These residual errors, inherent to the convergence process, have the capacity to adversely affect the system’s performance. In some cases, they may even lead to instability, posing significant challenges to the overall control effectiveness. Therefore, meticulous consideration of the convergence dynamics and their implications is essential when employing state estimation techniques within closed-loop systems. Such insights can inform the design of robust control strategies capable of mitigating the transient effects and ensuring stable and reliable system operation.
4. Design of ESO-Based CTC Controller
In this section, an AFTC technique using CTC is designed to overcome the effects of the unknown input with high control accuracy. Moreover, it is crucial to note that the control methodology outlined in this study is predicated on the assumption that only position sensors are accessible for system feedback. Normally, the real velocity signal is used in the design process and then replaced by the estimated velocity in the implementation phase. This method makes the control design process simpler but causes some elements of the control signal not to be fully considered. As a result, the system cannot achieve the best performance and will be unstable in some situations. This paper uses a novel design process to overcome the mentioned problem.
For the system (4) with unmeasurable velocity, the real velocity, , is replaced by in the first equation. The second one is replaced by the second equation of (5). Consequently, the robot system which is utilized to design the controller is the following:
Let us denote the preferred trajectories as and the preferred velocities as . These represent the desired positions and velocities that the robot manipulator aims to follow during its operation.
Based on the system (4), defining the position tracking and velocity errors as
To improve the robustness of the conventional CTC, a novel control law of the CTC with a compensator is proposed as
Theorem 2.
For the robot manipulator system provided in (4), if the control signal is constructed as in (16), then it ensures the global and asymptotic stability of the robot manipulator system.
Proof of Theorem 2.
Let , , , and .
Defining an error variable as follows:
Taking the time derivative of the error variable, we can obtain the following:
A Lyapunov function is chosen as the energy function that enables the analysis of the stability properties of the system with the formula as follows:
Taking derivative respect to the time of the Lyapunov function yields
Substituting the control rules in (16) to (20) yields
After convergence time, the term becomes zero; thus the Equation (21) becomes
where .
Thus, Theorem 2 is completely demonstrated. □
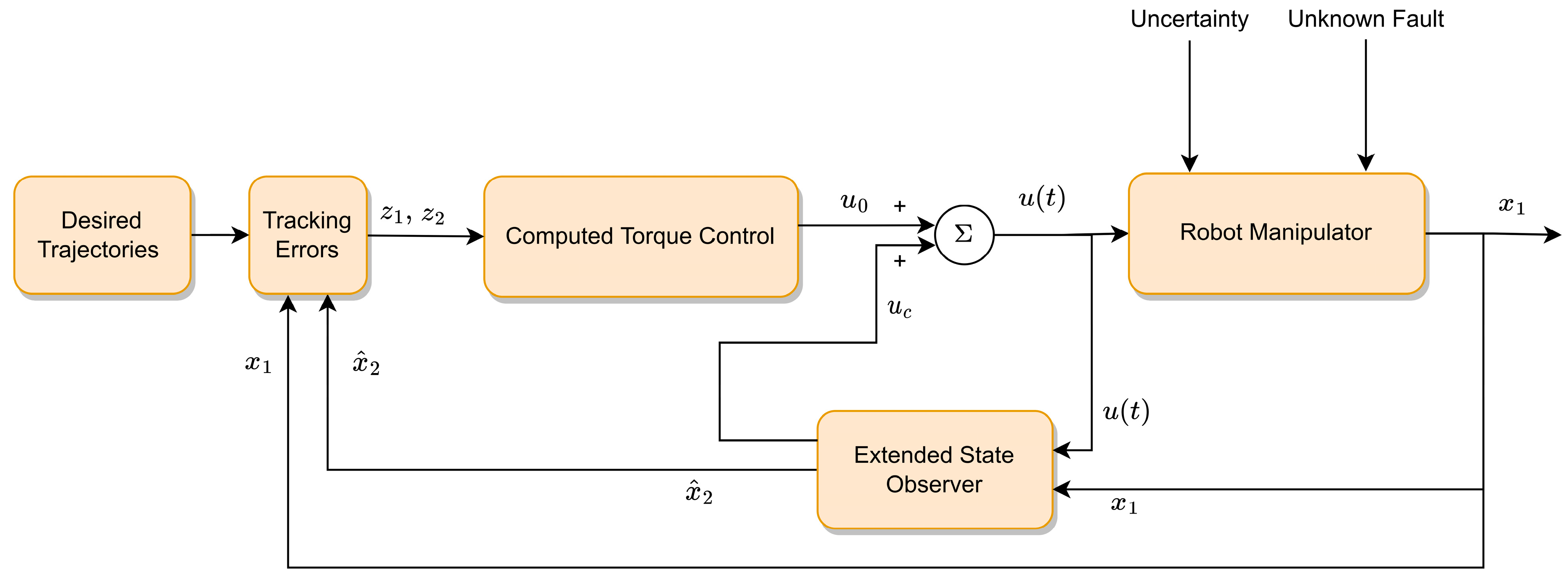
The Theorem 2 implies that the system will reach the stable equilibrium point globally and asymptotically over time, disregarding of the initial conditions. The control signal formulated in (16) is designed to regulate the system dynamics effectively, thereby ensuring stable and robust performance of the robot manipulator throughout its operational envelope. The organization of the suggested AFTC approach is expressed in Figure 1.
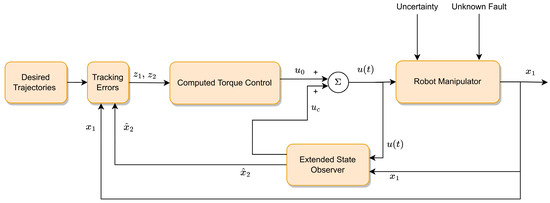
Figure 1.
Organization of the suggested AFTC approach.
5. Simulation Results
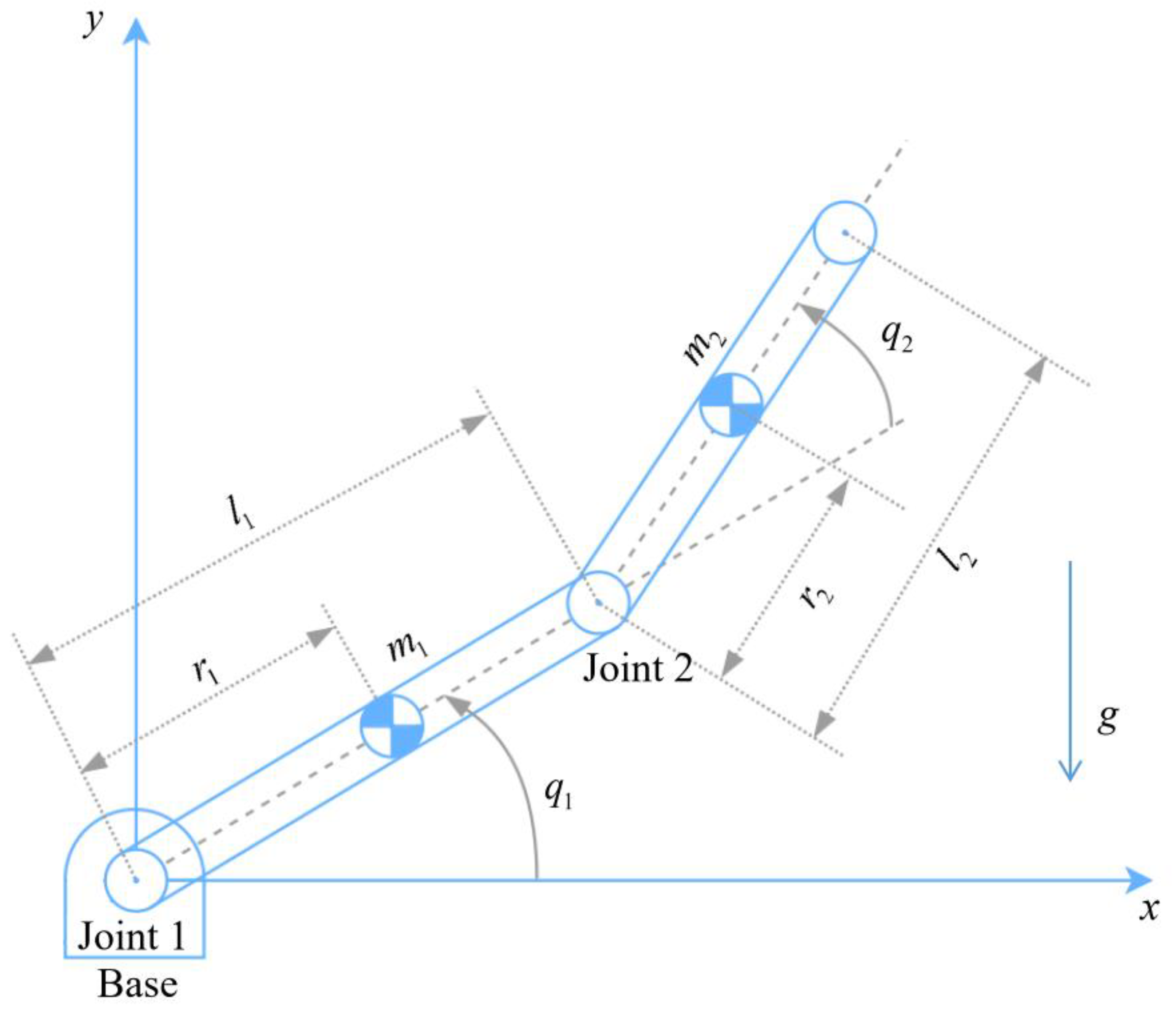
In this part, we embark on a comprehensive exploration through a series of simulations conducted on a serial 2-DOF robot manipulator. The primary objective is to meticulously demonstrate the efficiency and effectiveness of the proposed controller–observer method in regulating the manipulator’s behavior. Illustrated in Figure 2 is the configuration of the robot manipulator arm, providing a visual reference for its structural layout and design. To facilitate a detailed analysis, the dynamics model of the robot is meticulously outlined, incorporating specific parameters as detailed in Table 1. This comprehensive setup lays the groundwork for our extensive simulations, enabling a thorough evaluation of the proposed methodology across various scenarios and operational conditions. Through these simulations, we aim to elucidate the robustness, stability, and overall performance of the proposed controller–observer approach, offering valuable insights into its practical applicability and potential benefits in real-world settings.
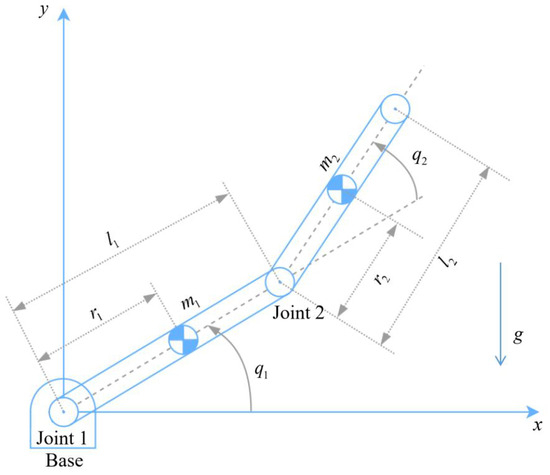
Figure 2.
Structure of the serial 2-DOF robot manipulator.

Table 1.
Specific parameters of the 2-DOF robot manipulator.
Inertia matrix
where
Coriolis and centripetal term
Gravitational term
In this simulation part, MATLAB/Simulink software is utilized, with sampling time is s.
The preferred trajectories are supposed as follows:
The friction and disturbance forces are supposed to be as follows:
The simulations include two parts. In the first part, the estimation results of the ESO will be shown. According to [25], the parameter values of the ESO in (5) are carefully chosen as , , , and . For the second part, to validate the efficiency of the suggested algorithm, its control performance is compared to two established controllers: (1) the conventional CTC, devoid of any observer compensation, and (2) the CTC integrated with ESO compensation in which the control signal is designed by traditional approach as in Appendix A. The parameters of the CTC are selected as . The simulations are performed for the robot manipulator under two working conditions as follows.
- Simulation case 1: In this working condition, incipient actuator faults are supposed to happen at joint 1 at occurrence time s, and happen at joint 2 at s with the evolution rate .
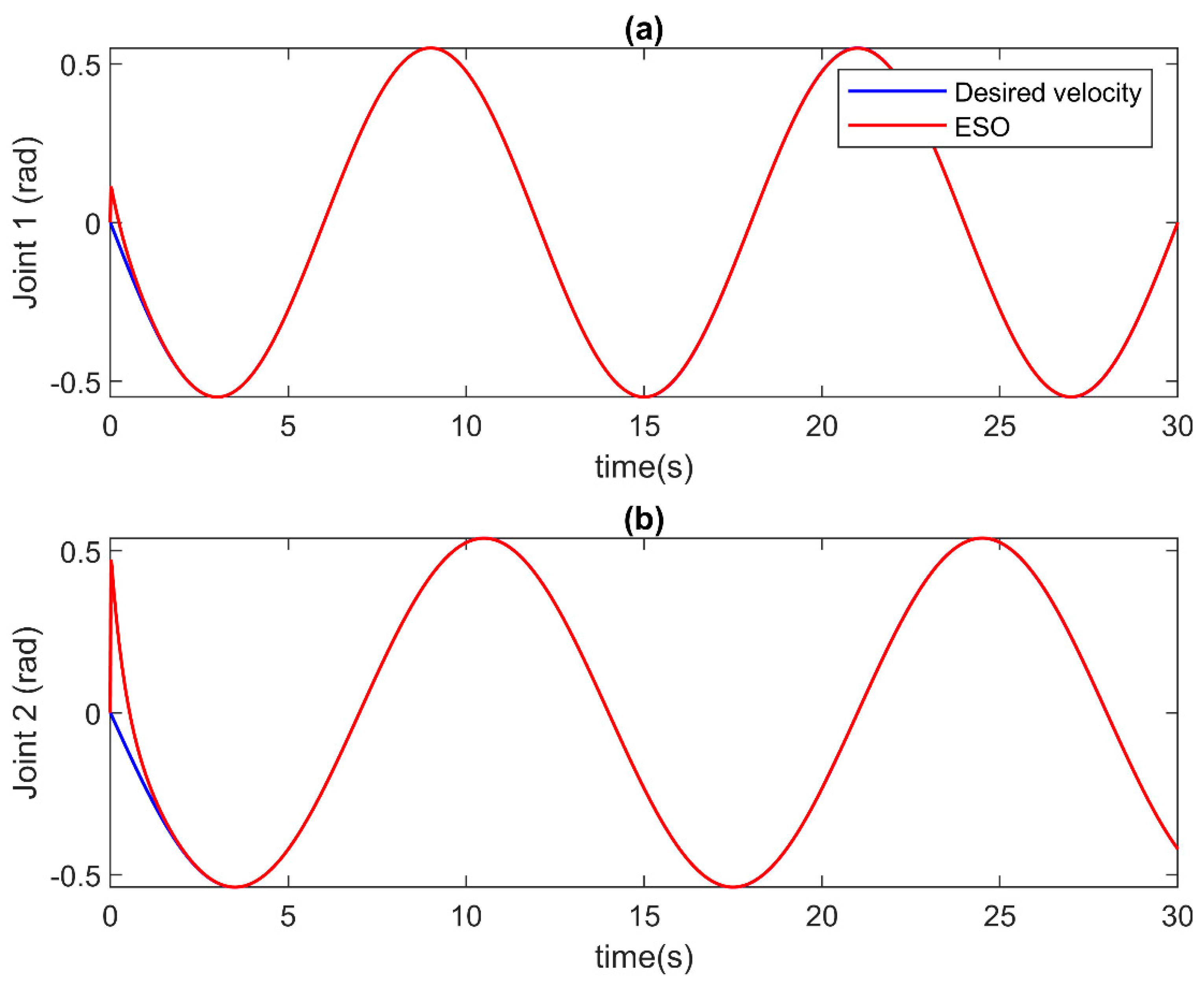
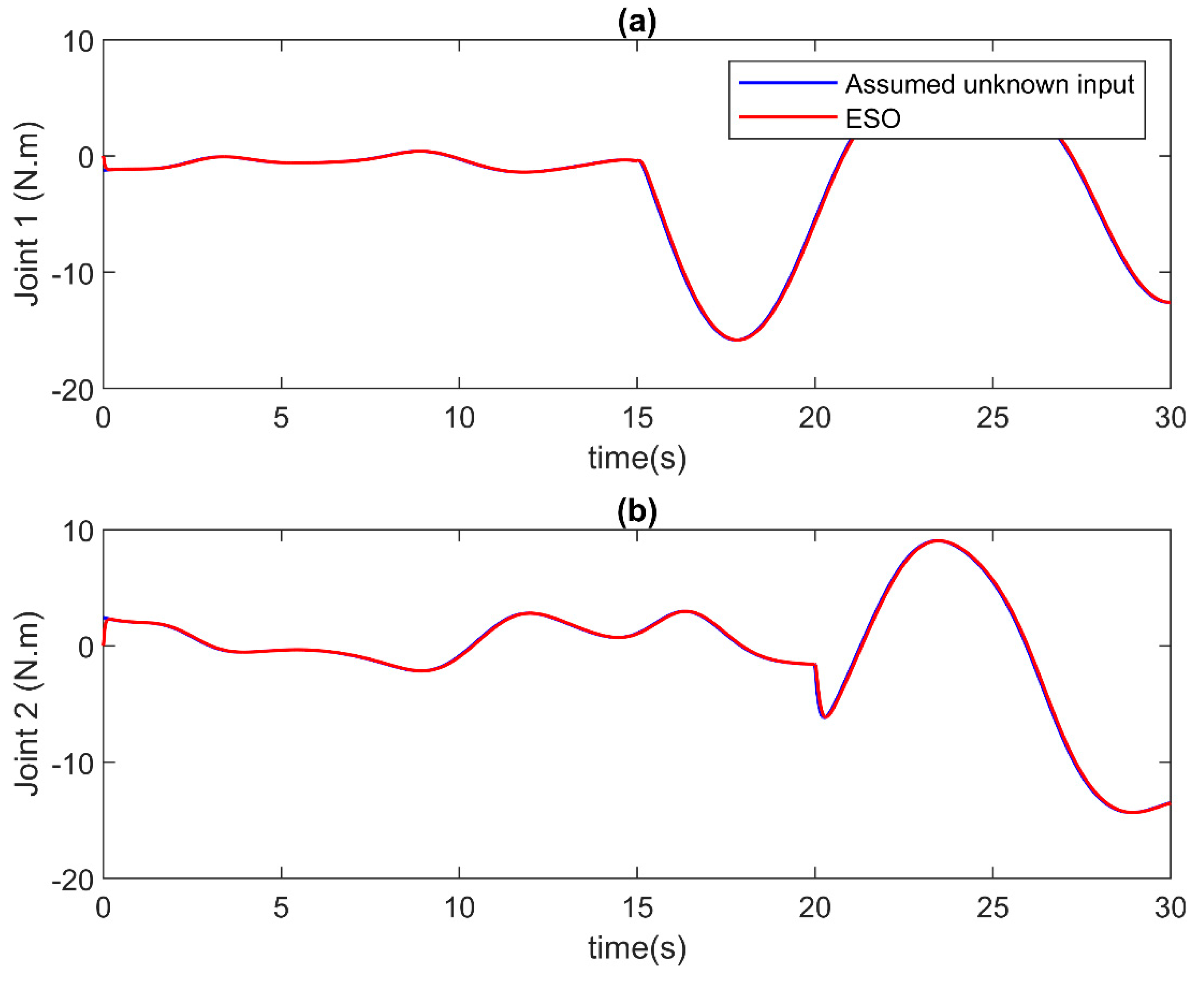
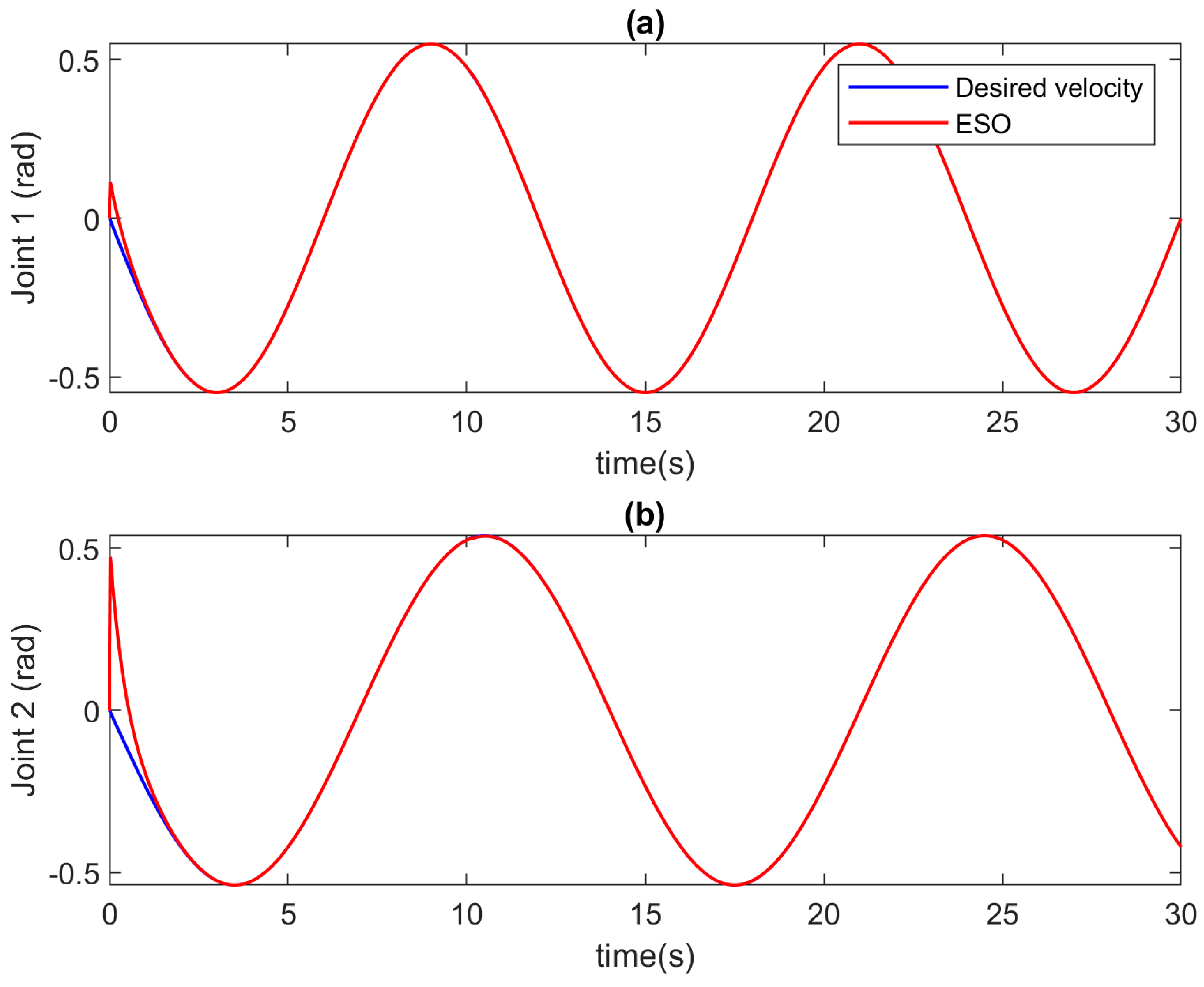
In this case, the faults are slowly developed in the robot system. The estimation outcomes generated by the ESO are visually depicted in Figure 3 and Figure 4. Figure 3 meticulously illustrates the velocity approximation results, while Figure 4 meticulously presents the estimation outcomes for unknown inputs at each joint. These figures collectively highlight the commendable performance of the ESO in providing accurate estimations for both velocity and unknown inputs. Moreover, it is noteworthy that the estimation process exhibits a remarkable speed, indicating the efficiency of the ESO in rapidly and accurately estimating the unknown input of the system under consideration.
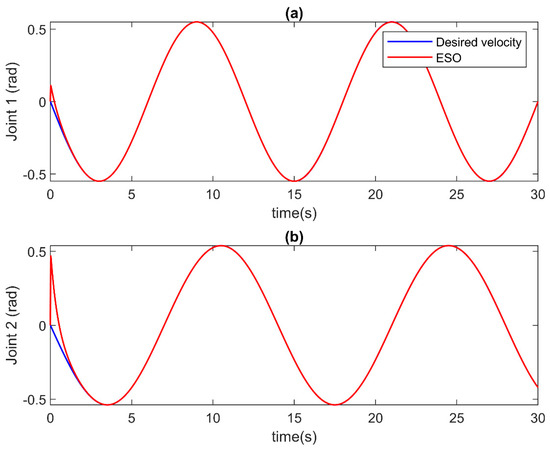
Figure 3.
The velocity estimation of ESO in case of incipient faults at (a) Joint 1, and (b) Joint 2.
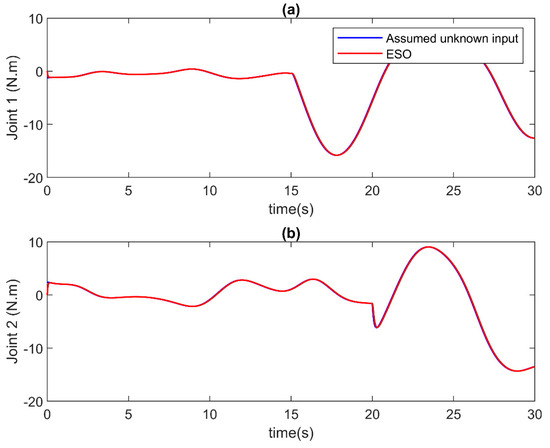
Figure 4.
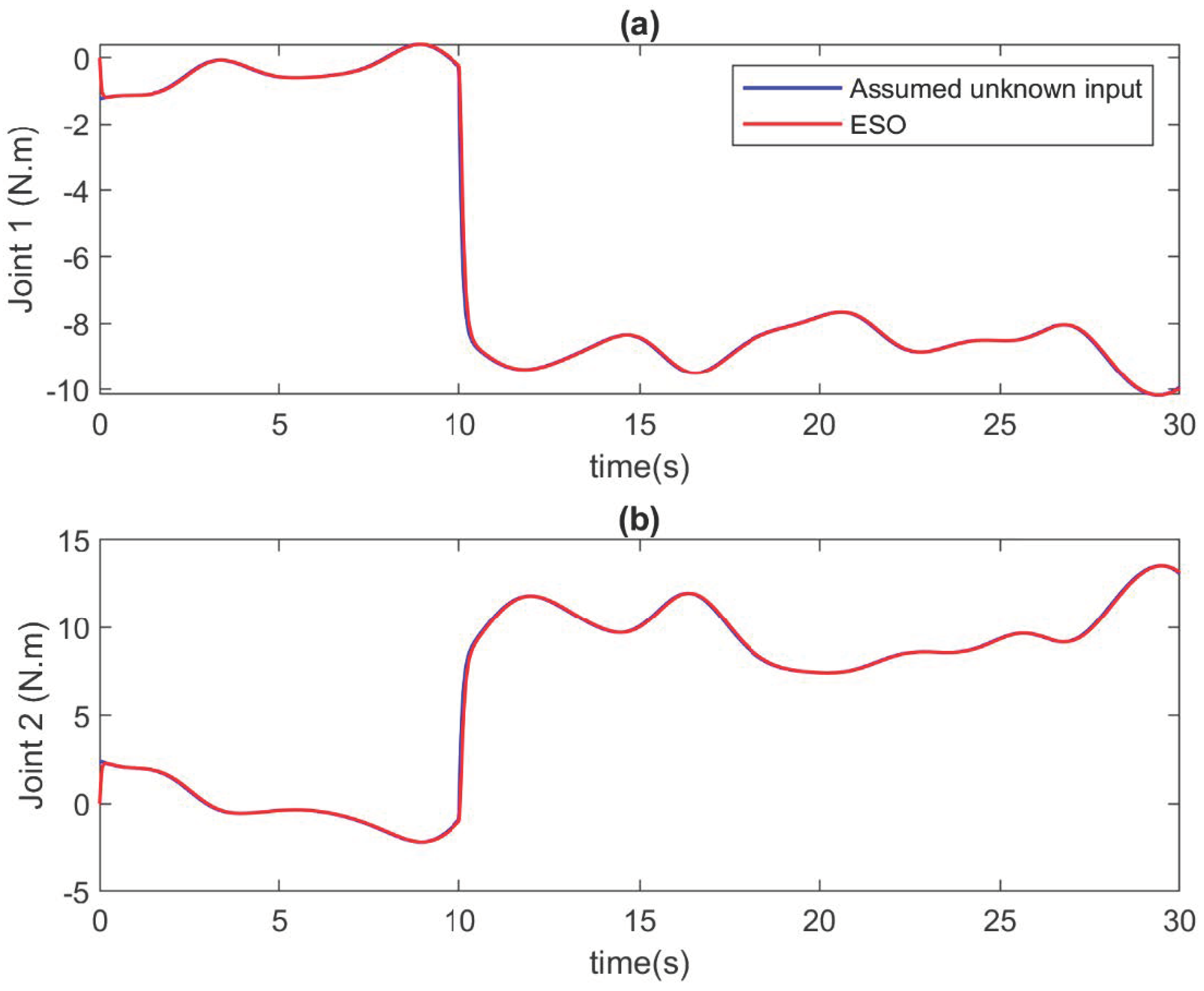
The unknown input estimation of ESO in case of incipient faults at (a) Joint 1, and (b) Joint 2.
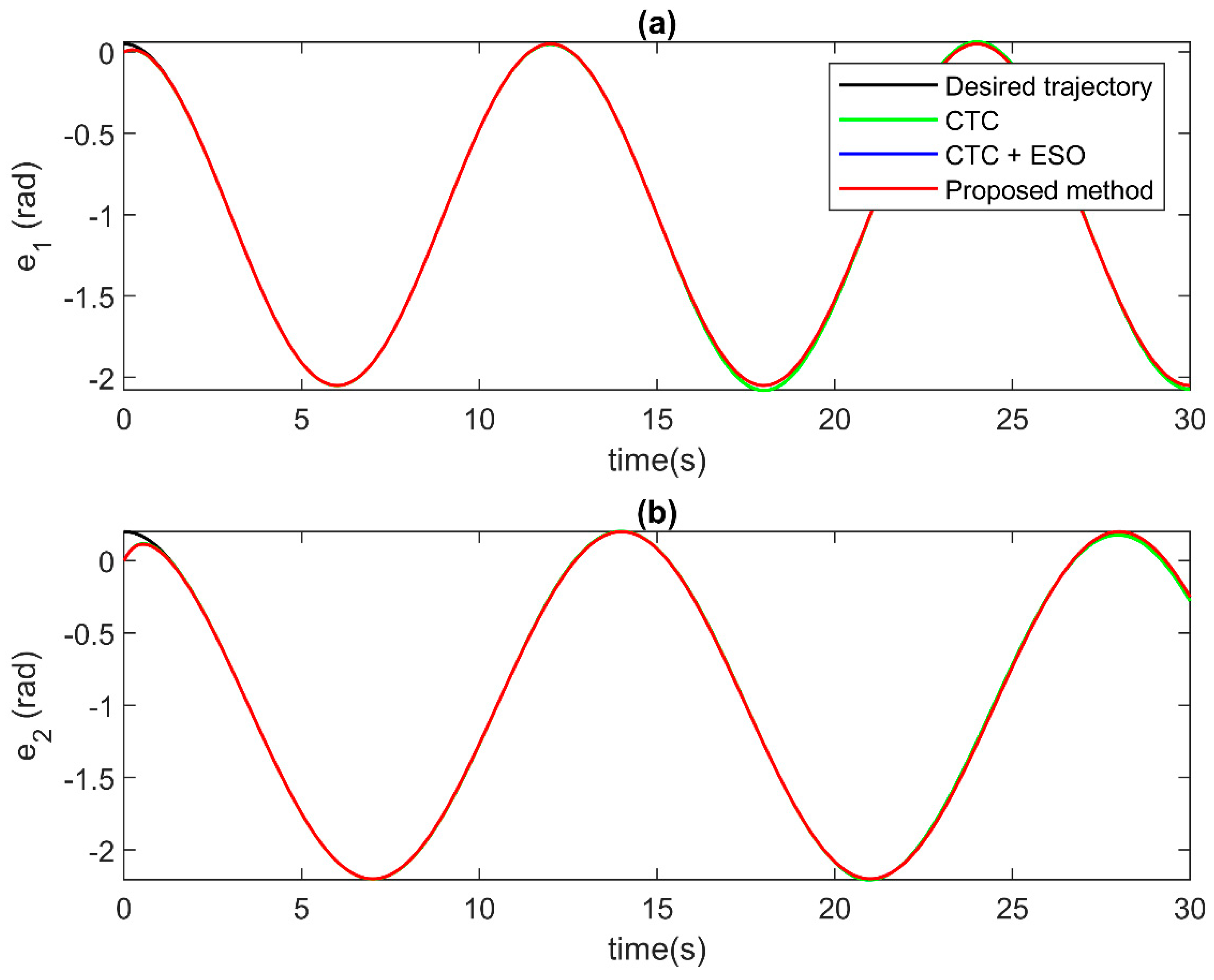
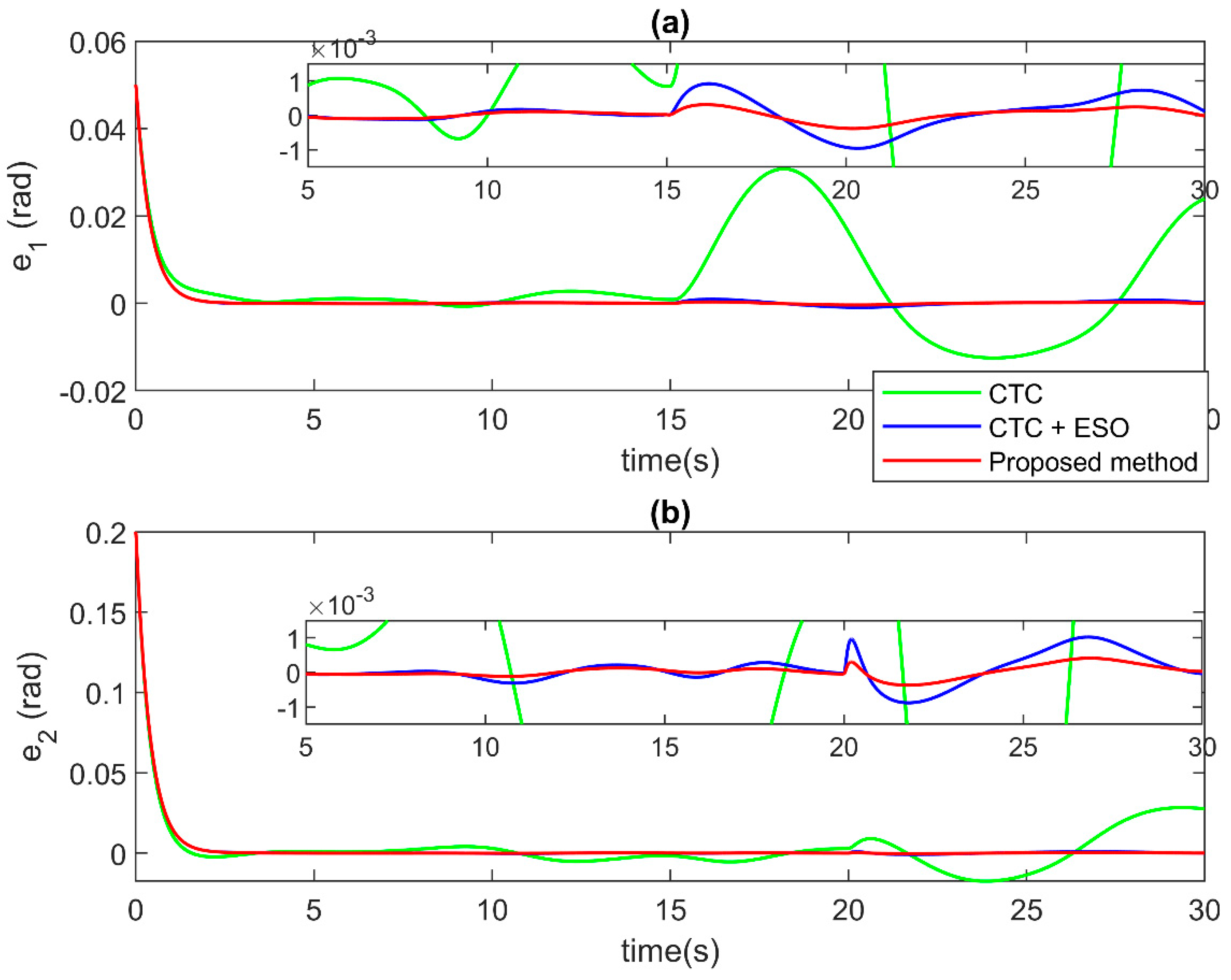
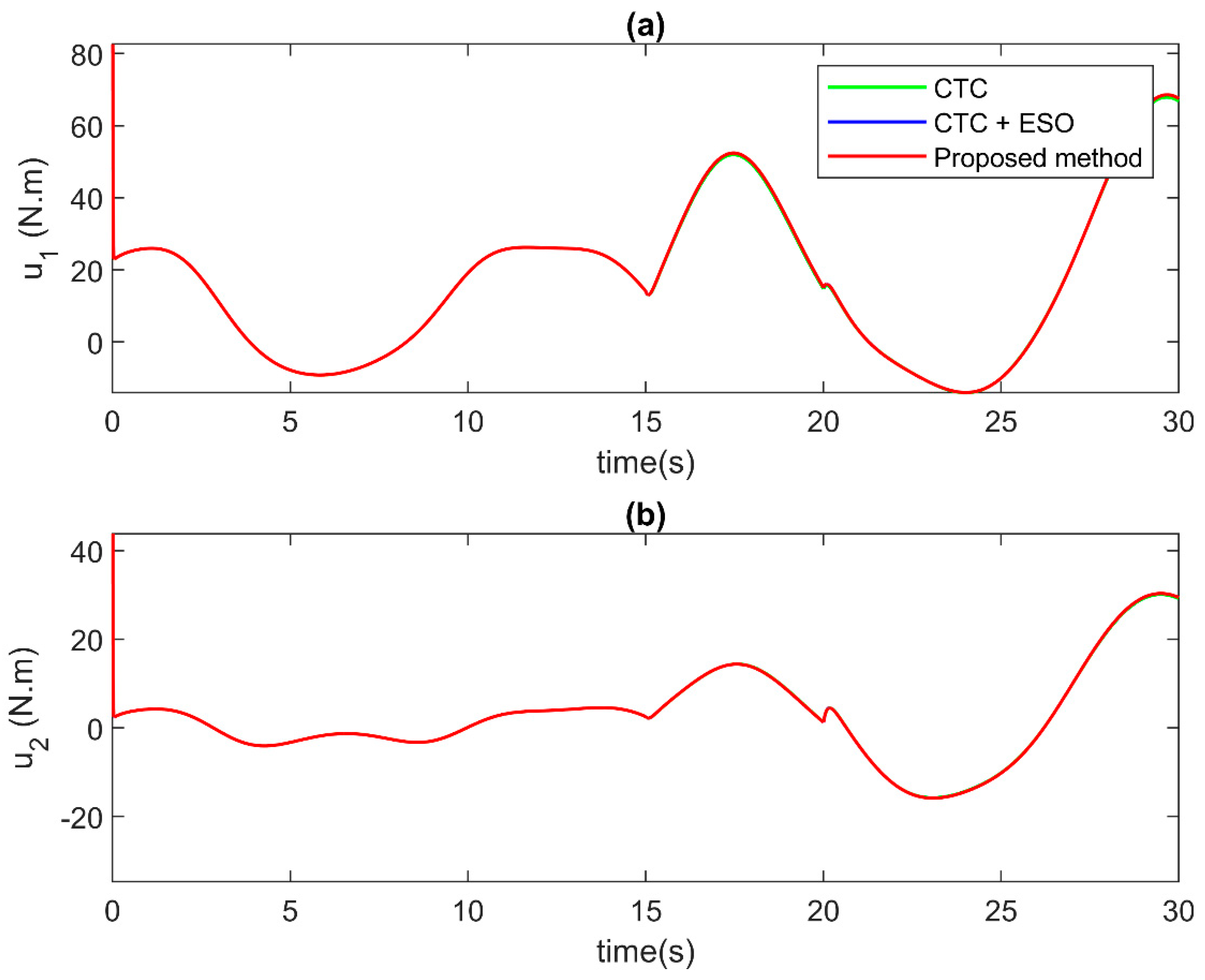
For the control performance validation, the comparison results among control algorithms are displayed in Figure 5, Figure 6 and Figure 7. Figure 5 and Figure 6 present the comparison of position tracking errors and the position tracking errors under the effect of incipient faults. As illustrated in the figures, the CTC without compensation (the green solid line) offers acceptable tracking performance before the occurrence of faults. However, when faults happen, its tracking accuracy becomes worse. For the CTC with the ESO compensation (the blue solid line), the tracking accuracy is higher than that of the CTC. The better tracking result is shown before faults occur and even under the effects of faults. For the proposed control algorithm, thanks to the special design approach, the compensator from ESO has a higher precision compensation signal. Therefore, the proposed AFTC technique (the red solid line) offers the best tracking performance among the three control methods. Notably, the proposed control signal not only helps to increase convergence speed but also reduces tracking errors. Figure 7 illustrates the comparison of the control input signal. As in the results, all three controllers provide control input without a chattering phenomenon; therefore, the proposed control algorithm is suitable for practical application.
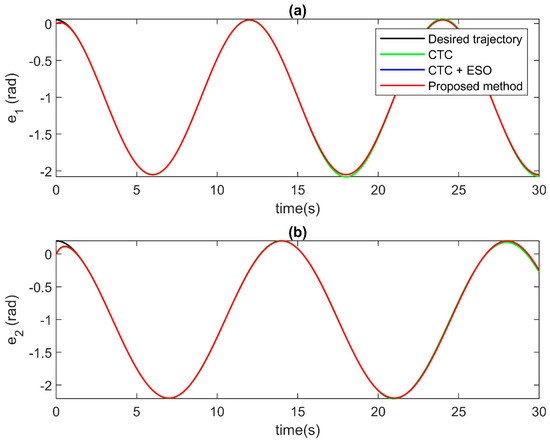
Figure 5.
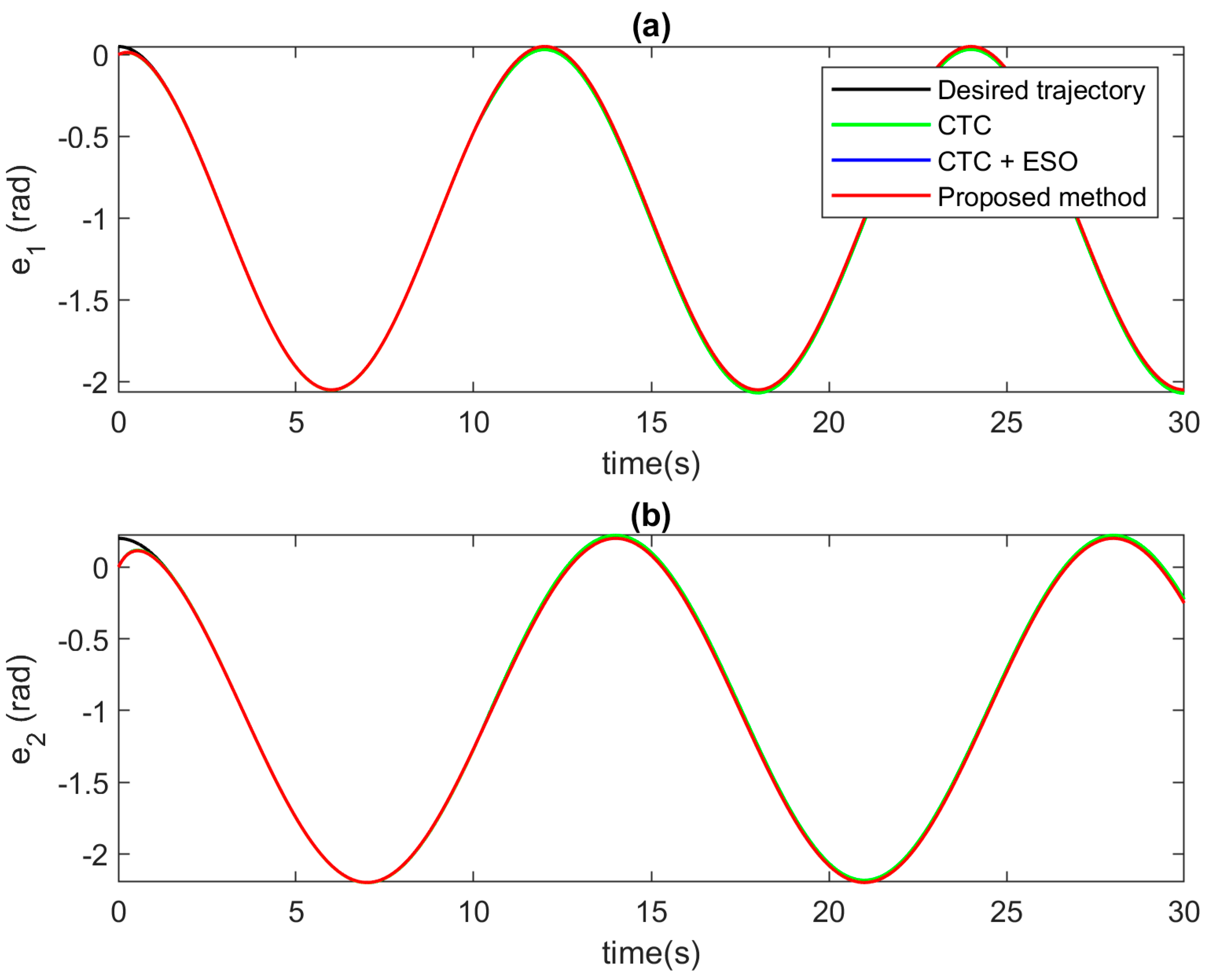
Position tracking at each joint in case of incipient faults at (a) Joint 1, and (b) Joint 2.
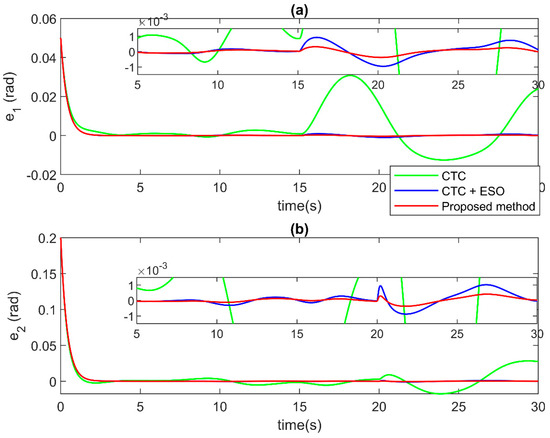
Figure 6.
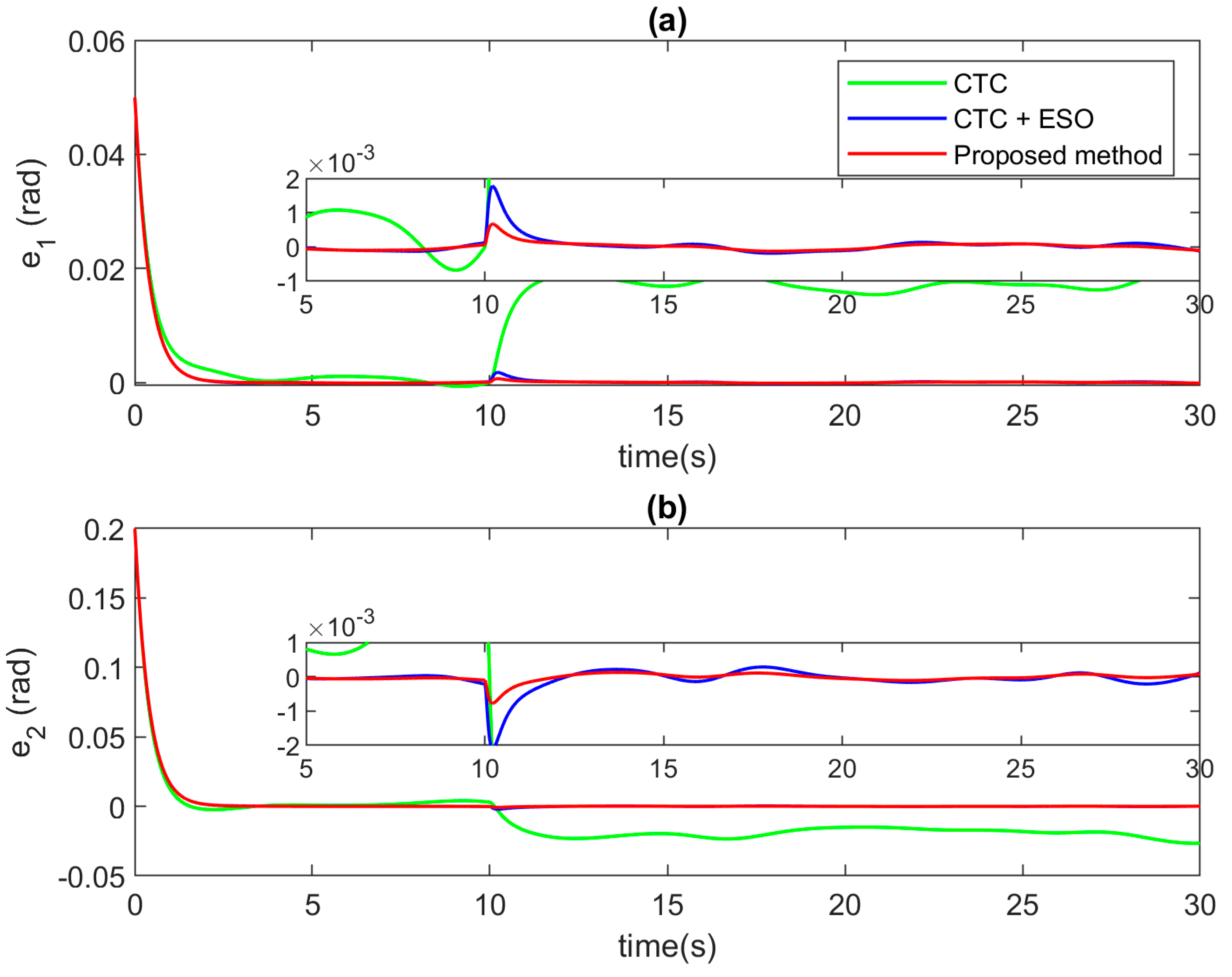
Comparison of tracking errors at each joint in case of incipient faults at (a) Joint 1, and (b) Joint 2.
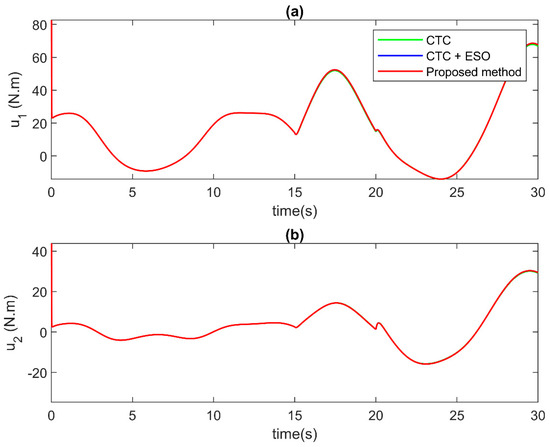
Figure 7.
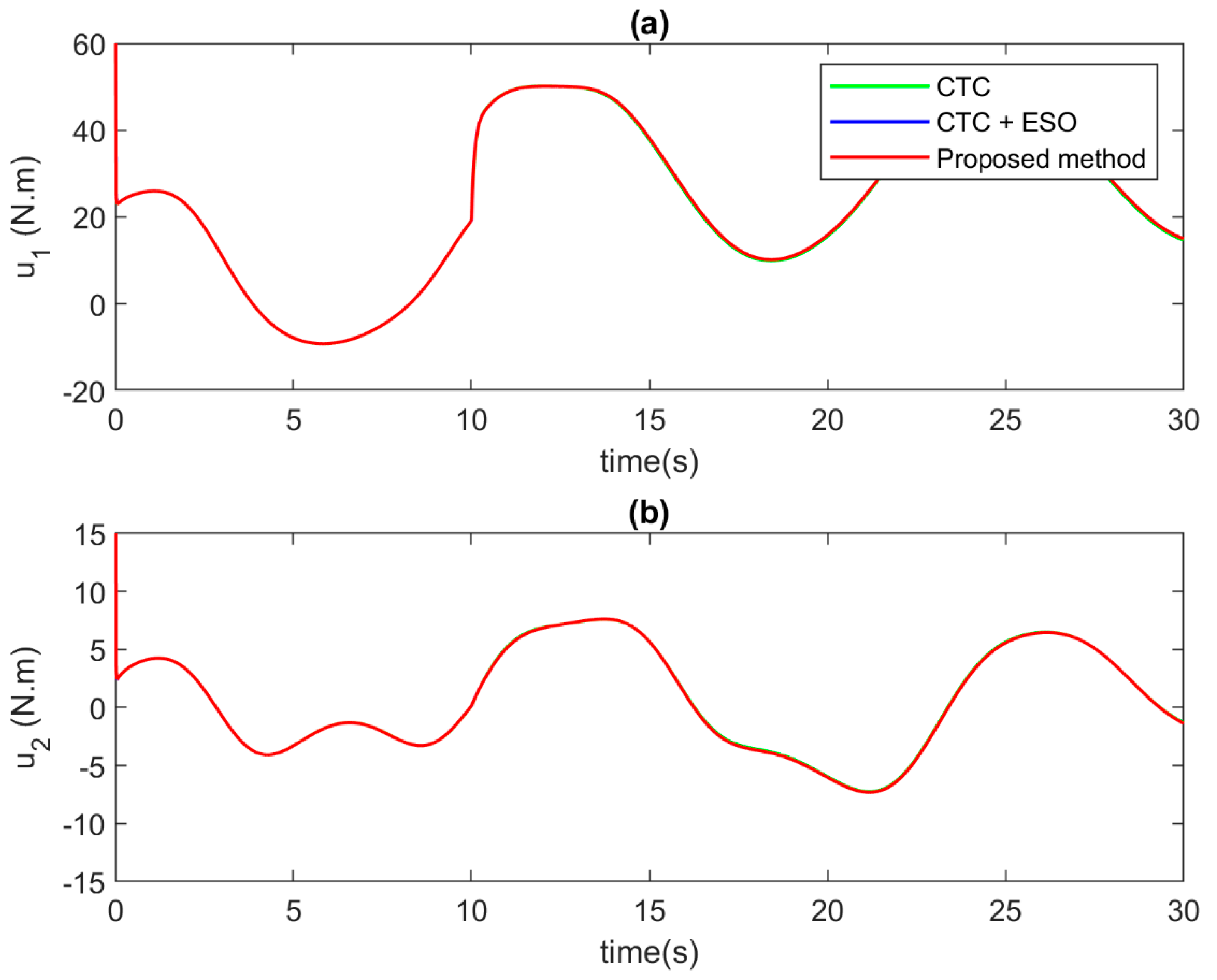
Comparison of the control input signal at each joint in case of incipient faults at (a) Joint 1, and (b) Joint 2.
- Simulation case 2: In this part, abrupt actuator faults are supposed to happen at both joint 1 and joint 2 at occurrence time s with the evolution rate . The fault function is assumed to be Θ .
In this case, the faults suddenly occur in the robot system. For this working condition, the estimation results of the ESO are indicated in Figure 8 and Figure 9. Figure 8 displays the velocity approximation results, and the Figure 9 presents the unknown input estimation at each joint. Similar to the simulation case 1, the results in figures show that the ESO provides good estimation performance for both velocity and unknown input. In addition, the estimation speed is quite fast, which helps to increase the tracking speed when using this signal in the compensator.
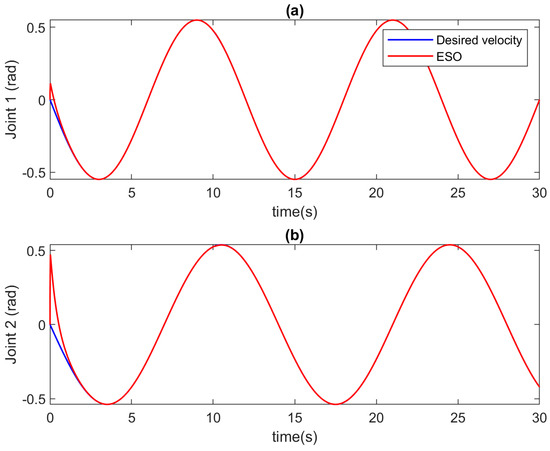
Figure 8.
The velocity estimation of ESO in case of abrupt faults at (a) Joint 1, and (b) Joint 2.
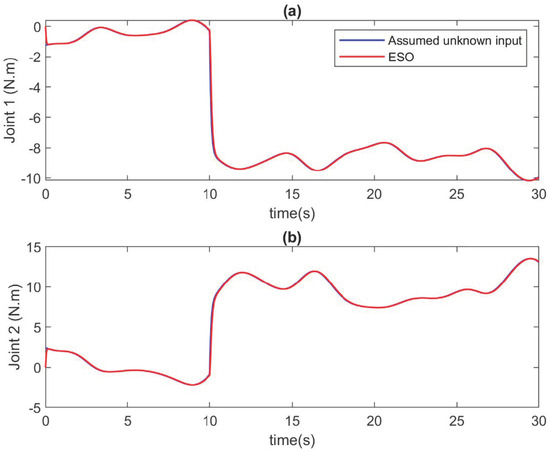
Figure 9.
The unknown input estimation of ESO in case of abrupt faults at (a) Joint 1, and (b) Joint 2.
For the control performance validation, the results are meticulously illustrated through the comprehensive depiction in Figure 10, Figure 11 and Figure 12. In Figure 10 and Figure 11, a detailed examination is undertaken to contrast position tracking performance and tracking errors across the three distinct control methodologies under the effect of abrupt faults. Initially, the conventional CTC, represented by the green solid line, showcases commendable tracking proficiency under standard operating conditions. However, its performance significantly deteriorates in the presence of faults, leading to a noticeable decline in tracking accuracy. In stark contrast, the utilization of ESO compensation, illustrated by the blue solid line, yields notably improved tracking accuracy, even amidst fault occurrences. For the proposed AFTC algorithm, the special design approach, denoted by the red solid line, emerges as the superior performer, showcasing unparalleled tracking performance. This improvement can be attributed to the meticulous design of the compensator within ESO, which enhances tracking precision significantly. Similarly to example 1, the proposed control signal can obtain both higher convergence speed and tracking performance. Figure 12 serves to elucidate the comparison of control input signals. Notably, all three controllers exhibit seamlessly smooth control inputs, devoid of any chattering phenomenon, thereby affirming the practical viability of the proposed control algorithm for real-world applications.
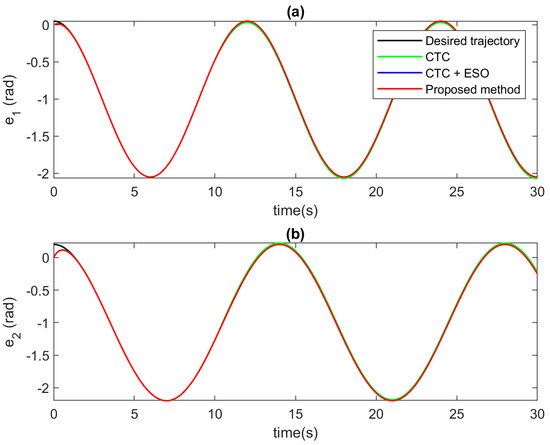
Figure 10.
Position tracking at each joint in case of abrupt faults at (a) Joint 1, and (b) Joint 2.
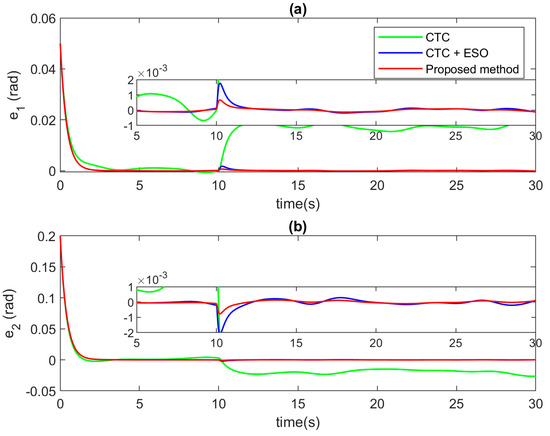
Figure 11.
Comparison of tracking errors at each joint in case of abrupt faults at (a) Joint 1, and (b) Joint 2.
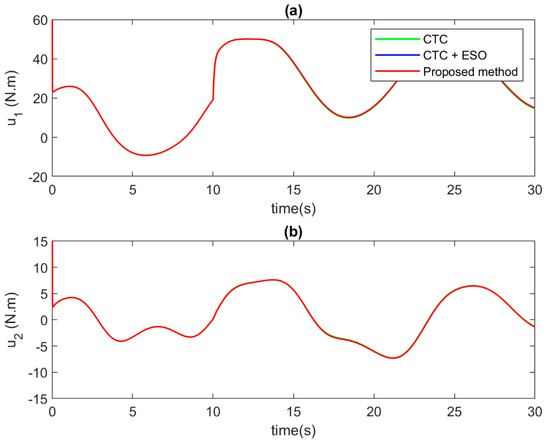
Figure 12.
Comparison of control input signal at each joint in case of abrupt faults at (a) Joint 1, and (b) Joint 2.
For further demonstration of the effectiveness of the novel control approach, the root mean square error (RMSE) of three comparing control methods among two simulation cases is calculated. In order to see the actual error values, the RMSE is calculated from the 3rd to 30th seconds of the simulation, and the results are presented in Table 2. The result shows that although using the same CTC and ESO methods with a special control design approach, the proposed novel control signal provides higher tracking performance compared to the traditional design approach.

Table 2.
Comparison of RMSE from three control methods among two simulation cases.
6. Conclusions
In this paper, an AFTC approach utilizing the CTC and the ESO for uncertain robot manipulators to eliminate the effects of the unknown input is suggested. The ESO offers estimation of velocities and the unknown input with good accuracy and quick convergence. The combination of the CTC and the ESO provides an effective control algorithm with good performance for the trajectory tracking problem of robot manipulator systems. Further, with a special design approach, this study proposed a novel control signal that provides higher control performance compared to the traditional design approach. The proposed method does not require velocity measurement in the design process. In addition, the proposed controller–observer tactic proved its ability to reduce the influences of the unknown input with outstanding precision, fast convergence, and no chattering. The global and asymptotic stability of the proposed strategy is proven through the Lyapunov stability theory. The efficiency of the suggested controller–observer method is validated by simulations on a 2-DOF robot manipulator.
Author Contributions
Conceptualization, X.-T.T., V.-C.N., and P.-N.L.; methodology, V.-C.N., P.-N.L., and X.-T.T.; software, X.-T.T., V.-C.N., and P.-N.L.; validation, X.-T.T. and V.-C.N.; formal analysis, V.-C.N., H.-J.K., and X.-T.T.; investigation, V.-C.N., P.-N.L., and X.-T.T.; resources, V.-C.N. and X.-T.T.; data curation, V.-C.N. and X.-T.T.; writing—original draft preparation, V.-C.N., P.-N.L., and X.-T.T.; writing—review and editing, V.-C.N., H.-J.K., and X.-T.T.; visualization, X.-T.T., V.-C.N., and P.-N.L.; supervision, H.-J.K.; project administration, H.-J.K.; funding acquisition, H.-J.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the BK21 FOUR (Fostering Outstanding Universities for Research, No.4120200913590) funded by the Ministry of Education (MOE, Korea) and National Research Foundation of Korea (NRF).
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A
Design of CTC with ESO Compensator
For the robot system in (4), defining the position tracking errors and velocity errors as follows:
where are the preferred trajectories and velocities, respectively.
To improve robustness, a control law of a CTC with a compensator from the ESO is designed as follows:
References
- Zhang, D.; Hu, J.; Cheng, J.; Wu, Z.-G.; Yan, H. A Novel Disturbance Observer Based Fixed-Time Sliding Mode Control for Robotic Manipulators with Global Fast Convergence. IEEE/CAA J. Autom. Sin. 2024, 11, 661–672. [Google Scholar] [CrossRef]
- Obuz, S.; Tatlicioglu, E.; Zergeroglu, E. Adaptive Cartesian Space Control of Robotic Manipulators: A Concurrent Learning Based Approach. J. Franklin Inst. 2024, 361, 106701. [Google Scholar] [CrossRef]
- Zhang, C.; Dai, M.-Z.; Dong, P.; Leung, H.; Wang, J. Fault-Tolerant Attitude Stabilization for Spacecraft with Low-Frequency Actuator Updates: An Integral-Type Event-Triggered Approach. IEEE Trans. Aerosp. Electron. Syst. 2020, 57, 729–737. [Google Scholar] [CrossRef]
- Van, M.; Sun, Y.; Mcllvanna, S.; Nguyen, M.-N.; Khyam, M.O.; Ceglarek, D. Adaptive Fuzzy Fault Tolerant Control for Robot Manipulators with Fixed-Time Convergence. IEEE Trans. Fuzzy Syst. 2023, 9, 3210–3219. [Google Scholar] [CrossRef]
- Stefanovski, J.D. Passive Fault Tolerant Perfect Tracking with Additive Faults. Automatica 2018, 87, 432–436. [Google Scholar] [CrossRef]
- Liu, L.; Zhang, L.; Hou, Y.; Tang, D.; Liu, H. Implementation of Adaptive Fault-Tolerant Tracking Control for Robot Manipulators with Integral Sliding Mode. Int. J. Robust Nonlinear Control 2023, 33, 5337–5364. [Google Scholar] [CrossRef]
- Shen, Q.; Yue, C.; Goh, C.H.; Wang, D. Active Fault-Tolerant Control System Design for Spacecraft Attitude Maneuvers with Actuator Saturation and Faults. IEEE Trans. Ind. Electron. 2018, 66, 3763–3772. [Google Scholar] [CrossRef]
- Nguyen, V.-C.; Le, P.-N.; Kang, H.-J. An Active Fault-Tolerant Control for Robotic Manipulators Using Adaptive Non-Singular Fast Terminal Sliding Mode Control and Disturbance Observer. Actuators 2021, 10, 332. [Google Scholar] [CrossRef]
- Ren, Y.; Sun, Y.; Liu, L. Fuzzy Disturbance Observers-Based Adaptive Fault-Tolerant Control for an Uncertain Constrained Automatic Flexible Robotic Manipulator. IEEE Trans. Fuzzy Syst. 2023, 32, 1144–1158. [Google Scholar] [CrossRef]
- Salgado, I.; Chairez, I. Adaptive Unknown Input Estimation by Sliding Modes and Differential Neural Network Observer. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 3499–3509. [Google Scholar] [CrossRef]
- Shen, Q.; Jiang, B.; Shi, P.; Lim, C.C. Novel Neural Networks-Based Fault Tolerant Control Scheme with Fault Alarm. IEEE Trans. Cybern. 2014, 44, 2190–2201. [Google Scholar] [CrossRef] [PubMed]
- Xi, R.-D.; Ma, T.-N.; Xiao, X.; Yang, Z.-X. Design and Implementation of an Adaptive Neural Network Observer–Based Backstepping Sliding Mode Controller for Robot Manipulators. Trans. Inst. Meas. Control 2024, 46, 1093–1104. [Google Scholar] [CrossRef]
- Qi, H.; Shi, Y.; Li, S.; Tian, Y.; Yu, D.-L.; Gomm, J.B. Fault Tolerant Control for Nonlinear Systems Using Sliding Mode and Adaptive Neural Network Estimator. Soft Comput. 2020, 24, 11535–11544. [Google Scholar] [CrossRef]
- Cho, C.N.; Hong, J.T.; Kim, H.J. Neural Network Based Adaptive Actuator Fault Detection Algorithm for Robot Manipulators. J. Intell. Robot. Syst. 2019, 95, 137–147. [Google Scholar] [CrossRef]
- Baek, J.; Kwon, W.; Kim, B.; Han, S. A Widely Adaptive Time-Delayed Control and Its Application to Robot Manipulators. IEEE Trans. Ind. Electron. 2019, 66, 5332–5342. [Google Scholar] [CrossRef]
- Van, M.; Ge, S.S.; Ren, H. Finite Time Fault Tolerant Control for Robot Manipulators Using Time Delay Estimation and Continuous Nonsingular Fast Terminal Sliding Mode Control. IEEE Trans. Cybern. 2017, 47, 1681–1693. [Google Scholar] [CrossRef] [PubMed]
- Jin, M.; Kang, S.H.; Chang, P.H. Robust Compliant Motion Control of Robot with Nonlinear Friction Using Time-Delay Estimation. IEEE Trans. Ind. Electron. 2008, 55, 258–269. [Google Scholar] [CrossRef]
- Kim, J.; Jin, M.; Choi, W.; Lee, J. Discrete Time Delay Control for Hydraulic Excavator Motion Control with Terminal Sliding Mode Control. Mechatronics 2019, 60, 15–25. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, J.; Tong, Y.; Liu, Y.; Ju, Z. Attitude Decoupling Control of Semifloating Space Robots Using Time-Delay Estimation and Supertwisting Control. IEEE Trans. Aerosp. Electron. Syst. 2021, 57, 4280–4295. [Google Scholar] [CrossRef]
- Xu, Q. Continuous Integral Terminal Third-Order Sliding Mode Motion Control for Piezoelectric Nanopositioning System. IEEE/ASME Trans. Mechatron. 2017, 22, 1828–1838. [Google Scholar] [CrossRef]
- Tran, X.-T.; Oh, H.; Kim, I.-R.; Kim, S. Attitude Stabilization of Flapping Micro-Air Vehicles via an Observer-Based Sliding Mode Control Method. Aerosp. Sci. Technol. 2018, 76, 386–393. [Google Scholar] [CrossRef]
- Mousavi, M.S.; Davari, S.A.; Nekoukar, V.; Garcia, C.; He, L.; Wang, F.; Rodriguez, J. Predictive Torque Control of Induction Motor Based on a Robust Integral Sliding Mode Observer. IEEE Trans. Ind. Electron. 2022, 70, 2339–2350. [Google Scholar] [CrossRef]
- Fang, L.; Zhang, Y.; Song, T. Tracking Control for Robotic Manipulators with Prescribed Performance and Adaptive Sliding Mode Disturbance Observer. Trans. Inst. Meas. Control 2024, 01423312241228921. [Google Scholar] [CrossRef]
- Khalil, H.K.; Praly, L. High-Gain Observers in Nonlinear Feedback Control. Int. J. Robust Nonlinear Control 2014, 24, 993–1015. [Google Scholar] [CrossRef]
- Le, Q.D.; Kang, H.-J. Implementation of Fault-Tolerant Control for a Robot Manipulator Based on Synchronous Sliding Mode Control. Appl. Sci. 2020, 10, 2534. [Google Scholar] [CrossRef]
- Khalil, H.K. High-Gain Observers in Feedback Control: Application to Permanent Magnet Synchronous Motors. IEEE Control Syst. Mag. 2017, 37, 25–41. [Google Scholar]
- Nguyen, V.-C.; Vo, A.-T.; Kang, H.-J. Continuous PID Sliding Mode Control Based on Neural Third Order Sliding Mode Observer for Robotic Manipulators. In Intelligent Computing Methodologies, Proceedings of the 15th International Conference, ICIC 2019, Nanchang, China, 3–6 August 2019; Springer: Cham, Switzerland, 2019; pp. 167–178. [Google Scholar]
- Song, Y.; Huang, X.; Wen, C. Robust Adaptive Fault-Tolerant PID Control of MIMO Nonlinear Systems with Unknown Control Direction. IEEE Trans. Ind. Electron. 2017, 64, 4876–4884. [Google Scholar] [CrossRef]
- Alibeji, N.; Sharma, N. A PID-Type Robust Input Delay Compensation Method for Uncertain Euler–Lagrange Systems. IEEE Trans. Control Syst. Technol. 2017, 25, 2235–2242. [Google Scholar] [CrossRef]
- Tutsoy, O.; Barkana, D.E. Model Free Adaptive Control of the Under-Actuated Robot Manipulator with the Chaotic Dynamics. ISA Trans. 2021, 118, 106–115. [Google Scholar] [CrossRef]
- Wang, H.; Bai, W.; Liu, P.X. Finite-Time Adaptive Fault-Tolerant Control for Nonlinear Systems with Multiple Faults. IEEE/CAA J. Autom. Sin. 2019, 6, 1417–1427. [Google Scholar] [CrossRef]
- Li, M.; Li, Y.; Ge, S.S.; Lee, T.H. Adaptive Control of Robotic Manipulators with Unified Motion Constraints. IEEE Trans. Syst. Man Cybern. Syst. 2016, 47, 184–194. [Google Scholar] [CrossRef]
- Wu, Y.; Huang, R.; Li, X.; Liu, S. Adaptive Neural Network Control of Uncertain Robotic Manipulators with External Disturbance and Time-Varying Output Constraints. Neurocomputing 2019, 323, 108–116. [Google Scholar] [CrossRef]
- Luan, F.; Na, J.; Huang, Y.; Gao, G. Adaptive Neural Network Control for Robotic Manipulators with Guaranteed Finite-Time Convergence. Neurocomputing 2019, 337, 153–164. [Google Scholar] [CrossRef]
- He, W.; Chen, Y.; Yin, Z. Adaptive Neural Network Control of an Uncertain Robot with Full-State Constraints. IEEE Trans. Cybern. 2016, 46, 620–629. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; Peng, K.; Han, L.; Guan, S. Modeling and Control of Robotic Manipulators Based on Artificial Neural Networks: A Review. Iran. J. Sci. Technol. Trans. Mech. Eng. 2023, 47, 1307–1347. [Google Scholar] [CrossRef]
- Wu, Z.; Zhang, T. Adaptive Finite-Time Tracking Control for Parameterized Nonlinear Systems with Full State Constraints. Int. J. Adapt. Control Signal Process. 2021, 35, 1768–1788. [Google Scholar] [CrossRef]
- Qiu, J.; Sun, K.; Rudas, I.J.; Gao, H. Command Filter-Based Adaptive NN Control for MIMO Nonlinear Systems with Full-State Constraints and Actuator Hysteresis. IEEE Trans. Cybern. 2019, 50, 2905–2915. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, V.-C.; Le, P.-N.; Kang, H.-J. Model-Free Continuous Fuzzy Terminal Sliding Mode Control for Second-Order Nonlinear Systems. In Proceedings of the International Conference on Intelligent Computing, Nanjing, China, 25–27 June 2021; pp. 245–258. [Google Scholar]
- Muñoz-Vázquez, A.J.; Treesatayapun, C. Model-Free Discrete-Time Fractional Fuzzy Control of Robotic Manipulators. J. Frankl. Inst. 2022, 359, 952–966. [Google Scholar] [CrossRef]
- Nguyen, V.-C.; Tran, X.-T.; Kang, H.-J. A Novel High-Speed Third-Order Sliding Mode Observer for Fault-Tolerant Control Problem of Robot Manipulators. Actuators 2022, 11, 259. [Google Scholar] [CrossRef]
- Cruz-Ortiz, D.; Chairez, I.; Poznyak, A. Non-Singular Terminal Sliding-Mode Control for a Manipulator Robot Using a Barrier Lyapunov Function. ISA Trans. 2022, 121, 268–283. [Google Scholar] [CrossRef]
- Najafi, A.; Vu, M.T.; Mobayen, S.; Asad, J.H.; Fekih, A. Adaptive Barrier Fast Terminal Sliding Mode Actuator Fault Tolerant Control Approach for Quadrotor UAVs. Mathematics 2022, 10, 3009. [Google Scholar] [CrossRef]
- Zhao, B.; Li, Y. Local Joint Information Based Active Fault Tolerant Control for Reconfigurable Manipulator. Nonlinear Dyn. 2014, 77, 859–876. [Google Scholar] [CrossRef]
- Codourey, A. Dynamic Modeling of Parallel Robots for Computed-Torque Control Implementation. Int. J. Rob. Res. 1998, 17, 1325–1336. [Google Scholar] [CrossRef]
- Sancak, K.V.; Bayraktaroglu, Z.Y. Nonlinear Computed Torque Control of 6-Dof Parallel Manipulators. Int. J. Control Autom. Syst. 2022, 20, 2297–2311. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).