A Tube-Based Model Predictive Control for Path Tracking of Autonomous Articulated Vehicle
Abstract
1. Introduction
- Integration of controllers for both path tracking and velocity tracking aims to account for the correlation between lateral and longitudinal motion, thereby enhancing lateral stability.
- The design of a reference tracking-based controller addresses the limitations of point tracking-based controllers and error dynamics defined for a fixed planned path, enabling the proposed controller to be applied to arbitrary desired paths.
- The utilization of tube-based MPC enhances robustness against external disturbances of sensors and modeling errors.
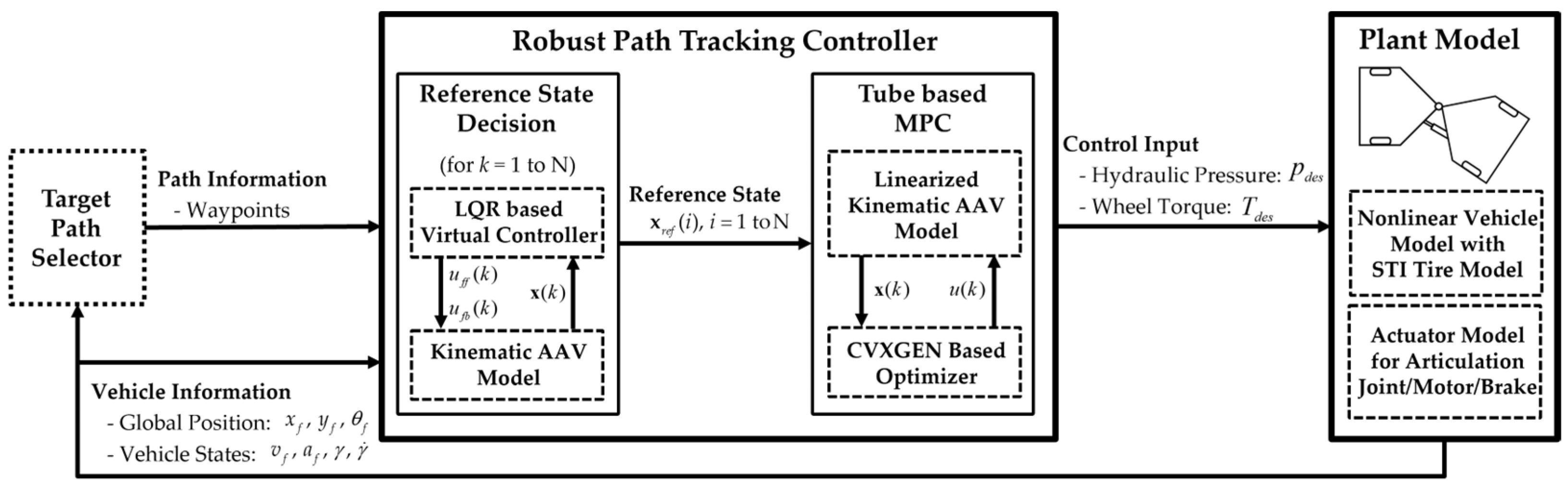
2. Overall Architecture
3. Vehicle Model
4. Robust Path Tracking Controller
4.1. Reference State Decision
4.2. Tube-Based MPC
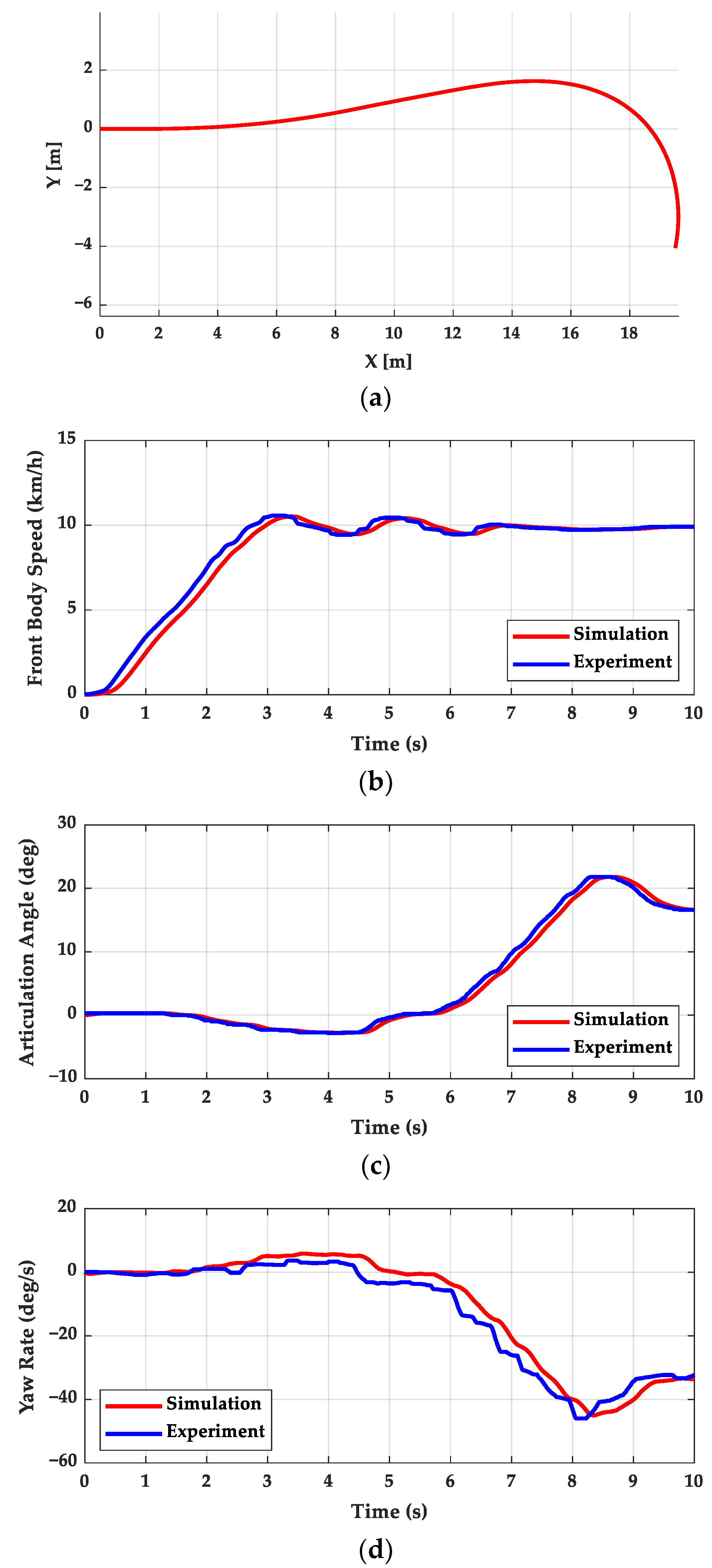
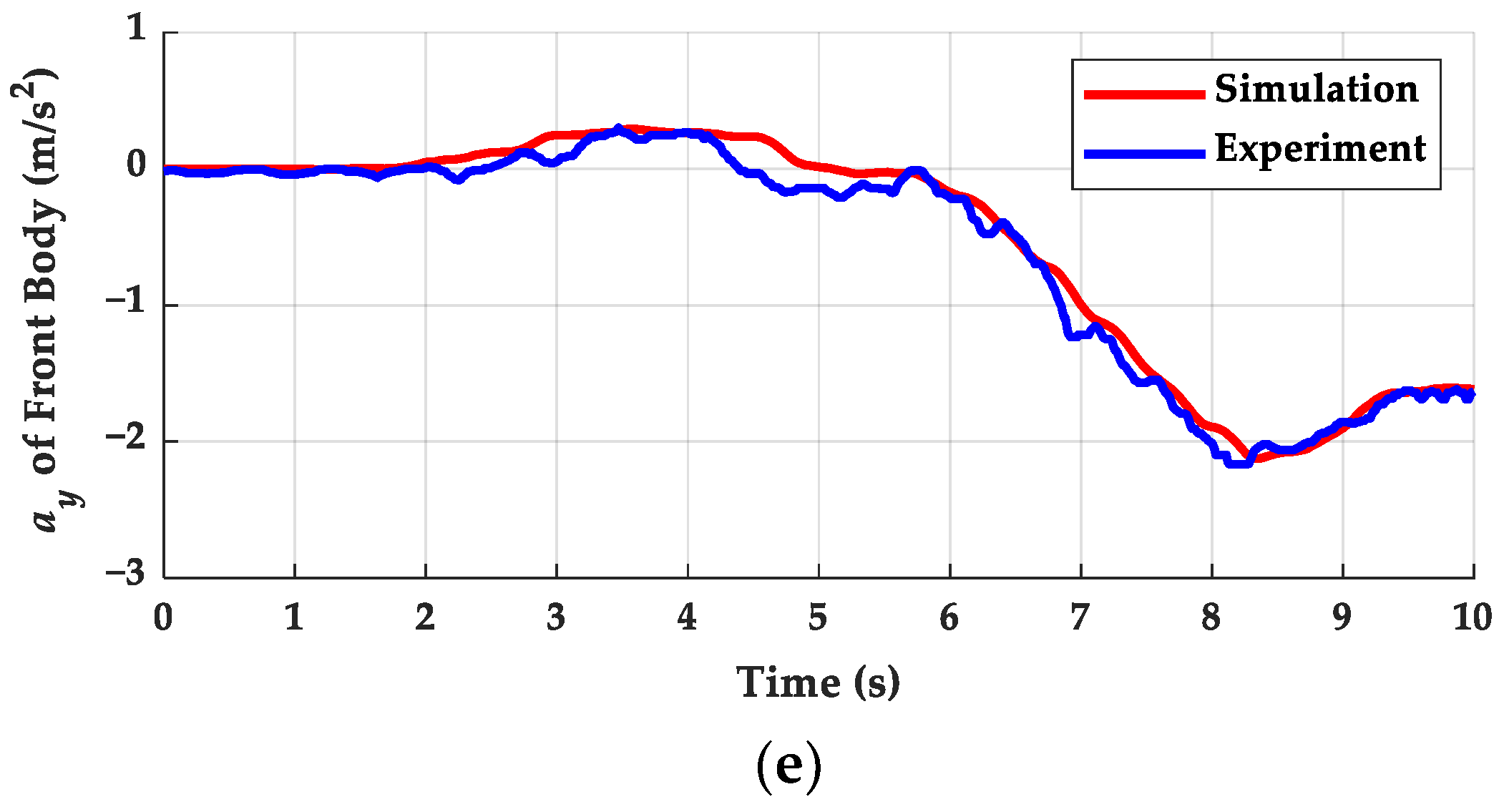
4.3. Vehicle Model Validation
4.4. Base Algorithms
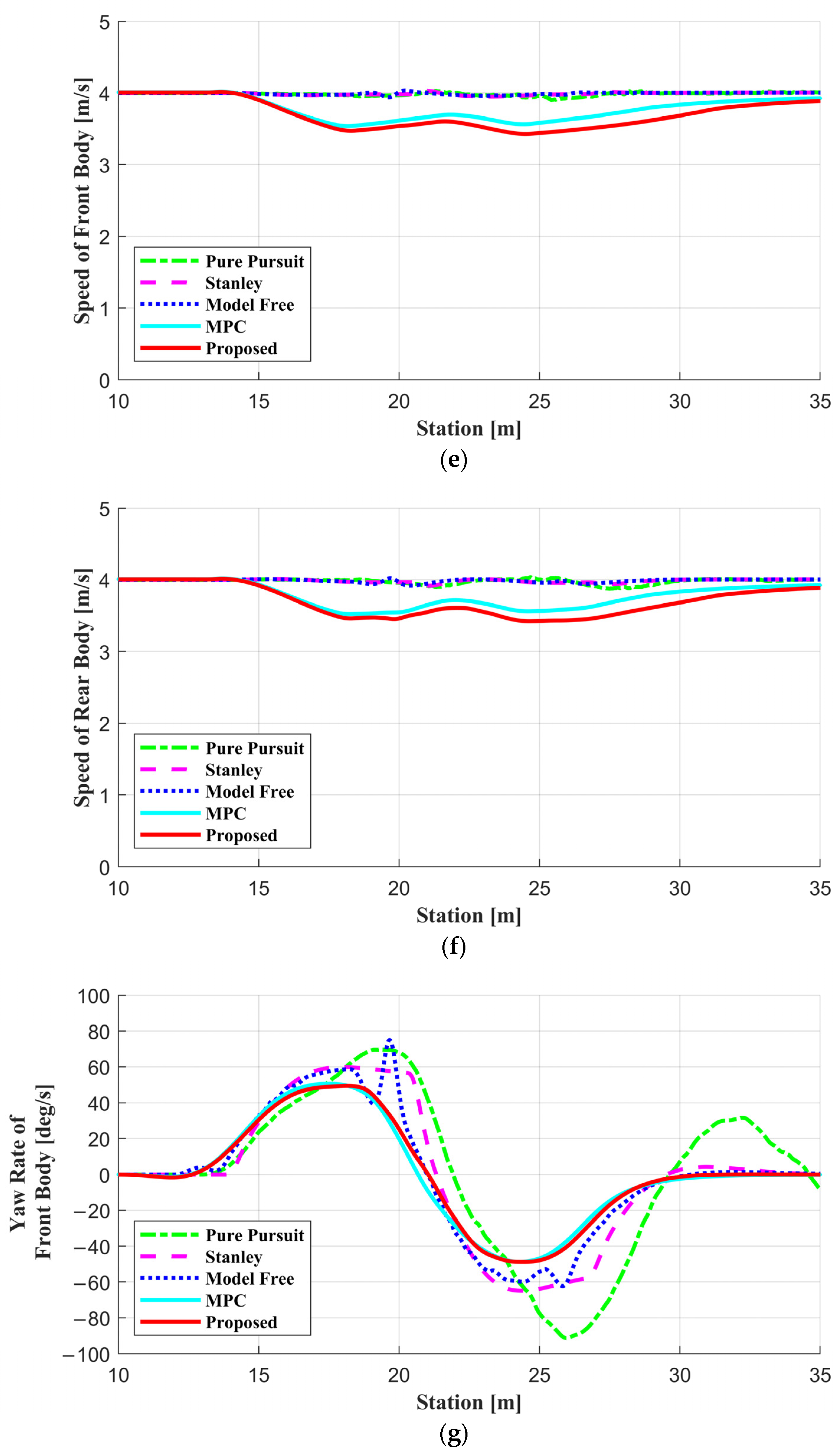
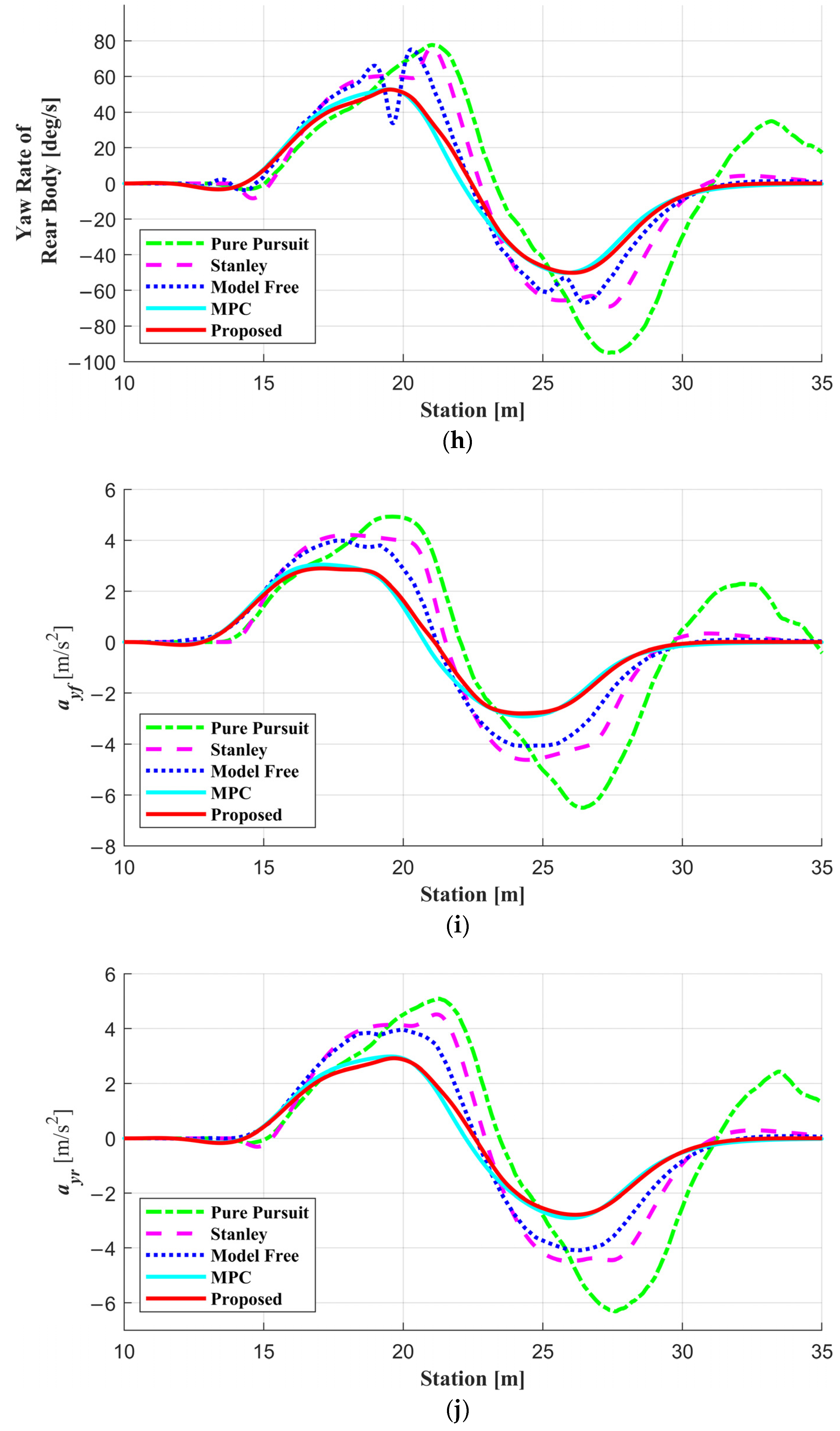
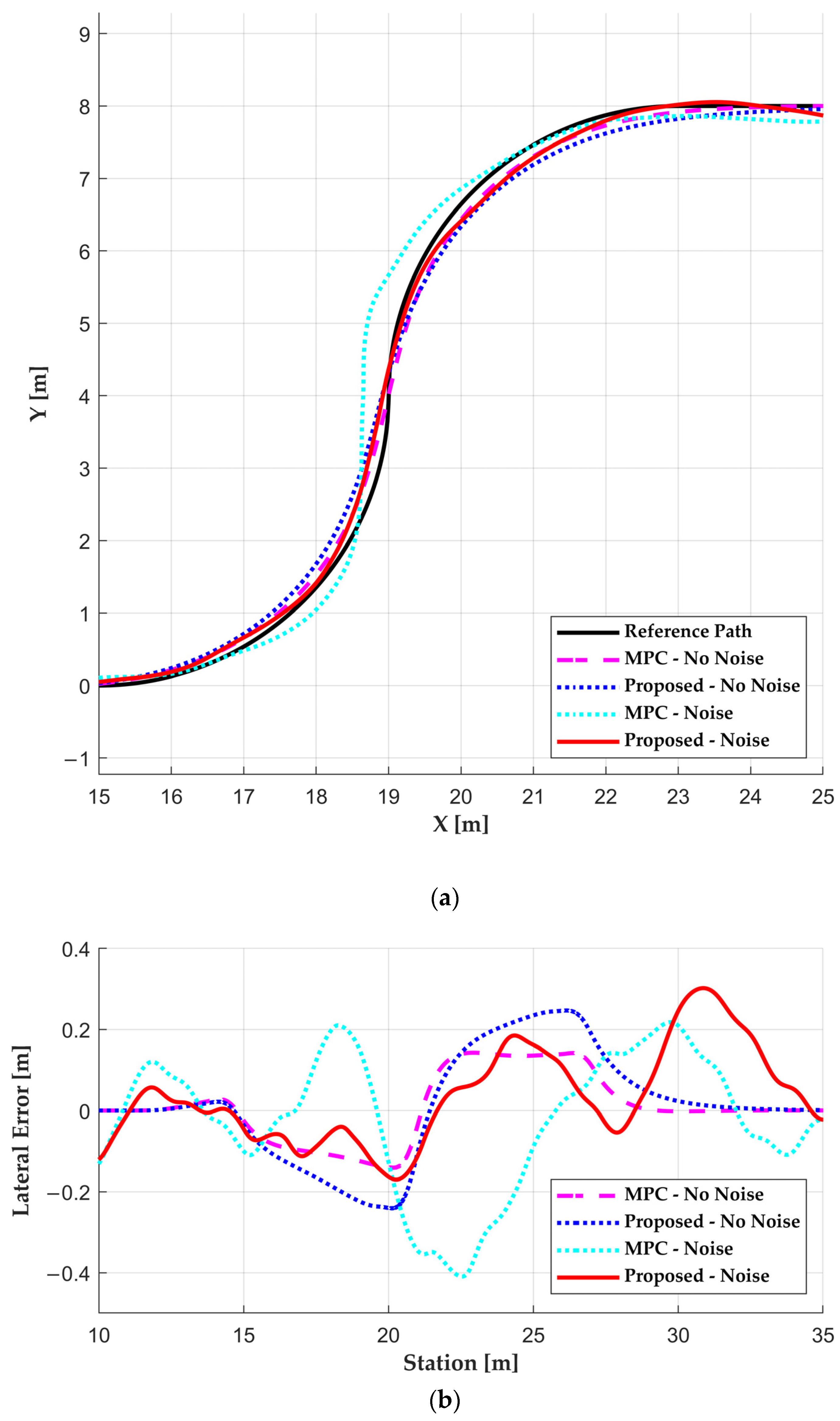
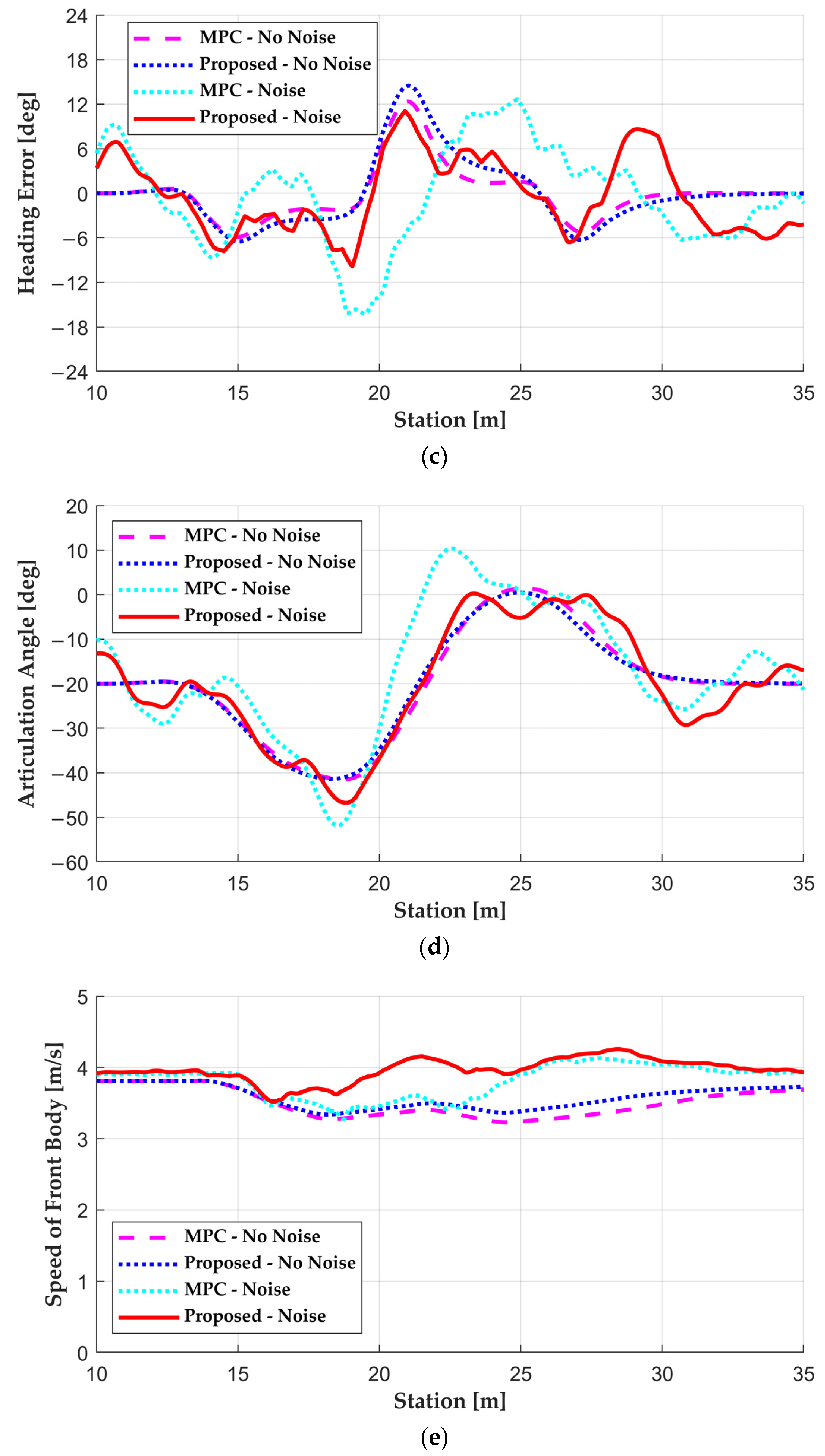
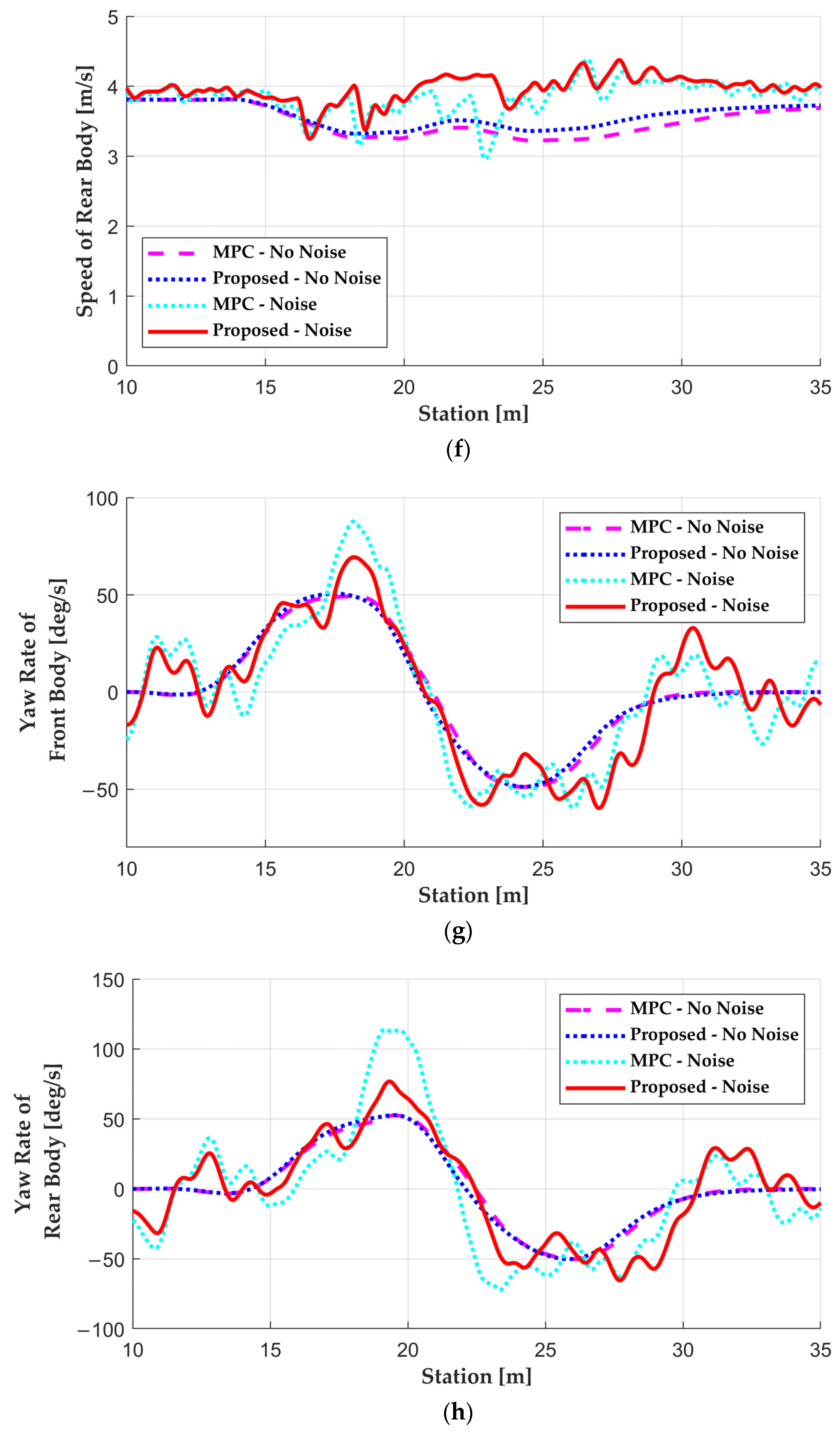
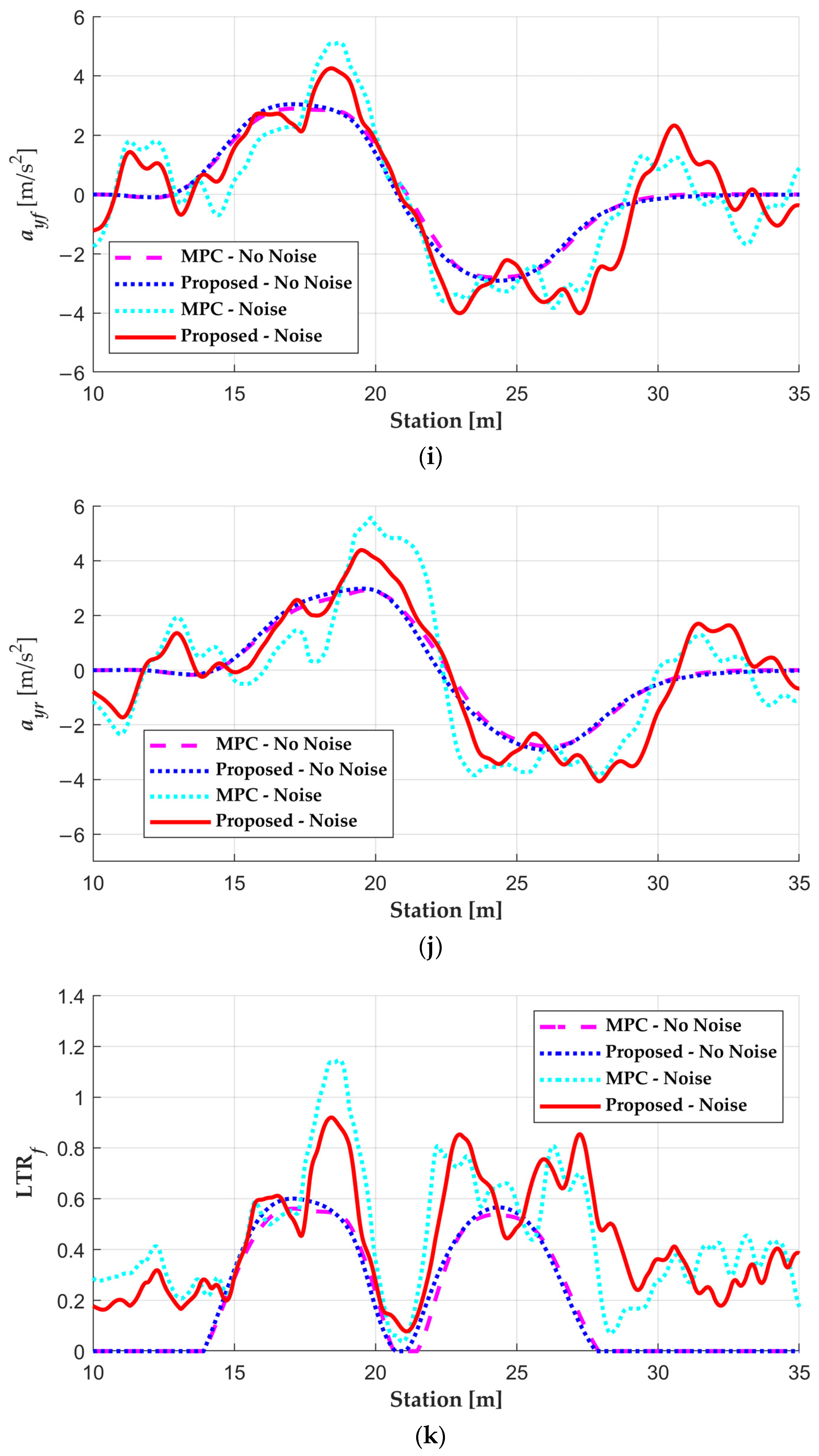
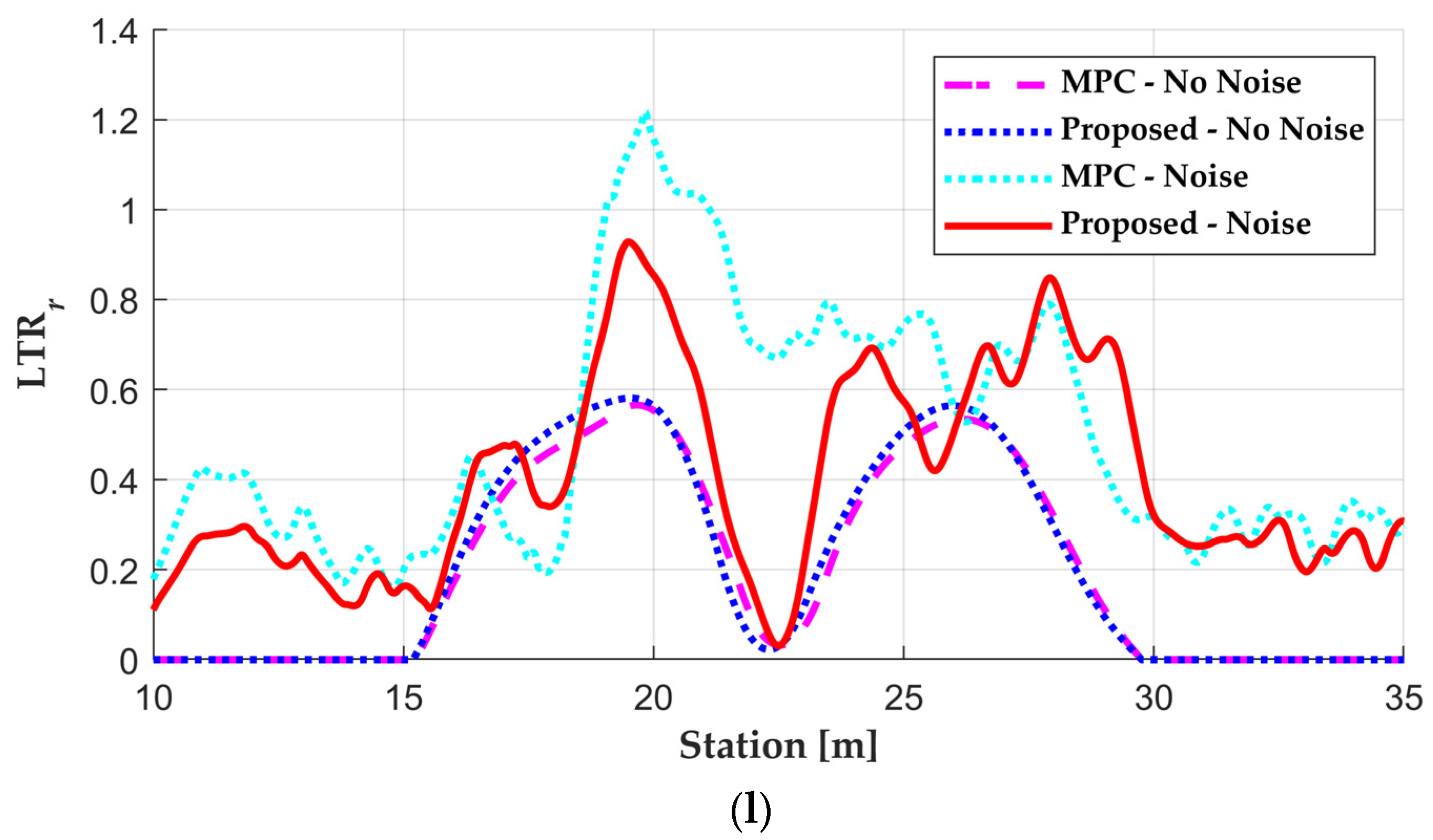
5. Results
5.1. Simulation Model and Environment
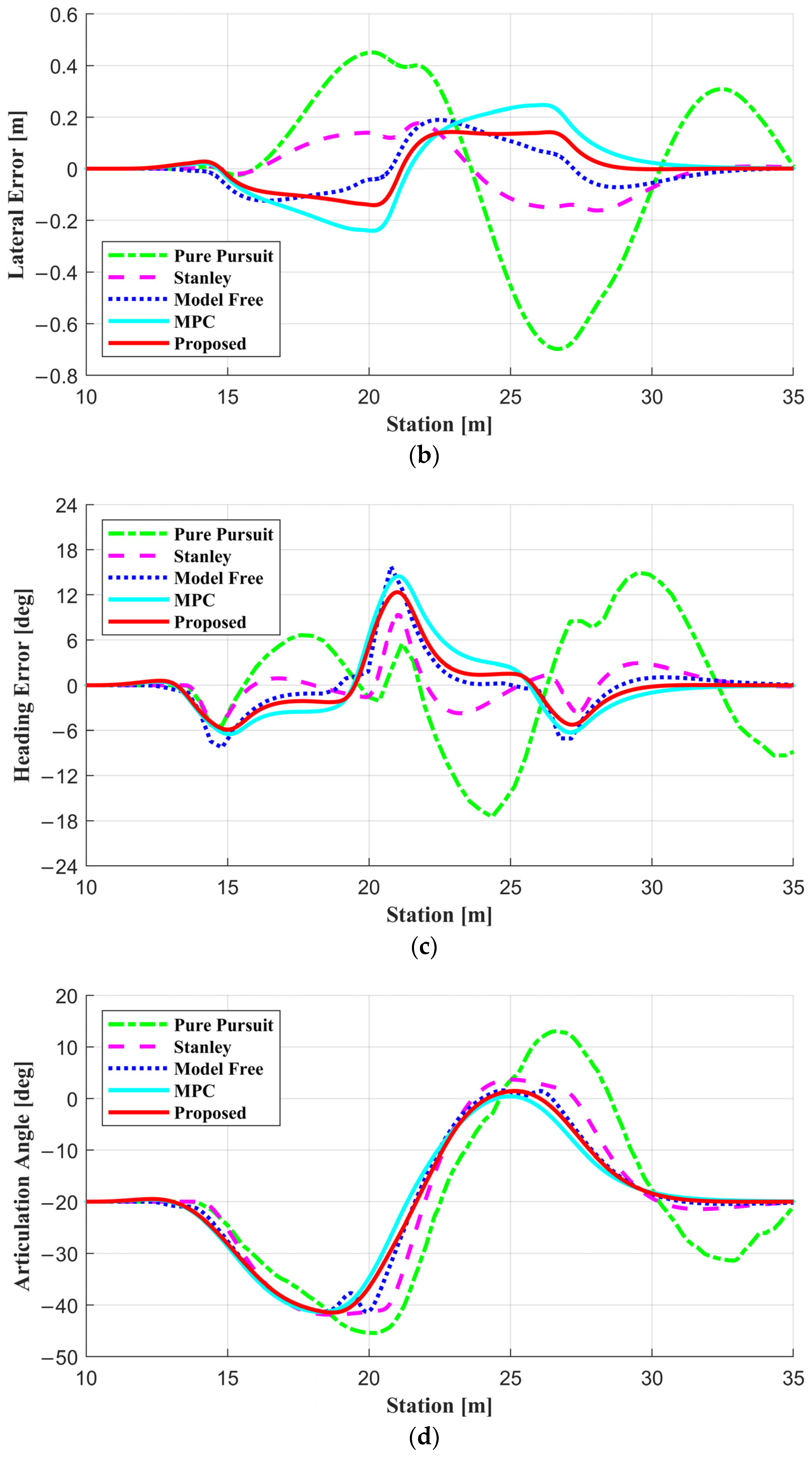
5.2. Simulation Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Viscelli, S. Driverless? Autonomous Trucks and the Future of the American Trucker, Center for Labor Research and Education; University of California, Berkely and Working Partnerships USA: San Francisco, CA, USA, 2018. [Google Scholar]
- Rana, M.M.; Hossain, K. Connected and autonomous vehicles and infrastructures: A literature review. Int. J. Pavement Res. Technol. 2021, 16, 264–284. [Google Scholar] [CrossRef]
- Iclodean, C.; Cordos, N.; Varga, B.O. Autonomous shuttle bus for public transportation: A review. Energies 2020, 13, 2917. [Google Scholar] [CrossRef]
- Jo, A.; Lee, H.; Seo, D.; Yi, K. Model-reference adaptive sliding mode control of longitudinal speed tracking for autonomous vehicles. Proc. Inst. Mech. Eng. D J. Automob. Eng. 2023, 237, 493–515. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, Y.; Ai, Z.; Feng, Y.; Zhang, J.; Murphey, Y.L. Estimation of electric mining haul trucks’ mass and road slope using dual level reinforcement estimator. IEEE Trans. Veh. Technol. 2019, 68, 10627–10638. [Google Scholar] [CrossRef]
- Hiraoka, T.; Nishihara, O.; Kumamoto, H. Automatic path-tracking controller of a four-wheel steering vehicle. Veh. Syst. Dyn. 2009, 47, 1205–1227. [Google Scholar] [CrossRef]
- Kang, J.; Kim, W.; Lee, J.; Yi, K. Design, implementation, and test of skid steering-based autonomous driving controller for a robotic vehicle with articulated suspension. J. Mech. Sci. Technol. 2010, 24, 793–800. [Google Scholar] [CrossRef]
- Yin, Y.; Rakheja, S.; Yang, J.; Boileau, P.E. Design optimization of an articulated frame steering system. Proc. Inst. Mech. Eng. D J. Automob. Eng. 2018, 232, 1339–1352. [Google Scholar] [CrossRef]
- Hang, P.; Chen, X.; Luo, F. LPV/H∞ controller design for path tracking of autonomous ground vehicles through four-wheel steering and direct yaw-moment control. Int. J. Automot. Technol. 2019, 20, 679–691. [Google Scholar] [CrossRef]
- Hiraoka, T.; Nishihara, O.; Kumamoto, H. Model-following sliding mode control for active four-wheel steering vehicle. Rev. Automot. Eng. 2004, 25, 305. [Google Scholar]
- Shamah, B.; Wagner, M.D.; Moorehead, S.; Teza, J.; Wettergreen, D.; Whittaker, W.L. Steering and control of a passively articulated robot. In Proceedings of the SPIE 4571, Sensor Fusion and Decentralized Control in Robotic Systems IV, Boston, MA, USA, 28–31 October 2001. [Google Scholar]
- Sunday, B. Stability analysis of a semi-trailer articulated vehicle: A review. Int. J. Automot. Sci. Technol. 2021, 5, 131–140. [Google Scholar]
- He, Y.; Khajepour, A.; McPhee, J.; Wang, X. Dynamic modelling and stability analysis of articulated frame steer vehicles. Int. J. Heavy Veh. Syst. 2005, 12, 28–59. [Google Scholar] [CrossRef]
- Lei, T.; Wang, J.; Yao, Z. Modelling and stability analysis of articulated vehicles. Appl. Sci. 2021, 11, 3663. [Google Scholar] [CrossRef]
- Shen, Y.; Xie, J.; Zhang, W. Study of hydraulic steering process for intelligent autonomous articulated vehicle. SAE Tech. Pap. 2018. [Google Scholar] [CrossRef]
- Sampei, M.; Tamura, T.; Kobayashi, T.; Shibui, N. Arbitrary path tracking control of articulated vehicles using nonlinear control theory. IEEE Trans. Control Syst. Technol. 1995, 3, 125–131. [Google Scholar] [CrossRef]
- Mohamed, A.; Ren, J.; Lang, H.; El-Gindy, M. Optimal path planning for an autonomous articulated vehicle with two trailers. Int. J. Autom. Control 2018, 12, 449–465. [Google Scholar] [CrossRef]
- Bolzern, P.; DeSantis, R.M.; Locatelli, A.; Masciocchi, D. Path-tracking for articulated vehicles with off-axle hitching. IEEE Trans. Control Syst. Technol. 1998, 6, 515–523. [Google Scholar] [CrossRef]
- Oreh, S.T.; Kazemim, R.; Azadi, S. A new desired articulation angle for directional control of articulated vehicles. Proc. Inst. Mech. Eng. K J. Multi-body Dyn. 2012, 226, 298–314. [Google Scholar] [CrossRef]
- Jeong, D.; Choi, S.B. Tube-based Robust Model Predictive Control for Tracking Control of Autonomous Articulated Vehicles. IEEE Trans. Intell. Veh. 2024, 9, 2184–2196. [Google Scholar] [CrossRef]
- Alshaer, B.J.; Darabseh, T.T.; Alhanouti, M.A. Path planning, modeling and simulation of an autonomous articulated heavy construction machine performing a loading cycle. Appl. Math. Model. 2013, 37, 5315–5325. [Google Scholar] [CrossRef]
- Meng, Y.; Gan, X.; Wang, Y.; Gu, Q. LQR-GA controller for articulated dump truck path tracking system. J. Shanghai Jiaotong Univ. (Sci.) 2019, 24, 78–85. [Google Scholar] [CrossRef]
- Nayl, T.; Nikolakopoulos, G.; Gustafsson, T. Effect of kinematic parameters on MPC based on-line motion planning for an articulated vehicle. Robot. Auton. Syst. 2015, 70, 16–24. [Google Scholar] [CrossRef]
- Nayl, T.; Nikolakopoulos, G.; Gustafsson, T. On-line path planning for an articulated vehicle based on model predictive control. In Proceedings of the 2013 IEEE international conference on control applications (CCA), Hyderabad, India, 28–30 August 2013. [Google Scholar]
- Nayl, T.; Nikolakopoulos, G.; Gustafsson, T. A full error dynamics switching modeling and control scheme for an articulated vehicle. Int. J. Control Autom. Syst. 2015, 13, 1221–1232. [Google Scholar] [CrossRef]
- Nayl, T.; Nikolakopoulos, G.; Gustafsson, T. Switching model predictive control for an articulated vehicle under varying slip angle. In Proceedings of the 2012 20th Mediterranean Conference on Control & Automation (MED), Barcelona, Spain, 3–6 July 2012. [Google Scholar]
- Marshall, J.; Barfoot, T.; Larsson, J. Autonomous underground tramming for center-articulated vehicles. J. Field Robot. 2008, 25, 400–421. [Google Scholar] [CrossRef]
- Rains, G.C.; Faircloth, A.G.; Thai, C.; Raper, R.L. Evaluation of a simple pure pursuit path-following algorithm for an autonomous, articulated-steer vehicle. Appl. Eng. Agric. 2014, 30, 367–374. [Google Scholar]
- Yao, D.; Xie, H.; Qiang, W.; Liu, Y.; Xiong, S. Accurate trajectory tracking with disturbance-resistant and heading estimation method for self-driving vibratory roller. IFAC-PapersOnLine 2018, 51, 754–758. [Google Scholar] [CrossRef]
- Liu, Z.; Yue, M.; Guo, L.; Zhang, Y. Trajectory planning and robust tracking control for a class of active articulated tractor-trailer vehicle with on-axle structure. Eur. J. Control. 2020, 54, 87–98. [Google Scholar] [CrossRef]
- Gao, Y.; Cao, D.; Shen, Y. Path-following control by dynamic virtual terrain field for articulated steer vehicles. Veh. Syst. Dyn. 2020, 58, 1528–1552. [Google Scholar] [CrossRef]
- Li, X.; Gong, X.; Huang, J.; Chen, Y.H. Trajectory-tracking controller for vehicles on inclined road based on Udwadia–Kalaba equation. Green Energy Intell. Transp. 2022, 1, 100021. [Google Scholar] [CrossRef]
- Fong, J.; Tan, Y.; Crocher, V.; Oetomo, D.; Mareels, I. Dual-loop iterative optimal control for the finite horizon LQR problem with unknown dynamics. Syst. Control Lett. 2018, 111, 49–57. [Google Scholar] [CrossRef]
- Lee, C.; Van Tran, Q.; Kim, J. Robust Path Tracking and Obstacle Avoidance using Tube-based Model Predictive Control for Surface Vehicles. IFAC-Pap. 2022, 55, 301–306. [Google Scholar] [CrossRef]
- Youness, G.; Phan, N.U.T.; Boulakia, B.C. BootBOGS: Hands-on optimizing Grid Search in hyperparameter tuning of MLP. In Proceedings of the AICCSA 2023: 20th ACS/IEEE International Conference on Computer Systems and Applications, Giza, Egypt, 4–7 December 2023. [Google Scholar]
- Korea IT News. Gwangju-Si and Korea Institute of Industrial Technology to Introduce Two Unmanned Special Vehicles Next Month. Available online: https://english.etnews.com/20201118200004 (accessed on 20 November 2020).
- Coulter, R. Implementation of the Pure Pursuit Path Tracking Algorithm; Carnegie Mellon University: Pittsburgh, PA, USA, 1990; pp. 1–9. [Google Scholar]
- Thrun, S.; Montemerlo, M.; Dahlkamp, H.; Stavens, D.; Aron, A.; Diebel, J.; Fong, P.; Gale, J.; Halpenny, G.; Lau, K.; et al. Stanley: The robot that won the DARPA Grand Challenge. J. Field Robot. 2006, 23, 661–692. [Google Scholar] [CrossRef]
- Liu, Q.; Solis, D.; Pan, W. Analysis of the STI tire Model. SAE Tech. Pap. 2002. [Google Scholar] [CrossRef]
- Jeong, Y. Integrated Vehicle Controller for Path Tracking with Rollover Prevention of Autonomous Articulated Electric Vehicle Based on Model Predictive Control. Actuators 2023, 12, 41. [Google Scholar] [CrossRef]
- Mattingley, J.; Boyd, S. CVXGEN: A code generator for embedded convex optimization. Optim. Eng. 2012, 13, 1–27. [Google Scholar] [CrossRef]




| Variable | Standard Deviation | Variable | Standard Deviation |
|---|---|---|---|
| xf | 0.5 m | vf | 1 m/s |
| yf | 0.5 m | af | 0.2 m/s2 |
| θf | 5 deg | γ | 0.5 deg |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Lf | 0.605 m | ΔT | 0.1 s |
| Lr | 0.895 m | Np | 20 |
| τf | 0.2 s | τa | 0.05 s |
| Qx | 1 | xmgn | 0.5 m |
| Qy | 75 | ymgn | 0.5 m |
| Qθ | 100 | θmgn | 3 deg |
| Qv | 10 | vf,min | 0 m/s |
| Qa | 20 | vf,max | 5 m/s |
| Qγ | 100 | af,min | −3 m/s2 |
| 150 | af,man | 1 m/s2 | |
| Rp | 0.1 | γman | 50 deg |
| Rτ | 0.01 | 90 deg/s | |
| pmax | 50 bar | τmax | 1500 Nm |
| Criteria | Noise | Pure Pursuit | Stanley | Model- | MPC | Proposed |
|---|---|---|---|---|---|---|
| Mean (SD) of lateral error [m] | Off | 0.1660 (0.1975) | 0.0422 (0.0585) | 0.0389 (0.0530) | 0.0696 (0.0893) | 0.0447 (0.0568) |
| On | - | - | - | 0.1286 (0.0983) | 0.0863 (0.0702) | |
| Max of lateral error [m] | Off | 0.6983 | 0.1770 | 0.1901 | 0.2470 | 0.1429 |
| On | - | - | - | 0.4093 | 0.3022 | |
| Mean (SD) of heading error [deg] | Off | 4.3795 (4.8417) | 0.9832 (1.6004) | 1.3902 (2.7911) | 2.2949 (3.1920) | 1.7151 (2.6232) |
| On | - | - | - | 4.8468 (3.8542) | 3.7865 (2.4860) | |
| Max of heading error [deg] | Off | 17.4951 | 9.3390 | 15.7492 | 14.4686 | 12.3413 |
| On | - | - | - | 16.2658 | 11.0544 | |
| Max of ay [m/s2] | Off | 5.8621 | 4.6436 | 4.2733 | 3.0435 | 2.9409 |
| On | - | - | - | 5.5699 | 4.3923 | |
| Max of LTR | Off | 1.7861 | 1.4252 | 1.2565 | 0.9139 | 0.8942 |
| On | - | - | - | 1.2175 | 0.9284 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, T.; Jeong, Y. A Tube-Based Model Predictive Control for Path Tracking of Autonomous Articulated Vehicle. Actuators 2024, 13, 164. https://doi.org/10.3390/act13050164
Lee T, Jeong Y. A Tube-Based Model Predictive Control for Path Tracking of Autonomous Articulated Vehicle. Actuators. 2024; 13(5):164. https://doi.org/10.3390/act13050164
Chicago/Turabian StyleLee, Taeyeon, and Yonghwan Jeong. 2024. "A Tube-Based Model Predictive Control for Path Tracking of Autonomous Articulated Vehicle" Actuators 13, no. 5: 164. https://doi.org/10.3390/act13050164
APA StyleLee, T., & Jeong, Y. (2024). A Tube-Based Model Predictive Control for Path Tracking of Autonomous Articulated Vehicle. Actuators, 13(5), 164. https://doi.org/10.3390/act13050164






