Abstract
The hydro-pneumatic suspension, known for enhancing vehicle ride comfort and stability, finds widespread use in engineering vehicles. Presently, the majority of mining trucks employ hydro-pneumatic suspension with a fixed damping hole, underscoring the critical importance of selecting appropriate damping hole parameters. Initially, an equilibrium mathematical model of the ¼ hydro-pneumatic suspension is established, and the influencing factors of the damping characteristics are analyzed. Subsequently, the simulation model and experimental bench for the hydro-pneumatic suspension are constructed. Sinusoidal signals with different frequencies and amplitudes serve as the excitation signals to analyze the variation trend of the force on the rod with displacement changes. The simulation and experimental results demonstrate a high degree of consistency, validating the rationality and validity of the simulation model. Building upon this foundation, various damping apertures are then selected to study the damping characteristics of the hydro-pneumatic suspension. The research indicates that as the damping aperture increases, the setting time of the hydro-pneumatic suspension system after excitation extends, accompanied by a decrease in the acceleration overshoot. As a result, a comprehensive evaluation index is developed, considering various factors, such as different weight setting times and peak longitudinal accelerations to assess the ride comfort of the suspension. This approach is then employed to determine the optimal damping aperture under both full-load and no-load conditions. The findings of this research offer valuable insights for the development of adaptive variable damping hydraulic suspensions, especially under variable load conditions.
1. Introduction
In the 1980s, hydro-pneumatic suspension began to be used in heavy vehicles [1]. Damping characteristics play a crucial role as a performance indicator for hydro-pneumatic suspension systems. Their nonlinear features are particularly well suited to meet the requirements of most construction vehicles [2,3]. As a result, the analysis and research on the damping characteristics of these suspension systems hold great significance and application value. The principle of the commonly used hydro-pneumatic suspension involves the combined action of the compressibility of inert gas, vibration reduction through the use of oil, and friction between components within a certain flow area. This combination aims to alleviate ground impact, reduce vehicle vibration, and enhance driving smoothness, vehicle safety, and ride comfort.
In recent years, with the growing demand for engineering vehicles, research on hydro-pneumatic suspension has gained prominence. For instance, Zhang Di et al. conducted a comparative analysis of the ride performance of a vehicle equipped with hydro-pneumatic suspension and the original vehicle. They evaluated the performance under two conditions: random road excitation and triangular pulse excitation. The conclusion drawn was that the vehicle employing hydro-pneumatic suspension exhibited significantly superior performance compared to the original vehicle [4]. You Zhuan et al. analyzed the response characteristics of hydro-pneumatic suspension to road excitation under both normal driving conditions and obstacle-crossing conditions through simulation [5]. Andrzej Zuska et al. investigated the influence of changes in stiffness and damping of tire wheels on the outcome of the condition assessment of motor vehicle shock absorbers [6]. Verros et al. analyzed the elastic and damping characteristics of the suspension under different road classes by building a nonlinear quarter-vehicle model and proposed an optimization method [7]. Cao Ruiyuan et al. selected the WC5 articulated mining vehicle as the research object and analyzed the changing trends in stiffness and damping characteristics of hydro-pneumatic suspension. This analysis was conducted after altering the initial conditions of various parameters, including the accumulator, inner diameter of the suspension cylinder, check valve, and hole diameter [8]. Tao Wei et al. introduced a semi-active seat suspension system for a loader, incorporating a damping multi-state switching shock absorber. Their analysis focused on identifying the recovery and compression damping coefficients of the shock absorber across four distinct damping states. The findings from this investigation significantly contributed to enhancing the vehicle’s ride performance [9]. Wang Shaohua et al. introduced a novel structure and control methodology for a rigidity-damped, multistage, adjustable pneumatic suspension system, leveraging a high-speed switching solenoid valve. They applied the particle swarm optimization algorithm to optimize and align the stiffness and damping characteristics of the oil–gas suspension system across various driving conditions. Additionally, they devised a mode-switching control approach to determine the optimal sequence for switching stiffness damping modes of the oil–gas suspension under diverse driving scenarios [10]. Goga employed a genetic algorithm to optimize both the damping and stiffness coefficients of the suspension system, with the evaluation criteria of passenger comfort and driving stability as the primary optimization objectives. The results indicated a substantial reduction in model amplitude following parameter optimization [11]. Sang et al. developed a two-chamber hydro-pneumatic suspension structure and employed both nonlinear vibration theory and fractional calculus theory to analyze its characteristics [12]. Han Shousong introduced a multi-system co-simulation methodology, utilizing particle swarm optimization, aimed at optimizing the damping parameters of semi-active oil–gas suspension systems. This approach addresses the segmental discontinuity inherent in damping force control and the challenges associated with accurately resolving dynamic performance indexes of suspensions [13]. Yuan Jiaqi et al. developed a mathematical model to characterize the stiffness and damping properties of the hydro-pneumatic suspension. Their simulations demonstrated that varying the throttle aperture resulted in changes to the damping force of the hydro-pneumatic suspension [14]. Wang Xu et al. utilized a mathematical model of a hydraulic system for interconnected oil–gas suspension to compare the stiffness and damping properties between interconnected and independent suspension, considering both vertical and roll conditions. Additionally, they conducted a parametric analysis to examine the damping characteristics of the interconnected suspension [15]. Liu Qihang investigated the output characteristics of interconnected suspension across various parameters and analyzed the evolving trends of body vibration characteristics. Their findings revealed a significant impact of damping hole diameter on the vibration state of the body [16]. Liu Yan et al. analyzed the working process of hydro-pneumatic suspension, the system’s response after excitation, the hole parameters of the check valve, and the characteristics of gas dissolved in oil. They reached the conclusion that, under continuous sinusoidal excitation, the change in hole size has a more significant impact on the external characteristics of hydro-pneumatic suspension compared to the size of the check valve [17]. This also highlights the importance of studying the influence of hole size variation on the specific performance parameters of hydro-pneumatic suspension.
In this paper, the damping characteristics of the hydro-pneumatic suspension system of a 90 ton heavy-duty truck are analyzed and studied. The working environment of heavy-duty vehicles is inherently hazardous, and there exists a substantial gap between full-load and no-load working conditions. Based on the structure and working principles of the hydro-pneumatic suspension system in heavy-duty vehicles, a mathematical model is established. A 1/4 simulation model of the front suspension of a heavy-duty car is constructed using AMESim, and its force conditions and performance are thoroughly analyzed. The validity of the simulation model is confirmed through comparison with experimental data. In conclusion, we utilize the simulation model to investigate the damping characteristics of the suspension with various hole sizes. This research offers theoretical guidance for selecting the optimal hole size and designing a suspension system with variable damping.
2. Modeling Analysis of Hydro-Pneumatic Suspension
As depicted in Figure 1, the single-chamber suspension is partitioned into two chambers: rodless chamber I and rod chamber II. These two chambers are interconnected through hole 4 and check valve 3. During the suspension’s stretch stroke, check valve 3 remains closed, allowing the hole to function independently. Conversely, during the compression stroke, check valve 3 opens and collaborates with hole 4.
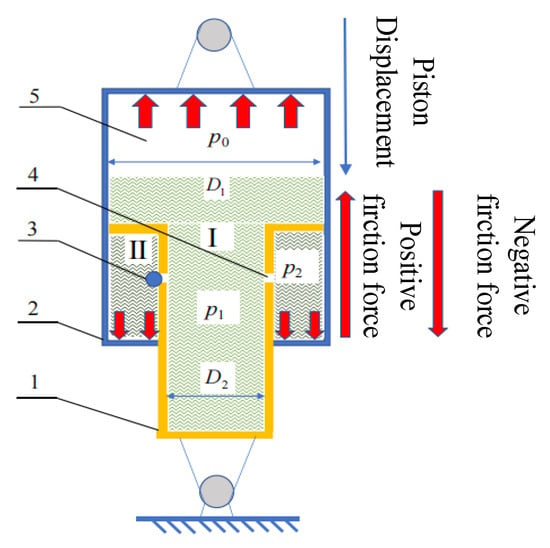
Figure 1.
Structure diagram of hydro-pneumatic suspension. 1. Rod, 2. cylinder, 3. check valve, 4. hole, and 5. air chamber.
Before establishing the mathematical model for a theoretical analysis of the structure and working principle of the single-chamber hydro-pneumatic suspension, several assumptions were made to facilitate the analysis [18]. The air–gas suspension system demonstrated excellent sealing performance, and oil leakage was disregarded in the analysis. Considering the brief travel change time of the hydro-pneumatic suspension, the heat generated by the alteration in gas volume was insufficient for effective heat exchange with the external environment. As a result, the inert gas within the suspension underwent an adiabatic process. The schematic diagram illustrating the forces acting on the hydro-pneumatic suspension is presented in Figure 1.
Under the assumption that the compression stroke of the suspension is considered positive, while the stretching stroke is negative, and building upon the previously mentioned assumptions and force analysis, the mathematical model of the hydro-pneumatic suspension was formulated.
Suspension force balance equation:
In the formula, , is the pressure of the rodless chamber, is the area of the rodless chamber, is the pressure of the rod chamber, is the area of the rod chamber, is the motion resistance of suspension, is the sprung force, and x is the piston displacement.
The motion resistance of the suspension comprises kinetic friction, static friction, and viscous resistance, which can be synthesized using the following equation [19]:
In the formula, is static friction, is kinetic friction, is the set speed when kinetic friction is fully achieved, and is the viscous damping coefficient.
The spring load force and the output force of the hydro-pneumatic suspension constitute a pair of action and reaction forces. The output force of the hydro-pneumatic suspension can be obtained as follows:
By employing the flow continuity equation for the check valve and the damping hole, the total oil flow through both the damping hole and the check valve can be determined as:
In the formula, = , is the number of holes and check valves, is the flow factors of the hole, is the overflow area of the hole, is the flow factor of the check valves, is the overflow area of the check valves, and is the density of the oil.
Taking into account the compressibility of the fluid, the total volume change of the fluid can be determined using the bulk modulus of elasticity:
where is the initial volume of the rodless cavity, is the initial volume of the rod cavity, and is the volumetric modulus of elasticity of the oil.
According to the hydro-pneumatic suspension flow equation, the alteration in the flow rate within the two oil chambers can be represented by:
According to Equations (4) and (6):
Considering nitrogen gas dissolved in an oil liquid, according to Henry’s law, the concentration of a gas in a solution at a given temperature is directly proportional to the equilibrium pressure of that gas above the liquid surface. Therefore, the volume of nitrogen dissolved in the oil liquid is [20]:
In the formula, is the gas solubility, is the initial-state gas pressure inside the gas chamber, and is the initial-state gas volume inside the gas chamber.
By applying the ideal gas equation, the rodless cavity pressure can be determined in the hydro-pneumatic suspension system. The ideal gas equation, considering an adiabatic process with a gas variability index of 1.4, is used to satisfy the following equation:
In the formula, are variables related to gas dissolution and oil compression.
From the coupling equations, (2) to (10), it can be obtained that the output force of the oil–air suspension is satisfied:
Considering the sprung mass of the hydro-pneumatic suspension system when the hydro-pneumatic suspension reaches equilibrium:
In the given formula, represents the mass of the spring load borne by the hydro-pneumatic suspension at unloaded static equilibrium, and denotes the height of the gas inside the airbag at static equilibrium.
Substituting Equation (11) into Equation (10) yields the output force of the oil–air suspension, as:
Equation (13) indicates that the output force of the hydro-pneumatic suspension is comprised of three components: the elastic force, , the damping force, , and the friction force, . The total output force can be expressed as follows:
The elastic force is obtained by deriving the displacement, providing a model for calculating the stiffness, of the hydro-pneumatic suspension cylinder:
The damping force is determined by deriving with respect to velocity, yielding a model for calculating the damping coefficient, , of the hydro-pneumatic suspension:
Equation (15) highlights that the stiffness, , of the hydro-pneumatic suspension exhibits a nonlinear relationship with the piston displacement, x. Additionally, the stiffness is influenced by various factors, including the initial filling height, of the hydro-pneumatic suspension, structural parameters of the suspension, the volume of dissolved gas, and the volume of oil compression.
Equation (16) indicates that the damping coefficient, , of the hydro-pneumatic suspension demonstrates a nonlinear relationship with the piston speed. The damping coefficient is not only dependent on the piston speed but is also influenced by various factors, including the number of check valves, , the through-flow area of the check valves, , the through-flow area of the hole, , and other parameters [21,22]. Additionally, the amount of oil compression plays a significant role in determining the damping coefficient.
The primary focus of this paper was to investigate the impact of different damping hole diameters on the damping characteristics of hydro-pneumatic suspension using a simulation-based approach to obtain the optimal damping aperture for hydro-pneumatic suspension under different loads.
3. Simulation Modeling and Validation of Hydro-Pneumatic Suspension
Initially, a simulation model of the hydro-pneumatic suspension was constructed. Experimental data were then utilized to identify the main parameters. The reasonableness and validity of the simulation model were subsequently verified by comparing its results with those obtained from experiments.
3.1. Simulation Model of Hydro-Pneumatic Suspension
The AMESim-2021.1 software was employed to establish a 1/4 oil–pneumatic suspension simulation model, as illustrated in Figure 2 [23,24]. The oil–pneumatic cylinder comprises two sets of parallel hole and check valves, and an accumulator was utilized to replicate the cylinder air chamber. The parameters of the simulation model are detailed in Table 1, facilitating easy configuration for each structural parameter of the oil–pneumatic suspension, motion resistance, air chamber parameters, oil properties, displacement signals, and other relevant factors.
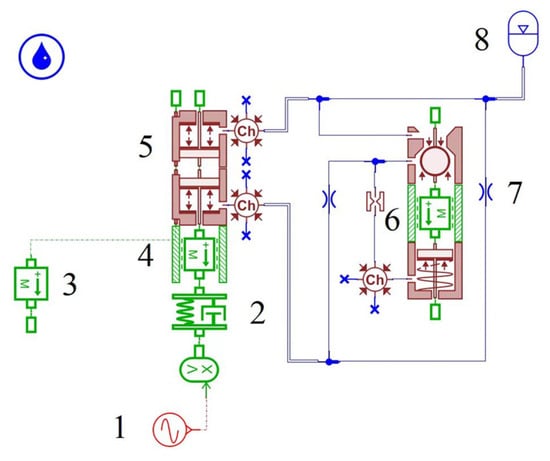
Figure 2.
1/4 Simulation model of hydro-pneumatic suspension. 1. Displacement signal, 2. tire model, 3. sprung mass, 4. piston and rod mass, 5. piston cylinder, 6. check valve, 7. hole, and 8. air chamber.

Table 1.
Simulation parameters of hydro-pneumatic suspension.
3.2. Hydro-Pneumatic Suspension Test Bench
Drawing inspiration from established hydro-pneumatic suspension experimental methods, we constructed an experimental bench utilizing an existing oil–air suspension system with a hole diameter of 5.3 mm [25,26]. The experimental bench is illustrated in Figure 3.

Figure 3.
Test bench of hydro-pneumatic suspension. 1. Upper computer, 2. test controller, 3. electro-hydraulic servo valve, 4. displacement sensor, 5. load cylinder, 6. tension sensor, 7. hydro-pneumatic suspension, and 8. fixed trestle.
For ease of loading, a dedicated fixing bracket (8) was designed to mount the hydro-pneumatic suspension (7) in reverse on the experimental bench. The upper computer (1) was responsible for configuring the mode and parameters of the input displacement excitation signal. Real-time displacement feedback was obtained through the displacement sensor (4) on the loading cylinder [27]. The electro-hydraulic servo valve (3) ensured that the loading cylinder moved in accordance with the displacement signal, while the tension sensor (6) provided feedback on the force exerted on the rod of the hydro-pneumatic suspension.
The hydraulic schematic diagram of the experimental bench is depicted in Figure 4. This experimental setup allowed for both force control and motion control [28]. Motion control was primarily achieved through the electro-hydraulic servo valve, which regulated the flow into the rod cavity and rodless cavity of the loading cylinder, thereby controlling the displacement and speed of the rod.
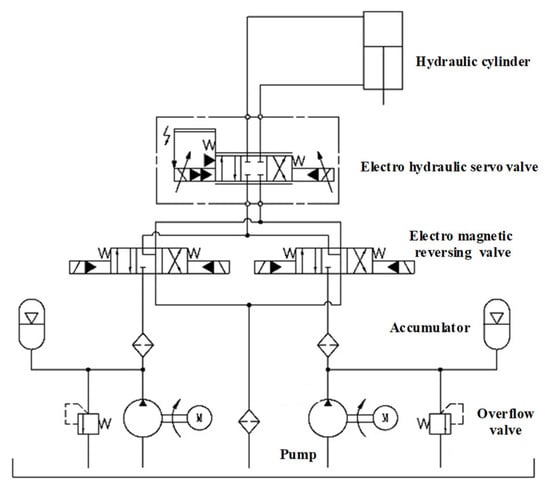
Figure 4.
Schematic diagram of the hydraulic principle of hydro-pneumatic suspension.
To simulate pavement excitation, sinusoidal signals with varying frequencies and amplitudes were carefully chosen. The parameters of these displacement excitation signals are outlined in Table 2, and the signals themselves are illustrated in Figure 5. These displacement excitation signals, possessing identical parameters, were then input into the simulation model.

Table 2.
Parameters of the displacement signal.
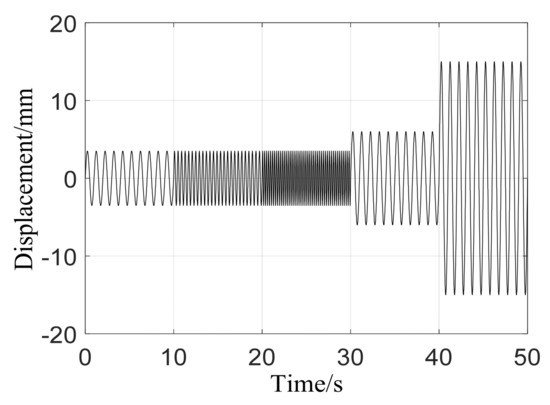
Figure 5.
Displacement signal.
The accuracy of the simulation model was validated by meticulously comparing the curves of force and displacement of the rod obtained through both experimentation and simulation.
3.3. Validation of Hydro-Pneumatic Suspension Model
The force–displacement curve of the rod of the oil–air suspension was generated with the rod displacement as the horizontal coordinate and the force on the rod relative to the equilibrium position as the vertical coordinate. The variations in force–displacement relative to the equilibrium position under displacement signals with amplitudes of 2.7 mm, 6 mm, and 15 mm, and frequencies of 1 Hz, 2.5 Hz, and 4.5 Hz, are depicted in Figure 6.
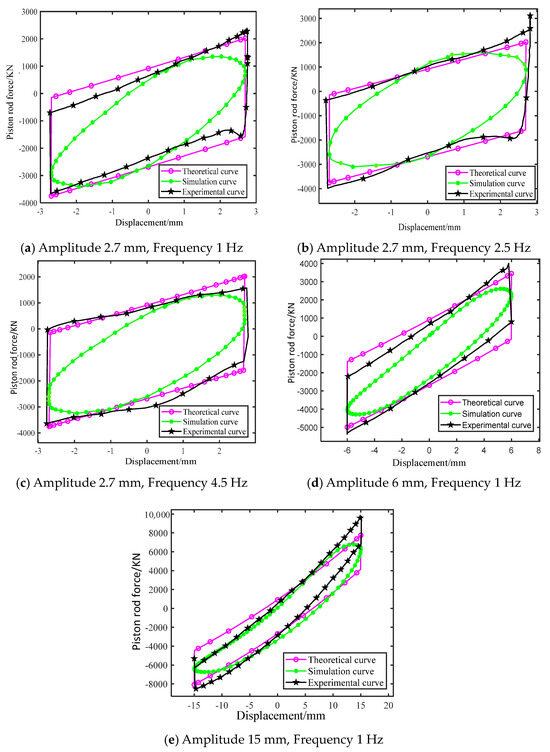
Figure 6.
Displacement–force curves of a rod under different excitation signals.
A comparison of the theoretical curve, simulation, and experimental curves indicated some differences. The primary reason for this variance was attributed to the larger size of the loading cylinder in the experimental platform, leading to fluctuations in the oil flow rate. These fluctuations were particularly notable when high-frequency displacement signals were applied. Furthermore, the oil leakage from the experimental platform had some impact on the experimental results. While the simulation could broadly capture the theoretical and experimental trends, notable discrepancies existed, particularly in the displacement limit position, where significant errors were observed. Specially, the simulation model overlooked the effects of oil leakage and flow rate fluctuations in the loading cylinder, resulting in a smoother simulation curve.
Comparing the force–displacement curves of the rod obtained from both the experiment and simulation indicated that under identical parameters, the rod experienced nearly equal magnitudes of force at the end of each positive and negative stroke. As the frequency increased at the same amplitude, the force fluctuation and the area enclosed by the curve both increased, indicating a rise in damping force generated by the hole. For an amplitude of 2.7 mm, the maximum force of the rod was approximately 3.8 KN. With an amplitude of 6 mm, the maximum force increased to about 5.1 KN, and for an amplitude of 15 mm, the maximum force rose to about 8 KN. Notably, as the amplitude increased, compression of the gas also increased, resulting in a rapid escalation of the maximum force.
In different displacement signals at the limit of displacement, the phenomenon where the displacement remains unchanged, but the force on the rod undergoes changes, is termed hysteresis. This hysteresis is primarily attributed to the lag in gas pressure from the hydro-pneumatic suspension accumulator behind the displacement changes caused by the opening and closing of the check valve during the conversion of the two strokes. Additionally, the alteration in the direction of friction also contributes to the hysteresis phenomenon. The trend of the rod force with displacement in the simulation closely aligned with the experimental results. Notably, altering the parameters of the displacement signal did not affect the consistency between the simulation and experimental results. This observation reinforces the validity of the simulation model.
4. Effect of Damping Aperture under Step Signals of Road Displacement
4.1. Step Response under No-Load Conditions
Damping characteristics of hydro-pneumatic suspensions were investigated through simulation models. The input road displacement signal is a step signal, and various sizes of holes were selected in the step response of the oil–air suspension under two distinct working conditions: no load and full load of the mining truck. This analysis encompassed the examination of the velocity and acceleration profiles of the rod of the oil–air suspension as they changed over time in response to excitation.
The setting time and peak longitudinal acceleration of the suspension following excitation serve as key indicators for assessing the damping and buffering performance of the suspension. In no-load conditions, the vehicle body often experiences vigorous shaking, with a more pronounced impact from acceleration. Conversely, under full-load conditions, enhanced setting is imperative, necessitating a minimal setting time for the system [29,30]. Hence, we proposed the introduction of a weight Table 3 and a comprehensive evaluation index that take into account both the setting time and acceleration.

Table 3.
Weight table.
To assess the damping and buffering performance of the suspension, key indices include the setting time required by the suspension after excitation, the peak longitudinal acceleration of the sprung mass, and the root-mean-square value of the weighted acceleration. Setting time, , is defined as the duration necessary for the piston speed to decrease by 90% from the peak speed following suspension excitation, ‘’ represents the value of piston acceleration, and ‘’ denotes the number of discrete times simulated during the setting time, with a simulation step of 0.001 s. The through-flow diameter of the hole was treated as a variable, and simulations were conducted with different hole diameters under no-load conditions. The results of these simulations are presented in Figure 7, Figure 8 and Figure 9.
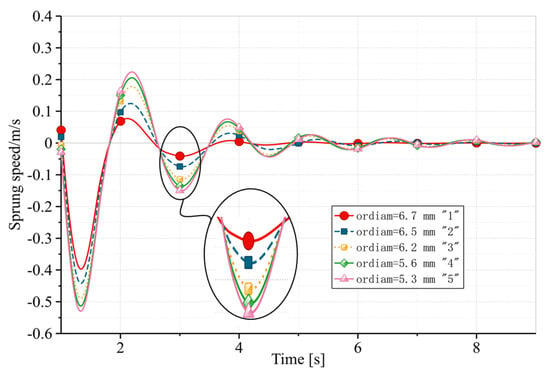
Figure 7.
Sprung speed with different diameters of the damping hole under no-load conditions. 1. Diameter 6.7 mm, 2. diameter 6.5 mm, 3. diameter 6.2 mm, 4. diameter 5.6 mm, and 5. diameter 5.3 mm.
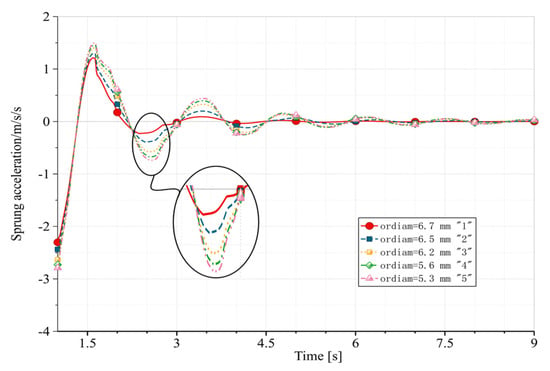
Figure 8.
Sprung acceleration with different diameters of the damping hole under no-load conditions. 1. Diameter 6.7 mm, 2. diameter 6.5 mm, 3. diameter 6.2 mm, 4. diameter 5.6 mm, and 5. diameter 5.3 mm.
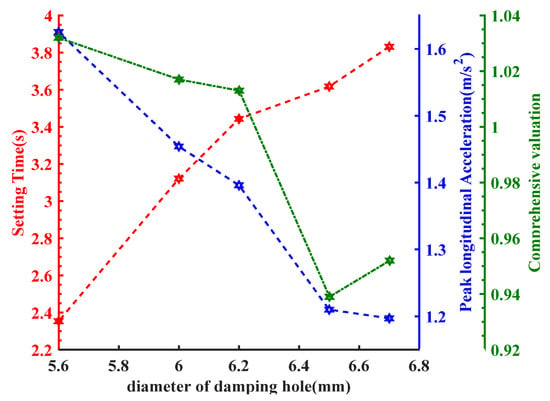
Figure 9.
Setting time, peak value of acceleration, and complete review under different diameters of the damping hole under the no-load condition.
Under no-load conditions, simulation results indicate the following characteristics for different damped hole sizes, as presented in Table 4.

Table 4.
Conclusion.
Due to the intense body-shaking phenomenon of the car under no-load conditions, acceleration had a significant impact. As a result, enlarging the damping hole diameter resulted in an increase in the setting time and a decrease in the peak longitudinal acceleration. As illustrated in Figure 9, the comprehensive evaluation value reached its lowest point.
4.2. Step Response under Full-Load Conditions
The simulation was conducted under full-load conditions, and the corresponding results are presented in Figure 10, Figure 11 and Figure 12.
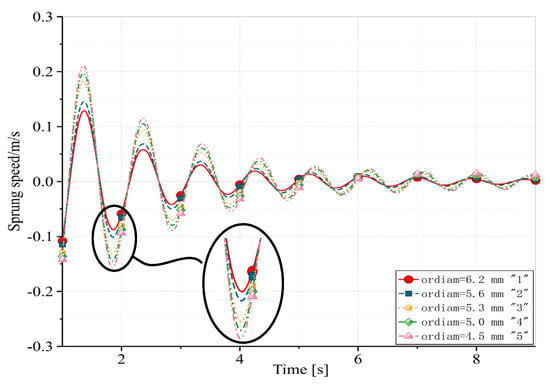
Figure 10.
Sprung speed under full-load conditions with different damping diameters. 1. Diameter 6.2 mm, 2. diameter 5.6 mm, 3. diameter 5.3 mm, 4. diameter 5 mm, and 5. diameter 4.5 mm.
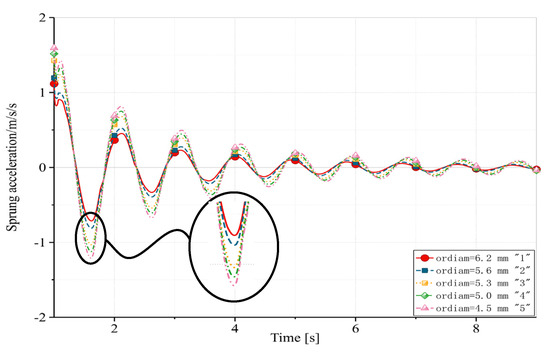
Figure 11.
Sprung acceleration under full-load conditions with different diameters of the damping hole. 1. Diameter 6.2 mm, 2. diameter 5.6 mm, 3. diameter 5.3 mm, 4. diameter 5 mm, and 5. diameter 4.5 mm.
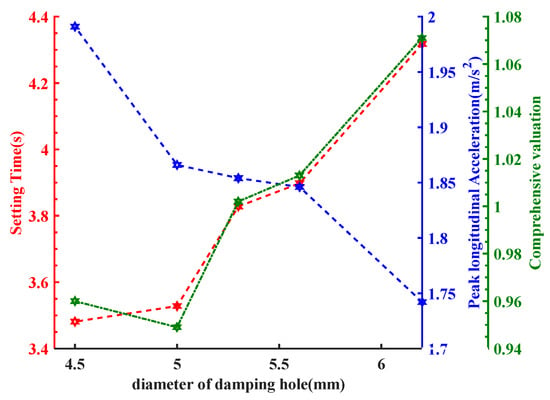
Figure 12.
Setting time, peak longitudinal value of acceleration, and complete review under different diameters of the damping hole under full-load conditions.
Under full-load conditions, simulation results indicate the following characteristics for different damped hole sizes, as presented in Table 5.

Table 5.
Conclusion.
In pursuit of enhanced stability for mining trucks under full-load conditions, minimizing the setting time of the system is crucial.
In a similar vein, when the vehicle operated under full-load conditions, an increase in the diameter of the damping hole resulted in a corresponding rise in the setting time and a decline in peak longitudinal acceleration. As depicted in Figure 12, the comprehensive evaluation value reached its minimum at a damping hole diameter of 5.0 mm, specifically measuring 0.949.
Taking into account the cushioning and vibration damping performance, the 5.0 mm hole was deemed more suitable for full-load working conditions.
5. Discussion and Conclusions
In this paper, we investigated the impact of the damping hole diameter on suspension damping characteristics and determined the optimal damping hole diameter under both no-load and full-load conditions by introducing comprehensive evaluation criteria. Our study utilized a test bench to analyze the influence of the damping hole diameter on suspension output characteristics, aligning with previous research findings [3,4]. However, unlike other studies, which typically discuss the optimal damping aperture range under a single working condition [16], or only outline the variation trend of damping force with aperture [14], our paper introduced a novel approach. By conducting research under various working conditions, we precisely determined the specific value of the optimal damping hole diameter, thus contributing a unique perspective to the field. We drew the following conclusions:
- (1)
- The equilibrium mathematical model of the hydro-pneumatic suspension was established, yielding expressions for the damping force and damping coefficient. The damping characteristics of the hydro-pneumatic suspension were not only dependent on piston speed, they were also influenced by structural parameters, including the number of holes and check valves, as well as the flow area of the check valves and holes. A simulation model for the hydro-pneumatic suspension and an experimental bench were constructed. The variation of force relative to the equilibrium position with the displacement of the rod was analyzed under different displacement excitation signals. The simulation and experimental results exhibited convergence, thereby validating the accuracy of the simulation model.
- (2)
- Utilizing the simulation model, the impact of the hole diameter on the damping characteristics of the hydro-pneumatic suspension was investigated. With an increase in hole diameter, the system’s setting time after excitation extended, accompanied by a corresponding decrease in peak longitudinal acceleration. A weight table and comprehensive evaluation index, which take into account both ride comfort and vehicle stability, were proposed. This methodology offers a systematic approach for selecting the optimal damping hole size under various working conditions. Furthermore, we determined the optimal damping hole diameter under both no-load and full-load conditions. Our study not only contributes to the optimization of damping hole selection for mining trucks but also provides a valuable methodology and insights applicable to other types of vehicles.
- (3)
- The optimal hole diameter for the hydro-pneumatic suspension was found to be 6.2 mm under no-load conditions, while the optimal diameter was 5.0 mm under full-load conditions. The results suggested the possibility of designing a variable damping hydro-pneumatic suspension with a hole diameter ranging between 5.0 and 6.2 mm to supply to various loading conditions. However, further research is needed to explore the variation trend of the damping hole flux area with piston displacement.
Author Contributions
Conceptualization, W.Z. and Z.Z.; methodology, W.Z. and X.C.; software, X.C.; validation, W.Z., X.C. and Z.Z.; formal analysis, X.Z.; investigation, Z.Z.; resources, M.Y.; data curation, C.C. and X.Z.; writing—original draft preparation, Z.Z. and X.Z.; writing—review and editing, Z.Z and M.M.A.; visualization, W.Z.; supervision, W.Z. and X.C.; project administration, X.C.; funding acquisition, W.Z., X.C. and C.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research received funding from the National Key Research and Development Program of China (2021YFB3400502), the Natural Science Basic Research Program of Shaanxi Province (2023-JC-QN-0472), the Postdoctoral Science Foundation of Anhui Province (2022B627), the Scientific Research Key Project of Anhui Provincial Department of Education (KJ2020A0364), and the Support Program for Outstanding Young Talents of Anhui Polytechnic University (2019YQQ023).
Data Availability Statement
Data can be obtained from the authors upon request.
Conflicts of Interest
Authors Wenfeng Zhu and Chuqing Cao was employed by the company Wuhu Hit Robot Technology Research Institute Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Nomenclature
| Value of piston acceleration | |
| Area of rodless chamber | |
| Area of rod chamber | |
| Overflow area of check valves | |
| Overflow area of hole | |
| Weight of setting time | |
| Damping coefficient | |
| Weight of peak longitudinal acceleration | |
| Flow factor of check valves | |
| Flow factor of hole | |
| Variables related to gas dissolution and oil compression | |
| Damping force | |
| Kinetic friction | |
| Friction force | |
| Static friction | |
| Elastic force | |
| Sprung force | |
| Acceleration of gravity | |
| The height of the gas at static equilibrium | |
| Stiffness | |
| Volumetric modulus of elasticity of the oil | |
| Mass of the spring load | |
| Initial-state gas pressure | |
| Pressure of rodless chamber | |
| Pressure of rod chamber | |
| Hydraulic oil flow | |
| Setting time | |
| Speed | |
| Initial-state gas volume | |
| Initial volume of the rodless chamber | |
| Initial volume of the rod chamber | |
| Volume of nitrogen dissolved | |
| Density | |
| Gas solubility | |
| Gas variability index |
References
- Sun, J. Application and key technologies of hydro-pneumatic suspension review. Coal Mine Mach. 2007, 28, 8–11. [Google Scholar]
- Liu, X.; Li, Y. Vehicle suspension technology of oil and gas research review. J. Southwest Jiaotong Univ. 2024, 3, 1–20. [Google Scholar]
- Repin, S.; Vasileva, P.; Evtykov, S.; Maksimov, S.; Ruchkina, I.; Eremeev, A. Theoretical study of throttle valve system operation in the hydropneumatic shock absorber of the transport and technological machinery undercarriage. Transp. Res. Procedia 2021, 57, 562–572. [Google Scholar] [CrossRef]
- Zhang, D.; Tian, J. Dump truck suspension characteristic simulation of hydro-pneumatic and comfort research. J. Chongqing Univ. Sci. Technol. (Nat. Sci.) 2017, 31, 45–52. [Google Scholar]
- You, Z.; He, R.; Liu, W. Based on the stiffness damping characteristics overloading car hydro-pneumatic suspension performance analysis. Mech. Des. Manuf. 2022, 3, 223–227. [Google Scholar]
- Zuska, A.; Jackowski, J. Influence of Changes in Stiffness and Damping of Tyre Wheels on the Outcome of the Condition Assessment of Motor Vehicle Shock Absorbers. Energies 2023, 16, 3876. [Google Scholar] [CrossRef]
- Verros, G.; Natsiavas, S.; Papadimitriou, C. Design optimization of quarter-car modelswith passive and semi-active suspensions under random road excitation. J. Vib. Control 2005, 11, 581–606. [Google Scholar] [CrossRef]
- Cao, R.; Zhang, H.; Xiong, S. Mine car Hydro-pneumatic suspension system modeling and simulation. Mech. Des. Manuf. 2011, 1, 239–241. [Google Scholar]
- Tao, W.; Liu, Z. Control of loader seat suspension based on damped state switching. J. Jiangsu Univ. (Nat. Sci. Ed.) 2019, 40, 504–505. [Google Scholar]
- Wang, S.; Zhai, X.; Sun, X.; Shi, D.; Yin, C. Analysis and control of a vehicle hydro pneumatic suspension system with multistage adjustable stiffness and damping characteristics. J. Vib. Shock. 2022, 41, 168–177. [Google Scholar]
- Goga, V.; Kľúčik, M. Optimization of vehicle suspension parameters with use of evolutionary computation. Procedia Eng. 2012, 48, 174–179. [Google Scholar] [CrossRef]
- Sang, Z.; Dong, M.; Gu, L. Numerical analysis of a dual-chamber hydro-pnematic suspension using nonlinear vibration theory and fractional calculus. Adv. Mech. Eng. 2017, 9, 1687814017705797. [Google Scholar] [CrossRef]
- Han, S.; Liu, X.; Chao, Z.; Li, H. Optimization of damping parameters of semi-active hydro-pneumatic suspension based on particle swarm Optimization. J. Ordnance Equip. Eng. 2020, 41, 53–57. [Google Scholar]
- Yuan, J.; Fan, J.; Zhou, Y.; Dou, H.; Song, F. Design of a Front Alxe Hydro-pneumatic Suspension with Controllable Stiffness and Damping. Mach. Tool Hydraul. 2019, 47, 135–141. [Google Scholar]
- Wang, X.; Gao, Q.-H.; Liu, Z.-H.; Feng, J.-T. Characteristics Analysis of Interconnected Hydro-pneumatic Suspension for Heavy Multi-axle Vehicle. Chin. Hydraul. Pneum. 2018, 15, 32–40. [Google Scholar]
- Liu, Q.; Feng, H.; Liu, S. Analysis of ride comfort in the suspension system of a mining dump truck using AMESim simulation software. J. Southwest JiaoTong Univ. 2024, 1–8. Available online: http://kns.cnki.net/kcms/detail/51.1277.U.20230922.1157.010.html (accessed on 26 April 2024).
- Liu, Y. Based on the characteristics of oil and gas on hydro-pneumatic suspension performance of Simulink analysis. Mach. Hydraul. 2017, 45, 152–158. [Google Scholar]
- Le, W. A Heavy Vehicle Hydro-Pneumatic Suspension Control Method Research. Master’s Thesis, Nanjing University of Science and Technology, Nanjing, China, 2016. [Google Scholar]
- Zhuang, D.; Liu, J.; Yu, F.; Lin, Y. Auto oil and gas spring nonlinear mathematical model and features. J. Shanghai Jiao Tong Univ. 2005, 39, 1441–1444. [Google Scholar]
- Huang, X.; Yang, J.; Shen, Y.; Feng, Y. Based on the dissolved gas and oil compressibility of hydro-pneumatic suspension performance study. J. Agric. Mach. 2013, 44, 14–18+13. [Google Scholar]
- Wang, G.; Wang, W.; Suo, X. Influence of structural parameters on dynamic characteristics of two-stage pressure type pneumatic suspension. Chin. Hydraul. Pneum. 2023, 47, 107–115. [Google Scholar]
- Tong, J.; Li, W.; Fu, S. Analysis of Influence of Main Parameters of Hydro-pneumatic Spring on Performance of Suspension System. J. Syst. Simul. 2008, 9, 2271–2274. [Google Scholar]
- Liu, G.; Chen, S.; Wang, W.; Zhao, Y. Simulation and Test of Oil-gas Suspension based on AMEsim and Simulink. J. Vib. Meas. Diagn. 2016, 36, 346–350+405. (In Chinese) [Google Scholar]
- Guo, Q.; Chi, Y. Simulation and Parameters Optimization of Hydro-pneumatic Suspension Based on AMESim. Coal Mine Mach. 2014, 35, 70–72. [Google Scholar]
- Zhang, X.-L.; Liu, J.; Nie, J.; Wei, H.; Chen, L. Simulation Analysis and Experiment Research on Hydro-Pneumatic ISD Suspension. Shock Vib. 2021, 2021, 2095350. [Google Scholar] [CrossRef]
- Zhen, L.; Zhang, W. Single chamber of hydro-pneumatic suspension simulation and experimental study. J. Mech. Eng. 2009, 45, 290–294. [Google Scholar] [CrossRef]
- Zhang, J.; Li, J.Y.; Wang, T.; Qian, Z.S. Influence of nozzle structure on theflow field of the prestage of nozzle flapper servo valve. Int. J. Hydromechatron. 2023, 6, 59–75. [Google Scholar] [CrossRef]
- Qian, P.; Liu, L.; Pu, C.; Meng, D.; Páez, L.M.R. Methods to improve motionservo control accuracy of pneumatic cylinders-review and prospect. Int. J. Hydromechatron. 2023, 6, 274–310. [Google Scholar] [CrossRef]
- Guo, Y.; Zhang, Z. Review on ride comfort control of active hydro-pneumatic suspension system for high speed and heavy load vehicles. Sci. Technol. Eng. 2022, 22, 4675–4686. [Google Scholar]
- Chen, K. Research on Ride Comfort Analysis and Collaborative Optimization of Heavy Commercial Vehicles Based on Nonlinear Mechanical Properties of Key Parts. Master’s Thesis, Guilin University of Electronic Technology, Guilin, China, 2022; pp. 23–24. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).