Defect Diagnosis of Rigid Catenary System Based on Pantograph Vibration Performance

Abstract

The condition of a catenary is significant to ensure a high current collection quality. Owing to the dynamic interaction between the pantograph and the catenary system, the vibration of the pantograph can be used to analyze the condition of the catenary system. Therefore, we developed a novel diagnosis system based on the correlation between catenary defects and pantograph vibration. The proposed system is capable of detecting the type and location of commonly encountered defects in rigid support catenary systems. Catenary positioning coefficient and enhanced sample entropy methods were proposed for the extraction of defect features, and subsequently, linear discriminate analysis was used to diagnose the type and location of the catenary defects. Finally, the proposed defect detection and diagnosis system was applied to a commercial metro line, and the results verified the reliability and effectiveness of this diagnosis system.

1. Introduction

In an electrified railway system, the power supplied by a pantograph–catenary system is vital for the normal operation of the vehicle [1]. The catenary system is usually classified into the flexible catenary and the rigid catenary based on their structural differences. The rigid catenary, which is widely used in metro lines due to its strong durability, convenient installation, low maintenance cost, low tunnel clearance requirements, and good wind resistance, operates in a high-frequency and long-term environment [2]. Long-term mechanical and electrical impact in harsh working environments leads to the formation of defects in the rigid catenary that can reduce the service life of the catenary as well as pose a threat to the safe operation of the vehicle. The online monitoring and defect diagnosis of the pantograph–catenary system can detect such defects and aid in the efficient elimination of their associated safety risks during normal operation [3,4]. Therefore, to reduce maintenance costs and ensure the safe operation of trains, the development of an effective monitoring and defect diagnosis system is significant and has attracted considerable attention in academics and industries.

Currently, mechanical sensor-based contact detection technology and vision-based detection technology have been widely utilized in pantograph–catenary systems for condition-based monitoring and defect diagnosis. Some scholars employ visual-based detection methods to extract the edges of catenary structures, thereby diagnosing faults in the catenary structures. In [5], Liu W. et al. located the bracing wire components of a catenary using an image acquisition system and detected the installation defects of the messenger wire bases via image processing. Lyu et al. [6] realized generic anomaly detection of catenary support components using an image-based approach, while Chen [7] proposed a deep learning model for the diagnosis of catenary current-carrying ring faults. Kang et al. [8,9] proposed a contact wire support and insulator defect detection system capable of localizing the key components of a catenary and evaluating its defect status using deep Bayesian segmentation neural networks and prior geometric knowledge. Liu Y et al. [10] introduced a robust image-based semantic segmentation model named ArcMSF for pantograph catenary arcing detection. While the visual-based detection method is effective in quickly identifying faulty components, it is limited to visible faults and lacks the ability to continuously monitor the status of the catenary in real time. Consequently, it cannot accurately detect the gradual degradation of the catenary status.

The mechanical sensor-based contact detection method utilizes sensors installed on the pantograph to indirectly monitor the real-time status of the catenary, thus diagnosing the catenary faults. Song Y et al. [11] presented a method for evaluating the quality of pantograph–catenary current collection on high-speed railways using the contact line height variability. Tian SX et al. [12] filtered the acceleration signal of the pantograph head with white noise using a global default threshold and utilized the characteristic signal to obtain a Hidden Markov Model for hard-point detection. Wang HR et al. [13] proposed a data-driven approach using a Bayesian network to integrate inspection data from high-speed railway catenaries into a key performance indicator for improved condition monitoring. Gao SB et al. [14] described the detailed architecture of the 6C system for automatic detection and monitoring of pantograph-catenary systems in China’s high-speed railways.

The objects of these studies are flexible catenaries, while there are limited studies on fault diagnosis of rigid catenaries.

At present, studies on monitoring and defect diagnosis of rigid catenary have mainly focused on condition monitoring by detecting the dynamic interaction parameters of the pantograph–catenary system. Bocciolone M et al. [15] and Carnevale M et al. [16] detected defects by observing the occurrence of high peaks in the measured contact force and vertical acceleration values. S. Gregori [17] used a simulation model to generate acceleration data of pantograph heads under fault conditions and used it to train a neural network model, achieving state assessment of the contact network and diagnosis of contact wire wear and irregularities. The condition monitoring of a catenary can realize the abnormal state detection of a rigid catenary; however, the diagnosis of defects remains a challenge and has not been effectively resolved as defect identification and separation are quite difficult.

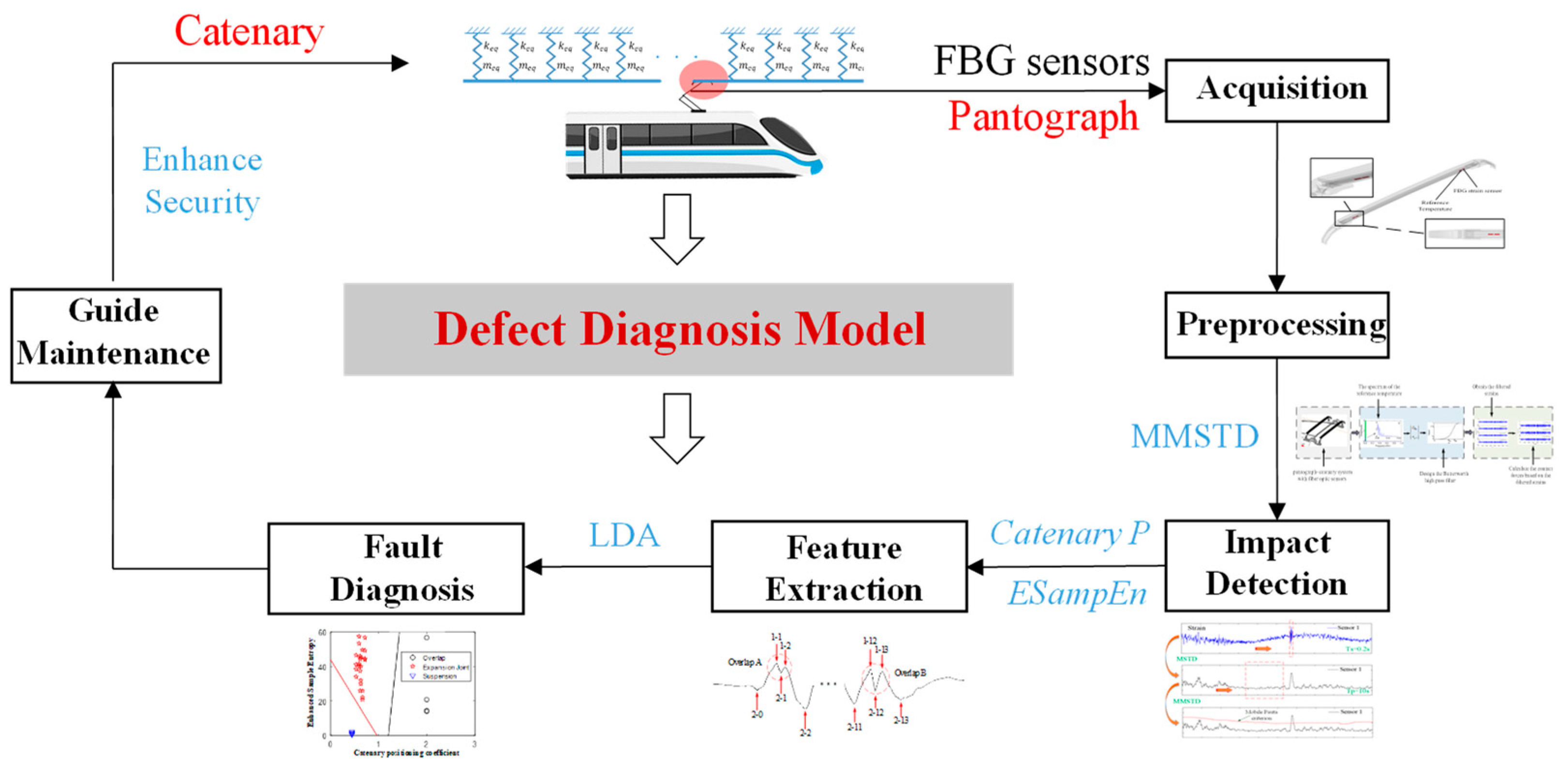
Due to the dynamic coupling relationship between the pantograph and the catenary, the pantograph’s vibration performance is intricately linked to the condition of the catenary. Diverse fault types lead to distinctive vibration patterns, giving rise to distinctive fluctuations in the dynamic interaction signal. Consequently, this paper introduces a defect diagnosis system based on pantograph vibrations for a rigid catenary. This system relies on strain signals as indicators, utilizing defect signature analysis to detect and identify various defects. This system offers the remarkable ability to pinpoint and synchronously locate catenary defects accurately, without the need for location equipment. It can be applied in real time and exhibits relatively high versatility. Furthermore, this system provides insights into the lifecycle of the catenary, particularly its early stages of degeneration, enabling defect prognosis and service life prediction.

2. Analysis of Common Defects in Rigid Catenary

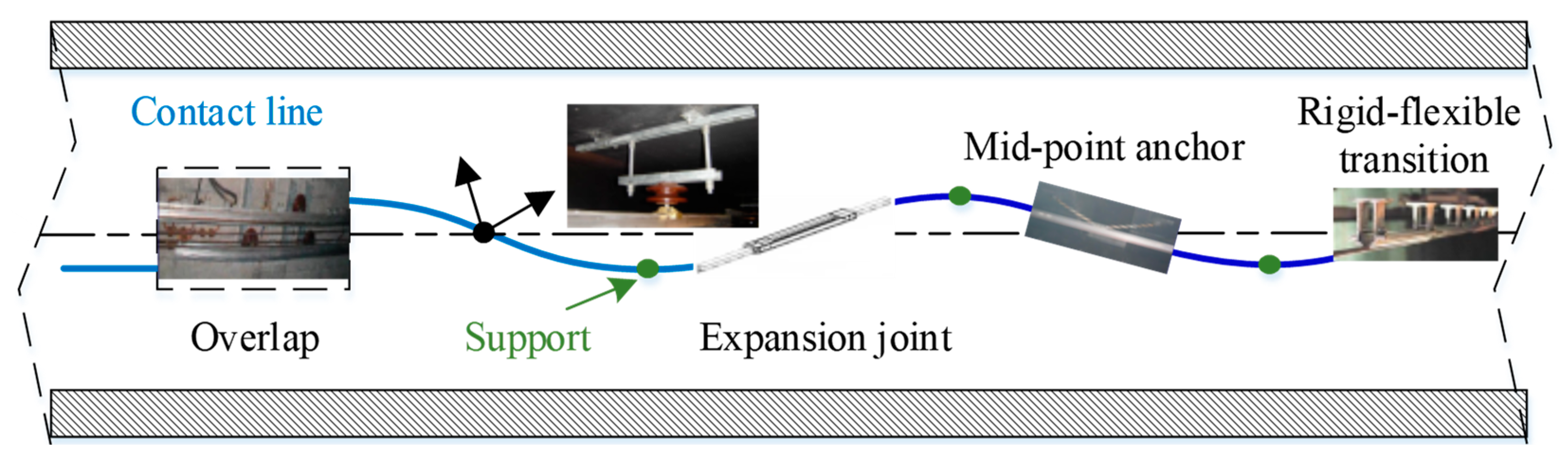
Railways have often adopted rigid overhead conductor lines for current collection in underground lines and tunnels. The rigid catenary is composed of contact wires, the conductor rails, and the supports (Figure 1). These supports are metal structures that are typically attached to the tunnel ceiling. The conductor rails are interconnected using bolted metal inserts, resulting in longer spans called anchoring sections. These mechanically independent anchoring sections form the entire catenary, which can minimize displacements due to thermal expansion or contraction. The overlap, expansion joint, and rigid–flexible transition are crucial structures that connect independent anchoring sections or different catenary components.

Metro operators have widely recognized that the majority of unfavorable behaviors between the pantograph and catenary—such as contact loss, impact, and arcing—tend to occur in specific sections like the overlap, expansion joint, and support spans. This is because the stiffness of the catenary varies in these unique spans, leading to an increase in vibrations caused by the interaction between the pantograph and the catenary. Over time, these intense vibrations can cause loosening, misalignment, and deformation of catenary components in the overlap, expansion joint, and support spans.

2.1. Misalignment of Overlap Section

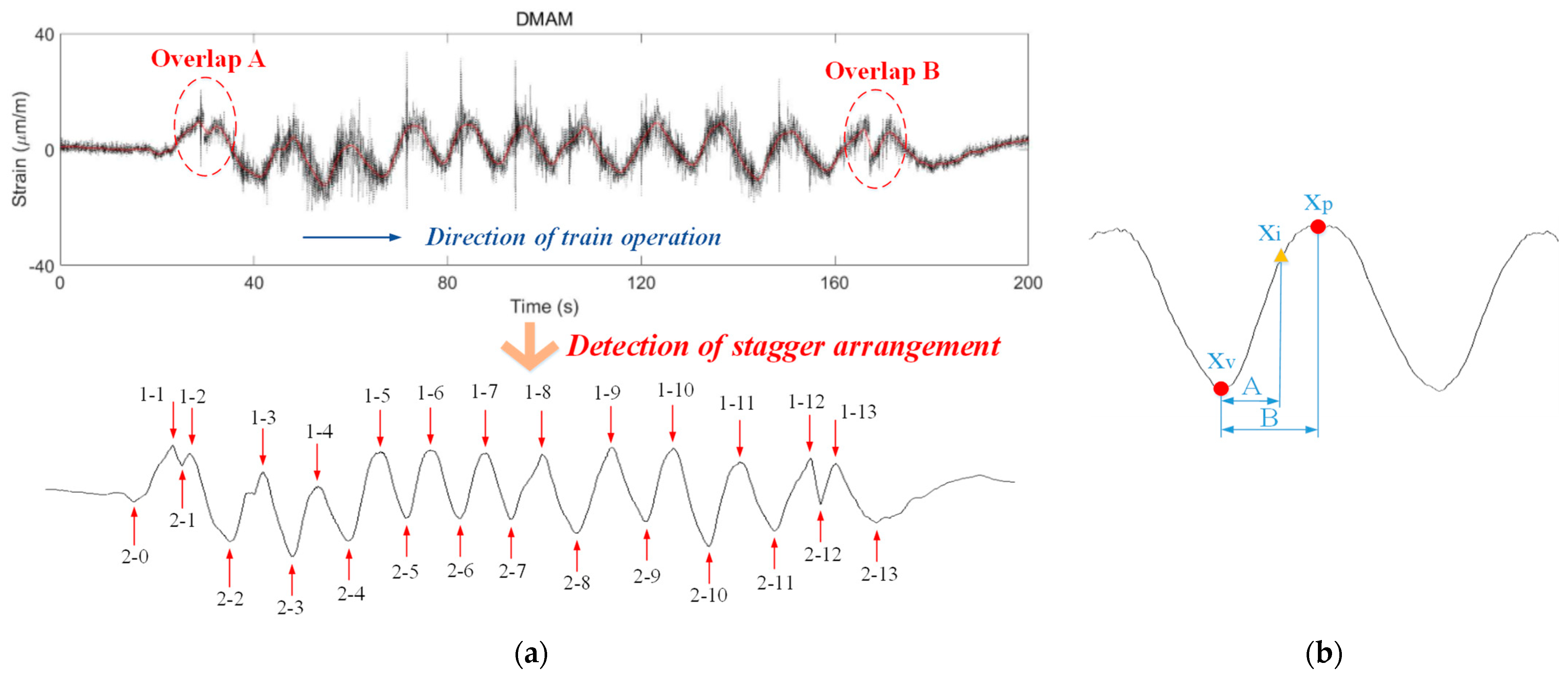
The overlap section is crucial for maintaining electrical continuity in the line and transferring mechanical load from one catenary section to the next. In the transition span, the two sections overlap side-by-side, allowing the pantograph to interact with either one or both sections. When the pantograph travels through the overlap spans, the dynamic interaction parameters measured will exhibit different fluctuations compared to those in the normal span. Long-term exposure to pantograph shock and vibration can cause changes in the vertical displacement of the catenary, leading to vertical misalignment of the two catenary sections in the overlap. This misalignment of overlap can create hard spots and more intense impacts on the pantograph–catenary system.

2.2. Deformation of Expansion Joint

The expansion joint is made up of two parallel aluminum alloy plates of the same size, designed to compensate for any deformation caused by thermal expansion and contraction. One aluminum alloy plate is firmly attached, while the other is free to adjust and compensate for the deformation of the two adjacent conductor rails. However, due to differences in the length and thermal expansion/contraction forces of the conductor rails at both ends of the expansion joint, the amount of deformation caused by the expansion/contraction of the aluminum alloy plates varies. Additionally, the status of the expansion joints can change over time as a result of mechanical and electrical interactions within the pantograph–catenary system. Inconsistencies in the deformation can lead to a shift in the barycenter within the expansion joint after multiple expansions and contractions caused by temperature. This barycenter offset causes a downward bending deformation in the contact line at this point, which can impact the pantograph–catenary system and generate sparks and arcs.

2.3. Loosening of Support

Over the long-term operation of trains, as travel density increases, the energy generated accumulates, and any excess energy is transferred into the support system. This can have a noticeable impact on the support system’s performance. A significant amount of released energy can cause the support system’s threads to slip and other components to become loose during operation, ultimately leading to the loosening of the support system and disrupting the smooth operation of the train.

3. Analysis of Defect Characteristic Based on Simulation Test

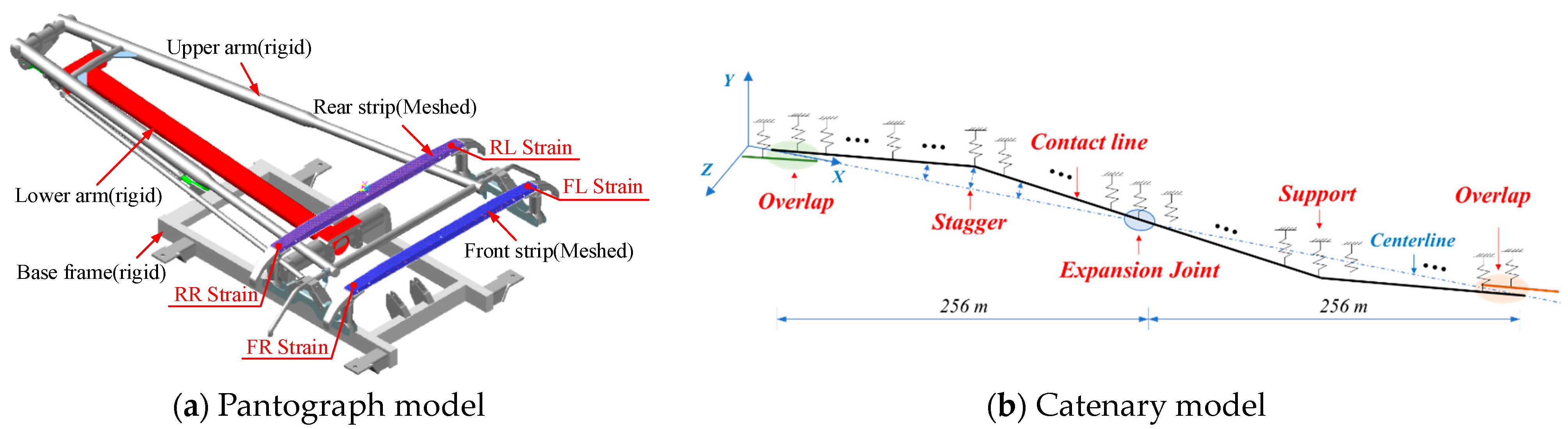
In order to analyze defect characteristics of misalignment of the overlap section, deformation of the expansion joint, and the loosening of support, a simulation model using Finite Element Models (FEM) was established. The pantograph is modeled with a rigid–flexible hybrid body, with two strips of the pantograph head as a flexible body and other parts of the pantograph as a rigid body, as shown in Figure 2a.

The rigid catenary support devices are simplified to a spring with mass, while the contact line and conductor rails are represented using the Euler–Bernoulli beam model. Furthermore, the stagger value is taken into account. The structure and parameters of the catenary used in this study are taken from a metro line in China. The catenary model includes two anchors, each 256 m long, connected by expansion joints. There are also overlapping sections at both ends of the catenary, as illustrated in Figure 2b.

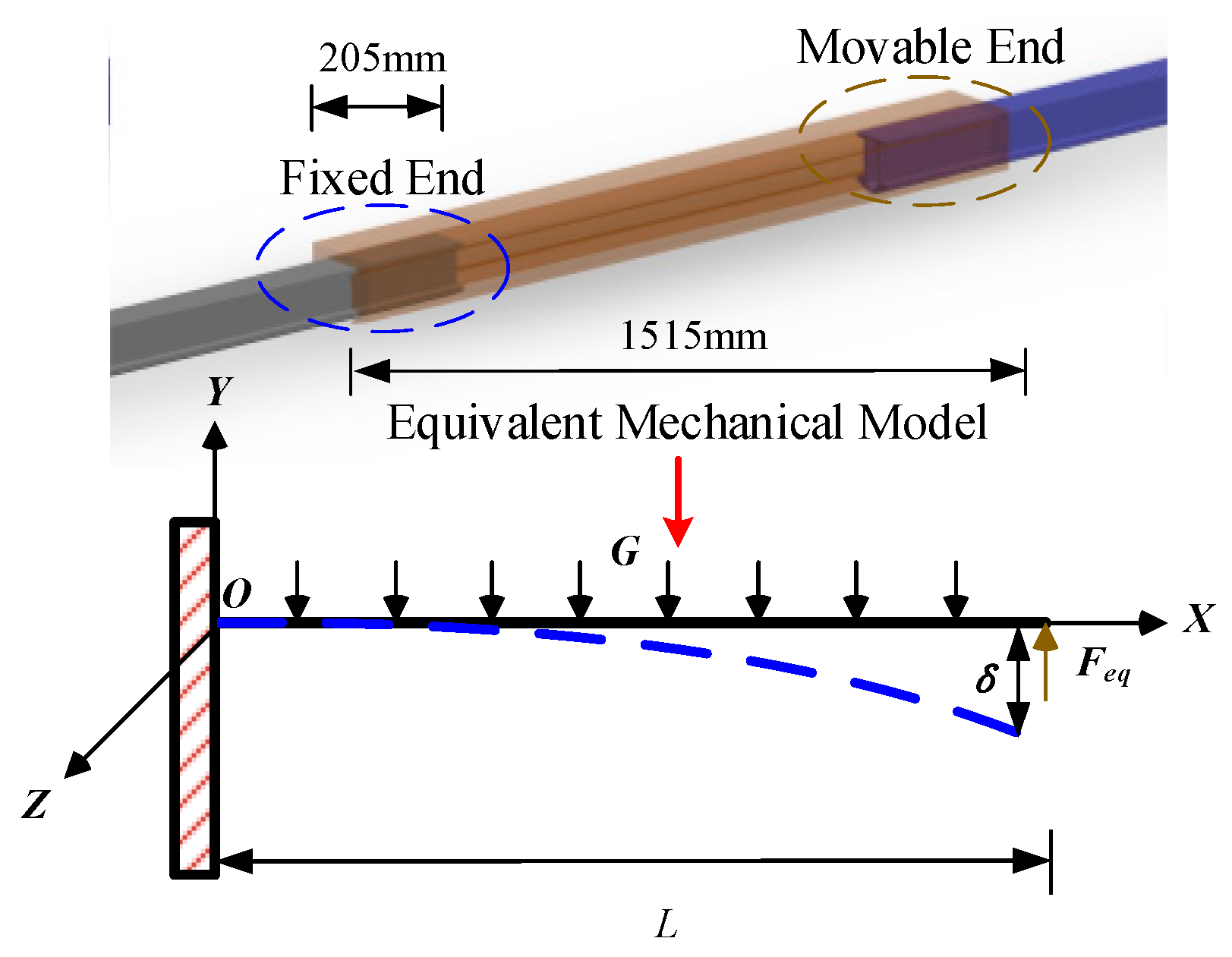
The expansion joint used in the experimental circuit in this paper is a dual auxiliary line expansion joint developed by the Furrer+Frey company from Guangzhou, China. Hence, we have chosen this specific type of expansion joint as our primary focus for the simulation. The expansion joint is composed of a fixed end and a movable end, which are both connected to different sections of the conductor rails. Given that the expansion joint experiences bending deformation during operation, it is represented as a beam model in our simulation. The fixed end is securely attached to the front anchor section, while the movable end is constrained using force elements to allow for a certain degree of freedom of movement along the conductor rail direction. This setup effectively simulates the thermal expansion and contraction of the conductor rails.

The expansion joint has a compensation range of 1000 mm, an overall length of 1515 mm, a mass of 60 kg, and a span of 4 m. The self-weight of the expansion joint, which is significantly heavier than the 6 kg/m mass of the conductor rail, enables sliding compensation for the conductor rail. However, due to the frequent reciprocating action of the pantograph and catenary, it is prone to loosening the connection between the expansion joint and the conductor rail. Coupled with its significant self-weight, this may result in the movable end of the expansion joint sinking, leading to an impact between the pantograph and catenary during passage. When the movable end of the expansion joint sinks due to gravity, the boundary conditions resemble those of a cantilever beam, allowing it to be equated to such a structure, as shown in Figure 3. Notably, the interaction between the movable end of the conductor rail and the expansion joint can be likened to a concentrated force Feq applied to the cantilever beam.

The combined deformation of the free end of the expansion joint, caused by the interaction of the equivalent force Feq and gravity G, results in the subsidence displacement, described in:

$$\delta =\frac{G{L}^3}{8EI}-\frac{F_{eq}{L}^3}{3EI}$$

(1)

where L is the length of the expansion joint, and EI is the bending stiffness of the expansion joint.

At the overlap section, there is no constraint relationship between the front and rear anchor sections. By modifying the vertical relative displacement between these two sections, a fault model with various height differences can be established.

Under prolonged and repeated vibrations and impacts, the threaded connections within the support of the rigid catenary are prone to loosening. In severe cases, this can even lead to the detachment of the insulator from the conducting rail. In this paper, the support device has been simplified as a spring structure with a mass. To simulate the loosening and detachment failures of the support, we adjust the stiffness of the spring.

We simulated the strain as a train speeds along at 100 km/h. After analyzing the strain signal’s spectrum (see Figure 4a), we discovered frequencies that align with the stagger (0.116 Hz) and dropper interval (3.47 Hz, 6.94 Hz, 10.41 Hz). This confirms the reliability of our simulation model.

To gain a better understanding of the fault characteristics of the catenary at various fault levels, we conducted simulation tests at 100 km/h with various fault levels.

Table 1. Simulation experiments setup.

Faults Type	Normal	Experiments Setup
Fault Degree			1	2	3	4
Misalignment displacement of overlap (mm)	0	2	3	4	5	6
The amount of deformation of expansion joint (mm)	0	1	2	3	4	5
Stiffness of support (N/m)	37,788,000	377,880	37,788	3778.8	37.788	0

outlines the setup of these simulation experiments.

Figure 4b shows the strain signal, contact force signal, and dynamic pantograph head displacement signal results of the simulated defects caused by misalignment of overlap (misalignment displacement is 3 mm), loosening of support (stiffness is 37,788 N/m), and deformation of expansion joints (the amount of deformation is 3 mm).

As we can see in Figure 4b, there are distinct differences in the waveforms of the faulty (blue curve) and fault-free (red curve) conditions at the overlap, support, and expansion joint sections. These variations are due to the distinct structures and failure modes of each section, which result in different vibration patterns and waveforms when there are defects. When the misalignment displacement of overlap reaches 3 mm, the simulated pantograph-head displacement is also approximately 3 mm, thereby verifying the reliability of the simulation results. By comparing the failure curve (blue curve) with the no-failure curve (red curve), it becomes evident that during the no-failure period, the pantograph–catenary vibration at the overlap, support, and expansion joint exhibited relatively regular patterns, with no notable impact. However, during the failure period, a significant impact was observed at the location of the failure.

A fault caused by misalignment of the overlap significantly impacts the strain and contact force signals. It also creates a noticeable difference in the pantograph–catenary displacement signal, as highlighted in the red box in Figure 4b. Moreover, the fault characteristics caused by positive misalignment (left red box) and negative misalignment (right red box) are distinctly different. When the support loosens, the vibration amplitude at the adjacent support increases, while the amplitude at the faulty support decreases, as shown in the green box in Figure 4b. Additionally, the deformation of the expansion joint leads to increased vibration at the faulty expansion joint, as indicated in the orange box.

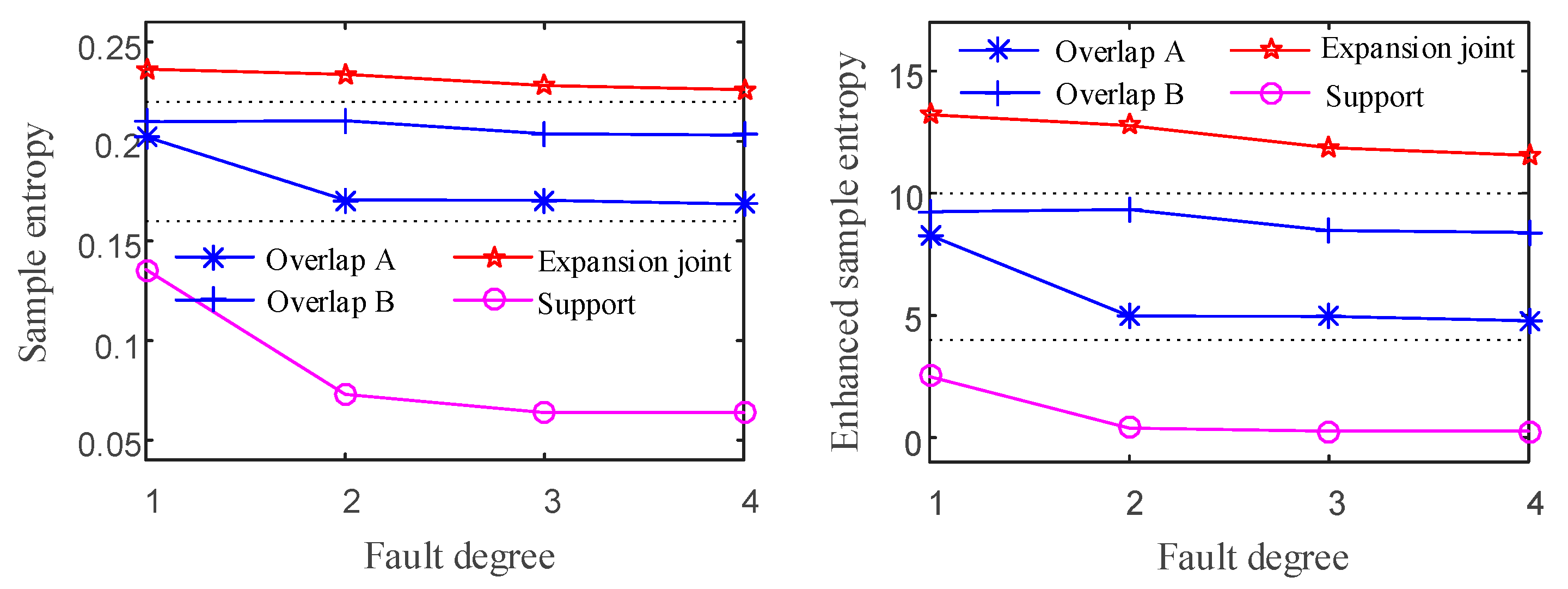
Furthermore, the faulty features present in strain, contact force, and dynamic pantograph head displacement signals due to defects in the support, expansion joints, and overlap are highly similar. This suggests that both the contact force and strain demonstrate a similar level of sensitivity toward dynamic interaction loads. Moreover, the strain signal is more responsive to the position of the load, particularly the contact point. Vibrations caused by stagger provide insights into the location of defects, whereas those caused by coupled contact offer insights into their cause. Therefore, the unique characteristics of the measured strain signal allowed for the diagnosis of defects.

4. Defect Diagnosis Approach

To monitor the catenary system in real time, we used a method that combines mobile standard deviation with the mobile Pauta criterion (MMSTD), as detailed in our prior work [18]. This method allowed us to detect the impact acting on the pantograph–catenary system for both flexible and rigid catenaries. Subsequently, we introduced a new feature extraction and defect diagnosis method to analyze the detected impact and pinpoint the cause and location of failures for rigid catenaries in this paper. Figure 5 provides a schematic of the diagnosis system.

In this defect diagnosis method, we extract the location feature based on the positioning coefficient of the catenary structure. Subsequently, we distinguish various defects based on their unique signal waveforms using enhanced sample entropy and linear discriminant analysis. We analyze the online data obtained during defect detection to extract key defect features. These features are then fed into a pre-trained linear discriminant analysis (LDA) classifier, which determines the cause and location of the defect. To ensure the accuracy of the defect diagnosis model, we utilize historical data to train the LDA classifier.

4.1. Feature Extraction of Defects in Rigid Catenary

4.1.1. Detection of Stagger Arrangement

The stagger in the catenary generates a strain signal trend that contains crucial information about the support points of the catenary. The trend of strain variation with the stagger exhibits a near-sinusoidal waveform, where the peak and valley values of the curve correspond to the maximum and minimum positions of the catenary stagger, respectively. By estimating these peak and valley values in the curve, we can pinpoint the location of a catenary defect between two control supports, significantly narrowing down the potential range of defects.

To detect the stagger arrangement, we employed a double moving average method (DMAM), which offers a straightforward algorithm and enables real-time identification of the stagger arrangement. The moving average method calculates the arithmetic average of a specified range of data in a time series, analyzing each item in the data column as the window slides, to generate a moving average. This moving average can be expressed as follows:

$$MAM(t)=\frac{1}{N}{\displaystyle {\sum }_{(i-N/2)}^{(t-N/2)}x(t)}$$

(2)

where N is the number of items for averaging, x(t) is the original signal, and t is time.

The DMAM is expressed as follows:

$$DMAM(t)=\frac{1}{N}{\displaystyle {\sum }_{(i-N/2)}^{(t-N/2)}MAM(t)}$$

(3)

Figure 6a displays the detection of the stagger arrangement through the strain signal of the pantograph head obtained through online tests utilizing the DMAM method. By utilizing DMAM, the stagger arrangement (depicted in red) was accurately identified from the strain signal (depicted in black). Subsequently, the control support points (labeled with numerals) were pinpointed and marked using an extreme value detection approach.

4.1.2. Catenary Positioning Coefficient

The strain signal from each component in the catenary structure exhibits unique stagger values, which can be exploited to extract the catenary positioning coefficient. This coefficient aids in pinpointing the location of defects within the strain signal.

1. Catenary positioning coefficient for overlap

As an important structure to realize the mechanical and electrical segmentation of the catenary, the overlap is usually installed at the entrance (Overlap A) and exits (Overlap B) of the train station, as shown in Figure 6a. This is because taking the train’s one-station spacing as an anchor segment interval can minimize the scope of failures and reduce the impact of catenary malfunctions on train operation. At the overlap section, the two conduct rail terminals are installed in parallel and staggered. When the pantograph passes through this overlap section, it transitions from the previous anchor section terminal to the next anchor section terminal, causing a sudden change in the stagger value, which is reflected in the stagger arrangement (as shown in 1-1, 1-2 and 1-13, 1-12 in Figure 6a). Drawing from these distinctive characteristics, we can establish an overlap positioning coefficient.

We numbered the extreme values detected in the stagger arrangement, with all peaks numbered 1 and all valleys numbered 2. We detected the overlap section based on the characteristic that the distance between the two adjacent extrema caused by the sudden change in the stagger at the overlap is much smaller than that of other segments. Hence, the judgment method for the overlap is described as:

(a) Judgment method for overlap A (overlap at the entrance of station). If the following conditions are met, it is detected as overlap A.

• $x_{1-\mathrm{overlapA}}=x_{1-1},x_{2-\mathrm{overlapA}}=x_{2-1}$;
• $x_{2-\mathrm{overlapA}}-x_{1-\mathrm{overlapA}}<\frac{1}{N-3}{\displaystyle \sum _{i=2}^{N-2}(x_{2-i}-x_{1-i})}$;

where $x_{2-\mathrm{overlapA}}$ and $x_{1-\mathrm{overlapA}}$ are the abscissa positions of overlap A at the first detected valley ($x_{2-1}$) and peak ($x_{1-1}$) values, respectively; N is the number of detected peaks, which is also the number of detected valleys. If the above conditions are met, it is detected as overlap A.

(b) Judgment method for overlap B (overlap at the exit of station). If the following conditions are met, it is detected as overlap B.

• $x_{1-\mathrm{overlapB}}=x_{1-(N-1)},x_{2-\mathrm{overlapB}}=x_{2-(N-1)}$;
• $x_{2-\mathrm{overlapB}}-x_{1-\mathrm{overlapB}}<\frac{1}{N-3}{\displaystyle \sum _{i=2}^{N-2}(x_{2-i}-x_{1-i})}$;

where $x_{2-\mathrm{overlapB}}$ and $x_{1-\mathrm{overlapB}}$ are the abscissa positions of the overlap B at the valley ($x_{2-(N-1)}$) and peak ($x_{1-(N-1)}$) values, respectively; $x_{1-(N-1)}$ and $x_{2-(N-1)}$ are the abscissa positions of the detected (N−1)th valley and (N−1)th peak, respectively.

By assigning different values to overlap A and overlap B, when the overlap is detected, the value of the catenary positioning coefficient facilitates the classification of overlap A and overlap B. Hence, we define the positioning coefficient of the overlap as:

$$OL=\left\{\begin{array}{l}2,\mathrm{Meet} \mathrm{the} \mathrm{judgment} \mathrm{condition} \mathrm{for} \mathrm{overlap} \mathrm{A}\\ 3,\mathrm{Meet} \mathrm{the} \mathrm{judgment} \mathrm{condition} \mathrm{for} \mathrm{overlap} \mathrm{B}\end{array}\right.$$

(4)

2. Catenary positioning coefficient for supports and expansion joints

To describe the locations of all typical catenary structures, we define the catenary positioning coefficient as:

$$CatenaryP=c_1\cdot PPDR+c_2\cdot OL$$

(5)

where OL = 2 or 3 (OL = 2 corresponds to overlap A and OL = 3 to overlap B, as described in Equation (4)). Overlap A is the overlap section where the pantograph moves into a new anchor, and overlap B is the overlap section where the pantograph moves out of the anchor. If the defect is caused by an overlap, the coefficient $c_1=0,c_2=1$; otherwise, $c_1=1,c_2=0$.

The peak-to-valley distance ratio (PPDR), as shown in Figure 6b, is evaluated as follows:

$$PPDR=\frac{x_i-x_v}{x_p-x_v}=\frac{A}{B}$$

(6)

where $x_i$ is the abscissa of the defect, $x_v$ is the abscissa of the nearest valley position to the left of $x_i$, and $x_p$ is the abscissa of the nearest peak position to the right of $x_i$.

The typical catenary structures, including control supports, expansion joints, supports, and overlap, were installed at distinct locations with a unique stagger value, as depicted in Figure 1. Generally, the control supports were situated at the maximum stagger value (PPDR is 0 or 1), while the expansion joints were positioned where the stagger value is zero based on their installation requirements. This results in a PPDR of 0.5 for an expansion joint. However, in actual train operation, due to variations in train speed and the asymmetric arrangement of control supports, the PPDR of the expansion joint is approximately 0.5, maybe 0.2~0.8. For this study, the peak-to-valley distance of the expansion joint was determined based on past experience. Additionally, supports were installed at intervals of approximately 6–8 m between the two control supports of the catenary to secure the conduct rails on top of the tunnel. Therefore, the PPDR of the supports are $0<PPDR<0.5$ or $0.5<PPDR<1$.

Although it is possible to use the catenary positioning coefficient to classify the control supports and overlap section, it remains difficult to distinguish between expansion joints and supports. Therefore, another defect characteristic parameter must be established.

4.1.3. Enhanced Sample Entropy

Sample Entropy (SampEn), which was first proposed by Richman [19] in 2000, is an improved algorithm for approximate entropy and is used to assess the complexity of time series data. The calculation of SampEn is independent of the data length. A lower SampEn value indicates a lower sequence complexity. The formula for SampEn is as follows:

$$SampEn(m,r,n)=-\ln \left[\frac{A^m(r)}{B^m(r)}\right]$$

(7)

where $B^m(r)=\frac{1}{n-m}{\displaystyle \sum _{i=1}^{n-m}{B}_i^m(r)}$ is the probability that two sequences will match for m points within a tolerance r, whereas $A^m(r)=\frac{1}{n-m}{\displaystyle \sum _{i=1}^{n-m}{A}_i^m(r)}$ is the probability that two sequences will match for m + 1 points. n is the length of the time series.

For a time series of n points, $X=\left\{x(1),x(2),\cdots ,x(n)\right\}$ can be reconstructed to be an m-dimensional vector:

$$X_m(1),\dots ,X_m(n-m+1)$$

(8)

where $X_m(i)=\left\{x(i),x(i+1),\dots ,x(i+m-1)\right\},1\le i\le n-m+1$.

The distance between vectors A and B is defined as the absolute value of the maximum difference of their corresponding scalar components:

$$d\left[X_m(i),X_m(j)\right]=\underset{k=0,\dots ,m-1}{\max }\left(\left|x(i+k)-x(j+k)\right|\right)$$

(9)

Let $B_i$ be the number of vectors $X_m(j)(1\le j\le n-m,j\ne i)$ within tolerance r of $X_m(i)(1\le i\le n-m)$. And let $A_i$ be the number of vectors $X_{m+1}(j)(1\le j\le n-m,j\ne i)$ within tolerance r of $X_{m+1}(i)(1\le i\le n-m)$. The probability that any vector $X_m(j)$ is within r of $X_m(i)$ is defined as $B_i^m(r)$, and the probability that any vector $X_{m+1}(j)$ is within r of $X_{m+1}(i)$ is defined as $A_i^m(r)$

$$A_i^m(r)=\frac{A_i}{n-m-1}, B_i^m(r)=\frac{B_i}{n-m-1}$$

(10)

To improve the effectiveness of defect classification and enhance the distinguishability of sample entropy between different defect types, an enhanced sample entropy has been proposed:

$$ESampEn(m,r,n)={\left[10\cdot SampEn(m,r,n)\right]}^3$$

(11)

The catenary defect characteristics can be extracted using the proposed methods: catenary positioning coefficient and enhanced sample entropy. Subsequently, the classifier can be trained using existing defect sample data using LDA to identify various defects based on the extracted catenary defect characteristics.

By analyzing simulation results, the most appropriate value of dimension mode m is 2, and the similar tolerance r is 0.15. The statistical results of the enhanced sample entropy of different defects are calculated in Figure 7, while the fault degree from 1 to 4 corresponds to the severity of the fault changes from minor to critical. The experiment setup of the simulation is described in Table 1. The results show that the defects caused by the deformation of the expansion joint, the misalignment of the overlap, and the loosening of control support can be readily differentiated using enhanced sample entropy. Thus, this method can be used along with the catenary positioning coefficient to assist in defect feature extraction.

4.2. Defect Diagnosis

LDA has been successfully used as a dimensionality reduction technique in several classification problems because of its high computational efficiency and classification accuracy [20,21,22]. Through the identification of an appropriate projection matrix, high-dimensional pattern samples are efficiently projected into the most discriminative vector space, thereby facilitating the extraction of classification information and effectively compressing the dimensionality of the feature space. The objective of LDA is to identify an optimal projection matrix that ensures the maximum inter-class distance and the minimum intra-class distance for samples in the new subspace.

Let ${\omega }_i=\left\{x_1^i,x_2^i,\cdots ,x_N^i\right\}$ be the defect feature value of defect feature i. The defect feature vector is $[{\omega }_1,{\omega }_2,\cdots ,{\omega }_i,\cdots ,{\omega }_C]$, where C is the number of feature classes. The optimal projection matrix $w$ can be given by maximizing the Fisher criterion:

$$J(w)=\frac{w^T{S}_{B}w}{w^T{S}_{W}w}$$

(12)

where $S_W={\displaystyle {\sum }_{i=1}^C{\displaystyle {\sum }_{x_k\in {\omega }_i}{N}_i(u_i-x_k){(u_i-x_k)}^T}}$ denotes within-class scatter matrices, and $S_B={\displaystyle {\sum }_{i=1}^C(u_i-\tilde{u}){(u_i-\tilde{u})}^T}$ denotes between-class scatter matrices.

The optimal projection matrix can be solved using the Lagrange multiplier method:

$$w={\displaystyle \sum _{i=1}^C{S}_W^{-1}(u_i-\tilde{u})}$$

(13)

where $N_i$ denotes the number of defect feature values, and $u_i$ and u are the mean of the ${\omega }_i$ and all classes, respectively.

When obtaining defect feature values, it is possible to partition the original values into training and testing datasets. The training data are utilized for deriving the projection matrix, while the discriminating feature matrix can be extracted by:

$$Y_T=w\times \left\{x_1^i,x_2^i,\cdots ,x_N^i\right\}$$

(14)

To verify the effectiveness of the proposed catenary diagnosis method, an analysis of simulation results was conducted. The fault characteristics of expansion joints, overlap A, and various fault locations of supports were identified. The detected fault features, CatenaryP and ESampEn, were fed into the LDA classifier. The projection process and classification detection outcomes resulting from LDA analysis are depicted in Figure 8. The projection matrix of expansion joints and support, expansion joints and overlap A, and overlap A and support are obtained as:

$$w_{es}=[0.108,8.609],w_{oe}=[85.348,-5.463],w_{os}=[85.456,3.146]$$

(15)

According to Figure 8, through the application of the optimal projection matrix, LDA has effectively mapped the fault features into a one-dimensional space. It is noteworthy that the fault features of the expansion joint, support, and overlap exhibit the largest interclass distance and the smallest within-class distance. These findings indicate that defects caused by expansion joint deformation, overlap misalignment, and control support loosening have been effectively distinguished. Consequently, it confirms the effectiveness of our proposed defect diagnosis method.

5. Experiments Results and Analysis

The catenary defect diagnosis system proposed in this study implements condition-based monitoring, impact detection, and defect diagnosis. As illustrated in Figure 9a, lightweight and compact optic fiber strain sensors were embedded into the inner surface of a pantograph aluminum support. Given that significant fluctuations in contact strip temperature can compromise the measurement accuracy of optic fiber strain sensors, four reference temperature sensors were installed in close proximity to the strain sensors for temperature compensation. For further details, please refer to our previously published paper [18].

Data from online tests utilizing the proposed monitoring system were collected from the metro line, with preprocessing employed to eliminate measurement noise and temperature-related drifts from the pantograph strain values obtained. To verify the reproducibility of experimental outcomes, two tests were conducted on the same line, separated by half a month. The Mann–Whitney U test and the Kruskal–Wallis test were utilized to analyze the correlation between these two tests. The correlation analysis results are summarized in

Table 2. Correlation analysis of strain signals from DATE1 and DATE2.

Method		Sensor 1 (DATE1/DATE2)	Sensor 2 (DATE1/DATE2)	Sensor 3 (DATE1/DATE2)	Sensor 4 (DATE1/DATE2)
Average	Case1	−0.38/0.17	0.37/−0.07	0.06/−0.36	−0.52/−0.13
	Case2	0.04/0.17	0.02/−0.41	0.16/−0.01	−0.16/−0.06
Standard deviation	Case1	5.72/6.06	5.88/6.20	6.46/7.14	5.81/5.96
	Case2	4.82/5.09	5.90/6.29	5.74/5.81	5.91/5.97
Pearson correlation coefficient	Case1	0.72	0.78	0.78	0.78
	Case2	0.83	0.89	0.89	0.87
Mann–Whitney U test	Case1	ID	ID	ID	ID
	Case2	ID	ID	ID	ID
Kruskal–Wallis test	Case1	ID	ID	ID	ID
	Case2	ID	ID	ID	ID

. Additionally, we analyzed two distinct rigid catenary segments, as represented in Figure 9b (Case1 and Case2). Notably, strain signals collected on DATE1 (30June) and DATE2 (15 July) exhibited highly similar trends and amplitudes. However, the amplitude of the strain signal on DATE2 was slightly greater than that on DATE1. This observation suggests that half a month of operation slightly degraded the catenary’s condition.

The correlation coefficient analysis demonstrates a strong linear correlation between the strain signals obtained on the two dates. Furthermore, the Mann–Whitney U test and Kruskal–Wallis test confirm that the two datasets exhibit identical distributions (ID) and significant correlation. These findings validate the reliability and reproducibility of the experimental results.

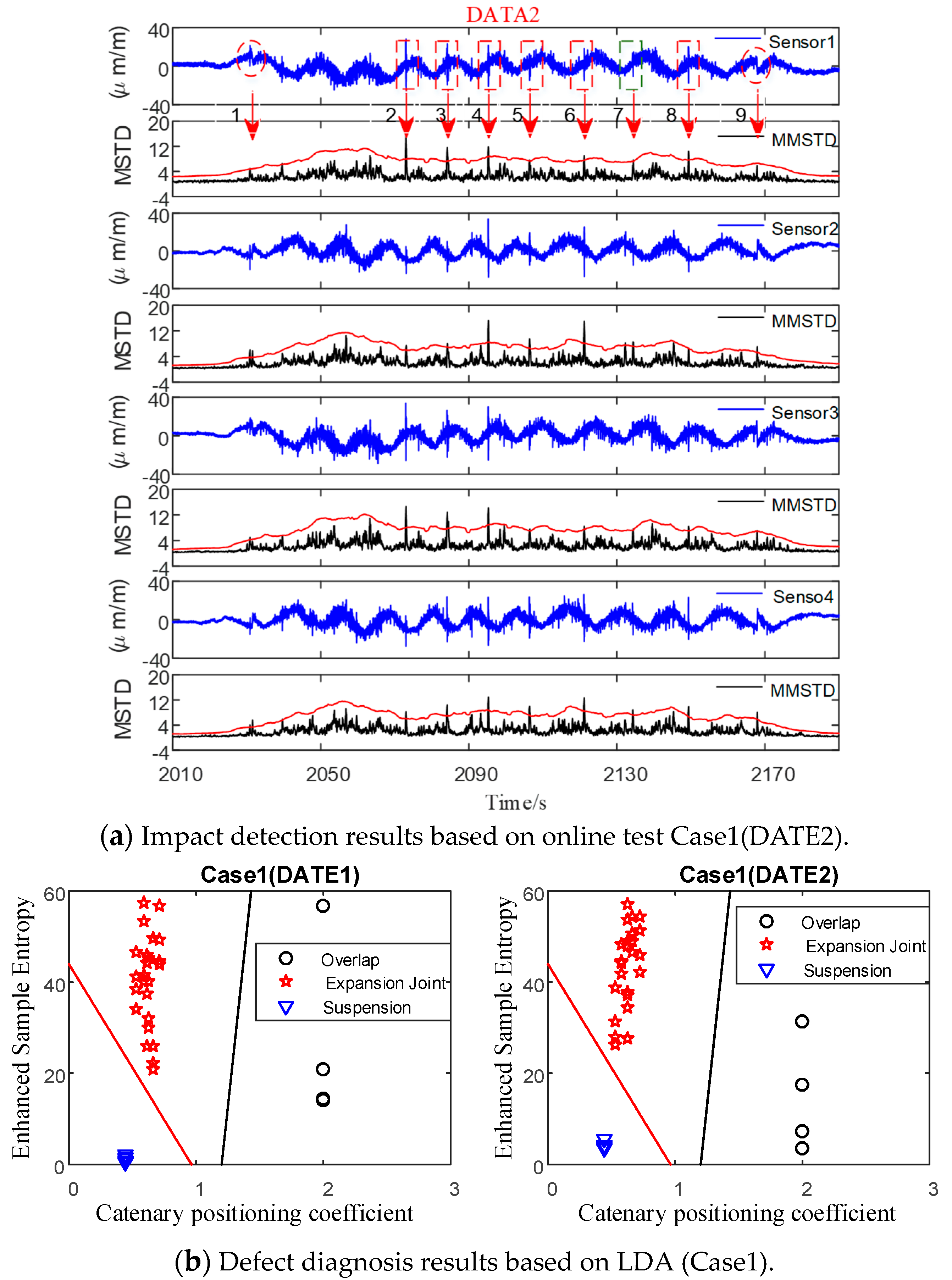
The strain signals obtained from two distinct rigid catenary segments (Case1 and Case2) were analyzed using the proposed defect diagnosis method. Figure 10 presents the strain signals captured by the four optic fiber strain sensors and the corresponding impact detection outcomes. The schematic of the corresponding rigid catenary segment (Case1) is provided at the top of Figure 10. This configuration comprises two overlap sections (highlighted in a red box), ten expansion joints, and eleven midpoint anchors.

It is evident that the MMSTD (right curve) effectively identified the real impact defects (1, 2, 3, 4, 5, 6, 7, 8, 9). Subsequently, the feature extraction methods were utilized to extract the catenary position and enhance the sample entropy of the detected impact defects. Furthermore, a detailed view (Figure 10c) reveals distinct defect characteristics among various defects, such as those caused by the deformation of expansion joints and loosening of control supports. These differences align with the simulation outcomes, highlighting the feasibility of the proposed diagnosis method to discriminate between different defects using enhanced sample entropy as a guiding feature.

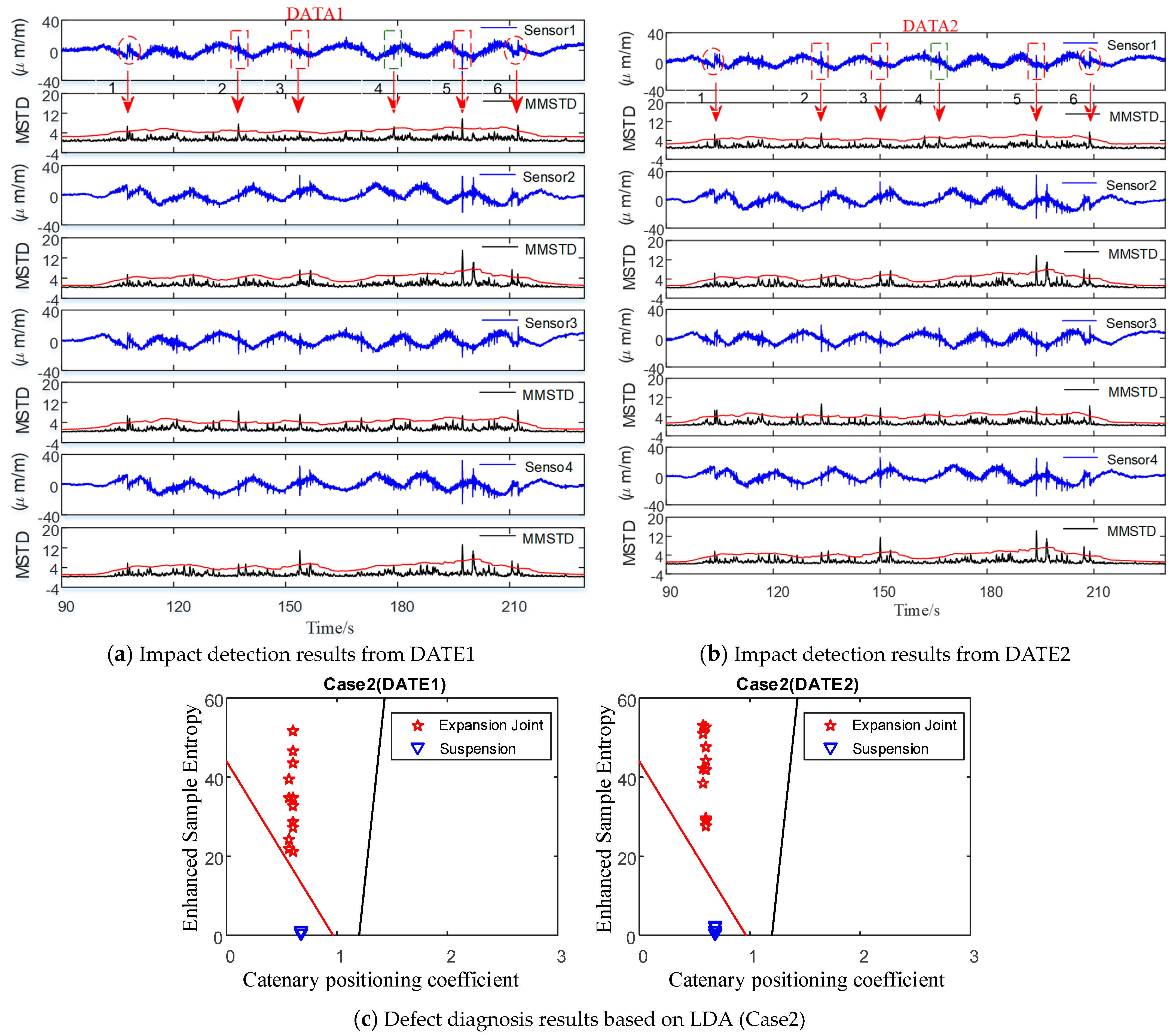
Figure 11 presents the defect monitoring and feature extraction results of Case1 obtained from DATA 2. The collection time of DATA 2 is half a month later than that of DATA 1. As evident from the results, the detected defects are consistent, indicating the reproducibility of the test and the reliability of the experimental data. Following impact detection, the newly proposed diagnosis method was utilized to analyze the defects, with the diagnosis outcomes presented in Figure 11b. As can be seen from Figure 11b, the classification accuracy obtained by feature selection based on LDA is 100%, which can completely separate the three types of faults.

In the provided example, Case1 possesses a diverse range of fault categories and numerous fault points, making it suitable as a training sample. However, in practical applications, a more extensive statistical analysis of the measured faults in operational catenary systems should be conducted to enrich the training fault samples further. Subsequently, by inputting the fault features into the trained LDA classifier, the fault diagnosis results can be obtained, as illustrated in Figure 12.

For the data collected from Case2, the MMSTD method was utilized to detect the defects, and a total of four defects were identified in Case2, as presented in Figure 12. The statistical characteristics of these defects are summarized in

Table 3. Defects feature extraction results from Case2.

Defect No.	2 (DATE1/DATE2)	3 (DATE1/DATE2)	4 (DATE1/DATE2)	5 (DATE1/DATE2)
Catenary P	0.562/0.583	0.604/0.600	0.670/0.686	0.597/0.603
ESampEn-S1	39.39/52.97	27.17/44.15	1.28/2.30	32.62/52.80
ESampEn-S2	24.33/38.41	21.31/29.41	0.40/2.66	51.68/41.71
ESampEn-S3	21.91/50.97	28.64/29.79	0.46/1.05	34.81/27.65
ESampEn-S4	34.77/42.26	46.75/29.02	0.41/0.55	43.55/47.68
Defect Type	Expansion Joint	Expansion Joint	Support	Expansion Joint

.

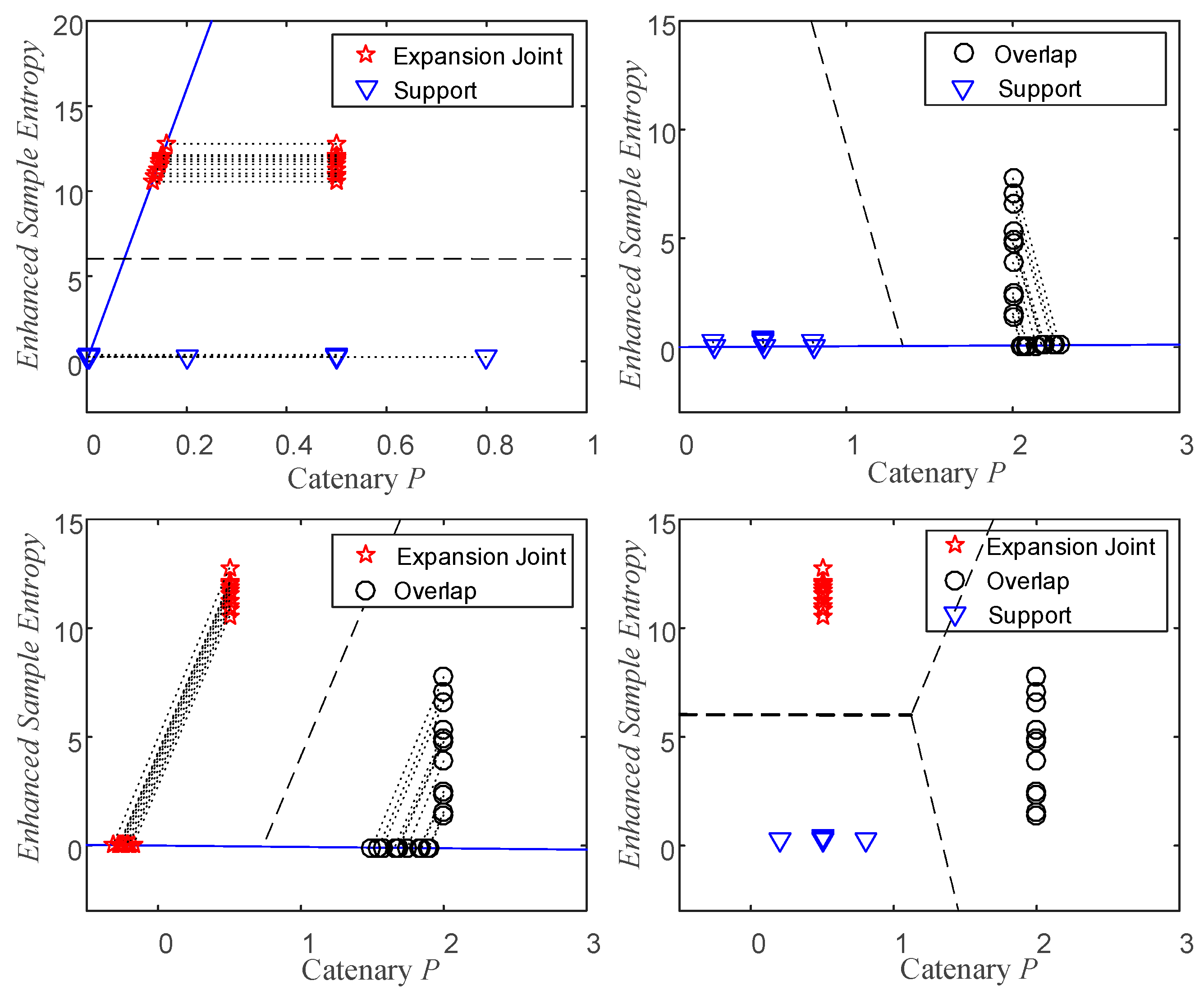
The analysis of Case1 and Case2 demonstrates that the fault feature extraction method proposed in this study renders the three prevalent catenary faults linearly separable. The findings indicate that the proposed approach enables discrimination between detected defects and provides information on their type and location. Furthermore, the diagnosis results were verified by the train operation company and were consistent with manual detection outcomes. The outcomes of the conducted analyses suggest that the proposed defect diagnosis method is highly effective.

6. Conclusions

In this study, we present a defect diagnosis system for a rigid catenary based on strain signals. The system architecture, key methods, and devices of the detection and monitoring system of the catenary are described in detail. We utilize pantograph head strain as a defect indicator, simplifying the detection system. The main conclusions are summarized as follows:

(1) The defects caused by the deformation of the expansion joint, the misalignment of overlap, and the loosening of control support result in different vibration patterns and waveforms in strain signals collected from the pantograph head.

(2) The simulation results show that the feature extraction methods—catenary positioning coefficient and enhanced sample entropy—can extract effective fault features for subsequent fault separation and diagnosis.

(3) Two tests that were conducted on the same commercial metro line, separated by half a month, exhibited highly similar trends and amplitudes. The correlation coefficient analysis demonstrates a strong linear correlation between the strain signals obtained on the two dates. Furthermore, the Mann–Whitney U test and Kruskal–Wallis test confirm that the two datasets exhibit identical distributions (ID) and significant correlation. These findings validate the reliability and reproducibility of the experimental data.

(4) The fault detection results from two tests on different dates are the same, and the classification accuracy obtained by feature selection based on LDA is 100%. These demonstrate that the proposed monitoring system can effectively detect the main defects in a catenary system caused by expansion joint deformation, overlap misalignment, and support loosening.

(5) The results are also verified through manual inspection, indicating the high effectiveness of our proposed catenary defect detection and diagnosis method.