Comparative Analysis of Force and Eddy Current Position Sensing Approaches for a Magnetic Levitation Platform with an Exceptional Hovering Distance
Abstract
1. Introduction
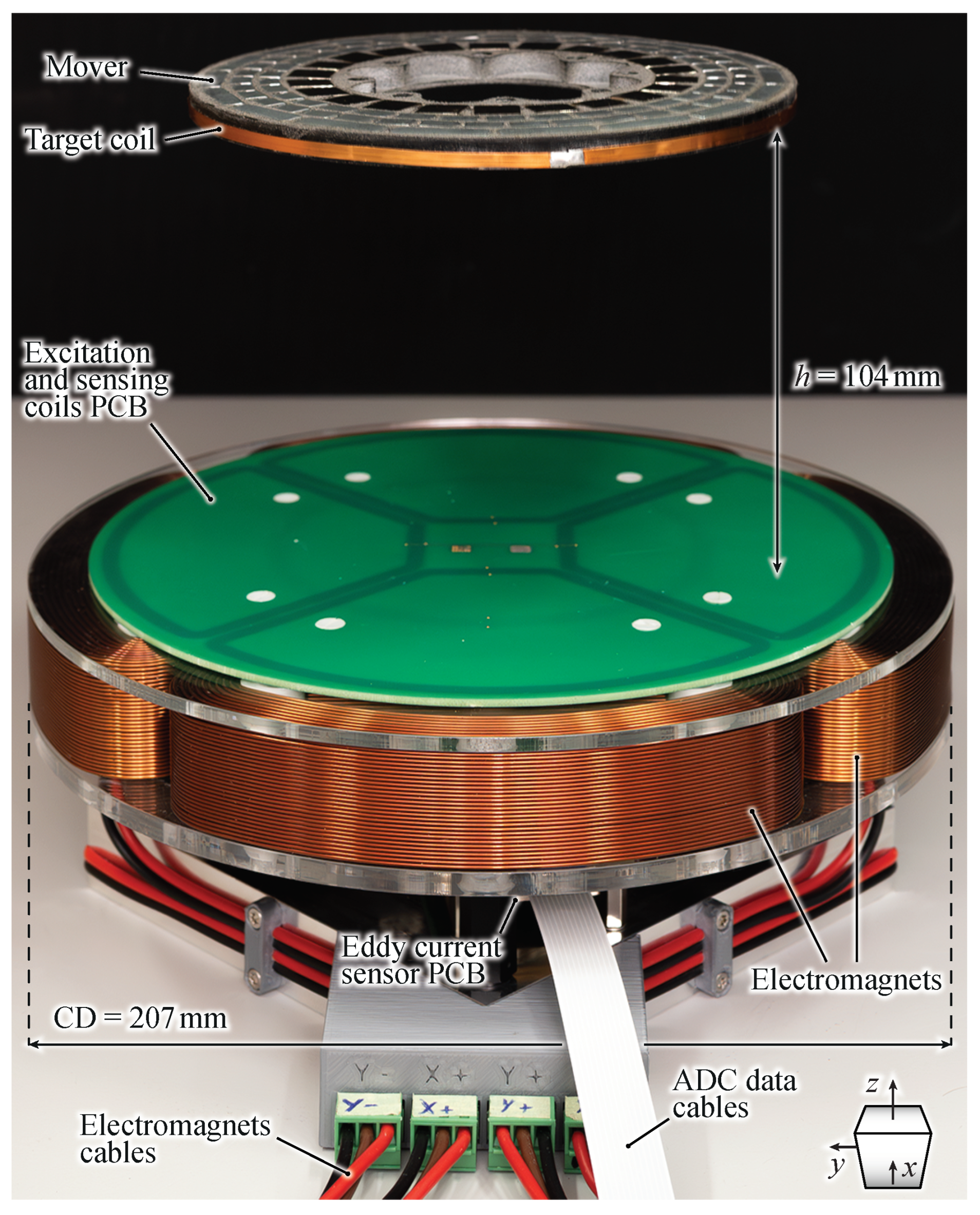
2. Eddy Current Position Sensor for the MLPs
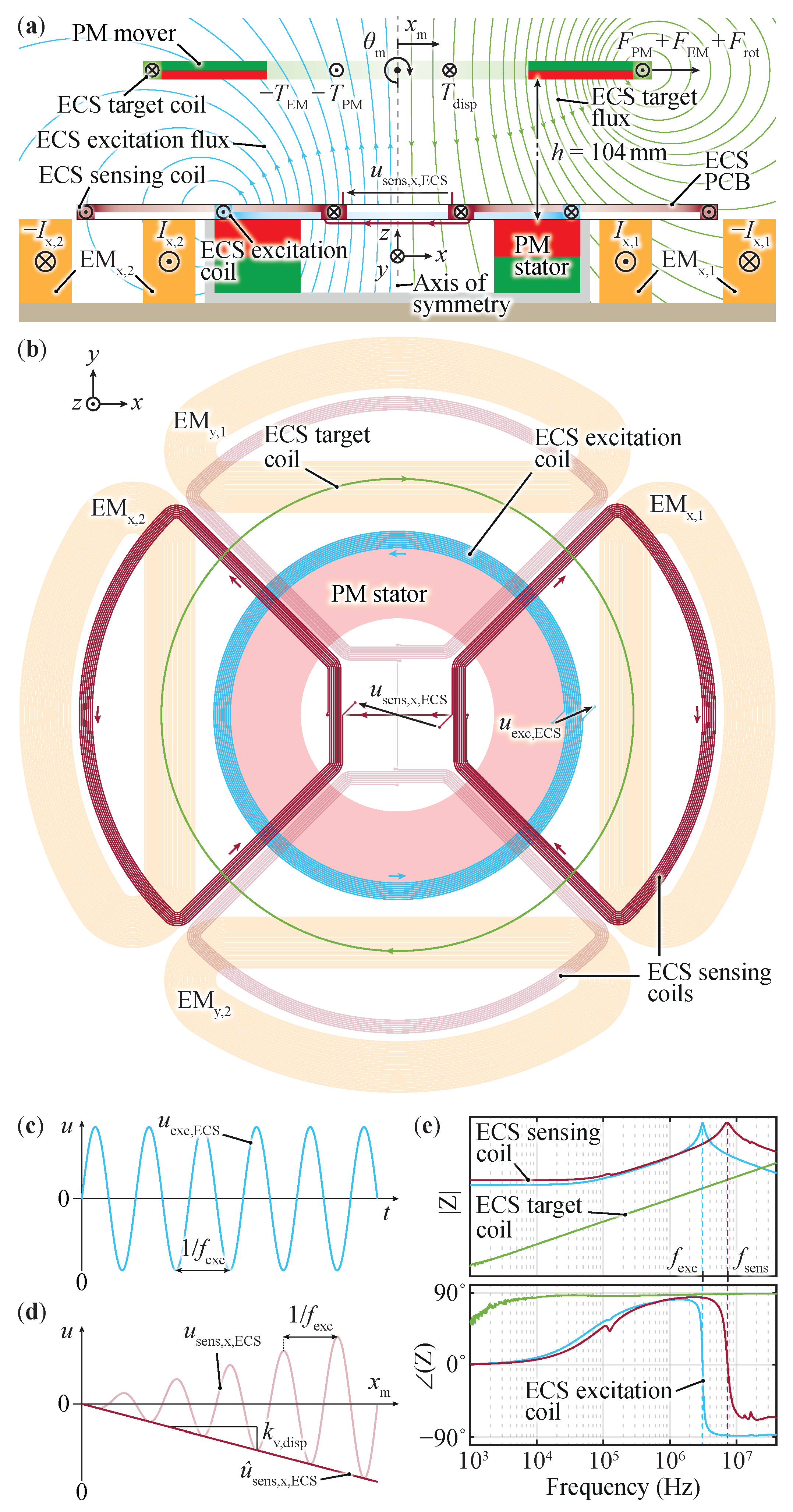
2.1. ECS Geometry and Operating Principle
2.2. ECS Design Considerations
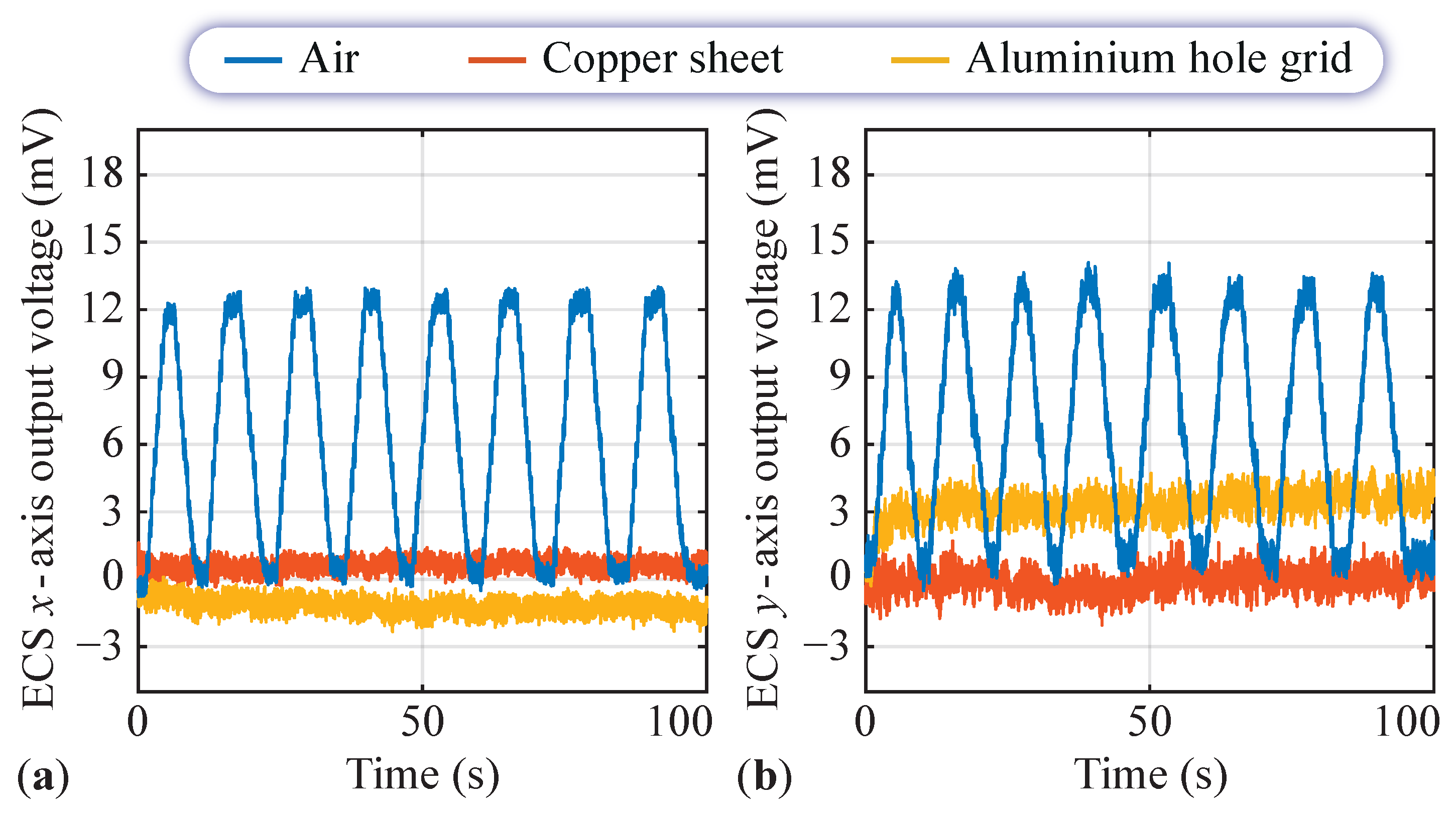
2.3. Impact of the Conductive Obstacles in the Air Gap
3. Reaction Force-Based Position Sensor
- The movement of the force sensor’s sensing side and the bending of the sensing element are linearly related to the applied force, i.e., , where is the stiffness of the force sensor.
- The stretch of the strain gauges, their resistance change, and the output voltage variation are linearly dependent on the movement of the force sensor’s sensing side, i.e., , where is a constant representing the mechanical-to-electrical signal conversion.
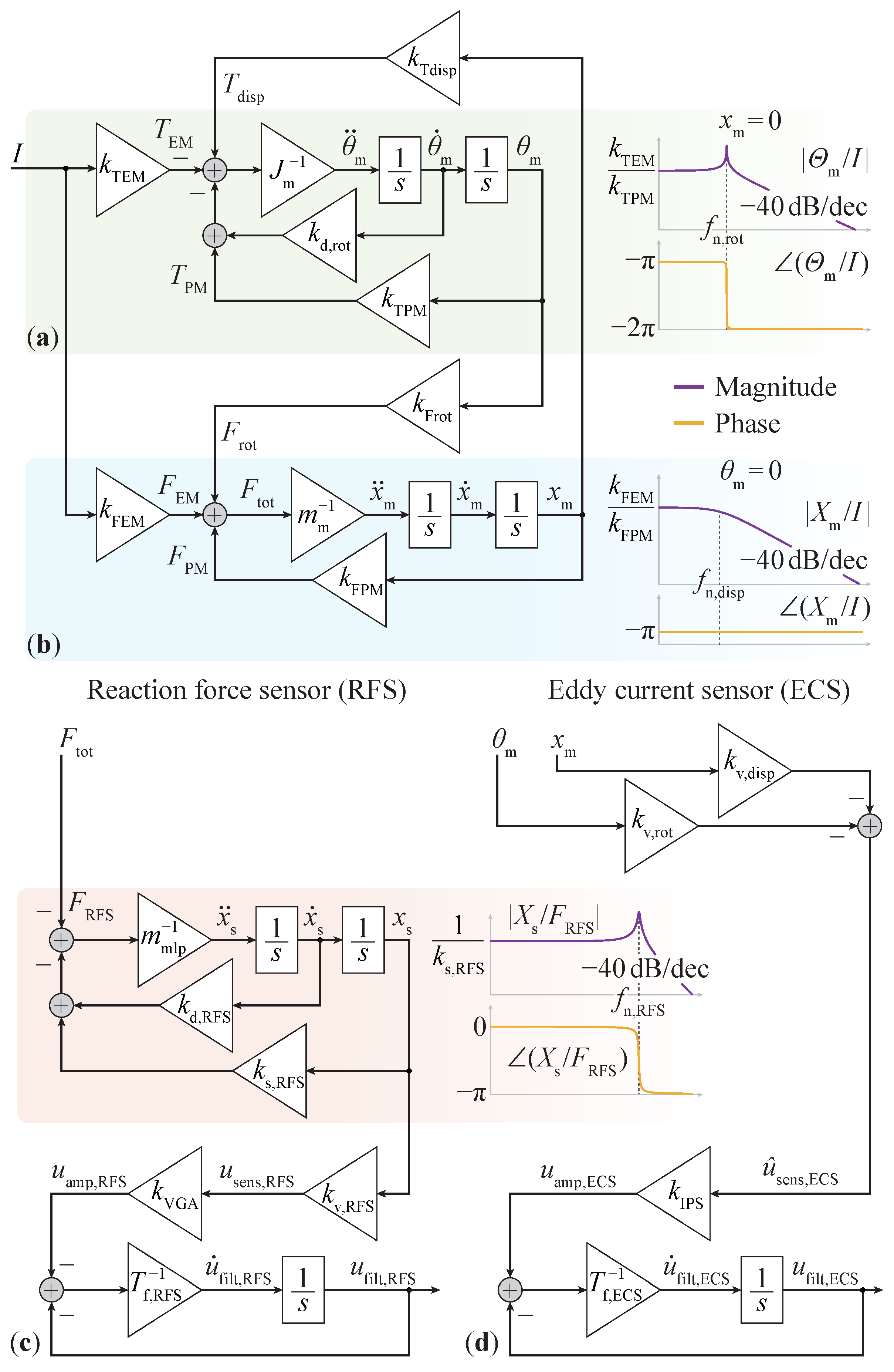
4. Dynamics Modeling and Verification
4.1. Dynamic Model
4.2. Dynamic Model Verification and Calibration
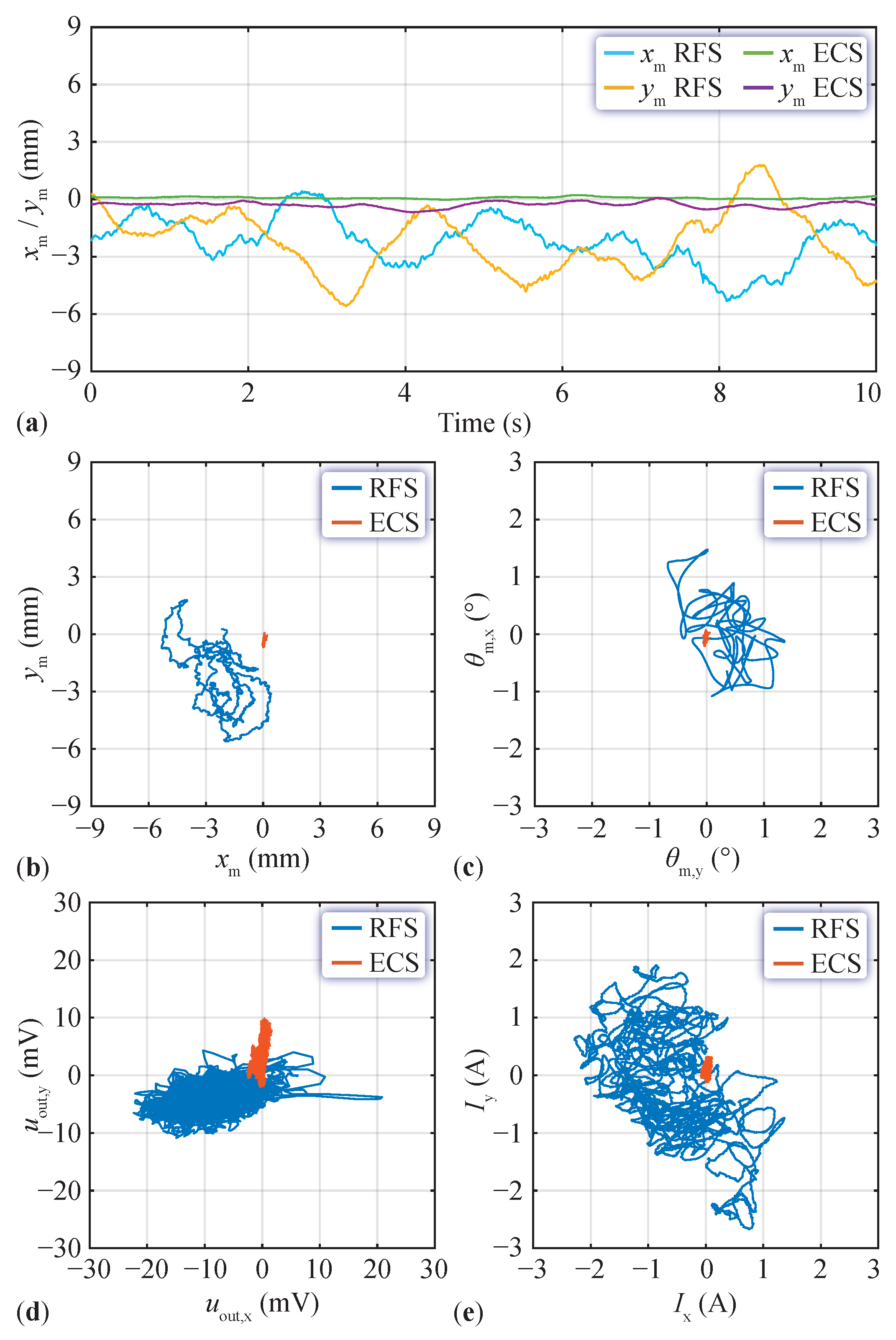
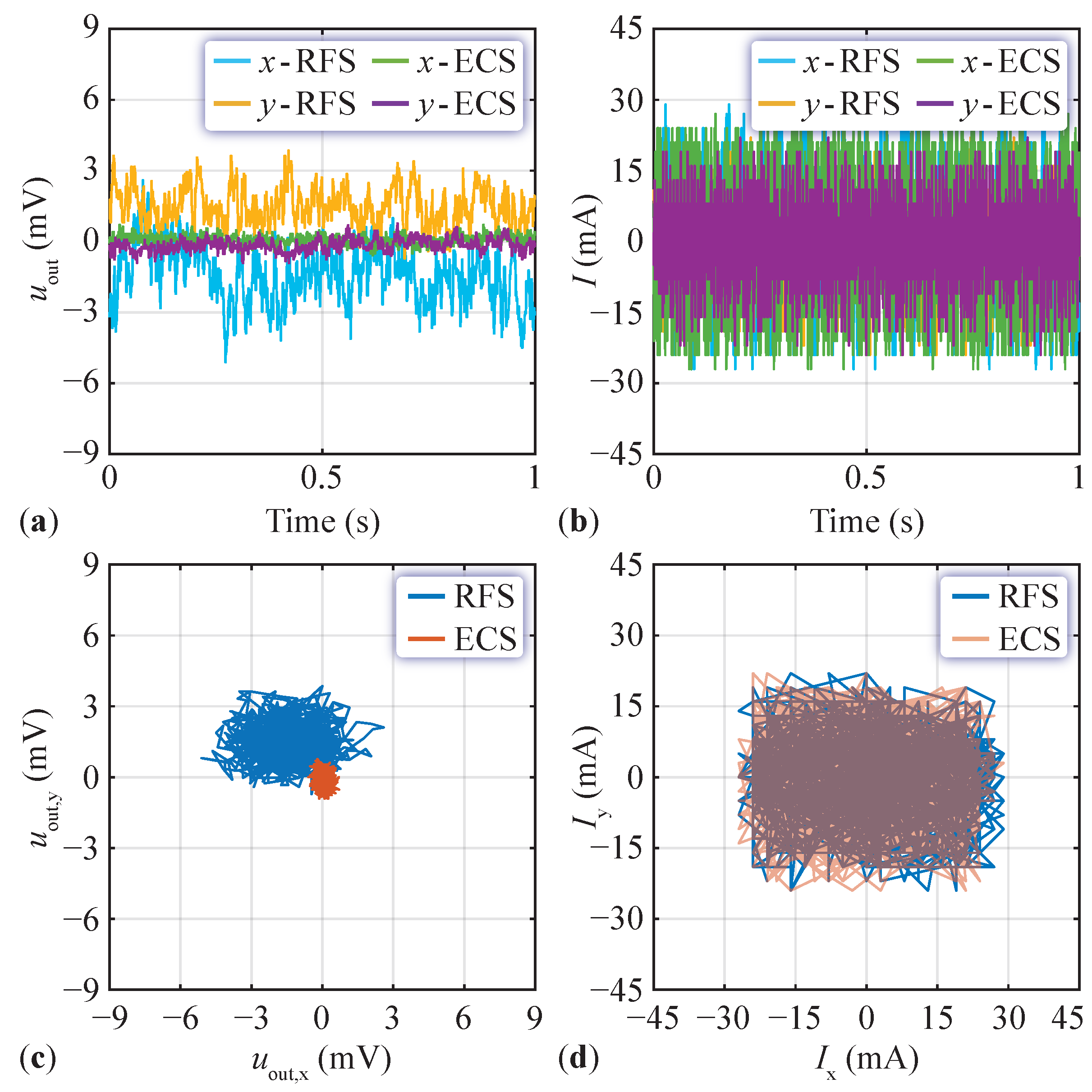
5. Comparative Results
5.1. Steady-State Levitation Comparison
5.2. Analysis of Performance Variance
6. Additional Experimental Results for the Eddy Current Sensor
6.1. Disturbance during Steady-State Levitation
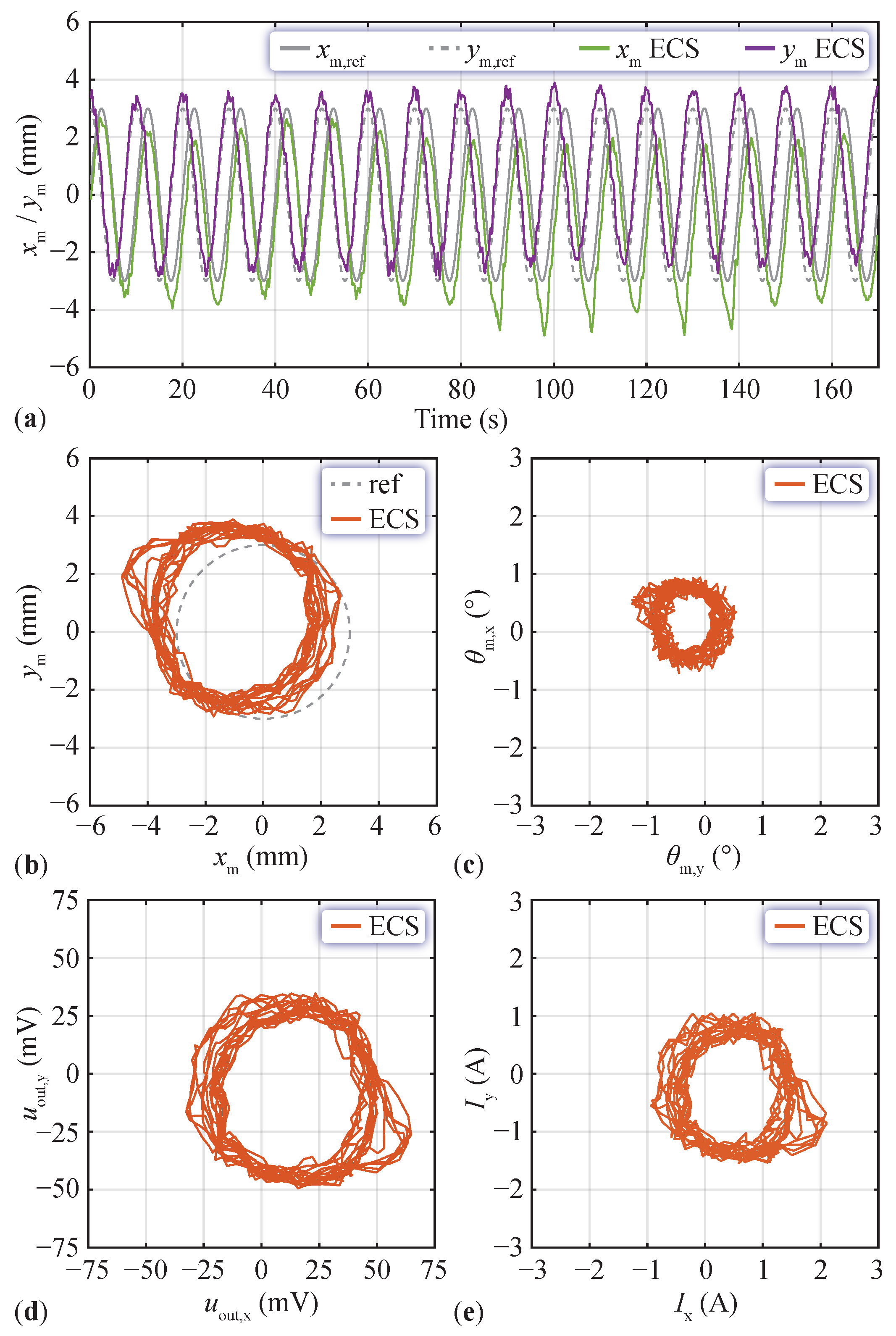
6.2. Position Reference Tracking
6.3. Position Reference Tracking with Payload
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yaghoubi, H. The Most Important MAGLEV Applications. J. Eng. 2013, 2013, 537986. [Google Scholar] [CrossRef]
- Csencsics, E.; Thier, M.; Hainisch, R.; Schitter, G. System and Control Design of a Voice Coil Actuated Mechanically Decoupling Two-Body Vibration Isolation System. IEEE/ASME Trans. Mechatron. 2017, 23, 321–330. [Google Scholar] [CrossRef]
- Trakarnchaiyo, C.; Khamesee, M.B. A Novel Wrench-Current Decoupling Strategy to Extend the Use of Small Lookup Data for a Long-Range MAGLEV Planar Motor. Actuators 2023, 12, 358. [Google Scholar] [CrossRef]
- Csencsics, E.; Doblinger, G.; Schitter, G. A Novel Magnetically Levitated Tip/Tilt Motion Platform. IFAC-PapersOnLine 2023, 56, 3379–3385. [Google Scholar] [CrossRef]
- Pechhacker, A.; Wertjanz, D.; Csencsics, E.; Schitter, G. Integrated Electromagnetic Actuator with Adaptable Zero Power Gravity Compensation. IEEE Trans. Ind. Electron. 2024, 71, 5055–5062. [Google Scholar] [CrossRef]
- Takahashi, M.; Ogawa, H.; Kato, T. Compact MAGLEV Stage System for Nanometer-Scale Positioning. Precis. Eng. 2020, 66, 519–530. [Google Scholar] [CrossRef]
- Zhang, H.; Lou, Y.; Zhou, L.; Kou, Z.; Mu, J. Modeling and Optimization of a Large-Load Magnetic Levitation Gravity Compensator. IEEE Trans. Ind. Electron. 2023, 70, 5055–5064. [Google Scholar] [CrossRef]
- Sun, F.; Pei, W.; Zhao, C.; Jin, J.; Xu, F.; Zhang, X. Permanent MAGLEV Platform using a Variable Flux Path Mechanism: Stable Levitation and Motion Control. IEEE Trans. Magn. 2022, 58, 8300410. [Google Scholar] [CrossRef]
- Matko, V.; Milanovič, M. Detection Principles of Temperature Compensated Oscillators with Reactance Influence on Piezoelectric Resonator. Sensors 2020, 20, 802. [Google Scholar] [CrossRef] [PubMed]
- Matko, V.; Milanovič, M. Temperature-Compensated Capacitance–Frequency Converter with High Resolution. Sens. Actuators A Phys. 2014, 220, 262–269. [Google Scholar] [CrossRef]
- Bonetti, R.; Bortis, D.; Beglinger, L.; Kolar, J.W. Exploring the Physical Limits of Axial Magnetic Bearings Featuring Extremely Large Vertical Levitation Distances. IEEE Trans. Ind. Appl. 2021, 57, 6931–6943. [Google Scholar] [CrossRef]
- Bonetti, R.; Beglinger, L.; Mirić, S.; Bortis, D.; Kolar, J.W. Reaction Force-Based Position Sensing for Magnetic Levitation Platform with Exceptionally Large Hovering Distance. In Actuators; Multidisciplinary Digital Publishing Institute: Basel, Switzerland, 2024. [Google Scholar]
- Berkelman, P.; Kang, S. Optimization of the Four Coil Configuration for Single Magnet Levitation from Below. In Proceedings of the IUTAM Symposium on Optimal Guidance and Control for Autonomous Systems, Honolulu, HI, USA, 15–17 March 2023; Volume 40, pp. 103–115. [Google Scholar]
- Berkelman, P.; Ohashi, N. Analysis and Testing of a Four Coil Magnetic Levitation Configuration. In Proceedings of the 48th Annual Conference of the IEEE Industrial Electronics Society (IECON), Brussels, Belgium, 17–20 October 2022; pp. 1–5. [Google Scholar]
- Engmark, H.A.; Hoang, K.T. Modeling and Control of a Magnetic Levitation Platform. IFAC-PapersOnLine 2023, 56, 7276–7281. [Google Scholar] [CrossRef]
- Song, H.; Lin, W.; Zhou, M.; Liu, G.; Pan, H.; Tong, M. Robust H∞ Control for Disturbance Rejection in a Magnetic Levitation Device. In Proceedings of the IEEE 28th International Symposium on Industrial Electronics (ISIE), Vancouver, BC, Canada, 12–14 June 2019; pp. 2170–2174. [Google Scholar]
- Kim, K.B.; Im, S.H.; Um, D.Y.; Park, G.S. Comparison of Magnetic Levitation Systems using Ring-Shaped Permanent Magnets. IEEE Trans. Magn. 2019, 55, 8300804. [Google Scholar] [CrossRef]
- Li, C.; Li, L. The Stable Magnetic Levitation of a Cylindrical Ferromagnetic Object. J. Supercond. Nov. Magn. 2014, 27, 2773–2778. [Google Scholar] [CrossRef]
- Bowler, N. Eddy-Current Nondestructive Evaluation; Springer Series in Measurement Science and Technology; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Renesas. Inductive Position Sensor IC. IPS2550 Datasheet. 2022. Available online: https://www.renesas.com/us/en/products/sensor-products/position-sensors/ips2550-inductive-position-sensor-high-speed-motor-commutation-automotive?gad_source=1&gclid=CjwKCAjwnv-vBhBdEiwABCYQAwEIv8x8h_mYch5X0NwHatWXxDzMgnqyRk2paKva1L-3DTKkCPSRuRoCvqQQAvD_BwE (accessed on 3 March 2024).
- Hanta, V.; Procházka, A. Rational Approximation of Time Delay. Inst. Chem. Technol. Prague Dep. Comput. Control Eng. Tech. 2009, 5, 28–34. [Google Scholar]
- Forsentek. 3 Axis Load Cell 0–100 N Multi-Axis Force Sensor. FNZ Datasheet. Available online: https://www.forsensor.com/sale-9906279-3-axis-load-cell-10n-20n-30n-50n-100n-multi-axis-force-sensor.html (accessed on 3 March 2024).
- Analog Devices. 0.25 ppm Noise, Low Drift Precision References. LTC6655/LTC6655LN Datasheet. 2021. Available online: https://www.google.com/url?sa=t&source=web&rct=j&opi=89978449&url=https://www.analog.com/media/en/technical-documentation/data-sheets/ltc6655-6655ln.pdf&ved=2ahUKEwi0wMLVsY6FAxXbs1YBHR2FB58QFnoECBYQAQ&usg=AOvVaw05jSdT6qdVI3T-jmJkTgoj (accessed on 3 March 2024).
- Texas Instruments. ADSxxx3 Dual, 1-MSPS, 16-, 14-, and 12-Bit, 4 × 2 or 2 × 2 Channel, Simultaneous Sampling Analog-to-Digital Converter. ADS8363 Datasheet. 2017. Available online: https://www.ti.com/ (accessed on 3 March 2024).
- Roriz, P.; Carvalho, L.; Frazão, O.; Santos, J.L.; Simões, J.A. From Conventional Sensors to Fibre Optic Sensors for Strain and Force Measurements in Biomechanics Applications: A Review. J. Biomech. 2014, 47, 1251–1261. [Google Scholar] [CrossRef] [PubMed]
- Jiang, J.; Chen, W.; Liu, J.; Chen, W.; Zhang, J. Optimum Design of a Dual-Range Force Sensor for Achieving High Sensitivity, Broad Bandwidth, and Large Measurement Range. IEEE Sens. J. 2015, 15, 1114–1123. [Google Scholar] [CrossRef]




| V/mm | 5 V/° | ||
| 240 V/V | ms | ||
| 35 Hz | Vpp | ||
| MHz | MHz | ||
| H | |||
| 15 | H | ||
| 2 | H | ||
| 110 pF | 16 pF | ||
| 10 | 16 |
| RFS | ECS | |
| Mover can be encapsulated in a stainless steel chamber | Yes | No |
| Trade-off between sensitivity and bandwidth | Yes | No |
| Electromagnetic and mechanical disturbances | Large | Small |
| Cross-coupling | Large | Negligible |
| mm | mm | |
| mm | mm | |
| dB | dB | |
| dB | dB |
| Magnetic levitation platform without payload | |||
| Levitation height | h | 104 mm | |
| Characteristic dimension | CD | 207 mm | |
| Mover weight | kg | ||
| Mover moment of inertia | gm2 | ||
| Radial stiffness | N/m | ||
| Displacement torque const. | Nm/m | ||
| Rotational stiffness | mNm/° | ||
| Rotational force const. | mNm/° | ||
| EMs force const. | 65 mN/A | ||
| EMs torque const. | mNm/A | ||
| Rotational damping | 2 Nms/° | ||
| Rotation natural frequency | 2 Hz | ||
| Radial disp. natural frequency | Hz | ||
| Magnetic levitation platform with payload of kg | |||
| h | 70 mm | kg | |
| N/m | gm2 | ||
| mNm/° | mN/A | ||
| 20 Nms/° | mNm/A | ||
| Hz | Hz | ||
| Eddy current sensor | |||
| V/mm | 250 V/° | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bonetti, R.; Mirić, S.; Kolar, J.W. Comparative Analysis of Force and Eddy Current Position Sensing Approaches for a Magnetic Levitation Platform with an Exceptional Hovering Distance. Actuators 2024, 13, 122. https://doi.org/10.3390/act13040122
Bonetti R, Mirić S, Kolar JW. Comparative Analysis of Force and Eddy Current Position Sensing Approaches for a Magnetic Levitation Platform with an Exceptional Hovering Distance. Actuators. 2024; 13(4):122. https://doi.org/10.3390/act13040122
Chicago/Turabian StyleBonetti, Reto, Spasoje Mirić, and Johann W. Kolar. 2024. "Comparative Analysis of Force and Eddy Current Position Sensing Approaches for a Magnetic Levitation Platform with an Exceptional Hovering Distance" Actuators 13, no. 4: 122. https://doi.org/10.3390/act13040122
APA StyleBonetti, R., Mirić, S., & Kolar, J. W. (2024). Comparative Analysis of Force and Eddy Current Position Sensing Approaches for a Magnetic Levitation Platform with an Exceptional Hovering Distance. Actuators, 13(4), 122. https://doi.org/10.3390/act13040122







