Abstract
The space instable target simulator (SITS) is a vital actuator for ground verification of on-orbital capture technology, the motion performance of which directly affects simulation credibility. Different delays reduce the stability of SITS and ultimately lead to its divergence. In order to achieve high-fidelity simulation, the impacts of force measurement delay, the discrete control cycle, and simulator response delay on stability are analyzed first. Then, the dynamic equation and transfer function identification model of the hybrid simulator is constructed, and the necessary and sufficient conditions of its stability and convergence are obtained using the Routh criterion. After that, a novel switching compensator with variable gain is proposed to reduce the superimposed effects of the three delays, the compensation principle diagram of which was built, and its mathematical model including the energy observer and nonlinear tracking differentiator is also established. Finally, three sets of numerical simulations were conducted to validate the correctness of the stability analysis and effectiveness of the proposed compensation method. The simulation results show that all three types of delays can cause SITS to lose stability under critical stable motion states, and the delay in force measurement has the greatest impact, followed by the influence of the control cycle. Compared with the force applied to the simulated target, the velocity, and the recovery coefficient of the space instable target using fixed gain and linear gain compensation, the proposed compensator has significantly better performance.
1. Introduction
With the increase in human space activities, the number of non-cooperative space objects such as defunct satellites and spacecraft debris continues to rise, significantly impacting the utilization of orbital resources and the space operational environment [1,2,3]. Active debris removal (ADR) technology involves the use of tools like robotic arms to repair and clean up space debris, effectively reducing the generation of space debris. This technology proves instrumental in mitigating the threats posed by uncontrolled debris in the space environment and alleviating congestion in orbital space [4,5,6,7].
Direct on-orbit application of ADR technology poses significant risks, generally necessitating comprehensive ground tests to address shortcomings in technical methods and validate its stability. Full physical simulation (FPS), semi-physical simulation (SPS), and digital simulation (DS) are currently the three most commonly applied ground experiment approaches. Full-sized simulators with complete physical characteristics are typically constructed in FPS, which incurs high costs. In addition, it is difficult to achieve frictionless movement along the direction of gravity in the simulation of 6-DoF spatial weightlessness motion [8,9,10]. DS, not reliant on physical hardware, conducts verification of debris removal processes only through mathematical modeling [11,12,13]. The mathematical model for the actual contact process cannot be accurately established, and it also lacks the capability to optimize and improve the real capture tool, thereby presenting certain limitations. SPS combines the advantages of FPS and DS, incorporating vital physical hardware into the test system to reduce the unnecessary costs of hardware [14,15,16,17,18]. Simultaneously, it utilizes mathematical spacecraft models with different mass and inertia characteristics, making it widely applicable in ground experiments for space mechanisms.
The ground capture SPS system for a space instable target (SIT) is a system with high real-time requirements. SITS is a critical device, and its motion performance is directly related to the accuracy of the simulation. Delays have significant effects on the stability and precision of the SPS system, leading to invalid test data or even damage to the simulator due to instability.
Research on the reasons and compensation methods for the delay of the simulator in the SPS system has made certain progress. M. Zebenay et al. [19] addressed the response time delay of the industrial robot controller in the European Proximity Operations Simulator (EPOS 2.0 c) and the impact of high robot stiffness on the safety and the authenticity of the experimental results. A contact collision model suitable for ground verification is proposed, combining impedance control with mechanical passive compliance, which builds the relationship between robot stiffness and test device stiffness. Based on estimating contact stiffness and damping, M. Zebenay introduced compensation into the dynamic model to achieve 1D hybrid simulation in 2015 [20]. By comparing the maximum contact force and velocity recovery coefficient of 1D movement with an air-floating test system, the feasibility of the hybrid simulator was verified. Aiming at the response delay of the 6-DoF parallel mechanism in a ground SPS platform, Chenkun Qi [21] investigated a real-time online identification method for contact stiffness, which was estimated through differential equations based on force, displacement, and velocity within three contact cycles. Adopting this information as the compensation for the dynamic input, system divergence was suppressed, and a velocity recovery coefficient of 0.9809 was achieved. To address the issues of system instability and simulation distortion caused by time delays and discrete integration of dynamics in the On-Orbit Servicing Simulator loop, Marco De Stefano [22] proposed a passive controller for adjusting the admittance dynamic input force and a speed modulation controller for maintaining energy characteristics. The instability suppression effect in satellite dynamics reproduction was verified on industrial robots. LAV Sanhith Rao [23] analyzed the motion divergence caused by the delay in the three-axis rotational semi-physical test platform for aerospace products. By compensating for the turntable angular velocity based on establishing the system transfer function, they successfully solved the problems of the undesired oscillations and inaccurate experiment results. The reason for the increase in system energy was identified through analysis of the phase relationship between force and velocity in a complex domain by Kohei Osaki [24]. The force compensation model was established and applied to 1D collision experiments, achieving a recovery coefficient of 0.97 with satisfactory results. However, due to neglecting the velocity phase variation caused by force lag, this method provides an approximate compensation effect. Satoko Abiko [25] presented a force compensation method based on the velocity recovery coefficient. By observing the velocity change online, they identified the compensation coefficient for the input force of the dynamic model and applied it to the planar 3-DoF collision tests.
There is considerable risk in identifying stiffness and damping in real time during actual capture processes, and the feasibility is weak, especially when the contact stiffness is high, that is, the contact time is also rather short. Moreover, relying solely on adjusting the impedance characteristics of the manipulator to indirectly extend the contact time and suppress divergence is not a fundamental approach to solving the divergence issue of the simulator. The integral lag in dynamics is just one aspect of control cycle delays. Only solving this problem while neglecting other lag impacts leaves the simulator in a divergent state. Similarly, sampling delay is only a part of system lag. The three-axis turntable conducts angular velocity control, and its angular velocity is derived from a high-precision measurement sensor. The compensation method is unsuitable for the simulator for an industrial robot that only precisely executes displacement commands. It is difficult to predict in advance the contact dynamic characteristics of the captured object. Therefore, the velocity recovery coefficient is also unknown, making it impractical to compensate for the input force of the hybrid simulator based on the velocity recovery coefficient.
It is hard to quantitatively prove the actual effect of delay compensation for complex 6-DoF movements. Complex systems are mixed with multiple influences and difficult to strictly control in engineering applications, so a simple and pure system is needed for delay compensation research. The usual approach is to abstract one-dimensional motion, study its compensator, conduct verification in one-dimensional experiments, prove its feasibility, and then expand it to six-dimensional motion. Ou Ma [26] proposed an experimental strategy for 1D peg-in-hole assembly and verified the effectiveness of the special purpose dexterous manipulator (SPDM) through data comparison. Considering the delay in force measurement, the transfer function of the 1D spring damping mass system in [20] was established using a linearized method, and 1D horizontal collision verification was conducted after analyzing system stability. Based on the building of a linear model of uniaxial collision of a simulator considering a pure time delay, Satoko Abiko [25] obtained the linearized compensation force. To further advance the servo-hydraulic compensation for a broader frequency bandwidth during real-time hybrid simulation, a FIR compensator was proposed by Saeid Hayati [27] on the basis of linearizing the system model using Z-transform, which was confirmed to have excellent compensation performance through numerical simulation and actual experiments. To compensate for the transmission delay of the actuator and the transducers of the hardware-in-the-loop simulator in the 1D vibration motion, Sahua [28] presented a delay estimation model on the basis of the linear phase system and demonstrated that the direct velocity feedback strategy is the most effective in improving system stability. Xu [29] established a first-order discrete transfer function model to represent 1D servo-hydraulic dynamics and investigated an easy-to-implement compensation method for real-time hybrid simulation. Qi [30] analyzed the delay in force measurement and dynamic calculation caused by communication delays, and conducted a simulation and experimental verification on the 1D vertical motion of a linear undamped spring mass system. He [31] validated the effectiveness of the proposed stiffness identification compensation method through 1D undamped motion simulation of a manipulator, and obtained a minor deviation from the theory value in the 1D collision experiment. To solve time delays introduced in the inherent dynamics of the eCVT with one rotational DoF, a tracking controller based on linearization of the actuation system into a second-order transfer function was proposed by Tsokanas [32] and achieved small tracking errors under uncertainties that were present during the real-time hybrid simulation.
The spring mass model, which is critically stable, is generally adopted to prove the stability of 1D motion in the above research. A system with damping is stable and may experience situations where there is a delay effect but it remains stable, which increases the difficulty of obtaining theoretical proof and is unnecessary. The 1D movement of SITS is researched according to the principle of the minimum envelope in this paper. Although the 1D motion of the robot end effector is the research object, all six axes of the simulator are in motion during the motion process. Compared to previous studies that considered one type of delay, we consider three different delays, with a maximum number of six motion axes; thus, the system also has a certain degree of complexity. It has been analyzed and proven that all three types of delays in current SPS can cause 1D motion divergence in a SIT in the absence of damping. On this basis, a hybrid simulation control block diagram is proposed, and its transfer function model is derived. A variable gain differential negative feedback with energy observer is presented to compensate for the input force of the dynamic model, and the effectiveness of the proposed method is verified through a simulation study.
The rest of the paper is organized as follows: the effect of different delays on SITS stability and mathematical modeling and stability analysis of the hybrid simulator are described in Section 2 and Section 3, respectively; the delay compensation method of the hybrid simulator and the results obtained from a series of simulations are presented in Section 4 and Section 5, respectively; and conclusions are drawn in Section 6.
2. Effect of Different Delays on SITS Stability
The simulator, a 6-DoF industrial robot, is used to conduct the spatial motion of a SIT in the hardware-in-the-loop-based ground capture test system. A six-axis force sensor is installed on the end flange of the simulator to measure the contact force during the capture process. After delayed sampling, it is input into the dynamic model of the SIT. Motion instructions obtained after dynamic calculation are transmitted to the host computer and sent to the simulator according to a certain control cycle. The simulator controller decomposes the instructions to the motor controllers of each joint, driving each joint motor to generate new contact force and follow the above process in a cyclic manner until the capture experiment is completed. The ground semi-physical test process of SITS is illustrated in Figure 1.
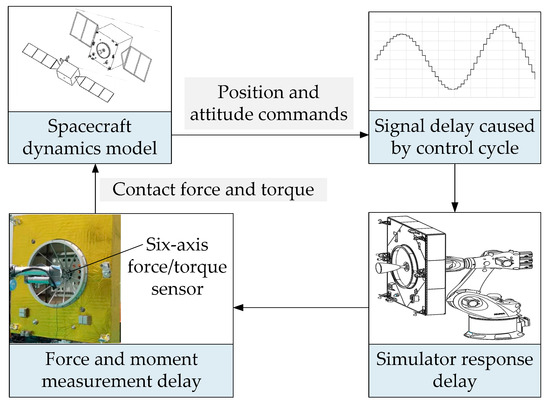
Figure 1.
Ground semi-physical test process of SITS.
During the above process, the simulator is affected by factors such as the force measurement delay, discrete control cycle, and response delay, resulting in reduced motion accuracy, decreased system stability, and even divergence. Force measurement delay includes the sampling delay of the force sensor itself and the data communication delay. The former is caused by the signal of the force sensor being amplified by charges, low-pass filtering, and power amplification, while the latter is determined by the hardware communication capability of the ground test system. At present, the sampling rate of the force sensor can reach 4 kHz, and the communication frame rate with Ethernet or EtherCAT can reach 8 kHz. Therefore, the delay caused by sampling is ignored, and only the delay in data transmission is considered. In actual physical systems, each module has a corresponding operating cycle. In order to ensure the unified issuance of instructions from the host computer to each module, the control cycle of the entire system should not be less time than the period of the simulator, which is 4 ms. Therefore, the issuance cycle of the dynamic command that takes 2 ms will be delayed to 4 ms, resulting in the delay of the control cycle. The simulator is an electromechanical system composed of six servo motors, and its response delay is inevitable. To illustrate the impact of different delays on simulator stability and determine the corresponding compensation method, considering the complexity of the system, the one-dimensional motion of a SIT is generally analyzed. The 1D motion of the simulator studied in this article is a combination of 6-axis robot motions. The 1D motion at the end of the simulator is representative of 3-DoF translational movement, which is the research focus that the ground test system can accurately assess. The undamped free vibration model is adopted here as shown in Figure 2.
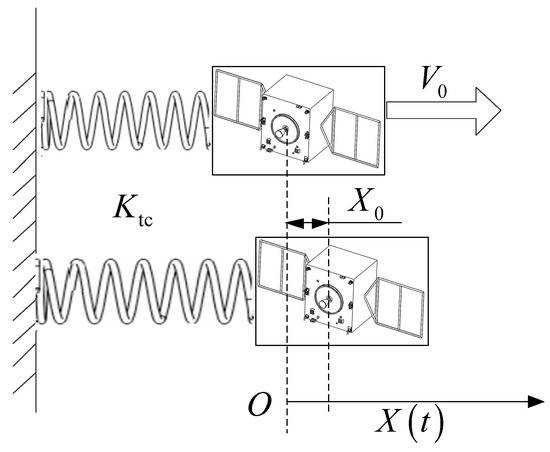
Figure 2.
The 1-DoF undamped free vibration of SIT.
In Figure 2, and are, respectively, the initial velocity and mass of the SIT, and is the spring stiffness. The SIT is theoretically in a free vibration state, and the system is critically stable. The corresponding dynamic equation is given by
where the natural frequency is .
2.1. Effect of Force Measurement Delay on System Stability
If the force measurement delay (FMD) is , the vibration differential equation of the SIT can be written as
If the Laplace transform is performed on Equation (2), the corresponding characteristic equation is
Equation (3) is a transcendental equation, which theoretically has countless characteristic roots. By substituting into the above equation, we can obtain
Separating the real and imaginary parts yields
By solving Equation (5), considering the symmetry of the eigenvalues and only considering solutions with , we can obtain
Obviously, when , is a pair of conjugate intercepts.
The real component of the derivative of the root locus at all intersection points can be expressed as
A pair of root trajectories enter the right side of the imaginary axis in the complex plane when , and they do not return to the left side when . Therefore, the undamped vibration of the SIT is unstable for .
To further demonstrate the stability of the time-domain solution in finite time [33], for Equation (2), when , the following is true:
Therefore, Equation (2) is about the stability of in a finite time interval, where and .
In summary, the undamped vibration of the SIT with a force measurement delay is stable in finite time, but as time approaches infinity, the system gradually diverges. In the ground experiment of space debris removal, the motion of the simulator includes the initial condition setting stage, pose maintenance stage, stable capture stage, and detumbling stage. Delay can lead to divergence in the latter two stages, with a duration ranging from a few seconds to several hundred seconds depending on the simulated operating conditions, and the simulator stops moving after the detumbling stage. However, no matter how long the simulator moves in the actual testing process, its convergence must be ensured; otherwise, the simulation is invalid and may even cause damage to the simulator, which is not allowed.
2.2. Effect of Control Cycle on System Stability
A discrete control cycle keeps the current displacement command for a period of time, which is equivalent to performing a zero-order hold on the command signal. The impact model of control cycle can be described as follows:
Performing the Laplace transform on Equation (9) yields
The undamped vibration model of the SIT considering only the effect of the control cycle (ECC) is
where is the displacement command considering the ECC.
By substituting Equation (10) into the Laplace transform of Equation (11) and performing the inverse Laplace transform, it can be obtained that
To prove its stability, we introduce the following inference.
For the equation , where
if has multiple non-negative roots, then its corresponding time-delay system is unstable, the equation for which is
We provide proof for the above inference. The corresponding characteristic equation for the third-order time-delay linear system mentioned in Equation (14) is
On the basis of the stability criterion of the control system, if there are multiple identical zero-real-part eigenvalues in Equation (15), then its corresponding system is unstable. If the pure imaginary root is , then by substituting it into Equation (15) and separating the real and imaginary components, we can obtain
Squaring and adding the above equations yields
If , then Equation (17) can be written as . Due to the presence of multiple non-negative roots in f, i.e., also having multiple positive real roots, the delay system is unstable.
Evidently, Equation (12) is one version of Equation (17). Therefore, it can be concluded that when considering the control cycle from the above inference, the undamped vibration system with 1-DoF is divergent.
2.3. Effect of Simulator Response Delay (SRD) on System Stability
Due to the reaction time of the electromechanical system, there is a certain delay in the motion response of SITS, and the corresponding differential equation can be written as
where is the time-varying delay function.
In terms of the characteristics of the control system, as the motion frequency increases, the phase delay becomes larger, and the response lag reduces the system adaptability to external interference and phase margin. Therefore, the 1-DoF undamped movement of SITS is divergent.
3. Mathematical Modeling and Stability Analysis of Hybrid Simulator
3.1. Mathematical Modeling of Hybrid Simulator
Even though the hardware in our system has high performance, the three types of delays mentioned above are still unavoidable. After our attempts, it is not effective to compensate for the force measurement delay of only 2 ms, and it is also difficult to independently compensate for the delay in the discrete control cycle and the response delay of the commercial robot. To solve the issues of simulation distortion and system divergence, a hybrid simulator was constructed by changing the semi-physical test architecture. The motion signals in the real system are processed and compensated to the dynamic model of one-dimensional undamped vibration of non-cooperative targets, thereby improving the stability of the system and reducing the impact of these three types of delay superpositions. The actual position signal of SITS is processed and compensated into the dynamic model of the SIT to improve the stability of the system.
The dynamic equations of the ground semi-physical experimental system, which takes into account FMD, ECC, and SRD before compensation, are as follows:
where is the input force of the dynamic model, is the equivalent mass, is the mass of the tracking spacecraft, is the displacement command input to SITS considering the control cycle, is the actual displacement output acquired from the SITS controller, and are, respectively, the orders of the SITS dynamic model, and . and are, respectively, the differential equation coefficients, and is the contact damping coefficient.
The force measurement delay signal is overlaid with the disposed velocity signal to correct the input of the dynamic model. If the compensation force is , then the sixth formula in Equation (19) can be written as follows:
where is the gain, which can be a fixed value or a time-varying value.
The Laplace transform can be performed on Equations (19) and (20), and the corresponding control block diagram of the hybrid simulator is shown in Figure 3.

Figure 3.
Control block diagram of the hybrid simulator.
The expressions of and in Figure 3 are
Due to the fact that is an infinite dimensional function, Pade approximation is used for linearization, which has good performance even when the delay time is long and the Taylor series does not converge [34,35,36]. The first-order Pade approximation expressions for and are as follows:
3.2. Model Identification of SITS
is the transfer function of the 1D motion of SITS, which mainly includes the forward kinematics model, control model of each joint, and inverse kinematics model, as shown in Figure 4. In practice, is generally obtained through system identification.
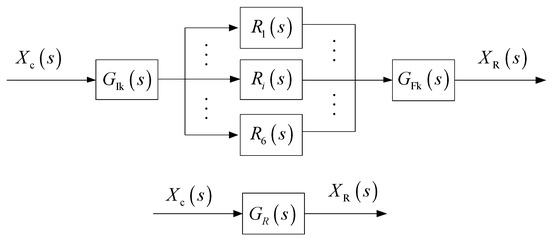
Figure 4.
Main constituent models of .
In order to comprehensively evaluate the performance of the simulator, a certain load is configured, and it is expected that as many axes as possible move simultaneously during the identification. In addition, the motion of the simulator should be obvious, making it convenient for real-time measurement by devices such as the laser tracker. The 1D motion trajectory is set as P0 → P1 → P0 → P2 → P0 → P1 → …, as shown in Figure 5.
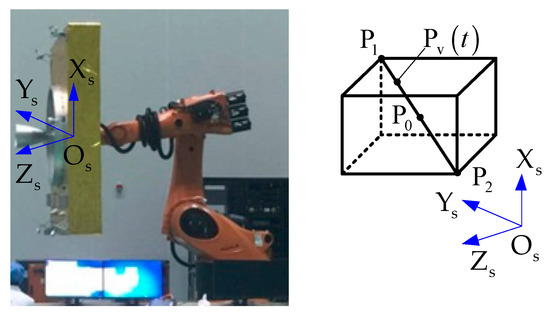
Figure 5.
The 1D motion trajectory for model identification of SITS.
The sweep path equation of the simulator is
where and are the amplitude and angular frequency, respectively.
The control point of the simulator is located at P0 at the initial moment, and the initial velocity is
If the coordinates of in the simulator’s base coordinate system are , this yields
The joint angular displacement corresponding to the above Cartesian trajectory can be obtained through the robot kinematics model, as follows:
where is the coordinate vector of P0 in the sixth axis coordinate system of SITS, and is the homogeneous transformation matrix of SITS.
The Z-transform function of SITS can be acquired by applying the least squares method to identify the above trajectory in the discrete-time domain.
The ARX model [37,38,39] of can be written as
where is the systematical error.
The difference equation corresponding to Equation (27) is
If the number of observed samples is , the least squares estimate of is
where
3.3. Stability and Steady-State Error Analysis
The control block diagram in Figure 3 satisfies
The zero and pole form of the identified is given by
where is the gain, and and are, respectively, the numbers of zeros and poles .
The transfer function of SITS can be obtained by performing the Laplace transform on the second formula in Equation (20) and substituting it into Equation (31) along with Equations (21), (22), and (32).
The characteristic equation of Equation (33) is given by
From the identification results in Section 5, there are two poles and one zero of , so and . Equation (34) is further simplified as
If the coefficients of the system characteristic equations are defined as , then Equation (35) can be rewritten as
where
Owing to the good stability and anti-interference ability of the industrial robot, and . Considering that and are relatively small, it can be clearly concluded from Equation (37) that , , , and .
In terms of the Routh stability criterion, the Routh array of Equation (36) is given by
To ensure the stability of SITS, the coefficients in the first column of the Routh array must be positive, as illustrated in Equation (39).
where
The steady-state error of the hybrid simulator can be drawn as
When is a step function with the expression , Equation (41) yields
From the above analysis, it can be concluded that when appropriate parameters are selected, the hybrid simulator proposed is convergent and can achieve stable ground experiments.
4. Delay Compensation Method of Hybrid Simulator
The hybrid simulation model for ground capture experiments on a SIT is elaborated on above in the continuous time domain using the linearization method. Due to the fact that the disposal in physical systems is based on sampled values, the compensation force needs to be discretized. Meanwhile, considering the continuous increase in system energy, a nonlinear energy observer is introduced to dynamically adjust the gain, and the principle diagram of delay compensation is illustrated in Figure 6.
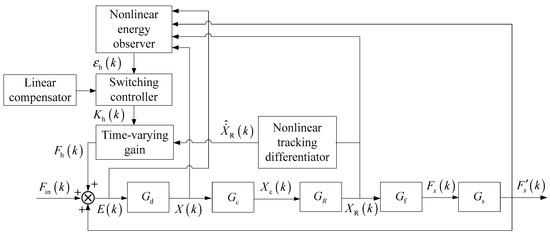
Figure 6.
Delay compensation principle diagram of hybrid simulator.
In Figure 6, is the estimation of obtained by the tracking differentiator, is the observed energy, and is the gain. The hybrid simulator in the discrete domain is obviously nonlinear and closer to the real system. The k-th force compensation value can be expressed as
where T is the system sampling time.
To quantify the performance of the proposed compensation method, evaluation indicators of the dynamic input force error , SIT velocity error , and recovery coefficient are introduced, the expressions of which are given by
where is the velocity of the SIT after compensation, and is the absolute value of when takes the maximum value within each vibration cycle.
When the delay compensation method for the hybrid simulator achieves a good force compensation effect, and should tend towards 0, and should be close to 1.
4.1. Modeling of Switching Compensator with Variable Gain
As the time of the ground hybrid simulation system increases, the differences between the velocity and recovery force of the hybrid simulator and the ideal system become larger without delay compensation, and the system energy continues to increase. If fixed gain is used for compensation (FGC for short), there will be better tracking performance in the early simulation stage and gradually increasing differences in the later stage. Although the feedback adjustment ability can vary with time when conducting linearized gain for compensation (named as LGC), the effectiveness of this compensation method is also limited when there is a significant nonlinear difference between force and velocity. According to the above analysis, a switching compensator with variable gain (SCVG) is constructed, which combines a linearized gain model and a variable gain model based on the energy observer, the latter of which can dynamically adjust with the change in system energy.
reflects the dynamic energy fluctuations during the movement of SITS, which can be drawn as
Because of the continuous oscillation of during the movement of SITS, its vibration frequency is twice the natural frequency of the SIT. If it is directly introduced into differential negative feedback, it is not conducive to system stability. Therefore, integrating to obtain the feedback gain, the relationship between and is
where is static gain, is variable gain, and is switching time.
According to Equation (37), it can be seen that when , varies linearly and also changes continuously with the change in system energy, which is related to and not entirely dependent on .
When the hybrid simulation system converges, the following is true:
In these circumstances, is finite and is bounded, so there exists , which satisfies
For the negative feedback imported by SCVG, is replaced by in Equation (39). In addition, can be acquired through iterative observation, which in turn provides constraints for and , which are also stability constraints for parameter tuning in the discrete domain.
4.2. Velocity Estimation Based on Tracking Differentiator
In the delay compensation approach shown in Figure 6, it is necessary to retrieve the displacement differential signal of the hybrid simulator. If the position signal is directly differentiated in the discrete-time domain, significant noise is involved and causes distortion in the velocity information, thereby leading to poor compensation performance. Owing to the capacity of the optimal tracking differentiator in discrete-time form to rapidly track input signals without overshoot, it has advantages in eliminating signal vibration and improving differentiation quality [40,41,42,43]. Therefore, the discrete optimal tracking differentiator with nonlinear characteristics is applied to estimate the SITS velocity.
The actual displacement signal is decomposed into and after passing through the tracking differentiator, where tracks and ; thus, . The nonlinear discrete optimal tracking differentiator is given by
where is the velocity factor, which determines the tracking speed of . The larger the r, the shorter the system step response time, and the faster the command tracking speed. is the filtering factor, which suppresses the noise in . is the optimal control synthesis function, expressed as follows:
5. Simulation Study
In order to verify the correctness of the theoretical analysis above and the effectiveness of the proposed delay compensation method, simulation studies were carried out sequentially. Although the control block diagram with delay compensation in the continuous time domain is linear, the nonlinearity of the proposed discretized compensator makes the simulation model of the hybrid simulator also nonlinear. Firstly, comparative analyses were conducted on the SITS stability of 1D undamped vibration under different delays. Then, the response characteristic of SITS identified by the ARX model was demonstrated. Finally, the effectiveness of different delay compensation methods on the hybrid simulator of the ground capture system for a SIT was compared. The parameters required for the simulation study are shown in Table 1.

Table 1.
The parameters and corresponding values required for numerical simulations.
5.1. Simulation Verification of Delay Effect on SITS Stability of 1D Undamped Vibration
To show the performances of system instability under three different delays, FMD, ECC, and SRD, the discrete method is used for the solution. The simulation step size for all simulations is set to 0.002 s, and the response lag model of the simulator adopts the transfer function identified in the next simulation.
The comparisons of velocity , force , and power of the SIT under different delay factors are shown in Figure 7. Figure 7a shows the comparison of speed and force between the ideal case and the case that only considers FMD. Figure 7b shows the speed and force comparison between FMD and ECC. Figure 7c shows the speed and force contrast between the ideal case and SRD. Figure 7d shows the power comparison of the SIT under the conditions of no delays and different delays.
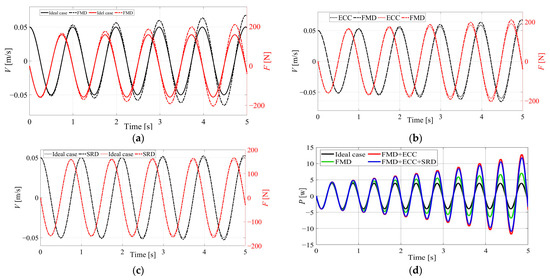
Figure 7.
The comparison of velocity, force, and power under different delay factors. ((a) Comparison of speed and force between ideal case and case only considering FMD, (b) speed and force comparison between FMD and ECC, (c) speed and force contrast between ideal case and SRD, (d) power comparison of SIT under the conditions of no delays and different delays).
It can be seen from Figure 7 that when there are the three different types of delays mentioned above, the 1D undamped system of the SIT diverges, but the velocity, force, and power are finite within a specific time interval, which also verifies the analysis and proof of system stability with the aforementioned lags. In the simulation, the delay of FMD has a greater impact than that of ECC, and SRD causes the system to diverge the slowest. Furthermore, the vibration amplitude and energy of SITS under different delay conditions continue to increase compared to the previous cycle. If corresponding compensation is not quickly carried out, this will lead to the loss of credibility of the ground capture simulation test results, and even damage to the simulator.
5.2. Identification Simulation of SITS
The sine sweep frequency curves corresponding to the relevant parameters in Table 1 are discretized and utilized as control instructions for identifying the discrete domain transfer function of SIST. Then, the instructions are mapped to the Cartesian coordinate system and the joint space of the robot through the kinematics model. The spatial trajectory of control point Pv is shown in Figure 8.
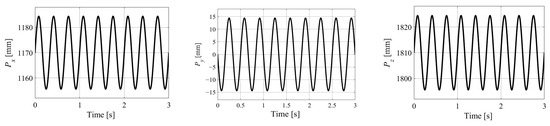
Figure 8.
The spatial trajectory of Pv.
Taking the above frequency sweep signal as the input and the simulated trajectory as the output, can be obtained through the above-mentioned identification algorithm, and can be obtained through transformation. The identified trajectory error is shown in Figure 9a, and its logarithmic frequency characteristic curve is drawn in Figure 9b.
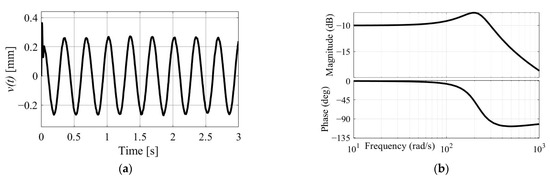
Figure 9.
Model identification results of SITS. ((a) Identified trajectory error, (b) logarithmic frequency characteristic of simulator).
As shown in Figure 9, the 1D sweep motion of the simulator has a large stability margin. Its amplitude frequency characteristics first increase and then decrease with frequency, while the phase lag continues to increase. At 10 Hz, its phase lag is −2.87°.
5.3. Simulation Verification of the Effect for SCVG
To verify the effectiveness of the tracking differentiator and optimize its tuning parameters, Figure 10a presents the original displacement curve and direct differential signal of the simulator. Figure 10b demonstrates differential signal estimation curves of the original signal corresponding to different tracking differentiator parameters. It can be seen from Figure 10a that there are significant spikes and oscillations in the differential signal, and directly applying it for feedback control would reduce system stability. From the partial enlarged view in Figure 10b, it can be seen that when r is set to a larger value, the estimated tracking speed of its differential signal increases significantly, but its amplitude overshoot also increases. When h takes a larger value, the differential signal becomes stable, but the signal is distorted due to excessive filtering. Therefore, the parameters of the tracking differentiator are selected as after comprehensive consideration, which not only has a fast tracking speed, but is also relatively stable and close to the real differential signal.
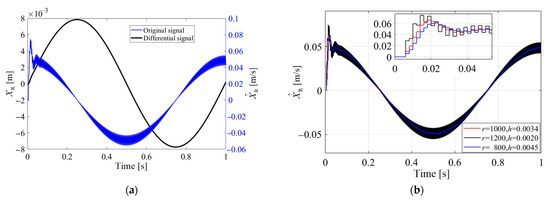
Figure 10.
Verification of the tracking differentiator’s effectiveness. ((a) Original displacement curve and differential signal of the simulator, (b) differential signal estimations under different tracking differentiator parameters).
To attain better dynamic compensation effects, plays an critical role in improving the ground experiment accuracy of the hybrid simulator in addition to parameter tuning of , , and . The evaluation indicators , , and in Equation (44) are the basis for determining the value of . When takes a better value, , , and all tend towards the ideal value. Here, is taken as an example to explain the selection process of . Figure 11a shows the comparison of when takes different values in SCVG, and its local magnification within 0–0.5 s is presented in Figure 11b.
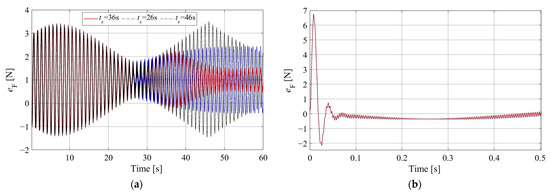
Figure 11.
The comparison of when takes different values in SCVG. ((a) Comparison of when takes different values in SCVG, (b) local magnification within 0–0.5 s of ).
From Figure 11, it can be seen that when , the linear compensator takes effect, and the maximum force error after compensation is 6.76 N. The nonlinear compensator based on the energy observer begins to take effect when , and the peak deviation between the compensated force and the ideal value when is slightly larger than , with a duration of 1 s and a maximum deviation of 5.39%. Afterwards, the force error is smaller than and , so it has a better compensation effect when , with decreasing from 6.76 N to 0.09 N, which will be used in the following simulations.
To prove the advantage of proposed compensator, the velocity error comparison of the SIT under different compensation methods, including FGC, LGC, and SCVG, is shown in Figure 12.
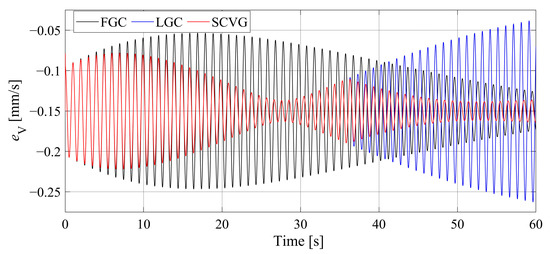
Figure 12.
Comparison of SIT velocity error under different compensators.
In Figure 12, it can be seen that the of LGC is better than that of FGC before the switching control takes effect. The maximum of the former is 0.14 mm/s, while that of the latter is 0.22 mm/s. If the nonlinear compensator based on the energy observer is not implemented, the velocity error amplitude of LGC exceeds that of FGC at 40.69 s. After implementing a nonlinear compensator based on the energy observer, is significantly reduced. At the end of the simulation, the amplitude of is only 0.028 mm/s when adopting SCVG, while those of LGC and FGC are 0.23 mm/s and 0.16 mm/s, respectively.
Although is relatively small within the simulation time, due to the continuous attenuation of the vibration velocity, the deviation of its vibration recovery coefficient from the ideal value may become larger. The comparison of the changes in for different compensators is shown in Figure 13.
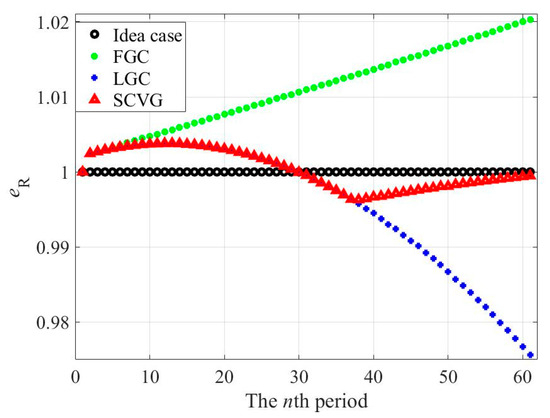
Figure 13.
The comparison of for different compensators during simulation.
From Figure 13, it can be seen that although the of LGC is greater than that of LGC in the later stage of the simulation, it reduces the energy of the system and thus increases its stability. The of SCVG remains between 0.995 and 1.005, and compared with FGC (1.0203) and LGC (0.9756), it gradually approaches 1 with a value of 0.9995, which also verifies the effectiveness of the proposed compensator.
The movement velocity of the SIT is closer to the ideal case without delays due to the adoption of SCVG, which also confirms that the dynamic input force approaches the true value. Figure 14 compares the using different compensators.
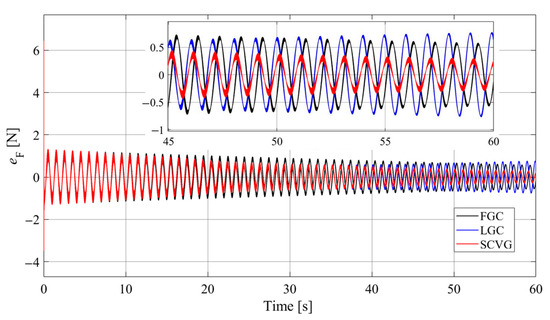
Figure 14.
Comparison of under different compensators.
As can be seen from Figure 14, input force errors of three types of compensators are basically the same in the initial phase of the simulation, while the differences increase gradually as time increases. The value of when applying SCVG decreases the fastest, and the peak value of at the end of the simulation in this case is only 0.29 N, compared with FGC (0.58 N) and LGC (0.77 N), which verifies the excellent compensation performance of SCVG in long-term hybrid simulation.
The variation in the observed energy of the SIT over time when adopting SCVG is revealed in Figure 15.
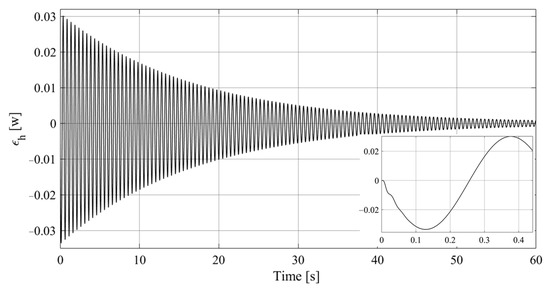
Figure 15.
The variation in when adopting SCVG.
It can be seen from Figure 15 that the value of starts from 0, with the amplitude increasing to 0.034 w within the first vibration period and decreasing to 8.37 × 10−4 w in the last simulation cycle, which implies that as the vibration period increases, it eventually tends towards 0, indicating that the system converges. The variation in over time in the proposed SCVG during simulation is shown in Figure 16.
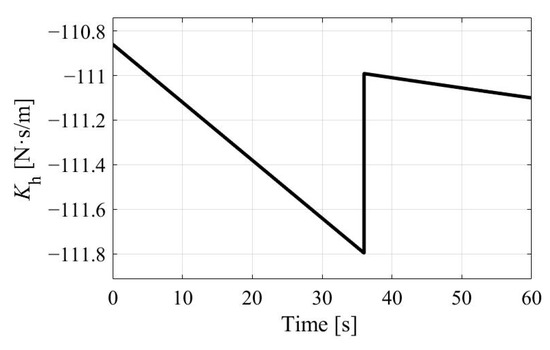
Figure 16.
The variation in in SCVG during simulation.
The feedback compensation gain varies linearly with time before the switching controller takes effect. As the system energy gradually stabilizes in the later phase of the simulation, it actually exhibits nonlinear changes, which means that SITS is corrected in a timely manner after the switch time.
Furthermore, the values of and can also be acquired, which are and , respectively. The SITS system has two characteristic roots with positive real parts when , and the system is unstable. It can be concluded that the eigenvalues all have negative real parts by substituting and into the characteristic Equation (36), and this simultaneously satisfies the stability constraints of Equation (39), indicating that the SITS is asymptotically stable. Therefore, the proposed hybrid simulation system with SCVG is stable.
Although the simulation model is nonlinear, it has been partly linearized and simplified in theoretical analyses, mainly including and . It is obvious that linearization introduces an error, but it is minor. Taking the force measurement delay as an example, the simulation model adopts a delay module, while the theoretical analysis uses the linearized model . and its error caused by linearization processing, defined as , are presented in Figure 17a and Figure 17b, respectively.
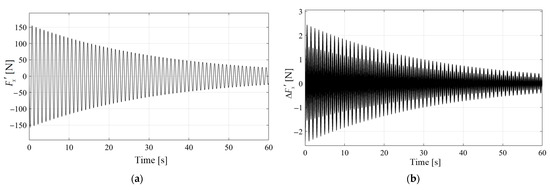
Figure 17.
and the error caused by linearization. ((a) Force curve caused by FMD, (b) error caused by linearization of FMD).
As can be seen from Figure 17, the amplitude of the error caused by linearization gradually decreases with the increase in simulation time, with a maximum error of 2.45 N. The vibration amplitude before the end of the simulation is 0.41 N. The ratio range of the amplitude of error in after linearization is 1.57~1.58%, indicating that the proportion of error caused by linearization remains basically unchanged. Therefore, appropriate linearization treatment during the modeling process in this article is reasonable.
6. Conclusions
(1) A hybrid simulator is proposed based on nonlinear SCVG after analyzing the instability of simulators in current SPS systems caused by three types of delays. The stability constraints of the proposed hybrid simulator were obtained through the Routh criterion, and the simulation study was employed to verify the effectiveness and stability of the proposed compensation method.
(2) The proposed nonlinear SCVG consists of the variable gain and velocity estimator, which modifies the input force of the dynamic model through switching control to compensate for the presence of three delays superimposed on each other. Velocity estimation is achieved by approximating tracking of the differential signal of the actual displacement when applying the optimal tracking differentiator. The nonlinear gain model automatically adjusts the feedback gain according to the current observed energy variation in the system.
(3) The peak errors of the dynamic input, velocity, and recovery coefficient when adopting SCVG in the last cycle before the end of the simulation are 0.29 N, 0.028 mm/s, and 0.0005, respectively. Compared with FGC and LGC, the performance improvements are at least 50.00%, 82.50%, and 97.54%.
(4) The proposed SCVG demonstrates excellent compensation effects for the 1D motion of the hybrid simulator in simulation of ground capture test systems. By analyzing the existing research progress in [20,25,26,27,28,29,30,31,32] and combining it with the research results in this paper, it can be ensured that the proposed compensator can play a useful role in practical systems. In future work, we will advance the divergence proof for the damping system with delays. We aim to extend the proposed compensator to 6-DoF spatial motion after experimental verification of the proposed SCVG in this paper, further enhancing the stability of the hybrid simulator. Future research will involve developing a universal hybrid simulator with high fidelity in ground capture mission trials.
Author Contributions
Conceptualization, X.B. and Z.X.; methodology, X.B. and X.L.; software, X.B. and M.L.; validation, H.L. and Z.Z.; writing—review and editing, X.B. and H.L.; supervision, X.L.; project administration, Z.Z. and Z.X. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the space debris mitigation research project (KJSP2020010303) funded by the State Administration of Science, Technology and Industry for National Defence, PRC.
Data Availability Statement
Data are contained within this article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Keles, O.F. Telecommunications and Space Debris: Adaptive Regulation Beyond Earth. Telecommun. Policy 2023, 47, 102517. [Google Scholar] [CrossRef]
- Takeichi, N.; Tachibana, N. A tethered plate satellite as a sweeper of small space debris. Acta Astronaut. 2021, 189, 429–436. [Google Scholar] [CrossRef]
- Witze, A. The quest to conquer earth’s space junk problem. Nature 2018, 561, 24–26. [Google Scholar] [CrossRef] [PubMed]
- Nanjangud, A.; Blacker, P.C.; Bandyopadhyay, S.; Gao, Y. Robotics and AI-Enabled On-Orbit Operations with Future Generation of Small Satellites. Proc. IEEE 2018, 106, 429–439. [Google Scholar] [CrossRef]
- Inaba, N.; Oda, M.; Asano, M. Rescuing a Stranded Satellite in Space-Experimental Robotic Capture of Non-Cooperative Satellites. Trans. Jpn. Soc. Aeronaut. Space Sci. 2006, 48, 213–220. [Google Scholar] [CrossRef]
- Papadopoulos, E.; Aghili, F.; Ma, O.; Lampariello, R. Robotic Manipulation and Capture in Space: A Survey. Front. Robot. AI 2021, 8, 686723. [Google Scholar] [CrossRef] [PubMed]
- Rybus, T. Obstacle avoidance in space robotics: Review of major challenges and proposed solutions. Prog. Aerosp. Sci. 2018, 101, 31–48. [Google Scholar] [CrossRef]
- Hatch, H.G.; Pennington, J.E.; Cobb, J.B. Dynamic Simulation of Lunar Module Docking with Apollo Command Module in Lunar Orbit; NASA Tech. Note TN D-3972; National Aeronautics and Space Administration: Washington, DC, USA, 1967; pp. 1–26. [Google Scholar]
- Uyama, N.; Fujii, Y.; Nagaoka, K.; Yoshida, K. Experimental evaluation of contact-impact dynamics between a space robot with a compliant wrist and a free-flying object. In Proceedings of the International Symposium on Artificial Intelligence, Robotics and Automation in Space, Turin, Italy, 4–6 September 2012. [Google Scholar]
- Wei, Y.; Yang, X.; Xu, Z.; Bai, X. Novel ground microgravity experiment system for a spacecraft-manipulator system based on suspension and air-bearing. Aerosp. Sci. Technol. 2023, 141, 108587. [Google Scholar] [CrossRef]
- Ma, O.; Wang, J. Model order reduction for impact-contact dynamics simulations of flexible manipulators. Robotica 2007, 25, 397–407. [Google Scholar] [CrossRef]
- Flores-Abad, A.; Ma, O.; Pham, K.; Ulrich, S. A review of space robotics technologies for on-orbit servicing. Prog. Aerosp. Sci. 2014, 68, 1–26. [Google Scholar] [CrossRef]
- Yaskevich, A. Real time math simulation of contact interaction during spacecraft docking and berthing. J. Mech. Eng. Autom. 2014, 4, 1–15. [Google Scholar]
- Roe, F.D.; Howard, R.T.; Murphy, L. Automated rendezvous and capture system development and simulation for NASA. Modeling, Simulation, and Calibration of Space-based Systems. In Proceedings of the Defense and Security, Orlando, FL, USA, 12–16 April 2004; SPIE: Bellingham, WA, USA, 2004; Volume 5420, pp. 118–125. [Google Scholar]
- Mitchell, J.D.; Cryan, S.P.; Baker, K.; Martin, T.; Goode, R.; Key, K.W.; Chien, C.H. Integrated docking simulation and testing with the Johnson space center six-degree-of-freedom dynamic test system. In Proceedings of the Space Technology and Applications International Forum, Albuquerque, NM, USA, 10–14 February 2008; pp. 709–716. [Google Scholar]
- Boge, T.; Ma, O. Using advanced industrial robotics for spacecraft Rendezvous and Docking simulation. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 1–4. [Google Scholar]
- Ma, O.; Flores-Abad, A.; Boge, T. Use of industrial robots for hardware-in-the-loop simulation of satellite rendezvous and docking. Acta Astronaut. 2012, 81, 335–347. [Google Scholar] [CrossRef]
- Wei, Y.Q.; Yang, X.; Bai, X.L.; Xu, Z.G. Hardware-in-the-loop based ground test system for space berthing and docking mechanism of small spacecraft. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2023, 237, 3486–3495. [Google Scholar] [CrossRef]
- Zebenay, M.; Lampariello, R.; Boge, T.; Choukroun, D. A new contact dynamics model tool for hardware-in-the-loop docking simulation. In Proceedings of the International Symposium on Artificial Intelligence, Robotics and Automation in Space, Turin, Italy, 4–6 September 2012. [Google Scholar]
- Zebenay, M.; Boge, T.; Krenn, R.; Choukroun, D. Analytical and experimental stability investigation of a hardware-in-the-loop satellite docking simulator. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2015, 229, 666–681. [Google Scholar] [CrossRef]
- Qi, C.; Ren, A.; Gao, F.; Zhao, X.; Wang, Q.; Sun, Q. Compensation of velocity divergence caused by dynamic response for hardware-in-the-loop docking simulator. IEEE/ASME Trans. Mechatron. 2016, 22, 422–432. [Google Scholar] [CrossRef]
- Stefano, M.D.; Balachandran, R.; Secchi, C. A Passivity-Based Approach for Simulating Satellite Dynamics with Robots: Discrete-Time Integration and Time-Delay Compensation. IEEE Trans. Robot. 2020, 36, 189–203. [Google Scholar] [CrossRef]
- Rao, L.S.; Rao, P.S.; Chhabra, I.M.; Kumar, L.S. Modeling and Compensation of Time-Delay Effects in HILS of Aerospace Systems. IETE Tech. Rev. 2022, 39, 375–388. [Google Scholar] [CrossRef]
- Osaki, K.; Konno, A.; Uchiyama, M. Delay time compensation for a hybrid simulator. Adv. Robot. 2010, 24, 1081–1098. [Google Scholar] [CrossRef]
- Abiko, S.; Satake, Y.; Jiang, X.; Tsujita, T.; Uchiyama, M. Delay time compensation based on coefficient of restitution for collision hybrid motion simulator. Adv. Robot. 2014, 28, 1177–1188. [Google Scholar] [CrossRef]
- Ma, O.; Wang, J.; Misra, S.; Liu, M. On the validation of SPDM task verification facility. J. Robot. Syst. 2004, 21, 219–235. [Google Scholar] [CrossRef]
- Hayati, S.; Song, W. Design and performance evaluation of an optimal discrete-time feedforward controller for servo-hydraulic compensation. J. Eng. Mech. 2018, 144, 04017163. [Google Scholar] [CrossRef]
- Sahu, G.N.; Vashisht, S.; Wahi, P.; Law, M. Validation of a hardware-in-the-loop simulator for investigating and actively damping regenerative chatter in orthogonal cutting. CIRP J. Manuf. Sci. Technol. 2020, 29, 115–129. [Google Scholar] [CrossRef]
- Xu, W.; Guo, T.; Chen, C.; Chen, M.; Chen, K. Experimental verification of a frequency domain evaluation index-based compensation for real-time hybrid simulation. Struct. Control. Health Monit. 2020, 27, e2641. [Google Scholar] [CrossRef]
- Qi, C.; Li, D.; Ma, W.; Wei, Q.; Zhang, W.; Wang, W.; Hu, H.; Gao, F. Distributed delay compensation for a hybrid simulation system of space manipulator capture. IEEE/ASME Trans. Mechatron. 2021, 27, 2367–2378. [Google Scholar] [CrossRef]
- He, J.; Shen, M. Hybrid Force/Velocity Control for Simulating Contact Dynamics of Satellite Robots on a Hardware-in-the-Loop Simulator. IEEE Access 2022, 10, 59277–59289. [Google Scholar] [CrossRef]
- Tsokanas, N.; Pastorino, R.; Stojadinovic, B. Adaptive model predictive control for actuation dynamics compensation in real-time hybrid simulation. Mech. Mach. Theory 2022, 172, 104817. [Google Scholar] [CrossRef]
- Khusainov, D.Y.; Diblík, J.; Růžičková, M.; Lukáčová, J. Representation of a solution of the Cauchy problem for an oscillating system with pure delay. Nonlinear Oscil. 2008, 11, 276–285. [Google Scholar] [CrossRef]
- Ricardo, L.G.G.; Lagomasino, G.L. Strong asymptotics of multi-level Hermite-Padé polynomials. J. Math. Anal. Appl. 2024, 531, 127801. [Google Scholar] [CrossRef]
- Đukić, D.; Mutavdžić Đukić, R.; Reichel, L.; Spalević, M. Optimal averaged Padé-type approximants. Electron. Trans. Numer. Anal. 2023, 59, 145–156. [Google Scholar] [CrossRef]
- Motoyama, Y.; Yoshimi, K.; Otsuki, J. Robust analytic continuation combining the advantages of the sparse modeling approach and the Padé approximation. Phys. Rev. B 2022, 105, 035139. [Google Scholar] [CrossRef]
- Mehmood, K.; Chaudhary, N.I.; Cheema, K.M.; Khan, Z.A.; Raja, M.A.Z.; Milyani, A.H.; Alsulami, A. Design of nonlinear marine predator heuristics for hammerstein autoregressive exogenous system identification with key-term separation. Mathematics 2023, 11, 2512. [Google Scholar] [CrossRef]
- Beltran-Perez, C.; Serrano, A.A.; Solís-Rosas, G.; Martínez-Jiménez, A.; Orozco-Cruz, R.; Espinoza-Vázquez, A.; Miralrio, A. A general use QSAR-ARX model to predict the corrosion inhibition efficiency of drugs in terms of quantum mechanical descriptors and experimental comparison for lidocaine. Int. J. Mol. Sci. 2022, 23, 5086. [Google Scholar] [CrossRef] [PubMed]
- Mehmood, K.; Chaudhary, N.I.; Khan, Z.A.; Cheema, K.M.; Raja, M.A.Z.; Shu, C.M. Novel knacks of chaotic maps with Archimedes optimization paradigm for nonlinear ARX model identification with key term separation. Chaos Soliton Fract. 2023, 175, 114028. [Google Scholar] [CrossRef]
- Wen, Q.; Wang, M.; Li, X.; Chang, Y. Learning-based design optimization of second-order tracking differentiator with application to missile guidance law. Aerosp. Sci. Technol. 2023, 137, 108302. [Google Scholar] [CrossRef]
- Park, J.H.; Park, T.S.; Kim, S.H. Asymptotically convergent higher-order switching differentiator. Mathematics 2020, 8, 185. [Google Scholar] [CrossRef]
- Feng, H.; Qian, Y. A linear differentiator based on the extended dynamics approach. IEEE Trans. Autom. Control 2022, 67, 6962–6967. [Google Scholar] [CrossRef]
- Oliveira, T.R.; Estrada, A.; Fridman, L.M. Global and exact HOSM differentiator with dynamic gains for output-feedback sliding mode control. Automatica 2017, 81, 156–163. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).