Decoupling Control for Module Suspension System of Maglev Train Based on Feedback Linearization and Extended State Observer
Abstract
:1. Introduction
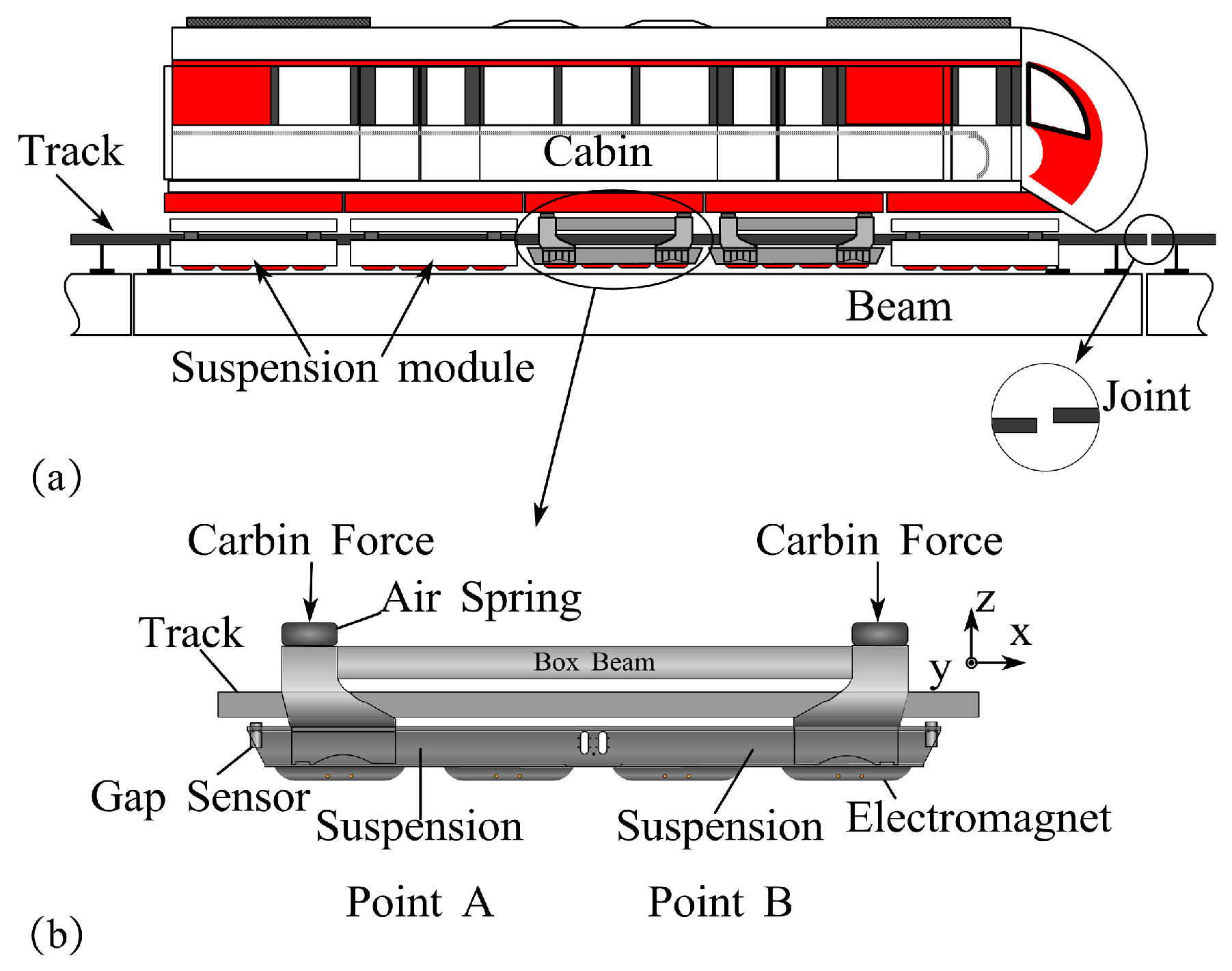
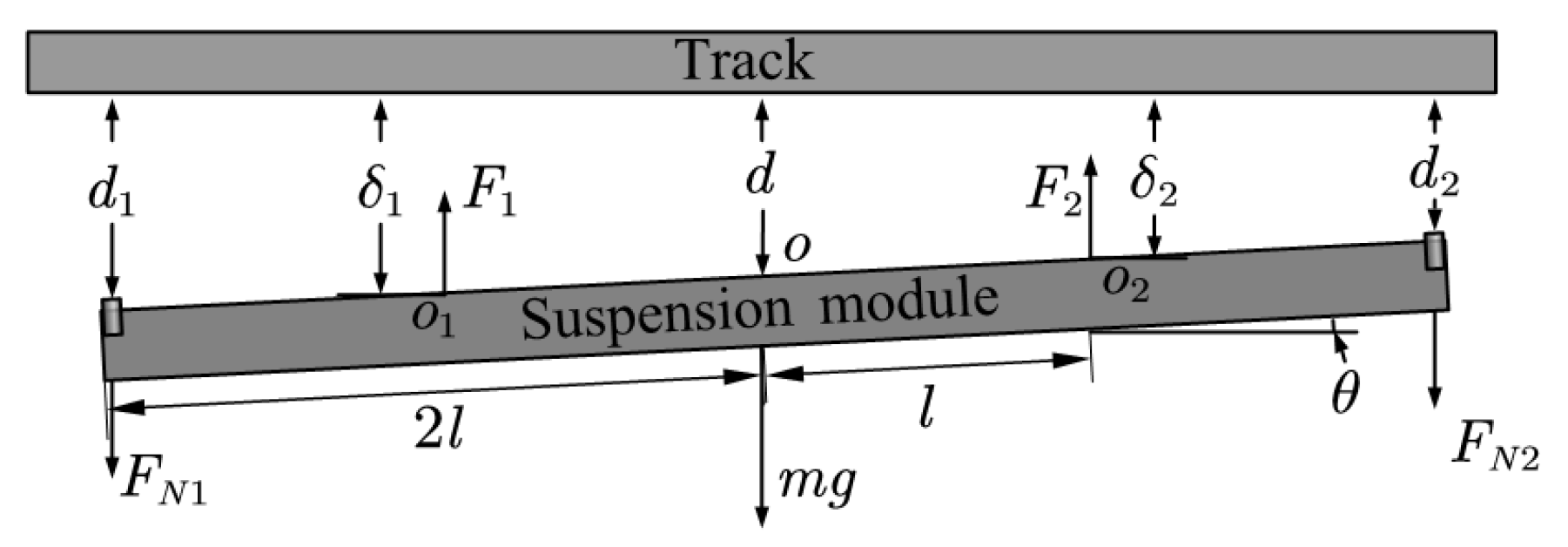
2. Modeling of the Module Suspension System
- Magnetic flux leakage of the winding and the magnetoresistance of the iron core and guide are ignored.
- There is no misalignment between the pole surface and the orbit of the electromagnet.
- The mass distribution of the suspension module is uniform.
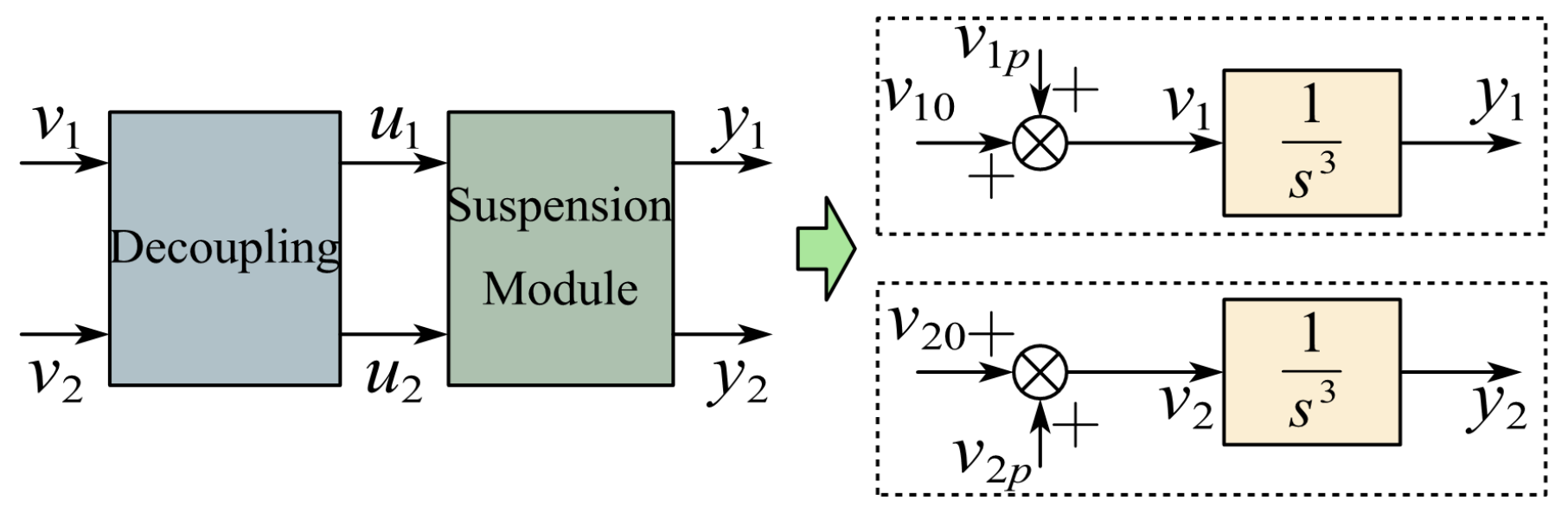
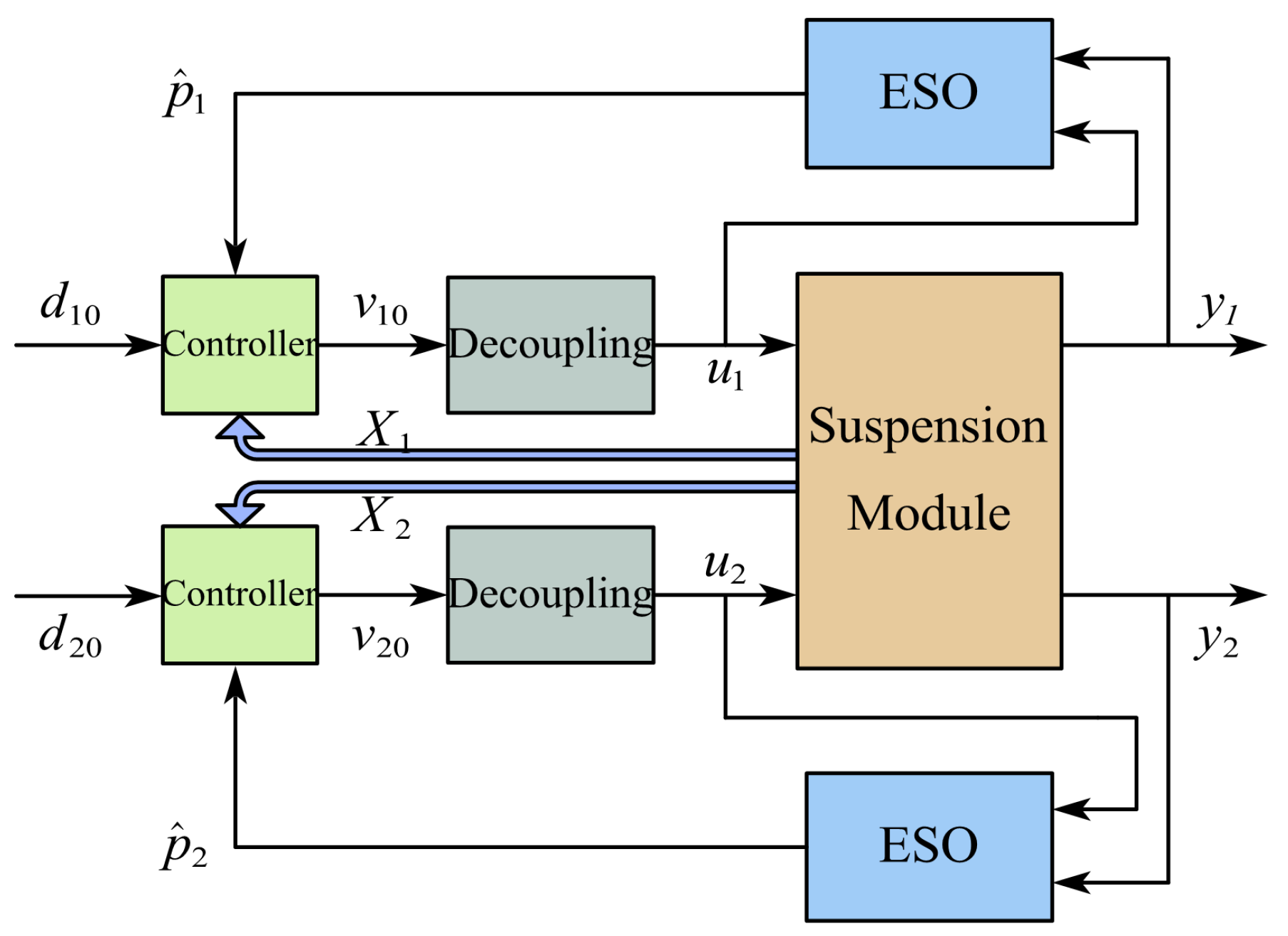
3. Decoupling Controller Design
3.1. Feedback Decoupling
3.2. State Feedback Control
- System overshoot: ;
- System peak time: .
3.3. Linear Extended State Observer
4. Simulation and Experimental Results
4.1. Numerical Simulations
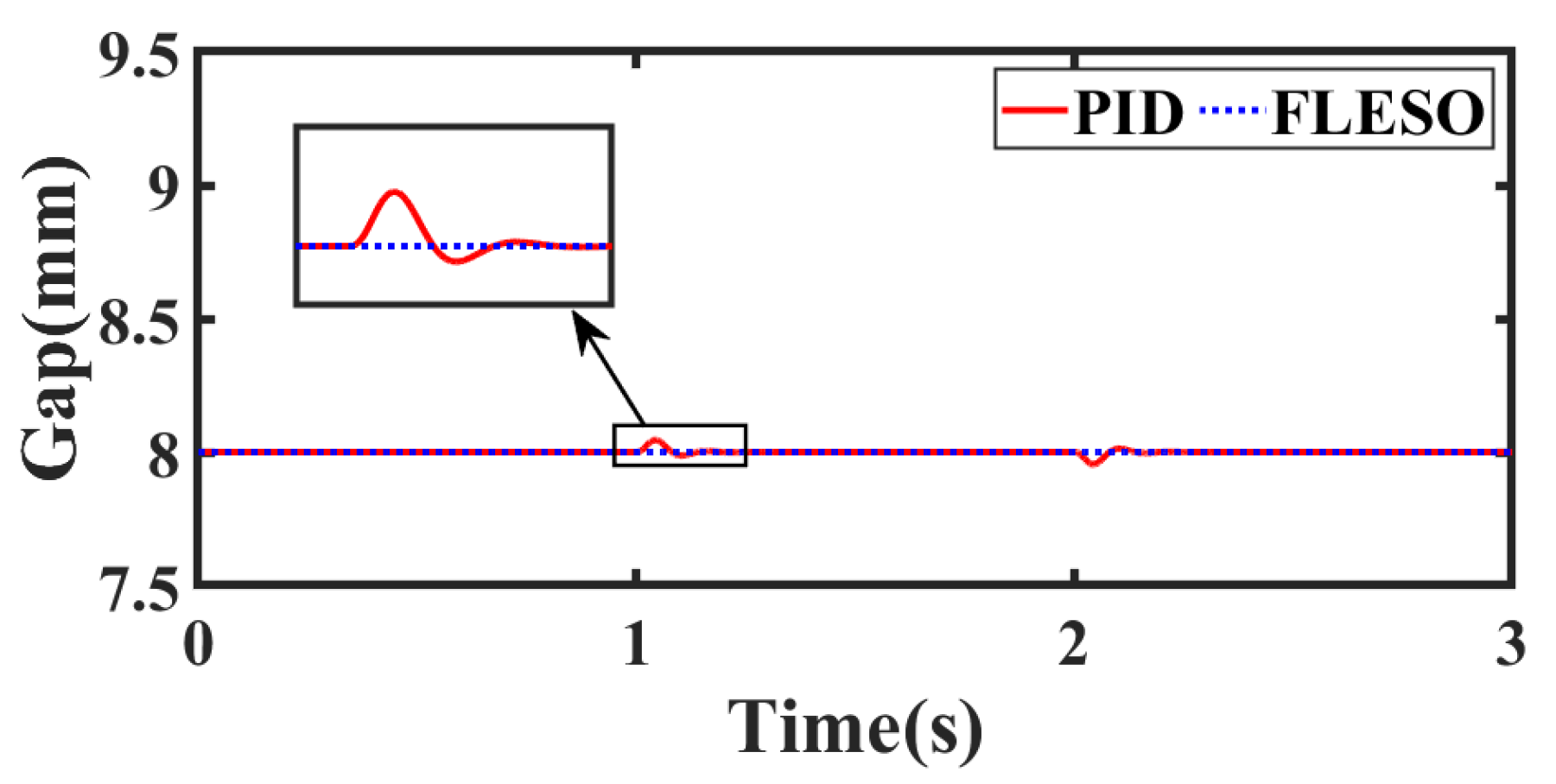
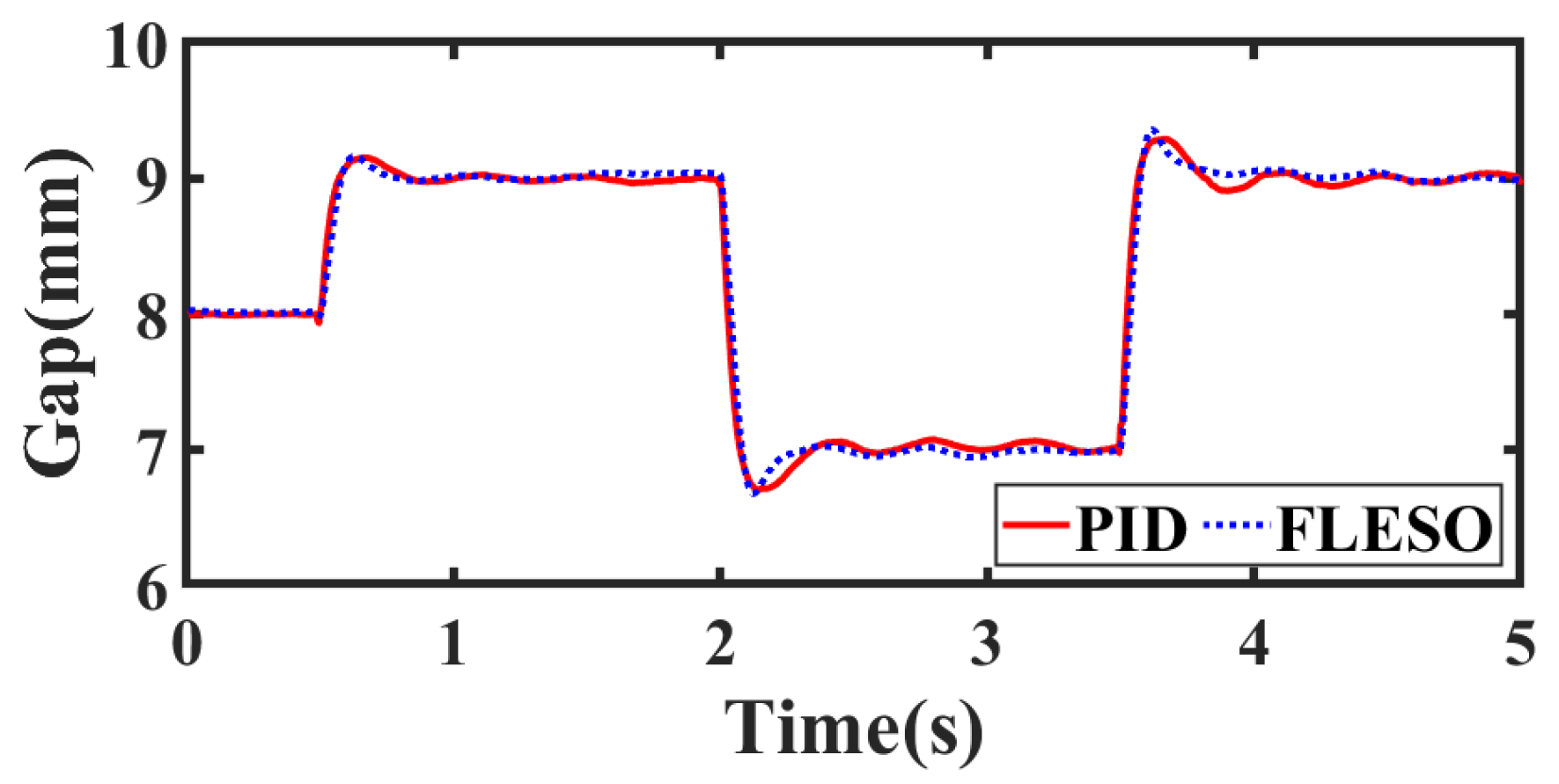
4.1.1. Case 1: Trajectory Tracking
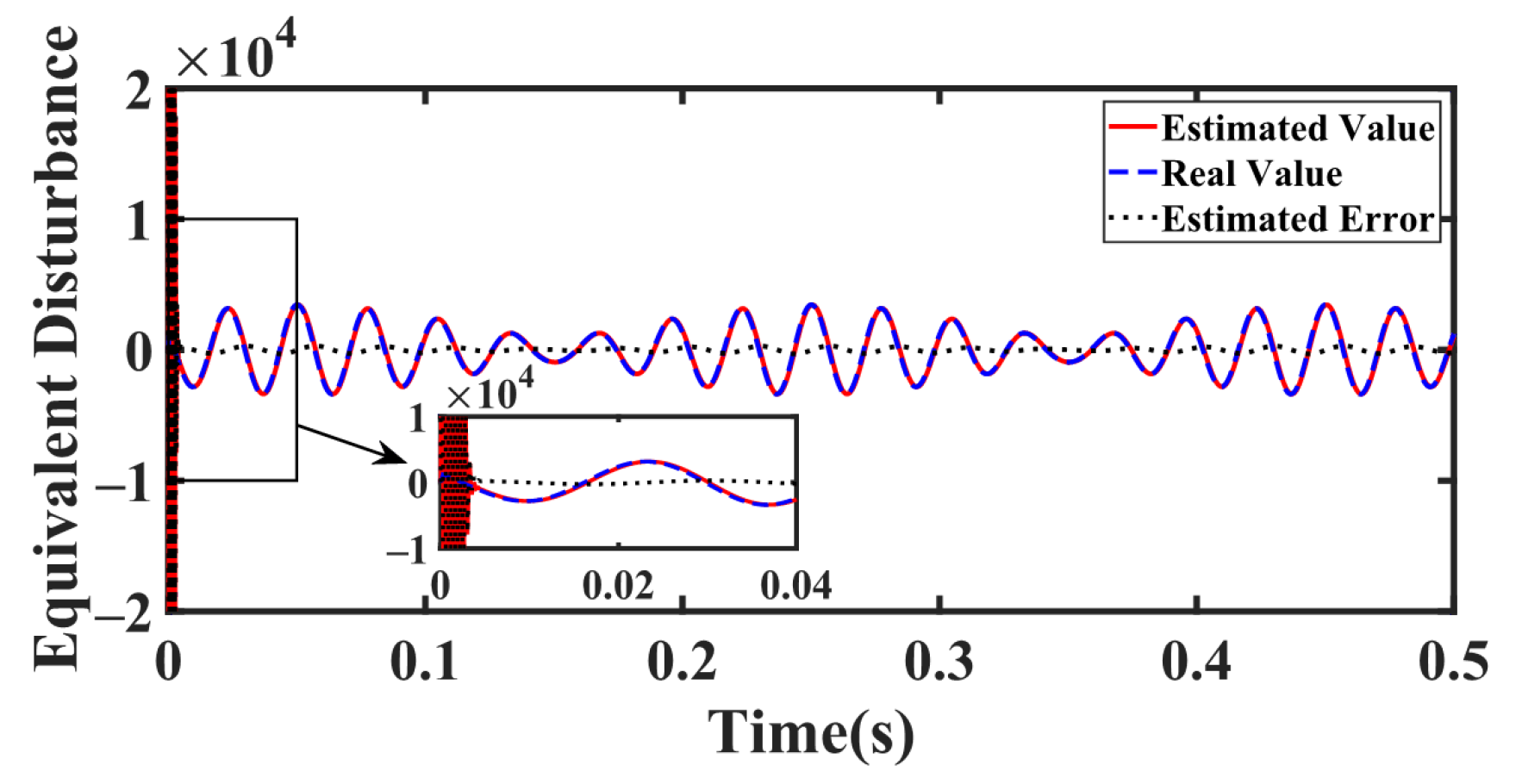
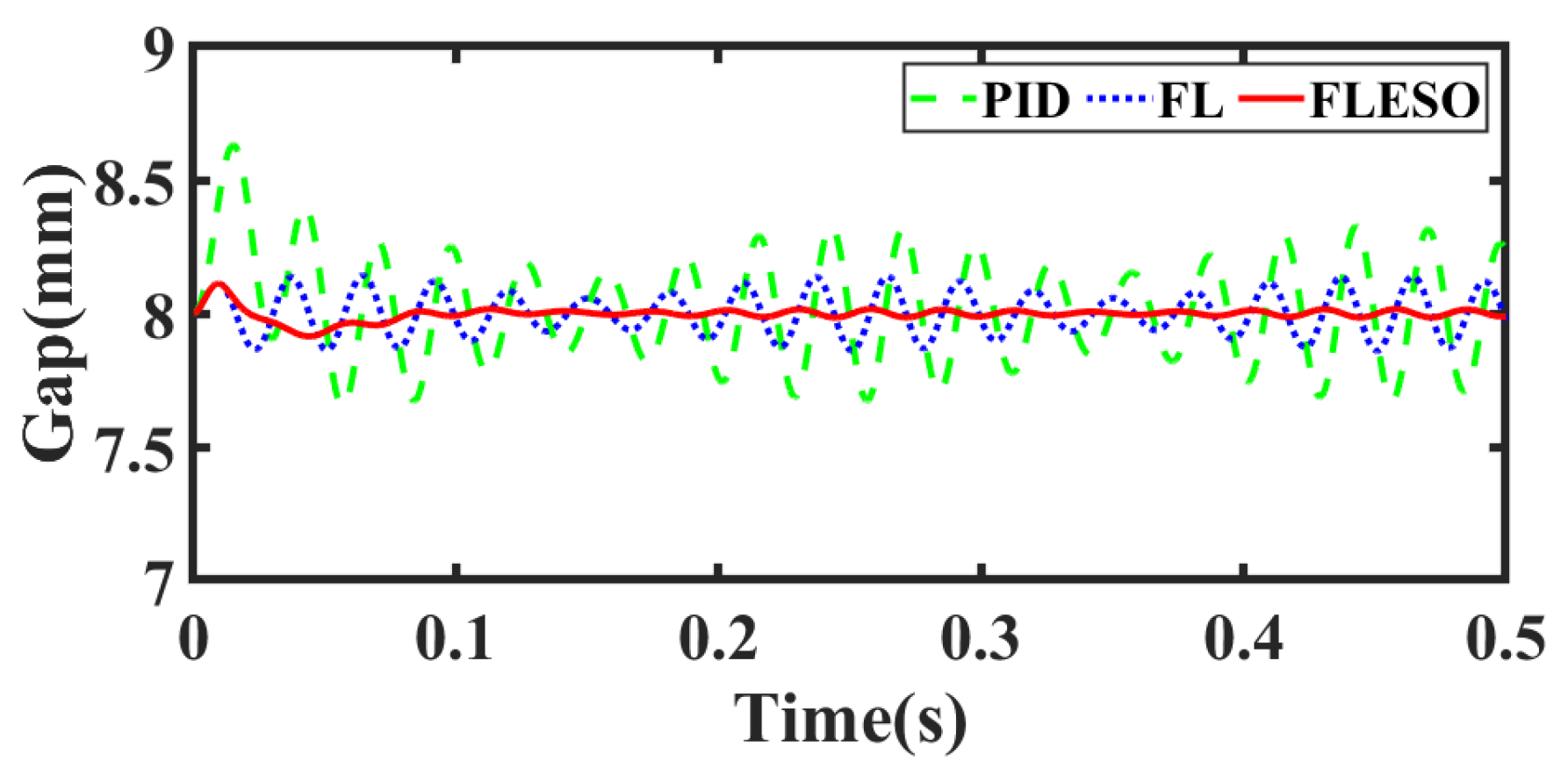
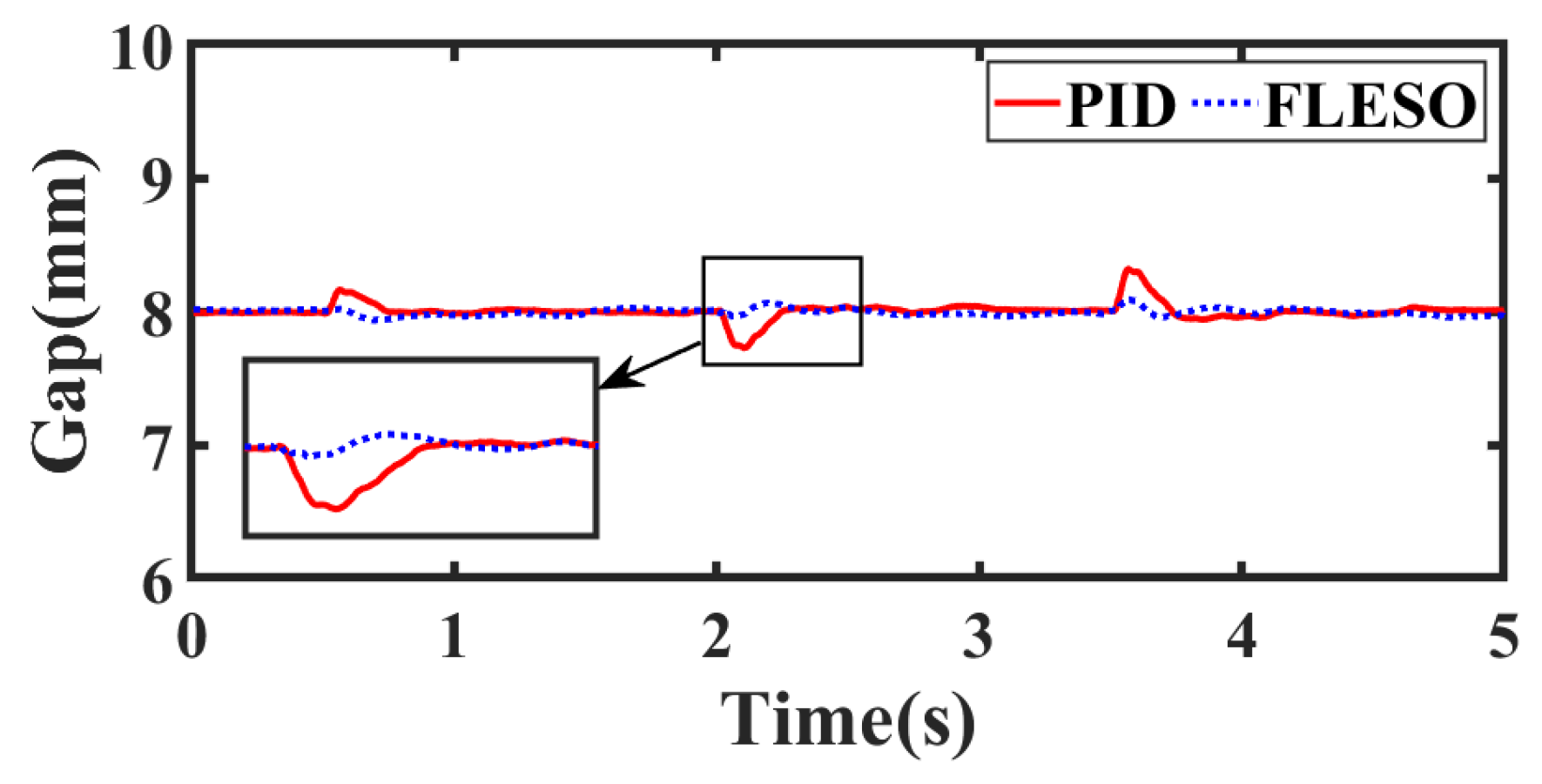
4.1.2. Case 2: Suspension with Periodic Perturbation
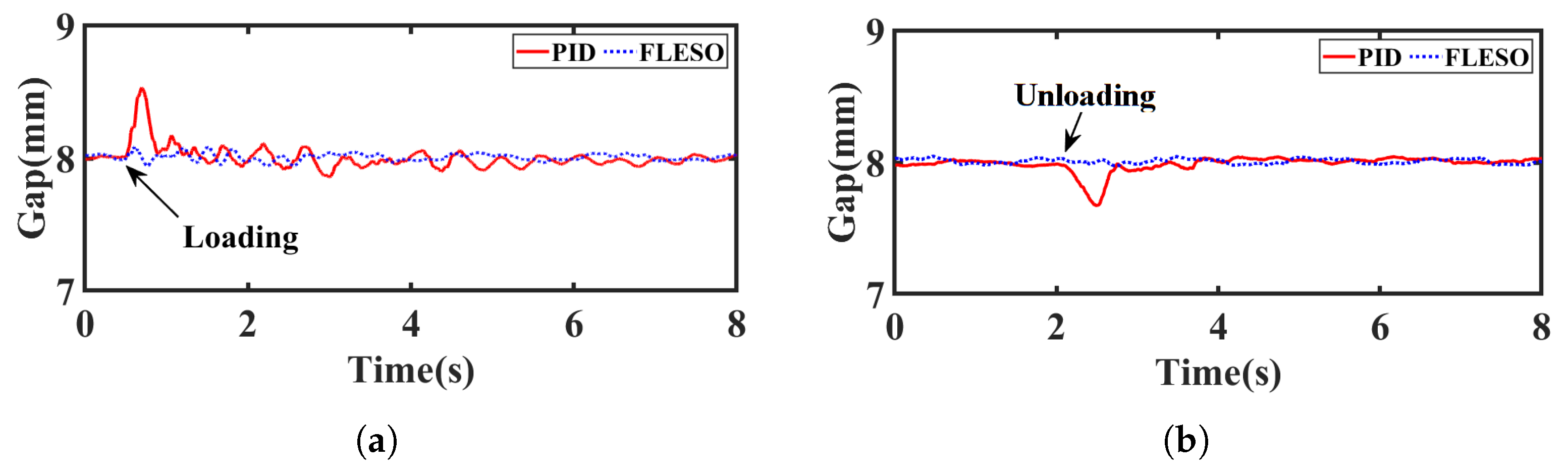
4.1.3. Case 3: Suspension with Load Disturbance
4.2. Experimental Results
4.2.1. Scenario 1: Trajectory Tracking
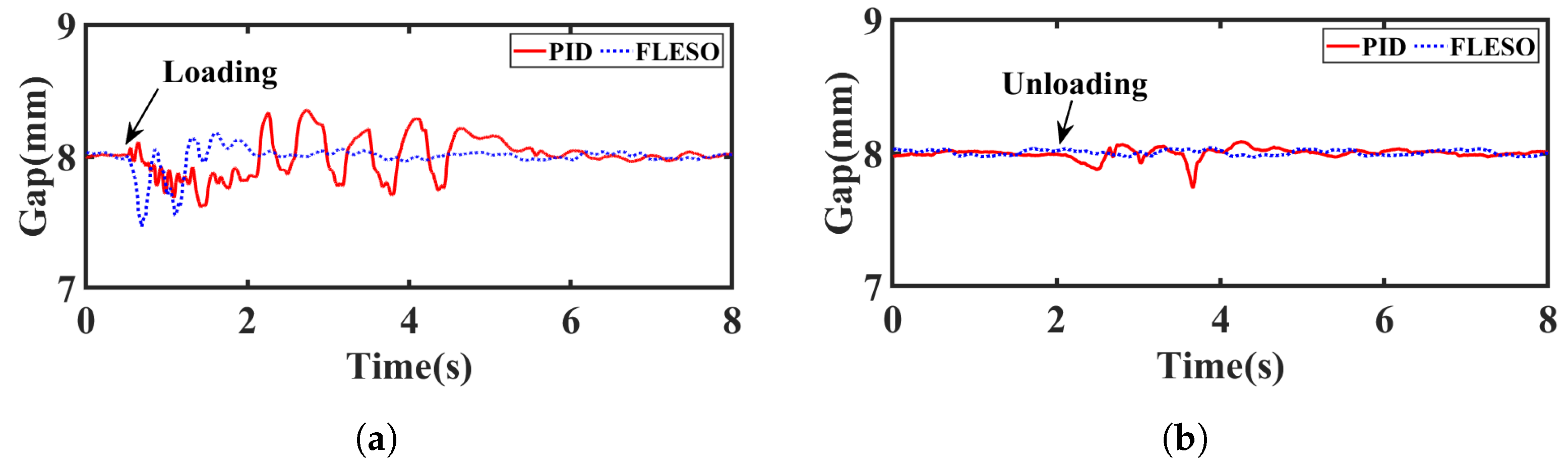
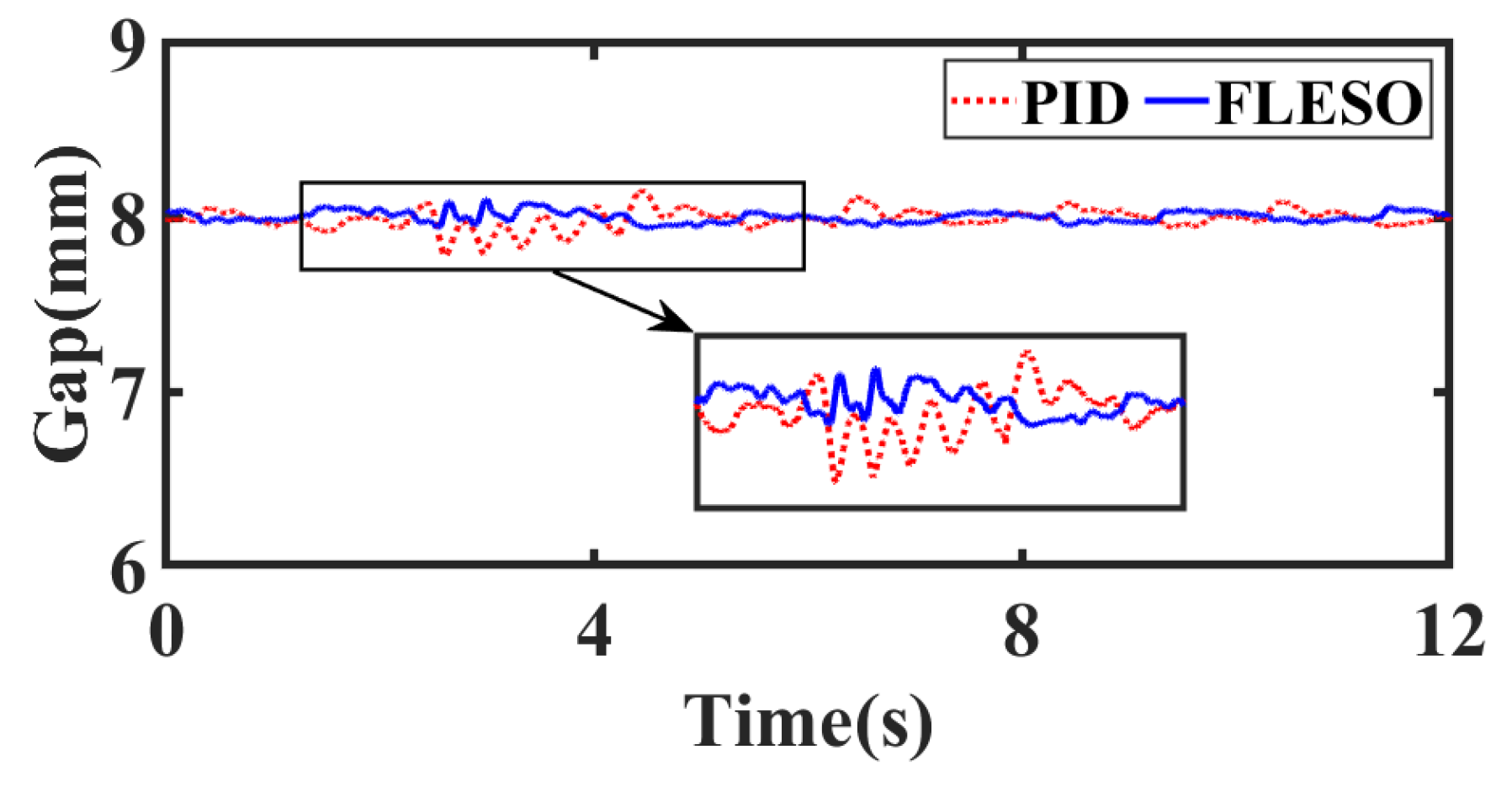
4.2.2. Scenario 2: Suspension with Load Disturbance
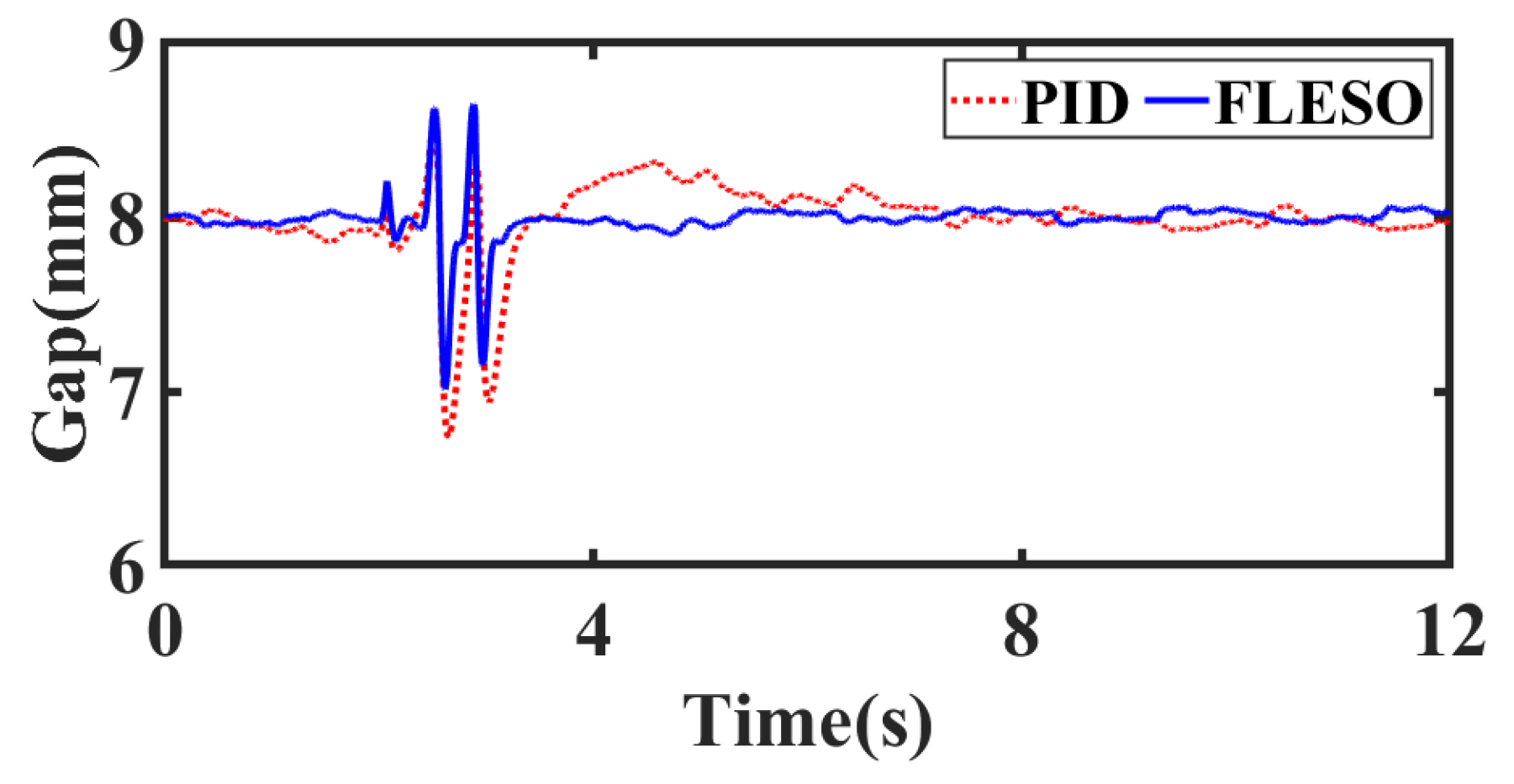
4.2.3. Scenario 3: Suspension with Track Step Disturbance
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lee, H.W.; Kim, K.C.; Lee, J. Review of maglev train technologies. IEEE Trans. Magn. 2006, 42, 1917–1925. [Google Scholar] [CrossRef]
- Gou, J. Development status and global competition trends analysis of maglev transportation technology based on patent data. Urban Rail Transit 2018, 4, 117–129. [Google Scholar] [CrossRef]
- Cassat, A.; Jufer, M. Maglev projects technology aspects and choices. IEEE Trans. Appl. Supercon. 2002, 12, 915–925. [Google Scholar] [CrossRef]
- Nakamura, S. Development of high speed surface transport system (HSST). IEEE Trans. Magn. 1979, 15, 1428–1433. [Google Scholar] [CrossRef]
- Park, D.Y.; Shin, B.C.; Han, H. Korea’s urban maglev program. Proc. IEEE 2009, 97, 1886–1891. [Google Scholar] [CrossRef]
- Yan, L. Progress of the maglev transportation in china. IEEE Trans. Appl. Supercon. 2006, 16, 1138–1141. [Google Scholar] [CrossRef]
- Dai, G.; Liu, G.; Liu, W.; Chen, Y.; Yang, L. Design and construction of concrete simply-supported guideway beam in the changsha maglev line, china. Struct. Eng. Int. 2017, 27, 569–574. [Google Scholar] [CrossRef]
- Xu, Y.; Zhao, Z.; Long, Z.; Wen, T. Performance optimization of maglev train’s electromagnetic levitation system: Control structure and algorithm. IEEE Trans. Autom. Sci. Eng. 2023, 1–11. [Google Scholar] [CrossRef]
- Zeng, J.; Xia, W.; Xiang, X.; Long, Z. Research on the mechanism and control characteristics of vehicle-track beam coupling vibration for medium-speed maglev vehicle. IEEE Trans. Transp. Electrif. 2022, 8, 3236–3246. [Google Scholar] [CrossRef]
- Yang, Q.; Chi, Z.; Wang, L. Uncertainty analysis of suspension system caused by horizontal misalignment and its suppression method. Machines 2022, 10, 977. [Google Scholar] [CrossRef]
- Li, Y.; Yu, P.; Zhou, D.; Li, J. Magnetic flux feedback strategy to suppress the gap fluctuation of low speed maglev train caused by track steps. In Proceedings of the 37th Chinese Control Conference (CCC 2018), Wuhan, China, 25–27 July 2018; pp. 983–989. [Google Scholar] [CrossRef]
- Nguyen, D.; Nguyen, T. Evaluate the stability of the vehicle when using the active suspension system with a hydraulic actuator controlled by the OSMC algorithm. Sci. Rep. 2022, 12, 19364. [Google Scholar] [CrossRef]
- Li, H.; Ke, Z.; Huang, H.; Li, Y.; Wang, S.; Deng, Z. Vibration suppression of high-temperature superconducting maglev system via semi-active suspension system. Phys. C Supercond. 2022, 601, 1354109–1354117. [Google Scholar] [CrossRef]
- Yu, P.; Li, J.; Wang, L. Research on the influence of track periodic short-wave irregularity on low-speed maglev train. In Proceedings of the 35th Chinese Control Conference (CCC 2016), Chengdu, China, 27–29 July 2016; pp. 9305–9310. [Google Scholar] [CrossRef]
- Munro, N. Applications of the inverse nyquist array design method. In Proceedings of the IEEE Conference on Decision and Control Including the 15th Symposium on Adaptive Processes, Clearwater, FL, USA, 1–3 December 1976; pp. 348–353. [Google Scholar] [CrossRef]
- Descusse, J.; Moog, C.H. Dynamic decoupling for right-invertible nonlinear systems. Syst. Control. Lett. 1987, 8, 345–349. [Google Scholar] [CrossRef]
- Lokesh, N.; Mishra, M.K. Design of a decoupled sliding mode control for four-leg distribution static compensator. IEEE Trans. Power Deliv. 2022, 37, 5014–5024. [Google Scholar] [CrossRef]
- Ding, J.; Wu, M.; Xiao, M. Nonlinear decoupling control with piλdμ neural network for mimo systems. IEEE Trans. Neural Netw. Learn. Syst. 2022, 1–8. [Google Scholar] [CrossRef]
- Liu, D.; Li, J.; Zhang, K. Design of Nonlinear Decoupling Controller for Double-electromagnet Suspension System. Acta Anat. Sin. 2006, 32, 321–328. [Google Scholar]
- Leng, P.; Li, Y.; Zhou, D.; Li, J.; Zhou, S. Decoupling control of maglev train based on feedback linearization. IEEE Access 2019, 7, 130352–130362. [Google Scholar] [CrossRef]
- He, G.; Li, J.; Cui, P. Nonlinear control scheme for the levitation module of maglev train. J. Dyn. Syst. Meas. Control Trans. ASME 2016, 138, 1–8. [Google Scholar] [CrossRef]
- Sun, Y.; Yang, L.; Xu, J.; Wang, S. Decoupling levitation control of maglev train based on backstepping control. In Proceedings of the 2021 International Conference on Sensing, Measurement & Data Analytics in the Era of Artificial Intelligence (ICSMD 2021), Nanjing, China, 21–23 October 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Xu, J.; Chen, C.; Sun, Y. Nonlinear dynamic characteristic modeling and adaptive control of low speed maglev train. Int. J. Appl. Electromagn. Mech. 2020, 62, 73–92. [Google Scholar] [CrossRef]
- Chen, C.; Xu, J.; Lin, G.; Sun, Y.; Gao, D. Fuzzy adaptive control particle swarm optimization based on t-s fuzzy model of maglev vehicle suspension system. J. Mech. Sci. Technol. 2020, 34, 43–54. [Google Scholar] [CrossRef]
- Sun, Y.; Xu, J.; Xu, H.; Cai, W.; Lin, G. Backstepping Sliding Mode Control for Magnetic Suspension System of Maglev Train with Parameter Perturbations and External Disturbance. In Proceedings of the Advances in Applied Nonlinear Dynamics, Vibration and Control (ICANDVC 2021), Hong Kong, China, 23–25 August 2021; pp. 253–267. [Google Scholar] [CrossRef]
- Ni, F.; Mu, S.; Kang, J.; Xu, J. Robust controller design for maglev suspension systems based on improved suspension force model. IEEE Trans. Transp. Electrif. 2021, 7, 1765–1779. [Google Scholar] [CrossRef]
- Leng, P.; Yu, P.; Gao, M.; Li, J.; Li, Y. Optimal Control Scheme of Maglev Train Based on The Disturbance Observer. In Proceedings of the Chinese Control Conference (CCC 2019), Guangzhou, China, 27–30 July 2019; pp. 1935–1940. [Google Scholar] [CrossRef]
- Verma, A.; Patel, V.; Guha, D. Disturbance Observer-based Resilient Controller for Nonlinear Maglev System. In Proceedings of the IEEE 9th Uttar Pradesh Section International Conference on Electrical, Electronics and Computer Engineering (UPCON 2022), Prayagraj, India, 2–4 December 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Sun, Y.; Xie, S.; Xu, J.; Lin, G. A Robust Levitation Control of Maglev Vehicles Subject to Time Delay and Disturbances: Design and Hardware Experimentation. Appl. Sci. 2020, 10, 1179. [Google Scholar] [CrossRef]
- Sun, Y.; Xu, J.; Wu, H.; Lin, G.; Mumtaz, S. Deep learning based semi-supervised control for vertical security of maglev vehicle with guaranteed bounded airgap. IEEE trans. Intell. Transp. Syst. 2021, 22, 4431–4442. [Google Scholar] [CrossRef]
- Chen, C.; Xu, J.; Ji, W.; Rong, L.; Lin, G. Sliding Mode Robust Adaptive Control of Maglev Vehicle’s Nonlinear Suspension System Based on Flexible Track: Design and Experiment. IEEE Access 2019, 7, 41874–41884. [Google Scholar] [CrossRef]
- Sun, Y.; Xu, J.; Lin, G. Adaptive neural network control for maglev vehicle systems with time-varying mass and external disturbance. Neural. Comput. Appl. 2023, 35, 12361–12372. [Google Scholar] [CrossRef]
- Wang, Z.; Long, Z.; Li, X. Track Irregularity Disturbance Rejection for Maglev Train Based on Online Optimization of PnP Control Architecture. IEEE Access 2019, 7, 12610–12619. [Google Scholar] [CrossRef]
- Sahoo, A.K.; Mishra, S.K.; Acharya, D.S.; Sahu, S.S.; Paul, S.; Gupta, V.K. Identification and control of Maglev system using fractional and integer order PID controller. J. Intell. Fuzzy Syst. 2023, 44, 7277–7289. [Google Scholar] [CrossRef]
- Teklu, E.A.; Abdissa, C.M. Genetic Algorithm Tuned Super Twisting Sliding Mode Controller for Suspension of Maglev Train with Flexible Track. IEEE Access 2023, 11, 30955–30969. [Google Scholar] [CrossRef]





| Symbol | Description | Value | Unit |
|---|---|---|---|
| m | Mass of a suspension module | 900 | |
| Forces from air springs | 12,000 | ||
| A | The effective area of each magnet pole | 0.0186 | |
| l | Length of an electromagnet | 0.65 | |
| Permeability of vacuum | 4 | ||
| R | Coil resistance of a set of electromagnets | 1 | |
| g | Acceleration of gravity | 9.8 | |
| Nominal air gap at the operation point | 8 | ||
| N | Number of coil turns of each electromagnet | 320 | – |
| Symbol | Description | Value | Unit |
|---|---|---|---|
| The proportional parameter of PID controller | 4500 | – | |
| The integral parameter of PID controller | 4 | – | |
| The differential parameter of PID controller | 950 | – | |
| The bandwidth of ESO | 5000 | – |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Q.; Leng, P.; Yu, P.; Zhou, D.; Li, J.; Qu, M. Decoupling Control for Module Suspension System of Maglev Train Based on Feedback Linearization and Extended State Observer. Actuators 2023, 12, 342. https://doi.org/10.3390/act12090342
Li Q, Leng P, Yu P, Zhou D, Li J, Qu M. Decoupling Control for Module Suspension System of Maglev Train Based on Feedback Linearization and Extended State Observer. Actuators. 2023; 12(9):342. https://doi.org/10.3390/act12090342
Chicago/Turabian StyleLi, Qicai, Peng Leng, Peichang Yu, Danfeng Zhou, Jie Li, and Minghe Qu. 2023. "Decoupling Control for Module Suspension System of Maglev Train Based on Feedback Linearization and Extended State Observer" Actuators 12, no. 9: 342. https://doi.org/10.3390/act12090342
APA StyleLi, Q., Leng, P., Yu, P., Zhou, D., Li, J., & Qu, M. (2023). Decoupling Control for Module Suspension System of Maglev Train Based on Feedback Linearization and Extended State Observer. Actuators, 12(9), 342. https://doi.org/10.3390/act12090342







