Quantitative Comparative Study on the Performance of a Valve-Controlled Actuator and Electro-Hydrostatic Actuator
Abstract
1. Introduction
- (1)
- A test platform and prototypes of a CVA and EHA were developed. Quantitative results of power losses under different test conditions are provided.
- (2)
- Parameter sensitivity analysis of different power losses was conducted, and suggestions for performance optimization of CVAs and EHAs are provided.
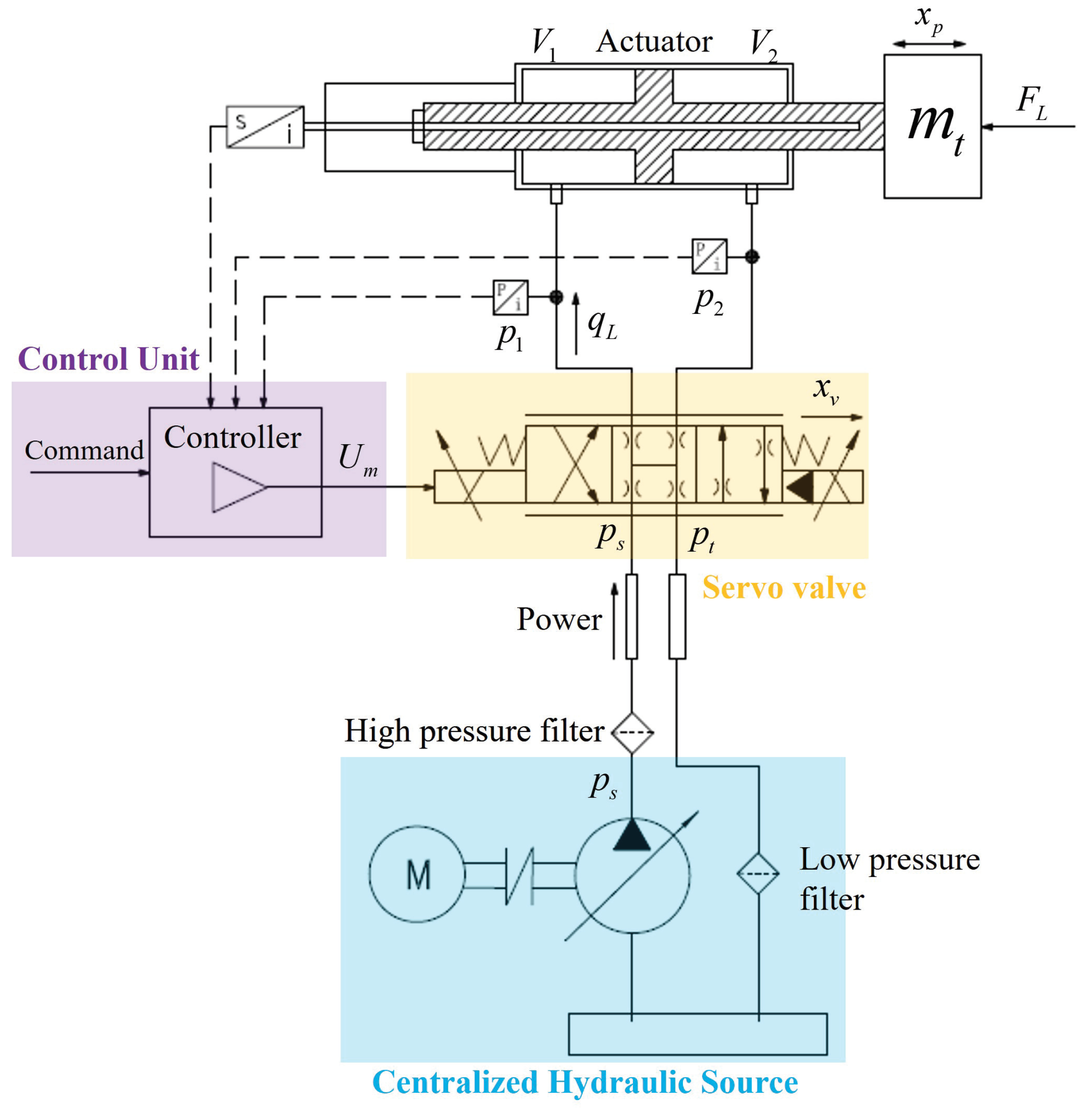
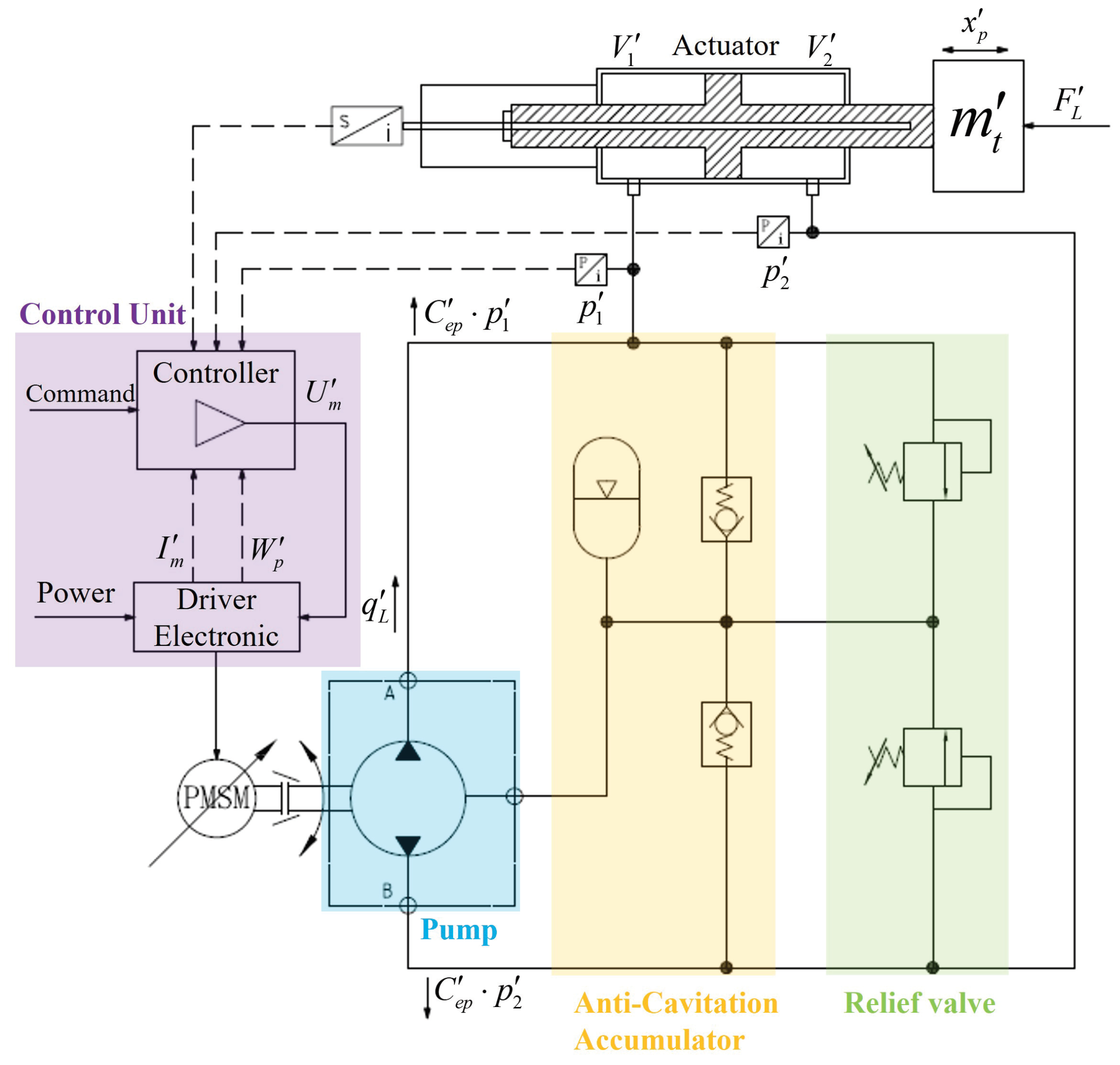
2. Modeling of CVAs and EHAs
2.1. Operating Principles
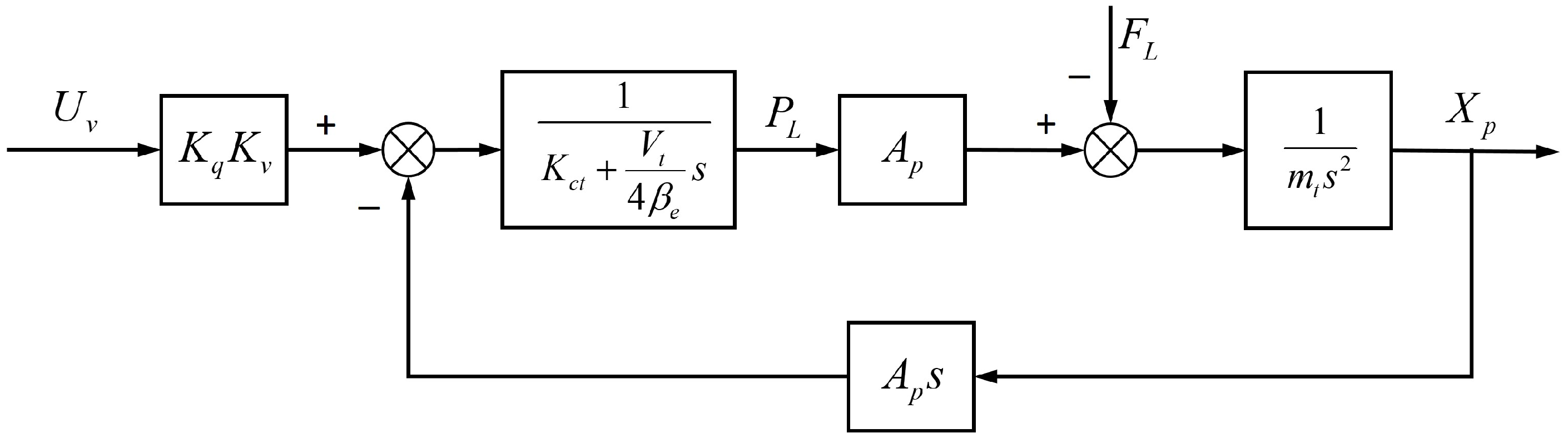
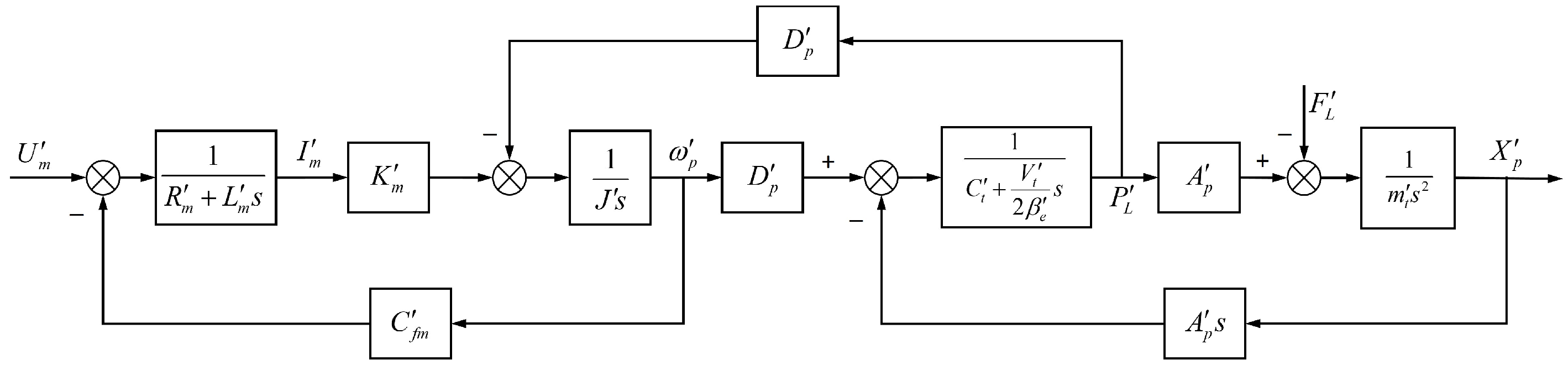
2.2. Modeling
- (1)
- Modeling of the CVA
- (2)
- Modeling of the EHA
3. Simulation Results and Analysis
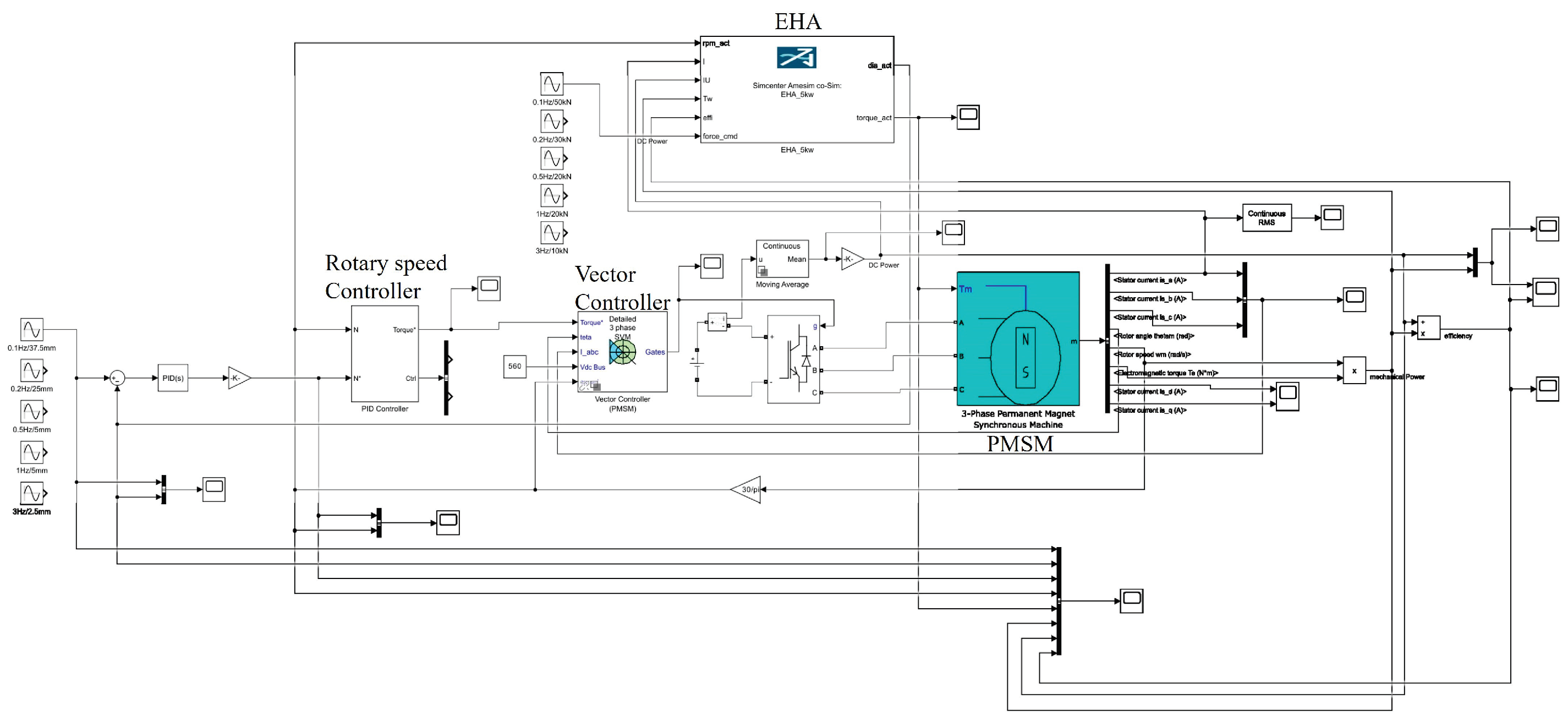
3.1. Simulation Model
3.2. Simulation Setup
- (1)
- Parameter settings
- (2)
- Simulation test design
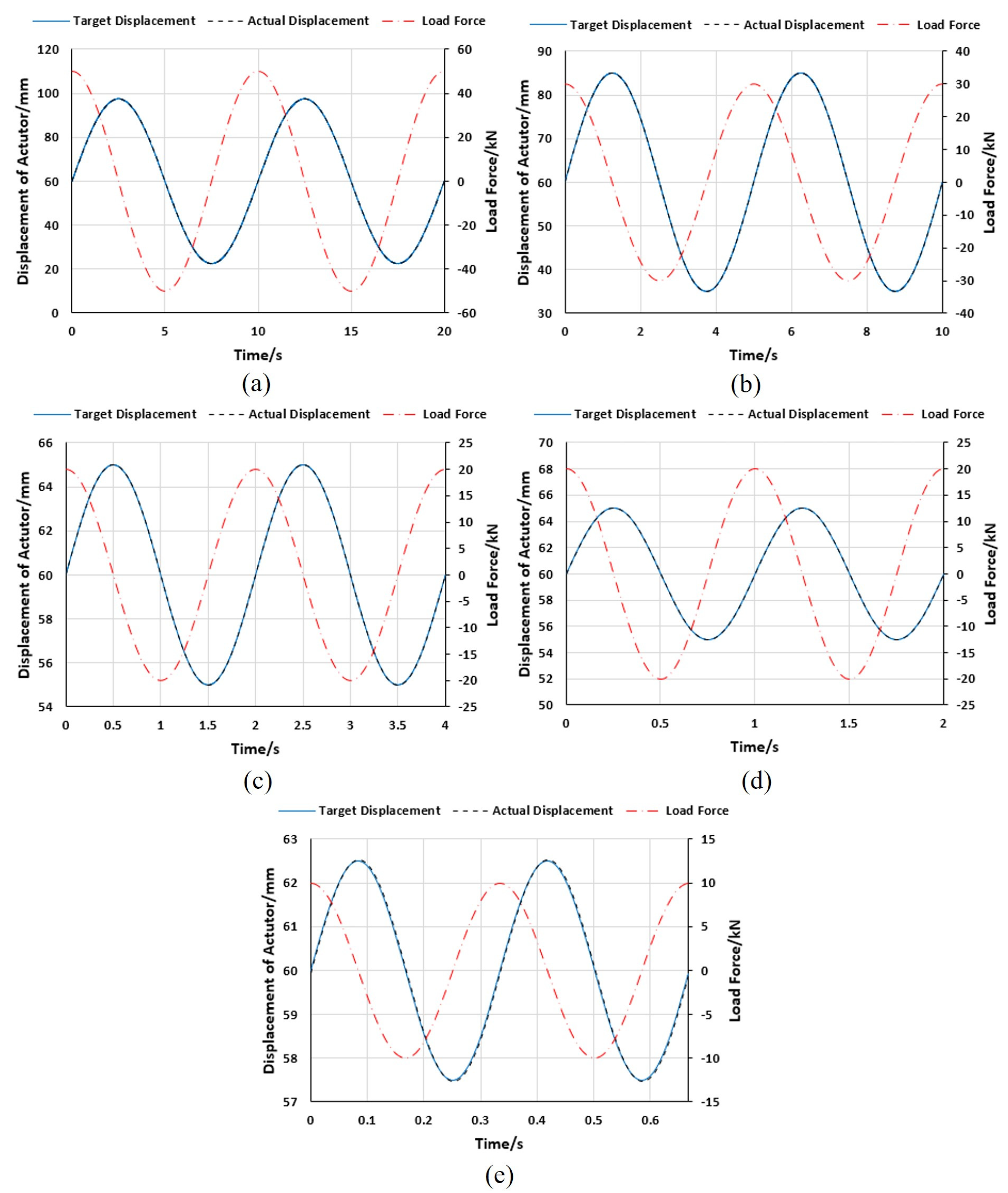
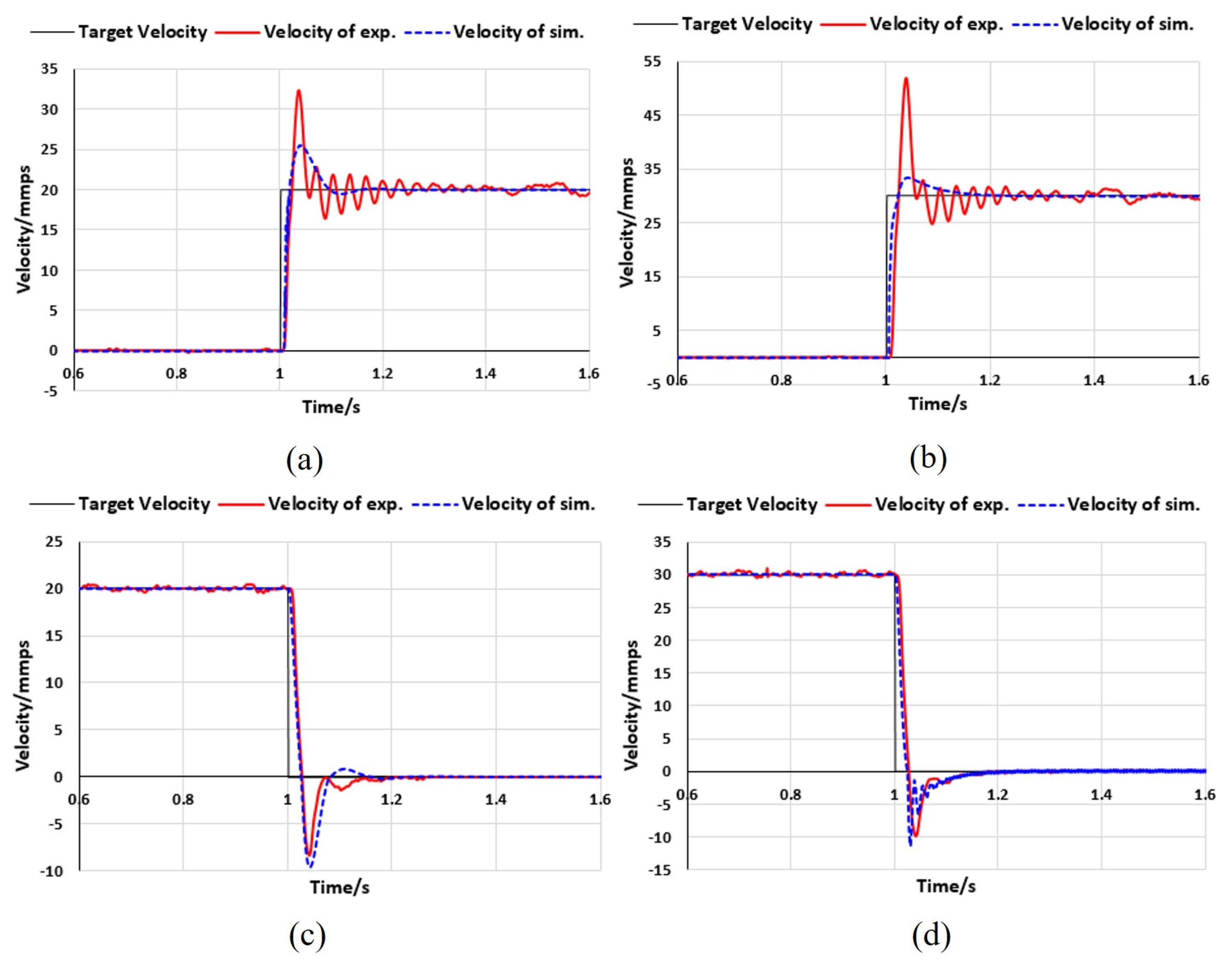
3.3. Simulation Results
- (1)
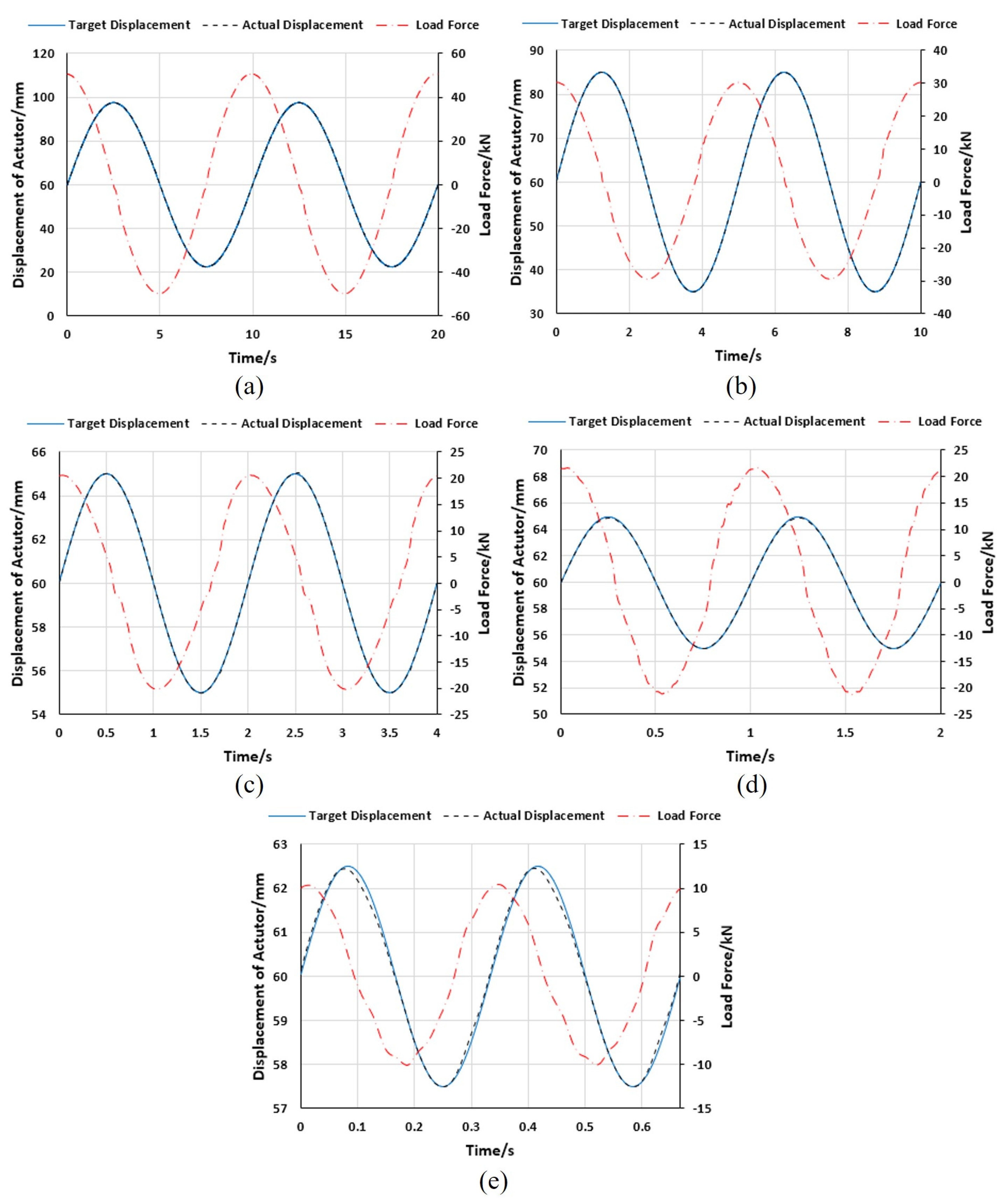
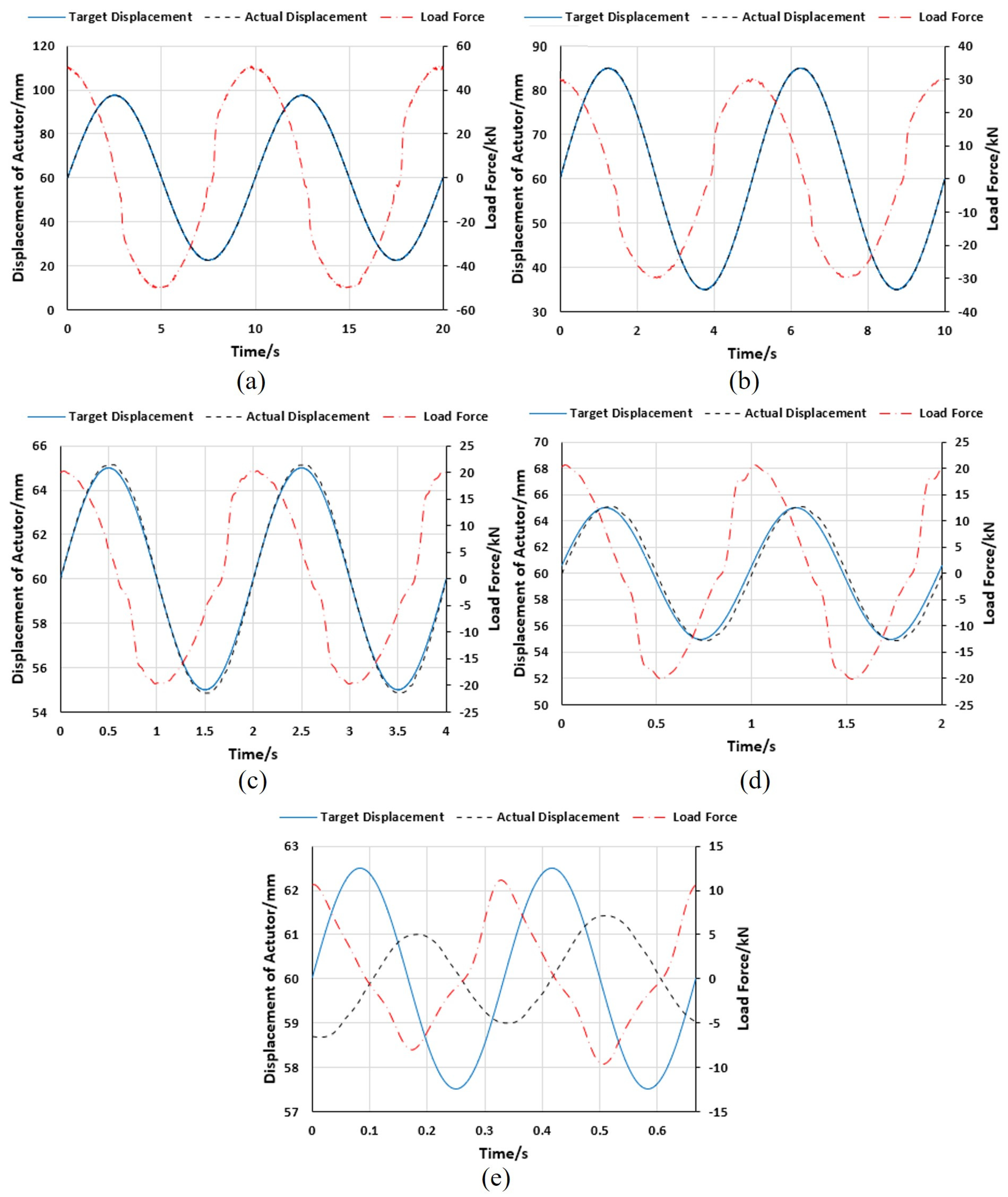
- Efficiency test results
| Conditions | Motor Power Losses (W) | Gear Pump Power Losses (W) | Leakage Power Losses in the Cylinder (W) | Output Power of EHA (W) | Overall Efficiency of EHA (%) |
|---|---|---|---|---|---|
| (a) | 233.6 | 117.7 | 27.6 | 592.3 | 61.0 |
| (b) | 271.1 | 124.9 | 16.7 | 473.8 | 53.4 |
| (c) | 115.9 | 47.8 | 7.6 | 158.4 | 48.0 |
| (d) | 180.9 | 75.8 | 8.8 | 328.3 | 55.3 |
| (e) | - | - | - | - | - |
- (2)
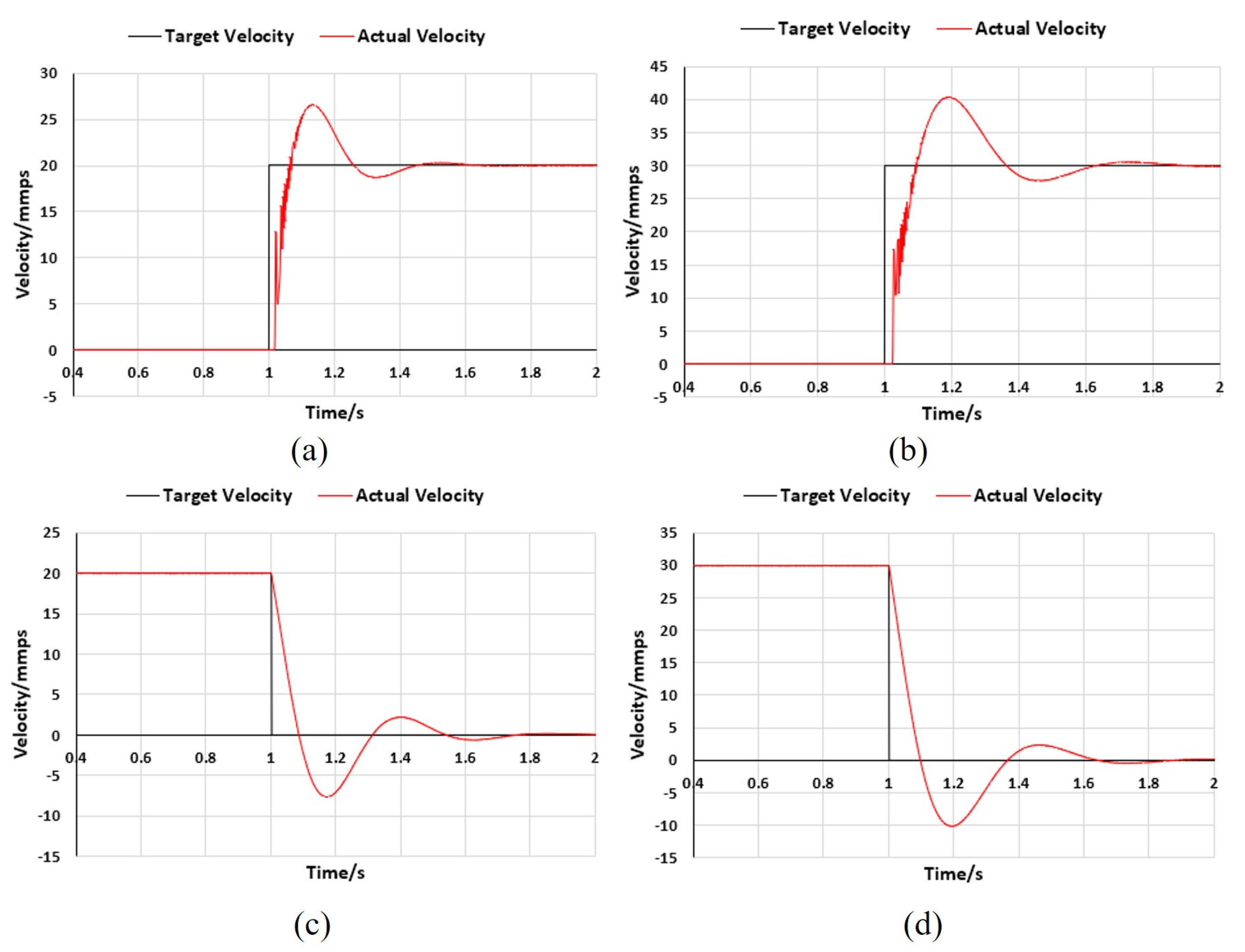
- Dynamic response test results
4. Experimental Results and Analysis
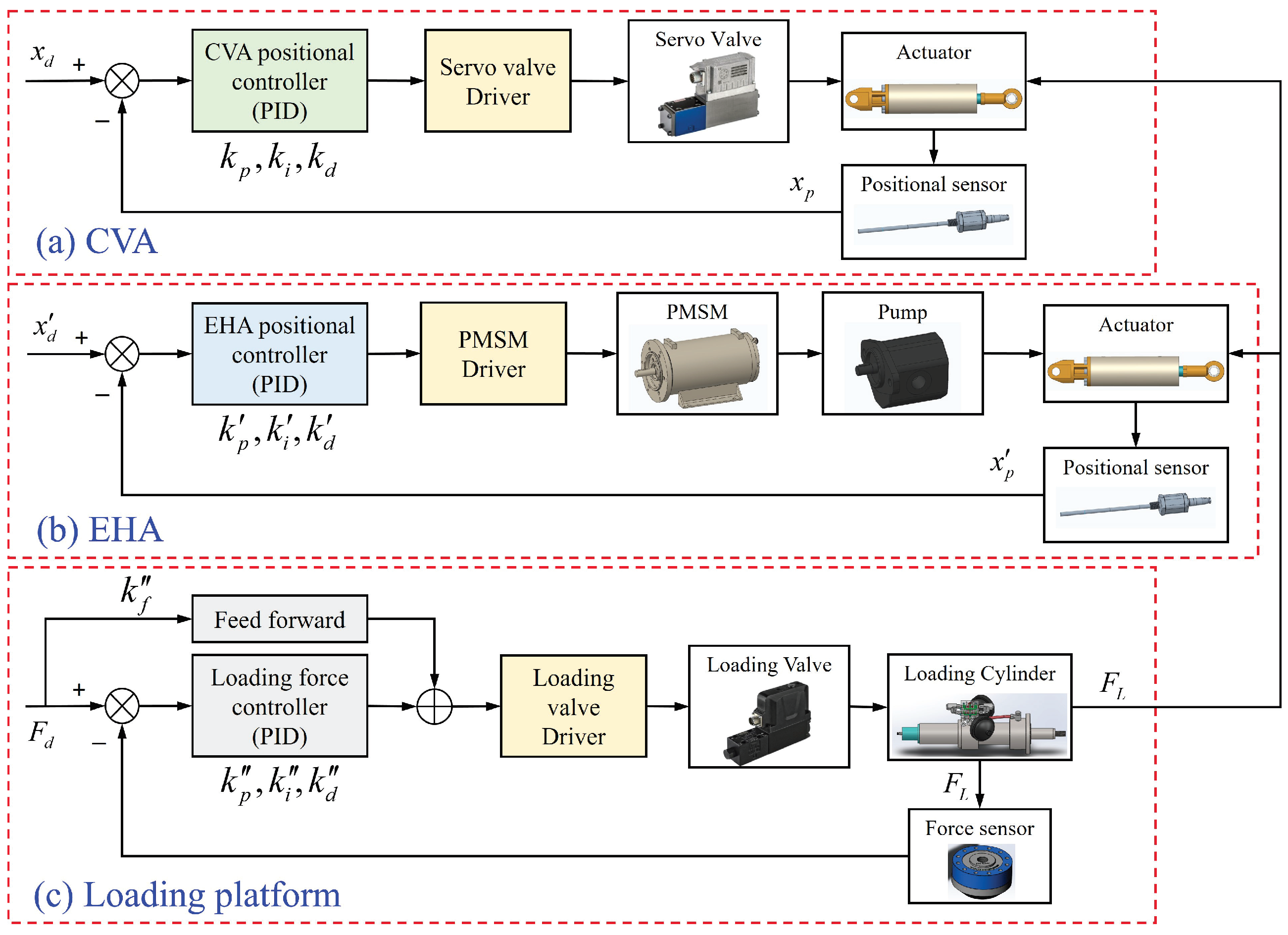
4.1. Experiment Setup
- (1)
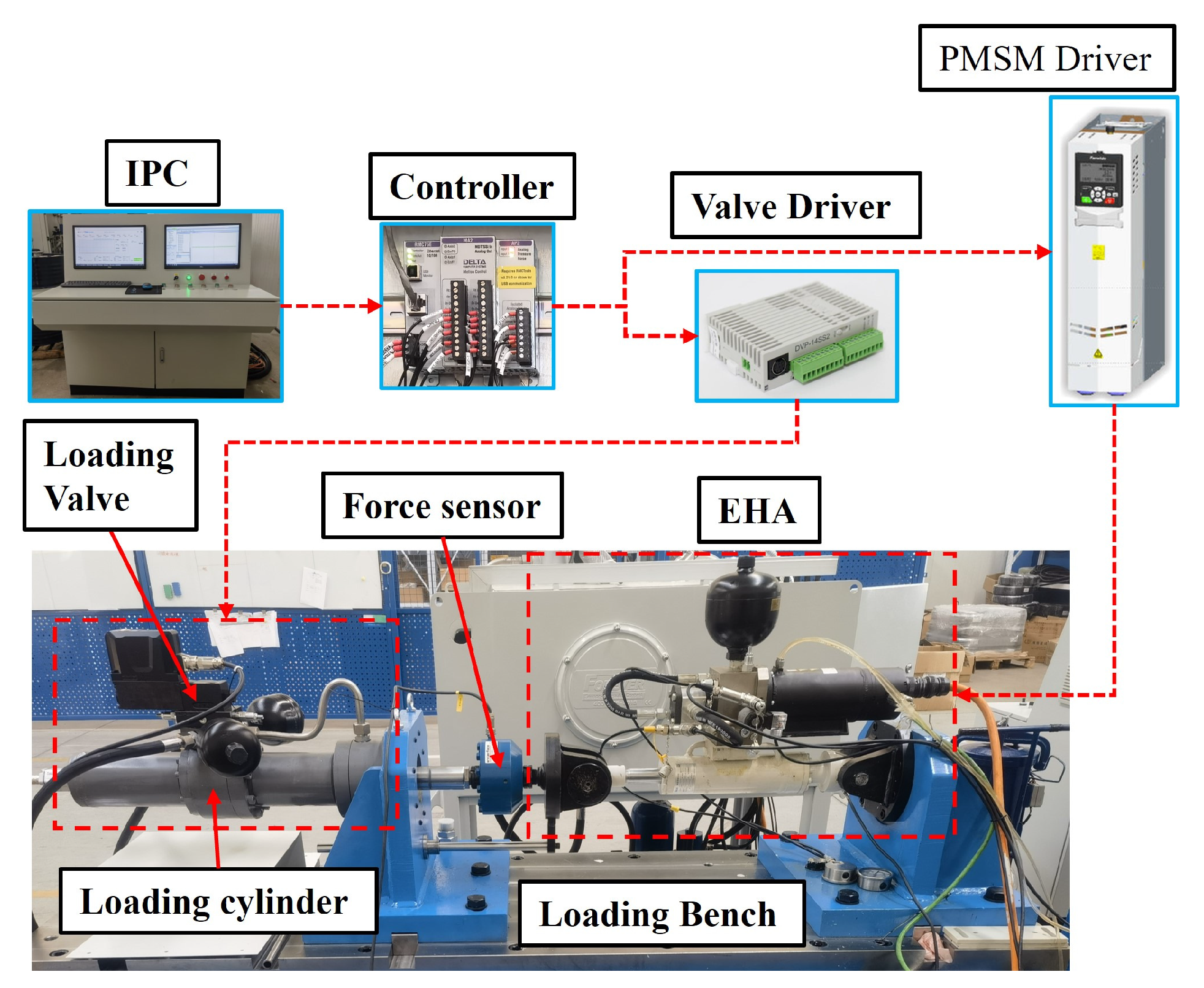
- Prototypes and test platform
- (2)
- Experiment design
| Components | Symbols | Values |
|---|---|---|
| Loading cylinder | Max Stroke (mm) | 300 |
| Max force (kN) | 150 | |
| Piston diameter (mm) | 100 | |
| Rod diameter (mm) | 63 | |
| Loading servo Valve | Nominal diameter (mm) | 6 |
| Nominal Flow (lpm) | 45 | |
| Response time (ms) | ≤10 | |
| Hysteresis (%) | ≤0.2 | |
| Force sensor | Max Force (kN) | 150 |
| Accuracy (%F.S.) | ±0.05 | |
| Position sensor | Stroke (mm) | 150 |
| Accuracy (mm) | 0.05 |
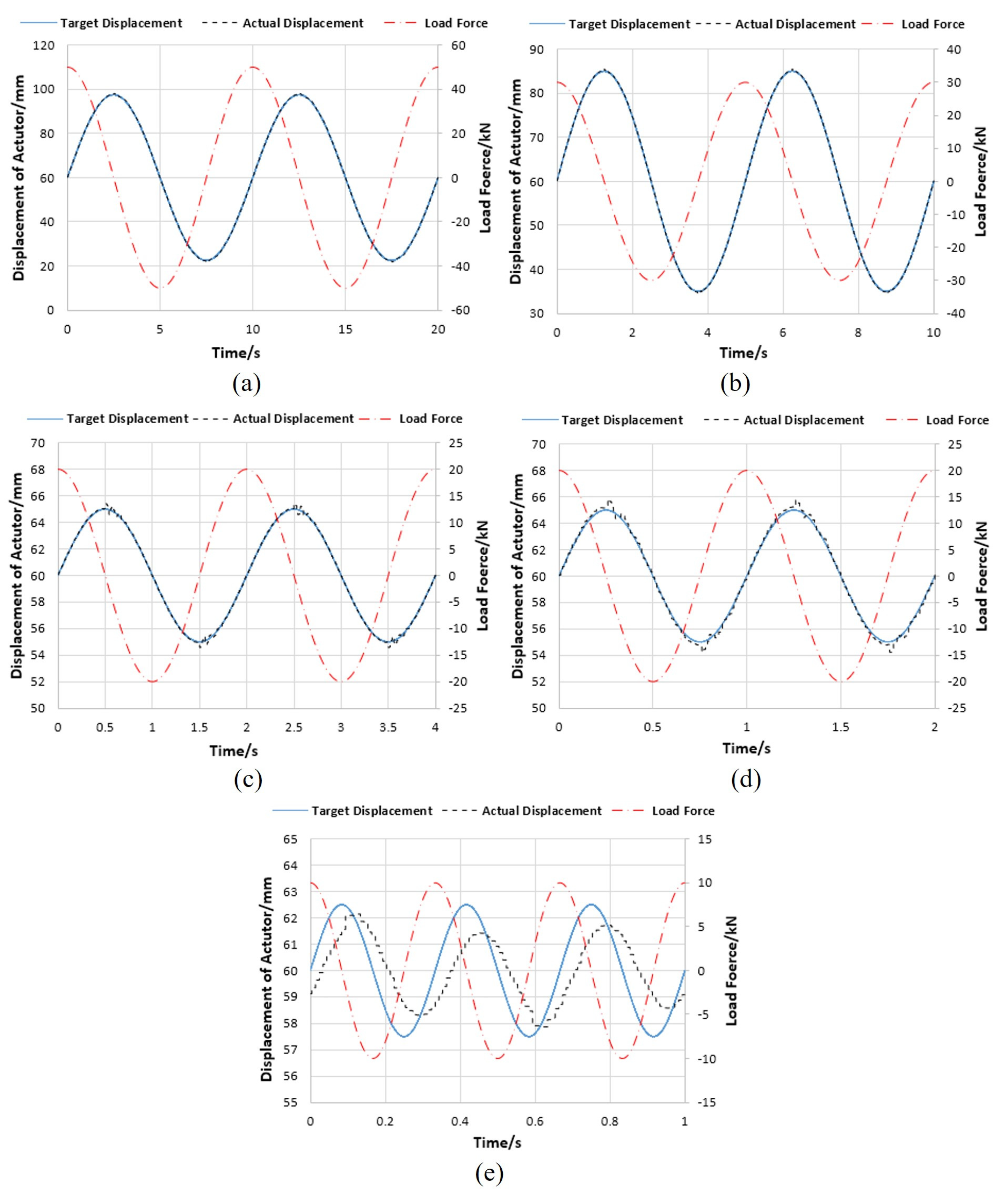
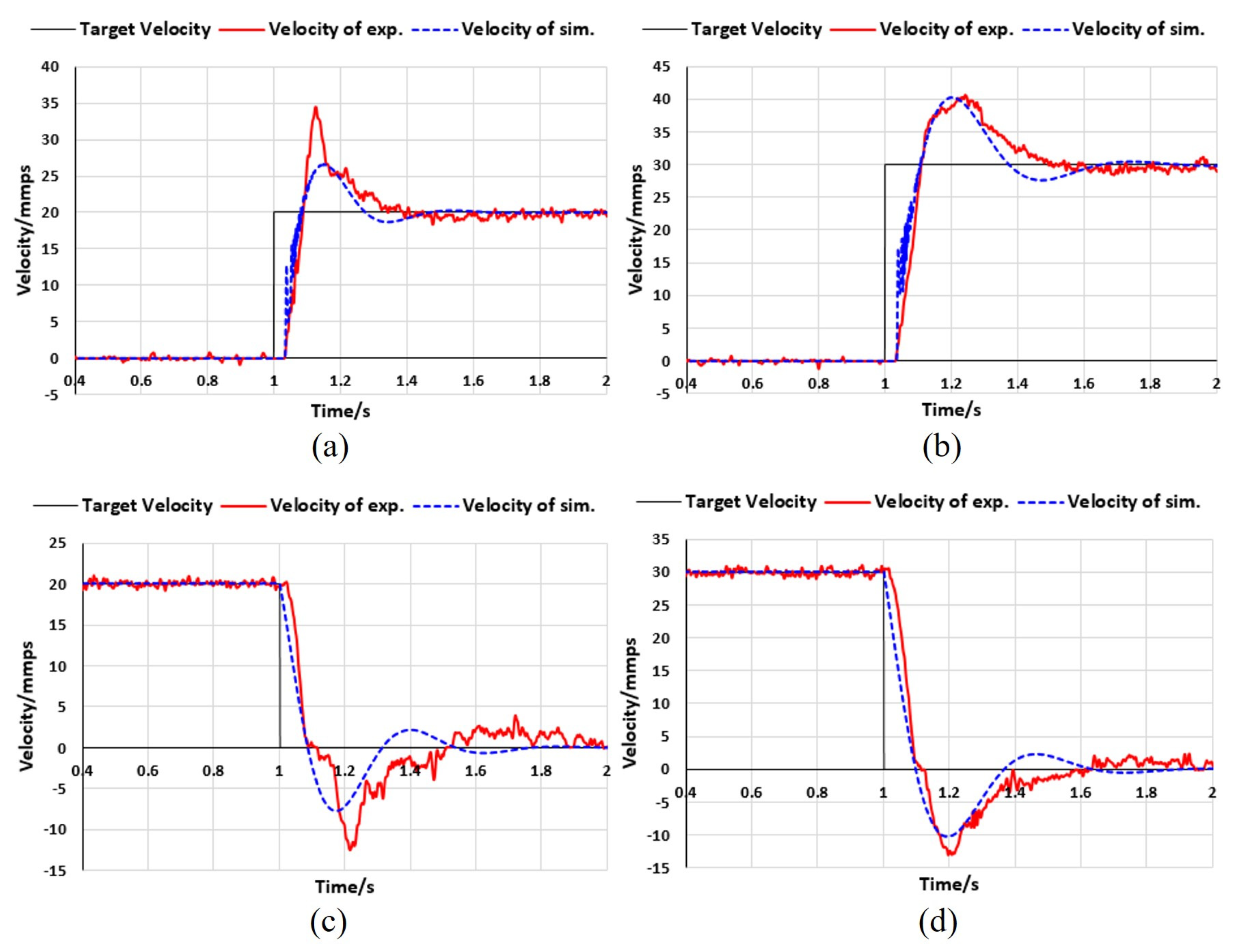
4.2. Experimental Results
- (1)
- Efficiency test results
- (2)
- Dynamic response test results
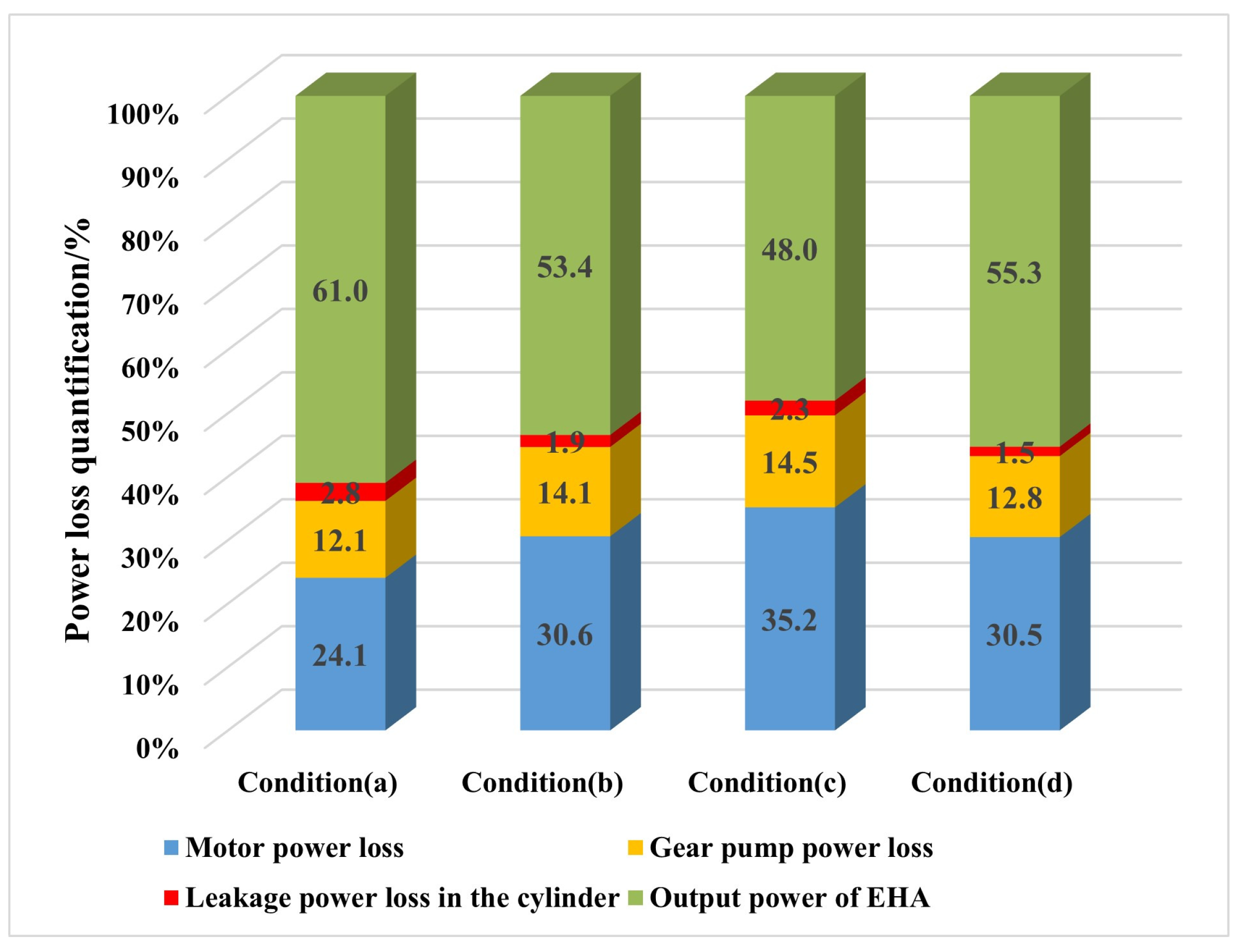
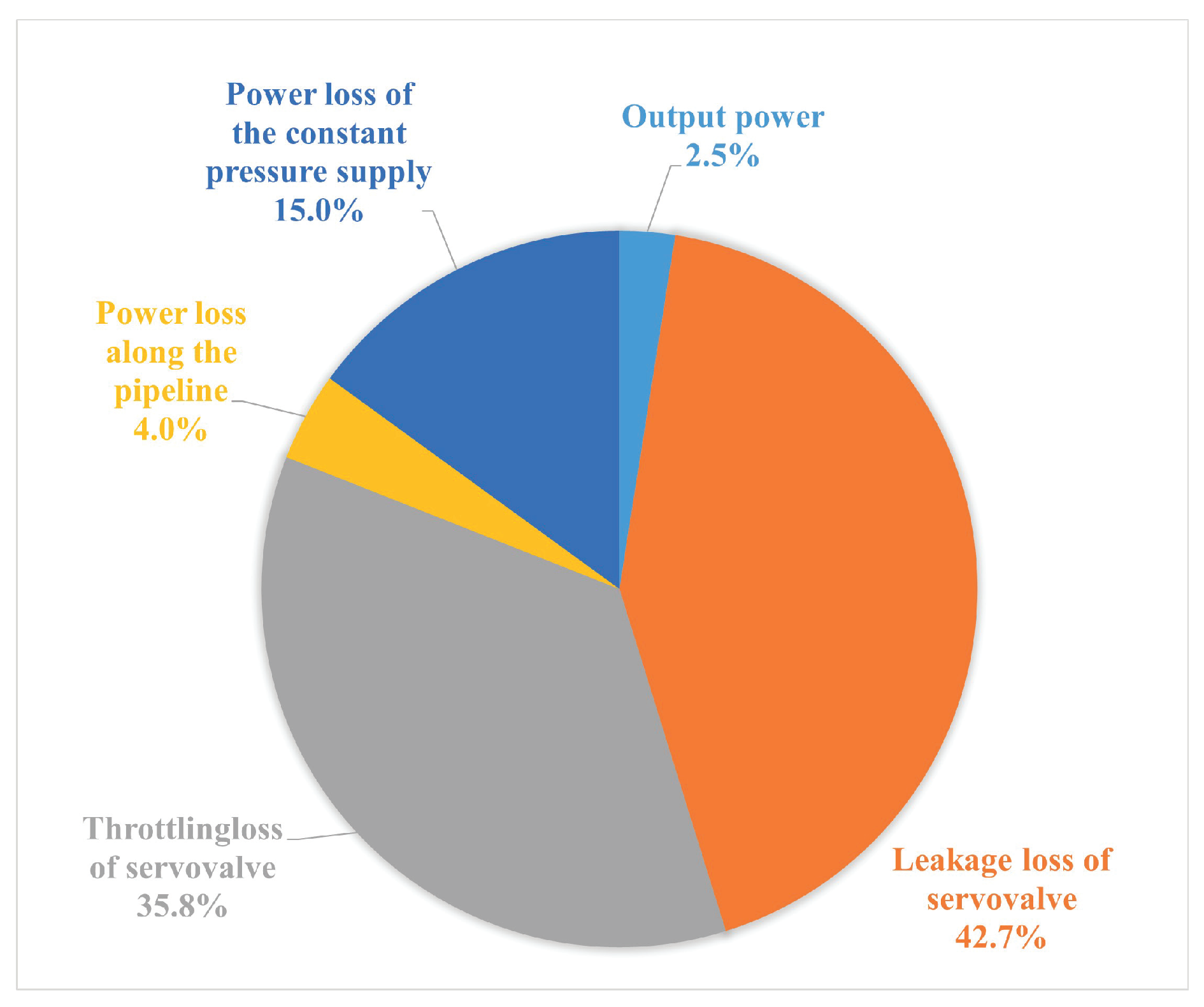
4.3. Discussions
- (1)
- Power loss quantification
- (2)
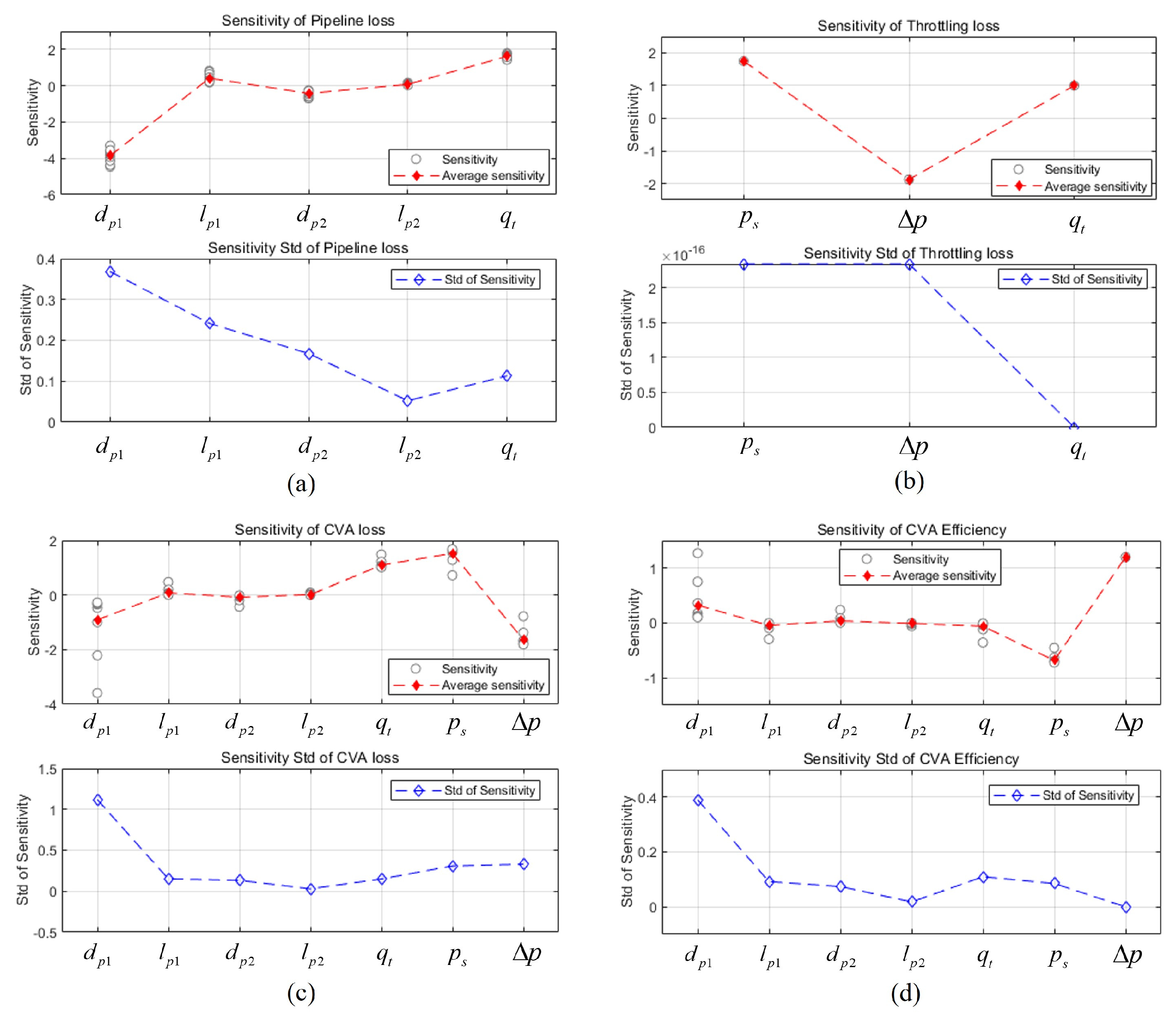
- Sensitivity analysis
- (3)
- Improvement methods
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| CVA | Centralized valve actuator |
| EDP | Engine-driven pump |
| EHA | Electro-hydrostatic actuator |
| FPVS | Fixed pump displacement variable motor speed |
| VPFS | Variable pump displacement fixed motor speed |
| VPVS | Variable pump displacement variable motor speed |
| PMSM | Permanent magnet synchronous motor |
Nomenclature
| Piston area of the hydraulic cylinder of CVA (m2) | |
| Piston area of the hydraulic cylinder of EHA (m2) | |
| B | Width of the gear of gear pump (m) |
| Piston leakage coefficient of CVA (m3/s/Pa) | |
| Internal leakage coefficient of the piston of CVA (m3/s/Pa) | |
| External leakage coefficient of the piston of CVA (m3/s/Pa) | |
| Overall flow coefficient of the hydraulic pump (m3/s/Pa) | |
| Internal leakage coefficient of the pump of EHA (m3/s/Pa) | |
| External leakage coefficient of the pump of EHA (m3/s/Pa) | |
| Total leakage coefficient of the cylinder of EHA (m3/s/Pa) | |
| Internal leakage coefficient of the cylinder of EHA (m3/s/Pa) | |
| External leakage coefficient of the cylinder of EHA (m3/s/Pa) | |
| Overall flow coefficient of EHA (m3/s/Pa) | |
| Counter electromotive force coefficient (-) | |
| Inner diameter of the adaptor on the high-pressure side (mm) | |
| Inner diameter of the adaptor on the low-pressure side (mm) | |
| Inner diameter of the pipeline on the high-pressure side (mm) | |
| Inner diameter of the pipeline on the low-pressure side (mm) | |
| Displacement of the gear pump (ml/rev) | |
| Energy loss per switch of each power switch (mJ) | |
| Operating frequency of the driver (Hz) | |
| External load force acting on the piston of CVA (N) | |
| External load force acting on the piston of EHA (N) | |
| Effective mass of the iron core lamination (kg) | |
| Current vectors in the d axis (A) | |
| Current of Permanent magnet Synchronous Motor (A) | |
| Nominal current of motor driver (A) | |
| Phase current of the motor (A) | |
| Current vectors in the q axis (A) | |
| Inertia moment of the motor and pump shaft (kg·m2) | |
| Empirical coefficient of iron loss (-) | |
| Flow-pressure coefficient of the servo valve (-) | |
| Total flow-pressure coefficient of CVA (-) | |
| Torque coefficient of the Permanent magnet Synchronous Motor (-) | |
| Flow gain of the servo valve (-) | |
| Electromagnet amplification factor of the servo valve (-) | |
| Quantity of elbows of the pipeline on the high-pressure side (-) | |
| Quantity of adaptors of the pipeline on the high-pressure side (-) | |
| Quantity of filters of the pipeline on the high-pressure side (-) | |
| Quantity of elbows of the pipeline on the low-pressure side (-) | |
| Quantity of adaptors of the pipeline on the low-pressure side (-) | |
| Quantity of filters of the pipeline on the low-pressure side (-) | |
| Length of the pipeline on the high-pressure side (m) | |
| Length of the pipeline on the low-pressure side (m) | |
| Equivalent inductances in the d axis (H) | |
| Equivalent inductances in the q axis (H) | |
| Inductance matrix in the phase coordinate system (H) | |
| Equivalent mass of the piston and the load of CVA (kg) | |
| Equivalent mass of the piston and the load of EHA (kg) | |
| Phase number of the motor winding (-) | |
| Number of power switches of motor driver (-) | |
| Pressure of the P port of servo valve (Pa) | |
| Pressure of the T port of servo valve (Pa) | |
| Pressure of the pressure compensated pump source (Pa) | |
| Pressure of the pressurized reservoir (Pa) | |
| Pressure of the cylinder inlet of CVA (Pa) | |
| Pressure of the cylinder outlet of CVA (Pa) | |
| Load pressure of CVA (Pa) | |
| Load pressure of EHA (Pa) | |
| Pressure of the cylinder inlet of EHA (Pa) | |
| Pressure of the cylinder outlet of EHA (Pa) | |
| Iron loss corresponding to the unit weight of the iron core lamination (W) | |
| Load flow of the hydraulic of CVA (lpm) | |
| Flow of the cylinder inlet of CVA (lpm) | |
| Flow of the cylinder outlet of CVA (lpm) | |
| Load flow of the hydraulic of EHA (lpm) | |
| Flow of the cylinder inlet of EHA (lpm) | |
| Flow of the cylinder outlet of EHA (lpm) | |
| Reynolds number of the oil (-) | |
| R | Radius of the pitch circle (m) |
| Radius of the addendum circle (m) | |
| Radius of the dedendum circle (m) | |
| Radius of the gear shaft (m) | |
| AC resistance of the winding () | |
| Thickness of the addendum (m) | |
| Friction torque of the Permanent magnet Synchronous Motor (N·m) | |
| Output torque of the Permanent magnet Synchronous Motor (N·m) | |
| Terminal voltage in the phase coordinate system (V) | |
| Command voltage signal of the servo valve (V) | |
| Oil flow velocity in the hydraulic pipeline (m/s) | |
| Initial oil inlet chamber volume of the cylinder of CVA (m3) | |
| Initial oil return chamber volume of the cylinder of CVA (m3) | |
| Total volume of the cylinder of CVA (m3) | |
| Initial oil inlet chamber volume of the cylinder of EHA (m3) | |
| Initial oil return chamber volume of the cylinder of EHA (m3) | |
| Collector-emitter voltage drop when forward conduction of motor driver (V) | |
| Freewheeling diode voltage drop of motor driver (V) | |
| Nominal voltage drop of motor driver (V) | |
| Total volume of the hydraulic cylinder of EHA (m3) | |
| Displacement of the servo valve spool (mm) | |
| Displacement of cylinder of CVA (mm) | |
| Displacement of cylinder of EHA (mm) | |
| Z | Number of gear teeth (-) |
| Number of teeth in the transition zone (-) | |
| Bulk modulus of oil (Pa) | |
| Average leakage power loss in hydraulic cylinder (W) | |
| Leakage power loss in hydraulic cylinder (W) | |
| Winding copper loss of Permanent magnet Synchronous Motor (W) | |
| Stator iron loss of Permanent magnet Synchronous Motor (W) | |
| Viscous friction loss between the gear side/liquid (W) | |
| Viscous friction loss between the addendum surface/pump body (W) | |
| Average power loss of Permanent magnet Synchronous Motor (W) | |
| Power loss of CVA under load-holding condition (W) | |
| Power loss of EHA under load-holding condition (W) | |
| Switching power loss of motor driver (W) | |
| Turn-on power loss of motor driver (W) | |
| Total power loss of the hydraulic pipeline on the high-pressure side (W) | |
| Total power loss of the hydraulic pipeline on the low-pressure side (W) | |
| Average power loss of the hydraulic pipeline in CVA (W) | |
| Average power loss of gear pump (W) | |
| Power loss of motor driver (W) | |
| Throttling power loss of servo valve (W) | |
| Average throttling power loss of servo valve in CVA (W) | |
| Engine-driven pump (EDP) volumetric loss under load-holding condition (W) | |
| Gear pump volumetric loss of EHA under load-holding condition (W) | |
| Servo valve leakage loss of CVA under load-holding condition (W) | |
| Pressure loss along the hydraulic pipeline on the low-pressure side (Pa) | |
| Pressure loss of a single elbow on the low-pressure side (Pa) | |
| Pressure loss of a single adaptor on the low-pressure side (Pa) | |
| Pressure loss of filters on the low-pressure side (Pa) | |
| Pressure loss along the hydraulic pipeline (Pa) | |
| Pressure loss of a single elbow on the high-pressure side (Pa) | |
| Pressure loss of a single adaptor on the high-pressure side (Pa) | |
| Pressure loss of filters on the high-pressure side (Pa) | |
| Total pressure loss of the hydraulic pipeline on the high-pressure side (Pa) | |
| Total pressure loss of the hydraulic pipeline on the low-pressure side (Pa) | |
| Leakage flow rate of the gear end face gap (lpm) | |
| Leakage flow of gear radial gap (lpm) | |
| Leakage flow of servo valve at 10 MPa differential pressure (lpm) | |
| Axial gap between the gear and the end face (m) | |
| Radial gap between the addendum and the pump case (m) | |
| Average efficiency of CVA (%) | |
| Average efficiency of EHA (%) | |
| Mechanical efficiency of the gear pump (%) | |
| Average efficiency of Permanent magnet Synchronous Motor (%) | |
| Overall efficiency of the gear pump (%) | |
| Volumetric efficiency of the gear pump (%) | |
| Wrap angles of transition zone in the gear pump (rad) | |
| Wrap angles of high-pressure zone in the gear pump (rad) | |
| Resistance coefficient along the pipeline (-) | |
| Dynamic viscosities of the oil (N·s/m2) | |
| Kinematic viscosity of the oil (mm2/s) | |
| Pipe elbow resistance coefficient (-) | |
| Resistance coefficient when the diameter of the pipeline changes from large to small (-) | |
| Resistance coefficient when the diameter of the pipeline changes from large to small (-) | |
| Hydraulic damping of CVA (-) | |
| Hydraulic damping ratio of EHA (-) | |
| Density of the oil (kg/m3) | |
| Number of pole pairs of Permanent magnet Synchronous Motor (-) | |
| Magnetic flux of the permanent magnet (Wb) | |
| Hydraulic natural frequency of CVA (Hz) | |
| Hydraulic natural frequency of EHA (Hz) | |
| Rotary speed of gear pump (rpm) |
References
- Chakraborty, I.; Mavris, D.N.; Emeneth, M.; Schneegans, A. A methodology for vehicle and mission level comparison of More Electric Aircraft subsystem solutions: Application to the flight control actuation system. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2015, 229, 1088–1102. [Google Scholar] [CrossRef]
- Chao, Q.; Zhang, J.; Xu, B.; Huang, H.; Pan, M. A Review of High-Speed Electro-Hydrostatic Actuator Pumps in Aerospace Applications: Challenges and Solutions. J. Mech. Des. 2019, 141, 050801. [Google Scholar] [CrossRef]
- Naayagi, R.T. A review of more electric aircraft technology. In Proceedings of the International Conference on Energy Efficient Technologies for Sustainability, Nagercoil, India, 10–12 April 2013. [Google Scholar]
- Yao, J.; Wang, P.; Yin, Y.; Li, M.; Li, Y. Power management of multi-source network hydraulic system with multiple actuators. Energy Convers. Manag. 2020, 223, 113247. [Google Scholar] [CrossRef]
- Wheeler, P.; Bozhko, S. The More Electric Aircraft: Technology and challenge. IEEE Electrif. Mag. 2014, 2, 6–12. [Google Scholar] [CrossRef]
- Ho, T.H.; Le, T.D. Development and Evaluation of Energy-Saving Electro-Hydraulic Actuator. Actuators 2021, 10, 302. [Google Scholar] [CrossRef]
- Maré, J.-C. From Douglas DC3 to Airbus A380–seventy years of innovation in aerospace hydraulics. In Proceedings of the 4th Internationales Fluidtechnisches Kolloquium, Dresden, Germany, 24–26 March 2004. [Google Scholar]
- Van Den Bossche, D. The A380 flight control electrohydrostatic actuators, achievements and lessons learnt. In Proceedings of the 25th International Congress of the Aeronautical Sciences, Hamburg, Germany, 3–8 September 2006. [Google Scholar]
- McCollom, N.N.; Brown, E.R. PHM on the F-35 fighter. In Proceedings of the IEEE Conference on Prognostics and Health Management, Denver, CO, USA, 20–23 June 2011. [Google Scholar]
- Shaw, J.C.; Fletcher, S.D.A.; Norman, P.J.; Galloway, S.J. More electric power system concepts for an environmentally responsible aircraft (N+2). In Proceedings of the 47th International Universities Power Engineering Conference, Uxbridge, UK, 4–7 September 2012. [Google Scholar]
- Tom, L.; Khowja, M.; Vakil, G.; Gerada, C. Commercial Aircraft Electrification-Current State and Future Scope. Energies 2021, 14, 8381. [Google Scholar] [CrossRef]
- Ma, Z.; Wang, S.; Shi, J.; Li, T.; Wang, X. Fault diagnosis of an intelligent hydraulic pump based on a nonlinear unknown input observer. Chin. J. Aeronaut. 2018, 31, 385–394. [Google Scholar] [CrossRef]
- Alle, N.; Hiremath, S.S.; Makaram, S.; Subramaniam, K.; Talukdar, A. Review on electro hydrostatic actuator for flight control. Int. J. Fluid Power 2016, 17, 125–145. [Google Scholar] [CrossRef]
- Wang, M.; Wang, Y.; Yang, R.; Fu, Y.; Zhu, D. A Sliding Mode Control Strategy for an ElectroHydrostatic Actuator with Damping Variable Sliding Surface. Actuators 2021, 10, 3. [Google Scholar] [CrossRef]
- Andersson, J.; Krus, P.; Nilsson, K. Optimization as a support for selection and design of aircraft actuation systems. In Proceedings of the 7th AIAA/USAF/NASA/ISSMO Symposium on Multidisciplinary Analysis and Optimization, St. Louis, MO, USA, 2–4 September 1998. [Google Scholar]
- Shang, Y.; Liu, X.; Jiao, Z.; Wu, S. An integrated load sensing valve-controlled actuator based on power-by-wire for aircraft structural test. Aerosp. Sci. Technol. 2018, 77, 117–128. [Google Scholar] [CrossRef]
- Agostini, T.; De Negri, V.; Minav, T.; Pietola, M. Effect of Energy Recovery on Efficiency in Electro-Hydrostatic Closed System for Differential Actuator. Actuators 2020, 9, 12. [Google Scholar] [CrossRef]
- Song, Y.; Ba, K.; Wang, Y.; Zhang, J.; Yu, B.; Zhang, Q.; Kong, X. Study on nonlinear dynamic behavior and stability of aviation pressure servo valve-controlled cylinder system. Nonlinear Dyn. 2022, 108, 3077–3103. [Google Scholar] [CrossRef]
- Quan, Z.; Quan, L.; Zhang, J. Review of energy efficient direct pump controlled cylinder electro-hydraulic technology. Renew. Sustain. Energy Rev. 2014, 35, 336–346. [Google Scholar] [CrossRef]
- Li, K.; Lv, Z.; Lu, K.; Yu, P. Thermal-hydraulic Modeling and Simulation of the Hydraulic System based on the Electro-hydrostatic Actuator. Procedia Eng. 2014, 80, 272–281. [Google Scholar] [CrossRef]
- Hu, W.; Zhou, L.; Tian, Y.; Jiao, Z.; Shang, Y.; Song, Z.; Yan, L. Analysis for the power loss of electro hydrostatic actuator and hydraulic actuator. In Proceedings of the IEEE International Conference on Advanced Intelligent Mechatronics, Busan, Republic of Korea, 7–11 July 2015. [Google Scholar]
- Navatha, A.; Bellad, K.; Hiremath, S.S.; Karunanidhi, S. Dynamic Analysis of Electro Hydrostatic Actuation System. Procedia Technol. 2016, 25, 1289–1296. [Google Scholar] [CrossRef]
- Maré, J.-C.; Budinger, M. Comparative analysis of energy losses in servo-hydraulic, electro-hydrostatic and electro-mechanical actuators. In Proceedings of the 11th Scandinavian International Conference on Fluid Power, Linköping, Sweden, 2–4 June 2009. [Google Scholar]
- Maré, J.-C. Towards more electric drives for embedded applications:(re) discovering the advantages of hydraulics. In Proceedings of the 7th International Fluid Power Conference, Aachen, Germany, 22–24 March 2010. [Google Scholar]
- Gaile, A.; Lue, Y. Electro Hydraulic Actuation (EHA) systems for primary flight control, landing gear and other type of actuation. In Proceedings of the IEEE International Conference on Aircraft Utility Systems, Beijing, China, 10–12 October 2016. [Google Scholar]
- Li, Z.; Shang, Y.; Jiao, Z.; Lin, Y.; Wu, S.; Li, X. Analysis of the dynamic performance of an electro-hydrostatic actuator and improvement methods. Chin. J. Aeronaut. 2018, 31, 2312–2320. [Google Scholar] [CrossRef]
- Waheed, U.R.; Wang, S.; Wang, X.; Fan, L.; Kamran, A.S. Motion synchronization in a dual redundant HA/EHA system by using a hybrid integrated intelligent control design. Chin. J. Aeronaut. 2016, 29, 789–798. [Google Scholar]
- Hu, X.; Mao, Z.; Jiao, Z.; Wu, S.; Yu, X.; Li, F. Analysis of the characteristics by modeling and simulation of actuator in flight control system. In Proceedings of the IEEE Chinese Guidance, Navigation and Control Conference, Yantai, China, 15 January 2015. [Google Scholar]
- Roboam, X.; Sareni, B.; De Andrade, A. More Electricity in the Air: Toward Optimized Electrical Networks Embedded in More-Electrical Aircraft. IEEE Ind. Electron. Mag. 2012, 6, 6–17. [Google Scholar] [CrossRef]
- Wang, Y.; Guo, S.; Dong, H. Modeling and control of a novel electro-hydrostatic actuator with adaptive pump displacement. Chin. J. Aeronaut. 2020, 33, 365–371. [Google Scholar] [CrossRef]
- Quan, L. Current State, Problems and the Innovative Solution of Electric-hydraulic Technology of Pump Controlled Cylinder. Chin. J. Mech. Eng. 2008, 44, 87–92. [Google Scholar] [CrossRef]
- Gao, Z.-X.; Deng, J.; Ge, X. Simulation of bubbly two-phase turbulent flow in circular pipe bend. J. Hydraul. Eng. 2009, 40, 696–702. [Google Scholar]
- Qu, S.; Zappaterra, F.; Vacca, A.; Busquets, E. An electrified boom actuation system with energy regeneration capability driven by a novel electro-hydraulic unit. Energy Conv. Manag. 2023, 293, 117443. [Google Scholar] [CrossRef]
- Thiagarajan, D.; Dhar, S.; Vacca, A. A Novel Fluid Structure Interaction-EHD Model and Optimization Procedure for an Asymmetrical Axially Balanced External Gear Machine. Tribol. Trans. 2015, 58, 274–287. [Google Scholar] [CrossRef]
- Torrent, M.; Gamez-Montero, P.J.; Codina, E. Model of the Floating Bearing Bushing Movement in an External Gear Pump and the Relation to Its Parameterization. Energies 2021, 14, 8553. [Google Scholar] [CrossRef]
- Dambrauskas, K.; Vanagas, J.; Zimnickas, T.; Kalvaitis, A.; Azubalis, M. A Method for Efficiency Determination of Permanent Magnet Synchronous Motor. Energies 2020, 13, 1004. [Google Scholar] [CrossRef]
- Iron Core One-Stop Solution. Available online: https://www.20wtg1500.com/ (accessed on 20 January 2024).
- Akoro, E.; Tevi, F.M.E.; Hamoud, F.; Maiga, A.S.; Doumbia, M.L. Comparative Study of Power Losses in Single and Parallel High-Power Photovoltaic Inverter Systems. In Proceedings of the 2020 1st International Conference on Innovative Research in Applied Science, Engineering and Technology, Meknes, Morocco, 16–19 April 2020. [Google Scholar]
- Zhou, F.; Sun, M.; Liu, H.; Ouyang, X.; Xu, L.; Yao, Y. An adaptive dead zone compensation control method for EHAs under low-speed conditions. Chin. J. Mech. Eng. 2022, in press. [CrossRef]
- Li, X.; Wang, S. Flow field and pressure loss analysis of junction and its structure optimization of aircraft hydraulic pipe system. Chin. J. Aeronaut. 2013, 26, 1080–1092. [Google Scholar] [CrossRef]
- Cooper, M.A. Simulating Actuator Energy Demands of an Aircraft in Flight. Ph.D. Thesis, Cranfield University, Bedford, UK, 2014. [Google Scholar]
- Dai, W.L.; Yan, Y.G. Development trend and current situation of starter-generator for aircraft engine. Aeronaut. Sci. Technol. 2010, 5, 28–32. [Google Scholar]
- Huang, B.; Wang, S.; Shi, J. Energy-saving optimization for intelligent pumps based on performance reliability restriction. J. Beijing Univ. Aeronaut. Astronaut. 2013, 39, 559–563. [Google Scholar]
- Zhang, K.; Zhang, J.; Gan, M.; Zong, H.; Wang, X.; Huang, H.; Su, Q.; Xu, B. Modeling and Parameter Sensitivity Analysis of Valve-Controlled Helical Hydraulic Rotary Actuator System. Chin. J. Mech. Eng. 2022, 35, 66. [Google Scholar] [CrossRef]
- Hall, J.W.; Boyce, S.A.; Wang, Y.; Dawson, R.J.; Tarantola, S.; Saltelli, A. Sensitivity Analysis for Hydraulic Models. J. Hydraul. Eng. 2009, 135, 1080–1092. [Google Scholar] [CrossRef]
- Goshtasbi, A.; Chen, J.; Waldecker, J.R.; Hirano, S.; Ersal1, T. Effective Parameterization of PEM Fuel Cell Models—Part I: Sensitivity Analysis and Parameter Identifiability. J. Electrochem. Soc. 2020, 167, 044504. [Google Scholar] [CrossRef]
- Goshtasbi, A.; Chen, J.; Waldecker, J.R.; Hirano, S.; Ersal1, T. Effective Parameterization of PEM Fuel Cell Models—Part II: Robust Parameter Subset Selection, Robust Optimal Experimental Design, and Multi-Step Parameter Identification Algorithm. J. Electrochem. Soc. 2020, 167, 044505. [Google Scholar] [CrossRef]
- Saltelli, A.; Ratto, M.; Andres, T.; Campolongo, F.; Cariboni, J.; Gatelli, D.; Saisana, M.; Tarantola, S. Global Sensitivity Analysis: The Primer; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 1998. [Google Scholar]
- Huang, H.; Mao, Y.; Sun, Y.; Pei, X. Test and Analysis of YH-15 Aviation Hydraulic Oil Viscosity-temperature Characteristics. Ordnance Ind. Autom. 2015, 34, 42–43. [Google Scholar]












| Components | Parameters | Values |
|---|---|---|
| Pipeline | (mm) | 10 |
| (m) | 10 | |
| (-) | 0.14 | |
| (mm) | 6 | |
| (-) | 0.42 | |
| (-) | 3.16 | |
| (-) | 6 | |
| (-) | 4 | |
| (-) | 1 | |
| (mm) | 16 | |
| (mm) | 9.6 | |
| (m) | 10 | |
| Servo valve | (lpm/mm) | 8 |
| (mm/V) | 0.5 | |
| (lpm) @ 100 bar | 0.5 | |
| Nominal flow @ 70 bar differential pressure (lpm) | 24 | |
| StepTime (ms) | ≤ 10 | |
| Hysteresis (%) | ≤ 0.2 | |
| Cylinder | (m2) | 0.00377 |
| (m3) | 0.000528 | |
| (m3/s/Pa) | 4 × 10−14 | |
| (m3/s/Pa) | 0 | |
| (kN) | 100 | |
| (mm) | ±60 | |
| (lpm) | 12 | |
| (kW) | 5 | |
| Other components | (Pa) | 1.6 × 109 |
| (mm2/s) @ 40 ∘C | 13.928 | |
| (kg/m3) | 840 | |
| (kg) | 7.2 |
| Components | Parameters | Values |
|---|---|---|
| Motor | (-) | 3 |
| () | 0.53 | |
| (kg) | 2.24 | |
| (-) | 0.519 | |
| (W/kg) | 1.059 | |
| (-) | 4 | |
| (kg·m2) | 0.00033 | |
| (H) | 2.9 | |
| (H) | 2.9 | |
| (Wb) | 0.01235 | |
| (Nm/A) | 0.868 | |
| (N·m) | 0 | |
| (V) | 323.3 | |
| (-) | 6 | |
| (kHz) | 10 | |
| (V) | 1.8 | |
| (V) | 1.3 | |
| (V/rad·s) | 31.1 | |
| Pump | (mL/r) | 2.1 |
| Z (-) | 11 | |
| m (mm) | 2 | |
| (rad) | /11 | |
| (rad) | /11 | |
| (m) | 8.5 × 10−3 | |
| (m) | 13 × 10−3 | |
| (m) | 7 × 10−3 | |
| B (m) | 7 × 10−3 | |
| (m) | 0.64 × 10−3 | |
| 2 | ||
| Cylinder | (m2) | 0.00377 |
| (m3) | 0.000671 | |
| (m3/s/Pa) | 4 × 10−14 | |
| (m3/s/Pa) | 0 | |
| (kN) | 100 | |
| Stroke (mm) | ±60 | |
| MaxFlow (lpm) | 12 | |
| Power (kW) | 5 | |
| Other components | (Pa) | 1.6 × 109 |
| (N·s/m2) | 0.012 | |
| (kg/m3) | 840 | |
| (kg) | 9.7 |
| Conditions | Displacement of Cylinder (mm) | Load Force (kN) |
|---|---|---|
| (a) | sin | sin |
| (b) | sin (m) | sin |
| (c) | sin | sin |
| (d) | sin | sin |
| (e) | sin | sin |
| Conditions | Initial Velocities (mm/s) | Terminal Velocities (mm/s) | Loading Forces (kN) |
|---|---|---|---|
| (a) | 0 | 20 | 50 |
| (b) | 0 | 30 | 100 |
| (c) | 20 | 0 | 50 |
| (d) | 30 | 0 | 100 |
| Parameters | Values | |||||
|---|---|---|---|---|---|---|
| (a) | (b) | (c) | (d) | (e) | ||
| CVA | 0.125 | 0.125 | 0.125 | 0.125 | 0.1875 | |
| 1.875 | 1.875 | 1.875 | 1.875 | 1.875 | ||
| 0 | 0 | 0 | 0 | 0 | ||
| EHA | 0.005 | 0.01 | 0.0117 | 0.0167 | 0.025 | |
| 0.27 | 1 | 3 | 3.3 | 4.2 | ||
| 0 | 0 | 0 | 0 | 0 | ||
| Loading platform | 10 | 10 | 12 | 12 | 15 | |
| 3.5 | 4.2 | 4.4 | 4.4 | 5.2 | ||
| 0.1 | 0.12 | 0.15 | 0.15 | 0.2 | ||
| 0.063 | 0.082 | 0.09 | 0.09 | 0.11 | ||
| Conditions | Power Losses along the Pipeline (W) | Throttling Power Losses of the Servo Valve (W) | Leakage Power Losses in the Cylinder (W) | Output Power of CVA (W) | Overall Efficiency of CVA (%) |
|---|---|---|---|---|---|
| (a) | 61.3 | 987.9 | 25.0 | 589.1 | 35.4 |
| (b) | 110.7 | 1598.0 | 12.1 | 471.4 | 21.5 |
| (c) | 108.8 | 873.9 | 6.0 | 157.3 | 13.7 |
| (d) | 208.9 | 1724.6 | 8.7 | 315.7 | 14.0 |
| (e) | 532.2 | 2703.3 | 5.8 | 238.8 | 6.9 |
| Conditions | Initial Velocities (mm/s) | Terminal Velocities (mm/s) | Loading Forces (kN) | Response Time (ms) |
|---|---|---|---|---|
| (a) | 0 | 20 | 50 | 21 |
| (b) | 0 | 30 | 100 | 24 |
| (c) | 20 | 0 | 50 | 23 |
| (d) | 30 | 0 | 100 | 25 |
| Conditions | Initial Velocities (mm/s) | Terminal Velocities (mm/s) | Loading Forces (kN) | Response Time (ms) |
|---|---|---|---|---|
| (a) | 0 | 20 | 50 | 75 |
| (b) | 0 | 30 | 100 | 98 |
| (c) | 20 | 0 | 50 | 85 |
| (d) | 30 | 0 | 100 | 99 |
| Components | Parameters | Values |
|---|---|---|
| Cylinder | Max speed (mm/s) | 50 |
| Max force (kN) | 100 | |
| Piston diameter (mm) | 80 | |
| Rod diameter (mm) | 40 | |
| Max stroke (mm) | 120 | |
| Max flow (lpm) | 12 | |
| Start pressure (MPa) | ≤0.1 | |
| Power (kW) | 5 | |
| Servo valve | Nominal diameter (mm) | 6 |
| Nominal Flow (lpm) | 24 | |
| Max pressure (MPa) | 35 | |
| Response time (ms) | ≤10 | |
| Hysteresis (%) | ≤0.2 | |
| Position sensor | Stroke (mm) | 150 |
| Accuracy (mm) | 0.05 |
| Components | Parameters | Values |
|---|---|---|
| Cylinder | Max speed (mm/s) | 50 |
| Max force (kN) | 100 | |
| Piston diameter (mm) | 80 | |
| Rod diameter (mm) | 40 | |
| Max stroke (mm) | 120 | |
| Max flow (lpm) | 12 | |
| Start pressure (MPa) | ≤0.1 | |
| Power (kW) | 5 | |
| Pump | Nominal displacement (ml/r) | 2.1 |
| Nominal speed (rpm) | 6000 | |
| Max pressure (MPa) | 28 | |
| Power (kW) | 5 | |
| Rotation direction (-) | Reversible | |
| Motor | Nominal Torque (N·m) | 10 |
| Nominal Speed (rpm) | 6000 | |
| Power (kW) | 6 | |
| Rotation Direction (-) | Reversible | |
| Driver Power (kW) | 10 | |
| Encoder Type | Absolute value | |
| Encoder Resolution (bit) | 23 | |
| Position sensor | Stroke (mm) | 150 |
| Accuracy (mm) | 0.05 |
| Conditions | Average Input Power (W) | Average Output Power (W) | Efficiency (%) |
|---|---|---|---|
| (a) | 1584.0 | 597.4 | 37.7 |
| (b) | 2114.0 | 476.9 | 22.6 |
| (c) | 1062.1 | 156.2 | 14.7 |
| (d) | 2090.3 | 330.8 | 15.8 |
| (e) | 3126.8 | 220.9 | 7.1 |
| Conditions | Average Input Power (W) | Average Output Power (W) | Efficiency (%) |
|---|---|---|---|
| (a) | 1064.3 | 629.1 | 59.1 |
| (b) | 885.6 | 492.8 | 55.7 |
| (c) | 337.1 | 161.4 | 47.9 |
| (d) | 532.4 | 309.5 | 58.1 |
| (e) | - | - | - |
| Conditions | Efficiency of CVA (%) | Efficiency of EHA (%) | ||
|---|---|---|---|---|
| Sim. | Exp. | Sim. | Exp. | |
| (a) | 35.4 | 37.7 | 61.0 | 59.1 |
| (b) | 21.5 | 22.6 | 53.4 | 55.6 |
| (c) | 13.7 | 14.7 | 48.0 | 47.9 |
| (d) | 14.0 | 15.8 | 55.3 | 58.1 |
| (e) | 6.9 | 7.0 | - | - |
| Average of (a)–(d) | 21.2 | 22.7 | 54.4 | 55.2 |
| Conditions | Initial Velocities (mm/s) | Terminal Velocities (mm/s) | Loading Forces (kN) | Response Time (ms) |
|---|---|---|---|---|
| (a) | 0 | 20 | 50 | 23 |
| (b) | 0 | 30 | 100 | 24 |
| (c) | 20 | 0 | 50 | 27 |
| (d) | 30 | 0 | 100 | 29 |
| Conditions | Initial Velocities (mm/s) | Terminal Velocities (mm/s) | Loading Forces (kN) | Response Time (ms) |
|---|---|---|---|---|
| (a) | 0 | 20 | 50 | 82 |
| (b) | 0 | 30 | 100 | 102 |
| (c) | 20 | 0 | 50 | 87 |
| (d) | 30 | 0 | 100 | 110 |
| Conditions | Response Time of CVA (ms) | Response Time of EHA (ms) | ||
|---|---|---|---|---|
| Simulation | Experiment | Simulation | Experiment | |
| (a) | 21 | 23 | 75 | 82 |
| (b) | 24 | 24 | 98 | 102 |
| (c) | 23 | 27 | 85 | 87 |
| (d) | 25 | 29 | 99 | 110 |
| Average | 23.3 | 25.8 | 89.3 | 95.3 |
| Conditions | Efficiency of CVA (%) | Efficiency of EHA (%) |
|---|---|---|
| (a) | 32.1 | 53.2 |
| (b) | 19.2 | 50.1 |
| (c) | 12.5 | 43.1 |
| (d) | 13.5 | 52.3 |
| Average of (a)–(d) | 19.3 | 49.7 |
| No. | F1 | F2 | F3 | F4 | F5 |
|---|---|---|---|---|---|
| Flight profile | Takeoff run | Climb | Cruise | Circling | Mission |
| Time | 1.90% | 3.50% | 22.10% | 22.20% | 9.60% |
| Load | Medium | Medium | Medium | High | High |
| Speed | Low | Medium | Low | High | High |
| No. | F6 | F7 | F8 | ||
| Flight profile | Cruise | Landing | Landing run | ||
| Time | 22.50% | 7.10% | 11.10% | ||
| Load | Medium | Medium | Medium | ||
| Speed | Low | Medium | Low |
| Symbols | Value Ranges | |
|---|---|---|
| (mm) | [5, 15] | |
| (mm) | [5, 15] | |
| (mm) | [10, 20] | |
| CVA | (mm) | [5, 15] |
| (lpm) | [0, 12] | |
| (MPa) | [14, 28] | |
| (MPa) | [5, 20] | |
| (rpm) | [0, 6000] | |
| EHA | (MPa) | [5, 20] |
| (mL/rev) | [1, 3] |
| Oil Temperatures (∘C) | Oil Kinematic Viscosities (mm2/s) | Oil Dynamic Viscosities (N·s/m2) |
|---|---|---|
| −55 | 1621.993 | 1.362 |
| −40 | 390.924 | 0.328 |
| −20 | 111.064 | 0.0933 |
| 0 | 42.734 | 0.0359 |
| 20 | 22.482 | 0.0189 |
| 40 | 13.928 | 0.0117 |
| 60 | 9.683 | 0.0081 |
| 80 | 7.088 | 0.0060 |
| 100 | 5.579 | 0.0047 |
| 135 | 4.027 | 0.0034 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, B.; Lu, Y.; Jiang, H.; Ling, Z.; Li, T.; Liu, H.; Ouyang, X. Quantitative Comparative Study on the Performance of a Valve-Controlled Actuator and Electro-Hydrostatic Actuator. Actuators 2024, 13, 118. https://doi.org/10.3390/act13040118
Yang B, Lu Y, Jiang H, Ling Z, Li T, Liu H, Ouyang X. Quantitative Comparative Study on the Performance of a Valve-Controlled Actuator and Electro-Hydrostatic Actuator. Actuators. 2024; 13(4):118. https://doi.org/10.3390/act13040118
Chicago/Turabian StyleYang, Bo, Yijie Lu, Haoyi Jiang, Zhenfei Ling, Tong Li, Hao Liu, and Xiaoping Ouyang. 2024. "Quantitative Comparative Study on the Performance of a Valve-Controlled Actuator and Electro-Hydrostatic Actuator" Actuators 13, no. 4: 118. https://doi.org/10.3390/act13040118
APA StyleYang, B., Lu, Y., Jiang, H., Ling, Z., Li, T., Liu, H., & Ouyang, X. (2024). Quantitative Comparative Study on the Performance of a Valve-Controlled Actuator and Electro-Hydrostatic Actuator. Actuators, 13(4), 118. https://doi.org/10.3390/act13040118







