Multi-Channel Phase-Compensated Active Disturbance Rejection Control with an Improved Backstepping Strategy for Electro-Optical Tracking Systems
Abstract
1. Introduction
- In the existing literature, such as [32,33], the study of the ESO does not consider the existence of lags in all observed states of the ESO, which reduces the observation accuracy of the ESO. Therefore, in this paper, a novel ESO (MPESO) is proposed, which for the first time considers and compensates for the lags of all the states of the system observed by the ESO, so that its estimation efficiency is further improved.
- The residual uncertainty in ESO compensation of the total disturbance is a challenge, and the treatment of this uncertainty has not been adequately considered in the existing literature [41]. In this paper, this residual uncertainty is introduced into the design of the Lyapunov function for backstepping control, which is estimated and compensated to achieve cancellation of this uncertainty.
- To demonstrate the stability of the proposed system, an equivalent control block diagram of the MPESO is presented, exploiting the small gain theorem’s original advantages, which is simple but powerful. While for special cases, equivalence may be established between small-gain conditions and Lyapunov-type conditions [42], small gain frequency domain testing is favored due to its numerical accuracy and computational efficiency.
2. Problem Formulation
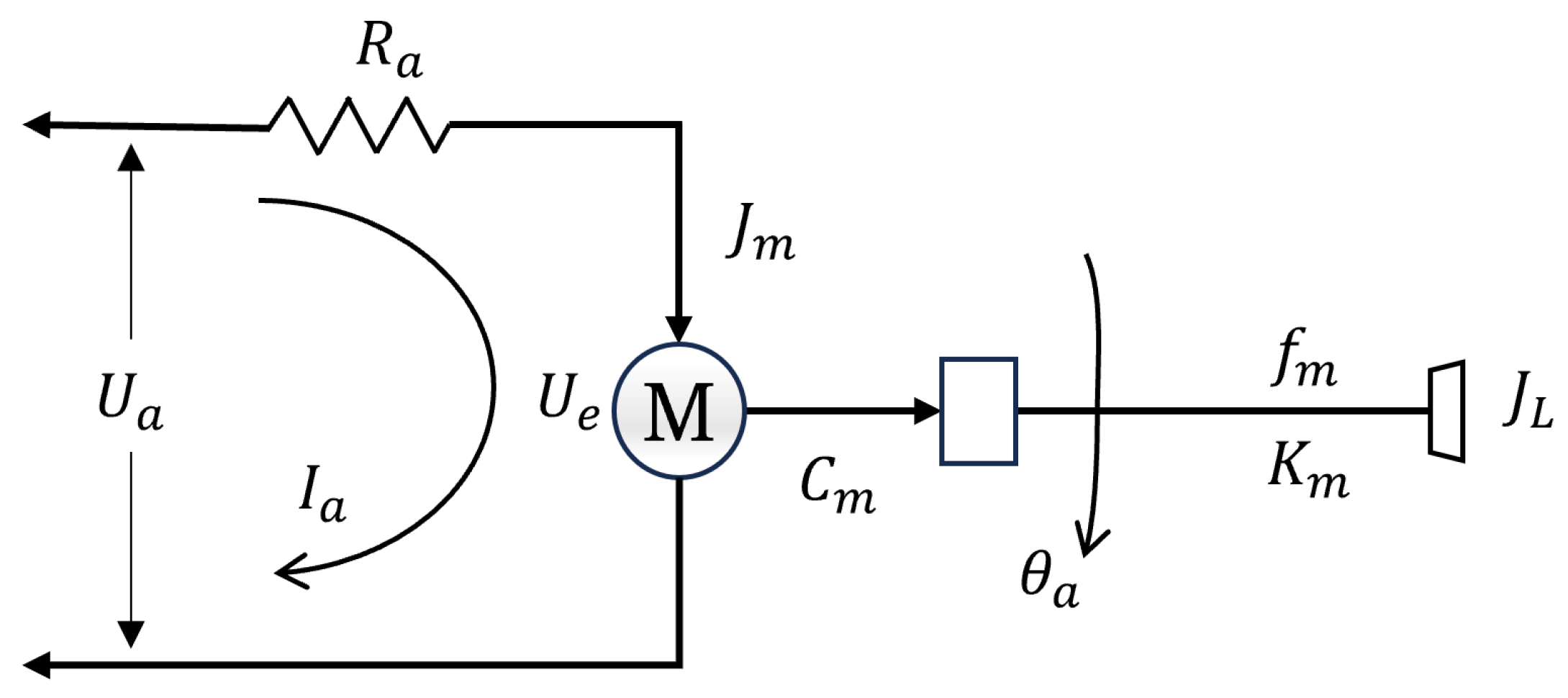
2.1. ETS Model Analysis
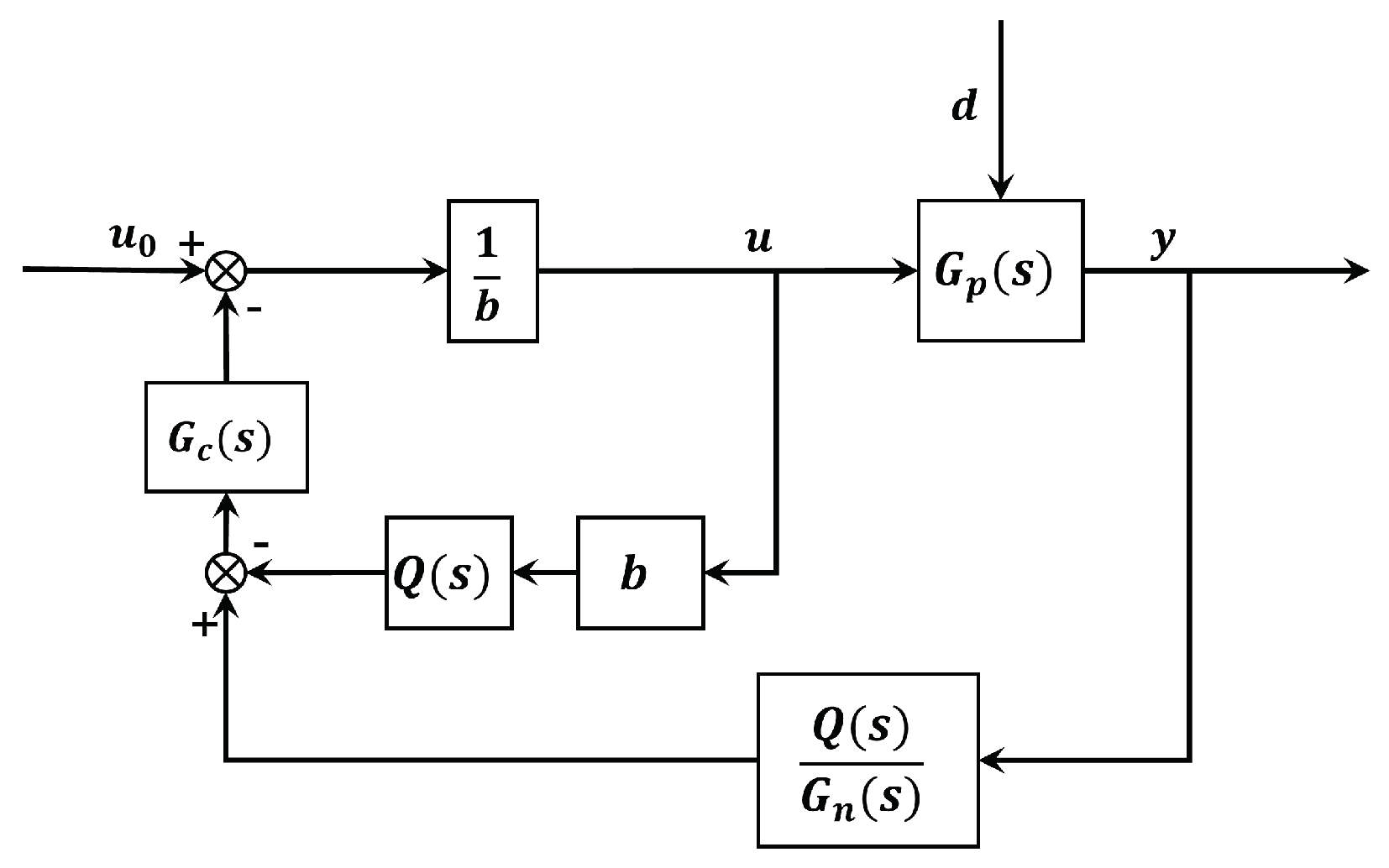
2.2. Linear Active Disturbance Rejection Control
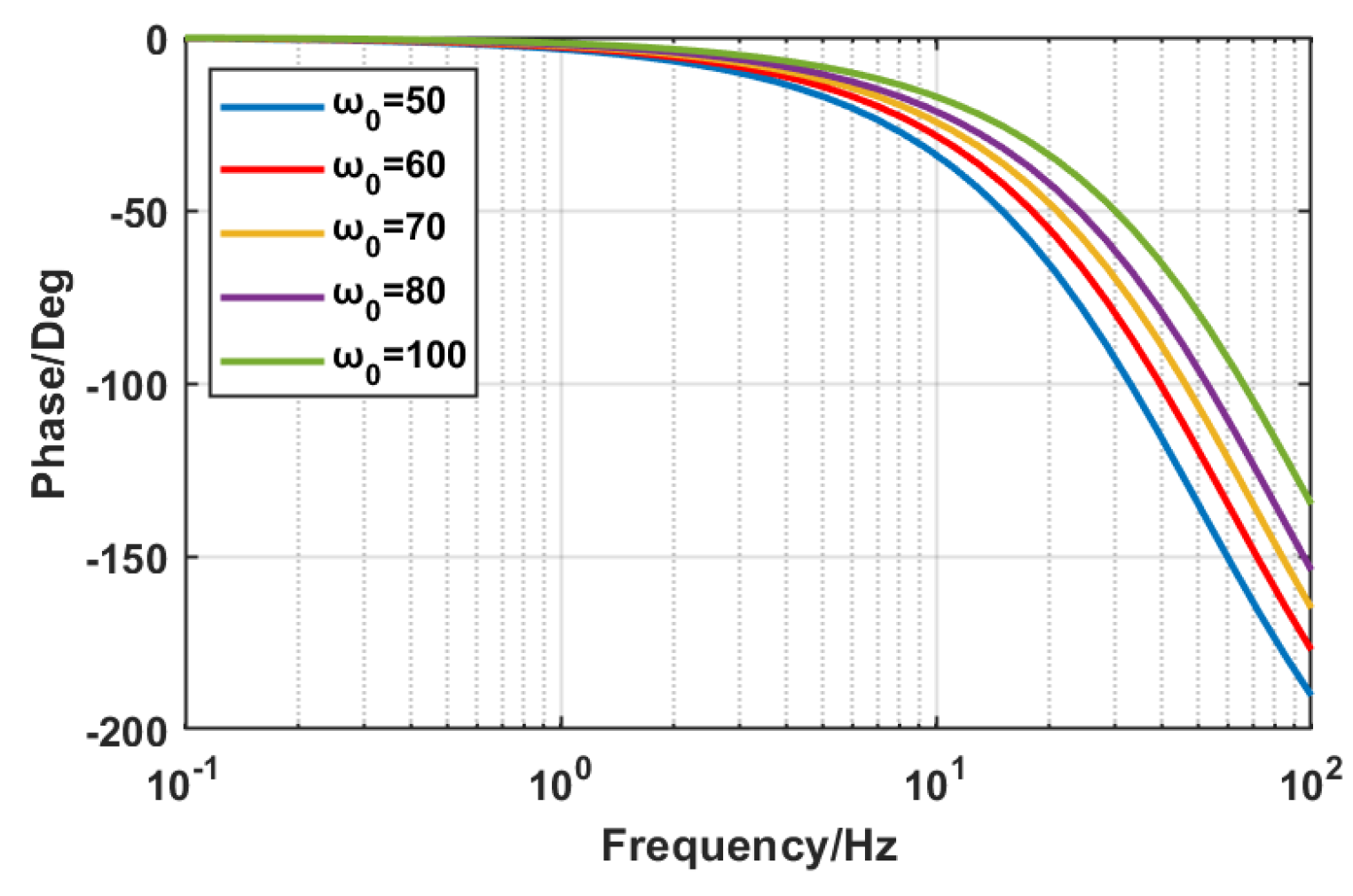
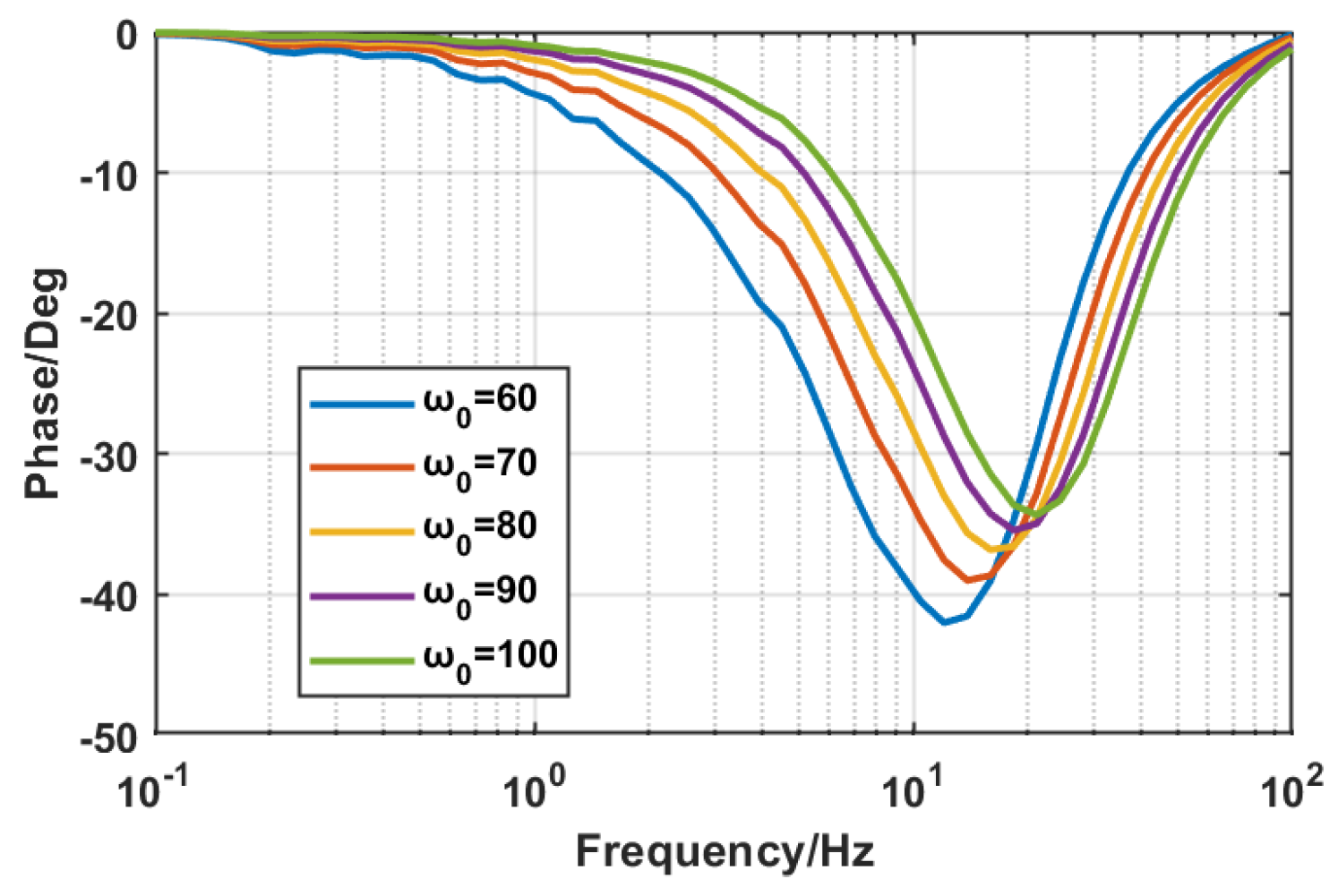
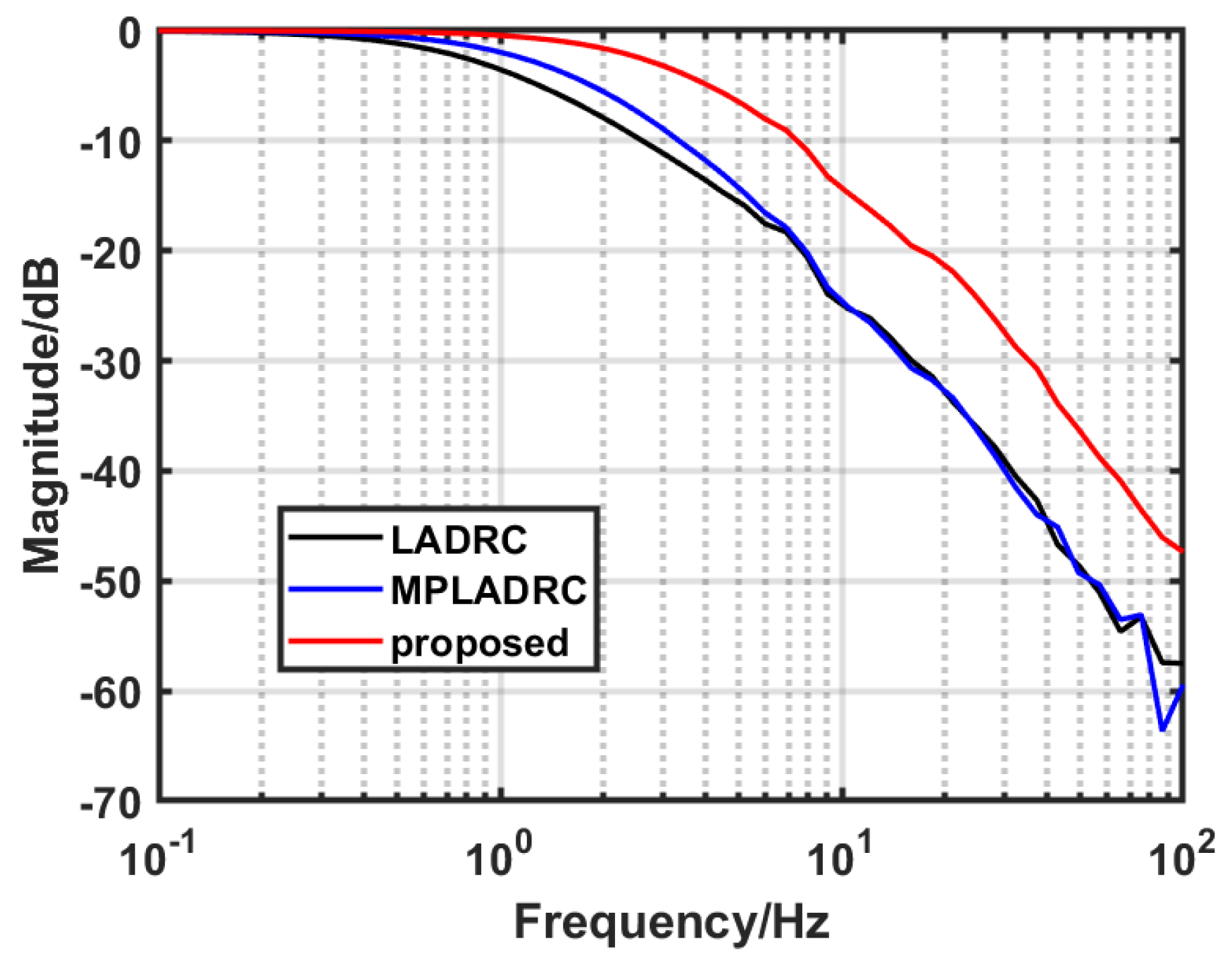
2.3. Phase Lag Analysis of the Conventional LESO
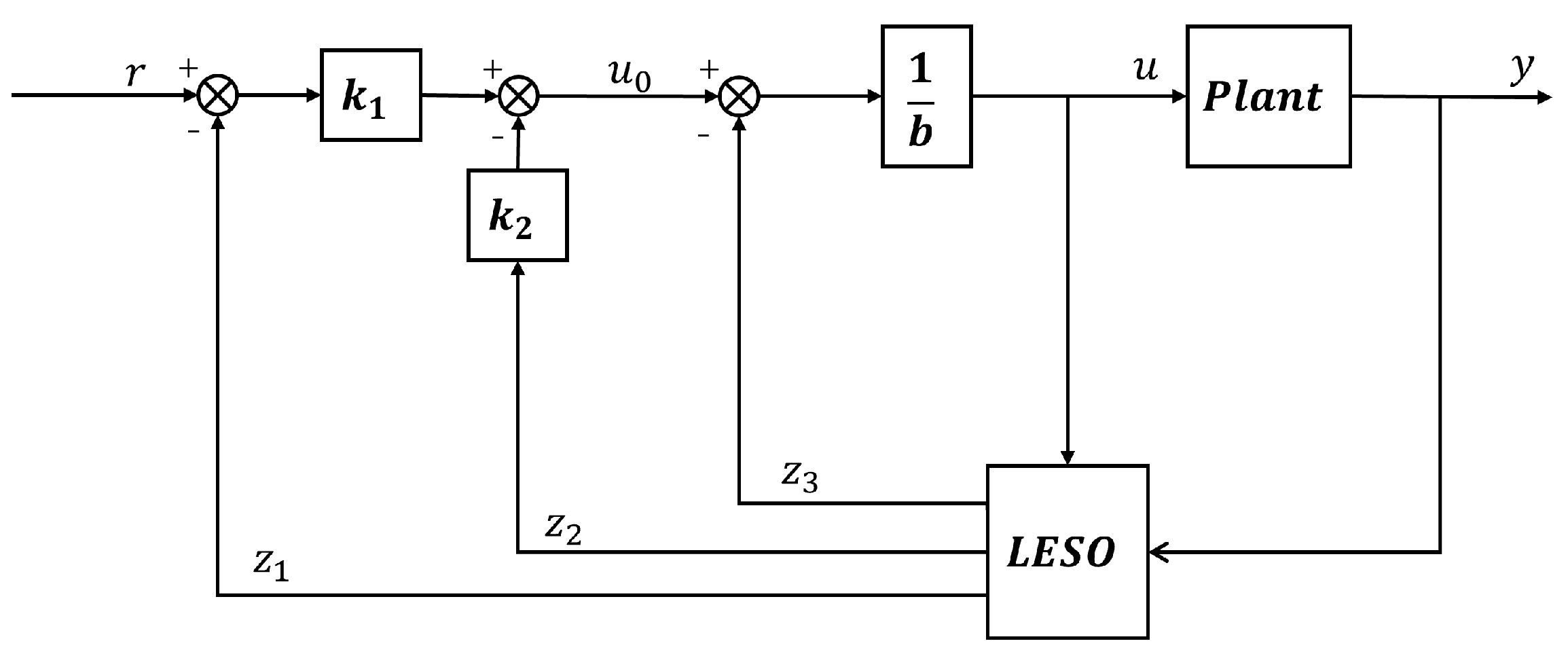
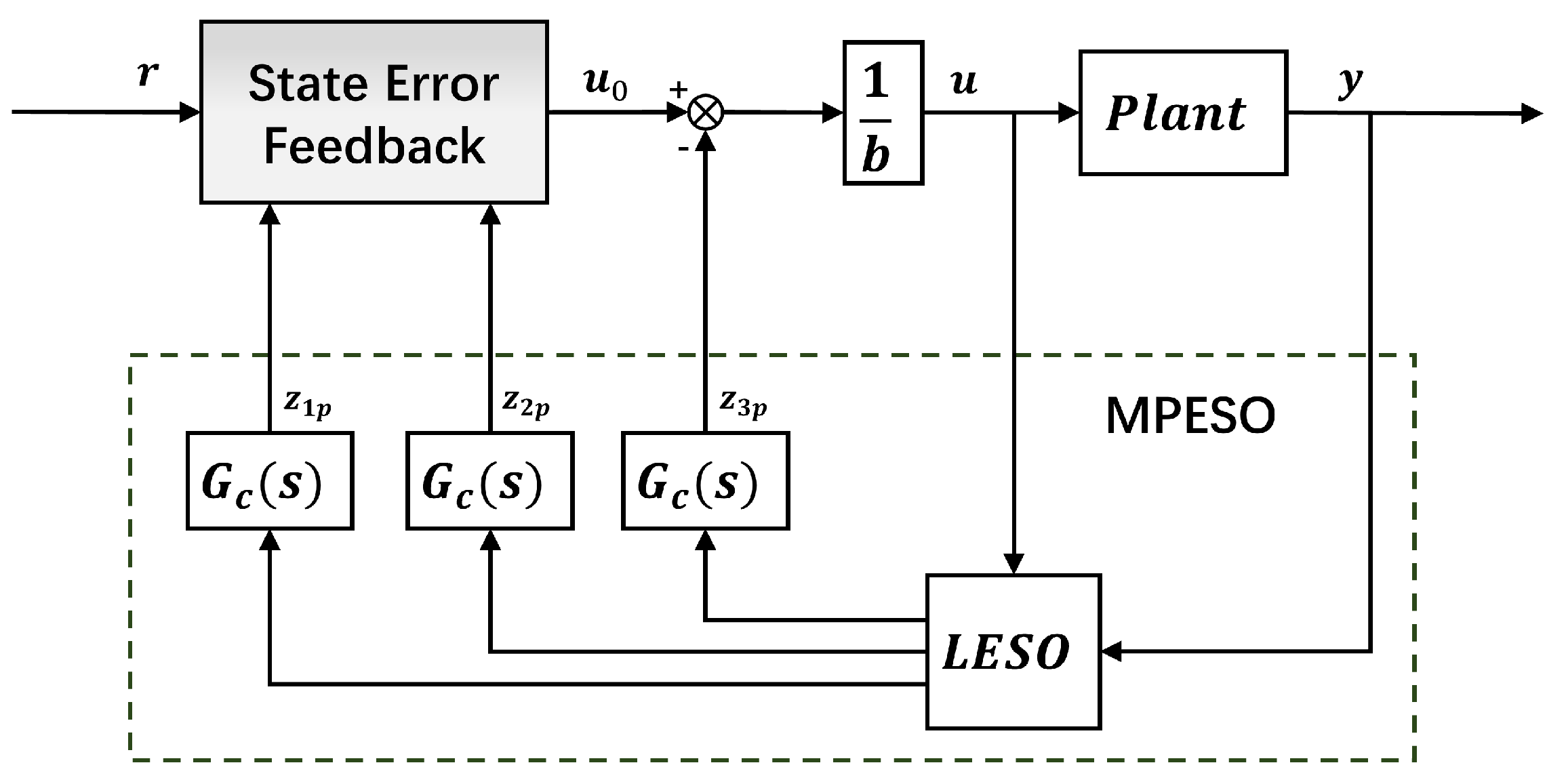
3. Design of the MPESO and Control Law
3.1. MPESO
3.2. Improved Backstepping Control Method Design
3.3. Stability Analysis
3.3.1. Analysis for the MPESO
3.3.2. Analysis for the Control Law
3.4. Parameter Selection Rules
- In the context of the ESO, the parameter is considered, and there is a need to maximize its value to enhance the convergence speed of the ESO observation error. However, an excessively large may amplify high-frequency noise in the system, leading to instability. Therefore, the selection of requires a careful balance between disturbance suppression and noise amplification;
- Then, , , and are tuned to achieve a balance between overshoot and rapid response while ensuring stability.
- For the parameters a and T, a nuanced adjustment is essential based on the system’s frequency response characteristics to simultaneously enhance the phase margin and meet the requirements for dynamic performance. Evaluating the closed-loop system response is required to ensure the avoidance of instability or other adverse characteristics.
4. Simulation and Experimental Verification
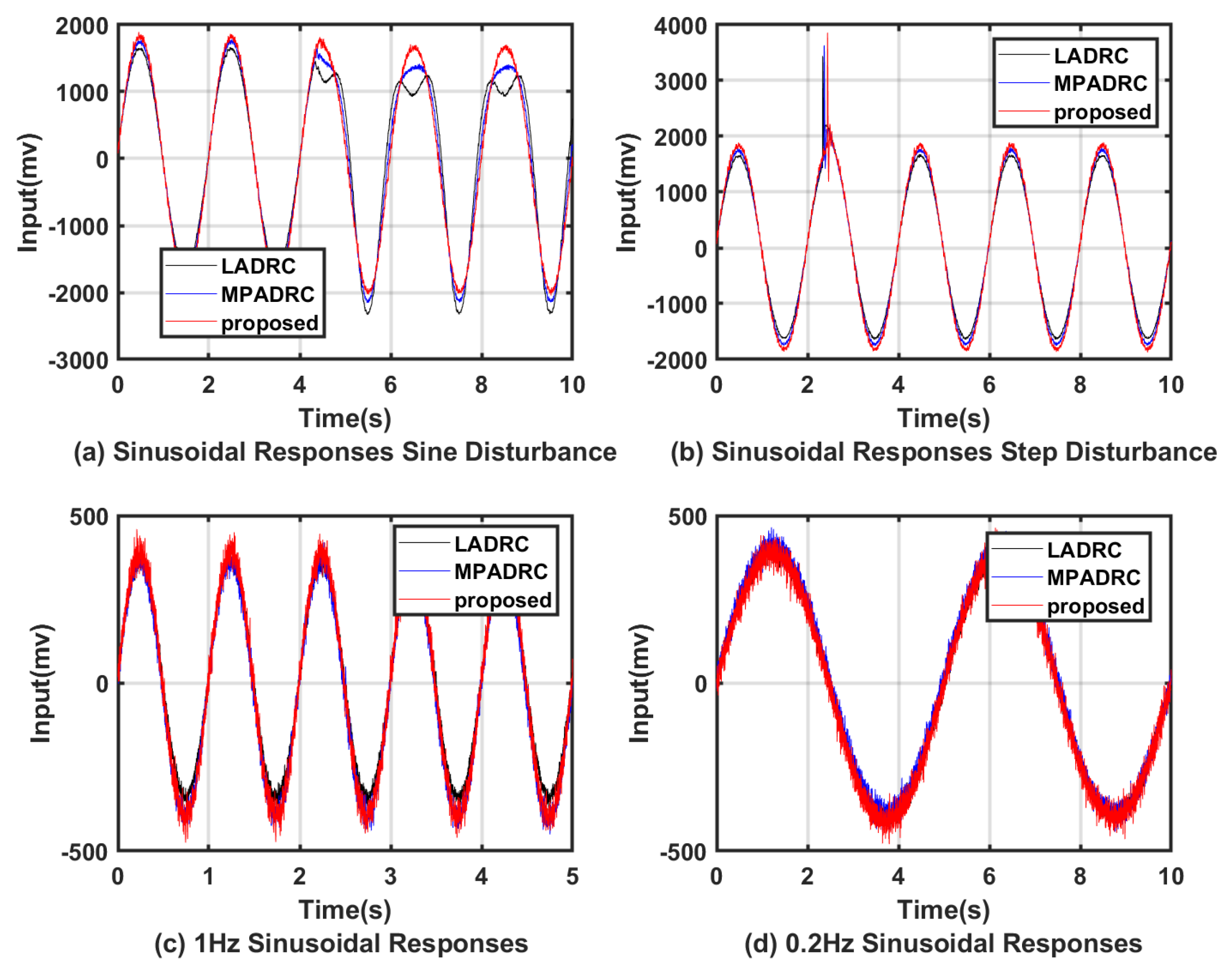
4.1. Simulation Verification
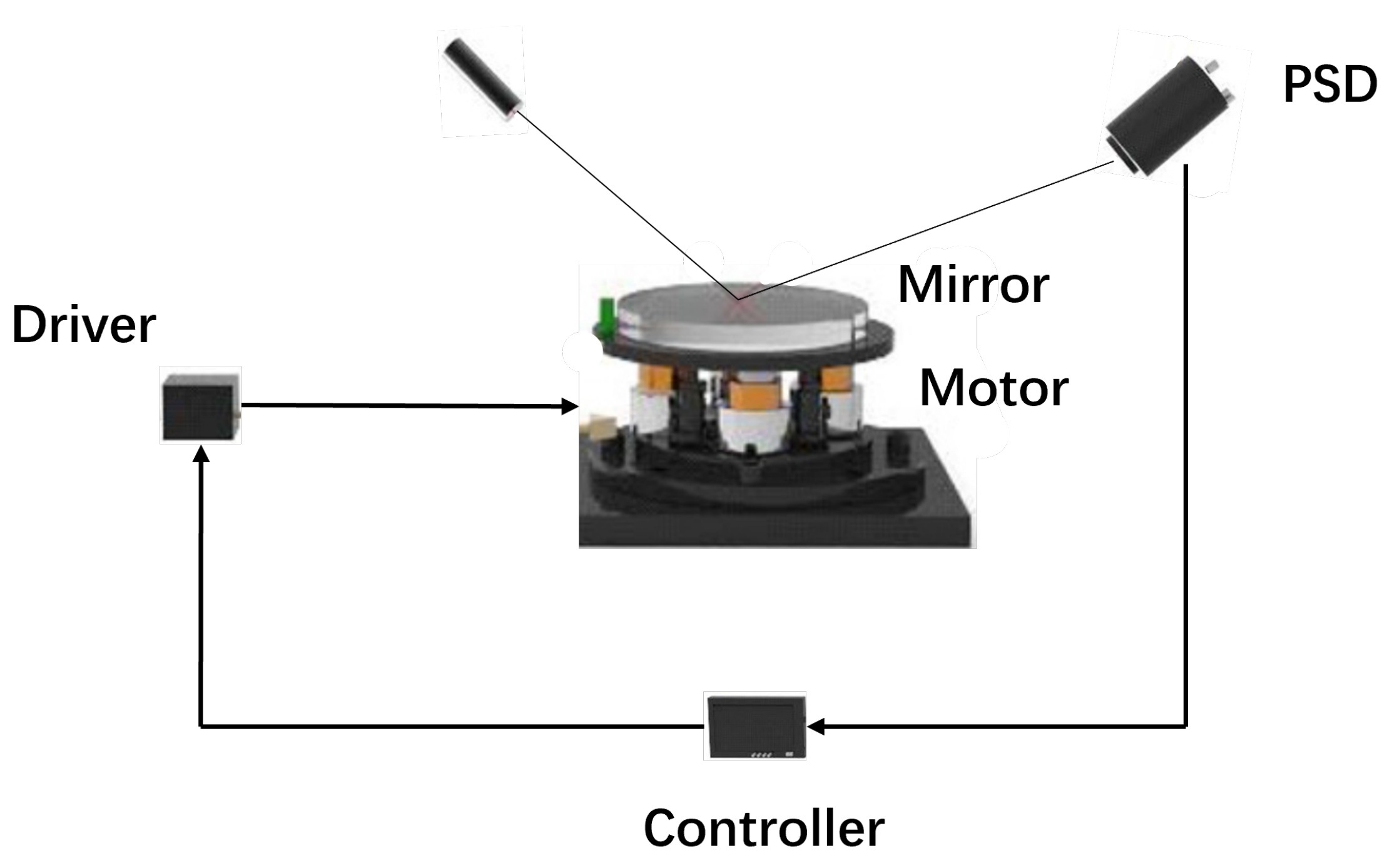
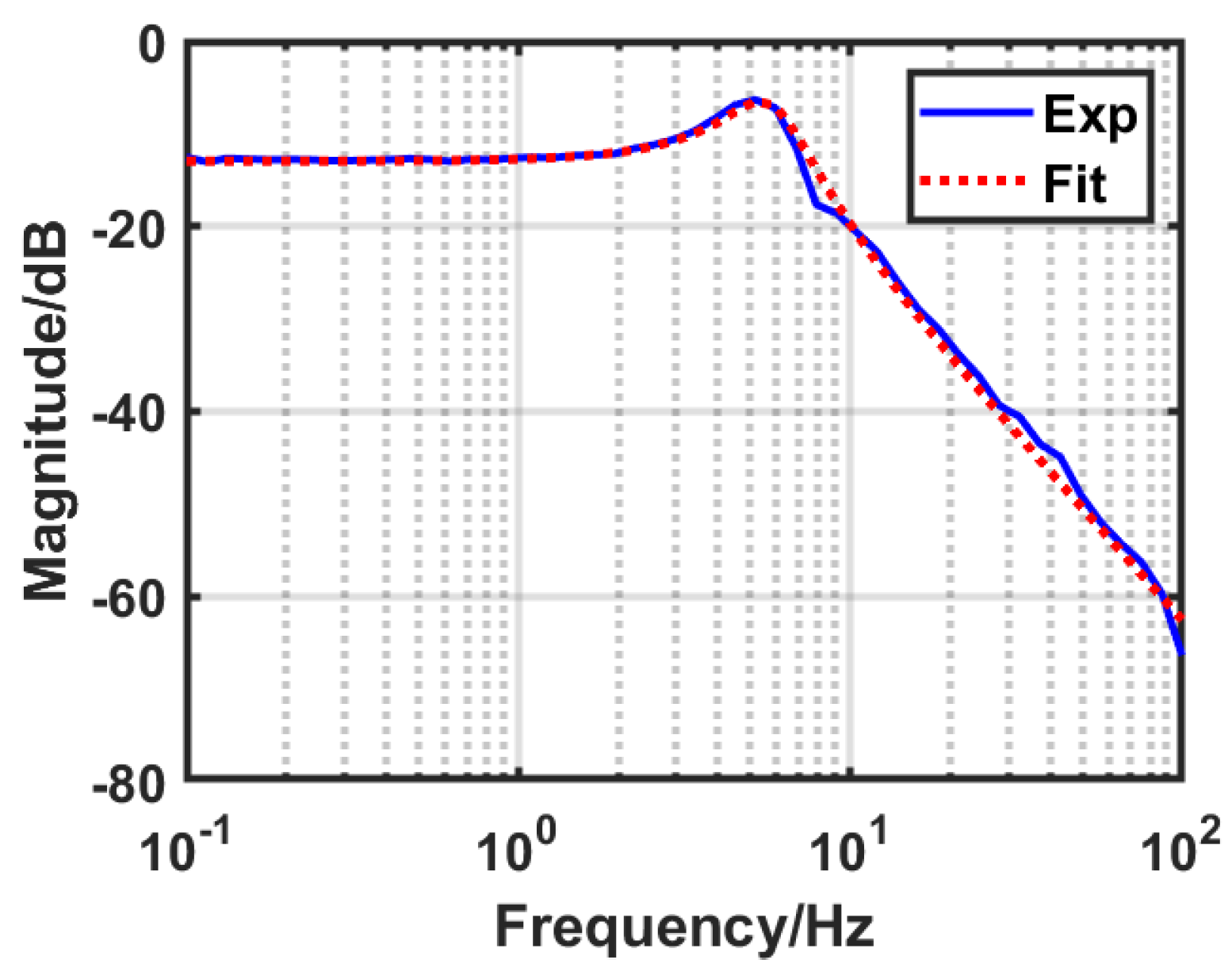
4.2. Experimental Verification
5. Summary and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Tao, T.; Jiaguang, M.; Hongbin, C.; Chengyu, F.; Hu, Y.; Ge, R.; Wenshu, Y.; Bo, Q.; Lei, C.; Mengwei, Z.; et al. A review on precision control methodologies for optical-electric tracking control system. Opto-Electron. Eng. 2020, 47, 200315. [Google Scholar]
- Kaidong, Y.; De’en, W.; Ying, Y.; Dangpeng, X.; Fang, W.; Hao, L. Inertial stabilization technology in optical-electric tracking system. High Power Laser Part. Beams 2022, 34, 081007. [Google Scholar]
- Deng, J.; Xue, W.; Liang, W.; Zhou, X.; Mao, Y. On adjustable and lossless suppression to disturbances and uncertainties for nonminimum-phase laser pointing system. ISA Trans. 2023, 136, 727–741. [Google Scholar] [CrossRef] [PubMed]
- Zhijun, L.; Yao, M.; Bo, Q.; Xi, Z.; Qiong, L.; Qian, Z. Research on control technology of single detection based on position correction in quantum optical communication. Opto-Electron. Eng. 2022, 49, 210311. [Google Scholar]
- Xu, C.; Huang, D.; Liu, J. Target Location of Unmanned Aerial Vehicles Based on the Electro-Optical Stabilization and Tracking Platform. Measurement 2019, 147, 106848. [Google Scholar] [CrossRef]
- Bi, Z.; Tian, Z.; Luo, T.; Fu, S. Study on Shipborne Video Electro-Optical Tracking System Based on FPGA. In Proceedings of the 5th International Conference on Electrical Engineering and Automatic Control, Khenchela, Algeria, 15–17 November 2016; pp. 521–529. [Google Scholar]
- Boroson, D.M.; Robinson, B.S.; Burianek, D.A.; Murphy, D.V.; Biswas, A. Overview and status of the Lunar Laser Communications Demonstration. In Proceedings of the SPIE—The International Society for Optical Engineering, Barcelona, Spain, 26–29 November 2012; Volume 8246, p. 7. [Google Scholar]
- Tang, T.; Qi, B.; Yang, T. Youla–Kucera Parameterization-Based Optimally Closed-Loop Control for Tip–Tilt Compensation. IEEE Sensors J. 2018, 18, 6154–6160. [Google Scholar] [CrossRef]
- Chaudhary, H.; Khatoon, S.; Singh, R.; Pandey, A. Fast steering mirror for optical fine pointing applications: A review paper applications: A review paper. In Proceedings of the 2018 3rd International Innovative Applications of Computational Intelligence on Power, Energy and Controls with their Impact on Humanity (CIPECH), Ghaziabad, India, 1–2 November 2018; pp. 1–5. [Google Scholar]
- Fan, Y.; He, Y.; Tan, U.X. Real-Time Compensation System via Gyroscope and Fast Steering Mirror for Wide-Bandwidth Multiple-Frequency Vehicle Disturbance. IEEE/ASME Trans. Mechatron. 2020, 25, 650–660. [Google Scholar] [CrossRef]
- Wang, L.; Liu, X.; Wang, C. Modeling and design of fast steering mirror in image motion compensation for backscanning step and stare imaging systems. Opt. Eng. 2019, 58, 103105. [Google Scholar] [CrossRef]
- Deng, J.; Xue, W.; Zhou, X.; Mao, Y. On disturbance rejection control for inertial stabilization of long-distance laser positioning with movable platform. Meas. Control 2020, 53, 1203–1217. [Google Scholar] [CrossRef]
- Nie, K.; Xue, W.; Zhang, C.; Mao, Y. Disturbance Observer-based Repetitive Control with Application to Optoelectronic Precision Positioning System. J. Frankl. Inst. 2021, 358, 8443–8469. [Google Scholar] [CrossRef]
- Tian, J.; Yang, W.; Peng, Z.; Tang, T. Inertial sensor-based multiloop control of fast steering mirror for line of sight stabilization. Opt. Eng. 2016, 55, 111602. [Google Scholar] [CrossRef]
- Zhang, B.; Nie, K.; Chen, X.; Mao, Y. Development of Sliding Mode Controller Based on Internal Model Controller for Higher Precision Electro-Optical Tracking System. Actuators 2022, 11, 16. [Google Scholar] [CrossRef]
- Wei, Q.; Wu, Z.; Zhou, Y.; Ke, D.; Zhang, D. Active Disturbance-Rejection Controller (ADRC)-Based Torque Control for a Pneumatic Rotary Actuator with Positional Interference. Actuators 2024, 13, 66. [Google Scholar] [CrossRef]
- Zhou, W.; Guo, S.; Guo, J.; Meng, F.; Chen, Z. ADRC-Based Control Method for the Vascular Intervention Master-Slave Surgical Robotic System. Micromachines 2021, 12, 1439. [Google Scholar] [CrossRef] [PubMed]
- Zhang, P.; Shi, Z.; Yu, B. Research on Friction Compensation Method of Electromechanical Actuator Based on Improved Active Disturbance Rejection Control. Actuators 2023, 12, 445. [Google Scholar] [CrossRef]
- Zhu, H.; Weng, F.; Makeximu; Li, D.; Zhu, M. Active control of combustion oscillation with active disturbance rejection control (ADRC) method. J. Sound Vib. 2022, 540, 117245. [Google Scholar] [CrossRef]
- Qi, X.; Li, J.; Xia, Y.; Wan, H. On stability for sampled-data nonlinear ADRC-based control system with application to the ball-beam problem. J. Frankl. Inst. 2018, 355, 8537–8553. [Google Scholar] [CrossRef]
- Han, J. From PID to Active Disturbance Rejection Control. IEEE Trans. Ind. Electron. 2009, 56, 900–906. [Google Scholar] [CrossRef]
- Han, J. Extended state observer for a class of uncertain plants. Control Decis. 1995, 10, 85–88. [Google Scholar]
- Gao, Z. Scaling and Parameterization Based Controller Tuning. In Proceedings of the American Control Conference, Denver, CO, USA, 4–6 June 2003. [Google Scholar]
- Zhou, X.; Li, X. Trajectory Tracking Control for Electro-Optical Tracking System Using ESO Based Fractional-Order Sliding Mode Control. IEEE Access 2021, 9, 45891–45902. [Google Scholar] [CrossRef]
- Hu, X.; Han, S.; Liu, Y.; Wang, H. Two-Axis Optoelectronic Stabilized Platform Based on Active Disturbance Rejection Controller with LuGre Friction Model. Electronics 2023, 12, 1261. [Google Scholar] [CrossRef]
- Zachi, A.R.; Correia, C.A.M.; A. Filho, J.L.; Gouvêa, J.A. Robust disturbance rejection controller for systems with uncertain parameters. IET Control Theory Appl. 2019, 13, 1995–2007. [Google Scholar] [CrossRef]
- Teixeira, A.; Gouvea, J.A.; Zachi, A.R.L.; Rodrigues, V.H.P.; Oliveira, T.R. Monitoring function-based active disturbance rejection control for uncertain systems with unknown control directions. Adv. Control Appl. Eng. Ind. Syst. 2021, 3, e66. [Google Scholar] [CrossRef]
- Gouvêa, J.A.; Fernandes, L.M.; Pinto, M.F.; Zachi, A.R. Variant ADRC design paradigm for controlling uncertain dynamical systems. Eur. J. Control 2023, 72, 100822. [Google Scholar] [CrossRef]
- Gouvêa, J.A.; Raptopoulos, L.S.C.; Pinto, M.F.; Díaz, E.Y.V.; Dutra, M.S.; Sousa, L.C.d.; Batista, V.M.O.; Zachi, A.R.L. Attitude Control of Ornithopter Wing by Using a MIMO Active Disturbance Rejection Strategy. Sensors 2023, 23, 6602. [Google Scholar] [CrossRef] [PubMed]
- Dong, Z.; Sun, Z.; Sun, H.; Wang, W.; Mei, X. A Novel Control Method for Permanent Magnet Synchronous Linear Motor Based on Model Predictive Control and Extended State Observer. Actuators 2024, 13, 34. [Google Scholar] [CrossRef]
- Liao, L.; Gao, L.; Ngwa, M.; Zhang, D.; Du, J.; Li, B. Adaptive Super-Twisting Sliding Mode Control of Underwater Mechanical Leg with Extended State Observer. Actuators 2023, 12, 373. [Google Scholar] [CrossRef]
- Wei, W.; Zhang, Z.; Zuo, M. Phase leading active disturbance rejection control for a nanopositioning stage. ISA Trans. 2021, 116, 218–231. [Google Scholar] [CrossRef]
- Dong, L.; Chen, Z.; Sun, M.; Sun, Q. Phase compensation active disturbance rejection control for shimmy vibration with magnetorheological damper of aircraft. Expert Syst. Appl. 2023, 213, 119126. [Google Scholar] [CrossRef]
- Du, Y.; Cao, W.; She, J. Analysis and design of active disturbance rejection control with an improved extended state observer for systems with measurement noise. IEEE Trans. Ind. Electron. 2022, 70, 855–865. [Google Scholar] [CrossRef]
- Fu, C.; Tan, W. Analysis and tuning of reduced-order active disturbance rejection control. J. Frankl. Inst. 2021, 358, 339–362. [Google Scholar] [CrossRef]
- Bartkowiak, P.; Pazderski, D. Position tracking control of a robotic joint using error-based ADRC with full and reduced order ESO. In Proceedings of the 2023 27th International Conference on Methods and Models in Automation and Robotics (MMAR), Miedzyzdroje, Poland, 22–25 August 2023; pp. 350–355. [Google Scholar]
- Doostdar, F.; Mojallali, H. An ADRC-based backstepping control design for a class of fractional-order systems. ISA Trans. 2022, 121, 140–146. [Google Scholar] [CrossRef]
- Li, S.; Li, H.; Wang, H.; Yang, C.; Gui, J.; Fu, R. Sliding Mode Active Disturbance Rejection Control of Permanent Magnet Synchronous Motor Based on Improved Genetic Algorithm. Actuators 2023, 12, 209. [Google Scholar] [CrossRef]
- Liu, J.; Gai, W.; Zhang, J.; Li, Y. Nonlinear adaptive backstepping with ESO for the quadrotor trajectory tracking control in the multiple disturbances. Int. J. Control Autom. Syst. 2019, 17, 2754–2768. [Google Scholar] [CrossRef]
- Patelski, R.; Pazderski, D. Parameter Identifying Disturbance Rejection Control With Asymptotic Error Convergence. IEEE Robot. Autom. Lett. 2023, 9, 1035–1042. [Google Scholar] [CrossRef]
- Li, J.; Zhang, L.; Luo, L.; Li, S. Extended state observer based current-constrained controller for a PMSM system in presence of disturbances: Design, analysis and experiments. Control Eng. Pract. 2023, 132, 105412. [Google Scholar] [CrossRef]
- Zhang, J.; Knopse, C.R.; Tsiotras, P. Stability of time-delay systems: Equivalence between Lyapunov and scaled small-gain conditions. IEEE Trans. Autom. Control 2001, 46, 482–486. [Google Scholar] [CrossRef]


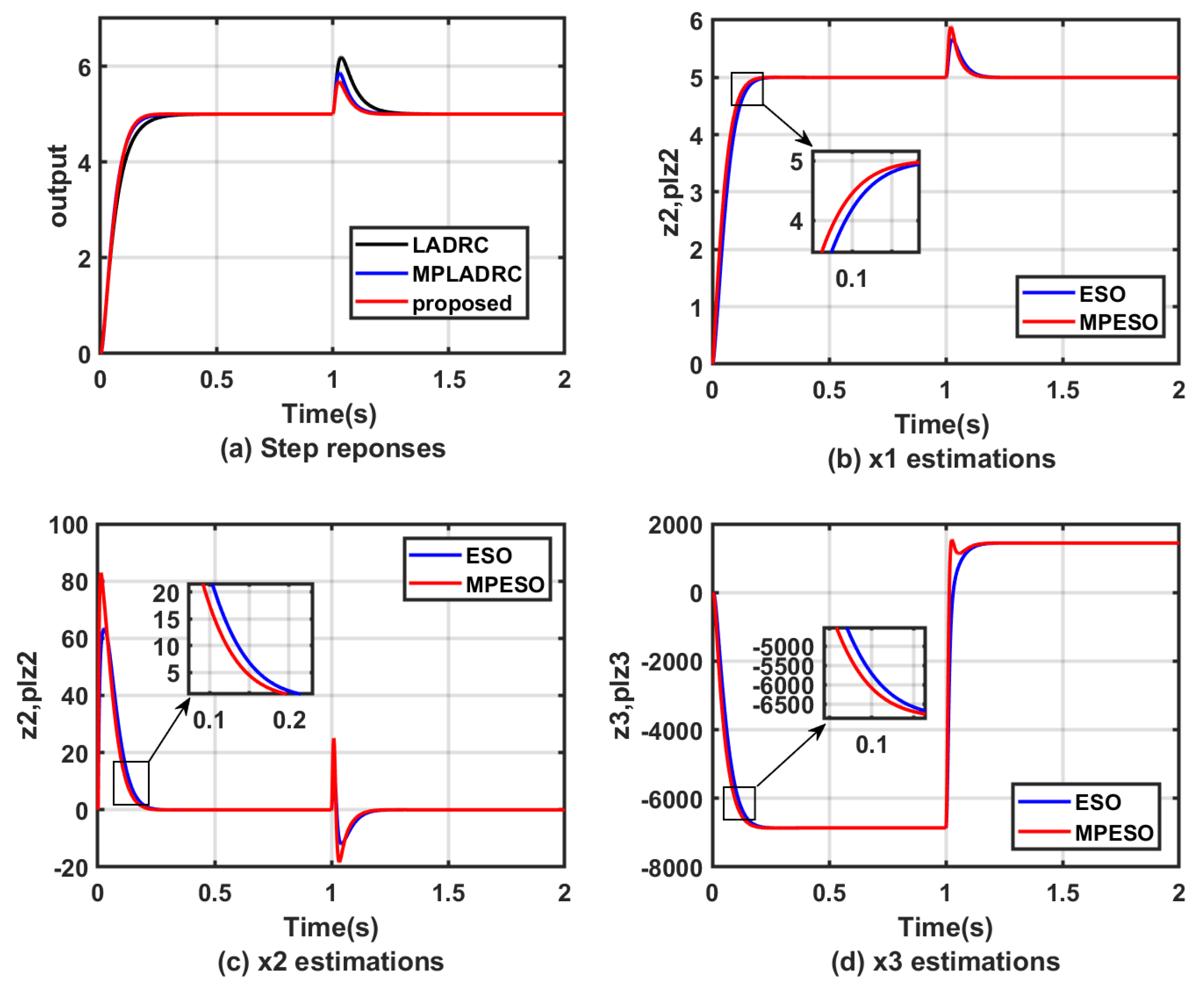
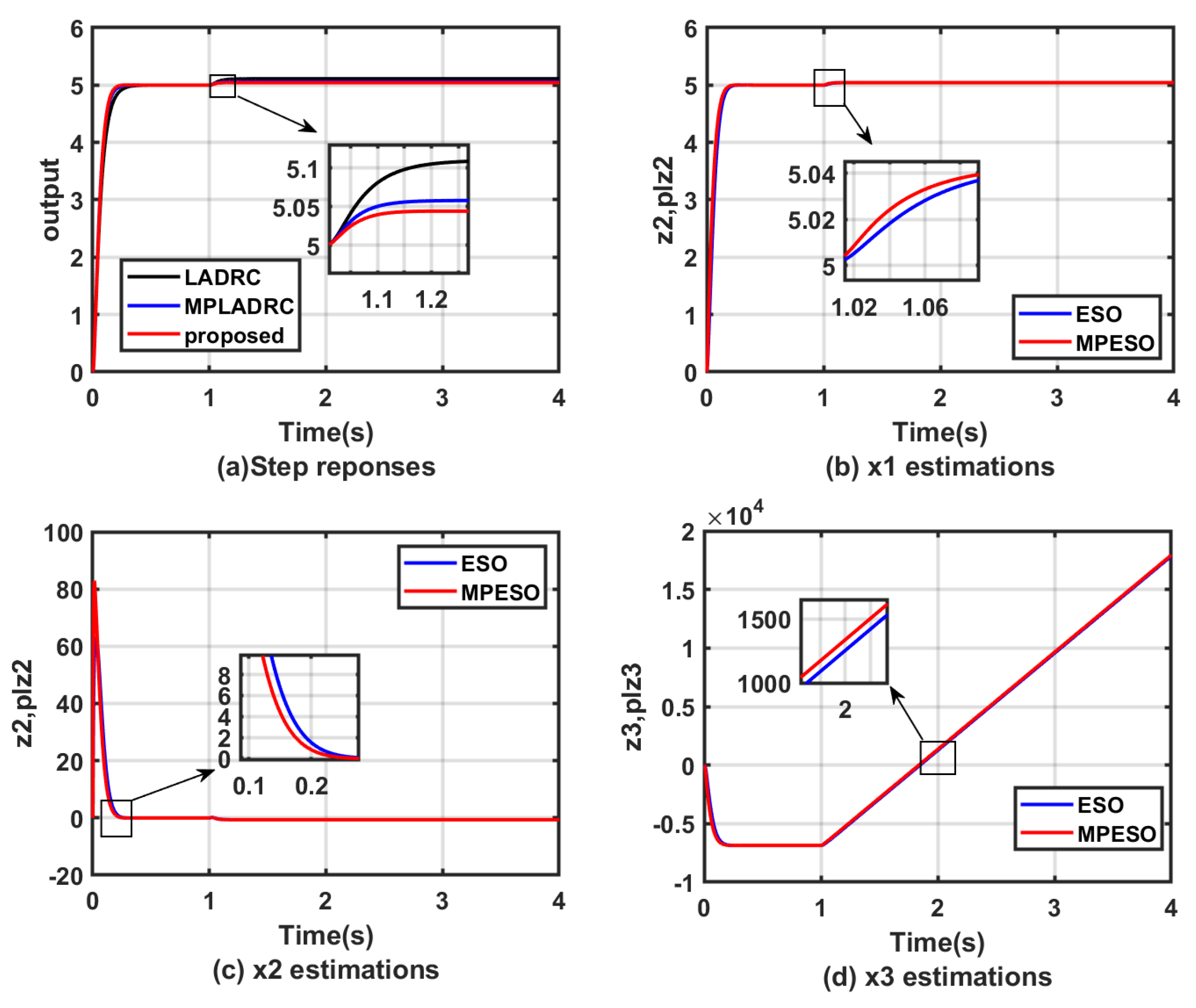
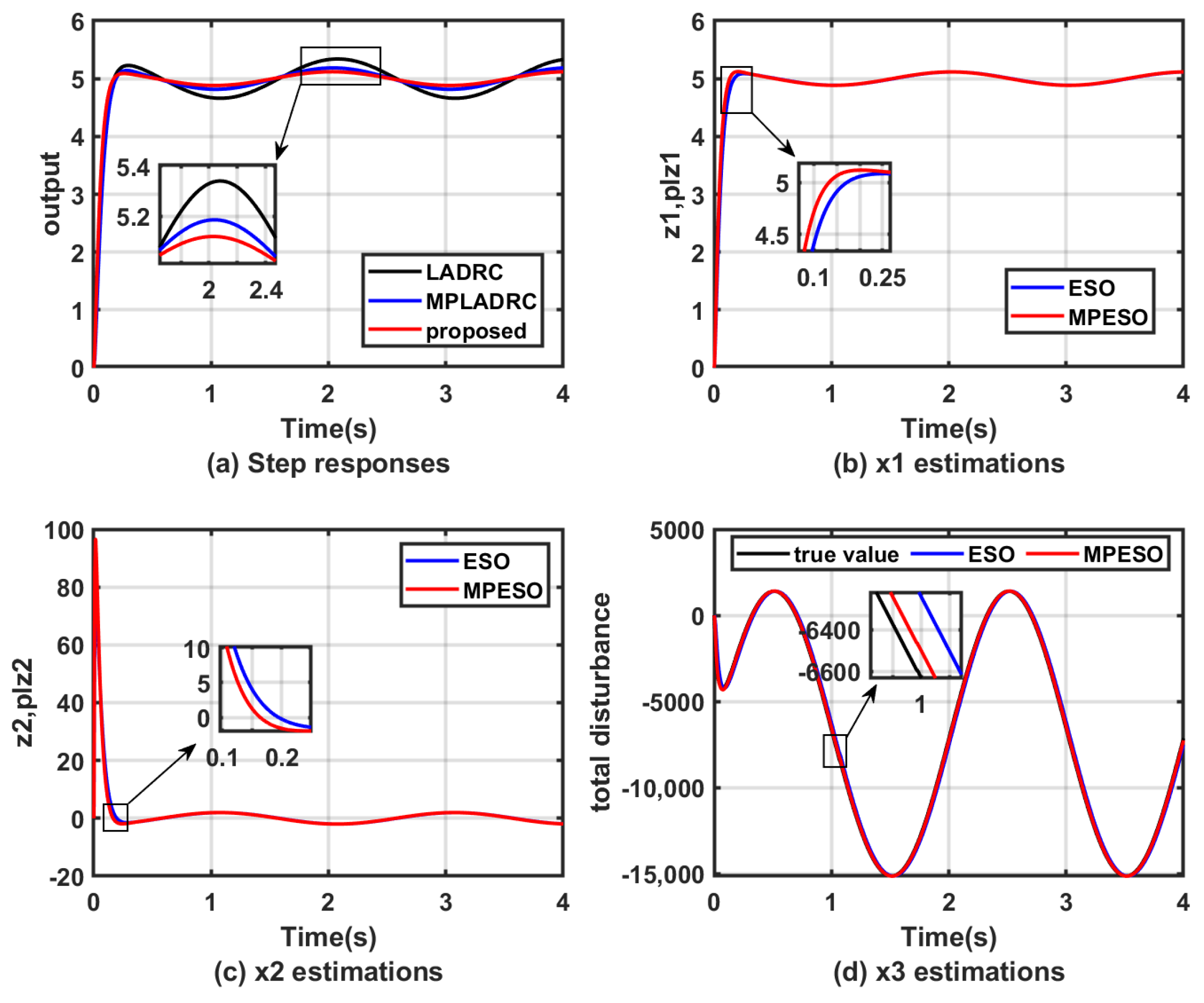
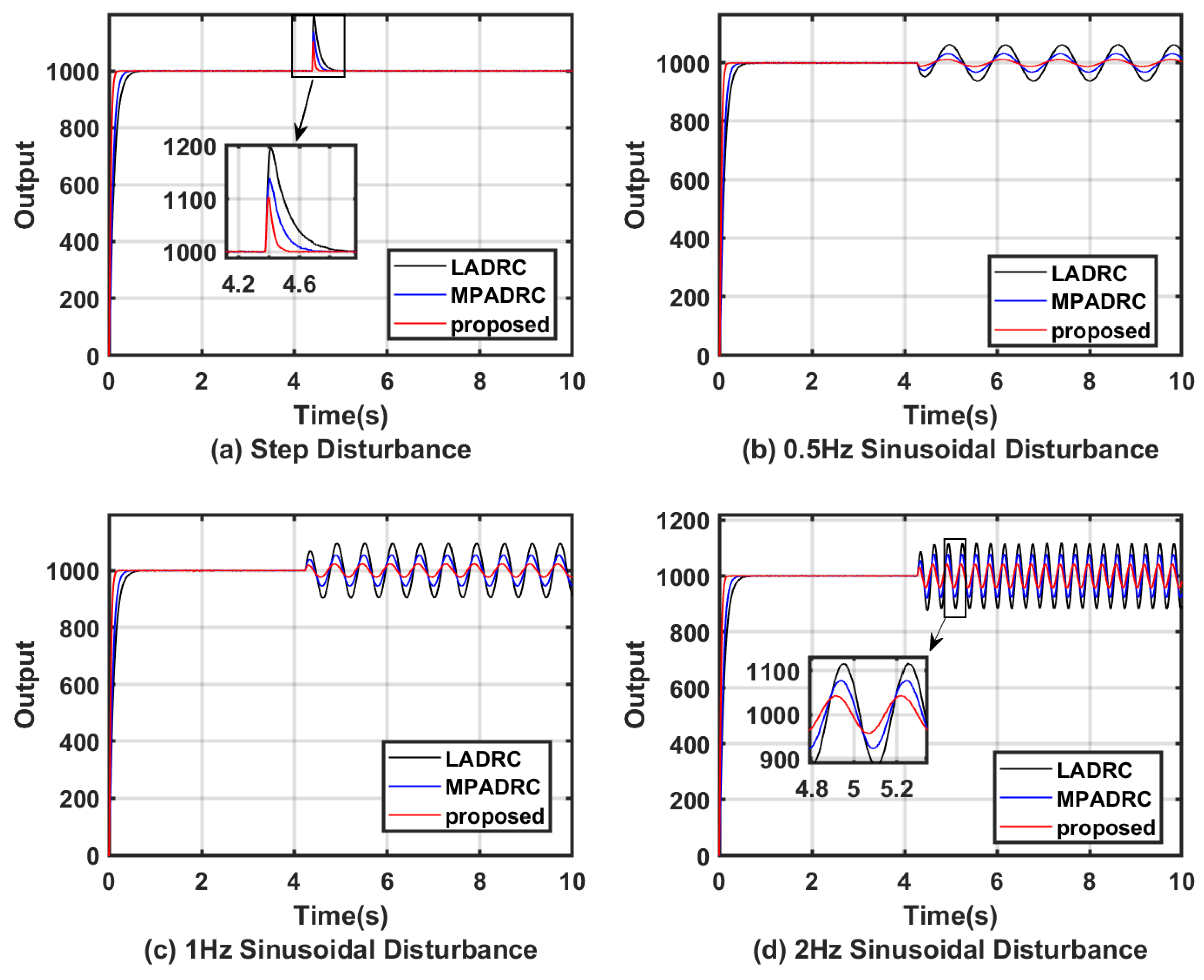
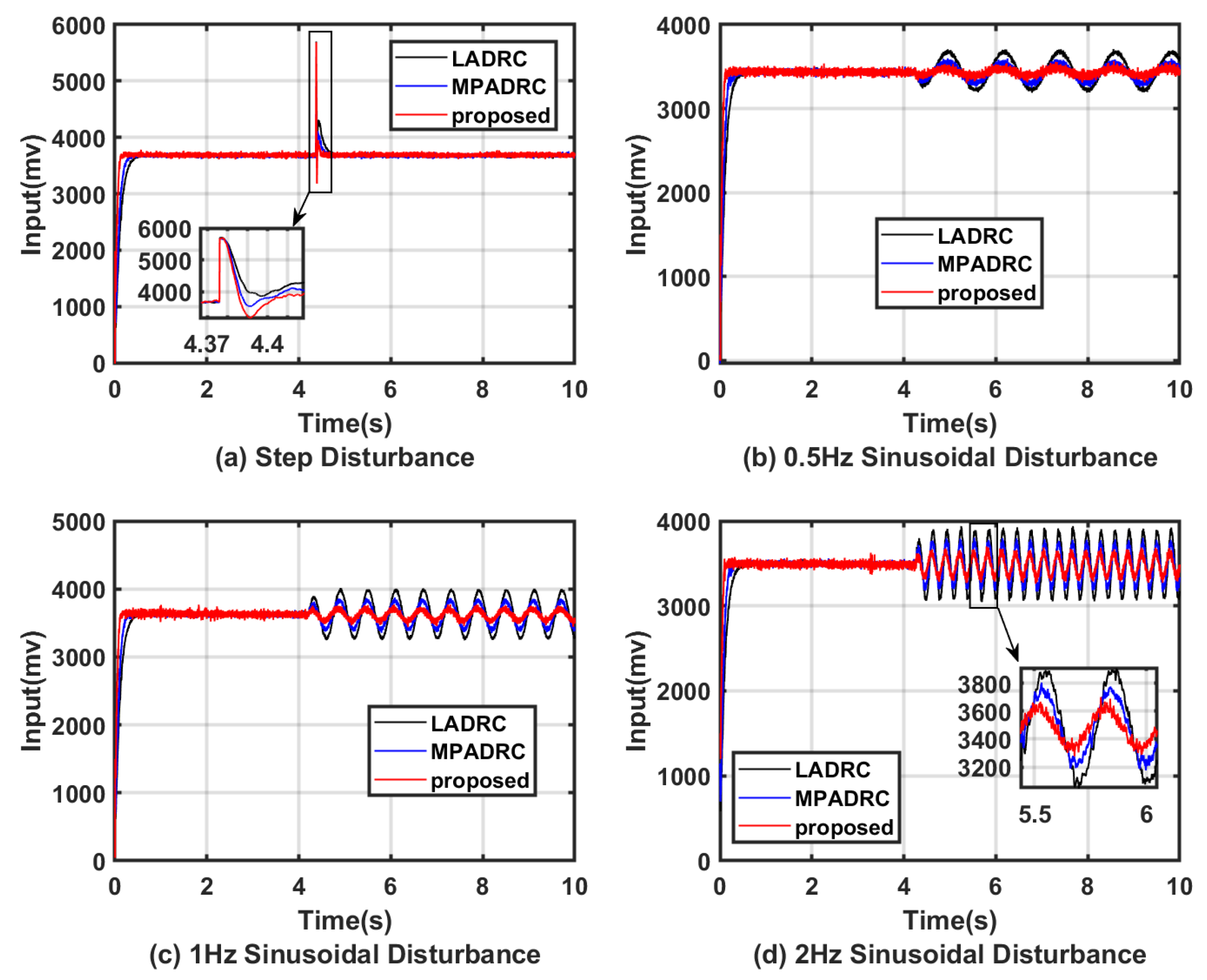
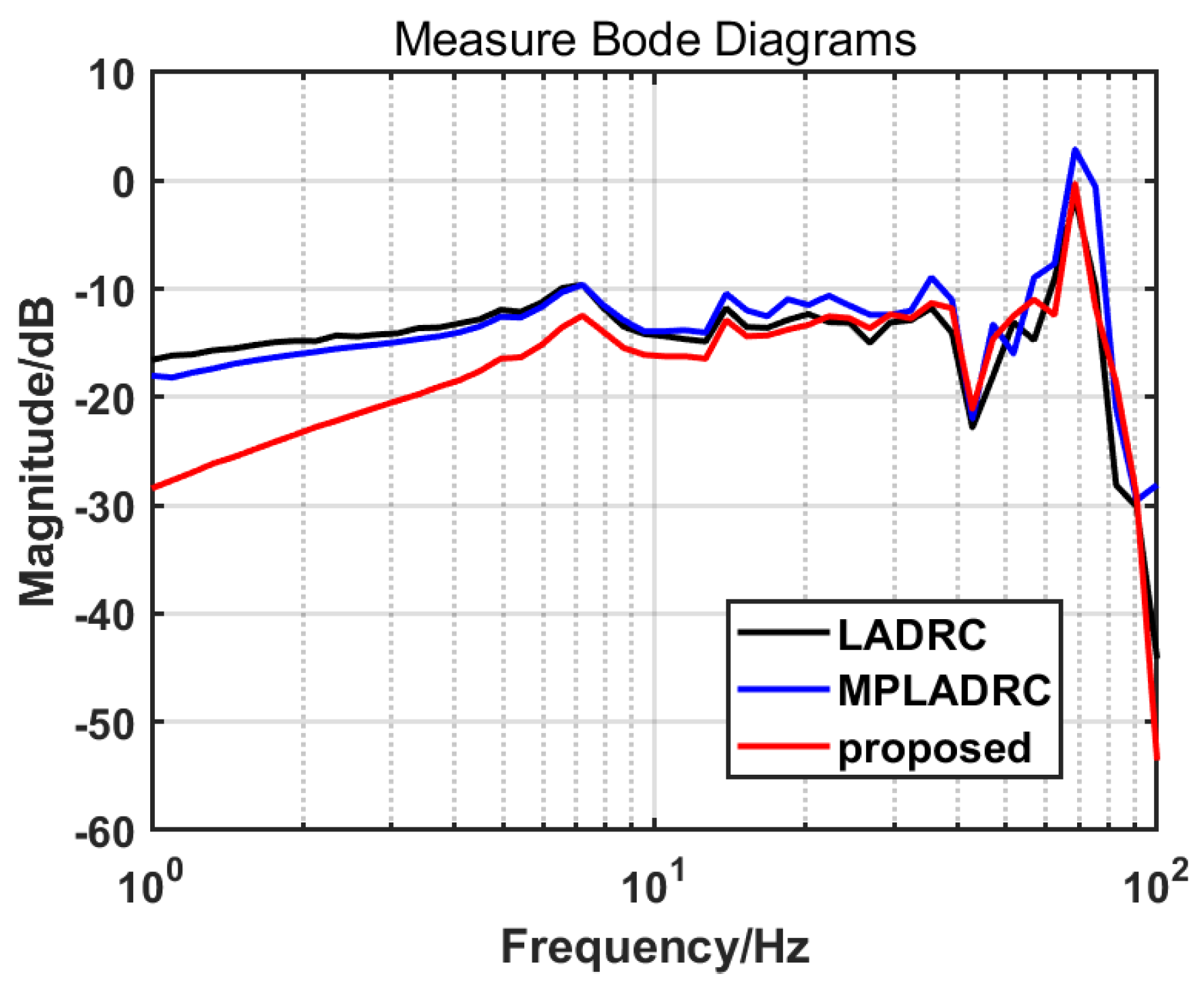
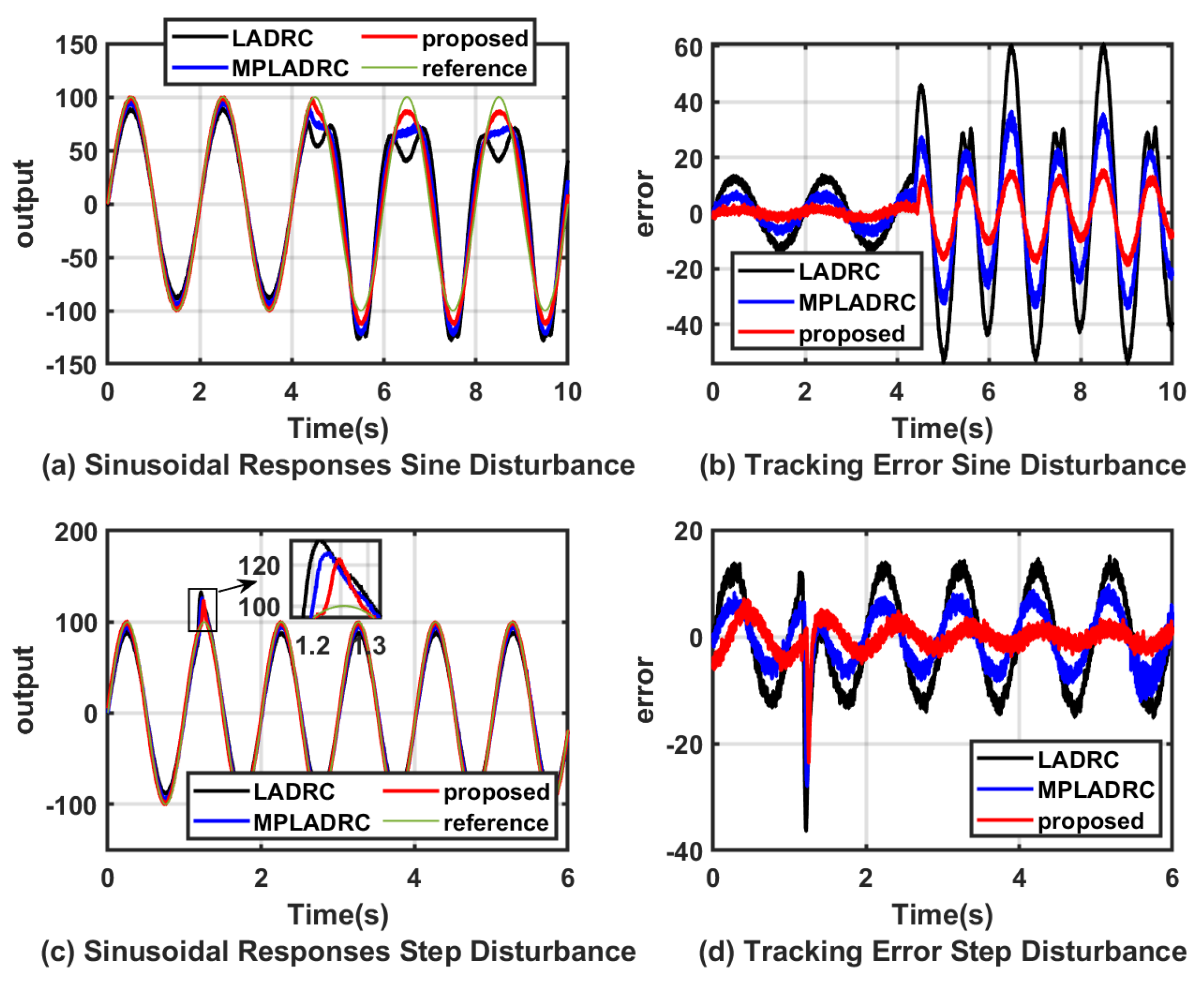
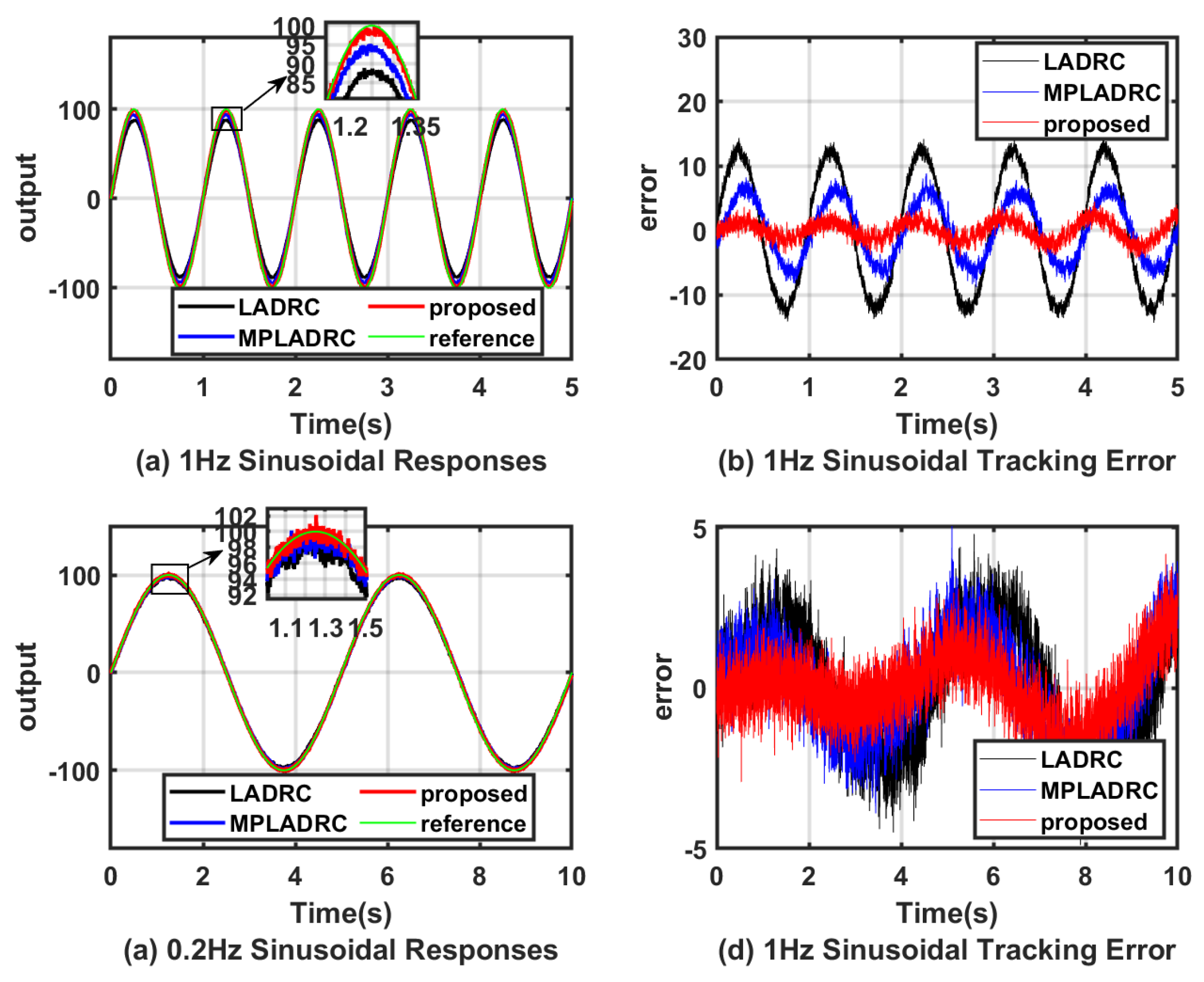
| Controllers | b | a | T | |||||
|---|---|---|---|---|---|---|---|---|
| LADRC | 830 | 40 Hz | 100 Hz | - | - | - | - | - |
| MPLADRC | 830 | 40 Hz | 100 Hz | 0.8 | 0.1 | - | - | - |
| Proposed | 830 | 40 Hz | 100 Hz | 0.8 | 0.1 | 40 | 40 | 20 |
| Controllers | Step Disturbance | Sine Disturbance | Ramp Disturbance |
|---|---|---|---|
| LADRC | 32.94 | 351.10 | 175.63 |
| MPLADRC | 27.26 | 292.17 | 144.32 |
| Proposed | 21.30 | 227.26 | 110.81 |
| Controllers | Step Disturbance | Sine Disturbance | Ramp Disturbance |
|---|---|---|---|
| LADRC | 43.47 | 234.54 | 55.07 |
| MPLADRC | 34.06 | 163.04 | 38.35 |
| Proposed | 24.17 | 99.70 | 24.16 |
| Controllers | 0.5 Hz Sine | 1 Hz Sine | 2 Hz Sine |
|---|---|---|---|
| LADRC | 3.3710 | 7.1378 | 2.0891 |
| MPLADRC | 1.7823 | 4.1364 | 1.4034 |
| Proposed | 0.7678 | 1.8514 | 0.7856 |
| Controllers | Step Response | Sine Response | Sine Response |
|---|---|---|---|
| (Step Disturbance) | (Step Disturbance) | (Sine Disturbance) | |
| LADRC | 3.3710 | 7.1378 | 2.0891 |
| MPLADRC | 1.7823 | 4.1364 | 1.4034 |
| Proposed | 0.7678 | 1.8514 | 0.7856 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhuang, S.; Li, J.; Wang, H.; Deng, J.; Mao, Y. Multi-Channel Phase-Compensated Active Disturbance Rejection Control with an Improved Backstepping Strategy for Electro-Optical Tracking Systems. Actuators 2024, 13, 117. https://doi.org/10.3390/act13030117
Zhuang S, Li J, Wang H, Deng J, Mao Y. Multi-Channel Phase-Compensated Active Disturbance Rejection Control with an Improved Backstepping Strategy for Electro-Optical Tracking Systems. Actuators. 2024; 13(3):117. https://doi.org/10.3390/act13030117
Chicago/Turabian StyleZhuang, Shanlin, Jiachen Li, Haolin Wang, Jiuqiang Deng, and Yao Mao. 2024. "Multi-Channel Phase-Compensated Active Disturbance Rejection Control with an Improved Backstepping Strategy for Electro-Optical Tracking Systems" Actuators 13, no. 3: 117. https://doi.org/10.3390/act13030117
APA StyleZhuang, S., Li, J., Wang, H., Deng, J., & Mao, Y. (2024). Multi-Channel Phase-Compensated Active Disturbance Rejection Control with an Improved Backstepping Strategy for Electro-Optical Tracking Systems. Actuators, 13(3), 117. https://doi.org/10.3390/act13030117






