Abstract
A modified Extended State Kalman Filter (ESKF)-based Model Predictive Control (MPC) algorithm is introduced to tailor the enhanced disturbance suppression in electro-optical tracking systems. Traditional control techniques, although robust, often struggle in scenarios with concurrent internal, external disturbances, and sensor noise. The proposed algorithm effectively overcomes these limitations by precisely estimating system states and actively mitigating disturbances, thus significantly boosting noise and perturbation control resilience. The primary contributions of this study include the integration of ESKF for accurate system state and disturbance estimation in noisy environments, the embedding of an ESKF estimation-compensation loop to simulate an improved disturbance-free system, and a simplified modeling approach for the controlled device. This designed structure minimizes the reliance on extensive system identification, easing the predictive control model-based constraints. Moreover, the approach incorporates total disturbance estimation into the optimization problem, safeguarding against actuator damage and ensuring high tracking accuracy. Through rigorous simulations and experiments, the ESKF-based MPC has demonstrated enhanced model error tolerance and superior disturbance suppression capabilities. Comparative analyses under varying model parameters and external disturbances highlight its exceptional trajectory tracking performance, even in the presence of model uncertainties and external noise.
1. Introduction
The electro-optical tracking system (ETS) plays a pivotal role in enabling the essential functions of acquisition, tracking, and precise pointing in various applications. ETSs are extensively utilized across diverse fields such as laser communication, astronomical observations [1], target tracking [2], space optical communication, quantum communication, and other fields [3,4]. The versatility of applications demands that these systems, often mounted on dynamic platforms like aircraft, satellites, and ships, meet increasingly stringent performance and parameter specifications.
Presently, numerous control methods are employed in ETS, including PID control [5], sliding mode control [6], and model predictive control [7]. These systems, operating in diverse environments, are susceptible to multiple external disturbances such as vibrations in airborne devices [8], wind disturbances [9], and friction torques [10]. Additionally, measurement noises stemming from sensor noise and complex environmental sounds impact these systems. Atmospheric environmental changes caused by non-terrestrial platforms disrupt the parameters of electrical components within the system, increasing uncertainty and reducing the modeling accuracy of ETS [11]. Some aforementioned control methods heavily rely on precise models; in the presence of measurement noise, external disturbances, and modeling errors, they significantly affect the stability of the Line of Sight (LOS), impacting tracking accuracy and potentially leading to system instability. Therefore, developing methods to improve the disturbance rejection is essential.
Currently, many methods have been proposed for disturbance rejection in electro-optical tracking systems. Techniques like adaptive control [12], disturbance observers (DOB) [13], active disturbance rejection control (ADRC) [14,15] are utilized for system disturbance rejection. These methods offer higher system adaptability, stronger disturbance resistance, and better capability to handle complex dynamic environments compared to PID control. Each disturbance estimation method has its strengths and weaknesses, potentially enhancing overall disturbance suppression performance. However, the complexity of boundary conditions and system uncertainties typically render it challenging to acquire an exact mathematical model of the controlled object. Consequently, these methods might not effectively suppress internal and external disturbances, making it challenging to achieve satisfactory disturbance rejection performance.
MPC determines optimal control values through an online optimization process, taking physical boundary constraints into account [16]. This method relies on a process model to predict future behavior at each sampling time. A Kalman Filter (KF)-based MPC is proposed [17] to suppress system disturbances and reduce output overshoot aspects. However, its performance significantly degrades in the presence of substantial internal and external disturbances, as MPC effectiveness depends on precise system and disturbance models [18]. Since KF is designed to solve linear system problems, many MPC methods based on EKF and UKF have been proposed to solve nonlinear system problems [19,20]. The trajectory tracking method based on MPC does not consider the impact of measurement noise, thereby failing to guarantee tracking accuracy. The Extended State Kalman Filter (ESKF) [21,22] is a filter designed for the timely estimation of unknown dynamics, offering enhanced robustness and higher estimation accuracy. ESKF considers internal and external disturbances as extended system state variables for estimation and compensation, without the need for an exact mathematical model of the system. This aspect of ESKF effectively addresses the shortcomings of MPC. Tackling these challenges, the present study introduces a methodology employing ESKF-based MPC, which comprehensively considers both internal and external disturbances as well as measurement noise, to improve tracking precision and robustness in practical applications. The principal contributions of this study are outlined as follows:
- The formulation of ESKF that estimates the states of the system and external perturbations, thereby enhancing the robustness of the electro-optical tracking system against both internal and external disturbances and mitigating the impact of system measurement noise.
- Integration of the ESKF estimation-suppression mechanism as an inner loop to ensure that the control system dynamics resemble those of an improved system without disturbances. This approach involves addressing the predictive control issue utilizing a stable discrete state-space model, which is of second-order, resembling a first-order model with an added integrator, despite potential discrepancies from the real characteristics of the system being managed. Furthermore, the criteria for both the practicality and nominal stability of the optimization challenge are provided.
- The estimation-suppression technique of the ESKF reduces the necessity for precise modeling of the controlled device, focusing instead on inherent system attributes like static gain and observable time constants. This approach simplifies the model-dependent aspects of predictive control and removes the requirement for intricate system identification.
The structure of the remainder of this article is outlined as follows: Section 2 details the electromechanical model pertinent to the electro-optical tracking system. In Section 3, the development and implementation of the proposed ESKF-based MPC for LOS regulation are discussed, highlighting how adopting error as a state variable streamlines the tracking and disturbance rejection design process. Following this, Section 4 and Section 5 showcase simulation and experimental outcomes, respectively, demonstrating the viability of the suggested control strategy. Finally, Section 6 offers concluding remarks.
2. Modeling of an Electro-Optical Tracking System
As a widely implemented ETS, this article validates experiments on an Inertial Stabilization Platform (ISP). Mounted above a disturbance platform, the ISP ensures the stability of the LOS, while the latter simulates complex external disturbances. LOS errors are deduced by calculating the central position deviations measured by the detector. A digital controller computes control commands from the received error signals to drive the ISP. Figure 1 presents the physical structural model of ISP, from which Equation (1) is derived using potential energy and torque balance equations [23].
where denotes the armature voltage and represents the armature current. and are the equivalent resistance and inductance in the motor drive circuit, respectively. is the motor torque coefficient, the load friction coefficient, the spring stiffness coefficient, the load inertia moment, and the rotational inertia of the motor. J is the sum of and , representing the equivalent inertia on the motor shaft. stands for external disturbances, is the back electromotive force generated by the coefficient , and , respectively, signify the system deflection angular velocity and angular displacement, and is the system angular displacement output, including the deflection and measurement noise n.
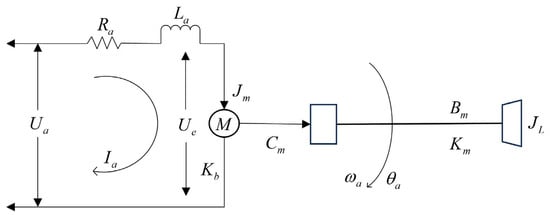
Figure 1.
The physical motion model diagram of the ISP.
Within the control frequency band, it is possible to derive the transfer function relating the armature voltage U to the angular displacement of the load :
where is the transfer function, , , .
The analytical representation of the ISP using a linear model often fails to capture a range of uncertainties. These include actuator saturation, back electromotive force (EMF) [24], hysteresis, and various complex nonlinear phenomena that naturally occur in the system structures, actuators, and sensors. When moving from theoretical models to practical simulations and experiments, these uncertainties and unaccounted-for specific parameters become evident in the results. In practice, robust control methods are required to effectively reject the real disturbances. Therefore, to validate the robustness of the proposed method, we take sinusoidal disturbances to simulate the real disturbances in experiments.
3. ESKF-Based MPC Design
MPC requires high fidelity in model accuracy; with a suitable model, MPC can be a robust algorithm, offering optimal control behavior satisfying process constraints, dependent on the feasibility of the optimization problem. However, this model-based characteristic can impair system performance significantly in cases of model mismatch, especially in processes characterized by intricate dynamics and varied operational states.
ESKF-based MPC is less dependent on model accuracy compared to traditional control methods. ESKF actively estimates the internal and external disturbance, encompassing model uncertainties and unknown perturbations, to achieve enhanced robustness and estimation accuracy. This allows for a certain degree of model error. It integrates unmodeled dynamics into estimated states without additional model information, providing appropriate control.
Moreover, the diagram illustrates a control system that integrates MPC with ESKF as shown in Figure 2. This architecture melds the disturbance rejection ability of ESKF with the forward-looking features of MPC. The MPC processes a reference signal to determine an initial control action, which is adjusted by a compensation factor from the ESKF that accounts for estimated disturbances. The combined control signal is then fed into the system, which reacts and produces an output. Meanwhile, the ESKF continually estimates the state of this system and the total perturbations, using this information to refine the disturbance compensation. The output of this system is also influenced by noise, which the ESKF attempts to filter out to ensure the system output closely follows the desired reference signal.
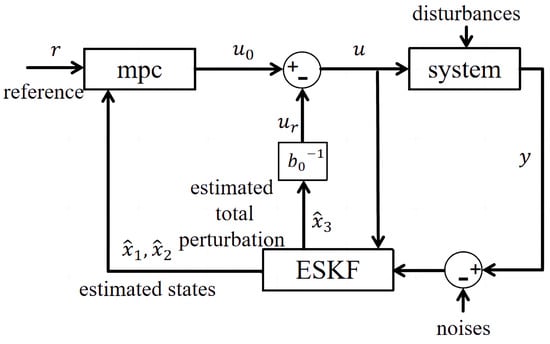
Figure 2.
Proposed control architecture.
3.1. ESKF Design
Based on the controlled object model in (2), a continuous varying nonlinear model can be obtained as follows:
Consider adopting a second-order integrator model to characterize the behavior of the revised device, with the anticipation that the ESKF will align with the actual dynamics observed. The variable to be controlled is expressed as y, the variable under manipulation is u, with K indicating the static gain, as the apparent time constant, and d is the total disturbances.
Employing a second-order integrator model to depict the updated process yields considerable merits: it creates a predetermined analytical structure with an explicit order for the control process, thereby streamlining the identification of parameters. It mirrors the integrative behavior that is typically present in industrial operations and simulates additional primary dynamics using a term influenced by a time constant. This additional temporal characteristic enhances the observer capacity for estimation, offering a more comprehensive dynamic insight than what is provided by a basic series of integrator. The continuous-time state-space representation is given in (4):
with ,, , . represents the system state, represents the control input, represents the comprehensive measurement, includes disturbances and unknown nonlinear dynamics, and and are standard Wiener processes in two and one dimensions, respectively. It is assumed that , and are independent. and , respectively, determine the covariances of the process and measurement noise.
Drawing upon the concept of an Extended State Observer (ESO) [25], the external disturbance is treated as an extended state, , which then allows for the design of an ESKF to estimate the system states and external disturbances as follows:
where . Let
Then, system can be rewritten as:
The ESKF design, which incorporates the advantages of both ESO and KF, is as follows:
with , , , .
The continuous-time ESKF design is presented to provide an intuitive understanding of its theoretical foundation and dynamic characteristics. However, for experimental implementations and real-time applications, the discrete form is employed, following standard practices in digital control systems. In our study, we discretize the continuous-time ESKF model using the forward Euler method.
3.2. MPC Design
At the k instant, the cost function J for prediction is expressed as:
where . J includes the sum of error weighting, input weighting, and terminal error. Here, N and M are weight coefficient matrices and both are diagonal matrices. The optimization objective is to minimize the cost, i.e., to . The expression for J involves two variables (the input u and the state e), which is one more variable compared to the general form of quadratic programming. Since the control goal is the control input, it is necessary to eliminate the variable e.
Assuming the prediction horizon is n, then the control inputs and states at the prediction boundary can be described as:
The system mathematical model can be rewritten through the tracking error :
with , d is considered as an uncertain variable. Let , then we have:
Let ; we can obtain that: . Now, can be expressed as:
where
Simplifying the cost function yields:
Substituting into the above equation, eliminating the variable and simplifying:
wherein .
Solving for the quadratic standard form cost function, the optimal output can be obtained. Taking the first item , the current optimal output is obtained.
4. Simulation
In this section, the ESKF-based MPC simulations are carried out, which is designed with the ISP in Equation (2) as the controlled objects. The key parameters of ESKF are as follows: is the apparent time constant, represents the static gain, , , , . The key parameters of MPC are as follows: the prediction horizon , the weight coefficient matrices , , . By using the forward Euler method, the continuous-time ESKF model is discretized into an algorithm form executable by a digital computer.
In the simulations, the tolerance to model errors and the disturbance suppression ability of the ESKF-based MPC were evaluated. Initially, in the absence of external disturbances, the model parameters of the controlled object state-transfer matric A in the closed-loop system were altered, as illustrated in Table 1. Under varying model conditions, the MPC method based on Kalman filters (KF-based MPC) exhibited increased amplitude and phase lagas, as shown in Figure 3. In contrast, the ESKF-based MPC method demonstrated superior tracking performance even when the model changed.

Table 1.
Uncertain parameters of model error simulations.
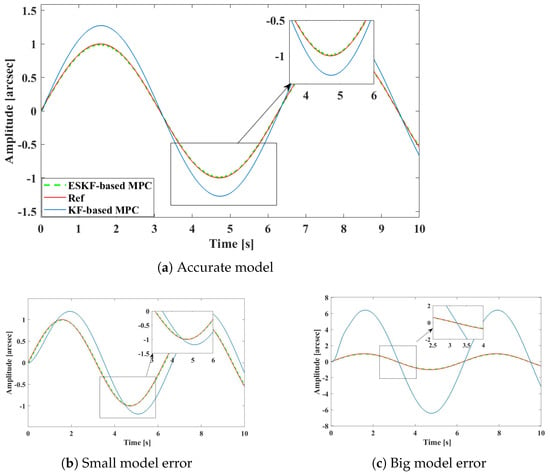
Figure 3.
Closed-loop response of ISP subject to KF-based MPC and ESKF-based MPC for sinusoidal signal.
Considering external disturbances, two sets of experiments were conducted with different types of disturbances: one with step disturbances and the other with sinusoidal disturbances. In the simulations, step disturbances with an amplitude of 2 and a step time of 5 were introduced, as well as mixed step disturbances with an amplitude of 1, a step time of 2, and an amplitude of 2 with a step time of 5, as shown in Figure 4. It was observed that, regardless of whether the disturbance was a step or sinusoidal, the ESKF-based MPC method outperformed the KF-based MPC method in terms of disturbance rejection.
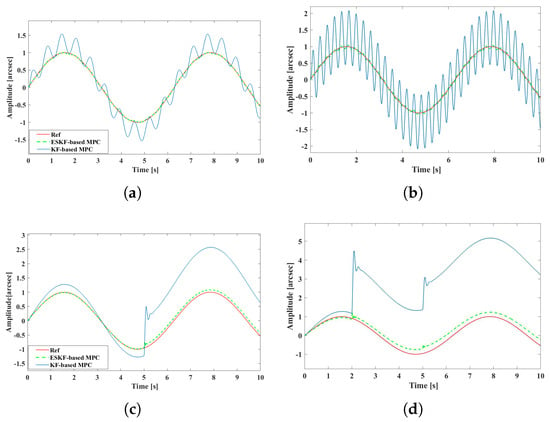
Figure 4.
Closed-loop response of ISP subject to KF-based MPC and ESKF-based MPC for sinusoidal reference. (a) Sinusoidal disturbance (amplitude = , frequency = ). (b) Sinusoidal disturbance (amplitude = , frequency = ). (c) Step disturbance amplitude = 1, step time = 5. (d) Multiple step disturbances amplitude = 1, step time = 5 s and amplitude = 2, step time = 2 s.
5. Experiments
5.1. Experiment Setup Description
The experimental setup of this study, as depicted in Figure 5, comprises three main components: a mechanical structure module, a driver module, and a control box module. The control box is primarily outfitted with a digital controller that operates on the VxWorks real-time operating system (RTOS), a flight board that utilizes a field-programmable gate array (FPGA), and a MOXA PC/104 serial card.

Figure 5.
ISP experiment setup.
The primary function of this apparatus is to ensure that the light signal remains centered on the position-sensitive detector. To achieve this, the disturbance platform replicates external disturbances, applying them to the electro-optical tracking system (ETS) to emulate real-world errors. In response to these simulated disturbances, the controller computes the necessary control values to counteract the errors. These corrective signals are then relayed to the driver module, which adjusts the ETS’s attitude accordingly, ensuring the stabilization of the Line of Sight (LOS). The experimental device operates at a working frequency of 5000 Hz, enabling it to respond rapidly to the dynamic conditions of the tracking environment.
5.2. Experiment Results
The subsequent experimental results were obtained to evaluate the performance of the KF-based MPC and the method proposed in this study. The specific parameter configurations for ESKF-based MPC are as follows: is the apparent time constant, represents the static gain, , , , . The key parameters of MPC are as follows: the prediction horizon , the weight coefficient matrices , , .The experiments setup is shown in Table 2.

Table 2.
Experiments setup.
Tracking performance is a fundamental performance indicator for electro-optical tracking systems. To validate the proposed method, we conducted comparative experiments on an experimental platform with a given signal of 1 Hz frequency and 100 arcsec amplitude, comparing the proposed method against KF-based MPC, Extended State Observer (ESO) and the Disturbance Observer (DOB). The results of Experiment E1 are depicted in Figure 6. It is evident that the maximum tracking error of the KF-based MPC reached 46.9 arcsec, while the proposed method reduced the maximum error to 5.2 arcsec, achieving an 88.9% reduction. The ESO observed a maximum tracking error of 84.8 arcsec, from which we can conduct that the ESKF-based MPC achieved a 93.9% reduction. The maximum tracking error of DOB was 77.99 arcsec, leading to the conclusion that the ESKF-based MPC realized a 93.3% reduction.
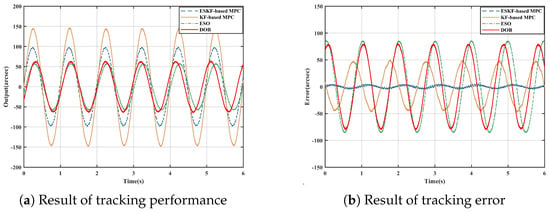
Figure 6.
Comparison of experiment E1.
With the expanding application scenarios of electro-optical tracking systems in complex environments, multiple disturbances have become the main factors affecting the stability of the LOS. In practical applications, step and sinusoidal disturbances are the most common perturbations impacting LOS stability. We have performed comparison experimental analysis on the proposed method against step and sinusoidal disturbances.
The experiment E2 results are shown in Figure 7, demonstrate that the proposed method effectively and accurately tracks the given sinusoidal signal compared to the KF-based MPC. It is evident that the maximum tracking error for the KF-based MPC reached 83.5 arcsec, whereas the proposed method achieved a maximum tracking error of 16.2 arcsec, representing a decrease of 80.5%. The maximum tracking error for the ESO reached 84.6 arcsec, representing a decrease of 80.9%. And the maximum tracking error for the DOB reached 76.8 arcsec, representing ESKF-based MPC realized a decrease of 78.9%.
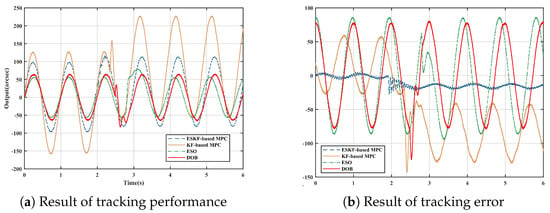
Figure 7.
Comparison of experiment E2 with step disturbance.
Disturbances affecting the performance of electro-optical tracking systems are primarily concentrated in the mid to low frequency range. In the experiments, we introduced a sinusoidal disturbance at a frequency of 5 Hz. The experiment E3 results are depicted in Figure 8, show that the proposed method can accurately track the given signal, significantly reducing the maximum error compared to the KF-based MPC, ESO and DOB. The maximum error reduction was 166.9 arcsec, 126.9 arcsec, 170.9 arcsec, respectively. To further clarify the impact of periodic disturbances on the system, a spectral analysis was conducted. The spectral analysis results, as shown in the figure, indicate that at 5 Hz, the amplitude reached by the proposed method, KF-based MPC, ESO, DOB was 16.7 dB, 37.2 dB, 30.6 dB and 35.9 dB. At 1 Hz, the amplitude reached by the proposed method, KF-based MPC, ESO, DOB was 4.4 dB, 26.2 dB, 32.5 dB and 31.7 dB. The results showed that both DOB and ESO have better disturbance rejection ability than KF-based MPC, but KF-based MPC has better tracking accuracy than ESO and DOB. More importantly, we can obtain the conclusion that ESKF-based MPC has the best disturbance suppression effect and the highest tracking accuracy among the four experimental methods.
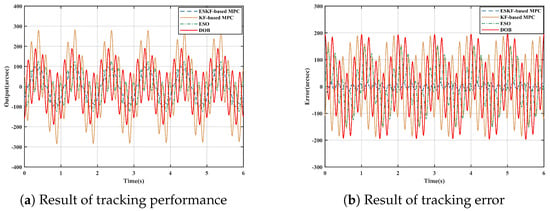
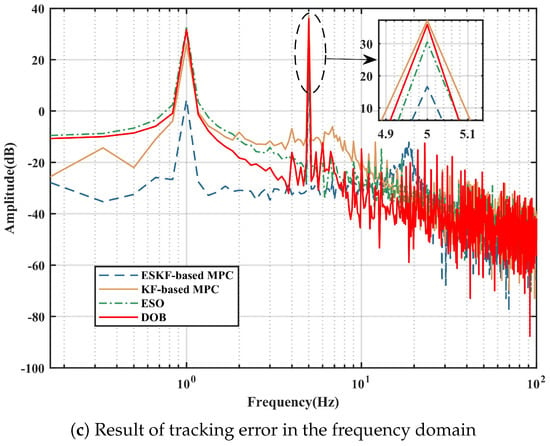
Figure 8.
Comparison of experiment E1 with sinusoidal disturbance.
Above all, the proposed method has exhibited outstanding performance in both tracking accuracy and disturbance suppression. Compared to the KF-based MPC, ESO and DOB, the proposed method has reduced the tracking error by 88.9%, 93.9%, 93.3%. On the other hand, in terms of disturbance suppression capability, the proposed method has shown significant effectiveness against both step and sinusoidal disturbances. Specifically, for sinusoidal disturbances, the amplitude at the disturbance frequency both 1 Hz and 5 Hz, ESKF-based MPC shows the best tracking accuracy and the best disturbance rejection, respectively.
6. Conclusions
Despite the excellent disturbance rejection capabilities of traditional electro-optical tracking control algorithms, their disturbance suppression performance can be degraded by concurrent internal and external disturbances, along with sensor noise. To achieve satisfactory disturbance suppression performance, this paper develops an ESKF-based MPC algorithm. Initially, the ESKF is designed to discern both the system states and the disturbances from inside and outside, actively offsetting these disturbances and mitigating the effects of measurement noise. Next, amid the influence of both internal and external disturbances, along with measurement noise, the ESKF-based MPC is developed. This controller devises an objective function that prioritizes the minimization of tracking discrepancies and the increments in control inputs, thereby transforming the task of trajectory tracking into an optimization challenge. Thirdly, the ESKF-based MPC prompts the actual process dynamics to align with a revised process model resembling a first-order integrator. Following this, a predictive control strategy is formulated based on a second-order state space, which is predicated on merely two parameters: the apparent time constant and the nominal control gain. This is in contrast to traditional MPC frameworks, which are extensively reliant on a meticulously recognized model. By characterizing the revised process model as a second-order integrator, the predictive model’s order is securely established. Thus, the intricacy of the optimization task tied to the derivation of the predictive control strategy hinges solely on the extent of the time horizon chosen. Finally, experimental results tracking trajectory after model parameter modifications and two different types of external disturbances demonstrate the effectiveness and robustness of the controller under external disturbances, measurement noise, and model uncertainties.
Author Contributions
Conceptualization, W.X. and T.G.; Methodology, W.X. and T.G.; Software, W.X. and L.Z.; Validation, W.X. and H.W.; Formal analysis, W.X.; Investigation, W.X.; Data curation, W.X. and H.W.; Writing—original draft, W.X. and L.Z.; Writing—review and editing, Y.M. and Q.B. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Natural Science Foundation of China (Grant No. 62271109).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- He, T.; Wu, Z. Multirate iterative learning disturbance observer with robustness to frequency deviation for high precision attitude stabilization of flexible spacecraft subject to complex disturbances. Aerosp. Sci. Technol. 2020, 96, 105583. [Google Scholar] [CrossRef]
- Han, B.; Jiang, Y.; Yang, W.; Xu, Y.; Yao, J.; Zao, Y. Kinematics characteristics analysis of a 3-UPS/S parallel airborne stabilized platform. Aerosp. Sci. Technol. 2023, 134, 108163. [Google Scholar] [CrossRef]
- Wang, X.-L.; Cai, X.-D.; Su, Z.-E.; Chen, M.-C.; Wu, D.; Li, L.; Liu, N.-L.; Lu, C.-Y.; Pan, J.-W. Quantum teleportation of multiple degrees of freedom of a single photon. Nature 2015, 518, 516–519. [Google Scholar] [CrossRef]
- Yin, J.; Cao, Y.; Li, Y.H.; Liao, S.-K.; Ren, J.-G.; Cai, W.-Q.; Li, B.; Dai, H.; Li, G.-B.; Lu, Q.-M.; et al. Satellite-based entanglement distribution over 1200 km. Science 2017, 356, 1140–1144. [Google Scholar] [CrossRef]
- Abdo, M.M.; Vali, A.R.; Toloei, A.R.; Arvan, M.R. Stabilization loop of a two axes gimbal system using self-tuning PID type fuzzy controller. ISA Trans. 2014, 53, 591–602. [Google Scholar] [CrossRef]
- Ding, Z.; Zhao, F.; Lang, Y.; Jiang, Z.; Zhu, J. Anti-Disturbance Neural-Sliding Mode Control for Inertially Stabilized Platform With Actuator Saturation. IEEE Access 2019, 7, 92220–92231. [Google Scholar] [CrossRef]
- Kamel, M.; Stastny, T.; Alexis, K.; Siegwart, R. Model predictive control for trajectory tracking of unmanned aerial vehicles using robot operating system. In Robot Operating System (ROS) the Complete Reference; Springer: Berlin/Heidelberg, Germany, 2017; Volume 2, pp. 3–39. [Google Scholar]
- Tang, T.; Niu, S.; Chen, X.; Qi, B. Disturbance observer-based control of tip-tilt mirror for mitigating telescope vibrations. IEEE Trans. Instrum. Meas. 2018, 68, 2785–2791. [Google Scholar] [CrossRef]
- Han, B.; Gao, H. Linear Parameter-Varying Model Predictive Control for Hydraulic Wind Turbine. Actuators 2022, 11, 292. [Google Scholar] [CrossRef]
- Zhou, X.; Zhao, B.; Liu, W.; Yue, H.; Yu, R.; Zhao, Y. A compound scheme on parameters identification and adaptive compensation of nonlinear friction disturbance for the aerial inertially stabilized platform. ISA Trans. 2017, 67, 293–305. [Google Scholar] [CrossRef]
- Su, Y.R.; Wang, Q.; Yan, F.B.; Huang, Y.M. Friction compensation for an m-Level telescope based on high-precision LuGre parameters identification. Res. Astron. Astrophys. 2021, 21, 19. [Google Scholar]
- Xu, Y.; Shao, X.; Hu, Q.; Song, B. Anti-disturbance fault-tolerant control with flexible performance for combined spacecraft attitude tracking under limited thrusts. Control Eng. Pract. 2023, 134, 105455. [Google Scholar] [CrossRef]
- Riel, T.; Galffy, A.; Janisch, G.; Wertjanz, D.; Sinn, A.; Schwaer, C.; Schitter, G. High performance motion control for optical satellite tracking systems. Adv. Space Res. 2020, 65, 1333–1343. [Google Scholar] [CrossRef]
- Li, J.; Zhang, L.; Li, S.; Su, J. A Time Delay Estimation Interpretation of Extended State Observer-Based Controller With Application to Structural Vibration Suppression. IEEE Trans. Autom. Sci. Eng. 2023. [Google Scholar] [CrossRef]
- Dong, Z.; Sun, Z.; Sun, H.; Wang, W.; Mei, X. A Novel Control Method for Permanent Magnet Synchronous Linear Motor Based on Model Predictive Control and Extended State Observer. Actuators 2024, 13, 34. [Google Scholar] [CrossRef]
- Yang, Z.; Wang, Z.; Yan, M. An Optimization Design of Adaptive Cruise Control System Based on MPC and ADRC. Actuators 2021, 10, 110. [Google Scholar] [CrossRef]
- Cao, Y.; Yan, P.; Lin, S.; Zhou, Z.; Zhang, W. KF-based MPC for the cascaded headbox system in papermaking process. In Proceedings of the 2017 36th Chinese Control Conference (CCC), Dalian, China, 26–28 July 2017; IEEE: New York, NY, USA, 2017; pp. 4369–4374. [Google Scholar]
- Yang, J.; Zheng, W.X. Offset-free nonlinear MPC for mismatched disturbance attenuation with application to a static var compensator. IEEE Trans. Circuits Syst. II Express Briefs 2013, 61, 49–53. [Google Scholar] [CrossRef]
- Dai, Y.; Yu, S.; Yan, Y.; Yu, X. An EKF-based fast tube MPC scheme for moving target tracking of a redundant underwater vehicle-manipulator system. IEEE/ASME Trans. Mechatron. 2019, 24, 2803–2814. [Google Scholar] [CrossRef]
- Gallego, A.J.; Sánchez, A.J.; Berenguel, M.; Camacho, E.F. Adaptive UKF-based model predictive control of a Fresnel collector field. J. Process. Control 2020, 85, 76–90. [Google Scholar] [CrossRef]
- Bai, W.; Xue, W.; Huang, Y.; Fang, H. On extended state based Kalman filter design for a class of nonlinear time-varying uncertain systems. Sci. China Inf. Sci. 2018, 61, 042201. [Google Scholar] [CrossRef]
- Xue, W.; Zhang, X.; Sun, L.; Fang, H. Extended state filter based disturbance and uncertainty mitigation for nonlinear uncertain systems with application to fuel cell temperature control. IEEE Trans. Ind. Electron. 2020, 67, 10682–10692. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, L.; Mao, Y.; Bao, Q. A novel fuzzy extended state observer-based control for electro-optical tracking system with disturbances and measurement noises: Design, analysis and experiments. Control Eng. Pract. 2024, 142, 105775. [Google Scholar] [CrossRef]
- Quattrocchi, G.; Berri, P.C.; Vedova, M.D.L.D.; Maggiore, P. Innovative Actuator Fault Identification Based on Back Electromotive Force Reconstruction. Actuators 2020, 9, 50. [Google Scholar] [CrossRef]
- Li, J.; Zhang, L.; Luo, L.; Li, S. Extended state observer based current-constrained controller for a PMSM system in presence of disturbances: Design, analysis and experiments. Control Eng. Pract. 2023, 132, 105412. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).