Abstract
The wheel slide protection control system for rail vehicles plays a crucial role in ensuring a consistent braking performance in all operating environments, making it a vital factor in the safety and efficiency of rail transportation. In this paper, a hybrid approach to wheel slide protection control is presented, which combines the rule-based control strategy and the model-based control methods using adhesion force estimation. Model-based control usually relies on mathematical models to characterize the vehicle dynamics, requiring online estimators to be designed or extra sensors to be added for practical application. Rule-based control operates on predefined rules and thresholds and the available data from vehicles in service. A comparative test was conducted between the traditional rule-based control strategy and the proposed combined control strategy using a semi-physical simulation test bench. The performance differences of the control strategies were analyzed from two perspectives: adhesion utilization and air consumption. It was observed that among the traditional 2-phase, 3-phase, 4-phase and the optimized 4-phase combined control method, the combined control strategy has the best adhesion utilization and the traditional 4-phase control strategy has the least air consumption.
1. Introduction
Due to the significant advancements in global rail infrastructure, the mileage of high-speed and urban transit lines has seen a steady rise, greatly contributing to the convenience of resident travel and promoting economic growth in local areas. Rail transport has the advantages of a large capacity, safety and punctuality, which means that the braking system needs to stop the train in the shortest distance. However, the wheel–rail adhesion is one of the constraints on the braking distance, as the most frequently used tread braking and disc braking both rely on adhesion. Adhesion characteristics are very susceptible to the influence of natural precipitation and track surface pollutants and other factors, with uncertainty [1,2]. When the adhesion condition deteriorates, the available adhesion will be significantly reduced, and skidding will occur during braking. If skidding is not detected and effectively suppressed, the wheels will slide directly on the surface of the rail. The uncontrolled friction may lead to serious damage to the rail surface and tread surface. At the same time, the actual utilization of adhesion is greatly reduced, which prolongs the braking distance, affects the normal running interval of trains and even causes safety accidents. Therefore, wheel slide protection (WSP) systems for improving adhesion utilization and avoiding wheel lock is one of the most significant functions for rail vehicles [3,4].
At present, the control strategies of WSP systems on rail vehicles are basically rule-based control. For engineering applications, rule-based control is easy to implement and is also more suitable for anti-skid valves with switching characteristics. This type of control generally uses speed difference, deceleration, slip ratio, etc. as the criterion. The values of the thresholds mainly rely on engineers’ experience and field tests [5]. The reference speed should be the running speed of the train, but due to the limitation of the train’s electrical architecture, the traditional WSP control system cannot obtain the train speed directly. Therefore, many methods have been developed for the calculation of the reference speed, such as the highest axle speed method, linear calculation method and the introduction of the radar or inertial measurement unit, as well as multi-sensor fusion approaches, etc. [6,7,8].
For rail vehicles, the number of axles in the train is much higher than that of general land transport. Based on the progress of train communication networks, taking the maximum axle speed of the whole train as the reference speed can be realized. Meanwhile, in order to ensure the speed reliability of the automatic train protection (ATP) system, there is an axle which will be fully released once it slides during braking; this means that the axle’s speed will recover to the same value as the car, which ensures the accuracy of the train speed measurement.
For the rule-based WSP system, the most important components are the criterion selection and threshold value. Through actual vehicle testing, low-adhesion rail surface conditions are artificially created, and the WSP control performance can be optimized by debugging the parameters of the embedded software in a large number of tests [9]; however, the required manpower and financial costs are too high. Some researchers use fuzzy logics to optimize the thresholds of WSP control, such as [10,11,12,13]. Nakazawa et al. [14,15] adopted the slip ratio as a WSP control criterion and designed a new threshold of the time to wheel-lock to optimize the re-adhesion control point. Chen et al. [16] developed a finite state machine approach to model the WSP control logic, which simplifies the programming complexity. However, pre-commissioning and engineering experience play a significant role in the implementation of these approaches.
Similar research has been conducted in the field of locomotive traction adhesion control, and the difference is that the actuator is changed from anti-skid valves to electric motors. Traction adhesion control also uses rule-based control algorithms, also called correction-based methods, for example, using measured values such as speed difference, acceleration, differential of acceleration, etc. [17]. The traction force will be quickly reduced after the slip of an axle is detected, and then slowly increases to slip again, and then the traction force reduces again. Repeat this cycle until the traction force can be restored to the target value without a slip of the wheels.
Model-based control often revolves around the optimal slip ratio; i.e., the adhesion peak. To obtain the optimal slip ratio, the adhesion coefficient information is required. The expected optimal slip ratio point is not fixed and will change under various adhesion conditions and with speed. Therefore, it is necessary to identify the adhesion characteristics and determine the peak point of the adhesion coefficient-slip ratio curve. There are many studies on wheel–rail adhesion characteristics. Theoretical calculation studies represented by Kalker’s theory [18] are mostly based on elastic contact mechanics. Experimental studies focus on the macro characteristics and influencing factors of the adhesion coefficient [19]. These studies help us understand the mechanism of adhesion, creep and slide and the characteristics of changes in the adhesion coefficient. However, due to the complexity of the wheel–rail interface, models or experimental curves have not been directly applied to railway vehicle control systems. Spiryagin et al. [20] used the adhesion coefficient under dry, wet and oily conditions as a benchmark, and compared the identified adhesion coefficient with the benchmark to determine the current rail surface condition. The accuracy of the rail surface condition judgment depends on the prior knowledge.
In addition, the macroscopic common feature that the slope of the adhesion–slip ratio curve at the peak point is 0 under different conditions is used to find the peak point. The key is to obtain the adhesion state between the wheel and rail in real time. However, direct online measurement of the adhesion coefficient is difficult to achieve, so it can be estimated through established models or methods. Shrestha et al. [21,22] designed an estimator with closed-loop characteristics in adhesion coefficient estimation, which is, in essence, a sliding mode observer. It is necessary to use high gain to approximate the angular velocity measurement value and the estimated value to estimate the adhesion coefficient. There are other methods to estimate the adhesion force, such as the disturbance observer [23,24] and maximum likelihood identification methods [25].
The calculation of the slip ratio is simple when the reference speed is known. Then, the optimal slip ratio can be identified. The literature [26,27,28,29] presents the acquisition and control methods of the optimal slip ratio. Sliding mode control and other methods [30,31,32] are used to continuously control the slip ratio in closed loop. In [33], a PI-based and fuzzy-logic-based sliding mode controller in locomotive traction adhesion control were compared, and it was found that the fuzzy-logic-based controller had a better performance at handling changes in the wheel–rail contact conditions.
In summary, the advantage of rule-based WSP is that it has strong control stability and safety in real vehicle deployment, and requires lower resources. The advantage of model-based control is that it incorporates the key information of wheel–rail adhesion, but due to the discontinuous characteristics of the anti-skid valves and the nonlinearity of the pneumatic system, its control is difficult. Moreover, in real vehicle applications, the slope-based optimal slip ratio searching method has limitations due to the influence of noise. Therefore, this paper proposes the adhesion estimation method and introduces adhesion information into the rule-based WSP control mode. This can take the advantages of both and facilitate actual vehicle application.
The following sections outline the structure of this paper. Section 2 introduces the WSP control system scheme. Section 3 explains the design method of the 4-phase rule-based WSP control. Section 4 undertakes the optimization of the 4-phase WSP control, utilizing the adhesion force estimation algorithm. Section 5 presents and discusses the test method and the outcomes of the proposed strategies. Lastly, Section 6 concludes the study and proposes further research recommendations.
2. Working Principle of Rail Vehicle WSP Systems in Service
2.1. System Components
The rail vehicle WSP system employs rule-based control strategies, utilizing periodic motion state detection and anti-skid valves switch control. The WSP control system consists of three primary components: the WSP controller, the anti-skid valves and the axle speed sensors. As depicted in Figure 1, the WSP controller receives the pulse signal from a speed sensor attached to the end of the shaft and computes the rotational speed and deceleration. Subsequently, it drives the anti-skid valves to release, hold or supply compressed air to the brake actuation unit (brake cylinder).
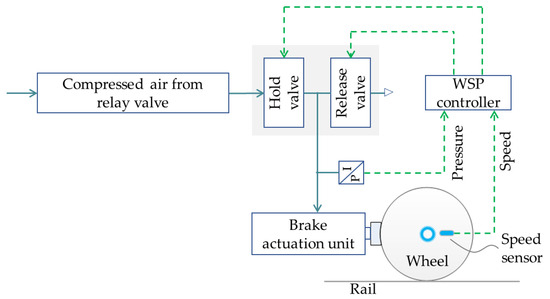
Figure 1.
Schematic diagram of the WSP system.
2.2. Working Principle
As shown in Figure 2a, the brake cylinder pressure and sliding axle’s speed are changing periodically during a WSP test. A typical WSP control cycle is shown in Figure 2b. As braking initiates, the brake cylinder pressure rises, and the vehicle and axles begin to decelerate. Under low-adhesion conditions, the axle’s deceleration increases rapidly, resulting in a large speed difference between the axle and the vehicle. When the axle’s deceleration or speed difference exceeds the threshold at point A, the wheel is considered to be skidding. Subsequently, the hold valve (HV) cuts off the upstream air supply to brake cylinders, and the release valve (RV) vents the air from the brake cylinders to the atmosphere. This state is called release mode. When the cylinder pressure drops down, the axle’s deceleration increases negatively to a maximum and then decreases until it becomes positive. Thus, the speed difference also decreases after reaching a maximum value. After detecting that the skidding tendency is effectively suppressed with the deceleration threshold at point B, the hold mode occurs. If the skidding continues to weaken, which means the speed difference decreases to satisfy the threshold at point C, the anti-skid valves will enter the supply mode and the brake cylinders will be recharged. If there no skidding occurs, the WSP control ends; otherwise, it will enter the next cycle. This WSP control method is cyclical, and different states exist in each control cycle, using wheelset deceleration, speed difference, etc. as the criteria for switching between the states.
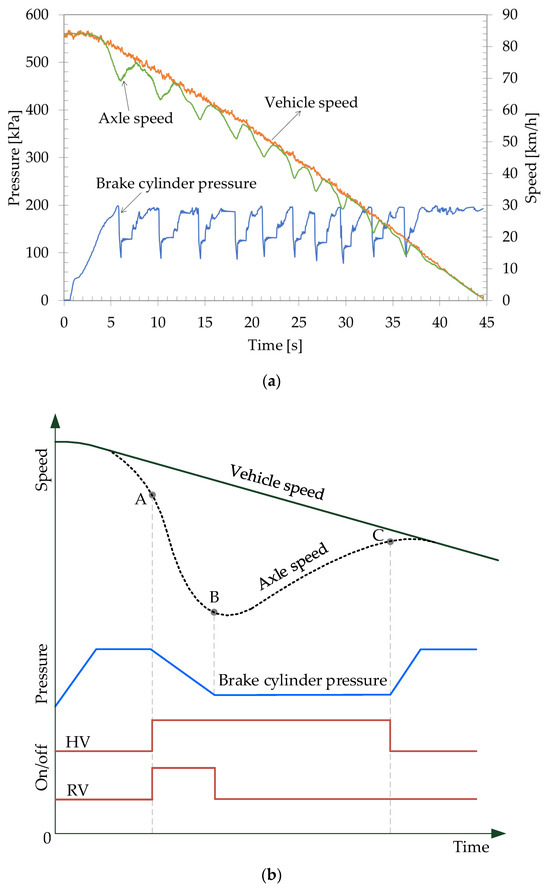
Figure 2.
Working principle of WSP control system in rail vehicles. (a) Curves from a WSP test. (b) A typical WSP control cycle.
3. Design of a 4-Phase WSP Control Mode
The rule-based WSP control strategy can be illustrated using automata theory. During the WSP control process, the adjustment of the braking force is achieved by supplying, holding and exhausting the air of the brake cylinders through anti-skid valves. The compressed air flows from the relay valve to the brake cylinders when in supply mode, and from the brake cylinders to the atmosphere when in release mode. Thus, an effective WSP control cycle should contain at least two states: supply and release.
As shown in Figure 3a, the 2-phase automaton is formed when the speed difference is greater than the threshold () for releasing and less than the other threshold () for supplying. Based on the principle of hysteresis loop, it can be seen that should be greater than , which forms the basis of cyclic WSP control.
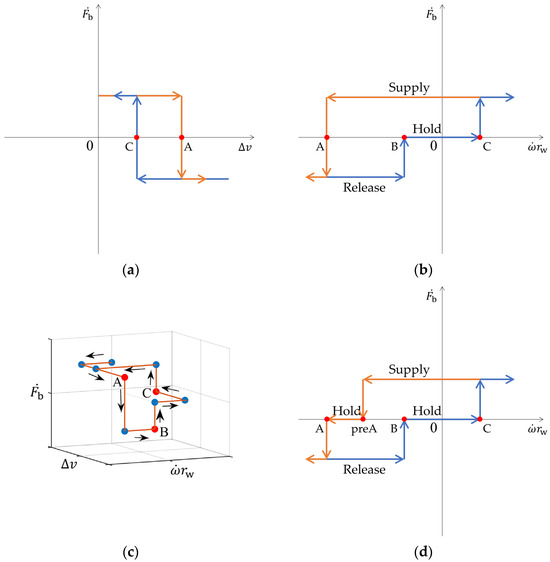
Figure 3.
Schematic diagrams of WSP control strategy. (a) 2-phase with a hysteresis loop based on speed difference. (b) 3-phase with a hysteresis loop and a dead zone from viewpoint of deceleration. (c) 3-phase with a hysteresis loop based on speed difference and a dead zone based on deceleration. (d) 4-phase control strategy from viewpoint of deceleration.
Furthermore, a pressure holding state, named the hold mode, is added to the control cycle, so that the braking force can be kept constant when skidding is effectively suppressed, constituting a 3-phase automaton (Figure 3b. The judgement of a skidding tendency often depends on the deceleration. When the axle’s deceleration satisfies , where , the hold mode occurs. The hold mode can be regarded as an actively added dead zone of deceleration. The three-dimension switching trajectory of the 3-phase WSP control automaton with speed difference a hysteresis loop and deceleration dead zone is shown in Figure 3c. For a viewpoint of the speed difference, . For a viewpoint of deceleration, and .
The speed difference criterion is the assurance of system stability. The deceleration criterion improves the sensitivity of control whilst also enhancing the fault tolerance of WSP in the scenario of reference speed failure. On this basis, in contrast to the process of the gradual elimination of skidding, the process of the gradual occurrence of skidding also introduces a hold mode; i.e., it constitutes a 4-phase automaton, depicted in Figure 3d.
The phase switching points of the automata and the corresponding criterion conditions are summarized in Table 1.

Table 1.
Phase switching points and its criterion of the WSP control system.
In the 4-phase WSP control mode, a closed trajectory, shown in Figure 4, is formed in the phase plane of the speed difference and braking force. This is the limit cycle of 4-phase WSP control. The upper edge of the trajectory is the maximum braking force in the WSP process, while the lower edge is the minimum braking force. The left and right edges are the speed difference fluctuation intervals. The formation of the trajectory is determined by four switching points. Traditional rule-based control cannot provide a theoretical basis for the design of these four switching points and can only rely on experience or extensive testing. Therefore, the adhesion threshold method is proposed in the next section to optimize it.

Figure 4.
Limit cycle of the 4-phase WSP control.
4. Optimization of 4-Phase Control Based on Adhesion Threshold
4.1. Adhesion Force Estimation
In the train braking process, if the adhesion force can be monitored online, the braking force can be adjusted according to the real-time usage of adhesion force and the actual state of the wheel. Thus, the wheel motion state and wheel–rail adhesion can be actively controlled. However, the use of adhesion force cannot be directly acquired, it can only be indirectly obtained according to other information that can be measured. Therefore, the research of new WSP control methods should first solve the problem of estimating the use of adhesion force.
The principle of adhesion estimation is shown in Figure 5. Firstly, according to the force relationship of the rotational motion of the wheel, it can be obtained as:
where is the moment of inertia of the wheelset; is the angular speed; is the adhesion force; is the braking force; is the radius of the wheel’s rolling circle.
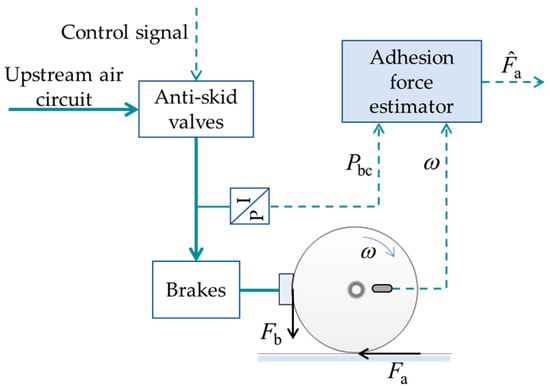
Figure 5.
Schematic diagram of adhesion force estimation method.
The adhesion force is an unknown quantity, which is expressed according to Equation (1), as:
As the angular acceleration is difficult to measure directly, the perturbation observer method is used to estimate the adhesion force. Firstly, the Laplace transform of Equation (2) is obtained as:
where is the Laplace operator.
To reduce the impact of the measurement noise, a first-order low-pass filter with a cut-off frequency of is applied to the right side of Equation (3) to obtain:
Transform Equation (4) as:
where is defined as:
By performing the inverse Laplace transform to Equation (6), we can derive:
Solving the differential equation shown in Equation (7) yields , with which we can determine the estimate of the adhesion force as:
4.2. Combined 4-Phase Adhesion Threshold Algorithm
Based on the WSP automaton framework and criterion design principles analyzed in the previous section, a combined 4-phase control strategy based on the adhesion threshold is proposed for the problem that the traditional rule-based control strategy may not be well adapted to complex adhesion conditions.
The adhesion information is introduced into the WSP automata model to optimize the criterion setting, and the thresholds, based on the estimated adhesion force, are presented as follows:
- (1)
- Point preA: , , where is the mass of a quarter vehicle.
- (2)
- Point A: and . It corresponds to points located to the right of the peak adhesion point and has a tendency for an increasing speed difference.
- (3)
- Point B: there are two choices, one is or , and the other is and . It corresponds to points located below the adhesion-limited braking force and has a tendency for a decreasing speed difference.
- (4)
- Point C: and . It corresponds to points located to the left of the peak adhesion point and has a tendency for a decreasing speed difference.
The simulation results are shown in Figure 6. From Figure 6a,c, it can be seen that the trajectory of the adhesion coefficient keeps moving along the peak adhesion point during the braking process. As the vehicle speed decreases, the peak adhesion point increases and the speed difference corresponding to the peak adhesion point decreases gradually; therefore, the adhesion force and braking force in Figure 6b are on the rise and the closed trajectory keeps moving in the direction of a decreasing speed difference. According to Figure 6b,d, it is evident that the braking force consistently maintains a higher level than the adhesion force during the braking process. Additionally, the adjustment range of the braking force gradually reduces over time.
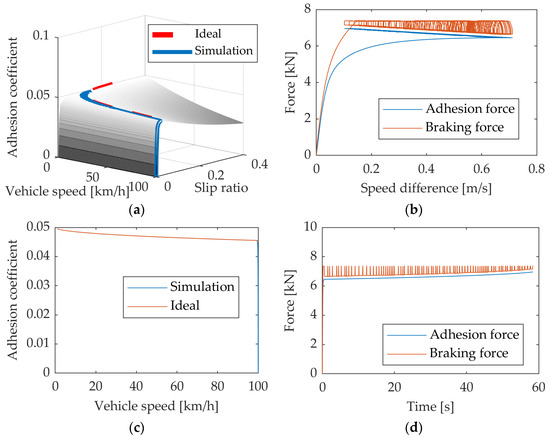
Figure 6.
Simulation results of optimized control strategy based on adhesion estimation. (a) Adhesion coefficient versus vehicle speed and slip ratio. (b) Phase plane of force versus speed difference. (c) Adhesion coefficient. (d) Adhesion force and braking force.
5. Test Verification and Results Discussion
In order to analyze and verify the actual performance of the control method proposed in this paper, a test via hardware-in-the-loop (HIL) simulation is performed. As the tests on actual railway lines with real vehicles requires a very high cost of investment and inter-organizational coordination, HIL testing is an affordable and sustainable way to evaluate WSP systems [33,34].
5.1. HIL Test Bench for the WSP System of Rail Vehicle
5.1.1. Architecture
The test bench (Figure 7a) adopts a combination of hardware and software, and the basic architecture is shown in Figure 7b. The WSP control algorithm is integrated in the real-time controller. The vehicle system and wheel–rail adhesion characteristics are simulated using software models, and the brake/WSP air circuit are physical. Among them, the host computer adopts Advantech’s industrial controller platform, equipped with an AIMB-706 industrial-grade motherboard, and the simulation computer adopts National Instrument’s PXI Express platform, equipped with a PXIe-8880 high-performance embedded controller, running a real-time operating system. Before the start of the test, the host computer will generate a real-time code for the WSP control program and download it to the simulation computer. During the test, the host computer and the simulation computer will interact with each other via ethernet, and the simulation computer is connected to the anti-skid solenoid valves and pressure sensors via data acquisition cards and signal conversion circuits.

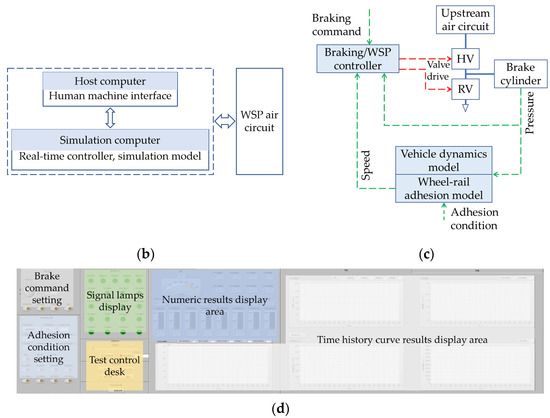
Figure 7.
HIL test bench for railway vehicle WSP. (a) Photography. (b) Architecture. (c) Test principle. (d) Human machine interface.
The basic principle of the WSP control test is depicted in Figure 7c. The WSP controller works according to the states of the vehicle, and the control effect causes the brake cylinder pressure to change, and the change in pressure is then reflected in the model to cause the change of vehicle states, thus forming a closed-loop verification environment. The human machine interface software is deployed in the host computer, which is shown in Figure 7d.
5.1.2. Model
During testing, the vehicle’s motion state is simulated using a model, which utilizes a simplified longitudinal dynamics model with one degree of freedom for longitudinal movement and four degrees of freedom for rotation of the wheelsets. The adhesion force between the wheel and rail is calculated using the adhesion model based on the vehicle speed and axle speed information.
(1) Vehicle longitudinal dynamics model
As the testing of the braking and WSP control process in this paper focuses on the longitudinal motion of the vehicle body and the rotational motion of the wheelsets, the simplified model is shown in Figure 8, with inputs of the braking force for the four axles and outputs of the axle speed and vehicle speed. The simplified longitudinal dynamics model is adopted because it requires less computation resources and is more convenient for real-time simulation. The inner vibration characteristics caused by the stiffness and damping inside the vehicle were ignored, which has less influence on the macro braking process.
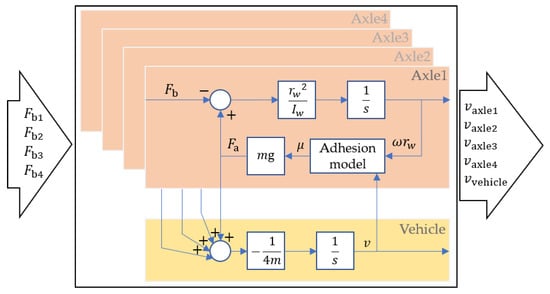
Figure 8.
Scheme of simplified vehicle longitudinal dynamics model.
(2) Wheel–rail adhesion force model for validation
There are many methods for modelling the wheel–rail creep and adhesion behaviour [35,36,37,38]. For braking application, Polach’s model (Figure 9) is commonly employed to simulate the adhesion force [36,37], which is demonstrated as follows:
in which:
where is adhesion coefficient; and are the adjustment parameters of the adhesion zone and slip zone in wheel–rail contact, respectively; is the static friction coefficient of the Polach model; and are adjustment parameters of the variable friction coefficient, respectively; is the shear modulus; and are the lengths of the long and short semi-axes of the wheel–rail contact ellipse; is the coefficient of Kalker’s theory [18]; is the normal force in wheel–rail contact; is the longitudinal slip ratio.
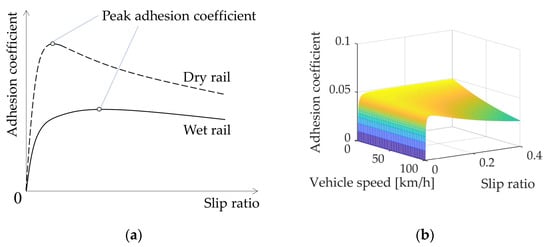
Figure 9.
Schematic representation of Polach’s model. (a) Typical shape of Adhesion coefficient-slip ratio function curves on wet and dry rail conditions. (b) Adhesion coefficient-slip ratio-vehicle speed three-dimensional relationship.
Polach’s model is adopted here, mainly for two reasons: (1) real-time: it can reflect the relationship between the vehicle speed, the slip ratio of the wheelset and the adhesion coefficient on a macro scale, and it is simple to compute, with a low demand for hardware resources, so it can support the real-time simulation and the HIL test; (2) accuracy: Polach’s model is a semi-empirical model, and it has fitted a large number of real vehicle test data in modelling, so it is more reflective of the real characteristics, especially its ability to simulate the adhesion state at the large slip ratio that exists in the braking process.
5.2. Test Results
In the tests, sliding was induced by setting one of the axles to operate in low adhesion conditions and the remaining axles to operate in dry rail conditions with no skidding. The complete braking process of the train is simulated, and the vehicle speed is reduced from the initial speed to the stop. The WSP control is cyclic, and the change of the vehicle speed in one cycle is relatively small compared with the change of the axle speed, so the speed difference is directly used to characterize the degree of skidding in the previous analysis. Here, the test needs to perform the whole braking process, and the fixed speed difference criterion needs to be adjusted at low speeds to avoid lock-up. The speed difference that changes with the vehicle speed can be regarded as the slip ratio, so the slip ratio criterion is used directly in the test, which can take the effect of the vehicle speed into account. The theoretical basis for the role of both the slip ratio and speed difference is equivalent here.
5.2.1. 2-Phase, 3-Phase and 4-Phase Control Strategy
Rule-based strategies, i.e., 2-phase, 3-phase and 4-phase WSP control, are tested in this section; the criterion values of the switch points are listed in Table 2. The test results are shown in Figure 10. It illustrates the dynamic adhesion utilization during the entire braking process, focusing on two aspects. Firstly, it demonstrates the relationship between the adhesion coefficient, slip ratio and vehicle speed. Secondly, it shows how the adhesion force varies with the braking force.

Table 2.
Criterion values of the rule-based WSP in the test.
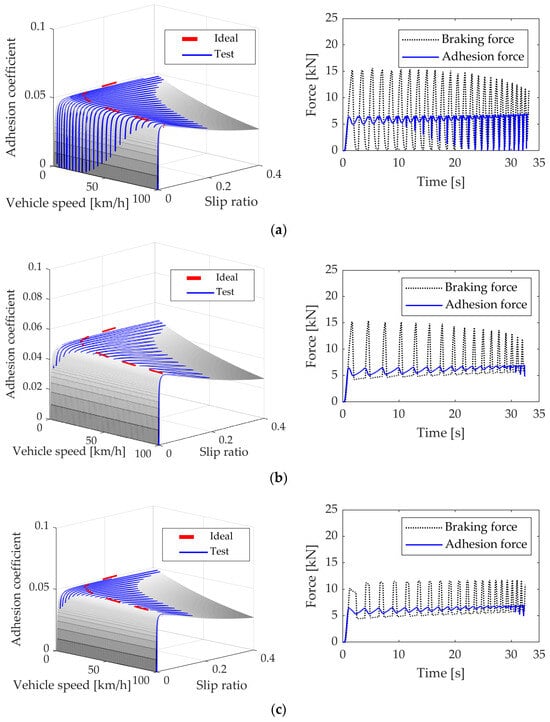
Figure 10.
Test results of various control strategy. (a) 2-phase WSP. (b) 3-phase WSP. (c) 4-phase WSP.
As shown in Figure 10a, the trajectory of adhesion coefficient utilization oscillates sharply on both sides of the peak adhesion points during braking. The adhesion force changes when the braking force rises and falls. As the minimum braking force in each cycle is too small, the adhesion force gradually reaches 0 when the speed declines. For 3-phase control, shown in Figure 10b, the low limit of the braking force is restricted. As for 4-phase control, the high and low limit of the braking force are both restricted, which is shown in Figure 10c.
5.2.2. Combined 4-Phase Control Strategy Based on Adhesion Threshold
The test results of the optimized control strategy based on the 4-phase combined adhesion threshold are shown in Figure 11. As shown in Figure 11a, the concentration of the adhesion coefficient trajectory is more improved than that of the combined 4-phase control strategy. Figure 11b shows that the adhesion coefficient is very close to the peak adhesion. Figure 11c shows that the change of the axle speed in each WSP control cycle is even smaller. From Figure 11d, it can be seen that the upper and lower limits of the braking force are close to the results of the 4-phase control strategy (Figure 10c).

Figure 11.
Test results of optimized control strategy based on adhesion force estimation. (a) Adhesion coefficient and slip ratio with vehicle speed. (b) Adhesion coefficient. (c) Vehicle speed and the sliding axle speed. (d) Adhesion force and braking force.
The adhesion conditions set in the above tests were all invariant low adhesion. To further verify the control performance of the combined 4-phase control strategy based on the adhesion estimation under changing adhesion conditions, a test of high-low-high adhesion conditions is conducted. The static friction coefficient of the Polach’s model is set to 0.25 → 0.05 → 0.25; that is, it is set to high adhesion (0.25) for vehicle speeds above 80 km/h and below 30 km/h, and low adhesion (0.05) for vehicle speeds of 80 km/h to 30 km/h.
The test results are shown in Figure 12. In the low-adhesion zone, the adhesion coefficient trajectory oscillates around and is close to the peak adhesion points, as shown in Figure 12a,b. And from Figure 12c,d, it can be seen that there is no skid in the high adhesion zone and the normal braking force is applied according to the braking command. The braking force and the axle speed change periodically in the middle section of the test, when in the low-adhesion condition.
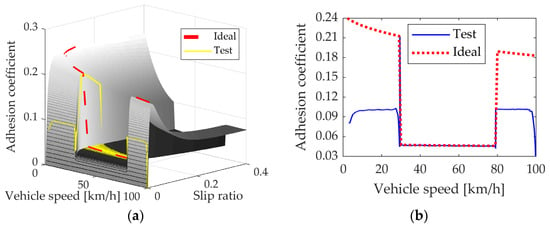
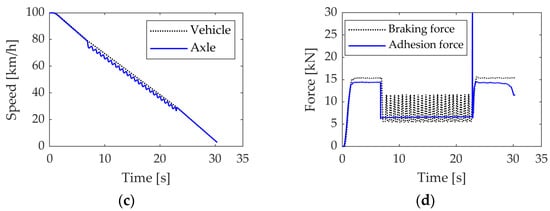
Figure 12.
Test results of optimized control strategy based on adhesion force estimation under special adhesion condition. (a) Adhesion coefficient and slip ratio with vehicle speed. (b) Adhesion coefficient. (c) Vehicle speed and the sliding axle speed. (d) Adhesion force and braking force.
The test results of the adhesion force estimation are shown in Figure 13 and Figure 14. During braking in the low-adhesion condition, Figure 13 demonstrates the implementation of WSP control and its successful estimation of adhesion force fluctuations. The tracking error of the estimated value is less than 0.1 kN, and the delay time is within 0.05 s. Figure 14 shows the results of the adhesion force estimation for the process of sliding until wheel lock under braking without WSP control. Note that the estimated value of the adhesion force can track the change of the reference value when sliding occurs but is not yet locked. However, once the wheel is locked, due to the complete stop of its rotation, the estimated value of the adhesion force will be increased to be in balance with the braking force. At this point, the estimation of the adhesion force is invalid, so special attention needs to be paid to the case of wheel lock in practical applications. If imminent wheel lock is detected, the braking force must be reduced as quickly as possible to allow for the rapid recovery of the wheel speed.
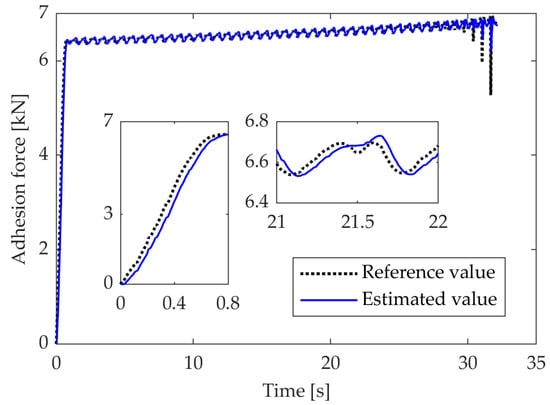
Figure 13.
Adhesion force estimation during the WSP control process.
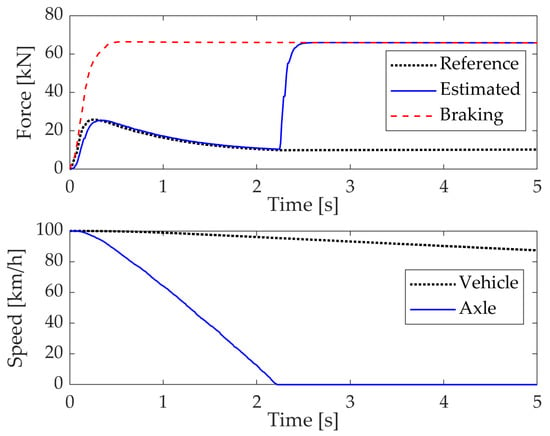
Figure 14.
Adhesion force estimation in the case of wheel locking without WSP control.
5.3. Comparison of Various Control Strategies
The most direct evaluation indicator of the WSP control performance is the braking distance. For pneumatic braking systems, the consumption of compressed air is also an indicator that needs attention. The braking system is driven by compressed air, and the availability of the braking function depends on sufficient compressed air. If the air consumption is too large, the air compressor may not be able to maintain the required pressure of the main reservoir, causing the pressure to be too low, which will lead to the occurrence of an unexpected emergency brake, and then the skidding is further aggravated, forming a vicious circle.
The braking distance of the test result is compared with the ideal braking distance, which is defined as the adhesion utilization indicator. The ideal braking distance can be calculated through the interpolation of the peak adhesion coefficient obtained directly from Polach’s adhesion model, which is shown in Figure 15.
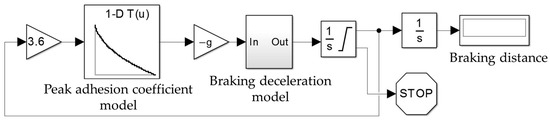
Figure 15.
Calculation of ideal braking distance.
The air consumption of the whole control process is also monitored in the test. The air consumption is obtained indirectly from the measurement of the system air flow, with the flow meter measurement point located at the inlet of the WSP air circuit. The relative air consumption of the WSP control is measured by calculating the air consumption increase ratio indicator, comparing the air consumption with the air consumption of a normal brake under the dry rail condition.
The definition equations for the adhesion utilization ratio and the air consumption increase ratio are as follows:
where is the ideal braking distance, which is the shortest value with theoretical limitation; is the actual braking distance; is the actual air consumption; is the air consumption under the dry rail condition.
The results of the different control strategies are shown in Table 3 and Figure 16. From the viewpoint of adhesion utilization, it can be found that the traditional 2-phase control strategy has the lowest adhesion utilization, the combined 4-phase control strategy based on the adhesion estimation has the best adhesion utilization and the 3-phase and 4-phase control strategies are similar. As the adhesion model used in the test is relatively simple, the control strategy with a fixed criterion has a fair performance. But the combined control strategy based on the adhesion threshold does not rely on a priori knowledge or experience and will have better adaptability under complex practical conditions.

Table 3.
Results of various control strategies.
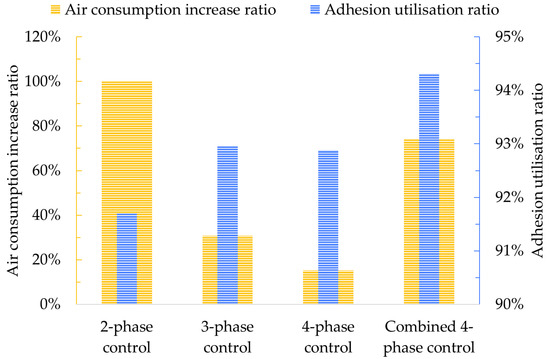
Figure 16.
Histogram of adhesion utilization ratio and air consumption increase ratio indicators for various control strategies.
From the viewpoint of air consumption, the air consumption of the control strategy from 2-phase and 3-phase to 4-phase becomes increasingly smaller due to the suppression of “over-supply” in the supply phase and “over-release” in the release phase. The air consumption of the combined 4-phase control strategy based on the adhesion estimation increases due to its relatively high control frequency, which can be further optimized for engineering application in the future. The potential solutions we are currently considering include: (1) adding dead zones to the switching conditions of the 4-phase WSP to reduce the action frequency of the solenoid valves; (2) further optimizing the holding phase by appropriately lengthening the duration of the holding, to reduce the air consumption of the supplying and exhausting process.
6. Conclusions
Using the theoretical basis of the traditional rule-based WSP control mode, a combined approach that optimizes the 4-phase control method with the estimation of adhesion force is proposed. The main contributions can be summarized as:
This method combines the model-based adhesion force estimator and the rule-based 4-phase limit cycle in the WSP control. The switching point and the upper and lower limits of the braking force in the cycle make the working range of the limit cycle more concentrated, thereby maximizing the utilization of wheel–rail adhesion. As the combined 4-phase control method can improve the adhesion utilization level, it can enhance the performance and consistency of the rail vehicle braking system under poor adhesion conditions and ensure a safe braking distance between trains. Thus, it can enhance the operational safety of the rail transport system.
Among the traditional 2-phase, 3-phase, 4-phase and the combined 4-phase control method, the combined 4-phase control strategy has the best adhesion utilization ratio at 94.3% and the shortest braking distance at 473.2 m. However, compared to the traditional 4-phase control strategy, it has a larger air consumption. For further study, the air consumption of the 4-phase combined adhesion threshold WSP should be reduced to save the compressed air in rail vehicles. Achieving a balance between air consumption and adhesion utilization is a significant task for engineering applications in the future.
Author Contributions
Conceptualization, T.M. and M.W.; methodology, T.M.; software, T.M.; validation, T.M., J.W. and C.T.; formal analysis, C.T.; investigation, J.W.; resources, M.W.; data curation, T.M. and J.W.; writing—original draft preparation, T.M.; writing—review and editing, C.T.; visualization, J.W.; supervision, M.W.; project administration, C.T.; funding acquisition, T.M., C.T. and M.W. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the China Postdoctoral Science Foundation, grant number 2021M702476; the Open Cooperative Innovation Foundation of the High Speed Wheel–Rail System Laboratory, grant number 2021YJ264; and the National Natural Science Foundation of China, grant number 52072266 and U1534205.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
Nomenclature
| deceleration () | |
| deceleration, subscript A, B, C and preA means the switching points of WSP system () | |
| deceleration of vehicle () | |
| speed difference () | |
| speed difference, subscript A, B and C means the switching points of WSP system () | |
| moment of inertia of the wheelset () | |
| vehicle speed () | |
| derivative of vehicle speed () | |
| angular speed () | |
| derivative of angular speed () | |
| slip ratio | |
| estimated value of adhesion force () | |
| adhesion force () | |
| maximum braking force in the WSP process () | |
| minimum braking force in the WSP process () | |
| braking force () | |
| radius of the wheel’s rolling circle () | |
| Laplace operator | |
| cut-off frequency of the first-order low-pass filter | |
| mass of a quarter vehicle () | |
| coefficient of inertial mass | |
| adhesion coefficient | |
| adjustment parameter of adhesion zone in wheel–rail contact | |
| adjustment parameter of slip zone in wheel–rail contact | |
| static friction coefficient of Polach’s model | |
| ratio of friction coefficients | |
| coefficient of exponential friction decreases () | |
| shear modulus () | |
| , | lengths of long and short semi-axes of wheel–rail contact ellipse () |
| coefficient of Kalker’s theory | |
| normal force in wheel–rail contact () | |
| adhesion utilization ratio | |
| air consumption increase ratio | |
| ideal braking distance () | |
| actual braking distance (m) | |
| actual air consumption () | |
| air consumption under dry rail condition () | |
| WSP | wheel slide protection |
| ATP | automatic train protection |
| HV | hold valve |
| RV | release valve |
| HIL | hardware-in-the-loop |
References
- White, B.; Nilsson, R.; Olofsson, U.; Arnall, A.; Evans, M.; Armitage, T.; Fisk, J.; Fletcher, D.; Lewis, R. Effect of the presence of moisture at the wheel–rail interface during dew and damp conditions. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2018, 232, 979–989. [Google Scholar] [CrossRef]
- Galas, R.; Omasta, M.; Shi, L.; Ding, H.; Wang, W.; Krupka, I.; Hartl, M. The low adhesion problem: The effect of environmental conditions on adhesion in rolling-sliding contact. Tribol. Int. 2020, 151, 106521. [Google Scholar] [CrossRef]
- UIC 541-05; Brakes—Manufacturing Specifications for Various Brake Parts—Wheel Slide Protection Device (WSP). International Union of Railways: Paris, France, 2016.
- BS EN 15595; Railway Applications—Braking—Wheel Slide Protection. BSI Standards Limited: London, UK, 2018.
- Challa, A.; Ramakrushnan, K.; Gaurkar, P.V.; Subramanian, S.C.; Vivekanandan, G.; Sivaram, S. A 3-phase combined wheel slip and acceleration threshold algorithm for anti-lock braking in heavy commercial road vehicles. Veh. Syst. Dyn. 2022, 60, 2312–2333. [Google Scholar] [CrossRef]
- Antonov, S.; Fehn, A.; Kugi, A. Unscented kalman filter for vehicle state estimation. Veh. Syst. Dyn. 2011, 49, 1497–1520. [Google Scholar] [CrossRef]
- Tsunashima, H.; Murakami, M.; Miyataa, J. Vehicle and road state estimation using interacting multiple model approach. Veh. Syst. Dyn. 2006, 44, 750–758. [Google Scholar] [CrossRef]
- Zhang, J.; Li, J. Estimation of vehicle speed and tire-road adhesion coefficient by adaptive unscented Kalman filter. J. Xi’an Jiaotong Univ. 2016, 50, 68–75. [Google Scholar] [CrossRef]
- Wei, H. EMU anti-slide performance experimental study on ultra-low adhesion rail surface. China Railw. Sci. 2017, 39, 67–73. [Google Scholar] [CrossRef]
- Li, C.; Zhao, H.; Huang, K.; Chen, Y.-H. Optimal design for anti-skid control of electric vehicles by fuzzy approach. Chin. J. Mech. Eng. 2021, 34, 125. [Google Scholar] [CrossRef]
- Yi, L.; Jiang, W.; Yi, Y.; Li, J.; Xie, C. Freight train speed active disturbance rejection tracking and wheel anti-slip based on fuzzy neural network with DBO optimization. Electr. Eng. 2023, 9, 1–4. [Google Scholar] [CrossRef]
- Mousavi, A.; Markazi, A.H.D.; Masoudi, S. Adaptive fuzzy sliding-mode control of wheel slide protection device for ER24PC locomotive. Lat. Am. J. Solids Struct. 2017, 14, 2019–2045. [Google Scholar] [CrossRef]
- Amirkhani, A.; Molaie, M. Fuzzy controllers of antilock braking system: A review. Int. J. Fuzzy Syst. 2023, 25, 222–244. [Google Scholar] [CrossRef]
- Nakazawa, S. Development of a new wheel slide protection system using a new detection algorithm. Q. Rep. RTRI 2011, 52, 136–140. [Google Scholar] [CrossRef]
- Nakazawa, S.; Hijikata, D. Improvement of response and efficiency of railway air brake system by modifying software for control. Q. Rep. RTRI 2017, 58, 28–35. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Chen, P.; Zhu, W.; Yu, C.; Sun, N.; Xue, W. Research on train braking model by improved Polach model considering wheel-rail adhesion characteristics. IET Intell. Transp. Syst. 2023, 17, 2432–2443. [Google Scholar] [CrossRef]
- Xu, K.; Xu, G.; Zheng, C. Novel determination of wheel-rail adhesion stability for electric locomotives. Int. J. Precis. Eng. Manuf. 2015, 16, 653–660. [Google Scholar] [CrossRef]
- Kalker, J. Three-Dimensional Elastic Bodies in Rolling Contact; Springer: Dordrecht, The Netherlands, 1990. [Google Scholar] [CrossRef]
- Chang, C.; Chen, B.; Cai, Y.; Wang, J. Experimental study on adhesion property of high speed wheel and rail in wet condition by full scale roller rig. China Railw. Sci. 2019, 40, 25–32. [Google Scholar] [CrossRef]
- Spiryagin, M.; Cole, C.; Sun, Y.Q. Adhesion estimation and its implementation for traction control of locomotives. Int. J. Rail Transp. 2014, 2, 187–204. [Google Scholar] [CrossRef]
- Shrestha, S.; Spiryagin, M.; Wu, Q. Friction condition characterization for rail vehicle advanced braking system. Mech. Syst. Signal Pr. 2019, 134, 106324. [Google Scholar] [CrossRef]
- Shrestha, S.; Wu, Q.; Spiryagin, M. Review of adhesion estimation approaches for rail vehicles. Int. J. Rail Transp. 2019, 7, 79–102. [Google Scholar] [CrossRef]
- Ma, T.; Wu, M.; Tian, C. Anti-skid control based on adhesion force observer for train pneumatic braking. J. Tongji Univ. 2020, 48, 1668–1675. [Google Scholar]
- Schwarz, C.; Brembeck, J.; Heckmann, B. Dynamics observer for the longitudinal behavior of a wheelset on a roller rig. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2019, 233, 1112–1119. [Google Scholar] [CrossRef]
- He, J.; Liu, G.; Zhang, C.; Sun, J.; Cheng, X. Maximum likelihood identification method for adhesion performance parameters of heavy duty locomotive. J. Electron. Meas. Instrum. 2017, 31, 170–177. [Google Scholar] [CrossRef]
- Peng, Q.; Liu, J.; Huang, Z.; Liu, W.; Li, H. Sliding model control based on estimation of optimal slip ratio for railway wheel slide protection using extremum seeking. In Proceedings of the Energy Conversion Congress and Exposition (ECCE), Milwaukee, WI, USA, 18–22 September2016; IEEE: Piscataway, NJ, USA, 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Uyulan, C.; Gokasan, M.; Bogosyan, S. Re-adhesion control strategy based on the optimal slip velocity seeking method. J. Mod. Transp. 2018, 26, 36–48. [Google Scholar] [CrossRef]
- Sun, D.; Jiao, Z.; Shang, Y.; Wu, S.; Liu, X. High-efficiency aircraft antiskid brake control algorithm via runway condition identification based on an on-off valve array. Chin. J. Aeronaut. 2019, 32, 2538–2556. [Google Scholar] [CrossRef]
- Liu, J.; Peng, Q.; Huang, Z.; Liu, W.; Li, H. Enhanced sliding mode control and online estimation of optimal slip ratio for railway vehicle braking systems. Int. J. Precis. Eng. Manuf. 2018, 19, 655–664. [Google Scholar] [CrossRef]
- Lee, N.-J.; Kang, C.-G. Sliding mode control for wheel slide protection in railway vehicles with pneumatic brake systems. Int. J. Precis. Eng. Manuf. 2017, 18, 285–291. [Google Scholar] [CrossRef]
- Ma, T.; Wu, M.; Tian, C. Slip ratio control in rail vehicle braking with sliding mode control method. In Proceedings of the 5th International Conference on Intelligent Transportation Engineering (ICITE), Beijing, China, 11–13 September 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 160–164. [Google Scholar] [CrossRef]
- Tian, Y.; Daniel, W.; Liu, S.; Meehan, P. Comparison of PI and fuzzy logic based sliding mode locomotive creep controls with change of rail-wheel contact conditions. Int. J. Rail Transp. 2015, 3, 40–59. [Google Scholar] [CrossRef]
- Pugi, L.; Paolieri, G.; Giorgetti, M.; Berzi, L.; Viviani, R.; Cabrucci, L.; Bocciolini, L. HIL testing of wheel slide protection systems: Criteria for continuous updating and validation. Railw. Eng. Sci. 2023, 31, 108–121. [Google Scholar] [CrossRef]
- Yamamoto, T. Recent activities in railway vehicle technology research and development. Q. Rep. RTRI 2022, 63, 225–228. [Google Scholar] [CrossRef]
- Vollebregt, E. Numerical modeling of measured railway creep versus creep-force curves with CONTACT. Wear 2014, 314, 87–95. [Google Scholar] [CrossRef]
- Polach, O. Creep forces in simulations of traction vehicles running on adhesion limit. Wear 2005, 258, 992–1000. [Google Scholar] [CrossRef]
- An, B.; Wang, P.; Xu, Y.; Xu, J.; Chen, R. Study on wheel/rail creep curve based on Polach’s method. J. Mech. Eng. 2018, 54, 124–131. [Google Scholar] [CrossRef]
- Trummer, G.; Buckley-Johnstone, L.; Voltr, P.; Meierhofer, A.; Lewis, R.; Six, K. Wheel-rail creep force model for predicting water induced low adhesion phenomena. Tribol. Int. 2017, 109, 409–415. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).