Analysis of Vibration Energy Harvesting Performance of Thermo-Electro-Elastic Microscale Devices Based on Generalized Thermoelasticity
Abstract
1. Introduction
2. The Establishment of Theory
2.1. Thermo-Electro-Elastic Constitutive Model
2.2. Generalized Thermoelastic Theory Model
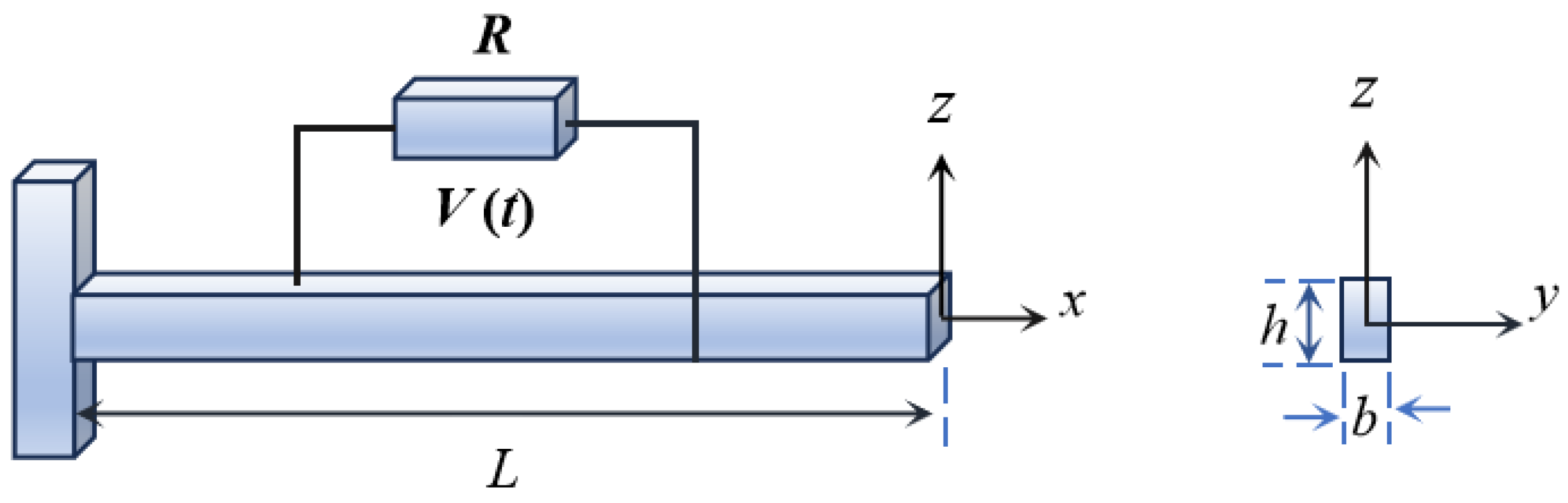
3. Modeling of Microbeam Structures
4. Analytical Solution
5. Numerical Results and Discussion
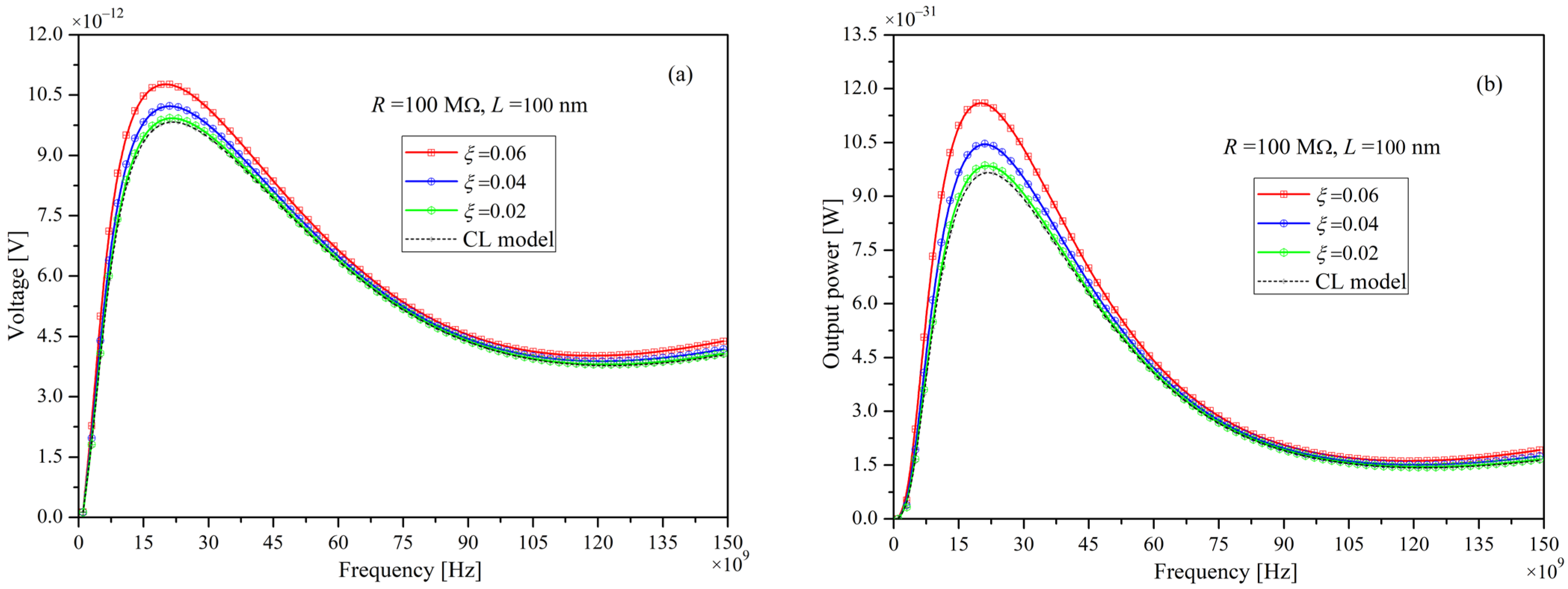
5.1. The Comparison of the Current Theoretical Analysis Model
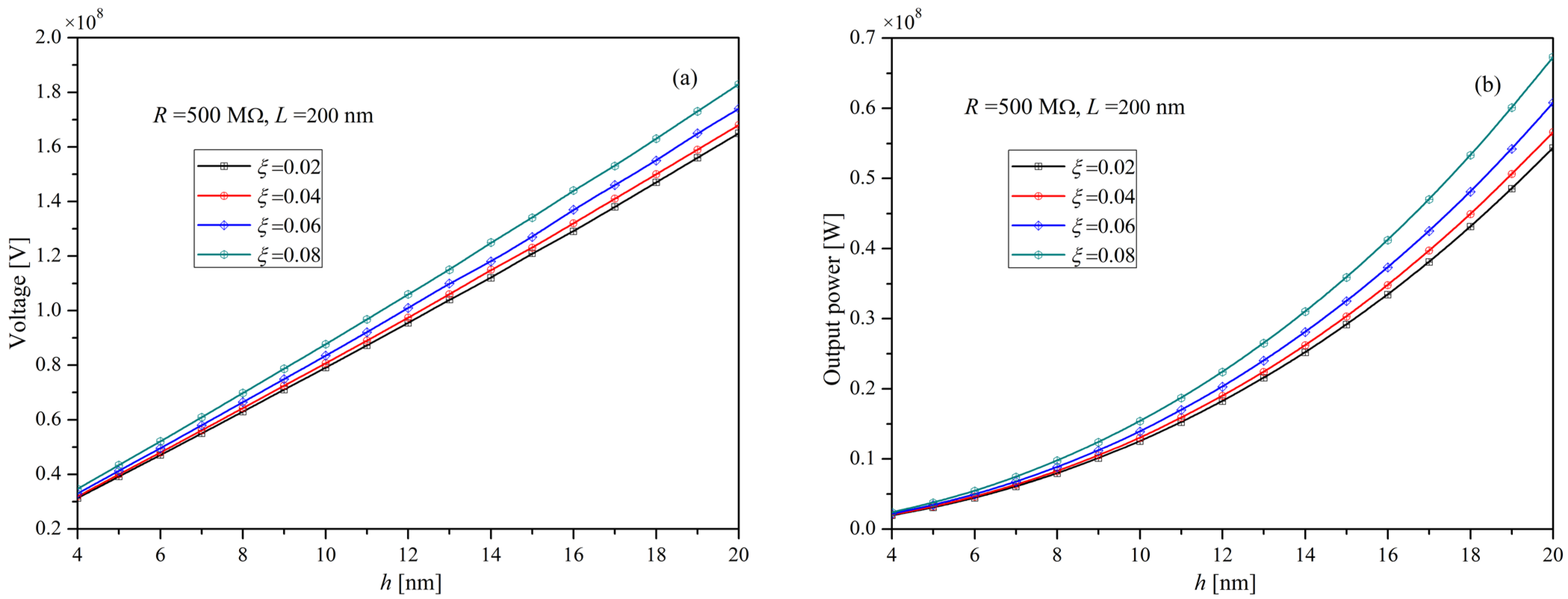
5.2. The Influence of Microscale Effect on the Performance of Energy Harvesting
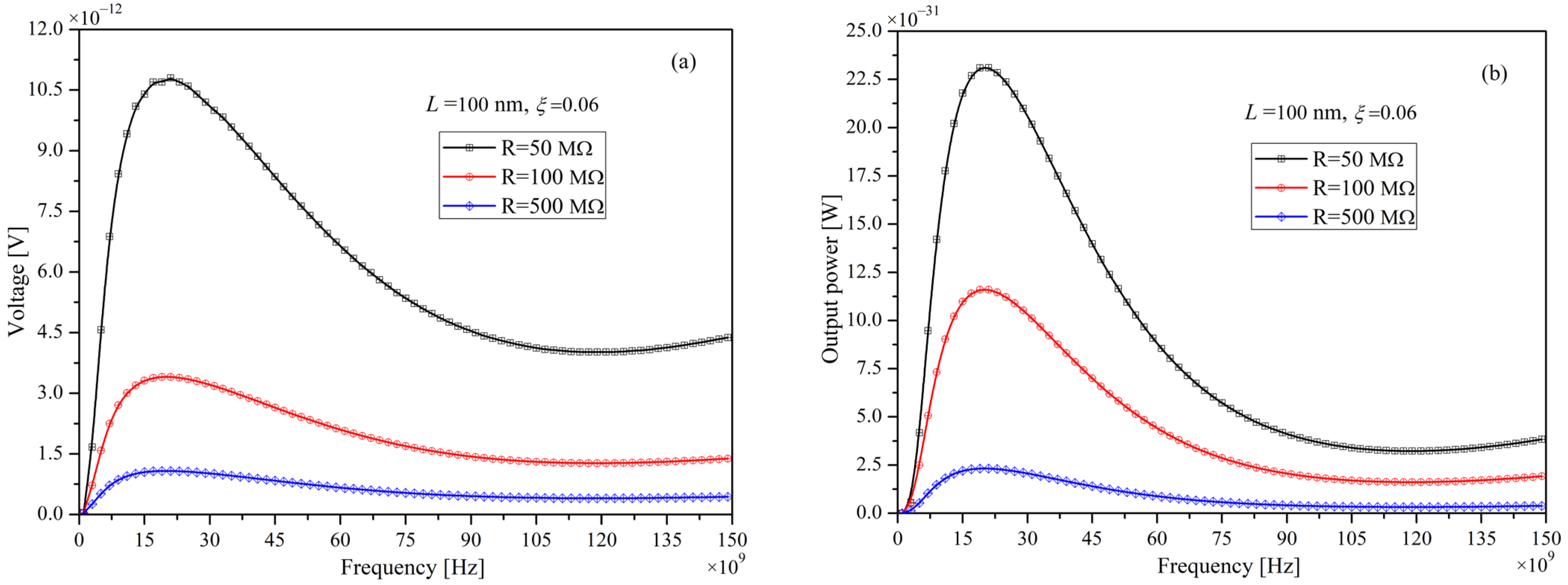
5.3. The Influence of Load Resistances on the Energy Harvesting Performance of Piezo-Flexoelectric Thermoelastic Microbeam
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fan, F.R.; Tang, W.; Wang, Z.L. Flexible Nanogenerators for Energy Harvesting and Self-Powered Electronics. Adv. Mater. 2016, 28, 4283–4305. [Google Scholar] [CrossRef] [PubMed]
- Sun, R.; Zhou, S.; Cheng, L. Ultra-low frequency vibration energy harvesting: Mechanisms, enhancement techniques, and scaling laws. Energy Convers. Manag. 2023, 276, 116585. [Google Scholar] [CrossRef]
- Abdollahzadeh Jamalabadi, M.Y. Effect of Tip Mass Length Ratio on Low Amplitude Galloping Piezoelectric Energy Harvest-ing. Acoustics 2019, 1, 763–793. [Google Scholar] [CrossRef]
- Kheibari, F.; Beni, Y.T.; Golestanian, H. On the generalized flexothermoelasticity of a microlayer. Acta Mech. 2024, 235, 3363–3384. [Google Scholar] [CrossRef]
- Aliakbari, F.; Amiri, A.; Talebitooti, R.; Daneshjou, K. On comprehensive nonlinear size-dependent analysis of nano-scale flexoelectric energy harvesters considering strain gradient, surface elasticity and thickness size effect. Eur. Phys. J. Plus 2023, 138, 807. [Google Scholar] [CrossRef]
- Liu, H.; Gao, S.; Wu, J.; Li, P. Study on the Output Performance of a Nonlinear Hybrid Piezoelectric-Electromagnetic Har-vester under Harmonic Excitation. Acoustics 2019, 1, 382–392. [Google Scholar] [CrossRef]
- Indenbom, V.; Loginov, E.; Osipov, M. Flexoelectric effect and structure of crystals. Kristallografiya 1981, 28, 1157–1162. [Google Scholar]
- Majdoub, M.S.; Sharma, P.; Cagin, T. Enhanced size-dependent piezoelectricity and elasticity in nanostructures due to the flexoelectric effect. Phys. Rev. B—Condens. Matter Mater. Phys. 2008, 77, 125424. [Google Scholar] [CrossRef]
- Zubko, P.; Catalan, G.; Tagantsev, A.K. Flexoelectric Effect in Solids. Annu. Rev. Mater. Res. 2013, 43, 387–421. [Google Scholar] [CrossRef]
- Van Minh, P.; Thai, L.M.; Dung, N.T.; Tounsi, A.; Nhung, N.T.C.; Van Thom, D. An overview of the flexoelectric phenomenon, potential applications, and proposals for further research directions. Int. J. Mech. Mater. Des. 2023, 19, 903–925. [Google Scholar] [CrossRef]
- Sun, R.; Liu, D.; Yan, Z. A finite element approach for flexoelectric nonuniform nanobeam energy harvesters. Mech. Adv. Mater. Struct. 2023, 30, 2430–2441. [Google Scholar] [CrossRef]
- Deng, Q.; Shen, S. The flexodynamic effect on nanoscale flexoelectric energy harvesting: A computational approach. Smart Mater. Struct. 2018, 27, 105001. [Google Scholar] [CrossRef]
- Deng, Q.; Kammoun, M.; Erturk, A.; Sharma, P. Nanoscale flexoelectric energy harvesting. Int. J. Solids Struct. 2014, 51, 3218–3225. [Google Scholar] [CrossRef]
- Managheb, S.A.M.; Ziaei-Rad, S.; Tikani, R. Energy harvesting from vibration of Timoshenko nanobeam under base excitation considering flexoelectric and elastic strain gradient effects. J. Sound Vib. 2018, 421, 166–189. [Google Scholar] [CrossRef]
- Baroudi, S.; Samaali, H.; Najar, F. Energy harvesting using a clamped–clamped piezoelectric–flexoelectric beam. J. Phys. D Appl. Phys. 2021, 54, 415501. [Google Scholar] [CrossRef]
- Li, A.; Zhao, W.; Zhou, S.; Wang, L.; Zhang, L. Enhanced energy harvesting of cantilevered flexoelectric micro-beam by proof mass. AIP Adv. 2019, 9, 115305. [Google Scholar] [CrossRef]
- Chen, X.; Yao, S.; Yvonnet, J. Dynamic analysis of flexoelectric systems in the frequency domain with isogeometric analysis. Comput. Mech. 2023, 71, 353–366. [Google Scholar] [CrossRef]
- Gao, P.; Zhang, Y.; Wang, X.; Zhou, Y. Interface Properties and Failures of REBCO Coated Conductor Tapes: Research Pro-gress and Challenges. Superconductivity 2023, 8, 100068. [Google Scholar] [CrossRef]
- Peshkor, V. Second sound in Helium II. J. Phys. 1944, 8, 381–382. [Google Scholar]
- Cattaneo, C. Sulla Conduzione del Calore; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- DeVoe, D.L. Thermal issues in MEMS and microscale systems. IEEE Trans. Compon. Packag. Technol. 2002, 25, 576–583. [Google Scholar] [CrossRef]
- Tzou, D.Y. A Unified Field Approach for Heat Conduction From Macro- to Micro-Scales. J. Heat Transf. 1995, 117, 8–16. [Google Scholar] [CrossRef]
- Roy Choudhuri, S.K. On a thermoelastic three-phase-lag model. J. Therm. Stress. 2007, 30, 231–238. [Google Scholar] [CrossRef]
- Zenkour, A.M.; Kutbi, M.A. Multi thermal relaxations for thermodiffusion problem in a thermoelastic half-space. Int. J. Heat Mass Transf. 2019, 143, 118568. [Google Scholar] [CrossRef]
- Mindlin, R. Equations of high frequency vibrations of thermopiezoelectric crystal plates. Int. J. Solids Struct. 1974, 10, 625–637. [Google Scholar] [CrossRef]
- Chandrasekharaiah, D. A generalized thermoelastic wave propagation in a semi-infinite piezoelectric rod. Acta Mech. 1988, 71, 39–49. [Google Scholar] [CrossRef]
- Ma, Y.; He, T. Dynamic response of a generalized piezoelectric-thermoelastic problem under fractional order theory of thermoelasticity. Mech. Adv. Mater. Struct. 2016, 23, 1173–1180. [Google Scholar] [CrossRef]
- Li, C.; Tian, X.; He, T. New insights on piezoelectric thermoelastic coupling and transient thermo-electromechanical responses of multi-layered piezoelectric laminated composite structure. Eur. J. Mech.-A/Solids 2022, 91, 104416. [Google Scholar] [CrossRef]
- Guha, S.; Singh, A.K.; Singh, S. Thermoelastic damping and frequency shift of different micro-scale piezoelectro-magneto-thermoelastic beams. Phys. Scr. 2024, 99, 015203. [Google Scholar] [CrossRef]
- Srivastava, A.; Mukhopadhyay, S. Analysis of the dynamic responses of a piezothermoelastic microbeam resonator under dual-phase-lag heat conduction. Wave Random Complex 2024, 1–22. [Google Scholar] [CrossRef]
- Gurevich, V.L. Dielectric relaxation and the thermopolarization effect in crystals. Sov. Phys. Uspekhi 1982, 25, 633. [Google Scholar] [CrossRef]
- Tagantsev, A.K. Pyroelectric, piezoelectric, flexoelectric, and thermal polarization effects in ionic crystals. Sov. Phys. Uspekhi 1987, 30, 588. [Google Scholar] [CrossRef]
- Yu, P.; Peng, L.; Suo, Y. Thermo-electro-elastic analysis of piezoelectric hollow cylinder with thermopolarization effect. J. Therm. Stress. 2024, 47, 250–262. [Google Scholar] [CrossRef]
- Hrytsyna, O.; Tokovyy, Y.; Hrytsyna, M. Local gradient theory of dielectrics incorporating polarization inertia and flexodynamic effect. Contin. Mech. Thermodyn. 2023, 35, 2125–2144. [Google Scholar] [CrossRef]
- Kulathunga, D.D.T.K.; Ang, K.K.; Reddy, J.N. Accurate modeling of buckling of single-and double-walled carbon nanotubes based on shell theories. J. Phys. Condens. Matter Inst. Phys. J. 2009, 21, 435301. [Google Scholar] [CrossRef]
- Zhang, H.; Inman, D.J.; Zhou, S. Coupled thermo-electric-elastic piezoelectric vibration energy harvester with axial movement: Modeling, verification, and analysis. J. Vib. Acoust. 2024, 146, 051002. [Google Scholar] [CrossRef]
- Gu, B.; He, A.; He, T.; Ma, Y. Investigation on the thermo-piezo-flexoelectric energy harvesting performance of self-powered microbeam devices considering strain gradient and dual-phase-lag effects. ZAMM-J. Appl. Math. Mech./Z. Angew. Math. Mech. 2024, 104, e202300777. [Google Scholar] [CrossRef]
- Toupin, R.A. The Elastic Dielectric. J. Ration. Mech. Anal. 1956, 5, 849–915. [Google Scholar] [CrossRef]
- Qi, L.; Zhou, S.; Li, A. Size-dependent bending of an electro-elastic bilayer nanobeam due to flexoelectricity and strain gradient elastic effect. Compos. Struct. 2016, 135, 167–175. [Google Scholar] [CrossRef]
- Lim, C.W.; Zhang, G.; Reddy, J.N. A higher-order nonlocal elasticity and strain gradient theory and its applications in wave propagation. J. Mech. Phys. Solids 2015, 78, 298–313. [Google Scholar] [CrossRef]
- Abouelregal, A.E.; Yao, S.W.; Ahmad, H. Analysis of a functionally graded thermopiezoelectric finite rod excited by a moving heat source. Results Phys. 2020, 19, 103389. [Google Scholar] [CrossRef]
- Chu, L.; Dui, G.; Zheng, Y. Thermally induced nonlinear dynamic analysis of temperature-dependent functionally graded flexoelectric nanobeams based on nonlocal simplified strain gradient elasticity theory. Eur. J. Mech.-A/Solids 2020, 82, 103999. [Google Scholar] [CrossRef]
- Mashat, D.S.; Zenkour, A.M. Modified DPL Green–Naghdi theory for thermoelastic vibration of temperature-dependent nanobeams. Results Phys. 2020, 16, 102845. [Google Scholar] [CrossRef]
- Erturk, A. Assumed-modes modeling of piezoelectric energy harvesters: Euler–Bernoulli, Rayleigh, and Timoshenko models with axial deformations. Comput. Struct. 2012, 106–107, 214–227. [Google Scholar] [CrossRef]
- Zheng, B.-J.; Gao, X.-W.; Yang, K.; Zhang, C.-Z. A novel meshless local Petrov–Galerkin method for dynamic coupled thermoelasticity analysis under thermal and mechanical shock loading. Eng. Anal. Bound. Elem. 2015, 60, 154–161. [Google Scholar] [CrossRef]
- Lam, T.T.; Fong, E. Heat diffusion vs. wave propagation in solids subjected to exponentially-decaying heat source: Analytical solution. Int. J. Therm. Sci. 2011, 50, 2104–2116. [Google Scholar] [CrossRef]
- Meirovitch, L. Fundamentals of Vibrations; Waveland Press: Long Grove, IL, USA, 2010. [Google Scholar]
- Faroughi, S.; Rojas, E.F.; Abdelkefi, A.; Park, Y.H. Reduced-order modeling and usefulness of non-uniform beams for flexoelectric energy harvesting applications. Acta Mech. 2019, 230, 2339–2361. [Google Scholar] [CrossRef]
- Li, Q.; Li, S.; Pisignano, D.; Persano, L.; Yang, Y.; Su, Y. On the evaluation of output voltages for quantifying the performance of pyroelectric energy harvesters. Nano Energy 2021, 86, 106045. [Google Scholar] [CrossRef]
- Ramazanov, M.A.; Ibragimova, K.S.; Abasov, S.A. Effect of the structure of piezoceramics on the dielectric and strength properties of composites based on polyvinylidene fluoride. Surf. Eng. Appl. Electrochem. 2012, 48, 380–383. [Google Scholar] [CrossRef]
- Chester, M. Second Sound in Solids. Phys. Rev. 1963, 131, 2013–2015. [Google Scholar] [CrossRef]
- Guo, F.L.; Jiao, W.J.; Wang, G.Q.; Chen, Z.Q. Distinctive features of thermoelastic dissipation in microbeam resonators at nanoscale. J. Therm. Stress. 2016, 39, 360–369. [Google Scholar] [CrossRef]
- Starkov, I.A.; Starkov, A.S. 8—Mathematical modeling of flexocaloric effect in ceramics. In Flexoelectricity in Ceramics and Their Application; Patel, S., Ed.; Elsevier: Amsterdam, The Netherlands, 2024; pp. 209–242. [Google Scholar] [CrossRef]
- Lam, D.C.C.; Yang, F.; Chong, A.C.M.; Wang, J.; Tong, P. Experiments and theory in strain gradient elasticity. J. Mech. Phys. Solids 2003, 51, 1477–1508. [Google Scholar] [CrossRef]


| Parameters | Unit | PVDF | |
|---|---|---|---|
| Elastic modulus | GPa | 3.7 | |
| Density | 1780 | ||
| Poisson’s ratio | 1 | 0.33 | |
| Thermal conductivity | |||
| Specific heat | |||
| Pyroelectric constants | |||
| Dielectric constants | |||
| Piezoelectric coefficient | |||
| Flexoelectric coefficient | |||
| Vacuum permittivity | |||
| Thermopolarization coefficient |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, A.; He, T.; Gu, B.; Li, Y. Analysis of Vibration Energy Harvesting Performance of Thermo-Electro-Elastic Microscale Devices Based on Generalized Thermoelasticity. Actuators 2024, 13, 533. https://doi.org/10.3390/act13120533
He A, He T, Gu B, Li Y. Analysis of Vibration Energy Harvesting Performance of Thermo-Electro-Elastic Microscale Devices Based on Generalized Thermoelasticity. Actuators. 2024; 13(12):533. https://doi.org/10.3390/act13120533
Chicago/Turabian StyleHe, Ailing, Tianhu He, Bingdong Gu, and Yuan Li. 2024. "Analysis of Vibration Energy Harvesting Performance of Thermo-Electro-Elastic Microscale Devices Based on Generalized Thermoelasticity" Actuators 13, no. 12: 533. https://doi.org/10.3390/act13120533
APA StyleHe, A., He, T., Gu, B., & Li, Y. (2024). Analysis of Vibration Energy Harvesting Performance of Thermo-Electro-Elastic Microscale Devices Based on Generalized Thermoelasticity. Actuators, 13(12), 533. https://doi.org/10.3390/act13120533





