Abstract
Aiming at the problems of low trajectory tracking accuracy, serious chattering and poor robust performance of ball screw feed systems in traditional sliding mode control (SMC), in this paper, a global nonsingular fast terminal sliding mode control (GNFTSMC) strategy based on improved double power reaching law (DPRL) and extended state observer (ESO) is proposed. Firstly, the system state variable is introduced into the power term of DPRL, so that the improved DPRL has the characteristics of variable speed reaching, which solves the contradiction between the reaching rate and the sliding mode chattering. Secondly, ESO is designed to observe the state of the system and match the external disturbance to improve the anti-interference performance of the system. Finally, GNFTSMC is designed for the ball screw feed system, and the global sliding mode factor is introduced to improve the trajectory tracking accuracy of the system. The results show that the proposed control strategy can effectively improve the tracking accuracy and anti-interference performance of the system.
1. Introduction
The ball screw feed system is widely used in the fields of CNC machine tools and mechanical processing transmission devices due to its high stiffness, smooth motion and high transmission efficiency. In the process of high-speed machining of CNC machine tools, the ball screw feed system needs to ensure that the workbench has a highly accurate positioning ability to achieve a smaller tracking error. In actual working conditions, many external uncertainties are often encountered, such as unmodeled parameter changes, external disturbances and model uncertainties.
In view of the above problems, many advanced control methods have been proposed, including neural network control [1,2,3], self-disturbance rejection control (ADRC) [4,5,6], model predictive control (MPC) [7,8,9,10], fuzzy control [11,12,13], sliding mode control (SMC) [14,15,16,17] and so on. SMC is widely used in ball screw feed systems, which has the advantages of high control precision and fast dynamic response. However, the traditional SMC will cause a high-frequency switching control signal after the system state variable reaches the sliding mode surface, which makes it difficult for the system to slide strictly along the sliding mode surface, thus causing the chattering problem of the system. This chattering phenomenon seriously affects the stability and control accuracy of the control system [18].
Aiming at the inherent chattering problem in traditional SMC, the continuous saturation function is used to replace the symbol function of traditional SMC, which can effectively reduce the chattering, but it will reduce the approaching rate and anti-interference performance of SMC [19]. In Reference [20], an enhanced exponential reaching law is designed based on the variable-speed direct-drive wind energy conversion system. The reaching law can effectively reduce the chattering of the SMC and improve the control performance of the system. In Reference [21], combined with hyperbolic sine function and power reaching law, a combined power reaching law SMC method is proposed to adjust the reaching speed at different stages. When maintaining the state of high-speed reaching rate of the system, the system chattering is greatly reduced, but the control system has many parameters and the adjustment is complicated.
In order to improve the robust performance of the system, the extended state observer (ESO) is used to compensate the external disturbance in Reference [22], which eliminates the uncertainty of the system model parameters and improves the robust performance of the control system. In Reference [23], a terminal sliding mode (TSM) control method is proposed, and a nonlinear function is introduced into the sliding mode surface. While improving the response speed of the control system, it ensures that the system can converge to zero in a finite time and improves the robust performance and tracking accuracy of the control system. However, the introduction of the nonlinear term will cause the system to have singular points near the equilibrium state. In order to solve this problem, a nonsingular terminal sliding mode (NTSM) control method is proposed in Reference [24], which can make the system converge in the effective time and avoid the singularity of the control. However, the sign function will cause reaching law chattering, resulting in lower control accuracy. In References [25,26,27], NTSM is designed to achieve high-precision tracking of the control system, and ESO is used to compensate for the influence of external disturbances, which solves the singularity problem of traditional TSM. However, the approaching speed of the system needs to be improved when it is far away from the sliding surface.
In view of the above problems, this paper proposes a global nonsingular fast terminal sliding mode control strategy for a ball screw feed system based on improved double power reaching law. The main contributions of this study are summarized as follows.
- (1)
- In DPRL, the state variables of the system are introduced, and the improved double power reaching law (IDPRL) is designed, so that the reaching law can be adjusted adaptively according to the state variables, and the improved double power reaching law can effectively reduce the chattering.
- (2)
- For the ball screw feed system, the global sliding mode factor is introduced into NFTSMC to improve the robust performance of the system. At the same time, ESO is designed to improve the anti-interference performance of the system.
- (3)
- The stability of the control system is proved by the Lyapunov method. The control strategy of IDPRL + GNFTSMC can obtain good anti-interference performance and control accuracy under external disturbance.
The structure of this paper is as follows: The second section introduces the dynamic model of the ball screw feed system. In the third section, IDPRL is designed to prove the effective time reachability of the reaching law. In the fourth and fifth sections, the composite strategies of ESO and GNFTSMC are designed for the ball screw feed system. In the sixth section, simulation examples are used to verify the effectiveness of the control strategy. The seventh section summarizes the work of this paper.
2. Dynamic Model of Ball Screw Feed System
As shown in Figure 1, the structure diagram of the ball screw feed system is shown. As a mechanical transmission device, it is mainly composed of a servo motor, coupling, ball screw and workbench. When the servo motor receives the output signal of the controller, the rotational torque generated by the servo motor drives the coupling to drive the screw to rotate. The ball screw and the workbench are connected by nuts, and the rotational motion of the screw is converted into the reciprocating linear motion of the workbench [28,29,30].
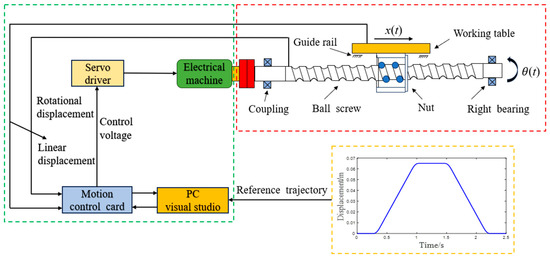
Figure 1.
Structure diagram of ball screw feed system.
The state space expression of the ball screw feed system is [31]:
where is the viscous damping coefficient of the ball screw feed system. is the equivalent rotational inertia of the system. is the current amplification gain, is the motor torque constant. is the ball screw pair transmission ratio.
Convert (1) into a second-order system expression:
where is the linear displacement of the ball screw, is the linear velocity of the ball screw, is the external uncertainty disturbance.
3. Design and Analysis of Improved Double Power Reaching Law
3.1. Design Improved Double Power Reaching Law
In the sliding mode control system, the existence of the chattering problem seriously hinders the stability of the control system. In order to improve the stability and control accuracy of the system, designing a reasonable reaching law has become an effective solution. The design of the reaching law needs to comprehensively consider the balance between chattering suppression and system response speed to achieve the best control effect.
The exponential reaching law (ERL) can be expressed as
where , is the sliding surface.
In ERL, increasing the exponential coefficient can effectively shorten the time for the system to reach the sliding mode surface, but the existence of the switching function will cause system chattering.
The double power reaching law (DPRL) can be expressed as
where , , . It can be seen from Equation (4) that when , the system can be stabilized at the equilibrium point. When , the switching gain of the power term can make the state variable approach the sliding mode surface quickly, which greatly improves the approaching speed of the system. When approaches 0, the power term of DPRL makes the switching gain of the system smaller when it is close to the sliding surface, which effectively weakens the chattering. However, when DPRL approaches the sliding surface, it cannot adaptively change the coefficient of the power term to further reduce the chattering.
By introducing the system state variables, the reaching law can adaptively adjust the reaching speed, which can effectively reduce the chattering.
The state variables exponential reaching law (SVERL) can be expressed as
When , compared with DPRL, SVERL adds to improve the approaching speed of the system when it is far away from the sliding surface. When approaches 0, the state variable can adaptively adjust the approaching speed, which effectively reduces the chattering. However, the addition of the exponential term also increases the control gain of the system and reduces the transient response performance of the system.
Combining the above two power reaching law analyses, this paper proposes an improved double power reaching law (IDPRL) that introduces system state variables
where , , , , . Select the appropriate and , so that .
When the system state condition is , Equation (6) can be written as , and the approaching speed of IDPRL is greater than that of DPRL and SVERL when it is far away from the sliding surface. When the system state condition is , Equation (6) can be written as , and can be adaptively adjusted with the state variables to effectively reduce the system chattering. The exponent term can improve the approaching speed of the reaching law and ensure the motion quality of the system state when approaching the sliding surface.
Select the Lyapunov function
According to the Lyapunov theorem,
According to the Lyapunov stability condition, only when , satisfying , can the system asymptotically converge to the sliding mode surface under the action of Equation (6).
3.2. Proof of Finite-Time Reachability of Reaching Law
For IPDRL, the initial state of is set to , then the sliding mode variables and can reach the sliding mode surface in a limited time, and the convergence time of the reaching law is less than :
Proof.
Assume that the initial state of the system , the system approach process is divided into two stages for calculation.
The reaching time of the sliding mode variable to is and Equation (6) can be written as:
where , , and play a leading role when away from the sliding surface, so Equation (11) is decomposed into . denotes that the approach time of the system is only affected by and . It can be seen that the approaching time of Equation (11) must be less than the solution of Equation . The solution process of Equation (11) is as follows:
The intermediate variables , can be transformed into and . can be expressed as:
Substituting (13) into (12),
Solving Equation (14),
where is a constant.
Substituting (15) into ,
When , , then the constant can be obtained,
Combined with formula (16), the solution of the equation can be obtained,
The reaching time of the sliding mode variable to is less than . Similarly, when the system is close to the sliding surface, the time required for the reaching law must be less than the solution of the equation . The time required for the sliding mode variable to reach is:
For IPDRL, the sliding mode variable can reach the sliding mode surface in a limited time, and the convergence time is less than . □
3.3. Analysis of Convergence Characteristics of Improved Double Power Reaching Law
Consider second-order nonlinear systems with disturbances:
where is the system state, is the external disturbance, is the control input.
The initial state of the system is set to [−0.1, −0.1], , . The reaching law parameters selected in this paper are: , , . Four reaching laws of EAL, DPRL, SVERL and IDPRL are used to design the control law. The second-order system is simulated to verify the effectiveness of the reaching law proposed in this paper.
Figure 2 shows the control performance effect diagrams of EAL, DPRL, SVERL and IDPRL. It can be seen from Figure 2a that ERL has a large chattering compared with the other three reaching laws, which seriously affects the stability of the control system. From Figure 2b,c, DPRL and SVERL can effectively reduce chattering compared with ERL, but the system state approaches the sliding mode surface. In the process, the control law will switch, the control input of the system will change between multiple states and the phase trajectory is not smooth enough. It can be seen from Figure 2d that the IDPRL proposed in this paper has a faster reaching speed than DPRL and SVERL when it is far away from the sliding mode surface and can reach the sliding mode surface faster. When the external disturbance is added, the reaching law cannot converge to the equilibrium point but converges to the interference steady-state region of the system. The above simulation verifies the effectiveness of the proposed reaching law.
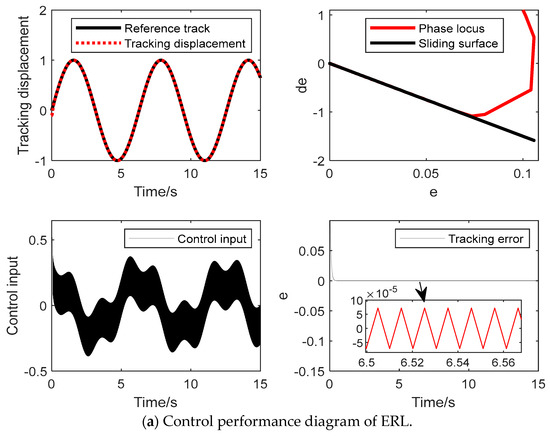
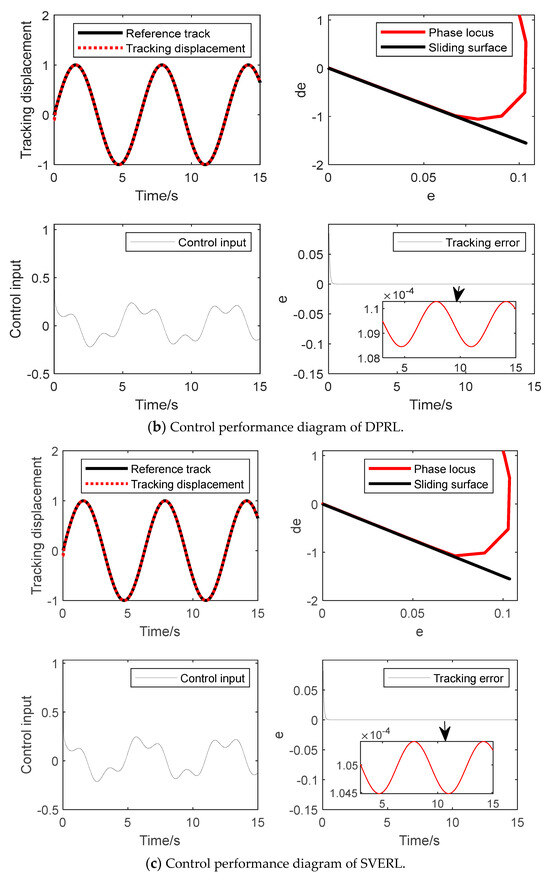
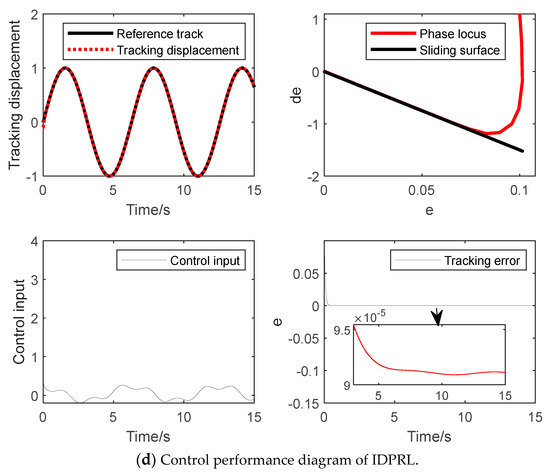
Figure 2.
Control performance diagrams of four reaching laws.
4. Design and Analysis of Extended State Observer
The second-order system is defined as:
where is the external interference of the system, has a known upper bound, , is derivable, is the control input.
In order to improve the robustness of the control system, ESO is designed to estimate the state of the disturbance.
When the system is disturbed by the outside world, ESO can estimate the state variables of the system by properly selecting the gain coefficient to improve the anti-interference performance of the system [32,33].
The error state equation of ESO can be expressed as
and can be expressed as
The characteristic equation of matrix is
According to Equation (25), we can obtain
In order to reduce the parameters required for the design and ensure a better transition process, the characteristic equation is converted into
and can be expressed as
According to Equation (28), choosing reasonable control parameters can make Hurwitz matrix and ensure the stability of ESO.
5. Global Nonsingular Fast Terminal Sliding Mode Control
For the ball screw feed system, a global nonsingular fast terminal sliding mode control strategy is designed in this paper. In Figure 3, the global nonsingular fast terminal sliding mode control frame diagram based on the improved double power reaching law is shown [34].
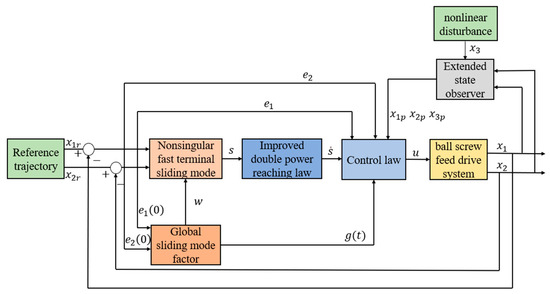
Figure 3.
GNFTSMC framework based on IDPRL.
The tracking error of the ball screw feed system is defined as:
where is the reference displacement of the system, is the displacement error of the system.
According to the design requirements of the controller, the global nonsingular fast terminal sliding mode surface is defined:
where , . , , , are all positive odd numbers, and , , is the global sliding mode factor.
The global sliding mode factor needs to satisfy the following three conditions simultaneously:
- (1)
- ;
- (2)
- When approaches infinity, approaches 0;
- (3)
- can be differentiated.
Condition (1) can ensure that the initial state of the system is located on the sliding surface; condition (2) can ensure that when the system state moves on the sliding surface, the system state tends to be stable; condition (3) means that the existence of sliding mode can be guaranteed. The global sliding mode factor is introduced into the nonsingular fast terminal sliding mode surface, and the system state can quickly converge to the sliding mode surface, which solves the problem of poor robustness of the traditional NFTSMC in the reaching stage.
The global sliding mode factor can be expressed as a monotonically decreasing function:
where is a constant, and is the function value of the global sliding mode factor at the initial time.
The derivation of (30) can be obtained:
When , the sliding mode equivalent control law can be obtained:
The switching control law can be obtained by using IDPRL:
The control law of GNFTSMC based on IDPRL can be expressed as:
In order to verify the stability of GNFTSMC, the Lyapunov function is defined:
The derivation of (36) can be obtained:
When is a positive real number, and are positive odd numbers. If , then . When , , the controller has a singular problem. Therefore, , then , and , avoiding the singular problem of the controller, when , , satisfying . In summary, the system will reach the sliding mode surface in a finite time, and the controller satisfies Lyapunov stability.
6. Simulation Verification and Analysis
In order to verify the effectiveness of IDPRL and GNFTSMC, the ball screw feed system model established in the second section is used for simulation verification. The model parameters of the ball screw feed system are shown in Table 1.

Table 1.
Model parameter values.
In order to further verify the effectiveness of the proposed control strategy, the following four controllers are selected as simulation comparison experiments.
- (1)
- Controller 1 (C1): The servo controller combining NFTSMC and DPRL is adopted, and ESO is designed to compensate the uncertainty and external disturbance of the model. The controller parameters are selected as follows: , , , , , and .
- (2)
- Controller 2 (C2): In order to form a set of comparative simulation experiments with C1, the effectiveness of GNFTSMC is verified. A servo controller combining IDPRL and GNFTSMC is used. The controller parameters are the same as C1. The global sliding mode factor is taken according to the initial state of the system.
- (3)
- Controller 3 (C3): In order to compare the influence of SVERL on system control performance, a servo controller combining SVERL and GNFTSMC is adopted.
- (4)
- Controller 4 (C4): C4 uses a controller that combines IDPRL and GNFTSMC. ESO compensates the model uncertainty and external disturbance. The global sliding mode factor coefficient , and the selection of other controller parameters is consistent with the other three control strategies.
Common error performance evaluation indicators include ISE, IAE, etc. In order to measure the gap between the actual tracking trajectory and the reference trajectory, this paper uses the ISE error performance evaluation index to reflect the fitting accuracy of the tracking trajectory by calculating the integral of the error square value to time. The expression of ISE is:
The ball screw feed system needs to perform accurate motion control according to the preset reference trajectory during the motion process. The selection of the reference trajectory is crucial for achieving high-precision tracking performance and smooth motion contour. When selecting the reference trajectory, the S-shaped motion curve is often used to achieve a smooth change in speed. However, there are discontinuous points in the S-shaped motion curve. This discontinuous point will cause the jump to mutate at a certain moment, resulting in flexible impact and mechanical vibration, which will affect the stability of the system. In order to solve the problems caused by the S-shaped motion curve, the quintic spline displacement curve can be used as the reference trajectory. The quintic spline curve has a continuous third-order derivative, which can ensure the smoothness and continuity of the jump curve of the feed system. Such characteristics can avoid structural vibration caused by sudden acceleration changes and improve the stability of the system. The reference trajectory acceleration equation used in this paper is expressed as [35]:
In order to reduce the influence of the mechanical stress and vibration of the ball screw feed system on the tracking accuracy and achieve a more stable speed change of the system, the acceleration constant is taken as , and the time interval is taken as 0.5 s. The speed and displacement curves of the ball screw feed system are obtained by one integral and two integrals. The reference displacement and reference speed of the ball screw feed system are input, and the obtained tracking curve and error are shown in Figure 4.
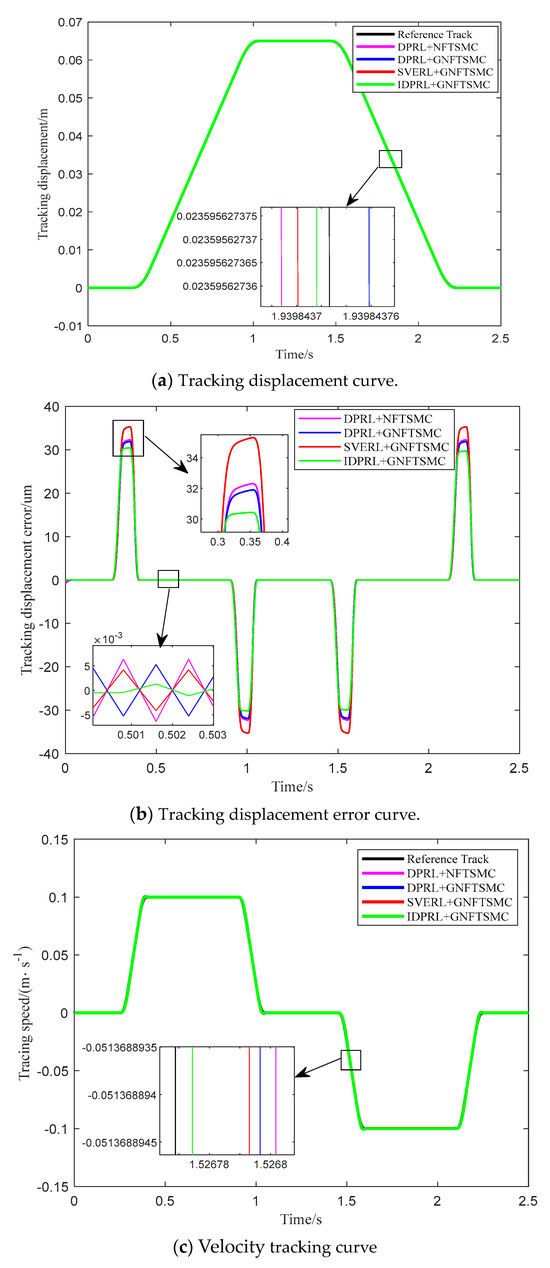
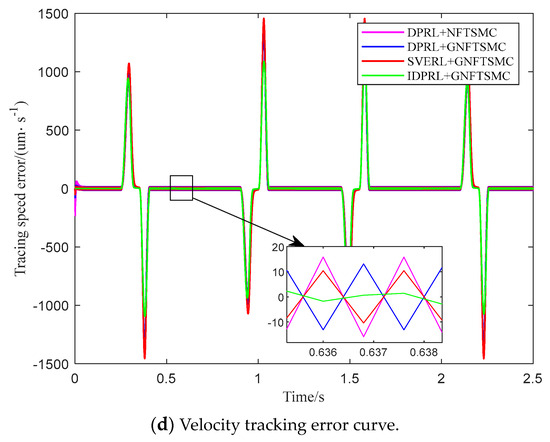
Figure 4.
Reference trajectory tracking curve.
From Figure 4a,b and Table 2, it can be seen that the displacement error performance evaluation function value of DPRL + GNFTSMC is 2.819, which is 14.81% higher than that of DPRL + NFTSMC. It is proved that the global sliding mode factor can effectively improve the tracking accuracy of the system. The maximum error values of DPRL + GNFTSMC and SVERL + GNFTSMC are 32.021 um and 35.824 μm, respectively. Although SVERL can reduce the chattering of the system, it will increase the maximum error value of the system. The displacement error performance evaluation function value of IDPL + GNFTSMC is only 1.371, which is 36.40%, 51.37% and 58.57% higher than that of SVERL + GNFTSMC, DPRL + GNFTSMC and DPRL + NFTSMC, respectively. IDPL + GNFTSMC maintains high tracking accuracy in each period of forward feed.

Table 2.
Tracking displacement performance index.
It can be seen from Figure 4c,d and Table 3 that the speed error performance evaluation function value of IDPRL + GNFTSMC is only 22.802, which is 40.02%, 61.56% and 69.46% higher than that of SVERL + GNFTSMC, DPRL + GNFTSMC and DPRL + NFTSMC, respectively. IDPRL + GNFTSMC effectively reduces the chattering of the system and improves the tracking accuracy of the system, which verifies the effectiveness of IDPRL + GNFTSMC.

Table 3.
Tracking speed performance index.
In order to improve the anti-interference of the system, it is necessary to simulate the influence of external interference on the tracking accuracy of the system to ensure the performance and reliability of the system in complex environments. In the control process, a nonlinear disturbance is added, as shown in Figure 5, which is a tracking trajectory diagram using ESO to observe nonlinear disturbances.
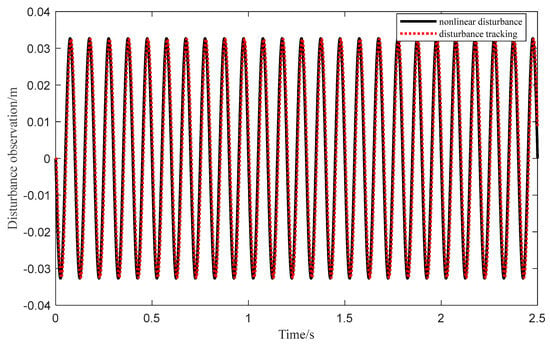
Figure 5.
Nonlinear interference observation curve.
It can be seen from Figure 5 that ESO can estimate the external disturbance of the system in real time, so as to effectively offset these uncertainties in the controller design and achieve accurate control of the system output. When the external interference is added, the reference displacement and reference speed of the ball screw feed system are input, and the tracking curve and error are shown in Figure 6.
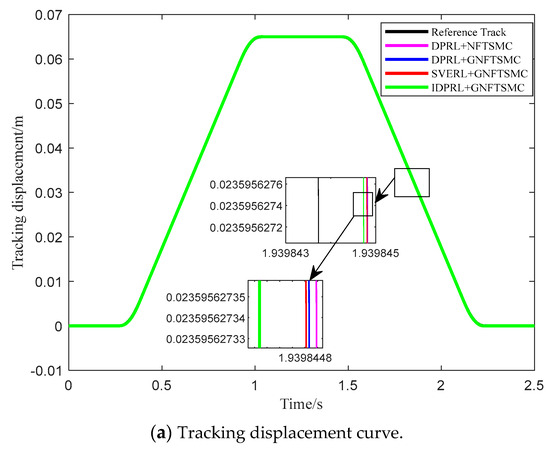
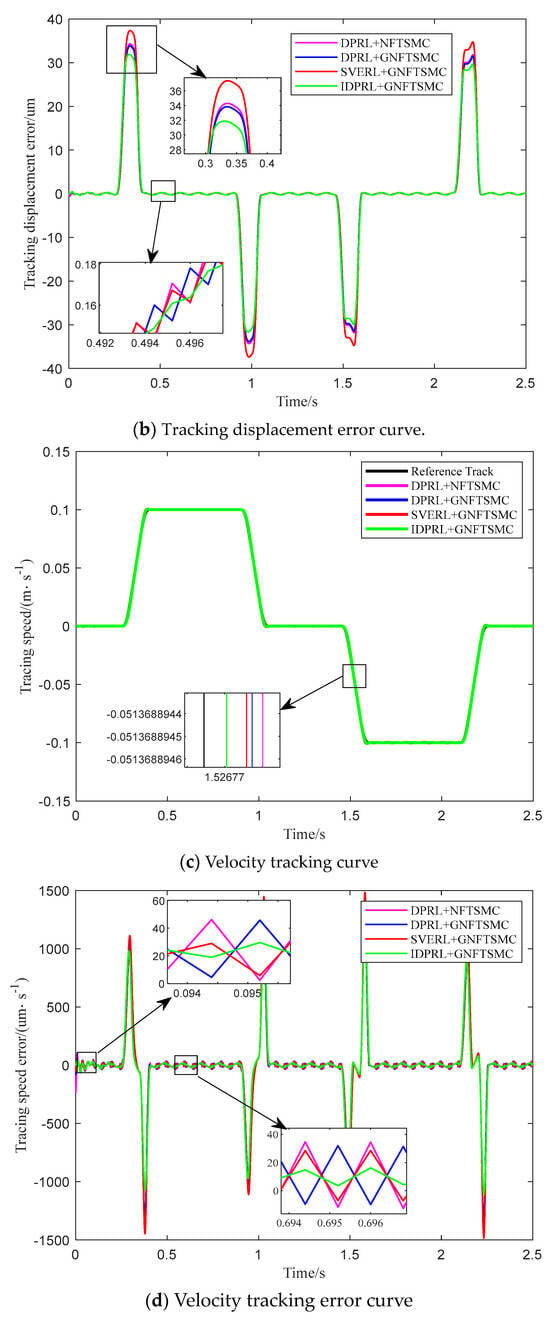
Figure 6.
Trajectory tracking curve with interference.
It can be seen from Figure 6a,b and Table 4 that after adding external interference, the average displacement error of IDPL + GNFTSMC is only 14.047 um, which is 15.14%, 15.93% and 16.83% lower than that of DPRL + GNFTSMC, DPRL + NFTSMC and SVERL + GNFTSMC.

Table 4.
Tracking displacement performance index when adding interference.
It can be seen from Figure 6c,d and Table 5 that the speed error performance evaluation function value of IDPRL + GNFTSMC is only 31.009 after adding external interference. Compared with DPRL + GNFTSMC, DPRL + NFTSMC and SVERL + GNFTSMC, it is increased by 55.59%, 64.37% and 65.01%, respectively. The simulation results show that IDPL + GNFTSMC can suppress external disturbances and improve the robustness of the system.

Table 5.
Performance index of tracking speed with interference.
7. Conclusions
Aiming at the dynamic model of ball screw feed system, an improved double power reaching law is designed in this paper. It is proved that the reaching law can reach the sliding mode surface in a finite time. The ESO is used to compensate the external disturbance, and the global sliding mode factor is introduced into the NFTSMC. The composite control strategy of IDPRL + GNFTSMC is proposed, and the stability of the control strategy is analyzed by Lyapunov theory. The simulation results show that IDPRL can greatly reduce the chattering of SMC. When external interference is added, the proposed IDPRL + GNFTSMC has better tracking accuracy and robust performance.
Author Contributions
Conceptualization, Q.W., S.Z. and X.W.; Methodology, Q.W., S.Z. and X.W.; Software, Q.W., S.Z. and X.W.; Validation, Q.W. and S.Z.; Formal analysis, Q.W. and X.W.; Investigation, X.W.; Writing—original draft, S.Z.; Writing—review and editing, S.Z.; Visualization, X.W.; Supervision, Q.W. and S.Z.; Project administration, Q.W. and X.W.; Funding acquisition, Q.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding
Data Availability Statement
Since the collection, collation and dissemination of data require a lot of time and resources, and the publication of these data may not produce sufficient benefits to make up for its costs, the data sets generated and/or analyzed in the current study are not publicly available, but can be obtained from the reasonable requirements of the corresponding authors.
Conflicts of Interest
The author Xinglian Wang was employed by the Lanzhou Petrochemical Company. All authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Wang, H.; Kang, S.; Zhao, X.; Xu, N.; Li, T. Command filter-based adaptive neural control design for nonstrict-feedback nonlinear systems with multiple actuator constraints. IEEE Trans. Cybern. 2021, 52, 12561–12570. [Google Scholar] [CrossRef] [PubMed]
- Ren, B.; Ge, S.S.; Tee, K.P.; Lee, T.H. Adaptive neural control for output feedback nonlinear systems using a barrier Lyapunov function. IEEE Trans. Neural Netw. 2010, 21, 1339–1345. [Google Scholar]
- Park, L.H.; Chung, S.; Kim, J.; Kwon, T. GradFuzz: Fuzzing deep neural networks with gradient vector coverage for adversarial examples. Neurocomputing 2023, 522, 165–180. [Google Scholar] [CrossRef]
- Zhang, S.; Xue, X.; Chen, C.; Sun, Z.; Sun, T. Development of a low-cost quadrotor UAV based on ADRC for agricultural remote sensing. Int. J. Agric. Biol. Eng. 2019, 12, 82–87. [Google Scholar] [CrossRef]
- Wang, F.; Wang, R.J.; Liu, E.H. Analysis and tuning for active disturbance rejection control. Math. Probl. Eng. 2019, 2019, 9641723. [Google Scholar] [CrossRef]
- Shi, S.; Zeng, Z.; Zhao, C.; Guo, L.; Chen, P. Improved active disturbance rejection control (ADRC) with extended state filters. Energies 2022, 15, 5799. [Google Scholar] [CrossRef]
- Vazquez, S.; Leon, J.I.; Franquelo, L.G.; Rodriguez, J.; Young, H.A.; Marquez, A.; Zanchetta, P. Model predictive control: A review of its applications in power electronics. IEEE Ind. Electron. Mag. 2014, 8, 16–31. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, Y.; Liang, X.; Guo, H.; Zhuang, X. Robust model predictive current control of PMSM based on nonlinear extended state observer. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 11, 862–873. [Google Scholar] [CrossRef]
- Dos Santos, T.B.; Oliani, I.; Figueiredo, R.; Albieiro, D.; Pelizari, A.; Sguarezi Filho, A.J. Robust finite control set model predictive current control for induction motor using deadbeat approach in stationary frame. IEEE Access 2022, 11, 13067–13078. [Google Scholar] [CrossRef]
- Yang, X.; Liu, G.; Le, V.D.; Le, C.Q. A novel model-predictive direct control for induction motor drives. IEEJ Trans. Electr. Electron. Eng. 2019, 14, 1691–1702. [Google Scholar] [CrossRef]
- Nguyen, A.T.; Taniguchi, T.; Eciolaza, L.; Campos, V.; Palhares, R.; Sugeno, M. Fuzzy control systems: Past, present and future. IEEE Comput. Intell. Mag. 2019, 14, 56–68. [Google Scholar] [CrossRef]
- Wang, H.; Bai, W.; Zhao, X.; Liu, P.X. Finite-time-prescribed performance-based adaptive fuzzy control for strict-feedback nonlinear systems with dynamic uncertainty and actuator faults. IEEE Trans. Cybern. 2021, 52, 6959–6971. [Google Scholar] [CrossRef] [PubMed]
- Le, T.L.; Ngo, V.B. The synchronization of hyperchaotic systems using a novel interval type-2 fuzzy neural network controller. IEEE Access 2022, 10, 105966–105982. [Google Scholar] [CrossRef]
- Wu, X.; Xu, K.; Lei, M.; He, X. Disturbance-compensation-based continuous sliding mode control for overhead cranes with disturbances. IEEE Trans. Autom. Sci. Eng. 2020, 17, 2182–2189. [Google Scholar] [CrossRef]
- Zaidi, A.; Dahech, K.; Damak, T. Maximum power point tracking of photovoltaic systems based on fast terminal sliding mode controller. Int. J. Renew. Energy Res. 2016, 6, 1435–1445. [Google Scholar]
- Ma, X.; Wong, P.K.; Zhao, J.; Xie, Z. Multi-Objective Sliding Mode Control on Vehicle Cornering Stability with Variable Gear Ratio Actuator-Based Active Front Steering Systems. Sensors 2016, 17, 49. [Google Scholar] [CrossRef] [PubMed]
- Deng, X.; Huang, Y.; Xu, B.; Tao, L. Position and Attitude Tracking Finite-Time Adaptive Control for a VTOL Aircraft Using Global Fast Terminal Sliding Mode Control. Mathematics 2023, 11, 2732. [Google Scholar] [CrossRef]
- Li, S.; Zhou, M.; Yu, X. Design and implementation of terminal sliding mode control method for PMSM speed regulation system. IEEE Trans. Ind. Inform. 2012, 9, 1879–1891. [Google Scholar] [CrossRef]
- Suryawanshi, P.V.; Shendge, P.D.; Phadke, S.B. A boundary layer sliding mode control design for chatter reduction using uncertainty and disturbance estimator. Int. J. Dyn. Control 2016, 4, 456–465. [Google Scholar] [CrossRef]
- Mozayan, S.M.; Saad, M.; Vahedi, H.; Fortin-Blanchette, H.; Soltani, M. Sliding mode control of PMSG wind turbine based on enhanced exponential reaching law. IEEE Trans. Ind. Electron. 2016, 63, 6148–6159. [Google Scholar] [CrossRef]
- Mobayen, S. Chaos synchronization of uncertain chaotic systems using composite nonlinear feedback based integral sliding mode control. ISA Trans. 2018, 77, 100–111. [Google Scholar] [CrossRef] [PubMed]
- Cui, M.; Liu, W.; Liu, H.; Jiang, H.; Wang, Z. Extended state observer-based adaptive sliding mode control of differential-driving mobile robot with uncertainties. Nonlinear Dyn. 2016, 83, 667–683. [Google Scholar] [CrossRef]
- Pan, H.; Zhang, G.; Ouyang, H.; Mei, L. A novel global fast terminal sliding mode control scheme for second-order systems. IEEE Access 2020, 8, 22758–22769. [Google Scholar] [CrossRef]
- Liu, W.; Chen, S.; Huang, H. Adaptive nonsingular fast terminal sliding mode control for permanent magnet synchronous motor based on disturbance observer. IEEE Access 2019, 7, 153791–153798. [Google Scholar] [CrossRef]
- Qiao, L.; Zhang, W. Adaptive non-singular integral terminal sliding mode tracking control for autonomous underwater vehicles. IET Control Theory Appl. 2017, 11, 1293–1306. [Google Scholar] [CrossRef]
- Feng, Y.; Yu, X.; Han, F. On nonsingular terminal sliding-mode control of nonlinear systems. Automatica 2013, 49, 1715–1722. [Google Scholar] [CrossRef]
- Qu, L.; Qiao, W.; Qu, L. An extended-state-observer-based sliding-mode speed control for permanent-magnet synchronous motors. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 9, 1605–1613. [Google Scholar] [CrossRef]
- Rushworth, A.; Axinte, D.; Raffles, M.; Cobos-Guzman, S. A concept for actuating and controlling a leg of a novel walking parallel kinematic machine tool. Mechatronics 2016, 40, 63–77. [Google Scholar] [CrossRef]
- Aslan, D.; Altintas, Y. On-line chatter detection in milling using drive motor current commands extracted from CNC. Int. J. Mach. Tools Manuf. 2018, 132, 64–80. [Google Scholar] [CrossRef]
- Ansoategui, I.; Campa, F.J. Mechatronics of a ball screw drive using an N degrees of freedom dynamic model. Int. J. Adv. Manuf. Technol. 2017, 93, 1307–1318. [Google Scholar] [CrossRef]
- Bao, D.F.; Tang, W.C.; Dong, L. Integral sliding mode control for flexible ball screw drives with matched and mismatched uncertainties and disturbances. J. Cent. South Univ. 2017, 24, 1992–2000. [Google Scholar] [CrossRef]
- Sun, H.; Gao, L.; Zhao, Z.; Li, B. Adaptive super-twisting fast nonsingular terminal sliding mode control with ESO for high-pressure electro-pneumatic servo valve. Control Eng. Pract. 2023, 134, 105483. [Google Scholar] [CrossRef]
- Li, P.; Yang, H.; Li, H.; Liang, S. Nonlinear ESO-based tracking control for warehouse mobile robots with detachable loads. Robot. Auton. Syst. 2022, 149, 103965. [Google Scholar] [CrossRef]
- Wang, H.; Yu, C.; Jing, Y. Global Sliding Mode Control for Nonlinear Network Systems with Input Constraints. J. Northeast. Univ. (Nat. Sci. Ed.) 2010, 31, 326. [Google Scholar]
- Shi, Y. Research on Trajectory Tracking Control Method of Ball Screw Feed System. Doctoral Dissertation, Southeast University, Nanjing, China, 2018. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).