Numerical and Experimental Study of a Wearable Exo-Glove for Telerehabilitation Application Using Shape Memory Alloy Actuators
Abstract
1. Introduction
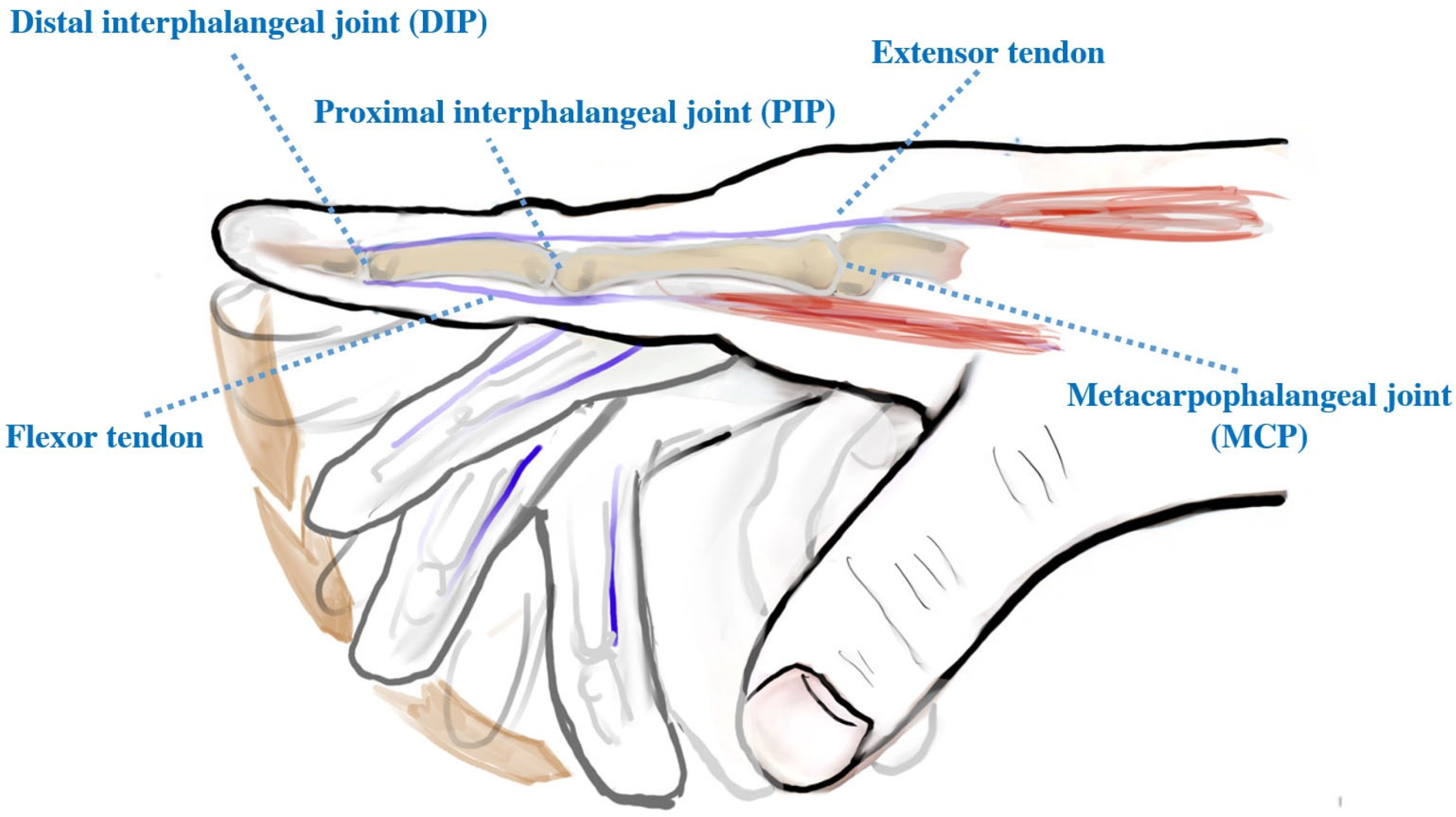
2. Materials and Methods
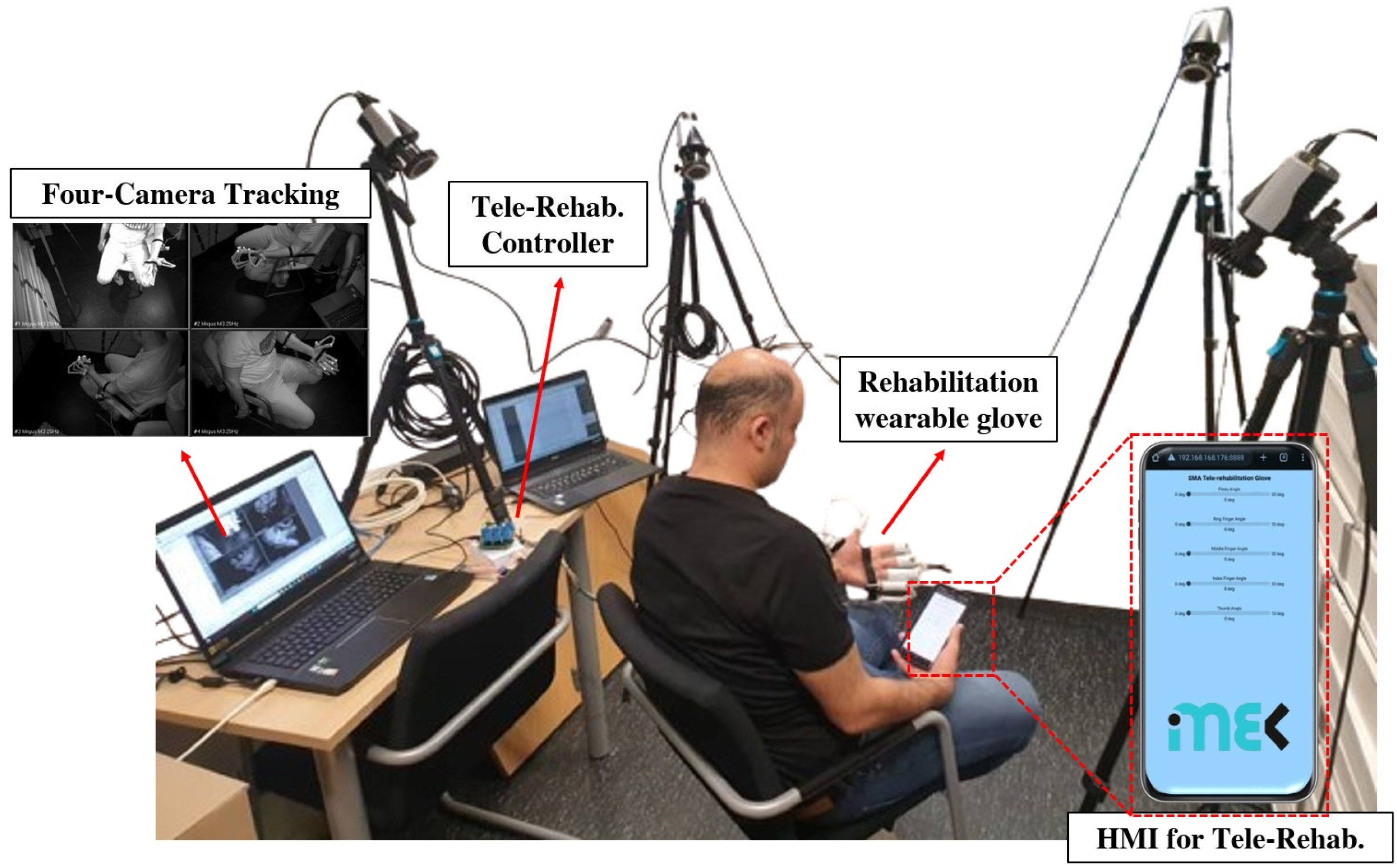
2.1. Experimental Setup
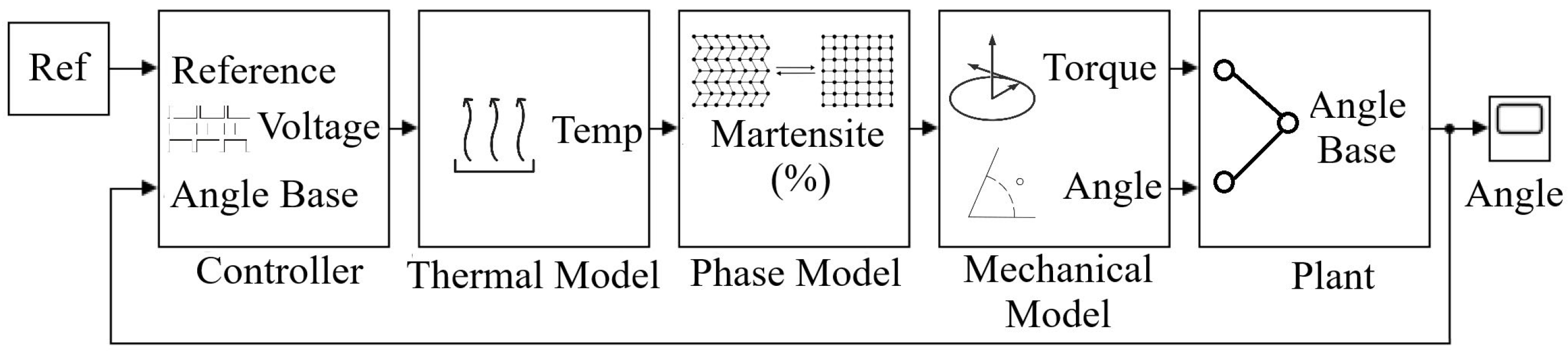
2.2. System Modeling and Control
2.3. Numerical Modeling of Shape Memory Alloy
2.4. Remote Control System
2.5. Measurement Scheme
2.5.1. Dynamic Measurement
2.5.2. Static Measurement
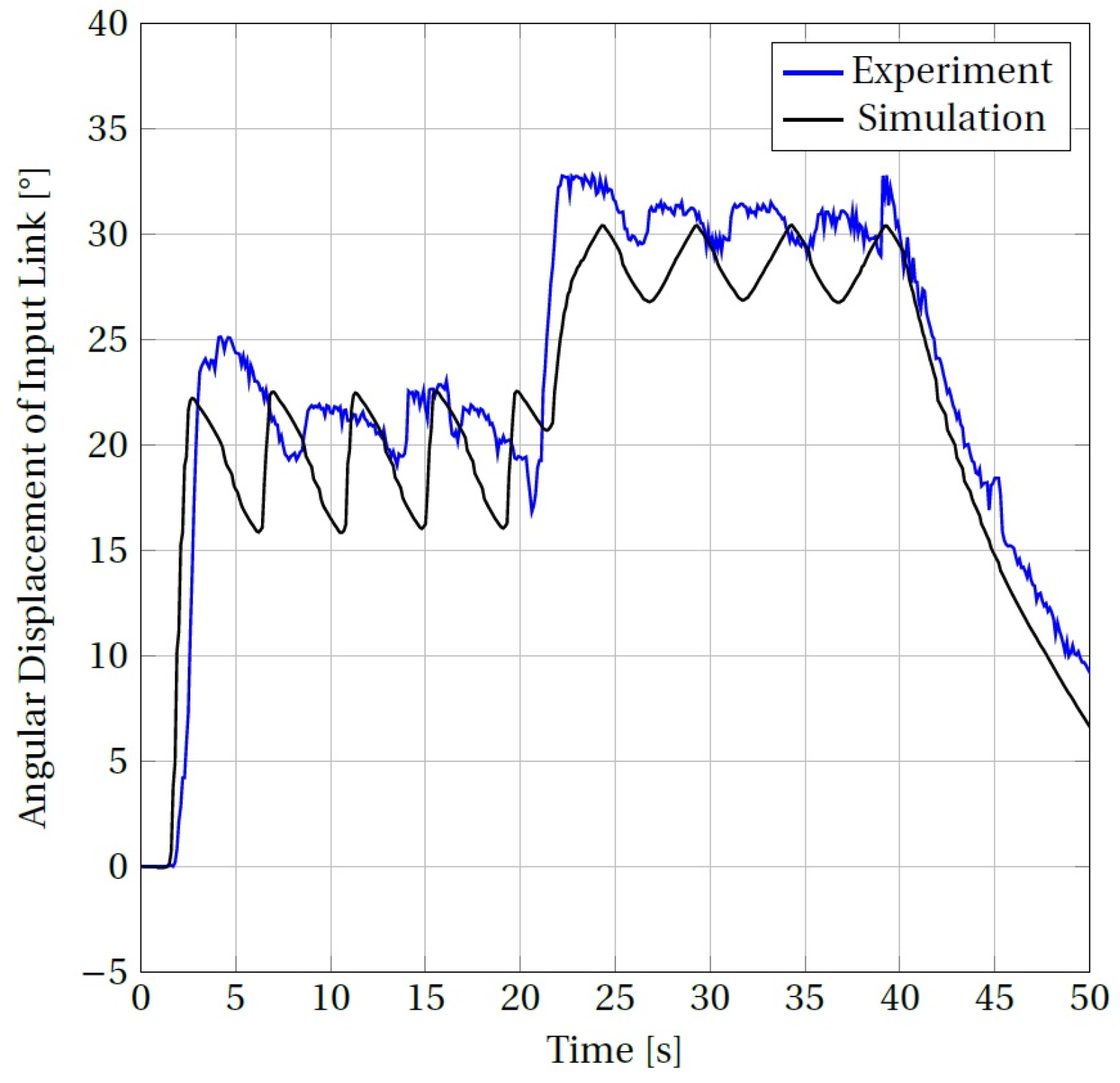
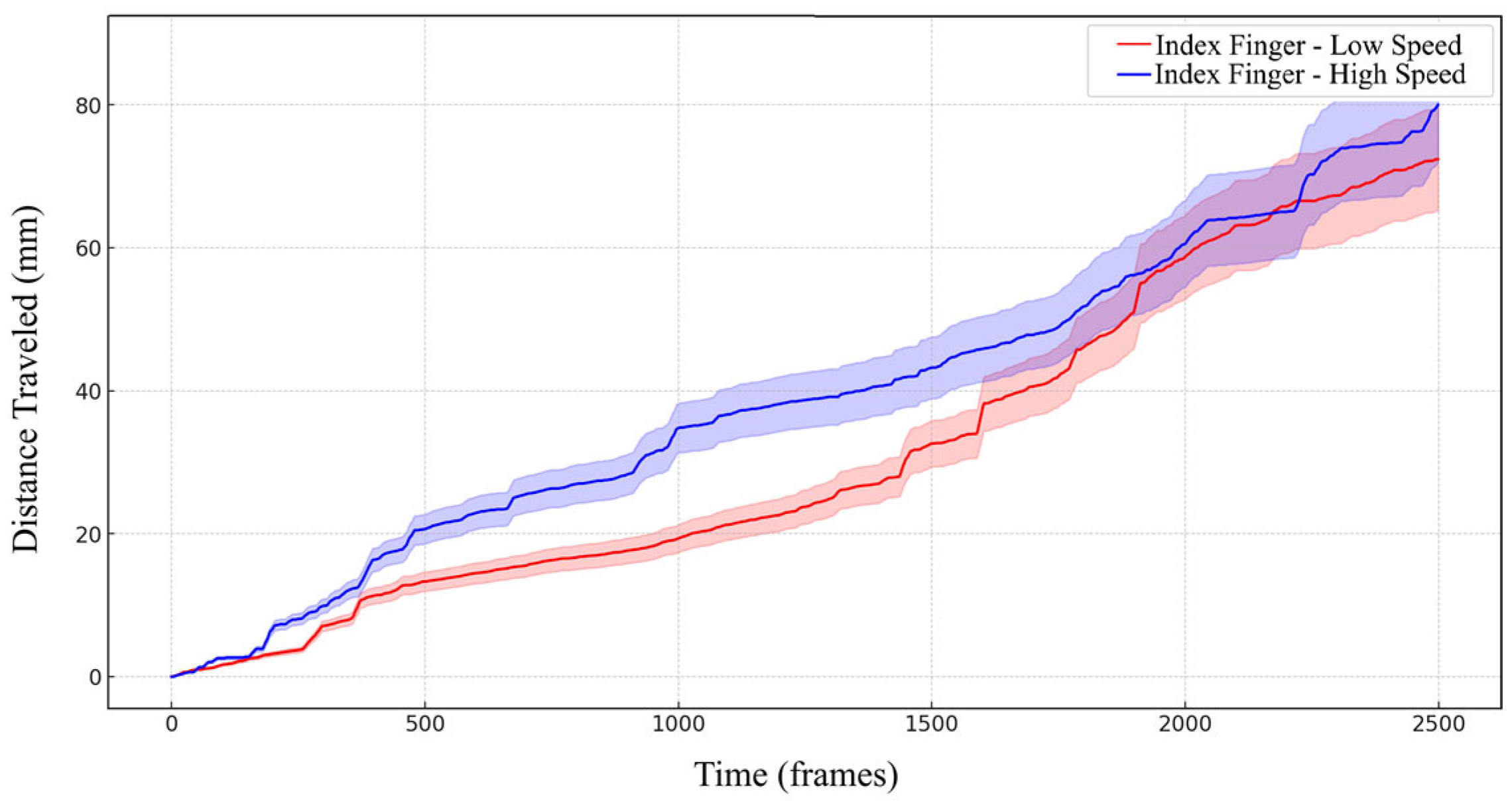
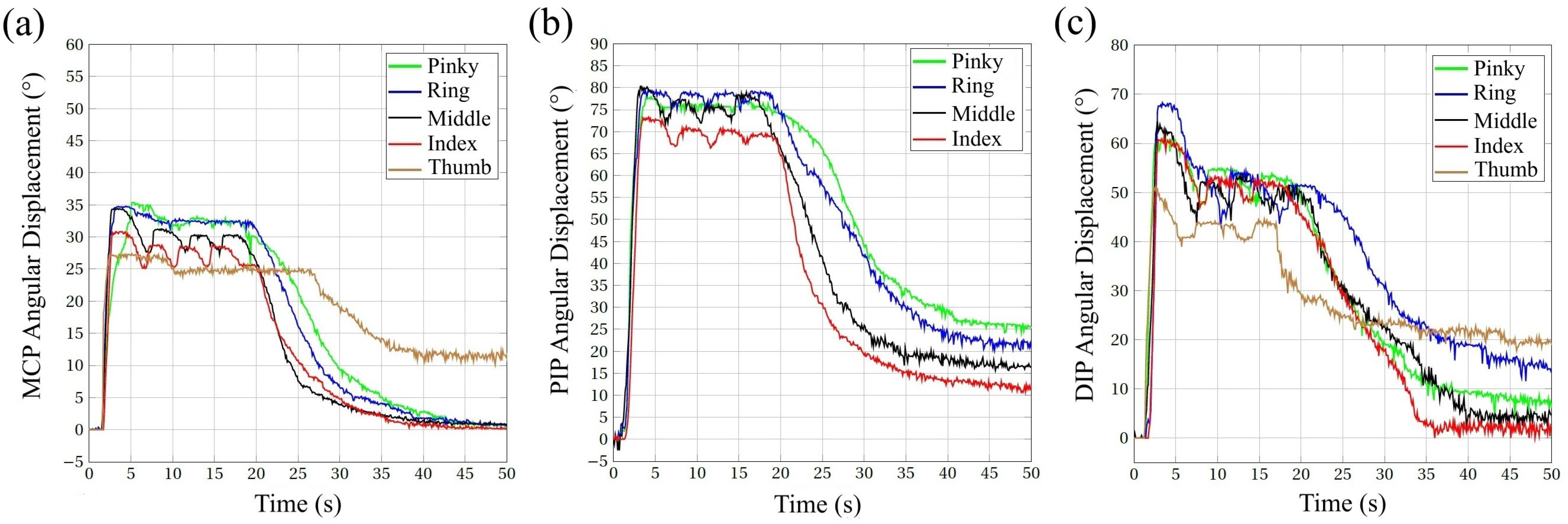
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B
| Description | Symbol | Value (Unit) |
|---|---|---|
| Length of link 1 | 0.05 () | |
| Length of link 2 | 0.14 () | |
| Length of link 3 | 0.08 () | |
| Length of link 4 | 0.11 () | |
| Initial link 2 angle | 2 () | |
| Mass of link 2 | 0.01 () | |
| Mass of link 3 | 0.007 () | |
| Mass of link 4 | 0.1 () | |
| Stiffness of torsional spring | 0.804 () | |
| PLA coefficient of friction | 0.45 () | |
| Clamping force on the link 2 joint | 15 () | |
| Inner diameter of friction hollow disk | 1.8 × 10−2 () | |
| Outer diameter of friction hollow disk | 5 × 10−3 () | |
| Length of the SMA wire | 0.67 () | |
| Electrical resistance of the SMA wire | 5.56 () |
Appendix C
| Material Parameter | Symbol | Value (Unit) |
|---|---|---|
| Maximum transformation strain | 0.056 () | |
| Slope of limit curve | 7.4 () | |
| Reference temperature | 265.5 | |
| Elastic domain radius | 129.5 | |
| Hardening modulus | 1.982 |
References
- Benjamin, E.J.; Blaha, M.J.; Chiuve, S.E.; Cushman, M.; Das, S.R.; Deo, R.; de Ferranti, S.D.; Floyd, J.; Fornage, M.; Gillespie, C.; et al. Heart disease and stroke statistics-2017 update: A report from the American Heart Association. Circulation 2017, 135, e146–e603. [Google Scholar] [CrossRef] [PubMed]
- Knecht, S.; Hesse, S.; Oster, P. Rehabilitation after stroke. Dtsch. Arztebl. Int. 2011, 108, 600–606. [Google Scholar] [CrossRef] [PubMed]
- Mackay, J.; Mensah, G. Atlas of Heart Disease and Stroke; World Health Organization, Nonserial Publication: Brighton, UK, 2004. [Google Scholar]
- Parker, V.M.; Wade, D.T.; Langton, H.R. Loss of arm function after stroke: Measurement, frequency, and recovery. Int. Rehabil. Med. 1986, 8, 69–73. [Google Scholar] [CrossRef] [PubMed]
- Marty, J.; Porcher, B.; Autissier, R. Hand injuries and occupational accidents. Statistics and prevention. Ann. Chir. Main. 1983, 2, 368–370. [Google Scholar] [CrossRef]
- van Stormbroek, K.; Buchanan, H. Novice therapists in a developing context: Extending the reach of hand rehabilitation. Hand Ther. 2017, 22, 141–152. [Google Scholar] [CrossRef]
- Lingampally, P.K.; Ramanathan, K.C.; Shanmugam, R.; Cepova, L.; Salunkhe, S. Wearable Assistive Rehabilitation Robotic Devices—A Comprehensive Review. Machines 2024, 12, 415. [Google Scholar] [CrossRef]
- Li, F.; Chen, J.; Ye, G.; Dong, S.; Gao, Z.; Zhou, Y. Soft robotic glove with sensing and force feedback for rehabilitation in virtual reality. Biomimetics 2023, 8, 83. [Google Scholar] [CrossRef]
- Janarthanan, V.; Assad-Uz-Zaman, M.; Rahman, M.H.; McGonigle, E.; Wang, I. Design and development of a sensored glove for home-based rehabilitation. J. Hand Ther. 2020, 33, 209–219. [Google Scholar] [CrossRef]
- Aly, A.A.I.; Abbasimoshaei, A.; Kern, T.A. Developing a VR training environment for fingers rehabilitation. In Proceedings of the 13th International Conference on Human Haptic Sensing and Touch Enabled Computer Applications, EuroHaptics 2022, Hamburg, Germany, 22–25 May 2022; pp. 331–333. [Google Scholar]
- Haghshenas-Jaryani, M.; Pande, C.; Wijesundara, B.M. Soft robotic bilateral hand rehabilitation system for fine motor learning. In Proceedings of the 2019 IEEE 16th International Conference on Rehabilitation Robotics (ICORR), Toronto, ON, Canada, 24–28 June 2019; pp. 337–342. [Google Scholar]
- Yang, S.-H.; Koh, C.-L.; Hsu, C.-H.; Chen, P.-C.; Chen, J.-W.; Lan, Y.-H.; Yang, Y.; Lin, Y.-D.; Wu, C.-H.; Liu, H.-K.; et al. An instrumented glove-controlled portable hand-exoskeleton for bilateral hand rehabilitation. Biosensors 2021, 11, 495. [Google Scholar] [CrossRef]
- Cisnal, A.; Gordaliza, P.; Pérez Turiel, J.; Fraile, J.C. Interaction with a hand rehabilitation exoskeleton in EMG-driven bilateral therapy: Influence of visual biofeedback on the users’ performance. Sensors 2023, 23, 2048. [Google Scholar] [CrossRef]
- Connolly, J.; Condell, J.; O’Flynn, B.; Sanchez, J.T.; Gardiner, P. IMU sensor-based electronic goniometric glove for clinical finger. movement analysis. IEEE Sens. J. 2017, 18, 1273–1281. [Google Scholar] [CrossRef]
- Lin, B.S.; Lee, I.J.; Yang, S.Y.; Lo, Y.C.; Lee, J.; Chen, J.L. Design of an inertial-sensor-based data glove for hand function evaluation. Sensors 2018, 18, 1545. [Google Scholar] [CrossRef] [PubMed]
- Saggio, G.; Riillo, F.; Sbernini, L.; Quitadamo, L.R. Resistive flex sensors: A survey. Smart Mater. Struct. 2015, 25, 013001. [Google Scholar] [CrossRef]
- Guo, S.; Gao, J.; Guo, J.; Zhang, W.; Hu, Y. Design of the structural optimization for the upper limb rehabilitation robot. In Proceedings of the 2016 IEEE International Conference on Mechatronics and Automation, Harbin, China, 7–10 August 2016; pp. 1185–1190. [Google Scholar]
- Richards, C.; MacKenzie, N.; Roberts, S.; Escorpizo, R. People with spinal cord injury in the United States. Am. J. Phys. Med. Rehabil. 2017, 96, S124–S126. [Google Scholar] [CrossRef] [PubMed]
- Popov, D.; Gaponov, I.; Ryu, J.H. Portable exoskeleton glove with soft structure for hand assistance in activities of daily living. IEEE ASME Trans. Mechatron. 2017, 22, 865–875. [Google Scholar] [CrossRef]
- Lee, B.J.; Williams, A.; Ben-Tzvi, P. Intelligent object grasping with sensor fusion for rehabilitation and assistive applications. IEEE Trans. Neural Syst. Rehabil. Eng. 2018, 26, 1556–1565. [Google Scholar] [CrossRef]
- Chen, X.; Gong, L.; Wei, L.; Yeh, S.-C.; Da Xu, L.; Zheng, L.; Zou, Z. A wearable hand rehabilitation system with soft gloves. IEEE Trans. Ind. Inform. 2021, 17, 943–952. [Google Scholar] [CrossRef]
- Lai, J.; Song, A.; Shi, K.; Ji, Q.; Lu, Y.; Li, H. Design and evaluation of a bidirectional soft glove for hand rehabilitation-assistance tasks. IEEE Trans. Med. Robot. Bionics 2023, 3, 730–740. [Google Scholar] [CrossRef]
- Schabowsky, C.N.; Godfrey, S.B.; Holley, R.J.; Lum, P.S. Development and pilot testing of HEXORR: Hand EXOskeleton rehabilitation robot. J. NeuroEng. Rehabil. 2010, 7, 36. [Google Scholar] [CrossRef]
- Shian, S.; Bertoldi, K.; Clarke, D.R. Dielectric elastomer based grippers for soft robotics. Adv. Mater. 2015, 27, 6814–6819. [Google Scholar] [CrossRef]
- Xiloyannis, M.; Cappello, L.; Khanh, D.B.; Yen, S.-C.; Masia, L. Modelling and design of a synergy-based actuator for a tendon-driven soft robotic glove. In Proceedings of the 6th IEEE International Conference on Biomedical Robotics and Biomechatronics, Singapore, 26–29 June 2016; pp. 1213–1219. [Google Scholar]
- Haptx. Available online: https://haptx.com/ (accessed on 2 July 2021).
- Wang, J.; Fei, Y.; Pang, W. Design, modeling, and testing of a soft pneumatic glove with segmented pneuNets bending actuators. IEEE ASME Trans. Mechatron. 2019, 24, 990–1001. [Google Scholar] [CrossRef]
- Feng, M.; Yang, D.; Gu, G. High-force fabric-based pneumatic actuators with asymmetric chambers and interference-reinforced structure for soft wearable assistive gloves. IEEE Robot. Autom. Lett. 2021, 6, 3105–3111. [Google Scholar] [CrossRef]
- Yi, J.; Chen, X.; Wang, Z. A three-dimensional-printed soft robotic glove with enhanced ergonomics and force capability. IEEE Robot. Autom. 2018, 3, 242–248. [Google Scholar] [CrossRef]
- Ge, L.; Chen, F.; Wang, D.; Zhang, Y.; Han, D.; Wang, T.; Gu, G. Design, modeling, and evaluation of fabric-based pneumatic actuators for soft wearable assistive gloves. Soft Robot. 2020, 7, 583–596. [Google Scholar] [CrossRef] [PubMed]
- Kubášová, K.; Drátovská, V.; Losertová, M.; Salvetr, P.; Kopelent, M.; Kořínek, F.; Havlas, V.; Džugan, J.; Daniel, M. A Review on Additive Manufacturing Methods for NiTi Shape Memory Alloy Production. Materials 2024, 17, 1248. [Google Scholar] [CrossRef] [PubMed]
- Chujo, T.; Sawada, H. The application of micro-vibratory phenomena of a shape-memory alloy wire to a novel vibrator. Vibration 2023, 6, 584–598. [Google Scholar] [CrossRef]
- Grigorie, T.L.; Botez, R.M. A self–tuning intelligent controller for a smart actuation mechanism of a morphing wing based on shape memory alloys. Actuators 2023, 12, 350. [Google Scholar] [CrossRef]
- Zhang, H.; Zhao, L.; Li, A.; Xu, S. Design and Hysteretic Performance Analysis of a Novel Multi-Layer Self-Centering Damper with Shape Memory Alloy. Buildings 2024, 14, 483. [Google Scholar] [CrossRef]
- Wang, Y.; Zheng, S.; Pang, J.; Li, S.; Li, J. Design and experiment of a hand movement device driven by shape memory alloy wires. J. Robot. 2021, 2021, 6611581. [Google Scholar] [CrossRef]
- Terrile, S.; Miguelañez, J.; Barrientos, A. A soft haptic glove actuated with shape memory alloy and flexible stretch sensors. Sensors 2021, 21, 5278. [Google Scholar] [CrossRef]
- Lee, S.M.; Park, J. A soft wearable exoglove for rehabilitation assistance: A novel application of knitted shape-memory alloy as a flexible actuator. Fash. Text. 2024, 11, 14. [Google Scholar] [CrossRef]
- Abdelaal, W.G.A.; Nagib, G. Modeling and simulation of sma actuator wire. In Proceedings of the 2014 9th International Conference on Computer Engineering & Systems (ICCES), Cairo, Egypt, 22–23 December 2014; pp. 401–405. [Google Scholar]
- Kazeminasab, S.; Hadi, A.; Alipour, K.; Elahinia, M. Force and motion control of a tendon-driven hand exoskeleton actuated by shape memory alloys. Ind. Robot. Int. J. 2018, 45, 623–633. [Google Scholar] [CrossRef]
- Auricchio, F.; Petrini, L. A three-dimensional model describing stress temperature induced solid phase transformations: Solution algorithm and boundary value problems. Int. J. Numer. Methods Eng. 2004, 61, 807–836. [Google Scholar] [CrossRef]
- Saharan, L.; de Andrade, M.J.; Saleem, W.; Baughman, R.H.; Tadesse, Y. iGrab: Hand orthosis powered by twisted and coiled polymer muscles. Smart Mater. Struct. 2017, 26, 105048. [Google Scholar] [CrossRef]
- Duanmu, D.; Li, X.; Huang, W.; Hu, Y. Soft Finger Rehabilitation Exoskeleton of Biomimetic Dragonfly Abdominal Ventral Muscles: Center Tendon Pneumatic Bellows Actuator. Biomimetics 2023, 8, 614. [Google Scholar] [CrossRef]





| Parameter (Diameter) | Sensor 1 (N) | Sensor 2 (N) | Sensor 3 (N) | Total Force (N) |
|---|---|---|---|---|
| Object A (60 mm) | 2.96 ± 1.02 | 1.12 ± 0.92 | 2.45 ± 1.52 | 6.53 |
| Object B (70 mm) | 3.27 ± 1.27 | 1.17 ± 1.04 | 2.87 ± 0.92 | 7.31 |
| Object C (80 mm) | 4.13 ± 0.85 | 1.43 ± 1.15 | 3.53 ± 1.23 | 9.09 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sadeghi, M.; Abbasimoshaei, A.; Kitajima Borges, J.P.; Kern, T.A. Numerical and Experimental Study of a Wearable Exo-Glove for Telerehabilitation Application Using Shape Memory Alloy Actuators. Actuators 2024, 13, 409. https://doi.org/10.3390/act13100409
Sadeghi M, Abbasimoshaei A, Kitajima Borges JP, Kern TA. Numerical and Experimental Study of a Wearable Exo-Glove for Telerehabilitation Application Using Shape Memory Alloy Actuators. Actuators. 2024; 13(10):409. https://doi.org/10.3390/act13100409
Chicago/Turabian StyleSadeghi, Mohammad, Alireza Abbasimoshaei, Jose Pedro Kitajima Borges, and Thorsten Alexander Kern. 2024. "Numerical and Experimental Study of a Wearable Exo-Glove for Telerehabilitation Application Using Shape Memory Alloy Actuators" Actuators 13, no. 10: 409. https://doi.org/10.3390/act13100409
APA StyleSadeghi, M., Abbasimoshaei, A., Kitajima Borges, J. P., & Kern, T. A. (2024). Numerical and Experimental Study of a Wearable Exo-Glove for Telerehabilitation Application Using Shape Memory Alloy Actuators. Actuators, 13(10), 409. https://doi.org/10.3390/act13100409






