Research on AGV Path Planning Based on Improved Directed Weighted Graph Theory and ROS Fusion
Abstract
1. Introduction
2. Path Planning Based on Improved Directed Weighted Graph Theory
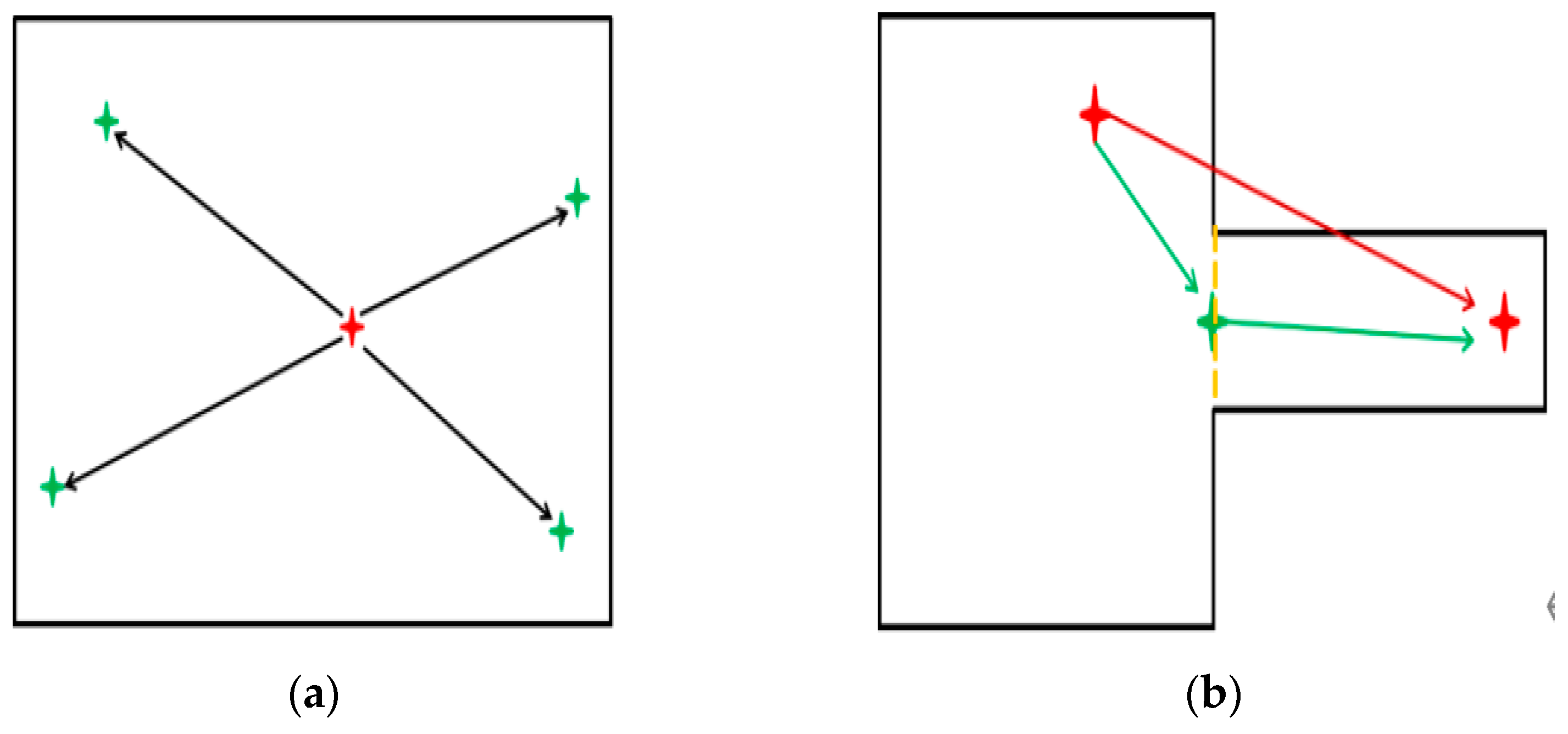
2.1. Traditional Directed Weighted Graph Theory
- Definition of a directed graph: A directed graph is composed of a set of vertices and a set of directed edges, each of which is represented by an ordered pair (u, v), where vertex u points to vertex v.
- Representation of weighted graphs: Based on a directed graph, edge weights are introduced, which represent the cost or distance from the source vertex to the target vertex.
- Paths and connectivity: A path is a series of vertices connected by an edge sequence in a graph. Formally, a path can be represented as (v0, v1, v2, …, vn), where vi represents a vertex and (vi, vi + 1) represents a directed edge from vi to vi + 1. If there is a path from vertex u to vertex v, then u and v are considered connected in the directed graph.
- Shortest path problem: The shortest path from one vertex to another refers to the path with the minimum sum of weights on the path. Usually d(u, v) is used to represent the weight of the shortest path from vertex u to vertex v.
- Dijkstra algorithm: This is an algorithm used to solve the shortest path of a single source in a weighted graph. The algorithm adopts a greedy strategy by continuously performing relaxation operations, selecting the vertex extension path of the currently known shortest path, until the shortest path from the source vertex to all other vertices is determined. It ultimately computes d(u,v).
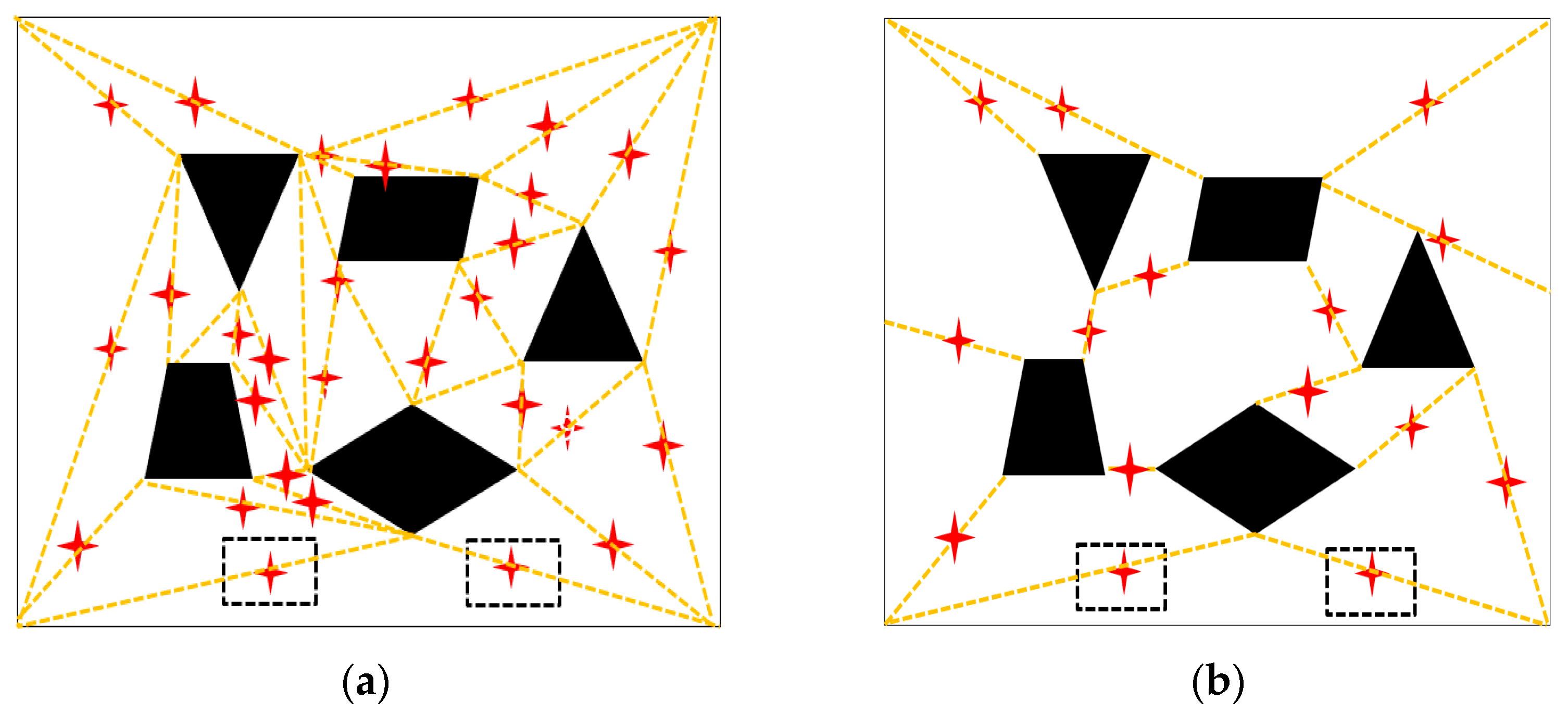
2.2. Improving the Application of Directed Weighted Graph in Path Planning
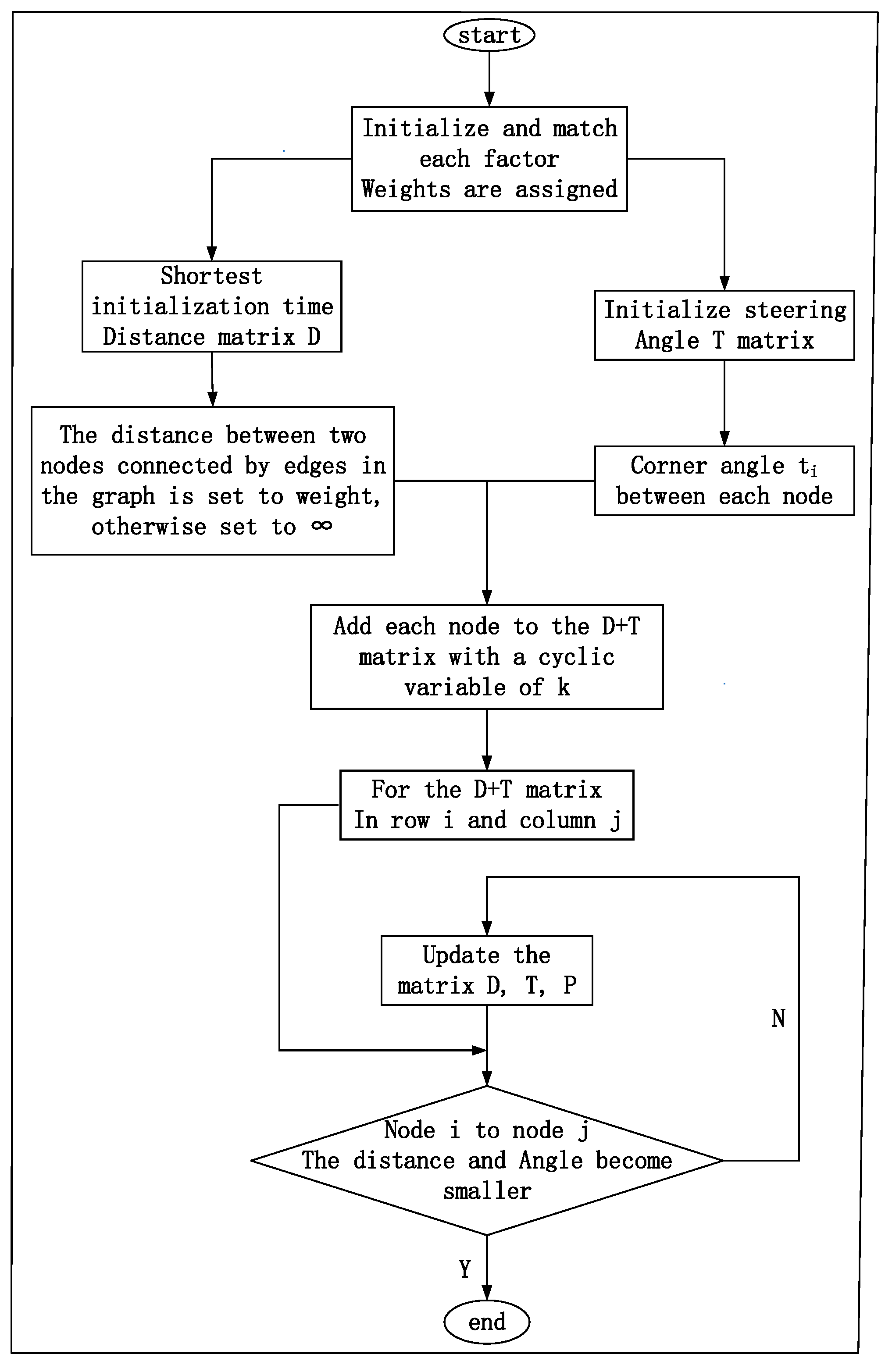
3. Solution and Application of Directed Weighted Graph Theory Based on the Floyd Algorithm
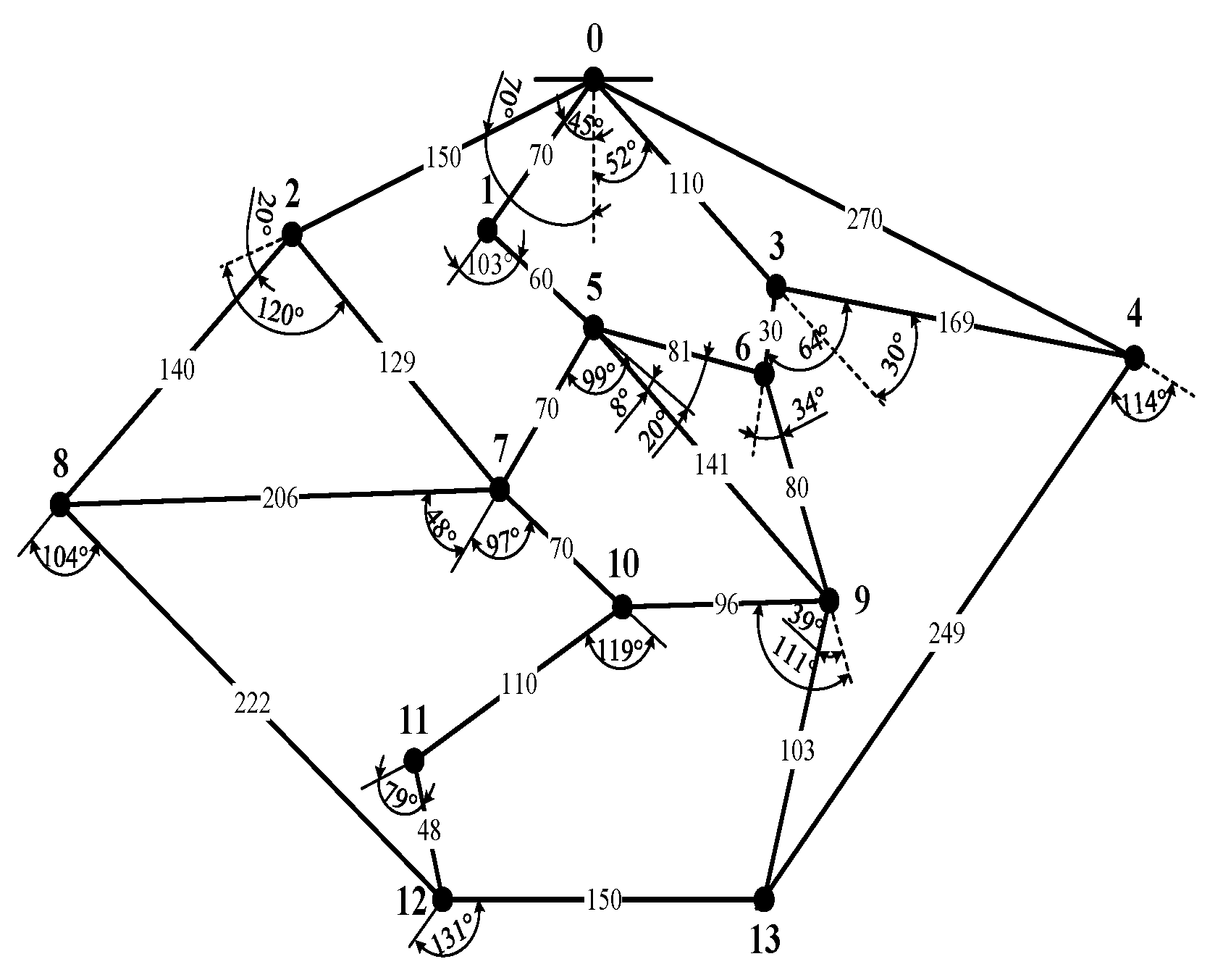
3.1. Floyd Algorithm Solution Design
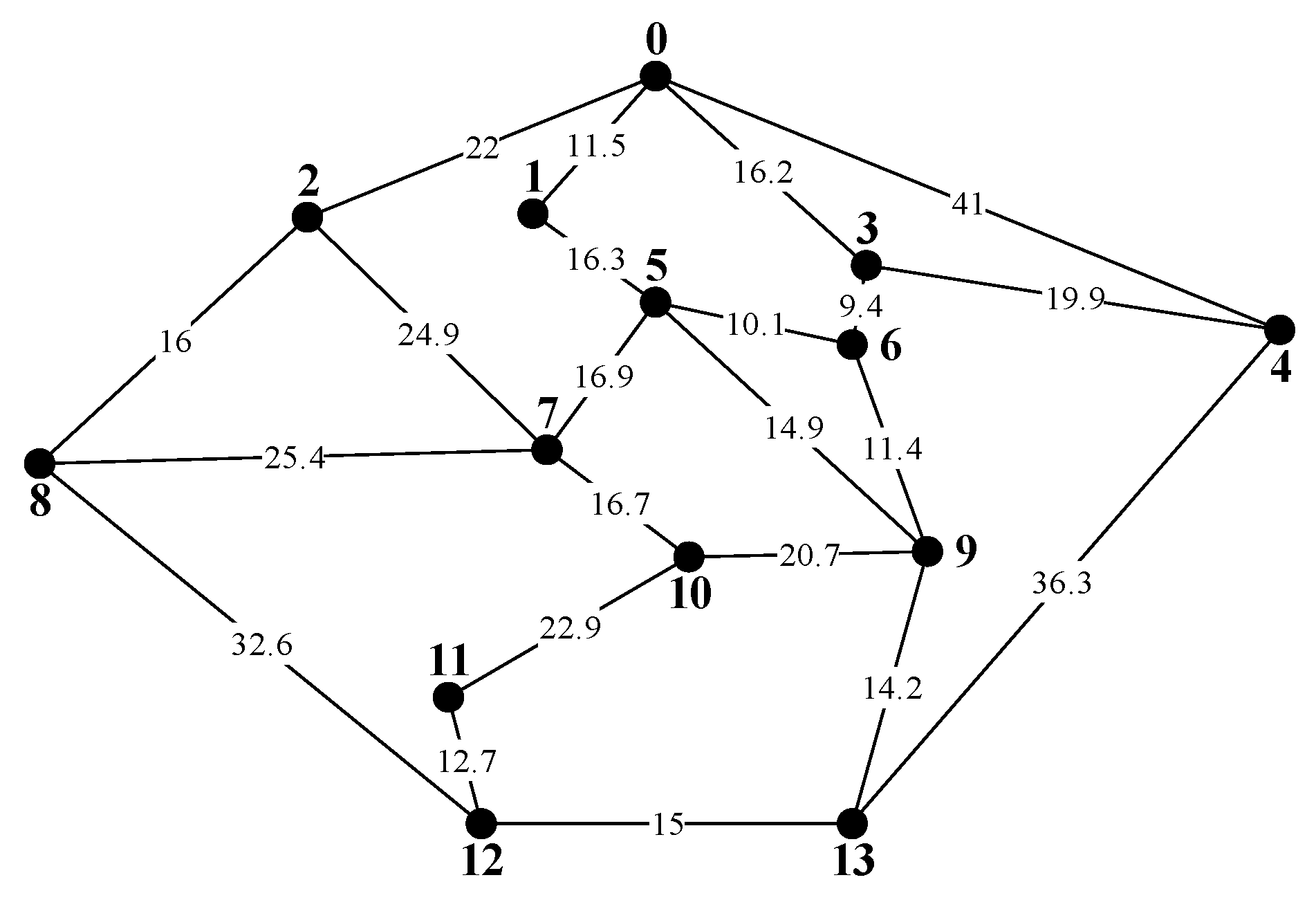
3.2. Solution Application of the Floyd Algorithm
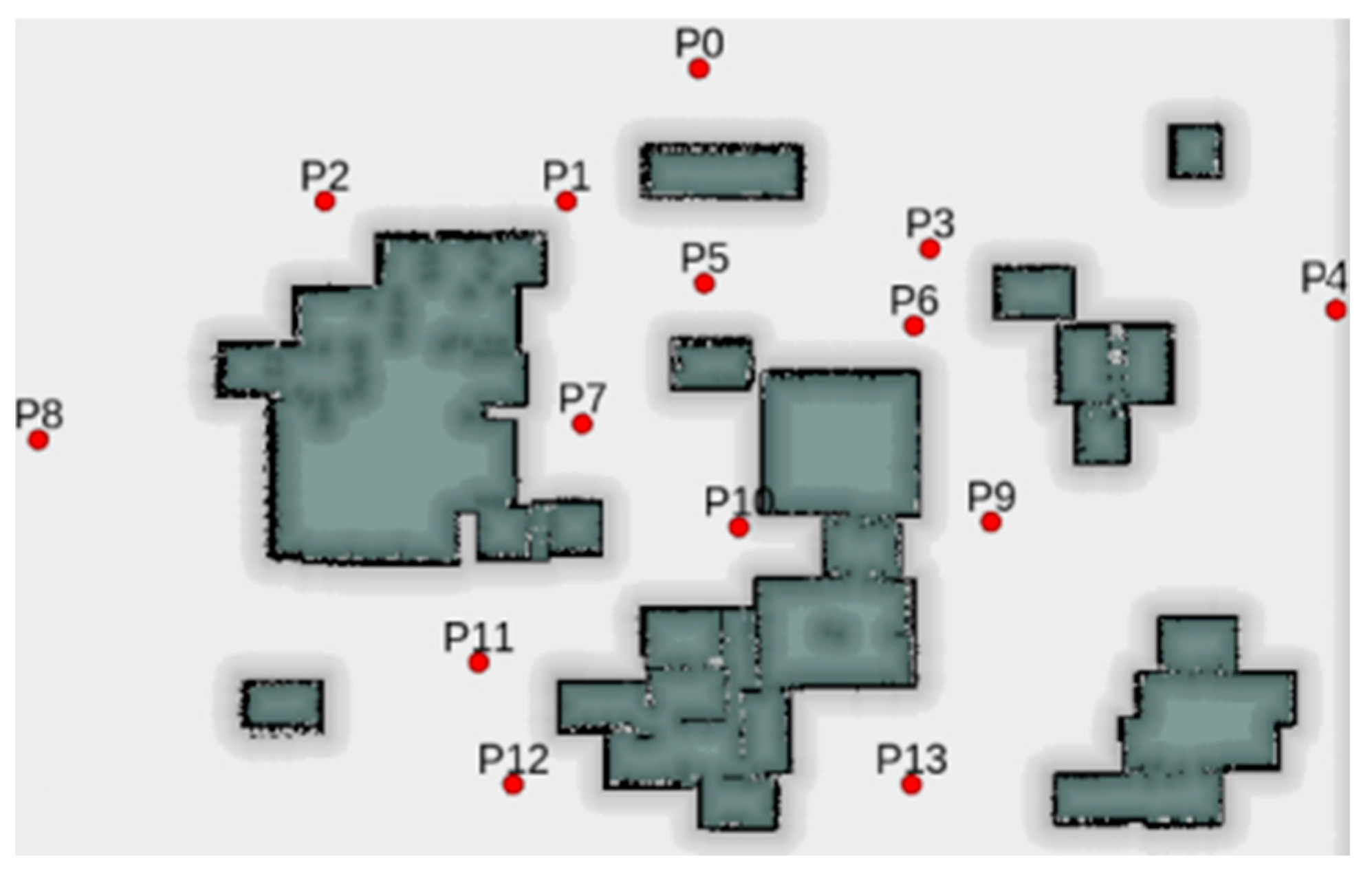
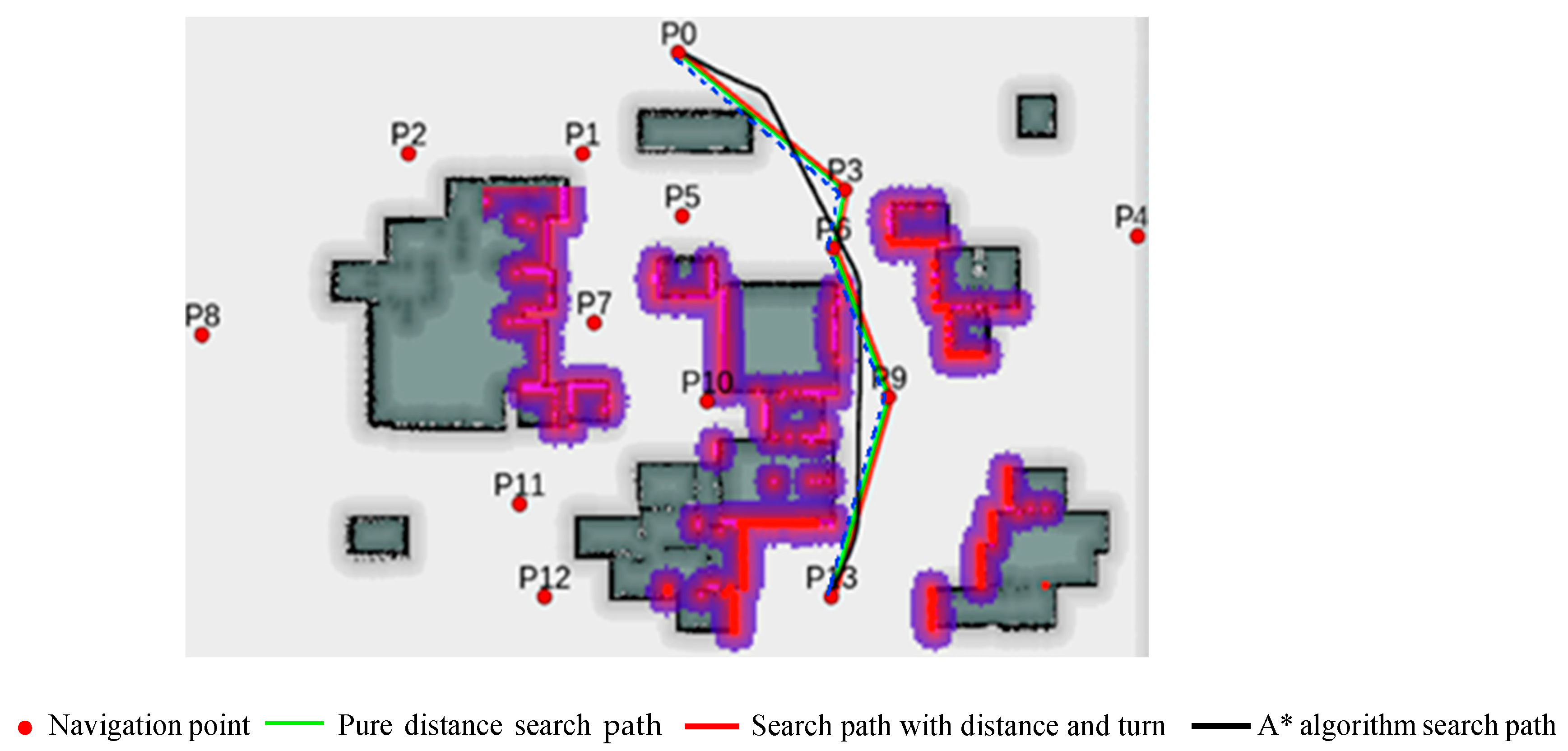
4. Simulation Experiment and Verification Analysis Based on the ROS
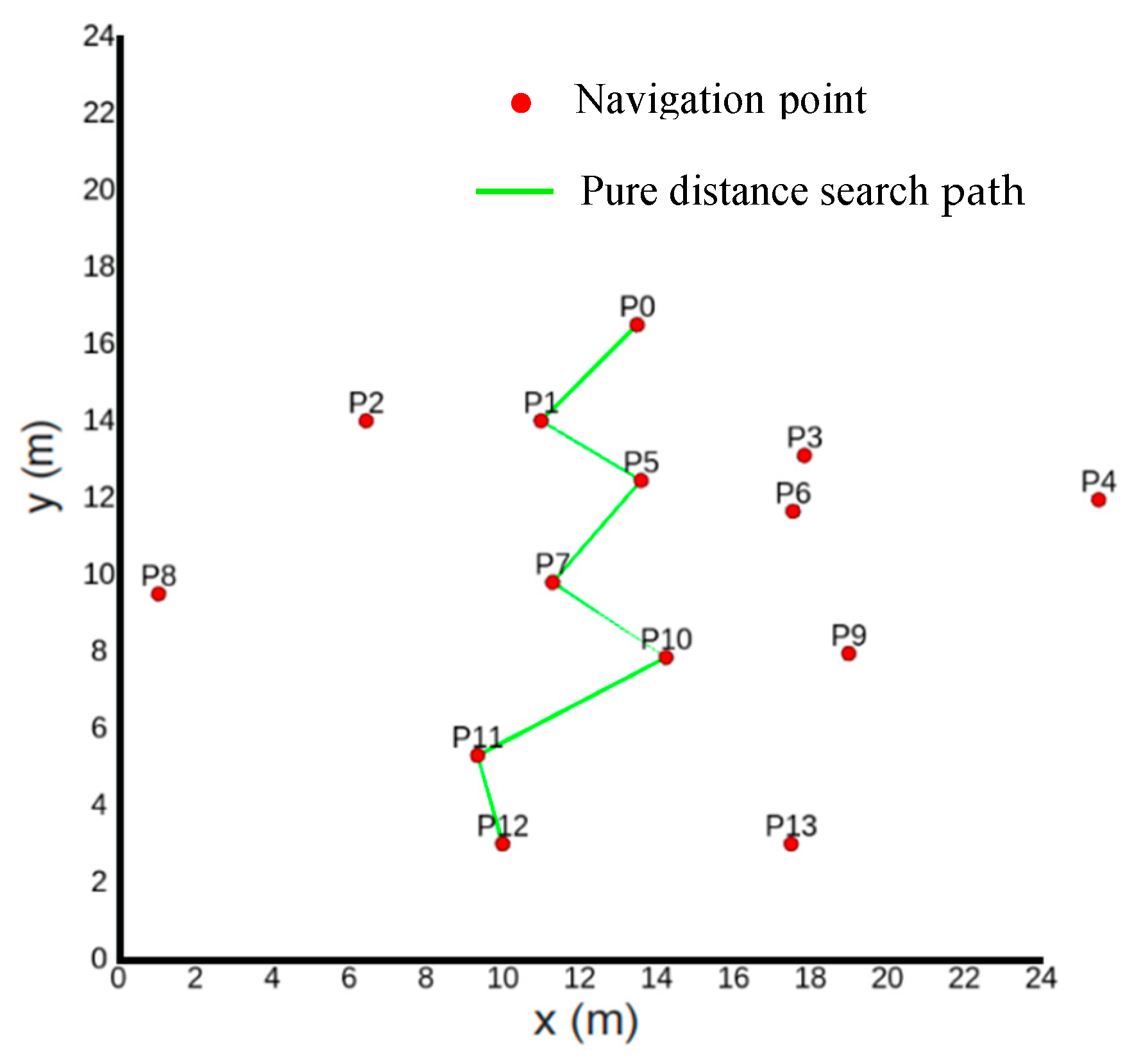
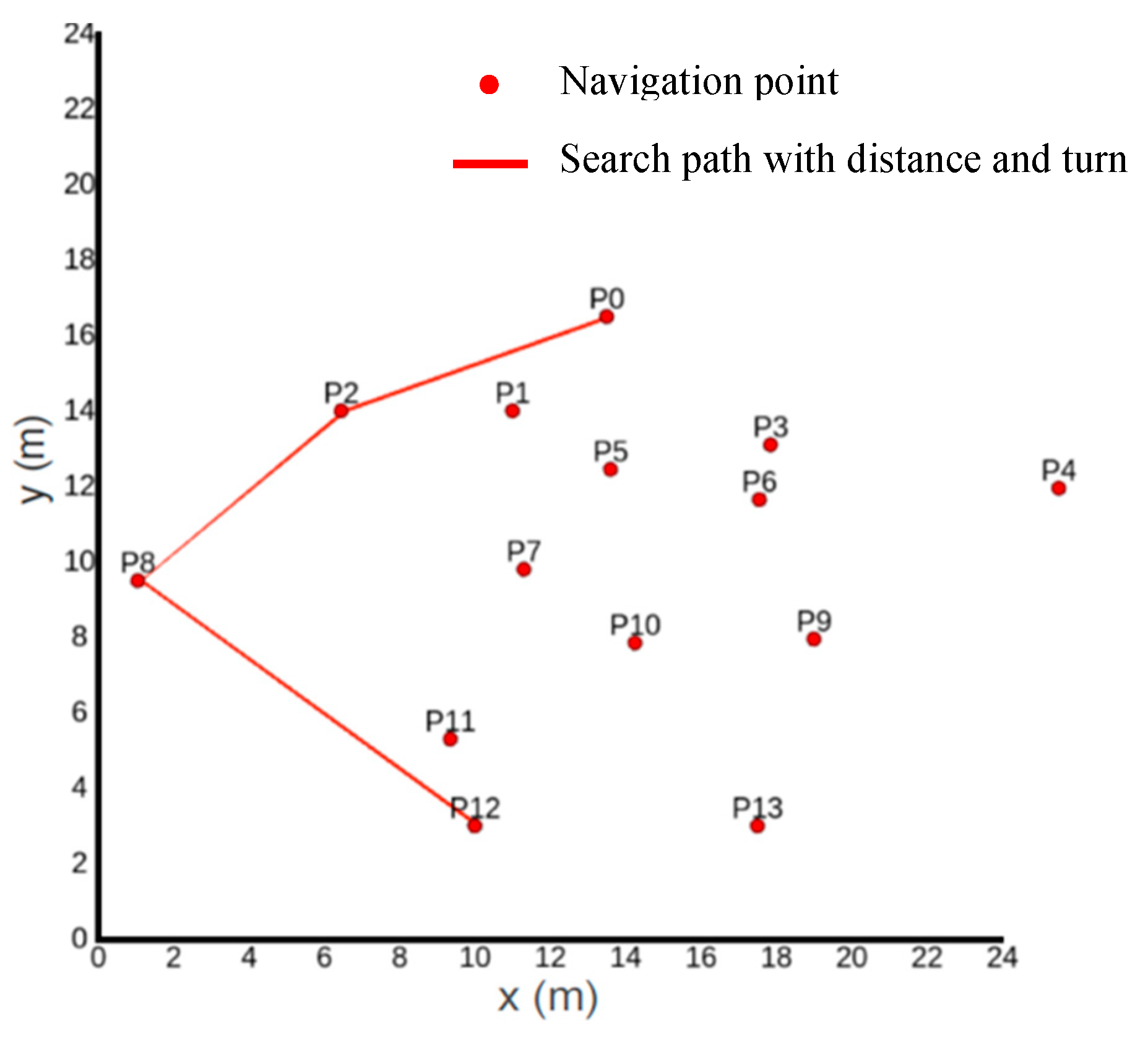
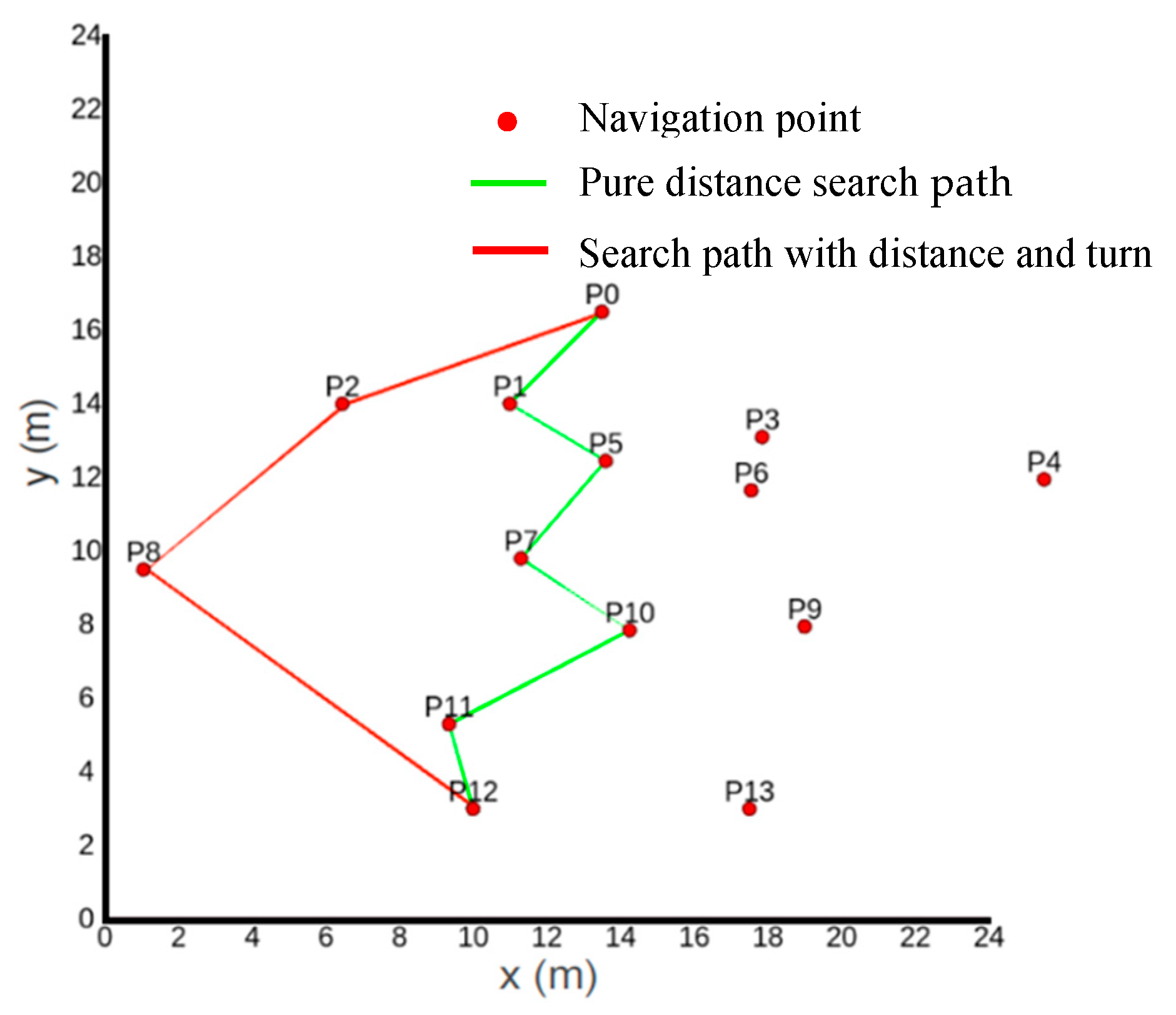
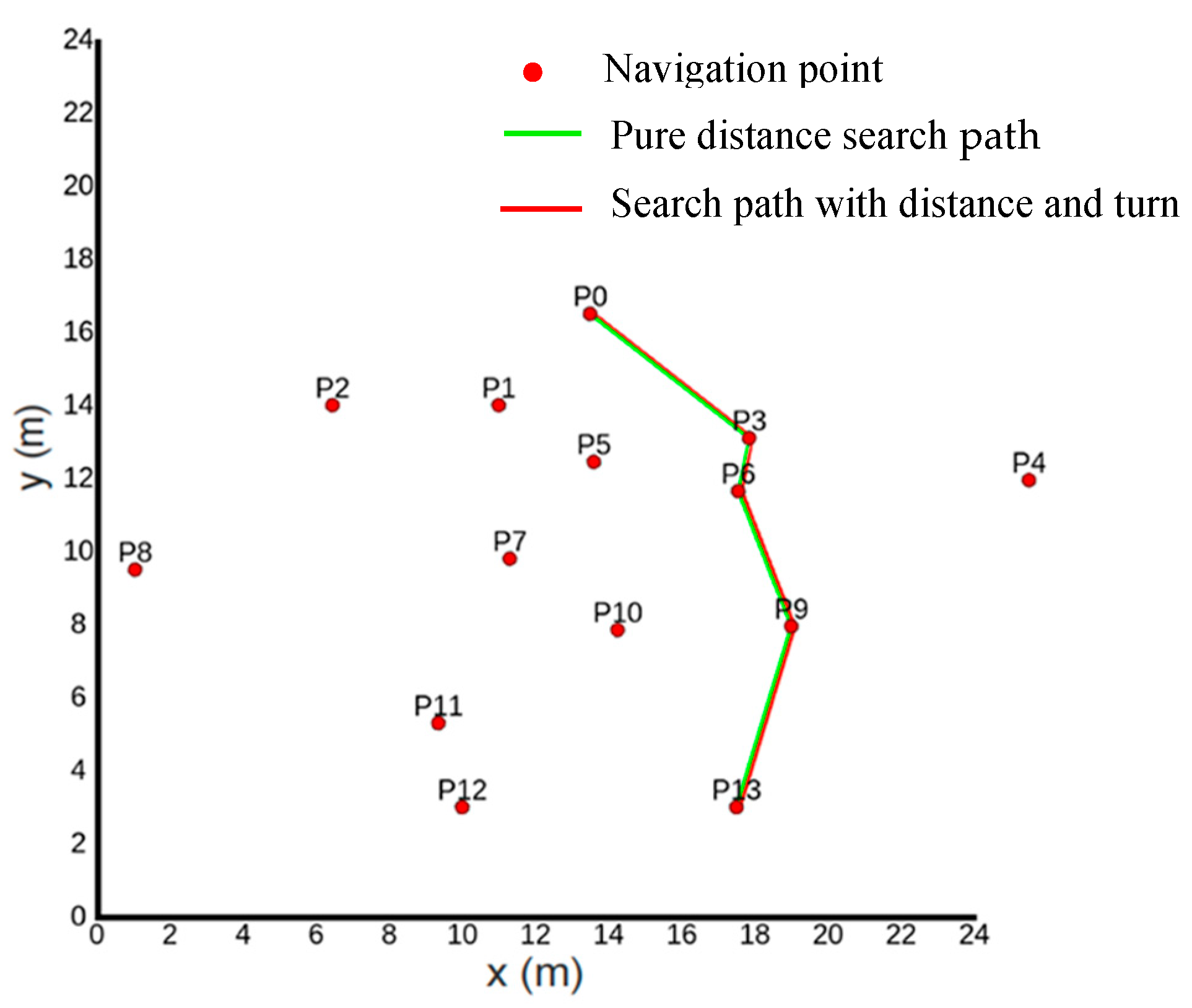
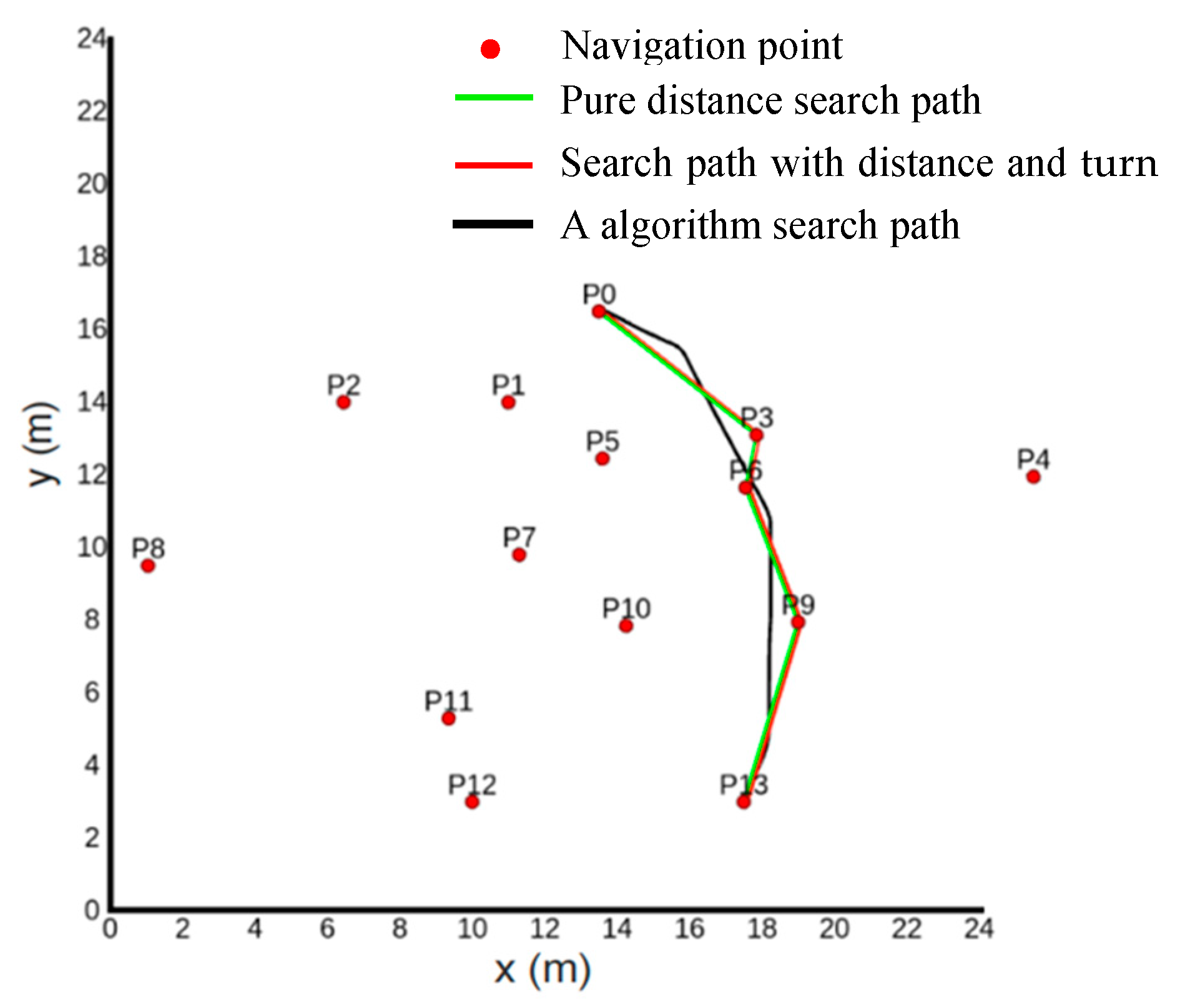
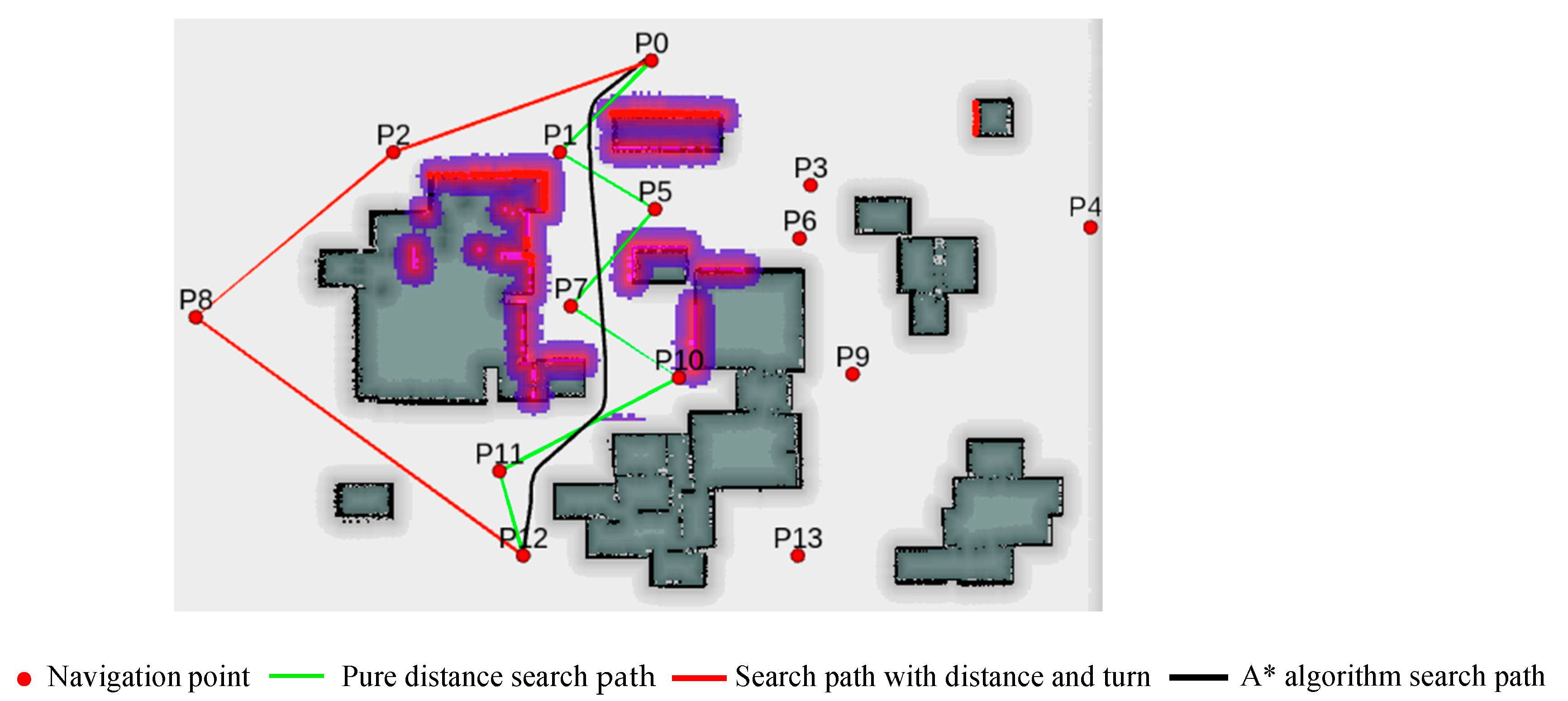
- Simulation Experiment 1
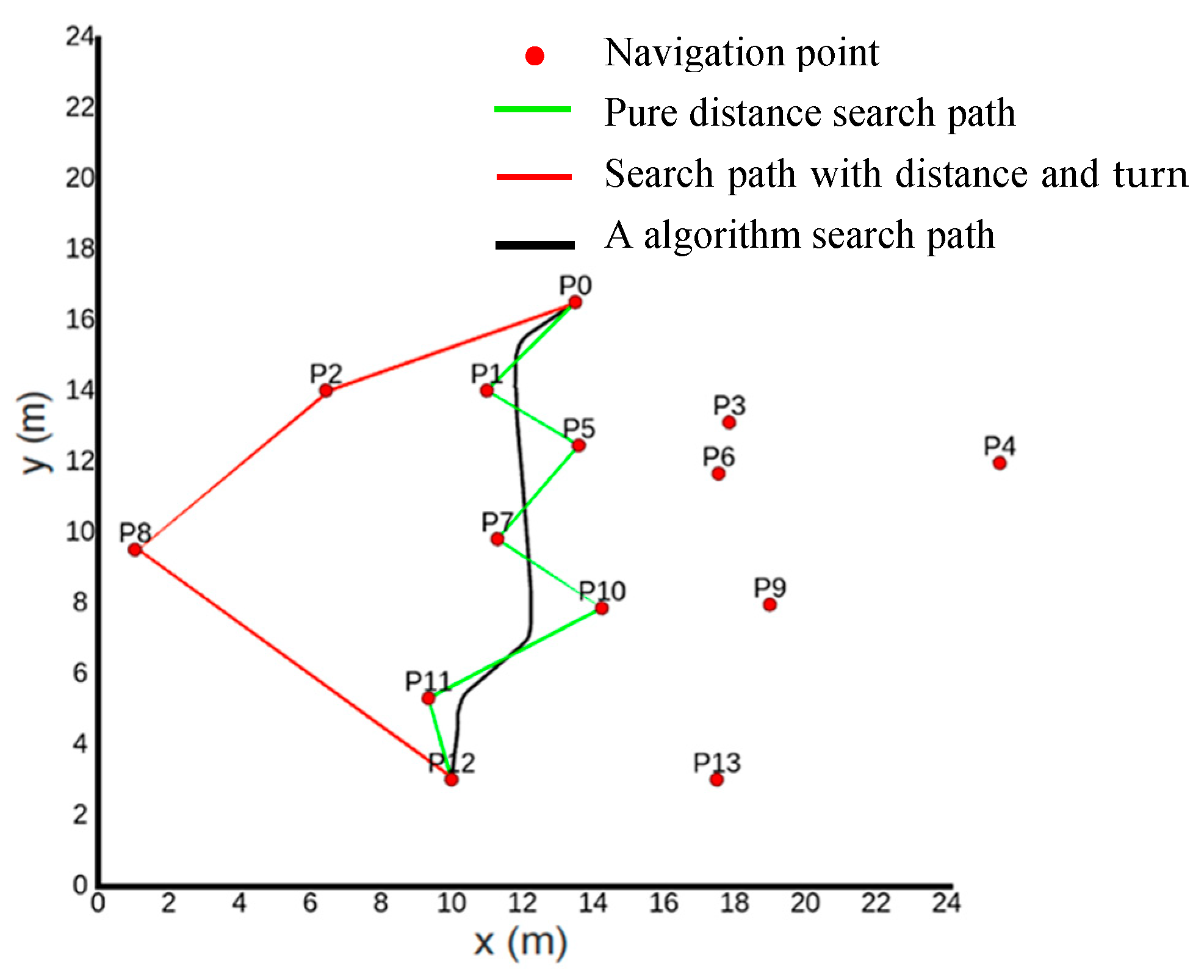
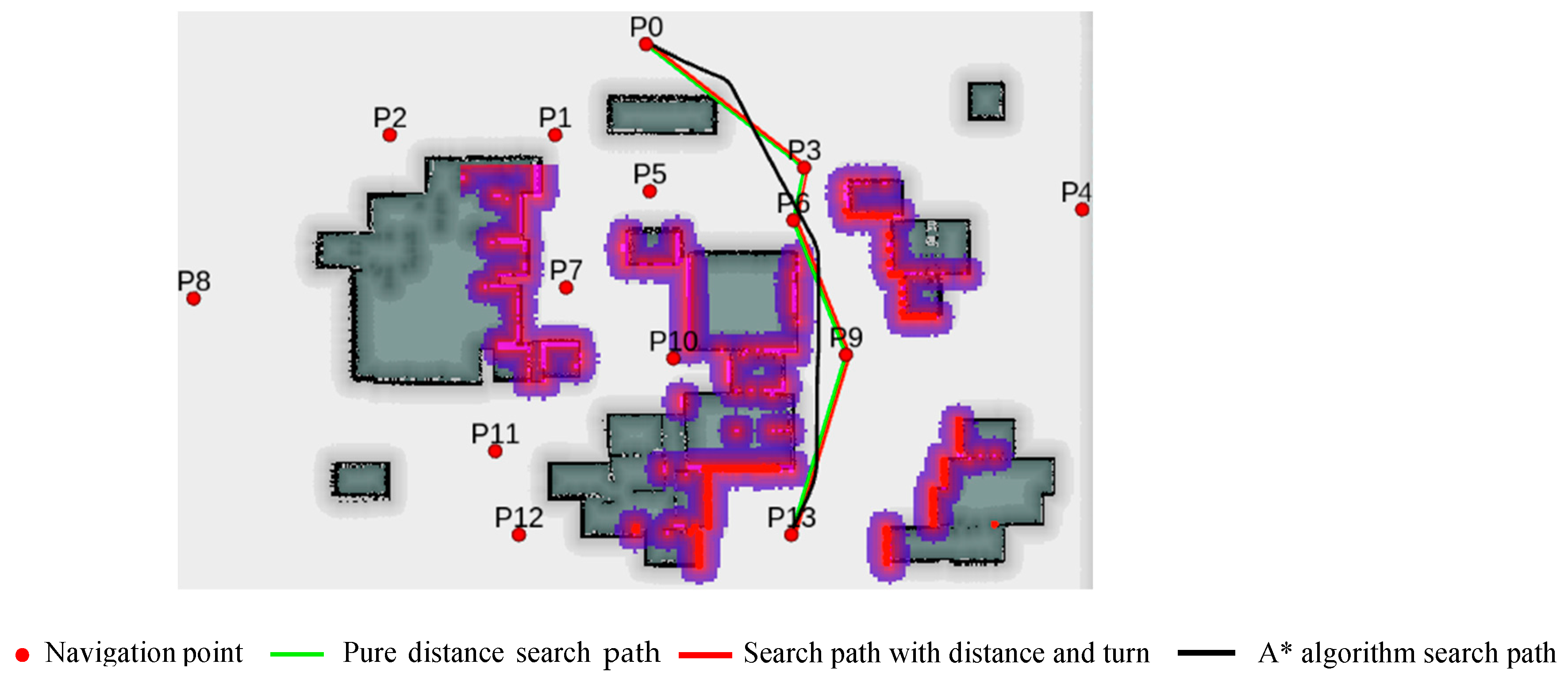
- Simulation Experiment 2
- (1)
- The A* path search is the most efficient in terms of distance cost, but its overall time cost is the highest, possibly due to real-time turning adjustments.
- (2)
- The pure distance-directed weighted graph search based on the Floyd algorithm has higher distance and turning costs, so the overall cost is always in the middle.
- (3)
- Based on Floyd’s distance plus a turning directed weighted graph search, a balanced solution is provided, where the distance cost is relatively high, but the turning cost is relatively low, resulting in the lowest overall cost time.
- (1)
- Floyd’s pure distance-based directed weighted graph search performance is balanced in all aspects, making it suitable for scenarios that require balancing various costs.
- (2)
- Floyd’s distance plus turning directed weighted graph search performs best in terms of turning cost, resulting in a more intuitive and smoother path, although the overall cost is slightly higher.
- (3)
- The A* path search performs best in terms of distance and overall time cost but has a high turning cost and poor path smoothness.
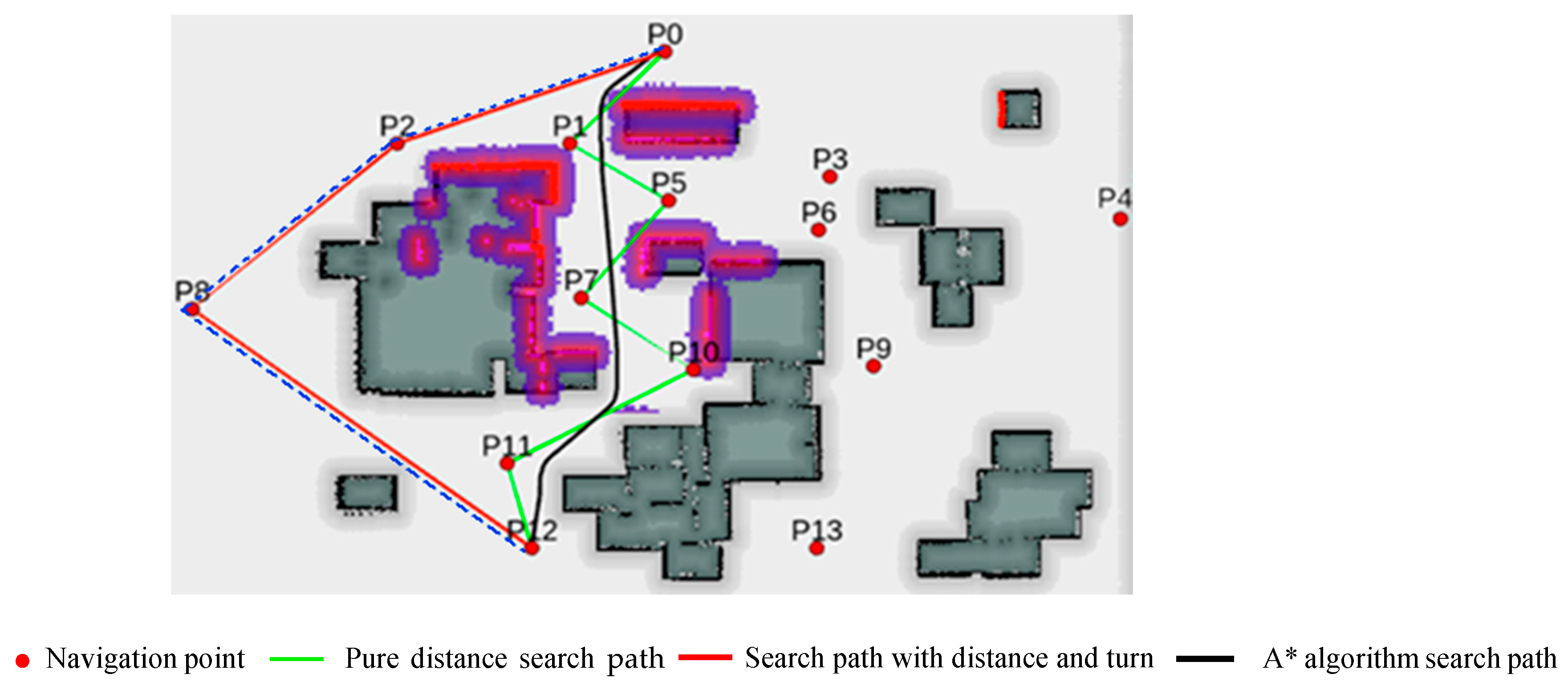
5. Real Vehicle Verification
- AGV configuration: The AGV is equipped with an industrial control computer (IPC), vehicle control unit (VCU), inertial measurement unit (IMU), DC module, battery compartment, laser radar, magnetic navigation and distance measurement sensors, and other equipment. It supports communication with the robot operating system (ROS).
- Test scenario: We simulated complex environments in actual industrial production, including various types of obstacles, paths, and target points.
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Shin, H.; Li, T.; Segura, A. Trajectory optimization and scheduling for AGVs in automated container terminals. J. Intellgent Robot. Syst. 2017, 86, 253–268. [Google Scholar]
- Lee, S.; Kahng, H.; Cheong, T.; Kim, S. Iterative two-stage hybrid algorithm for the vehicle lifter location problem in semiconductor manufacturing. J. Manuffacturing Syst. 2019, 51, 106–119. [Google Scholar] [CrossRef]
- Li, Z.; Li, P. Advanced 3D Navigation System for AGV in Complex Smart Factory Environments. Electronics 2024, 13, 130. [Google Scholar] [CrossRef]
- Islam, M.; Liu, X.; El Saddik, A. Hierarchical and Flexible Traffic Management of Multi AGV Systems in Industrial Environments. IEEE Access 2023, 11, 3054–3067. [Google Scholar]
- Rusakova, I.; Kubanova, J.; Benco, D.; Kadlecová, D. Implementation of Automated Guided Vehicles for the Automation of Selected Processes and Elimination of Collisions between Handling Equipment and Humans in the Warehouse. Sensors 2024, 24, 1029. [Google Scholar] [CrossRef]
- Saidi, S.; Li, H.; Ghandar, A. Optimized simultaneous conflict-free task assignment and path planning for multi-AGV systems in automated warehouses. IEEE Trans. Autom. Sci. Eng. 2023, 20, 1773–1786. [Google Scholar]
- Brown, M.; Smith, J.; Roberts, N. Real-Time Conflict-Free Task Assignment and Path Planning of Multi-AGV Systems in Complex Industrial Settings. IEEE Trans. Ind. Inform. 2023, 19, 840–850. [Google Scholar]
- De Ryck, M.; Versteyhe, M.; Debrouwere, F. Energy-efficient path planning for a multiload automated guided vehicle executing multiple transport tasks in a manufacturing workshop environment. Environ. Sci. Pollut. Res. 2020, 54, 152–173. [Google Scholar]
- Sun, Y.; Liu, Y.; Liu, L.; Lu, J. An Automated Guided Vehicle Path Planning Algorithm Based on Improved A* and Dynamic Window Approach Fusion. Appl. Sci. 2023, 13, 10326. [Google Scholar] [CrossRef]
- Fang, H.; Wei, Y.; Chen, J.; Xin, B. Flocking of Second-Order Multiagent Systems With Connectivity Preservation Based on Algebraic Connectivity Estimation. IEEE Trans. Cybern. 2017, 47, 1067–1077. [Google Scholar] [CrossRef]
- Li, H. Ambulance emergency rescue path planning based on an improved Floyd algorithm. J. Jiangsu Ocean Univ. Nat. Sci. Ed. 2022, 31, 47–53. [Google Scholar]
- Yu, j.; Ge, X. Optimal Route Planning of Parking Lot Based on Dijkstra Algorithm. In Proceedings of the 2017 International Conference on Robots & Intelligent System (ICRIS), Huaian, China, 15–16 October 2017; pp. 221–224. [Google Scholar]
- Zhang, L.; Lan, Y.; Hu, Y.; Ren, W. A dynamic scheduling method for self-organized AGVs in production logistics systems. Procedia CIRP 2021, 104, 381–386. [Google Scholar] [CrossRef]
- Zhang, X.; Li, N. A Distributed Conflict-Free Task Allocation Method for Multi-AGV Systems. Electronics 2023, 12, 3877. [Google Scholar] [CrossRef]
- Gallo, M.D.; Mazzuto, G.; Ciarapica, F.E.; Bevilacqua, M. Dynamic Scheduling and Optimization of AGV in Factory Logistics Systems Based on Digital Twin. Appl. Sci. 2023, 13, 1762. [Google Scholar] [CrossRef]
- Lu, S.; Zhou, M.; Peng, X. A Review of Real-Time Fault Diagnosis Methods for industrial Smart Manufacturing. Processes 2023, 11, 369. [Google Scholar] [CrossRef]
- Fenton, N.; Neil, M. Risk assessment and decision analysis with Bayesian networks. J. Risk Res. 2018, 21, 600–620. [Google Scholar]
- Hossain, M.S.; Muhammad, G. Cloud-assisted industrial internet of things (IIoT)–enabled framework for health monitoring. Comput. Netw. 2016, 101, 192–202. [Google Scholar] [CrossRef]
- Al-Turjman, F.; Alturjman, S. Context-sensitive access in industrial internet of things (IIoT) healthcare applications. IEEE Trans. Ind. Inform. 2018, 14, 2736–2744. [Google Scholar] [CrossRef]
- Gopinathan, D.; Nayyar, A.; Qureshi, B. An Overview of IoT Sensor Data Processing, Fusion, and Analysis Techniques. Sensors 2020, 20, 6076. [Google Scholar] [CrossRef]
- Li, X.; Gao, T.; Qian, H.; Yan, S. An Improved Unauthorized Unmanned Aerial Vehicle Detection Algorithm Using Radiofrequency-Based Statistical Fingerprint Analysis. Sensors 2023, 23, 3110–3127. [Google Scholar]
- Shahzad, M.; Khan, U.; Mahmood, Z. A Fast and Accurate Real-Time Vehicle Detection Method Using Deep Learning for Unconstrained Environments. Appl. Sci. 2023, 13, 3059. [Google Scholar] [CrossRef]
- Aparicio, J.; Resende, M. An Efficient Implementation of a Shortest Path Algorithm. J. Graph Algorithms Appl. 2023, 27, 123–141. [Google Scholar]
- Goldberg, A. Point-to-point shortest path algorithms with preprocessing. In Proceedings of the 33nd Conference on Current Trends in Theory and Practice of Computer Science, Harrachov, Czech Republic, 20–26 January 2007; pp. 88–102. [Google Scholar]
- Wayahdi, M.; Ginting, S.; Syahputra, D. Greedy, A-Star, and Dijkstra’s Algorithms in Finding the Shortest Path. Int. J. Adv. Data Inf. Syst. 2021, 2, 45–52. [Google Scholar] [CrossRef]
- Chen, R.; Gotsman, C. Efficient Fastest-Path Computations for Road Maps. Compact. Vis. Media 2021, 7, 267–281. [Google Scholar] [CrossRef]
- Holzinger, A.; Carrington, A.; Müller, H. Measuring the quality of explanations: The system causability scale (SCS). KI—Künstl. Intell. 2020, 34, 193–198. [Google Scholar] [CrossRef]
- Gong, L.; Cheng, Q. Exploiting edge features for graph neural networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 9211–9219. [Google Scholar]
- Ren, Z.; Zheng, Y.; Dong, X. Node importance estimation for neural networks on directed graphs. IEEE Trans Neural Netw. Learn. Syst. 2021, 32, 2152–2163. [Google Scholar]
- Hewa Welege, N.; Pan, W.; Kumaraswamy, M. Social network analysis applications in sustainable construction and built environment management: A review. Built Environ. Proj. Asset Manag. 2021, 11, 511–528. [Google Scholar] [CrossRef]
- He, Z.; Chen, W.; Wei, X.; Liu, Y. On the statistical significance of communities from weighted graphs. Sci. Rep. 2021, 11, 20304. [Google Scholar] [CrossRef]
- Huber, S.; Held, M. A fast straight-skeleton algorithm based on generalized motorcycle graphs. Int. J. Comput. Geom. Appl. 2012, 22, 471–498. [Google Scholar] [CrossRef]
- Choi, G.; Leung-Liu, Y.; Gu, X.; Lui, L. Parallelizable global conformal parameterization of simply-connected surfaces via partial welding. SIAM J. Imaging Sci. 2020, 13, 1049–1083. [Google Scholar] [CrossRef]
- Abel, Z.; Demaine, E.; Demaine, M. Reconfiguration of 3D Orthogonal Structures by Orthogonal Dissections. Discret. Comput. Geom. 2021, 66, 682–706. [Google Scholar]
- Lien, J.; Amato, N. Approximate Convex Decomposition of Polygons Computational. Geometry 2023, 35, 100–123. [Google Scholar]
- Goldberg, A.; Harrelson, C. Computing the shortest path: A* search meets graph theory. SIAM J. Comput. 2005, 34, 140–169. [Google Scholar]
- Anbarasi, J.; Izhar, L. A Systematic Review and Analysis of Intelligence-Based Pathfinding Algorithms in the Field of Video Games. Appl. Sci. 2022, 12, 5499. [Google Scholar] [CrossRef]
- Li, M.; Zhu, H. Efficiency of Floyd-Warshall Algorithm and its Variants in Network Analysis. Netw. Spat. Econ. 2021, 21, 509–523. [Google Scholar]
- Wang, H.; Yin, P.; Zheng, W.; Wang, H.; Zuo, J. Path Planning for Mobile Robots Based on Improved A* Algorithm and Dynamic Window Approach. Robotics 2020, 42, 346–353. [Google Scholar]
- Craus, M.; Bîrlescu, V.; Agop, M. Fractal Aspects in Classical Parallel Computing. Computers. 2016, 5, 19. [Google Scholar] [CrossRef]
- Jung, H.; Kim, D. A Comparative Study of All-Pairs Shortest Path Algorithms. J. Comput. Sci. 2022, 54, 101287. [Google Scholar]
- Oliveira, L.; de Moura, A. Floyd-Warshall Algorithm in Quantum Computing. Quantum Inf. Process. 2021, 20, 256. [Google Scholar]
- Park, J.; Kim, D. Obstacle Detection and Safely Navigate the Autonomous Vehicle from Unexpected Obstacles on the Driving Lane. Sensors 2020, 20, 4719. [Google Scholar] [CrossRef] [PubMed]
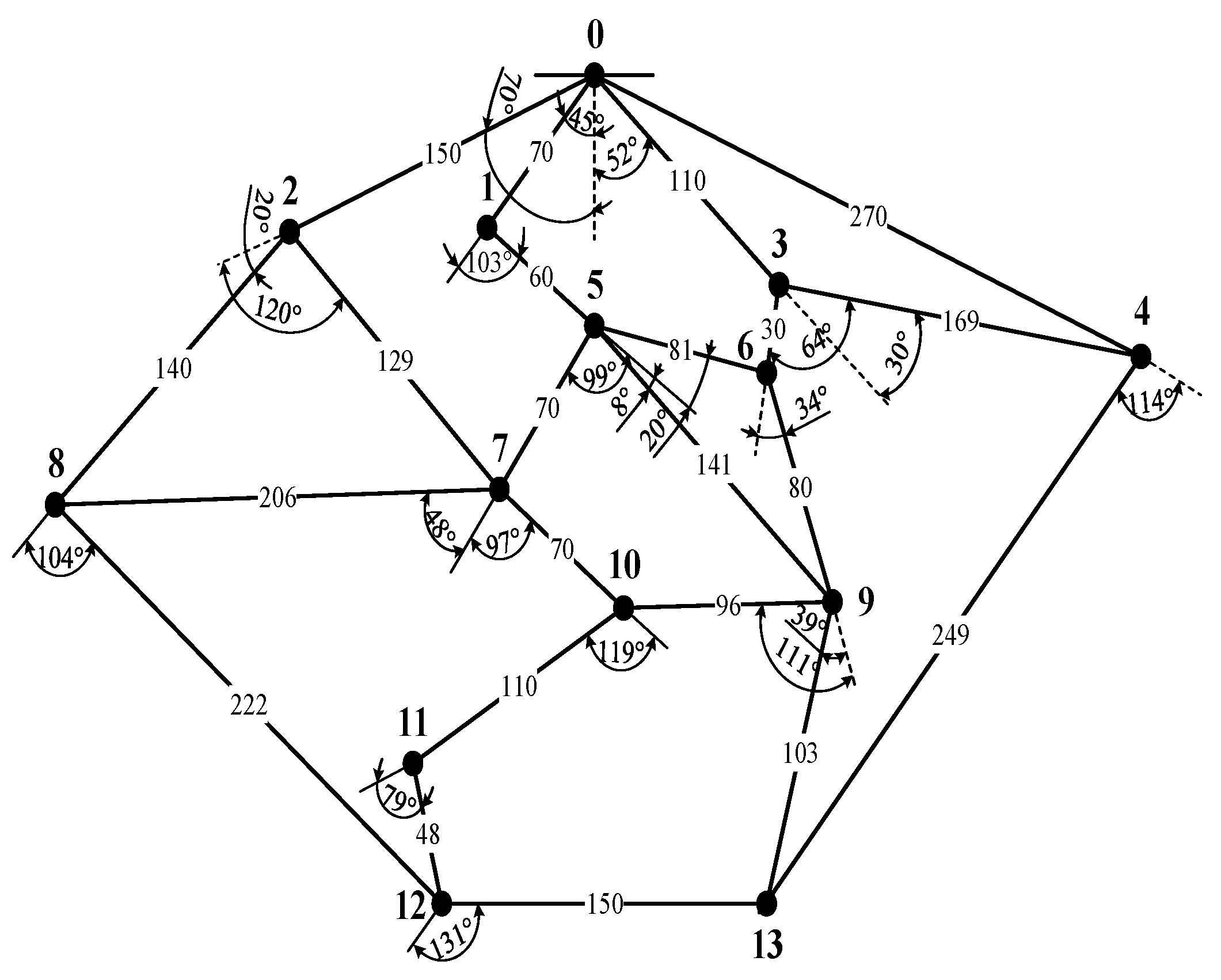


| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | |
| 0 | 0 | 7 | 15 | 11 | 27 | inf | inf | inf | inf | inf | inf | inf | inf | inf |
| 1 | inf | 0 | inf | inf | inf | 6 | inf | inf | inf | inf | inf | inf | inf | inf |
| 2 | inf | inf | 0 | inf | inf | inf | inf | 12.9 | 14 | inf | inf | inf | inf | inf |
| 3 | inf | inf | inf | 0 | 16.9 | inf | 3 | inf | inf | inf | inf | inf | inf | inf |
| 4 | inf | inf | inf | inf | 0 | inf | inf | inf | inf | inf | inf | inf | inf | 24.9 |
| 5 | inf | inf | inf | inf | inf | 0 | 8.1 | 7 | inf | 14.1 | inf | inf | inf | inf |
| 6 | inf | inf | inf | inf | inf | inf | 0 | inf | inf | 8 | inf | inf | inf | inf |
| 7 | inf | inf | inf | inf | inf | inf | inf | 0 | inf | inf | 7 | inf | inf | inf |
| 8 | inf | inf | inf | inf | inf | inf | inf | inf | 0 | inf | inf | inf | 22.2 | inf |
| 9 | inf | inf | inf | inf | inf | inf | inf | inf | inf | 0 | 9.6 | inf | inf | 10.3 |
| 10 | inf | inf | inf | inf | inf | inf | inf | inf | inf | inf | 0 | 11 | inf | inf |
| 11 | inf | inf | inf | inf | inf | inf | inf | inf | inf | inf | inf | 0 | 4.8 | inf |
| 12 | inf | inf | inf | inf | inf | inf | inf | inf | inf | inf | inf | inf | 0 | 15 |
| 13 | inf | inf | inf | inf | inf | inf | inf | inf | inf | inf | inf | inf | inf | 0 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | |
| 0 | 0 | 11.5 | 22 | 16.2 | 41 | inf | inf | inf | inf | inf | inf | inf | inf | inf |
| 1 | inf | 0 | inf | inf | inf | 16.3 | inf | inf | inf | inf | inf | inf | inf | inf |
| 2 | inf | inf | 0 | inf | inf | inf | inf | 24.9 | 16 | inf | inf | inf | inf | inf |
| 3 | inf | inf | inf | 0 | 19.9 | inf | 9.4 | inf | inf | inf | inf | inf | inf | inf |
| 4 | inf | inf | inf | inf | 0 | inf | inf | inf | inf | inf | inf | inf | inf | 36.3 |
| 5 | inf | inf | inf | inf | inf | 0 | 10.1 | 16.9 | inf | 14.9 | inf | inf | inf | inf |
| 6 | inf | inf | inf | inf | inf | inf | 0 | inf | inf | 11.4 | inf | inf | inf | inf |
| 7 | inf | inf | inf | inf | inf | inf | inf | 0 | inf | inf | 16.7 | inf | inf | inf |
| 8 | inf | inf | inf | inf | inf | inf | inf | inf | 0 | inf | inf | inf | 32.6 | inf |
| 9 | inf | inf | inf | inf | inf | inf | inf | inf | inf | 0 | 20.7 | inf | inf | 14.2 |
| 10 | inf | inf | inf | inf | inf | inf | inf | inf | inf | inf | 0 | 22.9 | inf | inf |
| 11 | inf | inf | inf | inf | inf | inf | inf | inf | inf | inf | inf | 0 | 12.7 | inf |
| 12 | inf | inf | inf | inf | inf | inf | inf | inf | inf | inf | inf | inf | 0 | 15 |
| 13 | inf | inf | inf | inf | inf | inf | inf | inf | inf | inf | inf | inf | inf | 0 |
| Path Search Algorithm | Distance Cost (Meters) | Turning Cost (Degrees) | Total Cost Time (Seconds) |
|---|---|---|---|
| Floyd-based Pure Distance Directed Weighted Graph Search | 13.28 | 542 | 23.34 |
| Floyd-based Distance plus Turning Directed Weighted Graph Search | 14.64 | 194 | 21.56 |
| A* Path Search | 12.36 | 854 | 24.78 |
| Path Search Algorithm | Distance Cost (Meters) | Turning Cost (Degrees) | Total Cost Time (Seconds) |
|---|---|---|---|
| Floyd-based Pure Distance Directed Weighted Graph Search | 12.18 | 489 | 23.87 |
| Floyd-based Distance plus Turning Directed Weighted Graph Search | 12.87 | 159 | 23.25 |
| A* Path Search | 10.21 | 758 | 22.13 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Liu, L. Research on AGV Path Planning Based on Improved Directed Weighted Graph Theory and ROS Fusion. Actuators 2024, 13, 404. https://doi.org/10.3390/act13100404
Li Y, Liu L. Research on AGV Path Planning Based on Improved Directed Weighted Graph Theory and ROS Fusion. Actuators. 2024; 13(10):404. https://doi.org/10.3390/act13100404
Chicago/Turabian StyleLi, Yinping, and Li Liu. 2024. "Research on AGV Path Planning Based on Improved Directed Weighted Graph Theory and ROS Fusion" Actuators 13, no. 10: 404. https://doi.org/10.3390/act13100404
APA StyleLi, Y., & Liu, L. (2024). Research on AGV Path Planning Based on Improved Directed Weighted Graph Theory and ROS Fusion. Actuators, 13(10), 404. https://doi.org/10.3390/act13100404






