Abstract
In the domain of bionic walking control for biped robots, optimizing the parameters of the central pattern generator (CPG) presents a formidable challenge due to its high-dimensional and nonlinear characteristics. The traditional particle swarm optimization (PSO) algorithm often converges to local optima, particularly when addressing CPG parameter optimization issues. To address these challenges, one improved particle swarm optimization algorithm aimed at enhancing the stability of the walking control of biped robots was proposed in this paper. The improved PSO algorithm incorporates a spiral function to generate better particles, alongside optimized inertia weight factors and learning factors. Evaluation results between the proposed algorithm and comparative PSO algorithms were provided, focusing on fitness, computational dimensions, convergence rates, and other metrics. The biped robot walking validation simulations, based on CPG control, were implemented through the integration of the V-REP (V4.1.0) and MATLAB (R2022b) platforms. Results demonstrate that compared with the traditional PSO algorithm and chaotic PSO algorithms, the performance of the proposed algorithm is improved by about 45% (two-dimensional model) and 54% (four-dimensional model), particularly excelling in high-dimensional computations. The novel algorithm exhibits a reduced complexity and improved optimization efficiency, thereby offering an effective strategy to enhance the walking stability of biped robots.
1. Introduction
The humanoid biped robot has attracted the attention of researchers because it can simulate the walking characteristics of human beings and shows potential to walk in complex terrains. In daily life and industrial production, biped robots have broad application prospects. The superior mobility and environmental adaptability of biped robots enable them to perform diverse tasks efficiently, thereby increasing production efficiency and reducing labor costs. The continuous progress in this field not only promotes the development of robot technology, but also provides important support for the construction of an intelligent society in the future [1]. However, the biped robot is a multi-rigid-body and nonlinear under-actuated system, and the stability control of its walking is a very challenging task [2].
In recent years, inspired by the principle of bionics, more and more researchers have added the central pattern generator (CPG) [3] to the study of walking control of bipedal or multi-legged robots. Based on the CPG model, Sun et al. [4] proposed a bionic control method based on the human–exoskeleton coupling dynamic model by using the human–exoskeleton interaction model. Li et al. [5] proposed a method combining the reinforcement of learning with CPG to enhance the terrain adaptability of hexapod robots in walking planning. CPG can generate self-sustaining multidimensional rhythm signals without any external input, thereby controlling the coordinated periodic motion of organisms [6]. The biped robot under the control of a CPG network has good anti-interference ability and adaptability to varying environments. However, the CPG network is usually controlled by multiple parameters. The adjustment of these parameters does not have uniform rules, and it is necessary to introduce an optimization algorithm to adjust them. The output control target of the CPG neural oscillator can be the joint torque of the two swing phases of the biped robot, which involves a large number of variables. The intelligent optimization algorithm can quickly find the appropriate oscillator parameters and provide preconditions for stable walking of the biped robot. The focus of this paper is to design a new intelligent optimization algorithm to optimize the parameters of the CPG network for biped walking control. It is expected that the optimized CPG network parameters can implement the stable walking of biped robots.
Among intelligent algorithms, PSO is simpler than the genetic algorithm (GA) [7], ant colony algorithm [8], neural network algorithm [9], tree structure encoding [10], fuzzy logic [11,12], gravitational search algorithm [13], grey wolf optimization (GWO) [14], and other intelligent algorithms. One of the main advantages of the PSO algorithm is the fast convergence speed. However, in the process of optimization, the PSO algorithm is prone to falling into the local optimal solution, and because the search accuracy of the global optimal solution is not high, the algorithm will stagnate for a long time. In order to solve the above problems, many scholars have improved the PSO algorithm. Zaman et al. [15] proposed to combine the backtracking search optimization algorithm with a particle swarm optimization algorithm and introduced a new mutation operator to improve the global search ability of the particle swarm optimization algorithm. Das et al. [16] used two evolutionary operators to improve the particle swarm optimization algorithm, which helped improve the convergence of the algorithm and remove the local optimal solution. Yuan et al. [17] used a differential evolution algorithm to improve the particle swarm optimization algorithm, which solved the limitations of traditional particle swarm optimization. Zhao et al. [18] proposed an adaptive weight adjustment strategy to improve the search ability of the algorithm. Shao et al. [19] applied it to the path planning of aerial robots based on the comprehensively improved particle swarm optimization algorithm. Song et al. [20] used the method of a continuous high-order Bessel curve to optimize the PSO algorithm and plan the smooth path of a mobile robot. Li et al. [21] proposed an improved hybrid algorithm based on the PSO algorithm and the GA algorithm, which can shorten the robot planning path and accelerate the convergence speed.
Tao et al. [22] proposed a walking optimization method based on the parallel comprehensive learning particle swarm optimizer (PCLPSO), which improved the fast and stable walking ability of humanoid robots. Although PCLPSO enhances the global search ability through multi-group parallel operation and information exchange between the master and slave groups, its efficiency may be affected when dealing with multimodal functions and high-dimensional space. Sahu et al. [23] designed an adaptive particle swarm optimization algorithm (APSO) and used this algorithm to plan the path for a biped robot. However, this method mainly focuses on the optimization of parameters such as the learning factors in a traditional particle swarm optimization algorithm, and as such, the improvement of the algorithm structure is limited.
In summary, although the traditional particle swarm optimization algorithm has been improved and optimized to a certain extent, in the face of high-dimensional and nonlinear models, such as biped robot gait planning and walking control, there are still problems, such as low computational efficiency, low optimization accuracy, and slow search speed, which need further improvement. In our previous research work [24,25,26], we optimized the structural parameters of the biped robot and designed the walking controller. These studies provided new ideas for the design of the bionic walking controller for a biped robot. In this paper, one improved particle swarm optimization algorithm was proposed, inspired by the idea of spiral function improvement, to provide a solution for the problem of the traditional PSO being prone to falling into the local optimal solution. Aiming at the parameter optimization problem of the CPG control network of biped robots, a new fitness function was designed and the improved particle swarm optimization algorithm was used to find the optimal parameters for the CPG network. This method helped to improve the stability and robustness of biped robot walking and promotes the performance of population intelligent algorithms in practical applications.
2. Biped Bionic Walking Control Based on CPG
2.1. Structural Design of the Biped Robot
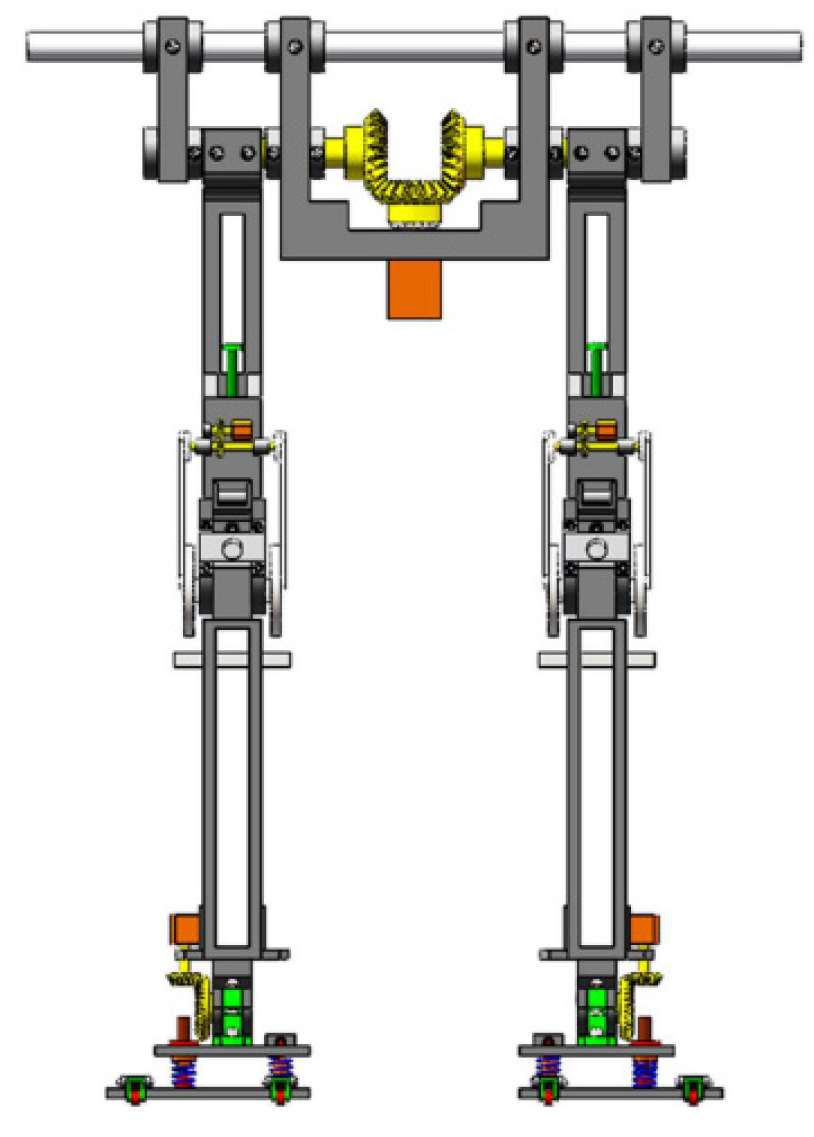
The structural design of the biped robot is mainly divided into three parts: hip joint, knee joint, and ankle joint. The overall design height of the biped robot is more than 0.85 m, and the number of degrees of freedom for the joints is 6. The overall structural design of the robot is shown in Figure 1:
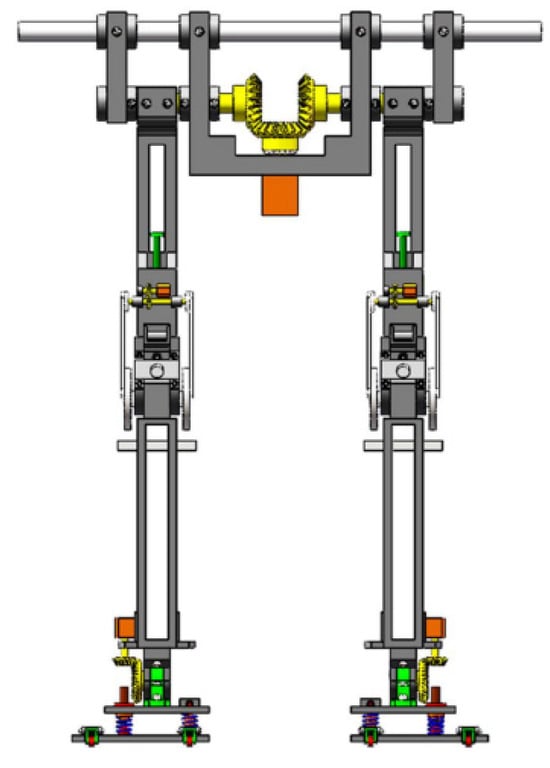
Figure 1.
The mechanical structure of the biped robot.
The main physical parameters of the biped robot are shown in Table 1. In the subsequent biped robot walking simulations, the physical parameters in Table 1 will be used as the input conditions.

Table 1.
The mechanical structure parameters of the biped robot.
2.2. Design of the Bionic Walking Control of the Biped Based on CPG
The walking generation of the biped robot based on CPG mimics the neural control mechanism of a biologically rhythmic motion. By establishing a CPG control network, the output of the CPG neural oscillator is used to control the joint angle or torque, thereby generating a stable biped robot during walking. By optimizing the parameters of the CPG control network through learning and training, the stability of the bipedal walking can be further improved.
Since the Hopf oscillator has benefits such as good stability and ease of generating periodic motion as a limit cycle, it is widely used in the walking planning of legged robots and has good stability. In this paper, the bionic walking control of the biped robot based on the Hopf oscillator is proposed. The following model is established:
where x and y are two stated variables of nonlinear differential equations, which are self-oscillating functions with respect to time; α and β can control the convergence speed of the oscillator; is the amplitude of the oscillator; and is the vibration frequency of the oscillator.
In order to control the torque of the biped robot joint, the Hopf output mapping function should be established:
where X and Y are the output of the Hopf oscillator, Xa and Ya are the offsets of the self-excited oscillation function relative to the initial position, and XR and YR are the amplitudes of the self-excited oscillation function curve.
The CPG walking controller established in this paper is the result of a multi-factor interaction. It is necessary to use the optimization algorithm to determine the parameters of α, β,, u, Xa, Ya, XR, YR and so on.
3. Improved Design of the Particle Swarm Optimization Algorithm
3.1. Overview of the Traditional Particle Swarm Optimization Algorithm
The particle swarm optimization algorithm is an efficient algorithm that imitates the foraging behavior of birds. It was proposed by Kennedy et al. in 1995 [27]. The algorithm finds the global optimal solution through the coordination and sharing of information among individuals in the bionic bird population. The main advantages of the traditional PSO algorithm consist of self-organizing ability, evolutionary ability and memory function, strong overall optimization ability, and a fast self-optimization speed. In the D-dimensional space, the particle swarm is composed of N particles. Then, the position vector of the i-th particle is as follows:
In the k-th iteration, the velocity update formula of the i-th particle is as follows:
where is the velocity inertia weight, is the best position for the i-th particle to pass by until the k-th iteration. is the best position for all particles to pass through by the k-th iteration. is the individual learning factor of the particle, is the social learning factor of the particle, and is a random number in the range of .
The position update formula of the i-th particle is as follows:
3.2. The Improved PSO Algorithm
In order to solve the problems that the traditional PSO algorithm has, which includes being prone to falling into the local optimum and having difficulties in escaping the search process, as well as optimization problems in high-dimensional, nonlinear, and other complex models, one improved PSO algorithm was proposed: a spiral function in the optimization strategy was used to improve the search ability and convergence speed of the algorithm.
The spiral function formula is as follows:
where a is the compression coefficient of the spiral, b is the rotation coefficient of the spiral, and θs is the angle of the spiral function.
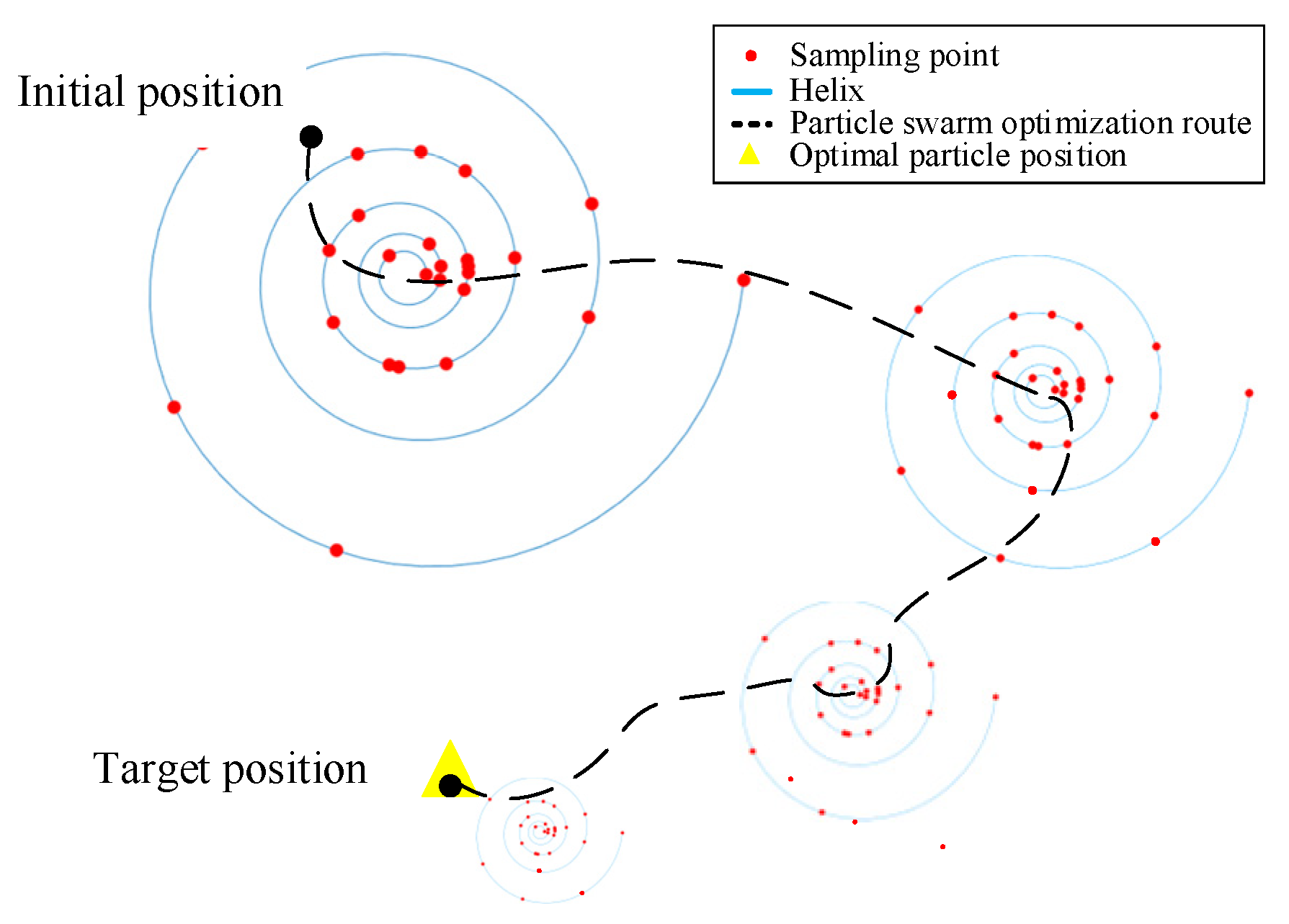
The spiral function is used to improve the optimization strategy of the traditional particle swarm optimization algorithm, which can effectively improve the global search ability of the particle swarm. The optimization process of this method is shown in Figure 2. When the particle update stagnation occurs, the spiral function is calculated with the current optimal particle as the center. With an increasing number of iterations, the spatial size of the spiral function distribution and the number of sampling points are gradually changed. The trend is that the dispersion space will become smaller and the number of sampling points will become greater, but the value of the dispersion space and the number of sampling points needs to be limited.
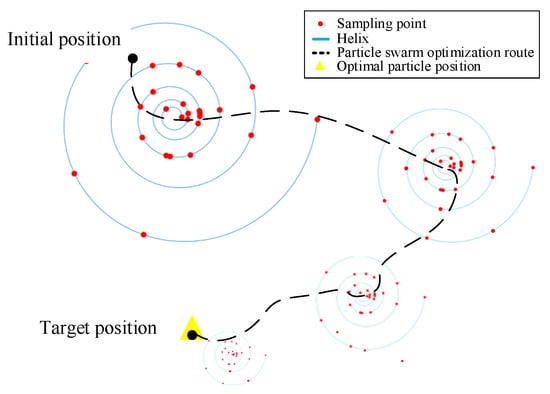
Figure 2.
A diagram of the improved particle swarm optimization algorithm.
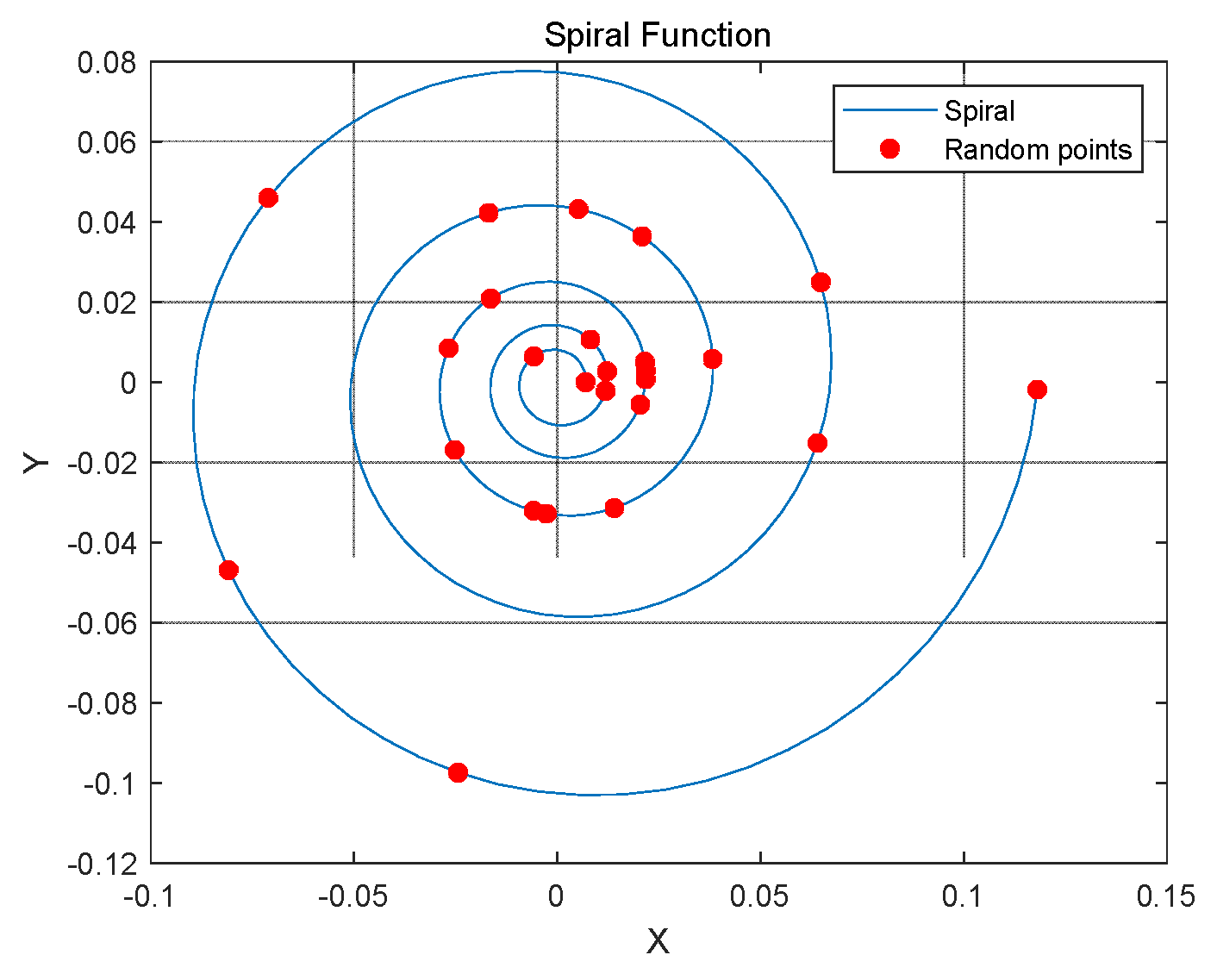
On the spiral function, the points are randomly selected via normal distribution, as shown in Figure 3. The red dots in Figure 3 are the points taken, with the starting and ending positions on the helix as the boundary and the middle part randomly selected.
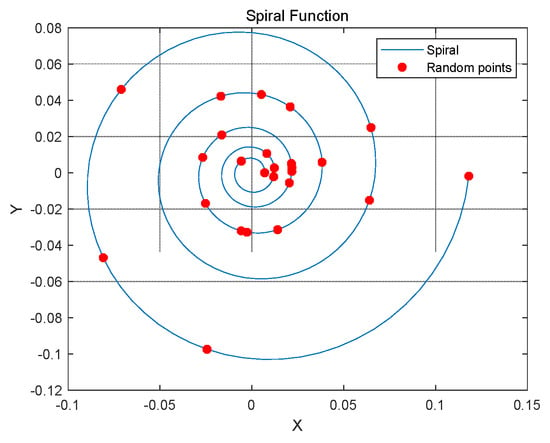
Figure 3.
Sampling plot of the normal distribution of the spiral function.
If d points are randomly sampled on the spiral function, then in n-dimensional space, the position of the i-th particle is as follows:
where is the global optimal value in traditional PSO and is the output particle value after taking a point on the spiral function. If the dimension is odd, or are added separately.
The fitness values of these obtained particles are calculated and compared with the fitness values of the particles . When a better particle than the particle appears, some particles are randomly taken from the spiral function to replace some of the particles in the particle swarm. The update is completed in this way every time.
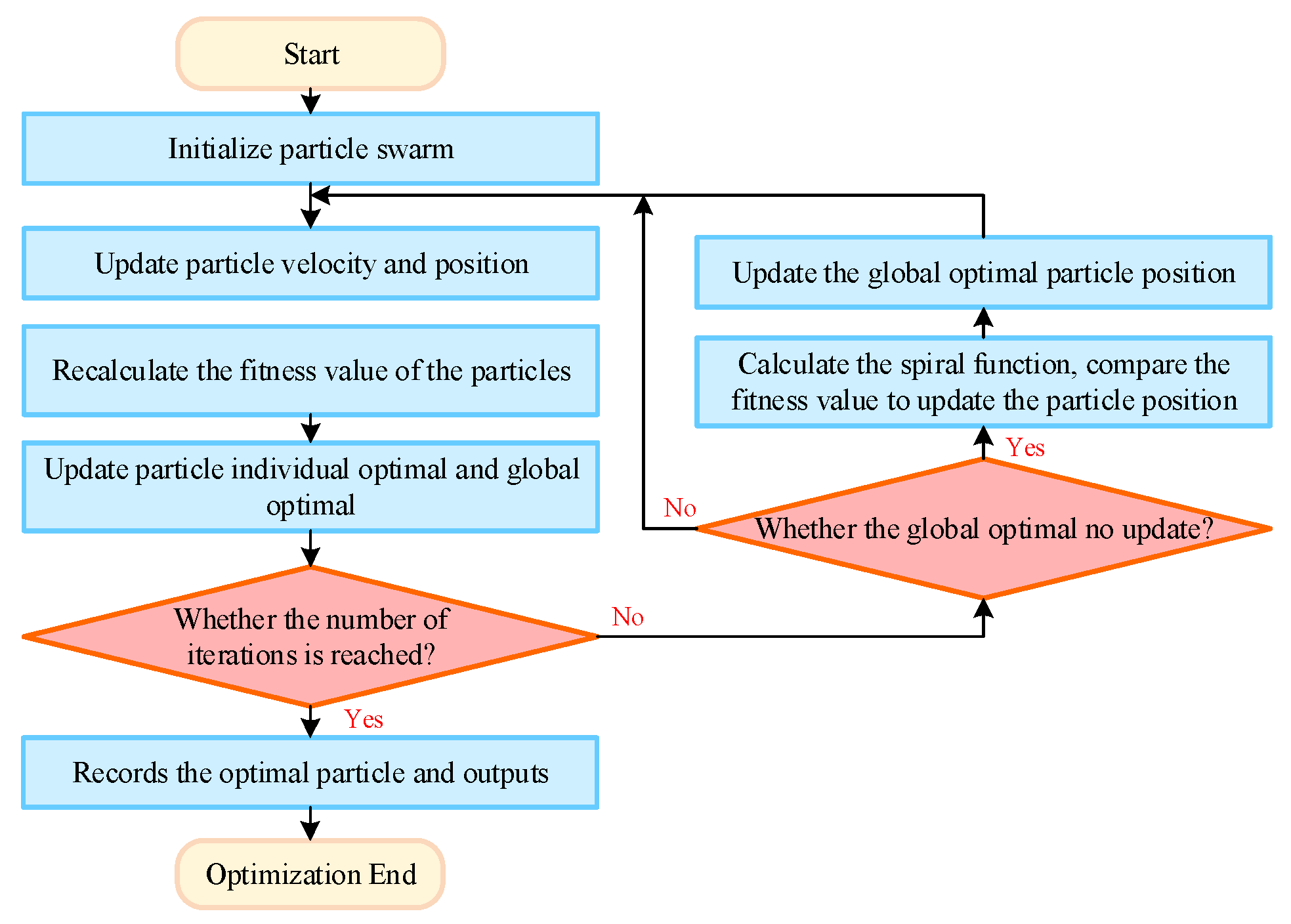
In the process of iteration, the PSO algorithm will have a long time for the iteration without updating the fitness value, indicating that the calculation of the particle swarm in this interval is of little significance or that the calculation results have not progressed. When this problem occurs, the improved particle swarm optimization algorithm is based on whether the same fitness value appears in the search. Before entering the next step of calculation, the spiral function centered on the global optimal value appearing in the current iteration number is preferentially calculated. Random sampling points are randomly selected on the generated spiral function in the form of a normal distribution, and the fitness values of these sampling points are calculated step by step. If there are better particles than the global optimal particle position in the current iteration, the algorithm will randomly replace the particles in the current iteration. Thus, a part of the particle population is updated quickly to improve the efficiency of the next iteration, and the newly generated particles can avoid falling near the local optimal solution. A flowchart of the improved particle swarm optimization algorithm based on the spiral function is shown in Figure 4. The pseudocode for the improved PSO algorithm is described as Algorithm 1.
| Algorithm 1. The particle swarm optimization algorithm based on the spiral function |
| Input: The optimization space of each CPG network parameter. |
| Output: Optimal CPG network parameters. |
| Step 1: Set the number of particles N, the number of iterations k, and then randomly set the initial position and velocity of the particles within a limited range. |
Step 2: Calculate the fitness value of the current particle.
|
Step 3: Using the spiral function to update the particles.
|
| Step 4: Iterate steps 2 and 3 until the maximum number of iterations k is reached. |
| Return the minimum fitness particle swarm |
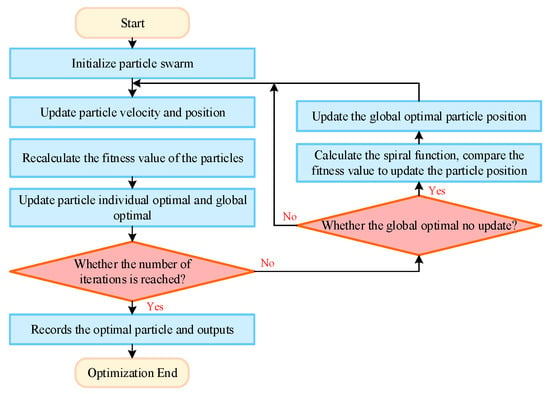
Figure 4.
The improved particle swarm algorithm flow chart.
4. The Biped Robot Walking Controller Optimization
The improved particle swarm optimization algorithm and the comparative optimization algorithms are used to optimize the parameters of the biped robot network based on CPG control. Based on the CPG network parameters obtained by optimization, the limit cycle of walking can be obtained by substituting the optimized parameters into the bipedal walking controller, so that the biped robot can achieve stable walking.
In order to fully reflect the efficient optimization ability of the particle swarm optimization algorithm based on the spiral function, this paper will present results from two-dimensional, four-dimensional, and ten-dimensional models, and other parameter optimization tests from low to high dimensions. The basic parameters of the algorithm are shown in Table 2.

Table 2.
The basic parameters of the algorithm.
The initial value of the biped robot walking control is set as follows:
x0 = [0.1925 −0.3919 −0.3921 −1.0746 1.5121 1.3789]
According to the characteristics of biped robot walking, the fitness function formula is set as follows:
where x0 is the initial value of the passive walking of the biped robot, x0[1, 1] is the position angle of the support leg under the generalized coordinate, L is the total length of the robot leg, θ is the angle between the slope and the ground, x0[2, 1] is the position angle of the swing leg under the generalized coordinate, B is the step size of the biped robot, and C is the step size difference of the biped robot.
The fitness function is a measure of the stability index of the biped robot during walking, and it is also an important part of the particle swarm optimization algorithm. The smaller the implicated fitness function value, the higher the walking stability of the biped robot and the better the control effect.
In order to evaluate the performance of the algorithm optimization, an evaluation index is proposed. According to the relationship between the fitness change of the algorithm and the number of iterations, the search efficiency (SE) of the algorithm can be obtained. The formula is as follows:
where is the fitness value at the beginning, is the fitness value at the end, and is the number of iterations of the algorithm.
When optimizing the parameters of different dimensions, this paper tests multiple comparative algorithms. These algorithms include the improved particle swarm optimization algorithm (IPSO), the traditional particle swarm optimization algorithm (TPSO), the chaotic particle swarm optimization algorithm 1 (CPSO1), and the chaotic particle swarm optimization algorithm 2 (CPSO2). Random numbers and were replaced by chaotic sequences in CPSO1 [28]. Additionally, a chaotic search was conducted as the inactive particles were randomly generated and incorporated in the new population in CPSO2 [29].
4.1. The Two-Dimensional Comparison Test
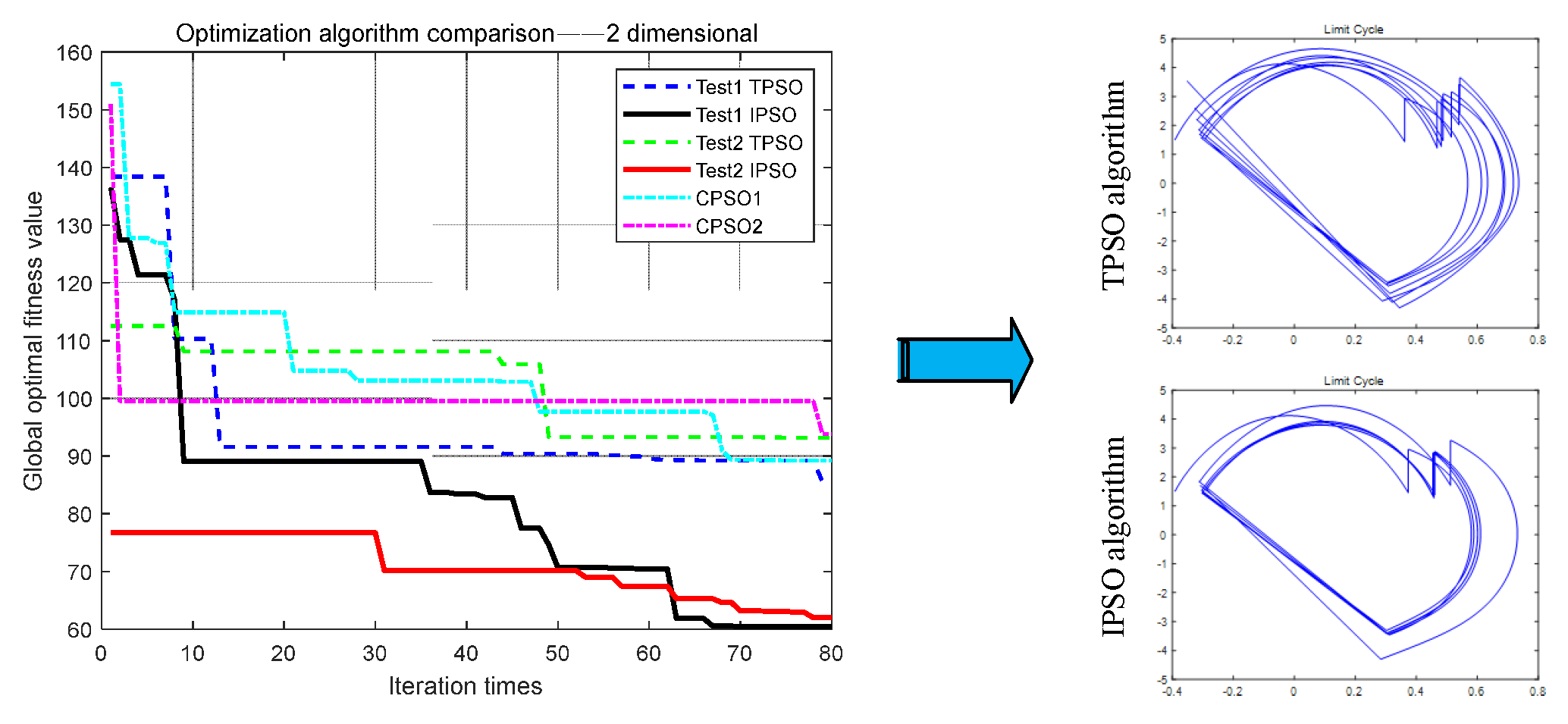
Some parameters in CPG [,] were introduced into the particle swarm optimization algorithm and the improved algorithm, respectively. The number of particles was 50 and the number of iterations was 80. In MATLAB (R2022b), several cases were run for the TPSO algorithm and the IPSO algorithm, respectively, and the optimization results are shown in Figure 5.
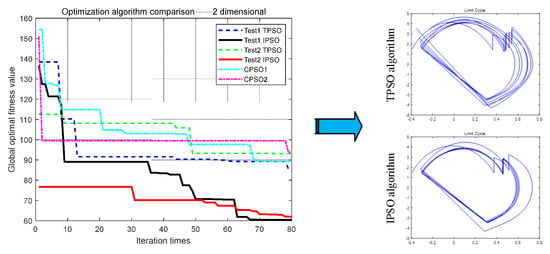
Figure 5.
The two-dimensional comparison test for the optimization algorithms.
The results from Figure 5 showed that the TPSO algorithm had about 15 iterations, and began to have a longer number of stagnation updates, with less updates until the 80th update. The IPSO algorithm had a strong update ability in the later stage and had a wide range of updates from the 30th time. Better results were gained via IPSO than the chaotic PSO algorithms. From the comparison of the IPSO and TPSO algorithms with an initial global optimal fitness value of about 140, the IPSO algorithm was about 45% more efficient than the TPSO algorithm. The calculation is as follows:
Using the calculated global optimal value, the limit cycle of biped robot walking can be obtained by substituting it into the mathematical model of biped robot hybrid dynamics. From the comparison of the two limit cycles, shown on the right side of Figure 5, the CPG parameters found by the IPSO algorithm were better, and the walking stability of the biped robot was higher. For low-dimensional parameter optimization, the IPSO algorithm had greater advantages than the TPSO algorithm.
4.2. The Four-Dimensional Comparison Test
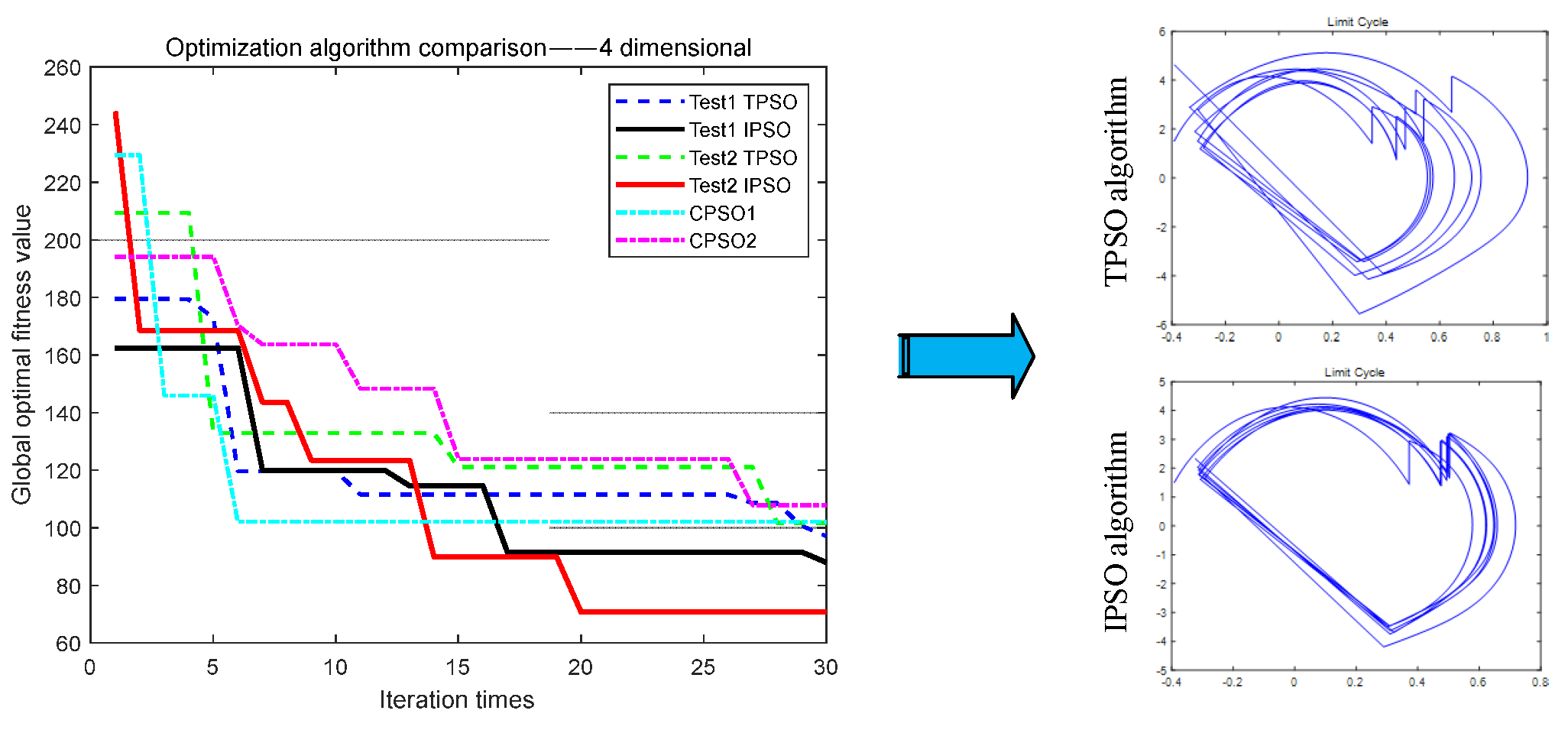
Some parameters [,,,] in CPG were introduced into the particle swarm optimization algorithm and the improved algorithm, respectively. The number of particles was 50 and the number of iterations was 30. In MATLAB, the TPSO algorithm and the IPSO algorithm were run several times, and the optimization results are shown in Figure 6.
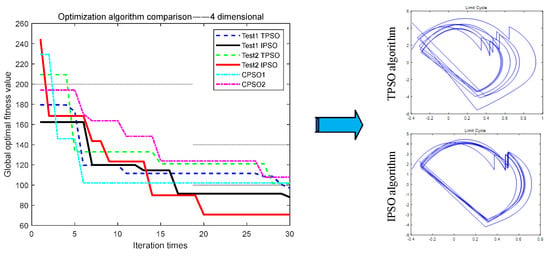
Figure 6.
The four-dimensional comparison test for the optimization algorithms.
The results from the graph show that the TPSO algorithm had about seven iterations and began to have a longer number of stagnation updates, with less updates until the 30th update. The IPSO algorithm still had a strong update ability in the later period, and it also had an update state after the 13th time. From the comparison of the IPSO and TPSO algorithms with the initial global optimal fitness value of about 210, the IPSO algorithm was about 54% higher than the traditional algorithm. The calculation is as follows:
Using the calculated global optimal value, the limit cycle of biped robot walking can be obtained by substituting it into the mathematical model of biped robot hybrid dynamics. From the comparison of the two limit cycles, shown on the right side of Figure 6, the IPSO algorithm had the strongest results in efficient optimization and better convergence of the limit cycle.
4.3. The Ten-Dimensional Comparison Test
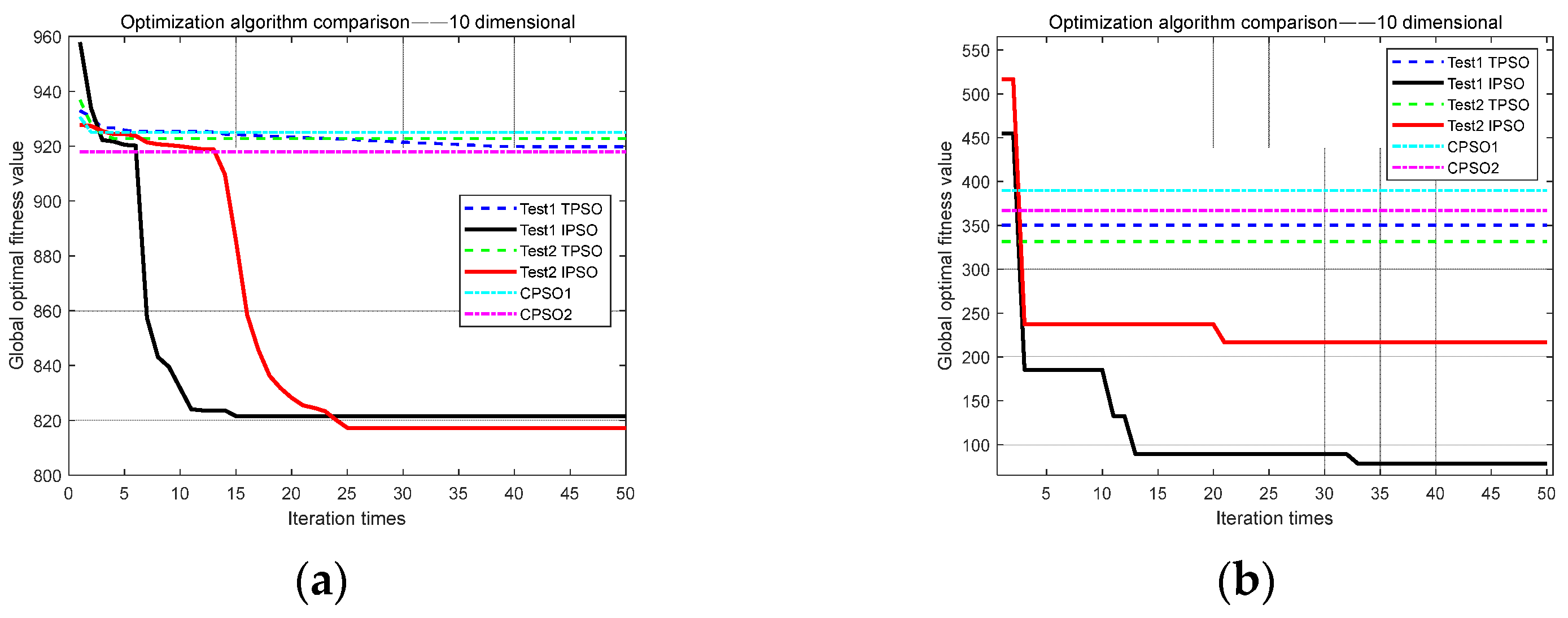
Some parameters [,,,,,,,,,] in CPG were introduced into the particle swarm optimization algorithm and the improved algorithm, respectively. The number of particles was 50 and the number of iterations was 50. In MATLAB, the TPSO algorithm and the IPSO algorithm were run several times, and the optimization results are shown in Figure 7.
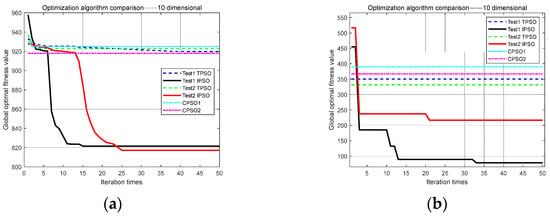
Figure 7.
The ten-dimensional comparison test for the optimization algorithms: (a) higher fitness value position; (b) lower fitness value position.
The results from Figure 7 show that under different initial positions, the TPSO algorithm had a very low optimization efficiency, very few iterative update fitness values, and the image tended to be horizontal, especially in the lower initial fitness values. It is possible that the TPSO algorithm needed more particles and iterations to continue to update the fitness value. However, the IPSO algorithm had a strong ability to update, and the update span was very large. Compared with TPSO and the chaotic PSO algorithms, the IPSO algorithm had a greater impact on the optimization efficiency whether the initial fitness value position was large or small.
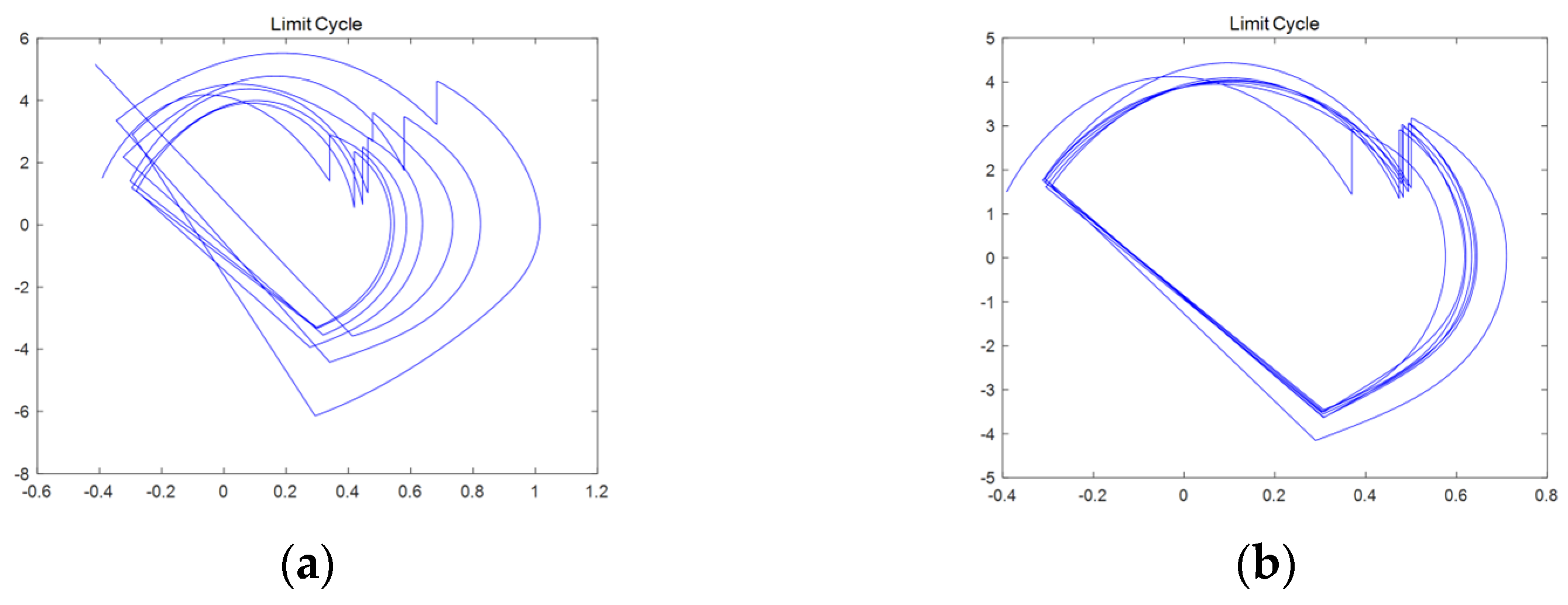
The calculated global optimal value was substituted into the hybrid dynamic mathematical model of the biped robot, and the limit cycle of the biped robot was obtained, as shown in Figure 8.
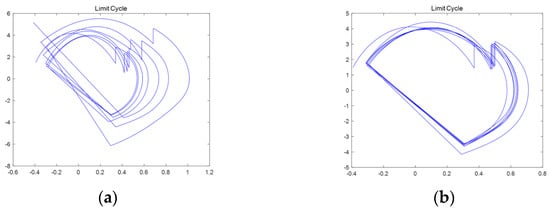
Figure 8.
Diagrams from the ten-dimensional limit cycle comparison: (a) TPSO algorithm; (b) IPSO algorithm.
Based on the above test data, the optimization performance of the algorithm in different dimensions was evaluated. For each algorithm test, the optimal calculation results were selected to calculate the SE value from Equation (10). The evaluation results are shown in Table 3. From the comparison results, the improved particle swarm optimization algorithm had a higher optimization ability, especially IPSO, which had better results in high-dimensional optimization.

Table 3.
Performance evaluation of the different algorithms.
The IPSO algorithm proposed in this paper does not produce very complex mathematical calculations. When the global optimal fitness value is stagnant and updated, the calculation of the spiral function starts to provide a new particle position for the next iteration. The computational complexity of the IPSO algorithm is proportional to the dimension of the input parameters and the number of stagnation updates of the fitness value. The proposed algorithm is more suitable for high-dimensional parameter optimization occasions, such as parameter optimization of the PID controller, time optimization of manipulator space planning, etc.
5. Walking Control Results of the Biped Robot
Using the ten-dimensional calculation results obtained by the IPSO algorithm, these were substituted into the CPG control network, and the walking simulation of the biped robot was performed using V-REP [30] and MATLAB. The parameters of the CPG walking controller, based on the improved PSO algorithm, are as follows:
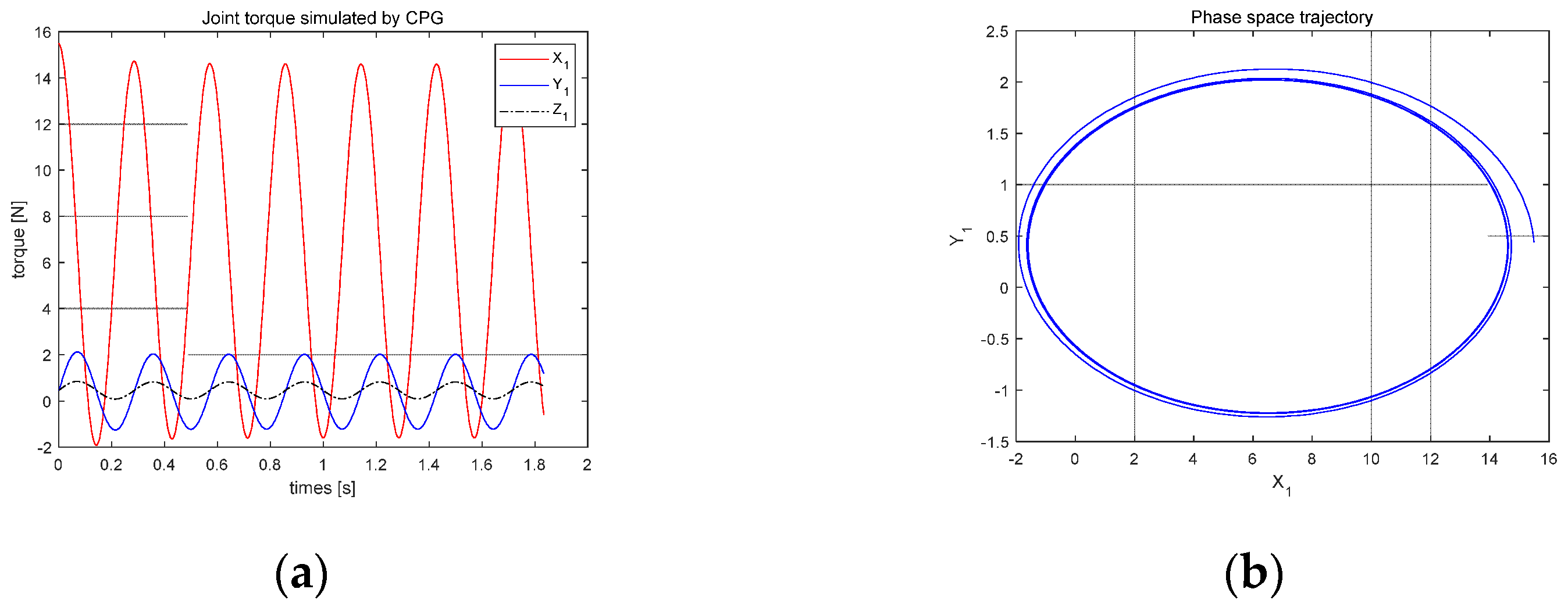
For the above parameters, the corresponding CPG oscillator output results are shown in Figure 9.
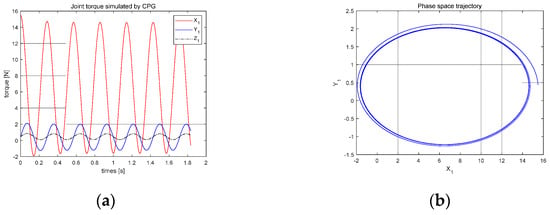
Figure 9.
The CPG oscillator output results: (a) joint torque simulated by CPG; (b) phase space trajectory.
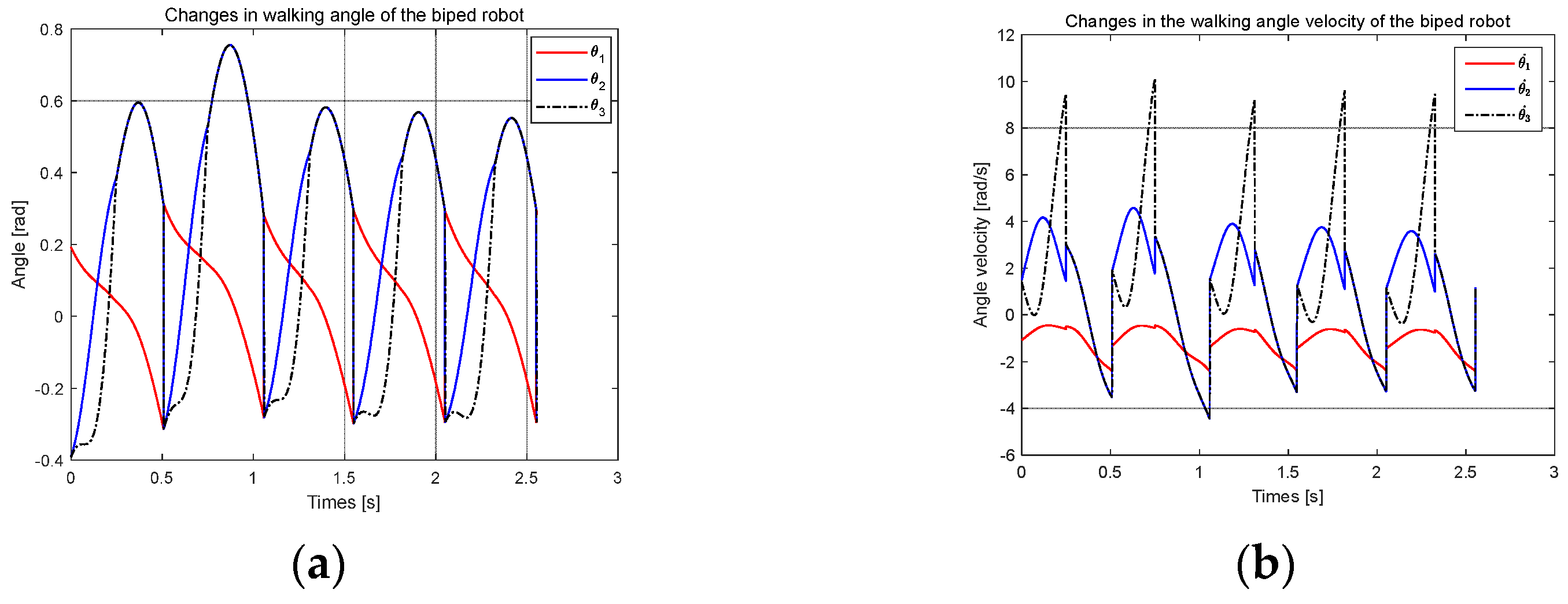
The data in Formula (13) were brought into the hybrid dynamic model of the biped robot [24]. In MATLAB, the joint angle and joint angular velocity of the biped robot were obtained by calculation, as shown in Figure 10.
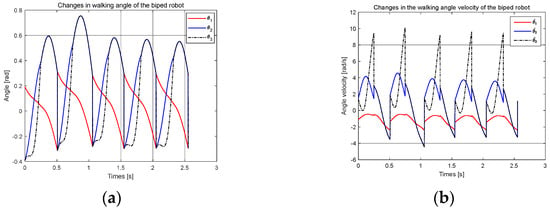
Figure 10.
The walking results of the biped robot: (a) changes in the walking angle of the biped robot; (b) changes in the walking angle velocity of the biped robot.
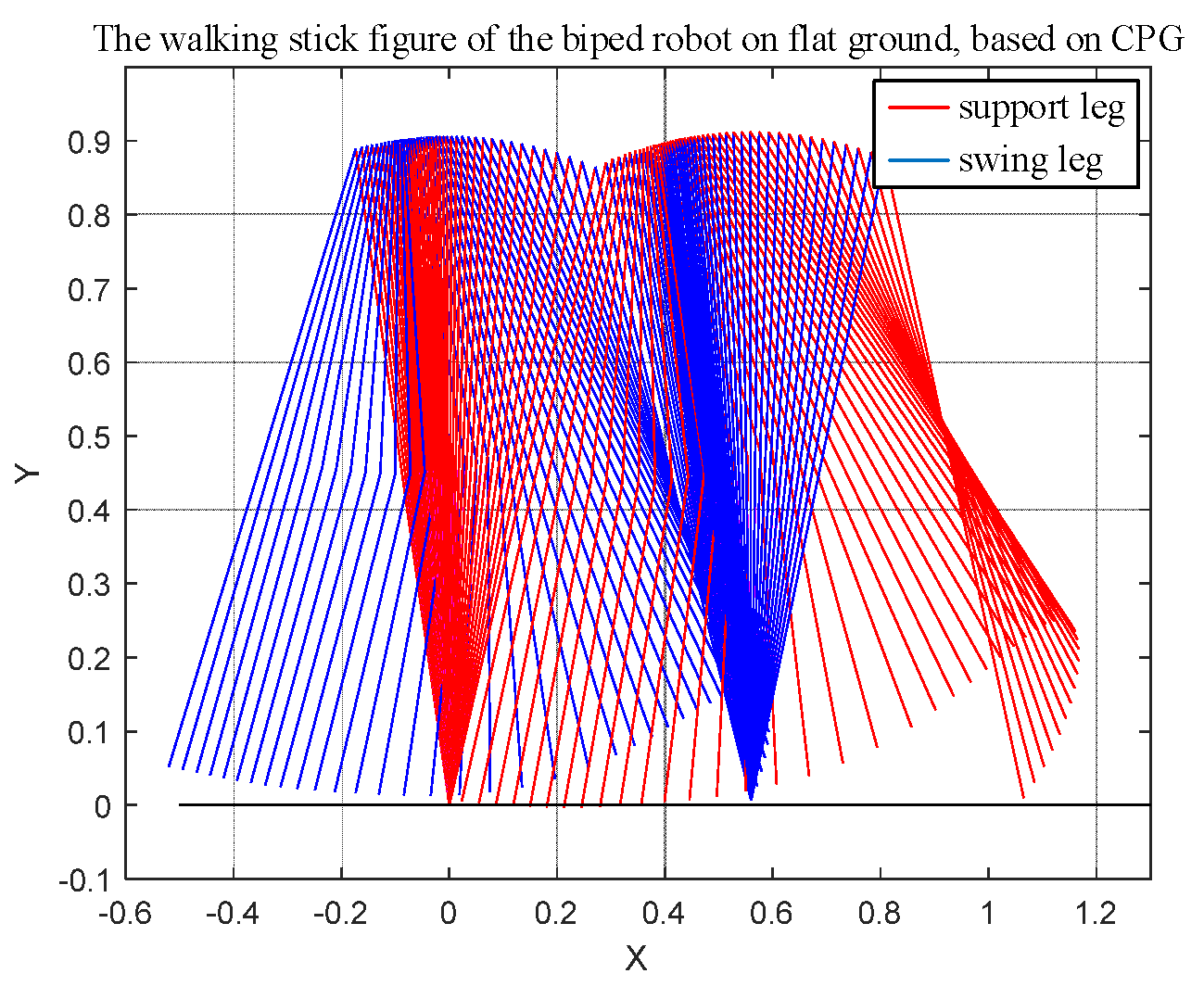
Using the joint data from Figure 10, the stick figure of the biped robot walking in a flat environment was obtained. As shown in Figure 11, during the walking process, the robot continued to walk stably and the walking state switched smoothly.
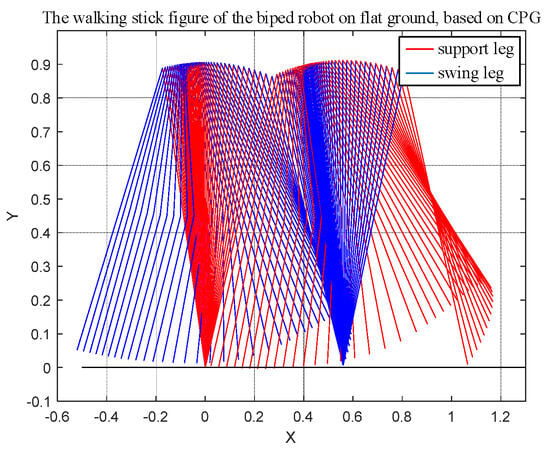
Figure 11.
The walking stick figure of the biped robot on flat ground, based on CPG.
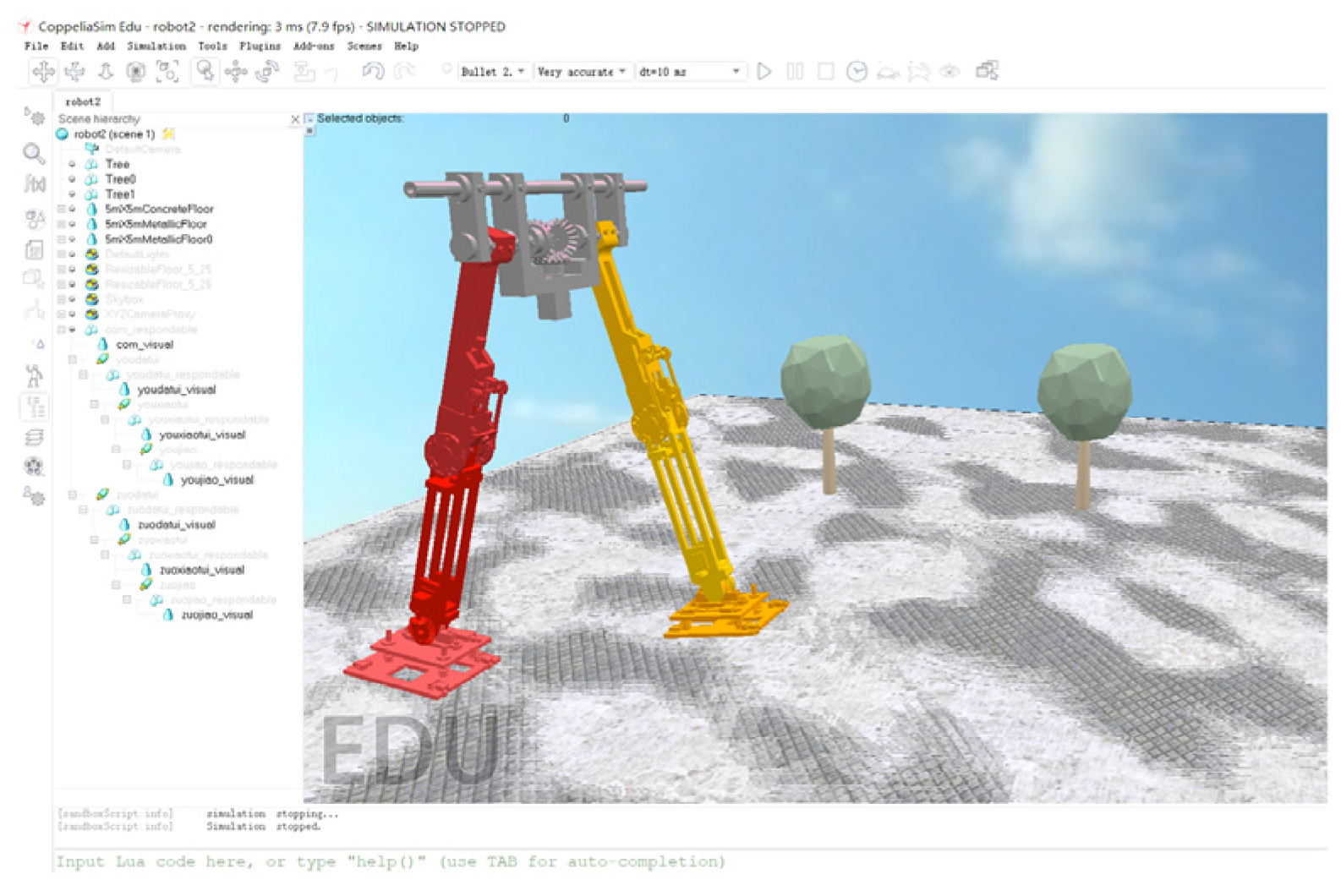
In order to simulate the biped robot walking on the flat ground, the robot’s mechanical model was imported into the cross-platform, open-source simulation software V-REP (V4.1.0). Additionally, MATLAB (R2022b) was used to conduct the optimization process and control the biped robot to walk.
The virtual prototype model of the biped robot was established in V-REP, as shown in Figure 12.
Figure 12.
The biped robot’s virtual prototype model.
In order to evaluate the performance of the CPG parameter optimization, two walking simulation tests were conducted for the biped robots in flat ground scenarios. Specifically, one walking simulation was used as a baseline, where the robot was controlled under the CPG network with unoptimized parameters, and the other was the experiment, where robot was simulated under CPG control with the optimized parameters gained by the improved PSO algorithm.
In the flat ground scene of V-REP, the one-step walking gait of the biped robot based on the unoptimized CPG parameters is shown in Figure 13. The robot could not maintain balance and easily fell.

Figure 13.
The biped robot’s gait simulation under the unoptimized CPG parameters.
In the flat ground scene of V-REP, the one-step walking gait of the biped robot based on the optimized CPG parameters is shown in Figure 14. It was seen that stable bipedal locomotion could be gained under the CPG optimized parameters by using the proposed IPSO algorithm. The step length of the bipedal locomotion was about 0.56 m and the single step walking time was about 0.5 s.

Figure 14.
The biped robot’s gait simulation under the optimized CPG parameters.
6. Conclusions and Future Work
The improved particle swarm optimization algorithm based on a spiral function that was proposed in this paper is effective in solving the problem of CPG parameter optimization. The improved particle swarm optimization algorithm had benefits such as a lower likelihood of falling into the local optimum and a high optimization efficiency.
The IPSO algorithm was compared with the TPSO algorithm, the CPSO1 algorithm, and the CPSO2 algorithm in the two-dimensional, four-dimensional, and ten-dimensional CPG parameter optimization. The optimization results showed that the efficiency of the IPSO algorithm was about 45% (for two-dimensional optimization) and 54% (for four-dimensional optimization) higher than that of the TPSO algorithm near the same initial position. The IPSO algorithm had a better optimization efficiency and faster convergence speed. The improved algorithm had a good performance, especially for high-dimensional optimization.
Through the joint simulation of V-REP and MATLAB, these results show that a biped robot based on CPG control using the IPSO algorithm can walk stably on flat ground. These optimized parameter results will be used to design real biped robot prototype experiments in the future.
Author Contributions
All authors contributed to this work. Conceptualization, Y.W. and S.Q.; methodology, Y.W. and B.T.; software, B.T.; validation, Y.W. and X.P.; writing—original draft preparation, B.T.; writing—review and editing, B.T. and Y.W.; funding acquisition, Y.W., S.Q. and X.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Research Foundation of Education Bureau of Hunan Province, China (22B0826, 22A0600), and the Science and Technology Innovation Program of Hunan Province (2022RC1138, 2023JJ30079).
Data Availability Statement
The data that support the findings of this study are available on request from the corresponding author. The data are not publicly available due to privacy and ethical restrictions.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Katayama, S.; Murooka, M.; Tazaki, Y. Model predictive control of legged and humanoid robots: Models and algorithms. Adv. Robot. 2023, 37, 298–315. [Google Scholar] [CrossRef]
- Wang, J.; Lu, S.; Chen, J. A CPG-based gait planning method for bipedal robots. Artif. Life Robot. 2024, 29, 340–348. [Google Scholar]
- Matsubara, T.; Morimoto, J.; Nakanishi, J.; Sato, M.A.; Doya, K. Learning CPG-based biped locomotion with a policy gradient method. Robot. Auton. Syst. 2006, 54, 911–920. [Google Scholar] [CrossRef]
- Sun, T.; Zhang, S.; Li, R.; Yan, Y. A Bionic Control Method for Human–Exoskeleton Coupling Based on CPG Model. Actuators 2023, 12, 321. [Google Scholar] [CrossRef]
- Li, D.; Wei, W.; Qiu, Z. Combined Reinforcement Learning and CPG Algorithm to Generate Terrain-Adaptive Gait of Hexapod Robots. Actuators 2023, 12, 157. [Google Scholar] [CrossRef]
- Ijspeert, A.J. Central pattern generators for locomotion control in animals and robots: A review. Neural Netw. 2008, 21, 642–653. [Google Scholar] [CrossRef]
- Urraca, R.; Sodupe-Ortega, E.; Antonanzas, J.; Antonanzas-Torres, F.; Martinez-de-Pison, F.J. Evaluation of a novel GA-based methodology for model structure selection: The GA-PARSIMONY. Neurocomputing 2018, 271, 9–17. [Google Scholar] [CrossRef]
- Wu, Y.; Gong, M.; Ma, W.; Wang, S. High-order graph matching based on ant colony optimization. Neurocomputing 2019, 328, 97–104. [Google Scholar] [CrossRef]
- Madani, T.; Daachi, B.; Benallegue, A. Adaptive variable structure controller of redundant robots with mobile/fixed obstacles avoidance. Robot. Auton. Syst. 2013, 61, 555–564. [Google Scholar] [CrossRef]
- Ju, M.Y.; Wang, S.E.; Guo, J.H. Path planning using a hybrid evolutionary algorithm based on tree structure encoding. Sci. World J. 2014, 2014, 746260. [Google Scholar] [CrossRef]
- Son, C. Intelligent rule-based sequence planning algorithm with fuzzy optimization for robot manipulation tasks in partially dynamic environments. Inf. Sci. 2016, 342, 209–221. [Google Scholar] [CrossRef]
- El Ferik, S.; Nasir, M.T.; Baroudi, U. A Behavioral Adaptive Fuzzy controller of multi robots in a cluster space. Appl. Soft Comput. 2016, 44, 117–127. [Google Scholar] [CrossRef]
- Purcaru, C.; Precup, R.E.; Iercan, D.; Fedorovici, L.O.; David, R.C.; Dragan, F. Optimal robot path planning using gravitational search algorithm. Int. J. Artif. Intell. 2013, 10, 1–20. [Google Scholar]
- Liu, E.; Yao, X.; Liu, M.; Jin, H. AGV path planning based on improved grey wolf optimization algorithm and its implementation prototype platform. Comput. Integr. Manuf. Syst. 2018, 24, 2779–2791. [Google Scholar]
- Zaman, H.R.R.; Gharehchopogh, F.S. An improved particle swarm optimization with backtracking search optimization algorithm for solving continuous optimization problems. Eng. Comput. 2022, 38, 2797–2831. [Google Scholar] [CrossRef]
- Das, P.K.; Jena, P.K. Multi-robot path planning using improved particle swarm optimization algorithm through novel evolutionary operators. Appl. Soft Comput. 2020, 92, 106312. [Google Scholar] [CrossRef]
- Yuan, Q.; Sun, R.; Du, X. Path planning of mobile robots based on an improved particle swarm optimization algorithm. Processes 2022, 11, 26. [Google Scholar] [CrossRef]
- Zhao, G.; Jiang, D.; Liu, X.; Tong, X.; Sun, Y.; Tao, B.; Kong, J.; Yun, J.; Liu, Y.; Fang, Z. A tandem robotic arm inverse kinematic solution based on an improved particle swarm algorithm. Front. Bioeng. Biotechnol. 2022, 10, 832829. [Google Scholar] [CrossRef]
- Shao, S.; Peng, Y.; He, C.; Du, Y. Efficient path planning for UAV formation via comprehensively improved particle swarm optimization. ISA Trans. 2020, 97, 415–430. [Google Scholar] [CrossRef]
- Song, B.; Wang, Z.; Zou, L. An improved PSO algorithm for smooth path planning of mobile robots using continuous high-degree Bezier curve. Appl. Soft Comput. 2021, 100, 106960. [Google Scholar] [CrossRef]
- Li, X.; Tian, B.; Hou, S.; Li, X.; Li, Y.; Liu, C.; Li, J. Path planning for mount robot based on improved particle swarm optimization algorithm. Electronics 2023, 12, 3289. [Google Scholar] [CrossRef]
- Tao, C.; Xue, J.; Zhang, Z.; Cao, F.; Li, C.; Gao, H. Gait optimization method for humanoid robots based on parallel comprehensive learning particle swarm optimizer algorithm. Front. Neurorobotics 2021, 14, 600885. [Google Scholar] [CrossRef] [PubMed]
- Sahu, C.; Parhi, D.R. Navigational strategy of a biped robot using regression-adaptive PSO approach. Soft Comput. 2022, 26, 12317–12341. [Google Scholar] [CrossRef]
- Wu, Y.; Qiao, S.; Yao, D. A hybrid chaotic controller integrating hip stiffness modulation and reinforcement learning-based torque control to stabilize passive dynamic walking. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2023, 237, 673–691. [Google Scholar] [CrossRef]
- Wu, Y.; Yao, D.; Xiao, X.; Guo, Z. Intelligent controller for passivity-based biped robot using deep Q network. J. Intell. Fuzzy Syst. 2019, 36, 731–745. [Google Scholar] [CrossRef]
- Wu, Y.; Yao, D.; Xiao, X. Optimal design for flexible passive biped walker based on chaotic particle swarm optimization. J. Electr. Eng. Technol. 2018, 13, 2493–2503. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle Swarm Optimization. In Proceedings of the IEEE International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; IEEE Press: Piscataway, NJ, USA, 1995; pp. 1942–1947. [Google Scholar]
- Yang, C.H.; Tsai, S.W.; Chuang, L.Y.; Yang, C.H. An improved particle swarm optimization with double-bottom chaotic maps for numerical optimization. Appl. Math. Comput. 2012, 219, 260–279. [Google Scholar] [CrossRef]
- Meng, H.J.; Zheng, P.; Wu, R.Y.; Hao, X.J.; Xie, Z. A hybrid particle swarm algorithm with embedded chaotic search. In Proceedings of the IEEE Conference on Cybernetics and Intelligent Systems, Singapore, 1–3 December 2004; pp. 367–371. [Google Scholar]
- Ao, T.; Li, M.; Liu, M.; Wang, H. Control Simulation of Dual-Arm Robot Based on Sliding Mode Controller. Process Autom. Instrum. 2019, 40, 34–38. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).