Study of Error Flow for Hydraulic System Simulation Models for Construction Machinery Based on the State-Space Approach
Abstract
:1. Introduction
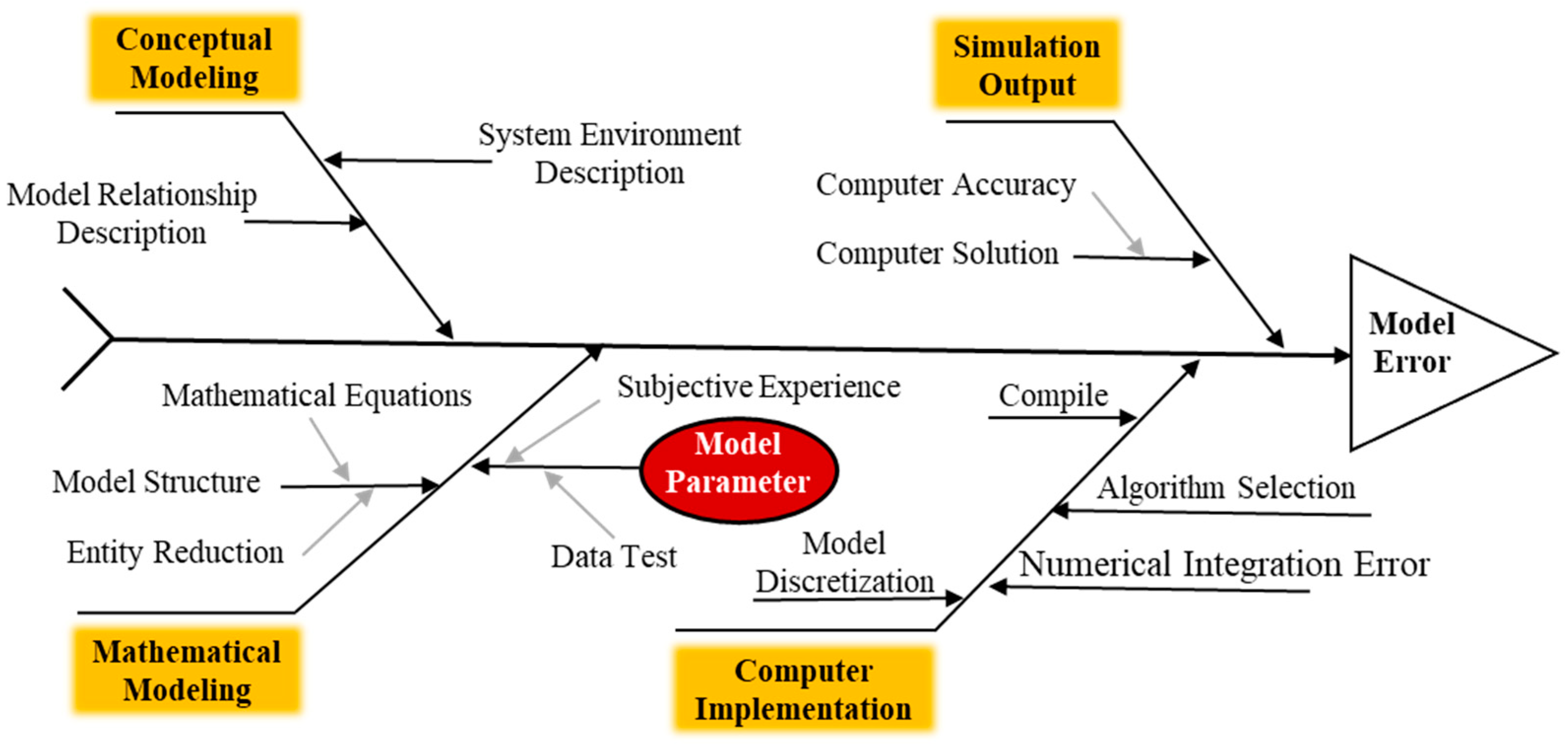
2. Error Analysis in Construction Machinery Simulation Modeling
3. Comprehensive Evaluation Metric for Simulation Model Accuracy
- (a)
- Generate radar charts based on the metrics.
- (b)
- Calculate the area enclosed by different metrics.
- (c)
- Calculate the area enclosed when all metrics are set to 1.
- (d)
- Compute the comprehensive evaluation metric based on the areas and . It falls within the range of [0, 1], where a higher value of “l” indicates greater model accuracy, with “1 − l” representing the model’s error characterization.
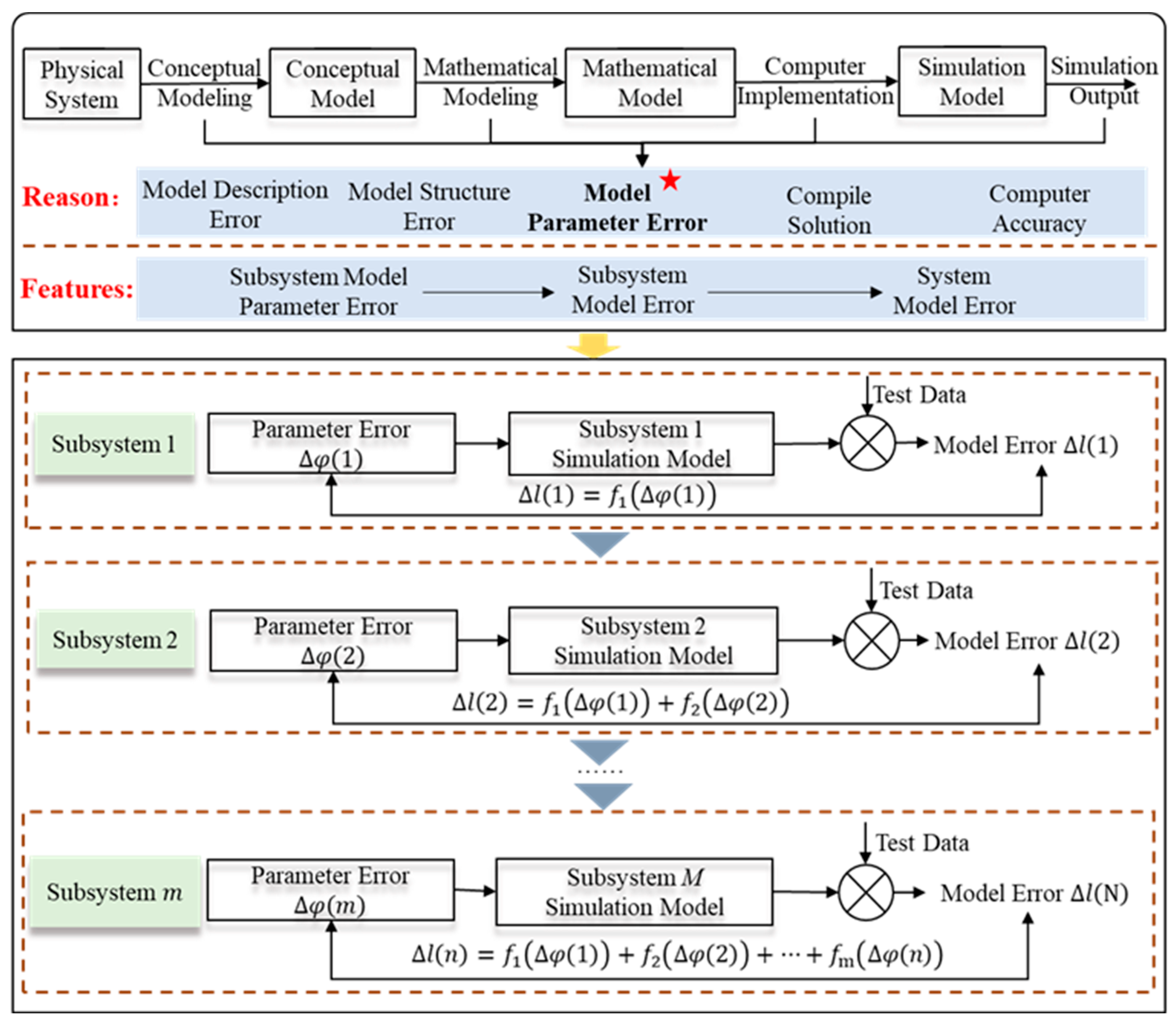
4. Error Flow Modeling Based on the State-Space Approach
- (1)
- Analysis and Characterization of Model Parameter Errors
- (2)
- Obtaining Reference Parameters
- (a)
- Establish the simulation model for the hydraulic system in construction machinery.
- (b)
- Obtain experimental data as reference data for the simulation model and refine it through multiple experiments to reduce gross errors and random errors.
- (c)
- Compare the output results of the simulation model with the reference data and assess the model’s accuracy using evaluation metric “l”.
- (d)
- As the optimization objective, seek to maximize evaluation metric “l” and employ optimization algorithms such as particle swarm optimization (PSO) [33] to solve for the reference parameters.
- (3)
- Model Expected Accuracy and Model Error Change Rate
- (4)
- Relationship between Model Parameters and Error Change Rate
- (5)
- Mathematical Formulation of Error Flow
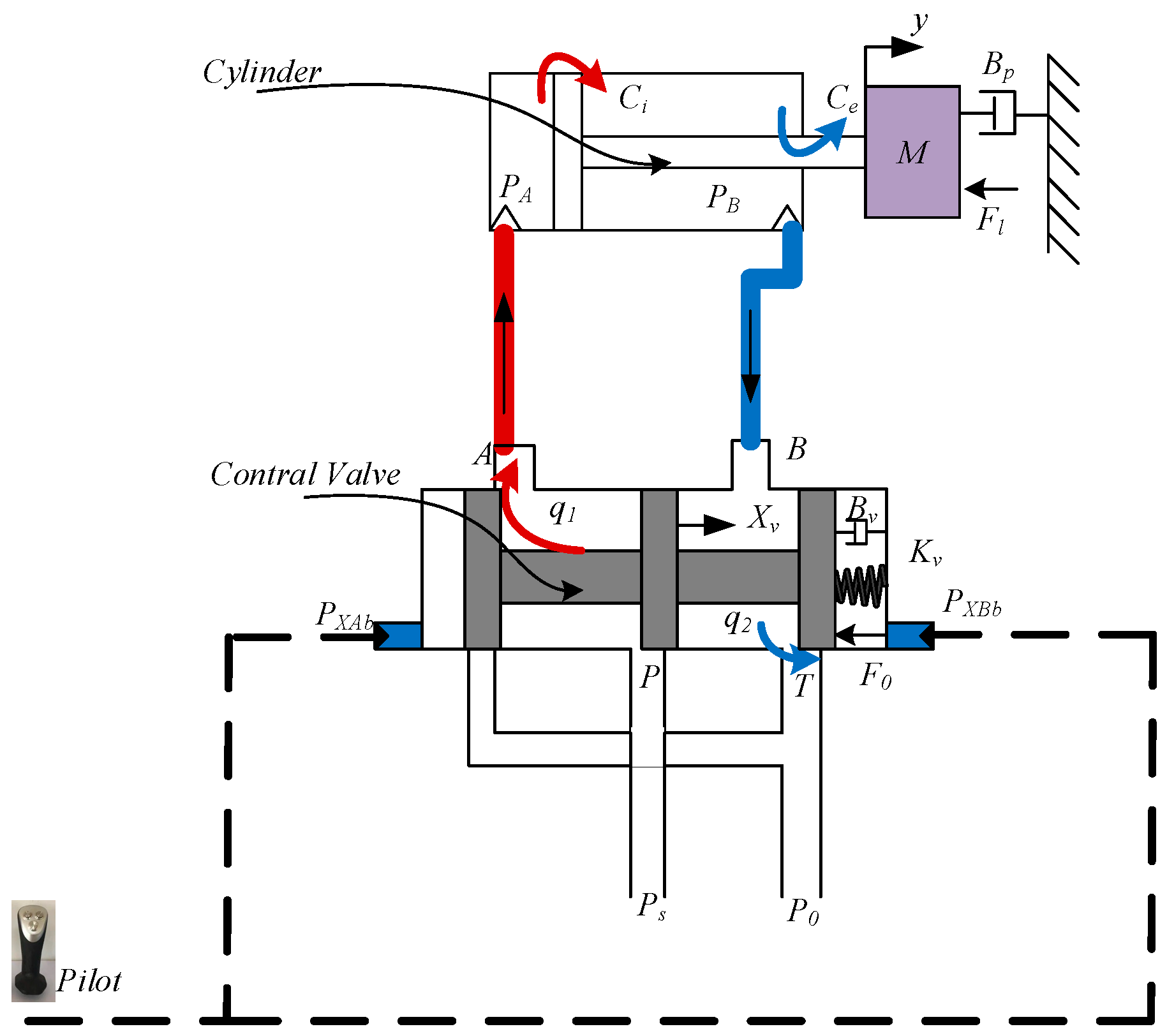
5. Case Study: Valve-Controlled Cylinder System
5.1. Error Sources of the Valve-Controlled Cylinder System Model
5.2. Error Flow Modeling of the Valve-Controlled Cylinder System
6. Results and Discussion
7. Conclusions
8. Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Khan, A.U.; Huang, L.Z.; Onstein, E.; Liu, Y.P. Overview of Emerging Technologies for Improving the Performance of Heavy-Duty Construction Machines. IEEE Access 2022, 10, 103315–103336. [Google Scholar] [CrossRef]
- Shariatfar, M.; Deria, A.; Lee, Y.C. Digital Twin in Construction Safety and Its Implications for Automated Monitoring and Management. In Proceedings of the Construction Research Congress 2022: Computer Applications, Automation, and Data Analytics, Arlington, VA, USA, 9–12 March 2022; pp. 591–600. [Google Scholar]
- Fu, T.; Zhang, T.; Lv, Y.L.; Song, X.G.; Li, G.; Yue, H.F. Digital twin-based excavation trajectory generation of Uncrewed excavators for autonomous mining. Autom. Constr. 2023, 151, 104855. [Google Scholar] [CrossRef]
- Wang, S.; Lai, X.N.; He, X.W.; Qiu, Y.M.; Song, X.G. Building a Trustworthy Product-Level Shape-Performance Integrated Digital Twin with Multifidelity Surrogate Model. J. Mech. Des. 2022, 144, 031703. [Google Scholar] [CrossRef]
- Zhang, L.; Zhou, L.F.; Horn, B.K.P. Building a right digital twin with model engineering. J. Manuf. Syst. 2021, 59, 151–164. [Google Scholar] [CrossRef]
- Yang, X.L.; Liu, X.M.; Zhang, H.; Fu, L.; Yu, Y.B. Meta-model-based shop-floor digital twin architecture, modeling and application. Robot. C-Int. Manuf. 2023, 84, 102595. [Google Scholar] [CrossRef]
- Robinson, S. Simulation: The Practice of Model Development and Use; Bloomsbury Publishing: London, UK, 2014. [Google Scholar]
- Fan, Z.X.; Yang, Z.F.; Yu, J. Error Bound Restriction of Linear Power Flow Model. IEEE Power Syst. 2022, 37, 808–811. [Google Scholar] [CrossRef]
- Qiu, N.; Park, C.Y.; Gao, Y.K.; Fang, J.G.; Sun, G.Y.; Kim, N.H. Sensitivity-Based Parameter Calibration and Model Validation Under Model Error. J. Mech. Des. 2018, 140, 011403. [Google Scholar] [CrossRef]
- Zhou, G.; Xie, Z.W.; Xu, X.H.; Li, Q. A new model of overall heat transfer coefficient of hot wax oil pipeline based on dimensionless experimental analysis. Case Stud. Therm. Eng. 2020, 20, 100647. [Google Scholar] [CrossRef]
- Hu, S.J.; Koren, Y. Stream-of-variation theory for automotive body assembly. Cirp. Ann. 1997, 46, 1–6. [Google Scholar] [CrossRef]
- Jin, J.; Shi, J. State space modeling of sheet metal assembly for dimensional control. J. Manuf. Sci. Eng. 1999, 121, 756–762. [Google Scholar] [CrossRef]
- Zhang, T.Y.; Shi, J.J. Stream of Variation Modeling and Analysis for Compliant Composite Part Assembly-Part II: Multistation Processes. J. Manuf. Sci. Eng. 2016, 138, 121004. [Google Scholar] [CrossRef]
- He, G.Y.; Guo, L.Z.; Li, S.Q.; Zhang, D.W. Simulation and analysis for accuracy predication and adjustment for machine tool assembly process. Adv. Mech. Eng. 2017, 9, 168781401773447. [Google Scholar] [CrossRef]
- Wang, K.; Li, G.L.; Du, S.C.; Xi, L.F.; Xia, T.B. State space modelling of variation propagation in multistage machining processes for variable stiffness structure workpieces. Int. J. Prod. Res. 2021, 59, 4033–4052. [Google Scholar] [CrossRef]
- Liu, C.H.; Jin, S.; Lai, X.M.; Wang, Y.L. Dimensional variation stream modeling of investment casting process based on state space method. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2015, 229, 463–474. [Google Scholar] [CrossRef]
- Ding, Y.; Ceglarek, D.; Shi, J.J. Design evaluation of multi-station assembly processes by using state space approach. J. Mech. Des. 2002, 124, 408–418. [Google Scholar] [CrossRef]
- Zhang, T.; Li, B.B.; Sun, H.; Zhao, S.Q.; Peng, F.Y.; Zhou, L.; Yan, R. A Knowledge-Embedded End-to-End Intelligent Reasoning Method for Processing Quality of Shaft Parts. Intell. Robot. Appl. 2022, 13458, 425–436. [Google Scholar]
- Pan, Y.; Xiong, Y.; Dai, W.; Diao, K.; Wu, L.; Wang, J. Crush and crash analysis of an automotive battery-pack enclosure for lightweight design. Int. J. Crashworthiness 2022, 27, 500–509. [Google Scholar] [CrossRef]
- Balci, O. How to Successfully Conduct Large-Scale Modeling and Simulation Projects. In Proceedings of the 2011 Winter Simulation Conference, Phoenix, AZ, USA, 11–14 December 2011; pp. 176–182. [Google Scholar]
- Wei, J.Y.; Zhang, X.M.; Mo, J.S.; Tong, Y.L. Error Modeling and Simulation of a 2-DOF High-Speed Parallel Manipulator. Lect. Notes Artif. Int. 2014, 8918, 100–110. [Google Scholar]
- Weens, W.; Vazquez-Gonzalez, T.; Salem-Knapp, L.B. Modeling Round-Off Errors in Hydrodynamic Simulations. Lect. Notes Comput. Sc. 2022, 13124, 182–196. [Google Scholar]
- Pan, Y.; Dai, W.; Huang, L.; Li, Z.; Mikkola, A. Iterative refinement algorithm for efficient velocities and accelerations solutions in closed-loop multibody dynamics. Mech. Syst. Signal Process. 2021, 152, 107463. [Google Scholar] [CrossRef]
- Oberkampf, W.L.; DeLand, S.M.; Rutherford, B.M.; Diegert, K.V.; Alvin, K.F. Error and uncertainty in modeling and simulation. Reliab. Eng. Syst. Safe 2002, 75, 333–357. [Google Scholar] [CrossRef]
- Mehmood, A.; Zameer, A.; Aslam, M.S.; Raja, M.A.Z. Design of nature-inspired heuristic paradigm for systems in nonlinear electrical circuits. Neural Comput. Appl. 2020, 32, 7121–7137. [Google Scholar] [CrossRef]
- Hu, J.X.; Yang, Y.; Zhou, Q.; Jiang, P.; Shao, X.Y.; Shu, L.S.; Zhang, Y.H. Comparative studies of error metrics in variable fidelity model uncertainty quantification. J. Eng. Des. 2018, 29, 512–538. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Gitau, M.W.; Pai, N.; Daggupati, P. Hydrologic and Water Quality Models: Performance Measures and Evaluation Criteria. Trans. ASABE 2015, 58, 1763–1785. [Google Scholar]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Wang, S.J.; Hou, L.; Lee, J.; Bu, X.J. Evaluating wheel loader operating conditions based on radar chart. Autom. Constr. 2017, 84, 42–49. [Google Scholar]
- He, L.; Pan, Y.; He, Y.; Li, Z.; Królczyk, G.; Du, H. Control strategy for vibration suppression of a vehicle multibody system on a bumpy road. Mech. Mach. Theory 2022, 174, 104891. [Google Scholar] [CrossRef]
- Peng, W.S.; Li, Y.H.; Fang, Y.W.; Wu, Y.; Li, Q. Radar Chart for Estimation Performance Evaluation. IEEE Access 2019, 7, 113880–113888. [Google Scholar] [CrossRef]
- Ma, R.; Guo, Q.; Hu, C.Z.; Xue, J.F. An Improved WiFi Indoor Positioning Algorithm by Weighted Fusion. Sensors 2015, 15, 21824–21843. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the Proceedings of the ICNN’95-international conference on neural networks, Perth, WA, Australia, 27 November–1 December 1995; IEEE: New York, NY, USA, 1995; pp. 1942–1948. [Google Scholar]
- Aashima, H.; Arun, N.; Manish, J.; Vikash, K.; Permender, R. Optimization and evaluation of gastrore-tentive ranitidine HCl microspheres by using design expert software. Int. J. Biol. Macromol. 2012, 51, 691–700. [Google Scholar]
- Vijay, Y.; Sanandiya, N.D.; Dritsas, S.; Fernandez, J.G. Control of Process Settings for Large-Scale Additive Manufacturing With Sustainable Natural Composites. J. Mech. Des. 2019, 141, 081701. [Google Scholar] [CrossRef]
- Weaver-Rosen, J.M.; Malak, R.J. Efficient Parametric Optimization for Expensive Single Objective Problems. J. Mech. Des. 2021, 143, 031711. [Google Scholar] [CrossRef]
- Rahmat, M.F.A.; Zulfatman, Z.; Husain, A.R.; Ishaque, K.; Sam, Y.M.; Ghazali, R.; Rozali, S.M. Modeling and controller design of an industrial hydraulic actuator system in the presence of friction and internal leakage. Int. J. Phys. Sci. 2011, 6, 3502–3517. [Google Scholar]
- Milecki, A.; Ortmann, J. Electrohydraulic linear actuator with two stepping motors controlled by overshoot-free algorithm. Mech. Syst. Signal Process. 2017, 96, 45–57. [Google Scholar] [CrossRef]
- Zhang, K.; Zhang, J.; Gan, M.; Zong, H.; Wang, X.; Huang, H.; Xu, B. Modeling and parameter sensitivity analysis of valve-controlled helical hydraulic rotary actuator system. Chin. J. Mech. Eng. 2022, 35, 66. [Google Scholar] [CrossRef]
- Kong, X.D.; Yu, B.; Quan, L.X.; Ba, K.X.; Wu, L.J. Nonlinear mathematical modeling and sensitivity analysis of hydraulic drive unit. Chin. J. Mech. Eng. 2015, 28, 999–1011. [Google Scholar] [CrossRef]
- Kong, X.D.; Ba, K.X.; Yu, B.; Cao, Y.; Wu, L.J.; Quan, L.X. Trajectory sensitivity analysis of first order and second order on position control system of highly integrated valve-controlled cylinder. J. Mech. Sci. Technol. 2015, 29, 4445–4464. [Google Scholar] [CrossRef]
- Ba, K.X.; Yu, B.; Kong, X.D.; Li, C.H.; Zhu, Q.X.; Zhao, H.L.; Kong, L.J. Parameters Sensitivity Characteristics of Highly Integrated Valve-Controlled Cylinder Force Control System. Chin. J. Mech. Eng. 2018, 31, 43. [Google Scholar] [CrossRef]
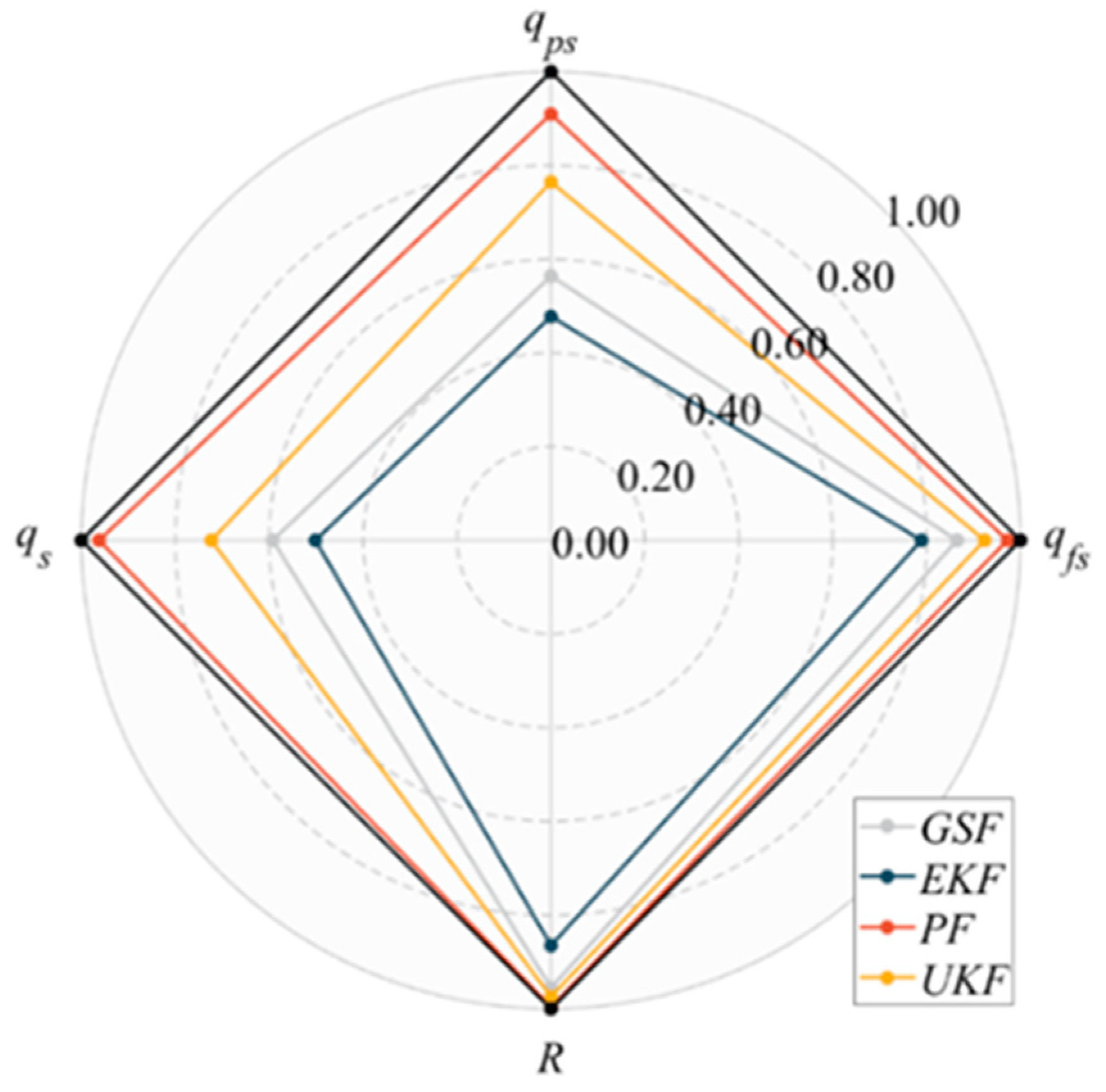




| Model | qfs | qps | qs | R2 |
|---|---|---|---|---|
| GSF | 0.865 | 0.564 | 0.593 | 0.955 |
| EKF | 0.789 | 0.477 | 0.502 | 0.865 |
| PF | 0.972 | 0.909 | 0.962 | 0.995 |
| UKF | 0.924 | 0.765 | 0.723 | 0.974 |
| Levels | /(N) | /(N/m) | /(Nm/s) | |
|---|---|---|---|---|
| −alpha | 257.324 | 105.285 | 259.386 | 0.495 |
| low | 277.324 | 120.285 | 279.386 | 0.595 |
| 0 | 297.324 | 130.285 | 299.386 | 0.695 |
| high | 317.324 | 150.285 | 319.386 | 0.795 |
| +alpha | 337.324 | 165.285 | 339.386 | 0.895 |
| Levels | /(mm3/MPa/s) | /(mm3/MPa/s) | /(MPa) | /(N·s/m) |
|---|---|---|---|---|
| −alpha | 2.878 | 2.351 | 758.414 | 78,514 |
| low | 3.378 | 2.726 | 858.414 | 80,514 |
| 0 | 3.878 | 2.976 | 958.414 | 82,514 |
| high | 4.378 | 3.476 | 1058.414 | 84,514 |
| +alpha | 4.878 | 3.851 | 1158.414 | 86,514 |
| Serial Number | /(N) | /(N/m) | /(Nm/s) | Error Change Rates | |
|---|---|---|---|---|---|
| 1 | 297.324 | 130.285 | 299.386 | 0.895 | 0.901534 |
| 2 | 317.324 | 150.285 | 319.386 | 0.795 | 0.836035 |
| 3 | 317.324 | 150.285 | 319.386 | 0.595 | 0.836035 |
| 4 | 297.324 | 90.285 | 299.386 | 0.695 | 0.0592399 |
| 5 | 297.324 | 130.285 | 299.386 | 0.695 | 0.901534 |
| 6 | 297.324 | 130.285 | 299.386 | 0.495 | 0.901534 |
| 7 | 317.324 | 110.285 | 319.386 | 0.795 | 0.495151 |
| 8 | 297.324 | 170.285 | 299.386 | 0.695 | 0.614629 |
| 9 | 317.324 | 110.285 | 319.386 | 0.595 | 0.495151 |
| 10 | 317.324 | 150.285 | 279.386 | 0.595 | 0.816725 |
| 11 | 277.324 | 110.285 | 279.386 | 0.595 | 0.549803 |
| 12 | 297.324 | 130.285 | 299.386 | 0.695 | 0.901534 |
| 13 | 277.324 | 150.285 | 279.386 | 0.595 | 0.816725 |
| 14 | 317.324 | 110.285 | 279.386 | 0.795 | 0.549803 |
| 15 | 277.324 | 110.285 | 319.386 | 0.595 | 0.495151 |
| 16 | 277.324 | 150.285 | 319.386 | 0.795 | 0.836035 |
| 17 | 277.324 | 150.285 | 279.386 | 0.795 | 0.816725 |
| 18 | 277.324 | 110.285 | 319.386 | 0.795 | 0.495151 |
| 19 | 297.324 | 130.285 | 339.386 | 0.695 | 0.867413 |
| 20 | 277.324 | 150.285 | 319.386 | 0.595 | 0.836035 |
| 21 | 317.324 | 150.285 | 279.386 | 0.795 | 0.816725 |
| 22 | 297.324 | 130.285 | 259.386 | 0.695 | 0.929980 |
| Serial Number | /(mm3/MPa/s) | /(mm3/MPa/s) | /(MPa) | /(N·s/m) | Error Change Rates |
|---|---|---|---|---|---|
| 1 | 437.808 | 347.641 | 1058.41 | 80,514 | 0.985792 |
| 2 | 387.808 | 297.641 | 958.412 | 82,514 | 0.985787 |
| 3 | 387.808 | 297.641 | 758.416 | 82,514 | 0.887663 |
| 4 | 387.808 | 297.641 | 958.412 | 82,514 | 0.887662 |
| 5 | 337.808 | 347.641 | 1058.41 | 84,514 | 0.996764 |
| 6 | 387.808 | 197.641 | 958.412 | 82,514 | 0.996764 |
| 7 | 437.808 | 347.641 | 1058.41 | 84,514 | 0.985792 |
| 8 | 337.808 | 247.641 | 1058.41 | 84,514 | 0.996768 |
| 9 | 287.808 | 297.641 | 958.412 | 82,514 | 0.985789 |
| 10 | 437.808 | 247.641 | 858.414 | 80,514 | 0.887665 |
| 11 | 437.808 | 247.641 | 1058.41 | 84,514 | 0.887663 |
| 12 | 337.808 | 247.641 | 858.414 | 84,514 | 0.985789 |
| 13 | 337.808 | 247.641 | 1058.41 | 80,514 | 0.996764 |
| 14 | 437.808 | 247.641 | 1058.41 | 80,514 | 0.985794 |
| 15 | 387.808 | 297.641 | 958.412 | 86,514 | 0.99677 |
| 16 | 487.808 | 297.641 | 958.412 | 82,514 | 0.990749 |
| 17 | 437.808 | 247.641 | 858.414 | 84,514 | 0.887663 |
| 18 | 337.808 | 347.641 | 1058.41 | 80,514 | 0.985794 |
| 19 | 337.808 | 247.641 | 858.414 | 80,514 | 0.996768 |
| 20 | 437.808 | 347.641 | 858.414 | 84,514 | 0.985794 |
| 21 | 387.808 | 297.641 | 958.412 | 82,514 | 0.99677 |
| 22 | 387.808 | 397.641 | 958.412 | 82,514 | 0.887663 |
| 23 | 337.808 | 347.641 | 858.414 | 84,514 | 0.887663 |
| 24 | 387.808 | 297.641 | 958.412 | 82,514 | 0.773039 |
| 25 | 437.808 | 347.641 | 858.414 | 80,514 | 0.996768 |
| 26 | 387.808 | 297.641 | 1158.41 | 82,514 | 0.985796 |
| 27 | 387.808 | 297.641 | 958.412 | 78,514 | 0.887663 |
| 28 | 337.808 | 347.641 | 858.414 | 80,514 | 0.985789 |
| Samples | The Control Valve Model Parameters | The Hydraulic Cylinder Model Parameters | ||||||
|---|---|---|---|---|---|---|---|---|
| 1 | 314.884 | 118.076 | 318.576 | 0.618 | 3.777 | 2.572 | 942.981 | 83,180.112 |
| 2 | 312.362 | 119.322 | 296.941 | 0.654 | 3.905 | 2.812 | 967.988 | 81,226.530 |
| 3 | 300.806 | 127.713 | 295.735 | 0.697 | 4.006 | 2.782 | 1055.024 | 81,198.484 |
| 4 | 285.634 | 122.729 | 303.182 | 0.612 | 3.670 | 3.333 | 918.705 | 80,644.403 |
| Samples | The Control Valve Model Parameter | The Hydraulic Cylinder Model Parameter | ||||
|---|---|---|---|---|---|---|
| Results of Stream of Variation Model | Results of Simulation Model | Relative Error | Results of Stream of Variation Model | Results of Simulation Model | Relative Error | |
| 1 | 10.55% | 10.39% | 1.54% | 11.67% | 11.43% | 2.10% |
| 2 | 8.32% | 8.56% | 2.72% | 8.89% | 8.69% | 2.40% |
| 3 | 1.77% | 1.84% | 3.68% | 2.47% | 2.55% | 2.97% |
| 4 | 6.06% | 6.29% | 3.73% | 6.95% | 6.76% | 2.86% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Su, D.; Rao, H.; Wang, S.; Pan, Y.; Xu, Y.; Hou, L. Study of Error Flow for Hydraulic System Simulation Models for Construction Machinery Based on the State-Space Approach. Actuators 2024, 13, 14. https://doi.org/10.3390/act13010014
Su D, Rao H, Wang S, Pan Y, Xu Y, Hou L. Study of Error Flow for Hydraulic System Simulation Models for Construction Machinery Based on the State-Space Approach. Actuators. 2024; 13(1):14. https://doi.org/10.3390/act13010014
Chicago/Turabian StyleSu, Deying, Hongyan Rao, Shaojie Wang, Yongjun Pan, Yubing Xu, and Liang Hou. 2024. "Study of Error Flow for Hydraulic System Simulation Models for Construction Machinery Based on the State-Space Approach" Actuators 13, no. 1: 14. https://doi.org/10.3390/act13010014
APA StyleSu, D., Rao, H., Wang, S., Pan, Y., Xu, Y., & Hou, L. (2024). Study of Error Flow for Hydraulic System Simulation Models for Construction Machinery Based on the State-Space Approach. Actuators, 13(1), 14. https://doi.org/10.3390/act13010014







