Adaptive Self-Triggered Control for Multi-Agent Systems with Actuator Failures and Time-Varying State Constraints

Abstract

This work focuses on the consensus problem for multi-agent systems (MASs) with actuator failures and time-varying state constraints, and presents a fixed-time self-triggered consensus control protocol. The use of time-varying asymmetrical barrier Lyapunov functions (BLF) avoids the violation of time-varying state constraints in MASs, ensuring stability and safety. Meanwhile, the system’s performance is further enhanced by leveraging the proposed adaptive neural networks (NNs) control method to mitigate the effects of actuator failures and nonlinear disturbances. Moreover, a self-triggered mechanism based on a fixed-time strategy is proposed to reach rapid convergence and conserve bandwidth resources in MASs. The mechanism achieves consensus within a predefined fixed time, irrespective of the system’s initial states, while conserving communication resources. Finally, the proposed method’s effectiveness is confirmed through two simulation examples, encompassing diverse actuator failure scenarios.

1. Introduction

Consensus control in multi-agent systems (MASs) is currently a prominent issue in the field of control. It refers to the continuous updating of their own states through mutual communication and local collaboration among agents in MASs, so that each agent reaches the same state [1,2,3]. Based on graph theory, MASs can achieve distributed communication by utilizing the state information and connectivity between corresponding agents and their neighbors. Distributed topology structures have advantages such as easy scalability and high fault tolerance, which have attracted extensive research [4,5,6,7,8]. In Ref. [6], a consensus constraint control method for MASs with random disturbances was proposed based on an undirected graph. Ref. [7] investigated a two-layer distributed control strategy for nonlinear MASs with unknown control directions. This strategy only requires relatively weak communication conditions. Ref. [8] proposed a consensus tracking protocol for a class of incommensurate fractional-order MAS with directed switching topologies.

The convergence speed is a key focus for the consensus control of MASs, and the aforementioned references mostly employed finite-time consensus control methods. Specifically, these methods facilitate the attainment of consensus and the fulfillment of the desired control objectives by MASs within a finite time period. Such methods offer notable advantages, including robustness, rapid convergence, and high precision in control [9,10]. However, it is important to note that the convergence time upper bound of finite-time control methods is contingent upon the initial states of the system. In situations where the initial states are unknown or exceedingly large, guaranteeing the convergence time becomes challenging [11]. Meanwhile, in practical applications, MASs may require achieving consensus within a specific time or achieving predictive convergence when the initial states are unknown. In response to these demands, fixed-time consensus control methods have been developed [12]. These methods alleviate the limitation of convergence time being dependent on the system’s initial values in MASs and allow for designing the desired fixed convergence time according to specific needs. At present, fixed-time control methods have been extensively utilized in the control of MASs [1,13,14,15,16]. In Ref. [13] and Ref. [14], fixed-time consensus control methods were developed for leaderless and leader-following MASs, respectively. In Ref. [15], a practical fixed-time consensus control method was introduced, which can reduce the state disagreement at the settling time by fine-tuning the parameters of time base generator. Ref. [16] presented a fixed-time control method for heterogeneous MASs, which was based upon only local information.

It is well known that MASs are evolving towards precise and efficient intelligence. Consequently, there is an imminent need to explore and address various factors that impact system control performance, with actuator failures being one such issue [17]. The effectiveness of control relies heavily on the normal operation of actuators in active control systems. However, in practical operations of industrial systems, actuators may fail due to various reasons [18]. If proper compensation is not employed when actuator failures occur, it may result in a range of consequences from decreased control performance to catastrophic system failures [19]. Consequently, numerous compensatory methods have been suggested to address the issue of actuator failures in MASs [20,21,22]. Ref. [20] developed a fault-tolerant consensus control protocol based on NNs and observer framework to prevent disturbances caused by actuator failures. In Ref. [21], an adaptive output-feedback consensus strategy was developed that took into account both actuator failures and unmatched actuator redundancy. In Ref. [22], the compensations for actuator faults, including gain fault, bias fault and unknown control direction, were achieved by using the Nussbaum function.

Furthermore, constraints that are frequently encountered in practical systems pose a significant influence on system performance. Constraints related concerns arise due to inherent system limitations or other factors, demanding careful consideration during the controller design process. Mishandling constraint issues may potentially result in safety hazards and economic losses [19]. In Ref. [23], the actuator input saturation constraints in the spacecraft formation were considered, and a distributed Lyapunov-based model predictive controller that was resilient against actuation attacks was proposed, eliminating the impact of input saturation constraints on the spacecraft formation control system. However, the design of the controller became more challenging when considering full-state constraints. Presently, research in the field of state constraints control primarily revolves around the incorporation of appropriate barrier Lyapunov functions (BLFs) to prevent the system from violating the corresponding constraint conditions [24,25,26,27]. To list a few, Ref. [24] utilized logarithmic asymmetric BLF (ABLF) to avoid the influence of full-state constraints in nonlinear systems. In Ref. [25], a higher-order tan-type BLF was formulated to address the limitation of traditional BLF in accommodating higher-order systems. In Ref. [26], a novel obstacle function was introduced to accommodate stochastic higher-order nonlinear systems with a non-triangular structure. Ref. [27] proposed a robust adaptive control scheme that can eliminate the restrictive conditions required for BLF-based control methods. It should be noted that the BLFs proposed in the aforementioned references were only applicable to constant constraints and cannot be directly applied to time-varying constraints. In order to achieve generality, this work constructs time-varying ABLFs based on the methodologies presented in Refs. [28,29].

On the other hand, the intermittent and missing data during the data transmission process, caused by the limited processing and storage capacity of individual agents, as well as the limited system network bandwidth, have attracted the attention of scholars. In commonly used time-triggered control, agents activate controllers at given time intervals [30]. Compared to continuous trigger methods, this approach can save communication resources to some extent. However, it still has many unnecessary triggers. In contrast, the event-triggered mechanism (ETM) does not need to adhere to a fixed trigger interval. It is based on a set of trigger conditions, and the controller communication is only updated when the agent meets those trigger conditions [10]. It is evident that, by designing appropriate trigger conditions, the sampling frequency can be effectively reduced, thereby conserving communication resources. Nevertheless, in practical terms, ETM requires a significant amount of detection hardware, increasing hardware costs. In Ref. [31], a sample-based ETM was proposed, which eliminated the need for the continuous detection of trigger conditions by only detecting them at sampling moments. However, detection hardware is still required in practical applications. Conversely, the self-triggered mechanism (STM) relies solely on information from the current time to calculate the next trigger instant [32,33,34]. They do not require continuous monitoring of error values, as in the case of ETM, to determine if the trigger conditions have been met. Specifically, the STM proposed in Ref. [32] only measures the states of itself and all neighboring agents at the triggering moment and calculates the next triggering moment according to the average measured states. The STMs proposed in Refs. [33,34] utilize the rate of change of control signals to calculate the next triggered time. These methods can effectively save communication resources. However, when the temporal derivative of control signals is too drastic, it may lead to system instability.

Guided by the above discussions, this work investigates the issue of consensus control in MASs with actuator failures and time-varying state constraints, and proposes a fixed-time self-triggered control strategy. This work makes contributions to the following aspects when compared to previous literature:

• In contrast to the finite-time control methods ([8,9,10,12,18,19]), a fixed-time STM is implemented, whose convergence time is unaffected by initial states. Additionally, the conservation of bandwidth resources makes the mechanism more practical. In comparison to prior studies ([33,34]), the proposed STM addresses the issues of system instability caused by rapid changes in the control signal.
• Different from the control schemes ([20,21,22]), this paper presents an adaptive NN control approach that effectively addresses both actuator failures and time-varying state constraints within a fixed-time framework. By combining radial basis function NNs with barrier Lyapunov functions, effective compensation can be achieved for actuator failures while ensuring that the system’s states do not violate time-varying constraints.

The outline of this article is as follows. Section 2 presents the system model and lemmas. Section 3 describes the design process and stability proof of the fixed-time self-triggered controller. To validate the effectiveness of the proposed method, Section 4 conducts two sets of simulation experiments and two sets of actuator failure cases. Section 5 provides a summary conclusion of this article.

2. System Modelling and Problem Formulation

2.1. Model Description

Consider a class of MASs as follows:

$$\left\{\begin{array}{c}{\dot{x}}_{i,\overline{g}}=x_{i,\overline{g}+1}+{\overline{n}}_{i,\overline{g}}\left({\overline{x}}_{i,\overline{g}}\right),\overline{g}=1,\dots ,n-1,\hfill \\ {\dot{x}}_{i,n}={\displaystyle \sum _{j=1}^r}{g}_{i,j}{\ell }_{i,j}\left({\overline{x}}_{i,j}\right)u_{i,j}+{\overline{n}}_{i,n}\left({\overline{x}}_{i,n}\right),\hfill \\ y_i=x_{i,1}.\hfill \end{array}\right.$$

(1)

The MASs consist of one virtual leader and l agents. In (1), n and $r(>1)$ represent the number of system’s states and actuators, respectively; $x_{i,g}(g=1,\dots ,n)$ and ${\overline{x}}_{i,g}={[x_{i,1},\dots ,x_{i,g}]}^T$ denote the state vectors of the i-th agent for $i=1,\dots ,l$; $u_{i,j}$ represents the output of the j-th actuator, $y_i$ denotes the agent output, ${\overline{n}}_{i,g}\left({\overline{x}}_{i,g}\right)$ and ${\ell }_{i,j}\left({\overline{x}}_{i,j}\right)$ are respectively unknown and known nonlinear functions, and $g_{i,j}$ represents an unknown constant.

In practical applications, actuators may experience failures. The fault model for the j-th actuator is defined as

$$\left\{\begin{array}{c}{u}_{i,j}={\sigma }_{i,j}{\overline{u}}_{i,j}+{\kappa }_{i,j},\forall t\ge t_j,\hfill \\ {\sigma }_{i,j}{\kappa }_{i,j}=0,\hfill \end{array}\right.$$

(2)

where ${\overline{u}}_{i,j}$ is the input of the j-th actuator, ${\sigma }_{i,j}\in [0,1]$ represents the fault severity, ${\kappa }_{i,j}$ represents the output when the j-th actuator fails completely, and $t_j$ represents the time at which the j-th actuator fails. Based on Equation (2), the operation of actuators can be classified into the following three cases:

Case I: ${\sigma }_{i,j}=1$, indicating normal operation of the j-th actuator, in this case, $u_{i,j}={\overline{u}}_{i,j}$.

Case II: ${\sigma }_{i,j}\in (0,1)$, indicating partial failure of the j-th actuator, in this case, $u_{i,j}={\sigma }_{i,j}{\overline{u}}_{i,j}$.

Case III: ${\sigma }_{i,j}=0$, indicating complete failure of the j-th actuator, in this case, $u_{i,j}={\kappa }_{i,j}$.

To facilitate further analysis, we establish the following definitions for sets $F_a$ and $F_b$. Set $F_a$ represents the collection of completely failed actuators, while set $F_b$ represents the ensemble of actuators that are functioning normally or experiencing partial failures. Based on these established definitions, we can deduce $F_a\cup F_b=\{1,\dots ,r\}$.

Assumption 1 

([21]). During the operation, at most $r-1$ actuators completely fail.

Based on the aforementioned analysis, the MAS (1) can be transformed into the following form:

$$\left\{\begin{array}{c}{\dot{x}}_{i,\overline{g}}=x_{i,\overline{g}+1}+{\overline{n}}_{i,\overline{g}}\left({\overline{x}}_{i,\overline{g}}\right),\overline{g}=1,\dots ,n-1,\hfill \\ {\dot{x}}_{i,n}={\displaystyle \sum _{j=1}^r}{g}_{i,j}{\ell }_{i,j}\left({\overline{x}}_i\right)({\sigma }_{i,j}{\overline{u}}_{i,j}+{\kappa }_{i,j})+{\overline{n}}_{i,n}\left({\overline{x}}_{i,n}\right),\hfill \\ y_i=x_{i,1}.\hfill \end{array}\right.$$

(3)

Furthermore, considering the constraints in practical applications, the system state $x_{i,g}$ needs to remain between the time-varying barrier functions $k_{c_i^g}\left(t\right)$ and ${\overline{k}}_{c_i^g}\left(t\right)$, i.e., $k_{c_i^g}\left(t\right)<x_{i,g}<{\overline{k}}_{c_i^g}\left(t\right)$.

Assumption 2 

([29]). $y_0\left(t\right)$ is known and bounded, i.e., $\left|y_0\left(t\right)\right|\le Y_0({\overline{k}}_{c_i^1}\left(t\right)>Y_0,k_{c_i^1}\left(t\right)<-Y_0)$. Additionally, the $j(j=1,\dots ,n)$-th order derivative of $y_0\left(t\right)$ satisfies $\left|y_0^{\left(j\right)}\left(t\right)\right|\le Y_j$, where $Y_0,Y_1,\dots ,Y_j$ represent positive constants.

Assumption 3 

([11]). There exist constants ${\overline{L}}_{i,g}^j$ and $L_{i,g}^j(j=0,\dots ,n)$ such that ${\overline{k}}_{c_i^g}\le {\overline{L}}_{i,g}^0$, $k_{c_i^g}\ge L_{i,g}^0$, ${\overline{k}}_{c_i^g}^{\left(j\right)}\le {\overline{L}}_{i,g}^j$, and $k_{c_i^g}^{\left(j\right)}\ge L_{i,g}^j$, where ${\overline{k}}_{c_i^g}^{\left(j\right)}$ and $k_{c_i^g}^{\left(j\right)}$ represent the j-th order derivatives of ${\overline{k}}_{c_i^g}$ and $k_{c_i^g}$, respectively.

2.2. Graph Theory

The communication topology structure between the leader and the rest of the agents in an MAS can be described using a directed graph ${\mathcal{G}}_d=\{\mathcal{P},\mathcal{F}\}$, where $\mathcal{P}=\{1,2,\dots ,l\}$ denotes the set of agents in the system, $\mathcal{F}\subseteq \mathcal{P}\times \mathcal{P}$ stands for the set of edges, which are the connections between the agents. $\mathcal{A}=\left[a_{ij}\right]\in {\mathcal{R}}^{l\times l}$ represents the adjacency matrix, when $a_{ij}>0$, we consider that the information from agent j can be transmitted to agent i. When $a_{ij}=0$, agent j’s information cannot be transmitted to agent i. Furthermore, by defining $d_i={\sum }_{j=1}^l{a}_{i,j}(i=1,2,\dots ,l)$, we can obtain the degree matrix $\mathcal{D}=diag(d_1,d_2,\dots ,d_l)$ and Laplacian matrix $\mathcal{L}=\mathcal{D}-\mathcal{A}$ of the system. In addition, define $b_i(\ge 0)$ to represent communication between the leader and agents, when direct communication exists, $b_i>0$; when direct communication does not exist, $b_i=0$.

Assumption 4 

([13]). $b_i(i=1,2,\dots ,l)$ cannot be all zeros, which means that at least one agent is capable of receiving information from the leader.

2.3. Preliminaries

Lemma 1 

([22]). For a system

$$\dot{x}\left(t\right)=f(x,t),x\left(0\right)=x_0,$$

(4)

where $f(·)$ is a continuous smooth nonlinear function, if there exists a positive definite, continuously differentiable Lyapunov function $V\left(x\right)$ such that $V\left(0\right)=0$, and the derivative of $V\left(x\right)$ satisfies

$$\dot{V}\left(x\right)\le -AV{\left(x\right)}^d-BV{\left(x\right)}^p+C,$$

(5)

where $A>0$, $B>0$, $C>0$, $1<d<\infty$ and $0<p<1$, then $V\left(x\right)$ is a set to

$$V\left(x\right)\le min\left\{{\left(\frac{C}{(1-\nu )A}\right)}^{\frac{1}{d}},{\left(\frac{C}{(1-\nu )B}\right)}^{\frac{1}{p}}\right\},$$

(6)

where $0<\nu <1$. Furthermore, the system is considered to be practically fixed-time stable and its convergence time T will not exceed

$$\overline{T}\le \frac{1}{A\nu (d-1)}+\frac{1}{B\nu (1-p)}.$$

(7)

Lemma 2 

([29]). Given arbitrary $\varsigma >0$, $o\in R$ satisfying

$$0\le \left|o\right|-otanh\left(\frac{o}{\varsigma }\right)\le 0.2785\varsigma .$$

(8)

Lemma 3 

([11]). If $0<\Omega <\infty$, $\tau =1,2,\dots ,l$, ${\delta }_1>1$ and $0<{\delta }_2\le 1$, then we have

$${\left({\displaystyle \sum _{\tau =1}^l}{\Omega }_{\iota }\right)}^{{\delta }_1}\le \frac{1}{l^{1-{\delta }_1}}{\displaystyle \sum _{\tau =1}^l}{\Omega }_{\tau }^{{\delta }_1},{\left({\displaystyle \sum _{\tau =1}^l}{\Omega }_{\iota }\right)}^{{\delta }_2}\le {\displaystyle \sum _{\tau =1}^l}{\Omega }_{\tau }^{{\delta }_2}.$$

(9)

Lemma 4 

([28]). For arbitrary $\left|\kappa \right|<1$ and a constant $\epsilon >0$, it can be stated that

$$ln\frac{1}{1-{\kappa }^{2\epsilon }}<\frac{{\kappa }^{2\epsilon }}{1-{\kappa }^{2\epsilon }}.$$

(10)

Lemma 5 

([19]). For any real numbers $h_1$ and $h_2$, we have

$$h_1{h}_2\le \frac{{\beta }_3}{{\beta }_2}{\left|h_1\right|}^{{\beta }_2}+\frac{1}{{\beta }_1{\beta }_3^{{\beta }_1}}{\left|h_2\right|}^{{\beta }_1},$$

(11)

where ${\beta }_1$, ${\beta }_2$ and ${\beta }_3$ are positive parameters, and they satisfy the condition $({\beta }_1-1)({\beta }_2-1)=1$.

Lemma 6 

([6]). Let $Y_0-Y$ denotes the set of tracking errors, where $Y_0=\stackrel{l}{\overbrace{[y_0,y_0,\dots ,y_0]}}$ and $Y=[y_1,y_2,\dots ,y_l]$, then it follows:

$$∥Y_0-Y∥\le \frac{∥Z∥}{{\xi }_{min}},$$

(12)

where $Z=[z_{1,1},z_{2,1},\dots ,z_{l,1}]$ represents the set of synchronization errors, ${\xi }_{min}$ denotes the minimum singular value of the matrix $\mathcal{L}+\mathcal{B}$.

Lemma 7 

([18]). For $\forall f_1\in R$ and $\forall f_2\in R$, the following inequality holds:

$${\left|f_1\right|}^{w_1}{\left|f_1\right|}^{w_2}\le \frac{w_1}{w_1+w_2}{w}_3{\left|f_1\right|}^{w_1+w_2}+\frac{w_2}{w_1+w_2}{w}_3^{-\frac{w_1}{w_2}}{\left|f_2\right|}^{w_1+w_2},$$

(13)

where $w_1>0$, $w_2>0$ and $w_3>0$.

Lemma 8 

([8]). For arbitrary continuous function $\overline{h}\left(G\right)$ with sufficiently large r in a compact set ${\Omega }_G\subset R^r$, there exists an NN approximator ${\vartheta }^{*T}\varpi \left(G\right)$ such that

$$\overline{h}\left(G\right)={\vartheta }^{*T}\varpi \left(G\right)+\epsilon \left(G\right),$$

(14)

where $G={[g_1,g_2,\dots ,g_k]}^T\in R^k\subset R^r$ denotes the input vector, ${\vartheta }^{*}={[{\vartheta }_1,{\vartheta }_2,\dots ,{\vartheta }_l]}^T\in R^r$ represents the ideal NN weight matrix, $\epsilon \left(G\right)$ is the approximation error and satisfies $\epsilon \left(G\right)\le \overline{\epsilon }$. $\varpi \left(G\right)={[{\varpi }_1\left(G\right),{\varpi }_2\left(G\right),\dots ,{\varpi }_r\left(G\right)]}^T$ denotes the radial basis function vector, where Gaussian function ${\omega }_i\left(G\right)(i=1,2,\dots ,r)$ expressed as

$${\varpi }_i\left(G\right)=-exp\left(\frac{{(G-{\eta }_i)}^T(G-{\eta }_i)}{o_i}\right),$$

(15)

where $o_i$ and ${\eta }_i$ refer to the width and center of the Gaussian function, respectively. The ideal weight matrix ${\vartheta }^{*}$ is given as

$${\vartheta }^{*}=arg{\displaystyle \underset{\vartheta \in R^r}{min}}\left\{{\displaystyle \underset{G\in {\Omega }_G}{sup}}\left|\overline{h}\left(G\right)-{\vartheta }^T\varpi \left(G\right)\right|\right\}.$$

(16)

3. Design and Stability Analysis of Fixed-Time Self-Triggered Consensus Controller

3.1. Fixed-Time Self-Triggered Consensus Controller Design

In this section, controllers and adaptive laws will be constructed using the backstepping technique for MASs with actuator faults and time-varying constraints. First, consider the following error systems:

$$\left\{\begin{array}{c}{z}_{i,1}={\displaystyle \sum _{j=1}^l}{a}_{ij}(y_i-y_j)+b_i(y_i-y_0),\hfill \\ z_{i,g}=x_{i,g}-{\phi }_{i,g-1},g=2,\dots ,n,\hfill \end{array}\right.$$

(17)

where $z_{i,1}$ and $z_{i,g}$, respectively, denote the synchronization error and virtual error of the i-th agent, ${\phi }_{i,g-1}$ represents the virtual controller.

Step 1: By considering (3) and (17), it can be deduced that

$${\dot{z}}_{i,1}=-b_i{\dot{y}}_0-{\displaystyle \sum _{k=1}^l}(x_{k,2}+{\overline{n}}_{k,1})+(b_i+d_i){\overline{n}}_{i,1}+(b_i+d_i)(z_{i,2}+{\phi }_{i,1}).$$

(18)

Given the function ${\overline{h}}_{i,1}\left(G_{i,1}\right)=-b_i{\dot{y}}_0-{\displaystyle \sum _{k=1}^l}(x_{k,2}+{\overline{n}}_{k,1})+(b_i+d_i){\overline{n}}_{i,1}$, according to the Lemma 8, the continuous function ${\overline{h}}_{i,1}\left(G_{i,1}\right)$ can be approximated by the following form:

$${\overline{h}}_{i,1}\left(G_{i,1}\right)={\vartheta }_{i,1}^{*T}{\varpi }_{i,1}\left(G_{i,1}\right)+{\epsilon }_{i,1}\left(G_{i,1}\right),$$

(19)

where $G_{i,1}=[x_{i,1},x_{k,1},x_{k,2},{\dot{y}}_0]$, ${\epsilon }_{i,1}\left(G_{i,1}\right)>0$.

Then, Equation (18) can be rewritten as

$${\dot{z}}_{i,1}={\vartheta }_{i,1}^{*T}{\varpi }_{i,1}\left(G_{i,1}\right)+{\epsilon }_{i,1}\left(G_{i,1}\right)+(b_i+d_i)(z_{i,2}+{\phi }_{i,1}).$$

(20)

Formulate the ABLF as follows:

$$V_{i,1}=\frac{(1-s_{i,1}\left(z_{i,1}\right))}{2}ln\frac{k_{a_i^1}^2\left(t\right)}{k_{a_i^1}^2\left(t\right)-z_{i,1}^2}+\frac{s_{i,1}\left(z_{i,1}\right)}{2}ln\frac{k_{b_i^1}^2\left(t\right)}{k_{b_i^1}^2\left(t\right)-z_{i,1}^2}+\frac{1}{2}{\tilde{\vartheta }}_{i,1}^T{W}_{i,1}^{-1}{\tilde{\vartheta }}_{i,1},$$

(21)

where ${\tilde{\vartheta }}_{i,1}={\widehat{\vartheta }}_{i,1}-{\vartheta }_{i,1}^{*}$ represents the error between the ideal weight matrix ${\vartheta }_{i,1}^{*}$ and its estimated value ${\widehat{\vartheta }}_{i,1}$, $W_{i,1}=W_{i,1}^{-1}$ is a positive constant gain matrix, the barrier functions $k_{a_i^1}\left(t\right)$ and $k_{b_i^1}\left(t\right)$ satisfy $k_{a_i^1}\left(t\right)={\xi }_{min}{\overline{k}}_{a_i^1}\left(t\right)$ and $k_{b_i^1}\left(t\right)={\xi }_{min}{\overline{k}}_{b_i^1}\left(t\right)$, where ${\overline{k}}_{a_i^1}\left(t\right)=y_0-k_{c_i^1}\left(t\right)$ and ${\overline{k}}_{b_i^1}\left(t\right)=k_{c_i^1}\left(t\right)-y_0$. ${\xi }_{min}$ represents the minimum singular value of $\mathcal{L}-\mathcal{A}$. The function $s_{i,g}\left(z_{i,g}\right)(g=1,2,\dots ,n)$ is defined as

$$s_{i,g}\left(z_{i,g}\right)=\left\{\begin{array}{c}1,z_{i,g}\ge 0,\hfill \\ 0,z_{i,g}<0.\hfill \end{array}\right.$$

(22)

Remark 1.

From the definition of $s_{i,g}\left(z_{i,g}\right)$, it can be observed that the designed ABLF can handle asymmetric barrier constraints.

For the purpose of simplifying the analysis procedure, the following transformation is performed:

$$\left\{\begin{array}{c}{\zeta }_{a_{i,g}}\left(t\right)=\frac{z_{i,g}}{k_{a_i^g}\left(t\right)},\hfill \\ {\zeta }_{b_{i,g}}\left(t\right)=\frac{z_{i,g}}{k_{b_i^g}\left(t\right)},\hfill \\ {\zeta }_{i,g}\left(t\right)=\frac{(1-s_{i,g}\left(z_{i,g}\right))z_{i,g}}{k_{a_i^g}\left(t\right)}+\frac{s_{i,g}\left(z_{i,g}\right)z_{i,g}}{k_{b_i^g}\left(t\right)}.\hfill \end{array}\right.$$

(23)

By combining (21) and (23), the derivative of $V_{i,1}$ is given by

$$\begin{array}{c}{\dot{V}}_{i,1}=\left(\frac{(1-s_{i,1}\left(z_{i,1}\right)){\zeta }_{a_{i,1}}}{k_{a_i^1}\left(t\right)(1-{\zeta }_{a_{i,1}}^2)}+\frac{s_{i,1}\left(z_{i,1}\right){\zeta }_{b_{i,1}}}{k_{b_i^1}\left(t\right)(1-{\zeta }_{b_{i,1}}^2)}\right){\dot{z}}_{i,1}+{\tilde{\vartheta }}_{i,1}^T{W}_{i,1}^{-1}{\dot{\widehat{\vartheta }}}_{i,1}\\ -\frac{(1-s_{i,1}\left(z_{i,1}\right)){\dot{k}}_{a_i^1}\left(t\right){\zeta }_{a_{i,1}}^2}{k_{a_i^1}\left(t\right)(1-{\zeta }_{a_{i,1}}^2)}-\frac{s_{i,1}\left(z_{i,1}\right){\dot{k}}_{b_i^1}\left(t\right){\zeta }_{b_{i,1}}^2}{k_{b_i^1}\left(t\right)(1-{\zeta }_{b_{i,1}}^2)}.\end{array}$$

(24)

Substituting (18) into (24), we have

$$\begin{array}{cc}\hfill {\dot{V}}_{i,1}=& \left(\frac{(1-s_{i,1}\left(z_{i,1}\right)){\zeta }_{a_{i,1}}}{k_{a_i^1}\left(t\right)(1-{\zeta }_{a_{i,1}}^2)}+\frac{s_{i,1}\left(z_{i,1}\right){\zeta }_{b_{i,1}}}{k_{b_i^1}\left(t\right)(1-{\zeta }_{b_{i,1}}^2)}\right)\hfill \\ \hfill & \times [{\vartheta }_{i,1}^{*T}{\varpi }_{i,1}\left(G_{i,1}\right)+{\epsilon }_{i,1}\left(G_{i,1}\right)+(b_i+d_i)(z_{i,2}+{\phi }_{i,1})]\hfill \\ \hfill & +{\tilde{\vartheta }}_{i,1}^T{W}_{i,1}^{-1}{\dot{\widehat{\vartheta }}}_{i,1}-\frac{(1-s_{i,1}\left(z_{i,1}\right)){\dot{k}}_{a_i^1}\left(t\right){\zeta }_{a_{i,1}}^2}{k_{a_i^1}\left(t\right)(1-{\zeta }_{a_{i,1}}^2)}-\frac{s_{i,1}\left(z_{i,1}\right){\dot{k}}_{b_i^1}\left(t\right){\zeta }_{b_{i,1}}^2}{k_{b_i^1}\left(t\right)(1-{\zeta }_{b_{i,1}}^2)}.\hfill \end{array}$$

(25)

Then, construct the following virtual controller:

$$\begin{array}{c}{\phi }_{i,1}=\frac{1}{(b_i+d_i)}[-c_{i,1,1}{\chi }_{i,1}{z}_{i,1}^3-c_{i,2,1}{\chi }_{i,1}^{p-1}{z}_{i,1}^{2p-1}-\frac{1}{2{\gamma }_{i,1}}{\chi }_{i,1}{z}_{i,1}\\ -\frac{1}{2}{(b_i+d_i)}^2{z}_{i,1}-{\Lambda }_{i,1}\left(t\right)z_{i,1}-{\widehat{\vartheta }}_{i,1}^T{\varpi }_{i,1}\left(G_{i,1}\right)],\end{array}$$

(26)

where $c_{i,1,1}$, $c_{i,2,1}$, and ${\gamma }_{i,1}$ are positive gain constants, and the design parameter p satisfies $p\in (0.5,1)$. The definitions of ${\chi }_{i,g}(g=1,2,\dots ,n)$ and ${\Lambda }_{i,g}\left(t\right)$ are given by Equations (27) and (28), respectively.

$${\chi }_{i,g}=\frac{(1-s_{i,g}\left(z_{i,g}\right))}{k_{a_i^g}^2\left(t\right)-z_{i,g}^2}+\frac{s_{i,g}\left(z_{i,g}\right)}{k_{b_i^g}^2\left(t\right)-z_{i,g}^2},$$

(27)

$${\Lambda }_{i,g}\left(t\right)=\sqrt{{\left(\frac{{\dot{k}}_{a_i^g}\left(t\right)}{k_{a_i^g}\left(t\right)}\right)}^2+{\left(\frac{{\dot{k}}_{b_i^g}\left(t\right)}{k_{b_i^g}\left(t\right)}\right)}^2+{\iota }_g},$$

(28)

where ${\iota }_g$ is a positive constant.

By further deriving from (28), we can obtain

$${\Lambda }_{i,1}\left(t\right)+\frac{(1-s_{i,1}\left(z_{i,1}\right)){\dot{k}}_{a_i^1}\left(t\right){\zeta }_{a_{i,1}}^2}{k_{a_i^1}\left(t\right)(1-{\zeta }_{a_{i,1}}^2)}+\frac{s_{i,1}\left(z_{i,1}\right){\dot{k}}_{b_i^1}\left(t\right){\zeta }_{b_{i,1}}^2}{k_{b_i^1}\left(t\right)(1-{\zeta }_{b_{i,1}}^2)}\ge 0.$$

(29)

The construction of the adaptive law is as follows:

$${\dot{\widehat{\vartheta }}}_{i,1}=W_{i,1}({\chi }_{i,1}{z}_{i,1}\varpi \left(G_{i,1}\right)-{\delta }_{i,1}{\widehat{\vartheta }}_{i,1}),$$

(30)

where ${\delta }_{i,1}>0$ is a constant.

By simultaneously considering (25) to (30), we have

$$\begin{array}{cc}\hfill {\dot{V}}_{i,1}\le & {\chi }_{i,1}{z}_{i,1}[-c_{i,1,1}{\chi }_{i,1}{z}_{i,1}^3-c_{i,2,1}{\chi }_{i,1}^{p-1}{z}_{i,1}^{2p-1}-\frac{1}{2{\gamma }_{i,1}}{\chi }_{i,1}{z}_{i,1}\hfill \\ \hfill & -\frac{1}{2}{(b_i+d_i)}^2{z}_{i,1}+(b_i+d_i)z_{i,2}+{\epsilon }_{i,1}\left(G_{i,1}\right)]-{\delta }_{i,1}{\tilde{\vartheta }}_{i,1}^T{\widehat{\vartheta }}_{i,1}.\hfill \end{array}$$

(31)

Based on the Lemma 5, inequalities (32) and (33) can be derived.

$${\chi }_{i,1}{z}_{i,1}{\epsilon }_{i,1}\left(G_{i,1}\right)\le \frac{1}{2{\gamma }_{i,1}}{\left({\chi }_{i,1}{z}_{i,1}\right)}^2+\frac{1}{2}{\gamma }_{i,1}{\overline{\epsilon }}_{i,1}^2,$$

(32)

$${\chi }_{i,1}(b_i+d_i)z_{i,1}{z}_{i,2}\le {\chi }_{i,1}(\frac{1}{2}{(b_i+d_i)}^2{z}_{i,1}^2+\frac{1}{2}{z}_{i,2}^2),$$

(33)

where ${\overline{\epsilon }}_{i,1}$ represents an upper bound for ${\epsilon }_{i,1}\left(G_{i,1}\right)$.

Obviously, from (32) and (33), we can obtain

$$\begin{array}{cc}\hfill {\dot{V}}_{i,1}\le & -c_{i,1,1}{\chi }_{i,1}^2{z}_{i,1}^4-c_{i,2,1}{\chi }_{i,1}^p{z}_{i,1}^{2p}\hfill \\ & +\frac{1}{2}{\gamma }_{i,1}{\overline{\epsilon }}_{i,1}^2+\frac{1}{2q}{\chi }_{i,1}{z}_{i,2}^2-{\delta }_{i,1}{\tilde{\vartheta }}_{i,1}^T{\widehat{\vartheta }}_{i,1}.\hfill \end{array}$$

(34)

Step $g (2\le g\le n-1)$: By considering (3) and (17), it can be deduced that

$${\dot{z}}_{i,g}={\phi }_{i,g}+z_{i,g+1}+{\overline{n}}_{i,g}-{\dot{\phi }}_{i,g-1},$$

(35)

where ${\dot{\phi }}_{i,g-1}={\displaystyle \sum _{j=0}^{g-1}}\frac{\partial {\phi }_{i,g-1}}{\partial y_0^{\left(j\right)}}{\dot{y}}_0+{\displaystyle \sum _{j=1}^{g-1}}\frac{\partial {\phi }_{i,g-1}}{\partial x_{i,j}}{x}_{i,j}+{\displaystyle \sum _{j=1}^{g-1}}\frac{\partial {\phi }_{i,g-1}}{\partial {\widehat{\vartheta }}_{i,j}}{\dot{\widehat{\vartheta }}}_{i,j}+{\displaystyle \sum _{j=1}^{g-1}}{\displaystyle \sum _{k=1}^l}\frac{\partial {\alpha }_{i,g-1}}{\partial x_{k,j}}{x}_{k,j}$

$+{\displaystyle \sum _{j=0}^{g-1}}\frac{\partial {\phi }_{i,g-1}}{\partial {\varphi }_{i,g-1}^{\left(j\right)}}{\varphi }_{i,g-1}^{(j+1)}$, ${\varphi }_{i,g-1}={[k_{a_i^1},\dots ,k_{a_i^{g-1}},k_{b_i^1},\dots ,k_{b_i^{g-1}}]}^T$.

Defining the function ${\overline{h}}_{i,g}\left(G_{i,g}\right)={\overline{n}}_{i,g}-{\dot{\phi }}_{i,g-1}$, according to Lemma 8, there exists an NN approximator ${\vartheta }_{i,g}^{*T}{\varpi }_{i,g}\left(G_{i,g}\right)$ and a positive parameter ${\epsilon }_{i,g}\left(G_{i,g}\right)$, such that ${\overline{h}}_{i,g}\left(G_{i,g}\right)$ can be expressed as

$${\overline{h}}_{i,g}\left(G_{i,g}\right)={\vartheta }_{i,g}^{*T}{\varpi }_{i,g}\left(G_{i,g}\right)+{\epsilon }_{i,g}\left(G_{i,g}\right),$$

(36)

where $G_{i,g}=[{\overline{x}}_{i,g}^T,{\overline{x}}_{k,g}^T,{\dot{y}}_0]$, ${\epsilon }_{i,g}\left(G_{i,g}\right)>0$.

Therefore, ${\dot{z}}_{i,g}$ can be rewritten as

$${\dot{z}}_{i,g}={\vartheta }_{i,g}^{*T}{\varpi }_{i,g}\left(G_{i,g}\right)+{\epsilon }_{i,g}\left(G_{i,g}\right)+z_{i,g+1}+{\alpha }_{i,g}.$$

(37)

The construction of the ABLF is given as

$$\begin{array}{cc}\hfill V_{i,g}=& V_{i,g-1}+\frac{(1-s_{i,g}\left(z_{i,g}\right))}{2}ln\frac{k_{a_i^g}^2\left(t\right)}{k_{a_i^g}^2\left(t\right)-z_{i,g}^2}\hfill \\ & +\frac{1}{2}{\tilde{\vartheta }}_{i,g}^T{W}_{i,g}^{-1}{\tilde{\vartheta }}_{i,g}+\frac{s_{i,g}\left(z_{i,g}\right)}{2}ln\frac{k_{b_i^g}^2\left(t\right)}{k_{b_i^g}^2\left(t\right)-z_{i,g}^2},\hfill \end{array}$$

(38)

where ${\tilde{\vartheta }}_{i,g}={\widehat{\vartheta }}_{i,g}-{\vartheta }_{i,g}^{*}$ represents the error between the ideal weight matrix ${\vartheta }_{i,g}^{*}$ and its estimated value ${\widehat{\vartheta }}_{i,g}$, $W_{i,g}=W_{i,g}^{-1}$ is a positive constant gain matrix.

Taking the derivative of (38), we obtain:

$$\begin{array}{cc}\hfill {\dot{V}}_{i,g}=& {\dot{V}}_{i,g-1}+\left(\frac{(1-s_{i,g}\left(z_{i,g}\right)){\zeta }_{a_{i,g}}}{k_{a_i^g}\left(t\right)(1-{\zeta }_{a_{i,g}}^2)}+\frac{s_{i,g}\left(z_{i,g}\right){\zeta }_{b_{i,g}}}{k_{b_i^g}\left(t\right)(1-{\zeta }_{b_{i,g}}^2)}\right){\dot{z}}_{i,g}\hfill \\ & +{\tilde{\vartheta }}_{i,g}^T{W}_{i,g}^{-1}{\dot{\widehat{\vartheta }}}_{i,g}-\frac{(1-s_{i,g}\left(z_{i,g}\right)){\dot{k}}_{a_i^g}\left(t\right){\zeta }_{a_{i,g}}^2}{k_{a_i^g}\left(t\right)(1-{\zeta }_{a_{i,g}}^2)}-\frac{s_{i,g}\left(z_{i,g}\right){\dot{k}}_{b_i^g}\left(t\right){\zeta }_{b_{i,g}}^2}{k_{b_i^g}\left(t\right)(1-{\zeta }_{b_{i,g}}^2)}.\hfill \end{array}$$

(39)

Substituting (37) into (39), it yields

$$\begin{array}{cc}\hfill {\dot{V}}_{i,g}=& {\dot{V}}_{i,g-1}+\left(\frac{(1-s_{i,g}\left(z_{i,g}\right)){\zeta }_{a_{i,g}}}{k_{a_i^g}\left(t\right)(1-{\zeta }_{a_{i,g}}^2)}+\frac{s_{i,g}\left(z_{i,g}\right){\zeta }_{b_{i,g}}}{k_{b_i^g}\left(t\right)(1-{\zeta }_{b_{i,g}}^2)}\right)\hfill \\ \hfill & \times [{\vartheta }_{i,g}^{*T}{\varpi }_{i,g}\left(G_{i,g}\right)+{\epsilon }_{i,g}\left(G_{i,g}\right)+z_{i,g+1}+{\phi }_{i,g}]\hfill \\ \hfill & +{\tilde{\vartheta }}_{i,g}^T{W}_{i,g}^{-1}{\dot{\widehat{\vartheta }}}_{i,g}-\frac{(1-s_{i,g}\left(z_{i,g}\right)){\dot{k}}_{a_i^g}\left(t\right){\zeta }_{a_{i,g}}^2}{k_{a_i^g}\left(t\right)(1-{\zeta }_{a_{i,g}}^2)}-\frac{s_{i,g}\left(z_{i,g}\right){\dot{k}}_{b_i^g}\left(t\right){\zeta }_{b_{i,g}}^2}{k_{b_i^g}\left(t\right)(1-{\zeta }_{b_{i,g}}^2)}.\hfill \end{array}$$

(40)

Designing the virtual controller and adaptive law as

$$\begin{array}{cc}\hfill {\phi }_{i,g}=& -c_{i,1,g}{\chi }_{i,g}{z}_{i,g}^3-c_{i,2,g}{\chi }_{i,g}^{p-1}{z}_{i,g}^{2p-1}-\frac{1}{2{\gamma }_{i,g}}{\chi }_{i,g}{z}_{i,g}\hfill \\ \hfill & -\frac{1}{2}{z}_{i,g}-\frac{{\chi }_{i,g-1}{z}_{i,g}}{2{\chi }_{i,g}}-{\Lambda }_{i,g}\left(t\right)z_{i,g}-{\widehat{\vartheta }}_{i,g}^T{\varpi }_{i,g}\left(G_{i,g}\right),\hfill \end{array}$$

(41)

$${\dot{\widehat{\vartheta }}}_{i,g}=W_{i,g}({\chi }_{i,g}{z}_{i,g}\varpi \left(G_{i,g}\right)-{\delta }_{i,g}{\widehat{\vartheta }}_{i,g}),$$

(42)

where $c_{i,1,g}$, $c_{i,2,g}$, ${\gamma }_{i,g}$ and ${\delta }_{i,g}$ are positive design parameters.

According to (41) and (42), we gain

$$\begin{array}{c}{\dot{V}}_{i,g}\le {\dot{V}}_{i,g-1}-c_{i,1,g}{\chi }_{i,g}^2{z}_{i,g}^4-c_{i,2,g}{\chi }_{i,g}^p{z}_{i,g}^{2p}+{\chi }_{i,g}{z}_{i,g}{\epsilon }_{i,g}\left(G_{i,g}\right)+{\chi }_{i,g}{z}_{i,g}{z}_{i,g+1}\\ -\frac{1}{2}{\chi }_{i,g}{z}_{i,g}^2-\frac{1}{2q}{\chi }_{i,g-1}{z}_{i,g}^2-\frac{1}{2{\gamma }_{i,g}}{\chi }_{i,g}^2{z}_{i,g}^2-{\delta }_{i,g}{\tilde{\vartheta }}_{i,g}^T{\widehat{\vartheta }}_{i,g}.\end{array}$$

(43)

Based on the Lemma 5, inequalities (44) and (45) can be derived.

$$\begin{array}{c}{\chi }_{i,g}{z}_{i,g}{\epsilon }_{i,g}\left(G_{i,g}\right)\le \frac{1}{2{\gamma }_{i,g}}{\left({\chi }_{i,g}{z}_{i,g}\right)}^2+\frac{1}{2}{\gamma }_{i,g}{\overline{\epsilon }}_{i,g}^2,\hfill \end{array}$$

(44)

$$\begin{array}{c}{\chi }_{i,g}{z}_{i,g}{z}_{i,g+1}\le {\chi }_{i,g}(\frac{1}{2}{z}_{i,g}^{2q}+\frac{1}{2}{z}_{i,g+1}^2),\hfill \end{array}$$

(45)

where ${\overline{\epsilon }}_{i,g}$ represents an upper bound for ${\epsilon }_{i,g}\left(G_{i,g}\right)$.

Obviously, from the above inequality, we can obtain

$$\begin{array}{c}{\dot{V}}_{i,g}\le {\dot{V}}_{i,g-1}-c_{i,1,g}{\chi }_{i,g}^2{z}_{i,g}^4-c_{i,2,g}{\chi }_{i,g}^p{z}_{i,g}^{2p}+\frac{1}{2}{\gamma }_{i,g}{\overline{\epsilon }}_{i,g}^2\\ -\frac{1}{2q}{\chi }_{i,g-1}{z}_{i,g}^2+\frac{1}{2q}{\chi }_{i,g}{z}_{i,g+1}^2-{\delta }_{i,g}{\tilde{\vartheta }}_{i,g}^T{\widehat{\vartheta }}_{i,g}.\end{array}$$

(46)

Through analysis, it can be deduced in step $g-1$ that:

$$\begin{array}{c}{\dot{V}}_{i,g-1}\le -{\displaystyle \sum _j^{g-1}}{c}_{i,1,j}{\chi }_{i,j}^2{z}_{i,j}^4-{\displaystyle \sum _j^{g-1}}{c}_{i,2,j}{\chi }_{i,j}^p{z}_{i,j}^{2p}\hfill \\ +\frac{1}{2}{\displaystyle \sum _j^{g-1}}{\gamma }_{i,j}{\overline{\epsilon }}_{i,j}^2+\frac{1}{2q}{\chi }_{i,g-1}{z}_{i,g}^2-{\displaystyle \sum _j^{g-1}}{\delta }_{i,j}{\tilde{\vartheta }}_{i,j}^T{\widehat{\vartheta }}_{i,j}.\hfill \end{array}$$

(47)

Hence, ${\dot{V}}_{i,g}$ can be written as

$$\begin{array}{c}{\dot{V}}_{i,g}\le -{\displaystyle \sum _j^g}{c}_{i,1,j}{\chi }_{i,j}^2{z}_{i,j}^4-{\displaystyle \sum _j^g}{c}_{i,2,j}{\chi }_{i,j}^p{z}_{i,j}^{2p}\hfill \\ +\frac{1}{2}{\displaystyle \sum _j^g}{\gamma }_{i,j}{\overline{\epsilon }}_{i,j}^2+\frac{1}{2q}{\chi }_{i,g}{z}_{i,g+1}^2-{\displaystyle \sum _j^g}{\delta }_{i,j}{\tilde{\vartheta }}_{i,j}^T{\widehat{\vartheta }}_{i,j}.\hfill \end{array}$$

(48)

Step n: To conserve system communication resources, an STM is established as shown below:

$$\left\{\begin{array}{c}{\overline{u}}_{i,j}={\omega }_{i,j}\left(t_g\right),\forall t\in [t_g,t_{g+1}),\hfill \\ t_{g+1}=\left\{\begin{array}{c}{t}_g+t^{*},{\dot{w}}_{i,j}\left(t\right)>v_2,\hfill \\ t_g+\frac{\eta \left|{\overline{u}}_{i,j}\right|+{\eta }_1}{max\{v_1,w_{i,j}\left(t\right)\}},{\dot{w}}_{i,j}\left(t\right)\le v_2,\hfill \end{array}\right.\hfill \end{array}\right.$$

(49)

where $w_{i,j}\left(t\right)=\left|{\dot{\omega }}_{i,j}\left(t\right){|}_{t=t_g}\right|$, ${\omega }_{i,j}\left(t\right)$ represents the intermediate control signal for the STM, which will be defined next. $t_g(g\in {\mathcal{N}}_{+})$ represents the triggering moment, $t^{*}$ denotes an arbitrarily small positive number, and ${\eta }_1$, $\eta$, $v_1$, and $v_2$ are positive design parameters.

Remark 2.

From (49), it can be observed that the designed STM calculates the next triggering moment at each trigger instant. The next triggering moment is determined by the values of η, ${\eta }_1$, $v_2$, $t^{*}$, and $max\{v_1,w_{i,j}\left(t\right)\}$. Accordingly, when the intermediate control signal undergoes significant changes, the next triggering moment occur earlier. Additionally, by introducing $v_1$, the system ensures that the signals are updated within a reasonable time frame to avoid prolonged periods without updates. $v_2$ represents the maximum tolerated rate of change for $w_{i,j}\left(t\right)$. Properly selecting the parameters for $v_1$ and $v_2$ guarantees both efficient utilization of communication resources and system stability.

The definition of the intermediate control signal is as provided below:

$$\begin{array}{cc}\hfill {\omega }_{i,j}\left(t\right)=& -(1+\eta )\left({\mu }_{i,j}tanh\left(\frac{z_{i,n}sign\left(g_{i,j}\right){\ell }_{i,j}\left({\overline{x}}_i\right){\mu }_{i,j}}{\varsigma }\right)\right.\hfill \\ \hfill & \left.+{\overline{\eta }}_{1}tanh\left(\frac{z_{i,n}sign\left(g_{i,j}\right){\ell }_{i,j}\left({\overline{x}}_i\right){\overline{\eta }}_1}{\varsigma }\right)\right),\hfill \end{array}$$

(50)

where $\varsigma$ denotes a positive constant and ${\mu }_{i,j}$ represents the control signal of the j-th actuator. Its design is as follows:

$${\mu }_{i,j}=\frac{sign\left(g_{i,j}\right){\theta }_{i,j}^T{\rho }_i}{{\ell }_{i,j}\left({\overline{x}}_i\right)},$$

(51)

where ${\theta }_{i,j}^T={\left[\begin{array}{cccc}\frac{1}{{\displaystyle \sum _{j\in F_b}}\left|g_{i,j}\right|{\sigma }_{i,j}}& {\theta }_{i,j,1}& \cdots & {\theta }_{i,j,r}\end{array}\right]}^T$, ${\rho }_i={\left[\begin{array}{cccc}{\phi }_{i,n}& {\rho }_{i,1}& \cdots & {\rho }_{i,r}\end{array}\right]}^T$, ${\rho }_{i,\overline{j}}={\ell }_{i,j}\left({\overline{x}}_i\right)$, ${\phi }_{i,n}$ denotes the virtual controller. Especially, if $\overline{j}\in F_a,{\theta }_{i,j,\overline{j}}=\frac{-g_{i,j}{\kappa }_{i,j}}{{\displaystyle \sum _{\overline{j}\in F_b}}\left|g_{i,j}\right|{\sigma }_{i,j}}$, else ${\theta }_{i,j,\overline{j}}=0$.

Consequently, it can be inferred that

$${\displaystyle \sum _{j\in F_b}}\left|g_{i,j}\right|{\sigma }_{i,j}{\theta }_{i,j}^T{\rho }_i={\phi }_{i,n}-{\displaystyle \sum _{j\in F_a}}\left|g_{i,j}\right|{\ell }_{i,j}\left({\overline{x}}_i\right){\kappa }_{i,j}.$$

(52)

Since ${\theta }_{i,j}$ cannot be obtained in advance, ${\widehat{\theta }}_{i,j}$ is used to estimate the value of ${\theta }_{i,j}$. The estimation error is represented by ${\tilde{\theta }}_{i,j}={\theta }_{i,j}-{\widehat{\theta }}_{i,j}$. Therefore, the expression for ${\mu }_{i,j}$ should be:

$${\mu }_{i,j}=\frac{sign\left(g_{i,j}\right){\widehat{\theta }}_{i,j}^T{\rho }_i}{{\ell }_{i,j}\left({\overline{x}}_i\right)}.$$

(53)

By considering (3) and (17), it can be deduced that

$${\dot{z}}_{i,n}={\displaystyle \sum _{j=1}^r}{g}_{i,j}{\ell }_{i,j}\left({\overline{x}}_i\right)({\sigma }_{i,j}{\overline{u}}_{i,j}+{\kappa }_{i,j})+{\overline{n}}_{i,n}\left({\overline{x}}_{i,n}\right)-{\dot{\phi }}_{i,n-1},$$

(54)

where ${\dot{\phi }}_{i,n-1}={\displaystyle \sum _{j=0}^{n-1}}\frac{\partial {\phi }_{i,n-1}}{\partial y_0^{\left(j\right)}}{\dot{y}}_0+{\displaystyle \sum _{j=1}^{n-1}}\frac{\partial {\phi }_{i,n-1}}{\partial x_{i,j}}{x}_{i,j}+{\displaystyle \sum _{j=1}^{n-1}}\frac{\partial {\phi }_{i,n-1}}{\partial {\widehat{\vartheta }}_{i,j}}{\dot{\widehat{\vartheta }}}_{i,j}+{\displaystyle \sum _{j=1}^{n-1}}{\displaystyle \sum _{k=1}^l}\frac{\partial {\alpha }_{i,n-1}}{\partial x_{k,j}}{x}_{k,j}+{\displaystyle \sum _{j=0}^{n-1}}\frac{\partial {\phi }_{i,n-1}}{\partial {\varphi }_{i,n-1}^{\left(j\right)}}{\varphi }_{i,n-1}^{(j+1)}.$

Given the function ${\overline{h}}_{i,n}\left(G_{i,n}\right)={\overline{n}}_{i,n}-{\dot{\phi }}_{i,n-1}+0.557\lambda {\displaystyle \sum _{j=1}^r}\left|g_{i,j}\right|{\sigma }_{i,j}$, according to the Lemma 8, the continuous function ${\overline{h}}_{i,n}\left(G_{i,n}\right)$ can be approximated by the following form:

$$\begin{array}{c}{\overline{h}}_{i,n}\left(G_{i,n}\right)={\vartheta }_{i,n}^{*T}{\varpi }_{i,n}\left(G_{i,n}\right)+{\epsilon }_{i,n}\left(G_{i,n}\right),\end{array}$$

(55)

where $G_{i,n}=[{\overline{x}}_{i,n}^T,{\overline{x}}_{k,n}^T,{\dot{y}}_0]$, ${\epsilon }_{i,n}\left(G_{i,n}\right)>0$.

Then, ${\dot{z}}_{i,n}$ can be rewritten as

$${\dot{z}}_{i,n}={\displaystyle \sum _{j=1}^r}{g}_{i,j}{\ell }_{i,j}\left({\overline{x}}_i\right)({\sigma }_{i,j}{\overline{u}}_{i,j}+{\kappa }_{i,j})+{\vartheta }_{i,n}^{*T}{\varpi }_{i,n}\left(G_{i,n}\right)+{\epsilon }_{i,n}\left(G_{i,n}\right)-0.557\varsigma {\displaystyle \sum _{j=1}^r}\left|g_{i,j}\right|{\sigma }_{i,j}.$$

(56)

In this step, the ABLF is chosen as

$$\begin{array}{cc}\hfill V_{i,n}=& V_{i,n-1}+\frac{(1-s_{i,n}\left(z_{i,n}\right))}{2}ln\frac{k_{a_i^n}^2\left(t\right)}{k_{a_i^n}^2\left(t\right)-z_{i,n}^2}+\frac{s_{i,n}\left(z_{i,n}\right)}{2}ln\frac{k_{b_i^n}^2\left(t\right)}{k_{b_i^n}^2\left(t\right)-z_{i,n}^2}\hfill \\ \hfill & +\frac{1}{2}{\tilde{\vartheta }}_{i,n}^T{W}_{i,n}^{-1}{\tilde{\vartheta }}_{i,n}+\frac{1}{2}{\displaystyle \sum _{j\in F_b}}\left|g_{i,j}\right|{\sigma }_{i,j}{\tilde{\theta }}_{i,j}^T{J}_{i,j}^{-1}{\tilde{\theta }}_{i,j},\hfill \end{array}$$

(57)

where ${\tilde{\vartheta }}_{i,n}={\widehat{\vartheta }}_{i,n}-{\vartheta }_{i,n}^{*}$ represents the error between the ideal weight matrix ${\vartheta }_{i,n}^{*}$ and its estimated value ${\widehat{\vartheta }}_{i,n}$, $W_{i,n}=W_{i,n}^{-1}$ and $J_{i,j}=J_{i,j}^{-1}$ represent positive constant gain matrices.

Differentiating Equation (57), we have

$$\begin{array}{cc}\hfill {\dot{V}}_{i,n}=& {\dot{V}}_{i,n-1}+\left(\frac{(1-s_{i,n}\left(z_{i,n}\right)){\zeta }_{a_{i,n}}}{k_{a_i^n}\left(t\right)(1-{\zeta }_{a_{i,n}}^2)}+\frac{s_{i,n}\left(z_{i,n}\right){\zeta }_{b_{i,n}}}{k_{b_i^n}\left(t\right)(1-{\zeta }_{b_{i,n}}^2)}\right){\dot{z}}_{i,n}+{\tilde{\vartheta }}_{i,n}^T{W}_{i,n}^{-1}{\dot{\widehat{\vartheta }}}_{i,n}\hfill \\ \hfill & +{\displaystyle \sum _{j\in F_b}}\left|g_{i,j}\right|{\sigma }_{i,j}{\tilde{\theta }}_{i,j}^T{J}_{i,j}^{-1}{\dot{\widehat{\theta }}}_{i,j}-\frac{(1-s_{i,n}\left(z_{i,n}\right)){\dot{k}}_{a_i^n}\left(t\right){\zeta }_{a_{i,n}}^2}{k_{a_i^n}\left(t\right)(1-{\zeta }_{a_{i,n}}^2)}-\frac{s_{i,n}\left(z_{i,n}\right){\dot{k}}_{b_i^n}\left(t\right){\zeta }_{b_{i,n}}^2}{k_{b_i^n}\left(t\right)(1-{\zeta }_{b_{i,n}}^2)}.\hfill \end{array}$$

(58)

Substituting (56) into (58), we obtain:

$$\begin{array}{cc}\hfill {\dot{V}}_{i,n}=& {\dot{V}}_{i,n-1}+{\tilde{\vartheta }}_{i,n}^T{W}_{i,n}^{-1}{\dot{\widehat{\theta }}}_{i,n}+{\displaystyle \sum _{j\in F_b}}\left|g_{i,j}\right|{\sigma }_{i,j}{\tilde{\theta }}_{i,j}^T{J}_{i,j}^{-1}{\dot{\widehat{\theta }}}_{i,j}+{\chi }_{i,n}{z}_{i,n}\times \hfill \\ \hfill & \left[{\displaystyle \sum _{j=1}^r}{g}_{i,j}{\ell }_{i,j}\left({\overline{x}}_i\right)({\sigma }_{i,j}{\overline{u}}_{i,j}+{\kappa }_{i,j})+{\vartheta }_{i,n}^{*T}{\varpi }_{i,n}\left(G_{i,n}\right)+{\epsilon }_{i,n}\left(G_{i,n}\right)-0.557\varsigma {\displaystyle \sum _{j=1}^r}\left|g_{i,j}\right|{\sigma }_{i,j}\right]\hfill \\ \hfill & -\frac{(1-s_{i,n}\left(z_{i,n}\right)){\dot{k}}_{a_i^n}\left(t\right){\zeta }_{a_{i,n}}^2}{k_{a_i^n}\left(t\right)(1-{\zeta }_{a_{i,n}}^2)}-\frac{s_{i,n}\left(z_{i,n}\right){\dot{k}}_{b_i^n}\left(t\right){\zeta }_{b_{i,n}}^2}{k_{b_i^n}\left(t\right)(1-{\zeta }_{b_{i,n}}^2)}.\hfill \end{array}$$

(59)

According to (49), we have ${\overline{u}}_{i,j}\left(t\right)=\frac{{\omega }_{i,j}\left(t\right)-o_1{\eta }_1}{1+o_2\eta }$, where $\left|o_1\right|<1$ and $\left|o_2\right|<1$. Further derivation leads to:

$$\begin{array}{cc}\hfill z_{i,n}sign\left(g_{i,j}\right){\ell }_{i,j}\left({\overline{x}}_i\right){\overline{u}}_{i,j}=& -z_{i,n}sign\left(g_{i,j}\right){\ell }_{i,j}\left({\overline{x}}_i\right)\hfill \\ \hfill & \times \left(\frac{1+\eta }{1+o_{i,2}\eta }\left({\mu }_{i,j}tanh\left(\frac{z_{i,n}sign\left(g_{i,j}\right){\ell }_{i,j}\left({\overline{x}}_i\right){\mu }_{i,j}}{\varsigma }\right)\right.\right.\hfill \\ \hfill & \left.\left.+{\overline{\eta }}_{1}tanh\left(\frac{z_{i,n}sign\left(g_{i,j}\right){\ell }_{i,j}\left({\overline{x}}_i\right){\overline{\eta }}_1}{\varsigma }\right)\right)+\frac{o_{i,1}{\eta }_1}{1+o_{i,2}\eta }\right).\hfill \end{array}$$

(60)

According to (60) and Lemma 2, it can be given as follows:

$$\begin{array}{cc}\hfill z_{i,n}sign\left(g_{i,j}\right){\ell }_{i,j}\left({\overline{x}}_i\right){\overline{u}}_{i,j}\le & -z_{i,n}sign\left(g_{i,j}\right){\ell }_{i,j}\left({\overline{x}}_i\right){\mu }_{i,j}tanh\left(\frac{z_{i,n}sign\left(g_{i,j}\right){\ell }_{i,j}\left({\overline{x}}_i\right){\mu }_{i,j}}{\varsigma }\right)\hfill \\ \hfill & -z_{i,n}sign\left(g_{i,j}\right){\ell }_{i,j}\left({\overline{x}}_i\right){\overline{\eta }}_{1}tanh\left(\frac{z_{i,n}sign\left(g_{i,j}\right){\ell }_{i,j}\left({\overline{x}}_i\right){\overline{\eta }}_1}{\varsigma }\right)\hfill \\ \hfill & +\left|z_{i,n}sign\left(g_{i,j}\right){\ell }_{i,j}\left({\overline{x}}_i\right)\frac{{\eta }_1}{1-\eta }\right|\hfill \\ \hfill \le & \left|z_{i,n}sign\left(g_{i,j}\right){\ell }_{i,j}\left({\overline{x}}_i\right){\mu }_{i,j}\right|\hfill \\ \hfill & -z_{i,n}sign\left(g_{i,j}\right){\ell }_{i,j}\left({\overline{x}}_i\right){\mu }_{i,j}tanh\left(\frac{z_{i,n}sign\left(g_{i,j}\right){\ell }_{i,j}\left({\overline{x}}_i\right){\mu }_{i,j}}{\varsigma }\right)\hfill \\ \hfill & -\left|z_{i,n}sign\left(g_{i,j}\right){\ell }_{i,j}\left({\overline{x}}_i\right){\mu }_{i,j}\right|+\left|z_{i,n}sign\left(g_{i,j}\right){\ell }_{i,j}\left({\overline{x}}_i\right)\frac{{\eta }_1}{1-\eta }\right|\hfill \\ \hfill & -z_{i,n}sign\left(g_{i,j}\right){\ell }_{i,j}\left({\overline{x}}_i\right){\overline{\eta }}_{1}tanh\left(\frac{z_{i,n}sign\left(g_{i,j}\right){\ell }_{i,j}\left({\overline{x}}_i\right){\overline{\eta }}_1}{\varsigma }\right)\hfill \\ \hfill \le & z_{i,n}sign\left(g_{i,j}\right){\ell }_{i,j}\left({\overline{x}}_i\right){\mu }_{i,j}+0.557\varsigma .\hfill \end{array}$$

(61)

Along with (53), (59) and (61), one gets

$$\begin{array}{cc}\hfill {\dot{V}}_{i,n}\le & {\dot{V}}_{i,n-1}+\left[{\displaystyle \sum _{j=1}^r}\left|g_{i,j}\right|{\sigma }_{i,j}{\widehat{\theta }}_{i,j}^T{\rho }_i+{\displaystyle \sum _{j=1}^r}\left|g_{i,j}\right|{\ell }_{i,j}\left({\overline{x}}_i\right){\kappa }_{i,j}+{\vartheta }_{i,n}^{*T}{\varpi }_{i,n}\left(G_{i,n}\right)+{\epsilon }_{i,n}\left(G_{i,n}\right)\right]\hfill \\ \hfill & \times z_{i,n}{\chi }_{i,n}+{\tilde{\vartheta }}_{i,n}^T{W}_{i,n}^{-1}{\dot{\widehat{\vartheta }}}_{i,n}+{\displaystyle \sum _{j\in F_b}}\left|g_{i,j}\right|{\sigma }_{i,j}{\tilde{\theta }}_{i,j}^T{J}_{i,j}^{-1}{\dot{\widehat{\theta }}}_{i,j}\hfill \\ \hfill & -\frac{(1-s_{i,n}\left(z_{i,n}\right)){\dot{k}}_{a_i^n}\left(t\right){\zeta }_{a_{i,n}}^2}{k_{a_i^n}\left(t\right)(1-{\zeta }_{a_{i,n}}^2)}-\frac{s_{i,n}\left(z_{i,n}\right){\dot{k}}_{b_i^n}\left(t\right){\zeta }_{b_{i,n}}^2}{k_{b_i^n}\left(t\right)(1-{\zeta }_{b_{i,n}}^2)}.\hfill \end{array}$$

(62)

According to ${\tilde{\theta }}_{i,j}={\theta }_{i,j}-{\widehat{\theta }}_{i,j}$ and (52), which yields

$$\begin{array}{cc}\hfill {\dot{V}}_{i,n}\le & {\dot{V}}_{i,n-1}+{\chi }_{i,n}{z}_{i,n}\left[{\phi }_{i,n}+{\displaystyle \sum _{j=1}^r}\left|g_{i,j}\right|{\sigma }_{i,j}{\tilde{\theta }}_{i,j}^T{\rho }_i+{\vartheta }_{i,n}^{*T}{\varpi }_{i,n}\left(G_{i,n}\right)\right]\hfill \\ \hfill & +{\chi }_{i,n}{z}_{i,n}{\epsilon }_{i,n}\left(G_{i,n}\right)+{\tilde{\vartheta }}_{i,n}^T{W}_{i,n}^{-1}{\dot{\widehat{\vartheta }}}_{i,n}+{\displaystyle \sum _{j\in F_b}}\left|g_{i,j}\right|{\sigma }_{i,j}{\tilde{\theta }}_{i,j}^T{J}_{i,j}^{-1}{\dot{\widehat{\theta }}}_{i,j}\hfill \\ \hfill & -\frac{(1-s_{i,n}\left(z_{i,n}\right)){\dot{k}}_{a_i^n}\left(t\right){\zeta }_{a_{i,n}}^2}{k_{a_i^n}\left(t\right)(1-{\zeta }_{a_{i,n}}^2)}-\frac{s_{i,n}\left(z_{i,n}\right){\dot{k}}_{b_i^n}\left(t\right){\zeta }_{b_{i,n}}^2}{k_{b_i^n}\left(t\right)(1-{\zeta }_{b_{i,n}}^2)}.\hfill \end{array}$$

(63)

Designing the virtual controller and adaptive laws as

$$\begin{array}{c}{\phi }_{i,n}=-c_{i,1,n}{\chi }_{i,n}{z}_{i,n}^3-c_{i,2,n}{\chi }_{i,n}^{p-1}{z}_{i,n}^{2p-1}-{\Lambda }_{i,n}\left(t\right)z_{i,n}\\ -\frac{1}{2{\gamma }_{i,n}}{\chi }_{i,n}{z}_{i,n}-\frac{{\chi }_{i,n-1}{z}_{i,n}}{2{\chi }_{i,n}}-{\widehat{\vartheta }}_{i,n}^T{\varpi }_{i,n}\left(G_{i,n}\right),\end{array}$$

(64)

$${\dot{\widehat{\vartheta }}}_{i,n}=W_{i,n}({\chi }_{i,n}{z}_{i,n}\varpi \left(G_{i,n}\right)-{\delta }_{i,n}{\widehat{\vartheta }}_{i,n}),$$

(65)

$${\dot{\widehat{\theta }}}_{i,j}=J_{i,j}(-{\chi }_{i,n}{z}_{i,n}{\rho }_i-{\upsilon }_{i,j}{\widehat{\theta }}_{i,j}),$$

(66)

where $c_{i,1,n}$, $c_{i,2,n}$, ${\gamma }_{i,n}$, ${\delta }_{i,n}$ and ${\upsilon }_{i,j}$ are positive design parameters.

Substituting (64)–(66) into (63), we obtain

$$\begin{array}{cc}\hfill {\dot{V}}_{i,n}\le & {\dot{V}}_{i,n-1}-c_{i,1,n}{\chi }_{i,n}{z}_{i,n}^3-c_{i,2,n}{\chi }_{i,n}^p{z}_{i,n}^{2p}-\frac{1}{2{\gamma }_{i,n}}{\left({\chi }_{i,n}{z}_{i,n}\right)}^2\hfill \\ & +{\chi }_{i,n}{z}_{i,n}{\epsilon }_{i,n}\left(G_{i,n}\right)-\frac{1}{2q}{\chi }_{i,n-1}{z}_{i,n}^2-{\delta }_{i,n}{\tilde{\vartheta }}_{i,n}^T{\widehat{\vartheta }}_{i,n}-{\displaystyle \sum _{j\in F_b}}\left|g_{i,j}\right|{\sigma }_{i,j}{\upsilon }_{i,j}{\tilde{\theta }}_{i,j}^T{\widehat{\theta }}_{i,j}.\hfill \end{array}$$

(67)

Applying the Lemma 5, one has

$${\chi }_{i,n}{z}_{i,n}{\epsilon }_{i,n}\left(G_{i,n}\right)\le \frac{1}{2{\gamma }_{i,n}}{\left({\chi }_{i,n}{z}_{i,n}\right)}^2+\frac{1}{2}{\gamma }_{i,n}{\overline{\epsilon }}_{i,n}^2,$$

(68)

where ${\overline{\epsilon }}_{i,n}$ represents an upper bound for ${\epsilon }_{i,n}\left(G_{i,n}\right)$.

Now, by inserting (68) into (67), one has

$$\begin{array}{cc}\hfill {\dot{V}}_{i,n}\le & {\dot{V}}_{i,n-1}-c_{i,1,n}{\chi }_{i,n}^2{z}_{i,n}^4-c_{i,2,n}{\chi }_{i,n}^p{z}_{i,n}^{2p}+\frac{1}{2}{\gamma }_{i,n}{\overline{\epsilon }}_{i,n}^2\hfill \\ & -\frac{1}{2}{\chi }_{i,n-1}{z}_{i,n}^2-{\delta }_{i,n}{\tilde{\vartheta }}_{i,n}^T{\widehat{\vartheta }}_{i,n}-{\displaystyle \sum _{j\in F_b}}\left|g_{i,j}\right|{\sigma }_{i,j}{\upsilon }_{i,j}{\tilde{\theta }}_{i,j}^T{\widehat{\theta }}_{i,j}.\hfill \end{array}$$

(69)

The following inequalities can be deduced in step $n-1$

$$\begin{array}{cc}\hfill {\dot{V}}_{i,n-1}\le & -{\displaystyle \sum _j^{n-1}}{c}_{i,1,j}{\chi }_{i,j}^2{z}_{i,j}^4-{\displaystyle \sum _j^{n-1}}{c}_{i,2,j}{\chi }_{i,j}^p{z}_{i,j}^{2p}\hfill \\ \hfill & +\frac{1}{2}{\displaystyle \sum _j^{n-1}}{\gamma }_{i,j}{\overline{\epsilon }}_{i,j}^2+\frac{1}{2}{\chi }_{i,n-1}{z}_{i,n}^2-{\displaystyle \sum _j^{n-1}}{\delta }_{i,j}{\tilde{\vartheta }}_{i,j}^T{\widehat{\vartheta }}_{i,j}.\hfill \end{array}$$

(70)

Substituting (70) into (69) leads to

$$\begin{array}{cc}\hfill {\dot{V}}_{i,n}\le & -{\displaystyle \sum _j^n}{c}_{i,1,j}{\chi }_{i,j}^2{z}_{i,j}^4-{\displaystyle \sum _j^n}{c}_{i,2,j}{\chi }_{i,j}^p{z}_{i,j}^{2p}\hfill \\ \hfill & +\frac{1}{2}{\displaystyle \sum _j^n}{\gamma }_{i,j}{\overline{\epsilon }}_{i,j}^2-{\displaystyle \sum _j^n}{\delta }_{i,j}{\tilde{\vartheta }}_{i,j}^T{\widehat{\vartheta }}_{i,j}-{\displaystyle \sum _{j\in F_b}}\left|g_{i,j}\right|{\sigma }_{i,j}{\upsilon }_{i,j}{\tilde{\theta }}_{i,j}^T{\widehat{\theta }}_{i,j}.\hfill \end{array}$$

(71)

Applying Lemma 3, it follows that

$$-{\displaystyle \sum _j^n}{c}_{i,1,j}{\left({\chi }_{i,j}{z}_{i,j}^2\right)}^2\le -{\displaystyle \sum _j^n}{c}_{i,1,j}{\left(s_{i,j}\left(z_{i,j}\right)ln\frac{k_{b_i^j}^2}{k_{b_i^j}^2-z_{i,j}^2}+(1-s_{i,j}\left(z_{i,j}\right))ln\frac{k_{a_i^j}^2}{k_{a_i^j}^2-z_{i,j}^2}\right)}^2,$$

(72)

$$-{\displaystyle \sum _j^n}{c}_{i,1,j}{\left({\chi }_{i,j}{z}_{i,j}^2\right)}^p\le -{\displaystyle \sum _j^n}{c}_{i,2,j}{\left(s_{i,j}\left(z_{i,j}\right)ln\frac{k_{b_i^j}^2}{k_{b_i^j}^2-z_{i,j}^2}+(1-s_{i,j}\left(z_{i,j}\right))ln\frac{k_{a_i^j}^2}{k_{a_i^j}^2-z_{i,j}^2}\right)}^p.$$

(73)

According to Lemma 7, two inequalities can be obtained as

$$\begin{array}{cc}\hfill -{\displaystyle \sum _j^n}{\delta }_{i,j}{\tilde{\vartheta }}_{i,j}^T{\widehat{\vartheta }}_{i,j}-{\displaystyle \sum _{j\in F_b}}\left|g_{i,j}\right|{\sigma }_{i,j}{\upsilon }_{i,j}{\tilde{\theta }}_{i,j}^T{\widehat{\theta }}_{i,j}\le & -{\displaystyle \sum _j^n}{\delta }_{i,j}{\tilde{\vartheta }}_{i,j}^T({\tilde{\vartheta }}_{i,j}+{\vartheta }_{i,j}^{*})-{\displaystyle \sum _{j\in F_b}}\left|g_{i,j}\right|{\sigma }_{i,j}{\upsilon }_{i,j}{\tilde{\theta }}_{i,j}^T({\tilde{\theta }}_{i,j}+{\theta }_{i,j}^{*})\hfill \\ \hfill \le & -{\displaystyle \sum _j^n}\frac{1}{2}{\delta }_{i,j}{∥{\tilde{\vartheta }}_{i,j}∥}^2-\frac{1}{2}{\displaystyle \sum _{j\in F_b}}\left|g_{i,j}\right|{\sigma }_{i,j}{\upsilon }_{i,j}{∥{\tilde{\theta }}_{i,j}∥}^2\hfill \\ \hfill & +{\displaystyle \sum _j^n}\frac{1}{2}{\delta }_{i,j}{∥{\vartheta }_{i,j}^{*}∥}^2+\frac{1}{2}{\displaystyle \sum _{j\in F_b}}\left|g_{i,j}\right|{\sigma }_{i,j}{\upsilon }_{i,j}{∥{\theta }_{i,j}^{*}∥}^2.\hfill \end{array}$$

(74)

Along with (71)–(74), one gets

$$\begin{array}{cc}\hfill {\dot{V}}_{i,n}\le & -{\displaystyle \sum _j^n}{c}_{i,1,j}{\left(s_{i,j}\left(z_{i,j}\right)ln\frac{k_{b_i^j}^2}{k_{b_i^j}^2-z_{i,j}^2}+(1-s_{i,j}\left(z_{i,j}\right))ln\frac{k_{a_i^j}^2}{k_{a_i^j}^2-z_{i,j}^2}\right)}^2\hfill \\ \hfill & -{\displaystyle \sum _j^n}{c}_{i,2,j}{\left(s_{i,j}\left(z_{i,j}\right)ln\frac{k_{b_i^j}^2}{k_{b_i^j}^2-z_{i,j}^2}+(1-s_{i,j}\left(z_{i,j}\right))ln\frac{k_{a_i^j}^2}{k_{a_i^j}^2-z_{i,j}^2}\right)}^p\hfill \\ \hfill & +\frac{1}{2}{\displaystyle \sum _j^n}{\gamma }_{i,j}{\overline{\epsilon }}_{i,j}^2-{\displaystyle \sum _j^n}\frac{1}{2}{\delta }_{i,j}{∥{\tilde{\vartheta }}_{i,j}∥}^2+{\displaystyle \sum _j^n}\frac{1}{2}{\delta }_{i,j}{∥{\vartheta }_{i,j}^{*}∥}^2\hfill \\ & -\frac{1}{2}{\displaystyle \sum _{j\in F_b}}\left|g_{i,j}\right|{\sigma }_{i,j}{\upsilon }_{i,j}{∥{\tilde{\theta }}_{i,j}∥}^2+\frac{1}{2}{\displaystyle \sum _{j\in F_b}}\left|g_{i,j}\right|{\sigma }_{i,j}{\upsilon }_{i,j}{∥{\theta }_{i,j}^{*}∥}^2.\hfill \end{array}$$

(75)

By applying Lemma 7, one can obtain

$${\left({\displaystyle \sum _j^n}\frac{{∥{\tilde{\vartheta }}_{i,j}∥}^2}{2}\right)}^p\le (1-p)p^{\frac{p}{1-p}}+{\displaystyle \sum _j^n}\frac{{∥{\tilde{\vartheta }}_{i,j}∥}^2}{2},$$

(76)

$${\left({\displaystyle \sum _{j\in F_b}}\frac{\left|g_{i,j}\right|{\sigma }_{i,j}{∥{\tilde{\theta }}_{i,j}∥}^2}{2}\right)}^p\le (1-p)p^{\frac{p}{1-p}}+{\displaystyle \sum _{j\in F_b}}\frac{\left|g_{i,j}\right|{\sigma }_{i,j}{∥{\tilde{\theta }}_{i,j}∥}^2}{2}.$$

(77)

According to (76), (77) and Lemma 3, (75) can be rewritten as

$$\begin{array}{cc}\hfill {\dot{V}}_{i,n}\le & -{\alpha }_{i,1}{\left({\displaystyle \sum _j^n}{s}_{i,j}\left(z_{i,j}\right)ln\frac{k_{b_i^j}^2}{k_{b_i^j}^2-z_{i,j}^2}+{\displaystyle \sum _j^n}(1-s_{i,j}\left(z_{i,j}\right))ln\frac{k_{a_i^j}^2}{k_{a_i^j}^2-z_{i,j}^2}\right)}^2\hfill \\ \hfill & -{\beta }_{i,1}{\left({\displaystyle \sum _j^n}{s}_{i,j}\left(z_{i,j}\right)ln\frac{k_{b_i^j}^2}{k_{b_i^j}^2-z_{i,j}^2}+{\displaystyle \sum _j^n}(1-s_{i,j}\left(z_{i,j}\right))ln\frac{k_{a_i^j}^2}{k_{a_i^j}^2-z_{i,j}^2}\right)}^p\hfill \\ \hfill & -{\alpha }_{i,2}{\left({\displaystyle \sum _j^n}\frac{{∥{\tilde{\vartheta }}_{i,j}∥}^2}{2}\right)}^2+{\alpha }_{i,2}{\left({\displaystyle \sum _j^n}\frac{{∥{\tilde{\vartheta }}_{i,j}∥}^2}{2}\right)}^2-{\beta }_{i,2}{\left({\displaystyle \sum _j^n}\frac{{∥{\tilde{\vartheta }}_{i,j}∥}^2}{2}\right)}^p\hfill \\ \hfill & -{\alpha }_{i,3}{\left({\displaystyle \sum _{j\in F_b}}\frac{\left|g_{i,j}\right|{\sigma }_{i,j}{∥{\tilde{\theta }}_{i,j}∥}^2}{2}\right)}^2+{\alpha }_{i,3}{\left({\displaystyle \sum _{j\in F_b}}\frac{\left|g_{i,j}\right|{\sigma }_{i,j}{∥{\tilde{\theta }}_{i,j}∥}^2}{2}\right)}^2\hfill \\ \hfill & -{\beta }_{i,2}{\left({\displaystyle \sum _{j\in F_b}}\frac{\left|g_{i,j}\right|{\sigma }_{i,j}{∥{\tilde{\theta }}_{i,j}∥}^2}{2}\right)}^p+\frac{1}{2}{\displaystyle \sum _j^n}{\gamma }_{i,j}{\overline{\epsilon }}_{i,j}^2+2{\beta }_{i,2}(1-p)p^{\frac{p}{1-p}}\hfill \\ \hfill & +{\displaystyle \sum _j^n}\frac{1}{2}{\delta }_{i,j}{∥{\vartheta }_{i,j}^{*}∥}^2+\frac{1}{2}{\displaystyle \sum _{j\in F_b}}\left|g_{i,j}\right|{\sigma }_{i,j}{\upsilon }_{i,j}{∥{\theta }_{i,j}^{*}∥}^2,\hfill \end{array}$$

(78)

where ${\alpha }_{i,1}=\frac{min\{c_{i,1,1},\dots ,c_{i,1,n}\}}{n}$, ${\alpha }_{i,2}=\frac{min\{{\delta }_{i,1}{\lambda }_{min}\left(W_{i,1}\right),{\delta }_{i,1}{\lambda }_{min}\left(W_{i,1}\right),\cdots ,{\delta }_{i,n}{\lambda }_{min}\left(W_{i,n}\right)\}}{n}$,

${\alpha }_{i,3}=\frac{min\{{\upsilon }_{i,1}{\lambda }_{min}\left(J_{i,1}\right),{\upsilon }_{i,2}{\lambda }_{min}\left(J_{i,2}\right)\cdots ,{\upsilon }_{i,j}{\lambda }_{min}\left(J_{i,j}\right)\}}{j}$, ${\beta }_{i,1}=min\{c_{i,2,1},\dots ,c_{i,2,n}\}$,

${\beta }_{i,2}=min\{{\delta }_{i,1}{\lambda }_{min}\left(W_{i,1}\right),{\delta }_{i,1}{\lambda }_{min}\left(W_{i,1}\right),\cdots ,{\delta }_{i,n}{\lambda }_{min}\left(W_{i,n}\right),{\upsilon }_{i,j}{\lambda }_{min}\left(J_{i,j}\right)\}$.

Then, based on (57), (78) and Lemma 3, it holds that

$${\dot{V}}_{i,n}\le -A_i{V}_{i,n}^2-B_i{V}_{i,n}^p+C_i.$$

(79)

where $A_i=\frac{min\{{\alpha }_{i,1},{\alpha }_{i,2},{\alpha }_{i,3}\}}{2}$, $B_i=min\{{\beta }_{i,1},{\beta }_{i,2}\}$, $C_i={\alpha }_{i,2}{\left({\displaystyle \sum _j^n}\frac{{∥{\tilde{\vartheta }}_{i,j}∥}^2}{2}\right)}^2+2{\beta }_{i,2}(1-p)p^{\frac{p}{1-p}}+{\alpha }_{i,3}{\left({\displaystyle \sum _{j\in F_b}}\frac{\left|g_{i,j}\right|{\sigma }_{i,j}{∥{\tilde{\theta }}_{i,j}∥}^2}{2}\right)}^2+\frac{1}{2}{\displaystyle \sum _j^n}{\gamma }_{i,j}{\overline{\epsilon }}_{i,j}^2+{\displaystyle \sum _j^n}\frac{1}{2}{\delta }_{i,j}{∥{\vartheta }_{i,j}^{*}∥}^2+\frac{1}{2}{\displaystyle \sum _{j\in F_b}}\left|g_{i,j}\right|{\sigma }_{i,j}{\upsilon }_{i,j}{∥{\theta }_{i,j}^{*}∥}^2$.

Remark 3.

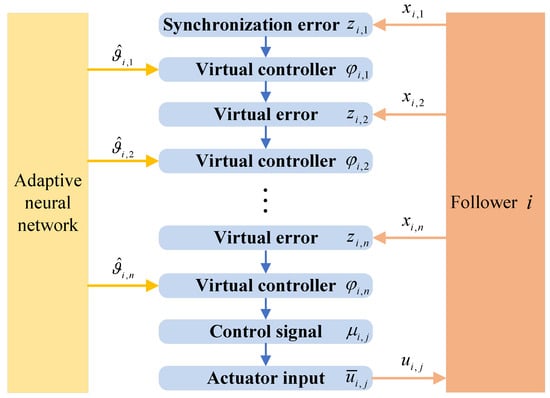
This paper proposes an adaptive NN control method based on radial basis function neural networks to deal with uncertain nonlinearities among agents. The structure of the adaptive NN control method used in this paper is shown in Figure 1, and it only requires online updating of the neural network weights. Then, in combination with adaptive control, the ideal weight ${\vartheta }_{i,g}^{*}(g=1,\dots ,n)$ is estimated using ${\widehat{\vartheta }}_{i,g}$. Following that, the adaptive backstepping technology is employed to construct the virtual controller ${\dot{\phi }}_{i,g}$ and the adaptive law ${\dot{\widehat{\vartheta }}}_{i,g}$, which ensures the stability of the system.

Figure 1. Schematic diagram of the adaptive NN control method.

3.2. System Stability Analysis

Theorem 1.

Under the Assumptions 1–4, the proposed method using virtual controllers (26), (41), (64), adaptive laws (30), (42), (65), (66), STM (49), control signal (51), and intermediate control signal (50) can guarantee the following characteristics for MASs (3) with actuator faults and time-varying state constraints:

• The system states will not violate the specified constraints and all system signals are bounded.
• Zeno-behavior will not occur.

Proof. 

1. Construct the Lyapunov function V for the system as follows:

$$V={\displaystyle \sum _{i=1}^l}{V}_{i,n}.$$

(80)

According to (80) and the Lemma 3, it yields

$$\begin{array}{c}\dot{V}\le -{\displaystyle \sum _{i=1}^l}{A}_i{V}_{i,n}^2-{\displaystyle \sum _{i=1}^l}{B}_i{V}_{i,n}^p+{\displaystyle \sum _{i=1}^l}{C}_i\hfill \\ \le -A{\left({\displaystyle \sum _{i=1}^l}{V}_{i,n}\right)}^2-B{\left({\displaystyle \sum _{i=1}^l}{V}_{i,n}\right)}^p+C\hfill \\ \le -A{V}^2-B{V}^p+C,\hfill \end{array}$$

(81)

where $A=\frac{\{A_1,\dots ,A_l\}}{l}$, $B=min\{B_1,\dots ,B_l\}$, $C={\displaystyle \sum _{i=1}^l}{C}_i$.

According to Lemma 1, it can be concluded that the convergence time T of the MASs (3) is practical fixed-time, and it satisfies

$$T\le \frac{1}{A\nu }+\frac{1}{B\nu (1-p)},$$

(82)

where $0<\nu <1$, furthermore, the solution of the MASs (3), is to a set of

$$\Theta \in min\left\{V(\Theta )\le {\left(\frac{C}{(1-\nu )A}\right)}^{\frac{1}{2}},{\left(\frac{C}{(1-\nu )B}\right)}^{\frac{1}{p}}\right\}.$$

(83)

Remark 4.

According to (82), it can be seen that the convergence time T of the MASs (3) is independent of the initial states and only depends on the system parameters. Therefore, the MAS is practically fixed-time stable.

Due to each term in V being positive, it can be deduced that

$$\frac{1}{2}ln\frac{1}{1-{\zeta }_{i,g}^2}\le V\le \Theta .$$

(84)

By further inference, we can derive the following inequalities:

$$\left\{\begin{array}{c}{z}_{i,g}\ge {\Delta }_{i,g},\hfill \\ z_{i,g}\le {\overline{\Delta }}_{i,g},\hfill \end{array}\right.$$

(85)

where ${\Delta }_{i,g}=-k_{a_i^g}\left(t\right){\left(1-\frac{1}{e^{2\Theta }}\right)}^{\frac{1}{2}}$, ${\overline{\Delta }}_{i,g}=k_{b_i^g}\left(t\right){\left(1-\frac{1}{e^{2\Theta }}\right)}^{\frac{1}{2}}$.

Then, according to the Lemma 6, we can deduce

$$\left\{\begin{array}{c}∥y-Y_0∥\ge \frac{{\Delta }_{i,1}}{{\xi }_{min}}\ge \frac{-k_{a_i^1}\left(t\right)}{{\xi }_{min}},\hfill \\ ∥y-Y_0∥\le \frac{{\overline{\Delta }}_{i,1}}{{\xi }_{min}}\le \frac{k_{b_i^1}\left(t\right)}{{\xi }_{min}}.\hfill \end{array}\right.$$

(86)

By the definition of ${\overline{k}}_{a_i^1}\left(t\right)$ and ${\overline{k}}_{b_i^1}\left(t\right)$, it follows that

$$\left\{\begin{array}{c}{x}_{i,1}\ge -{\overline{k}}_{a_i^1}\left(t\right)+y_0\left(t\right),\hfill \\ x_{i,1}\le {\overline{k}}_{b_i^1}\left(t\right)+y_0\left(t\right).\hfill \end{array}\right.$$

(87)

Therefore, the system state $x_{i,1}$ satisfies

$$\left\{\begin{array}{c}{x}_{i,1}\ge k_{c_i^1}\left(t\right),\hfill \\ x_{i,1}\le {\overline{k}}_{c_i^1}\left(t\right).\hfill \end{array}\right.$$

(88)

From Equation (88), it can be concluded that the output state of the system is bounded. Additionally, from (85), it can be inferred that the error $z_{i,1}$ is also bounded. ${\dot{k}}_{a_i^1}\left(t\right)$ and ${\dot{k}}_{b_i^1}\left(t\right)$ are composed of $y_0^{\left(1\right)}\left(t\right)$, ${\overline{k}}_{c_i^1}^{\left(1\right)}$ and $k_{c_i^1}^{\left(1\right)}$. It can be inferred from Assumptions 2 and 3 that $y_0^{\left(1\right)}\left(t\right)$, ${\overline{k}}_{c_i^1}^{\left(1\right)}$ and $k_{c_i^1}^{\left(1\right)}$ are both bounded. Therefore, ${\dot{k}}_{a_i^1}\left(t\right)$ and ${\dot{k}}_{b_i^1}\left(t\right)$ are also bounded. Then, according to the definition of ${\widehat{\vartheta }}_{i,1}$, ${\widehat{\vartheta }}_{i,1}$ is bounded. Due to ${\phi }_{i,1}$ composed of ${\dot{k}}_{a_i^1}\left(t\right)$, ${\dot{k}}_{b_i^1}\left(t\right)$, ${\widehat{\vartheta }}_{i,1}$ and $y_0^{\left(1\right)}\left(t\right)$, ${\phi }_{i,1}$ exists an upper bound ${\overline{\phi }}_{i,1}$. According to $z_{i,2}=x_{i,2}+{\phi }_{i,1}$ and by selecting $-k_{c_i^2}\left(t\right)={\Delta }_{i,2}\left(t\right)+{\overline{\phi }}_{i,1}$, ${\overline{k}}_{c_i^2}\left(t\right)={\overline{\Delta }}_{i,2}\left(t\right)+{\overline{\phi }}_{i,1}$, it can be obtained that $k_{c_i^2}\left(t\right)\le x_{i,2}\le {\overline{k}}_{c_i^2}\left(t\right)$, which means $x_{i,2}$ is within the constraint ranges.

In view of the above analysis, using the same approach, we can determine that all states of the system will always remain within the constraints and, furthermore, all signals of the system are bounded.

2. According to (49), when $w_{i,j}\left(t\right)>v_2$, we have $t_{g+1}-t_g=t^{*}>0$. When $w_{i,j}\left(t\right)\le v_2$, due to the boundedness of ${\overline{u}}_{i,j}$ and $w_{i,j}\left(t\right)=\left|{\dot{\omega }}_{i,j}\left(t\right){|}_{t=t_g}\right|$, we can conclude that $\frac{\eta \left|{\overline{u}}_{i,j}\right|+{\eta }_1}{max\{v_1,w_{i,j}\left(t\right)\}}$ is also bounded. Therefore, there exists a constant $\overline{t}=\frac{\eta \left|{\overline{u}}_{i,j}\right|+{\eta }_1}{max\{v_1,w_{i,j}\left(t\right)\}}$ such that $t_{g+1}-t_g=\overline{t}>0$. Evidently, the occurrence of Zeno-behavior is precluded. □

4. Simulation Results

In this section, two sets of experiments are employed to substantiate the efficacy of the proposed fixed-time self-triggered control method.

4.1. Example 1

Consider a class of MASs with a communication structure as presented in Figure 2, where node 0 represents the leader, and 1–4 represent the followers. The model for each follower is given below.

$$\left\{\begin{array}{c}{\dot{x}}_{i,1}=x_{i,2}+{\overline{n}}_{i,1}\left({\overline{x}}_{i,1}\right),\hfill \\ {\dot{x}}_{i,2}={\displaystyle \sum _{j=1}^2}{g}_{i,j}{\ell }_{i,j}\left({\overline{x}}_i\right)({\sigma }_{i,j}{\overline{u}}_{i,j}+{\kappa }_{i,j})+{\overline{n}}_{i,2}\left({\overline{x}}_{i,2}\right),\hfill \\ y_i=x_{i,1},\hfill \end{array}\right.$$

(89)

where $i=1,2,\dots ,4$, the selection of the nonlinear functions are ${\ell }_{i,j}\left({\overline{x}}_i\right)=3+0.1sin\left(x_{i,1}\right)$, ${\overline{n}}_{i,1}\left({\overline{x}}_{i,1}\right)=0.1sin\left(x_{i,1}\right)$ and ${\overline{n}}_{i,2}\left({\overline{x}}_{i,1}\right)=0.2sin\left(x_{i,1}{x}_{i,2}^2\right)$. The system’s constraint functions and the leader’s signal are chosen as ${\overline{k}}_{c_i^1}\left(t\right)=0.9+0.4sin\left(t\right)$, $k_{c_i^1}\left(t\right)=-0.8+0.3sin\left(t\right)$, ${\overline{k}}_{c_i^2}\left(t\right)=2.9+0.7cos\left(t\right)$, $k_{c_i^2}\left(t\right)=-3+0.2cos\left(t\right)$ and $y_0=sin\left(t\right)$, respectively. The other system parameters and controller parameters are listed in Table 1.

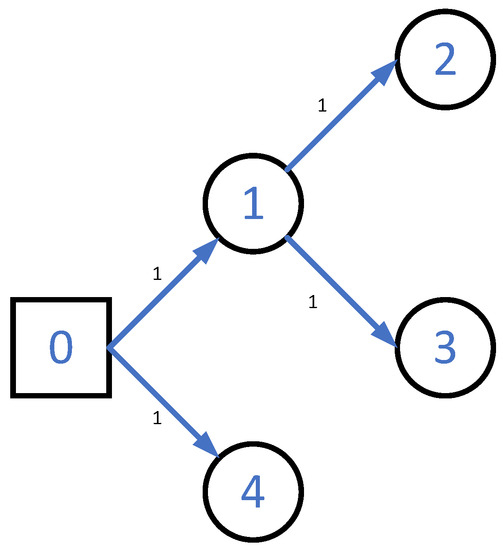
Figure 2. Communication structure graph.

Table 1. The other system parameters and controller parameters of Example 1.

The initial values of system	${[{\mathit{x}}_{1,1}\left(0\right),{\mathit{x}}_{2,1}\left(0\right),{\mathit{x}}_{3,1}\left(0\right),{\mathit{x}}_{4,1}\left(0\right)]}^{\mathit{T}}={[0.2,0.2,0.3,0.4]}^{\mathit{T}}$,
	${[x_{1,2}\left(0\right),x_{2,2}\left(0\right),x_{3,2}\left(0\right),x_{4,2}\left(0\right)]}^T={[0,0,0,0]}^T$,
	${\widehat{\vartheta }}_{i,1}\left(0\right)={\widehat{\vartheta }}_{i,2}\left(0\right)=0,{\widehat{\theta }}_{i,1}\left(0\right)={\widehat{\theta }}_{i,2}\left(0\right)={[0.4,0,0]}^T$,
	${[{\overline{u}}_{1,1},{\overline{u}}_{1,2}]}^T={[{\overline{u}}_{2,1},{\overline{u}}_{2,2}]}^T={[{\overline{u}}_{3,1},{\overline{u}}_{3,2}]}^T={[{\overline{u}}_{4,1},{\overline{u}}_{4,2}]}^T={[0,0]}^T.$
The parameters of controllers	${[c_{1,1,1},c_{2,1,1},c_{3,1,1},c_{4,1,1}]}^T={[44,42,47,46]}^T$, ${\iota }_1=25$, ${\iota }_2=30$,
	${[c_{1,2,1},c_{2,2,1},c_{3,2,1},c_{4,2,1}]}^T={[1,3,1,1]}^T$, ${\gamma }_{i,1}=4$, ${\gamma }_{i,2}=2$,
	${[c_{1,1,2},c_{2,1,2},c_{3,1,2},c_{4,1,2}]}^T={[4,4,5,2]}^T$, $W_{i,1}=0.8I_{15\times 15}$,
	${[c_{1,2,2},c_{2,2,2},c_{3,2,2},c_{4,2,2}]}^T={[8,4,3,3]}^T$, $W_{i,2}=0.6I_{15\times 15}$,
	$J_{i,1}=J_{i,2}=0.1I_{3\times 3}$, ${\delta }_{i,1}={\delta }_{i,1}=0.1$, ${\upsilon }_{i,1}={\upsilon }_{i,2}=0.01$.
The parameters of STM	$\eta =0.1$, ${\eta }_1=0.01$, $\varsigma =0.5$, $v_1=20$, $v_2=50,t^{*}=0.01$.

Furthermore, we account for two types of actuator failures:

Case I: At time $t=15$ s, actuator 1 experiences a failure rate of 20% for each agent, while actuator 2 experiences a failure rate of 40%.

Case II: At time $t=15$ s, actuator 1 continues to function normally for each agent, while actuator 2 completely fails.

The simulation results for Example 1 are shown in Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8 and Figure 9. From the simulation result graphs, it can be observed that the proposed method is effective for MASs with actuator faults and time-varying state constraints. Figure 3 and Figure 4 depict the tracking performance of each agent in response to the leader’s trajectory and the associated synchronization errors. It is evident that, under both instances of actuator failures, the agents achieve rapid convergence and maintain small tracking errors. Furthermore, the time-varying constraints on the output states are effectively satisfied. Figure 5, Figure 6, Figure 7 and Figure 8 depict the input signals of the STM and the system’s input signals. From the figures, it is evident that the system’s trigger interval are irregular and the signal update frequency is reduced based on the constructed STM. Notably, despite encountering actuator failures of varying magnitudes at 15 s, the system successfully attains the intended control objectives. Figure 9 depicts a comparison of the actuator 1 triggering number between the conventional continuous-time trigger mechanism and the developed STM. It is evident from the figure that the STM significantly decreases the triggering number, leading to substantial savings in system communication resources. The specific rate of communication resource savings is provided in Table 2.

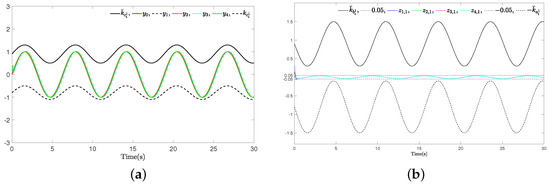
Figure 3. Example 1 (Case I): (a) Trajectories of leader $y_0$ and agents $y_i$; (b) The synchronization errors $z_{i,1}$.

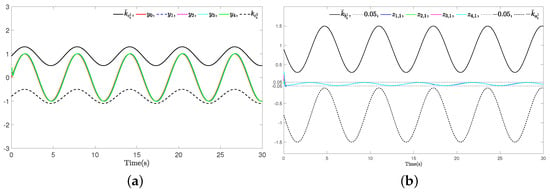
Figure 4. Example 1 (Case II): (a) Trajectories of leader $y_0$ and agents $y_i$; (b) The synchronization errors $z_{i,1}$.

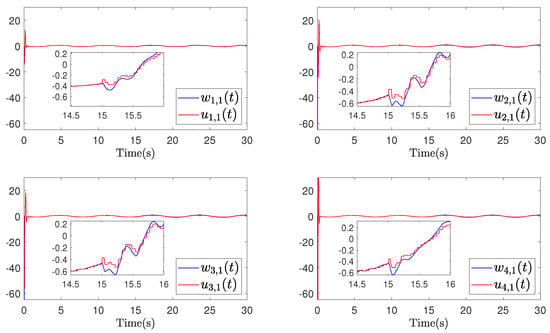
Figure 5. Example 1 (Case I): Trajectories of ${\omega }_{i,1}$ and $u_{i,1}$.

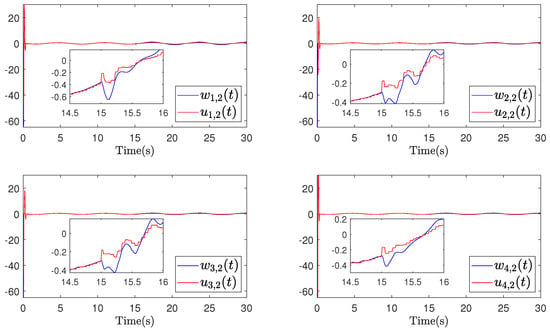
Figure 6. Example 1 (Case I): Trajectories of ${\omega }_{i,2}$ and $u_{i,2}$.

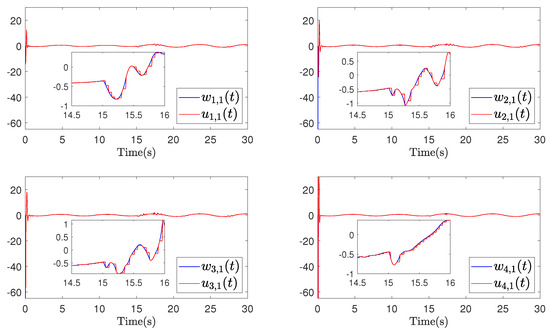
Figure 7. Example 1 (Case II): Trajectories of ${\omega }_{i,1}$ and $u_{i,1}$.

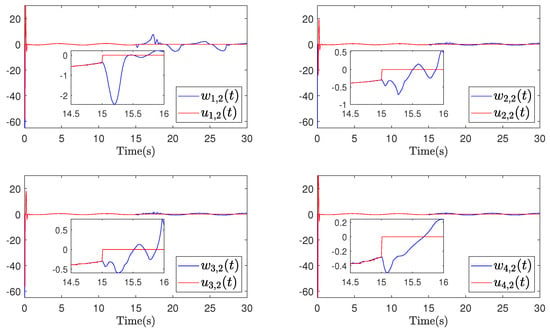
Figure 8. Example 1 (Case II): Trajectories of ${\omega }_{i,2}$ and $u_{i,2}$.

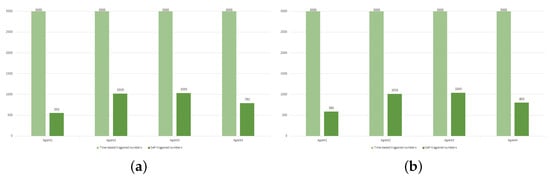
Figure 9. Example 1: (a) Comparison of trigger frequencies in Case I; (b) Comparison of trigger frequencies in Case II.

Table 2. The bandwidth saving rate of Example 1.

Case	Agent 1	Agent 2	Agent 3	Agent 4
Case I	81.57%	66.03%	65.57%	73.60%
Case II	80.50%	66.17%	65.23%	73.23%

To validate the fixed-time convergence property of the system, three sets of different initial states were selected to compare the convergence time of the synchronization errors. The selections of each set of initial states are displayed in Table 3, and the corresponding simulation results are illustrated in Figure 10. As can be seen from Figure 10, regardless of the initial states, the system’s convergence time remains around 0.1 s, which aligns with our expectations.

Table 3. Three different initial conditions of Example 1 Case I.

State	${\mathit{x}}_{\mathit{i},1}\left(0\right)$	${\mathit{x}}_{\mathit{i},1}\left(0\right)$	${\mathit{x}}_{\mathit{i},1}\left(0\right)$	${\mathit{x}}_{\mathit{i},1}\left(0\right)$
State I	0.2	0.2	0.3	0.4
State II	0.4	0.3	0.2	0.1
State III	−0.2	0	0.3	−0.1

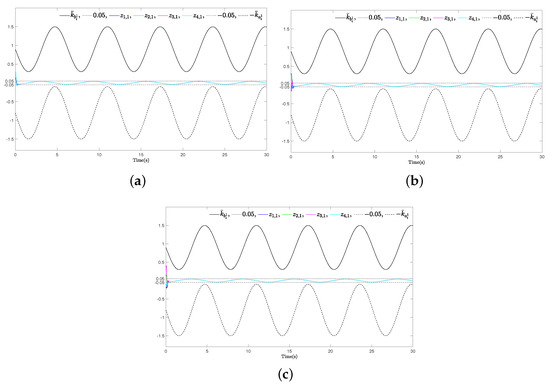
Figure 10. Example 1 (Case I): (a) The synchronization errors of State I; (b) The synchronization errors of State II; (c) The synchronization errors of State III.

4.2. Example 2

This section considers a class of MASs composed of multiple single-link robotic arms. The dynamics model of the system is as follows:

$$\left\{\begin{array}{c}{\dot{x}}_{i,1}=x_{i,2},\hfill \\ {\dot{x}}_{i,2}=\frac{1}{J}\left({\displaystyle \sum _{j=1}^2}\frac{g_{i,j}{\ell }_{i,j}\left({\overline{x}}_i\right)}{l}({\sigma }_{i,j}{\overline{u}}_{i,j}+{\kappa }_{i,j})-D{x}_{i,2}-MGLsin{x}_{i,1}\right),\hfill \\ y_i=x_{i,1},\hfill \end{array}\right.$$

(90)

where $G=9.8$ m/s ${}^2$ and $D=1$ kg/s represent the gravitational acceleration and damping factor, $L=1$ m and $M=2$ kg represent the length and mass of the robotic arm, respectively, and J represents the moment of inertia. The system’s constraint functions and the leader’s signal are chosen as ${\overline{k}}_{c_i^1}\left(t\right)=1.2+0.4sin\left(t\right)$, $k_{c_i^1}\left(t\right)=-1.2+0.3sin\left(t\right)$, ${\overline{k}}_{c_i^2}\left(t\right)=2.9+0.7cos\left(t\right)$, $k_{c_i^2}\left(t\right)=-3+0.2cos\left(t\right)$ and $y_0=sin\left(t\right)$ respectively. The other system parameters and controller parameters are listed in Table 4. Similarly, we adopt two types of actuator failure cases from Example 1.

Table 4. The other system parameters and controller parameters of Example 2.

The initial values of system	${[{\mathit{x}}_{1,1}\left(0\right),{\mathit{x}}_{2,1}\left(0\right),{\mathit{x}}_{3,1}\left(0\right),{\mathit{x}}_{4,1}\left(0\right)]}^{\mathit{T}}={[0.3,0.4,0.2,0.5]}^{\mathit{T}}$,
	${[x_{1,2}\left(0\right),x_{2,2}\left(0\right),x_{3,2}\left(0\right),x_{4,2}\left(0\right)]}^T={[0,0,0,0]}^T$,
	${\widehat{\vartheta }}_{i,1}\left(0\right)={\widehat{\vartheta }}_{i,2}\left(0\right)=0,{\widehat{\theta }}_{i,1}\left(0\right)={\widehat{\theta }}_{i,2}\left(0\right)={[0.4,0,0]}^T$,
	${[{\overline{u}}_{1,1},{\overline{u}}_{1,2}]}^T={[{\overline{u}}_{2,1},{\overline{u}}_{2,2}]}^T={[{\overline{u}}_{3,1},{\overline{u}}_{3,2}]}^T={[{\overline{u}}_{4,1},{\overline{u}}_{4,2}]}^T={[0,0]}^T.$
The parameters of controllers	${[c_{1,1,1},c_{2,1,1},c_{3,1,1},c_{4,1,1}]}^T={[38,27,33,34]}^T$, ${\iota }_1=30$, ${\iota }_2=30$,
	${[c_{1,2,1},c_{2,2,1},c_{3,2,1},c_{4,2,1}]}^T={[2,3,2,1]}^T$, ${\gamma }_{i,1}=2$, ${\gamma }_{i,2}=2$,
	${[c_{1,1,2},c_{2,1,2},c_{3,1,2},c_{4,1,2}]}^T={[2,2,5,4]}^T$, $W_{i,1}=0.8I_{15\times 15}$,
	${[c_{1,2,2},c_{2,2,2},c_{3,2,2},c_{4,2,2}]}^T={[6,4,3,3]}^T$, $W_{i,2}=0.8I_{15\times 15}$,
	$J_{i,1}=J_{i,2}=0.1I_{3\times 3}$, ${\delta }_{i,1}={\delta }_{i,1}=0.1$, ${\upsilon }_{i,1}={\upsilon }_{i,2}=0.01$.
The parameters of STM	$\eta =0.1$, ${\eta }_1=0.01$, $\varsigma =0.5$, $v_1=20$, $v_2=50,t^{*}=0.01$.

The corresponding simulation results are illustrated in Figure 11, Figure 12, Figure 13, Figure 14, Figure 15, Figure 16 and Figure 17. Consistent with the findings from Example 1, employing the proposed control method ensures that the MAS can still achieve consensus within a fixed time even in the presence of actuator failures and time-varying constraints. Furthermore, while ensuring fast convergence and small tracking errors, the system effectively saves communication resources (see Table 5).

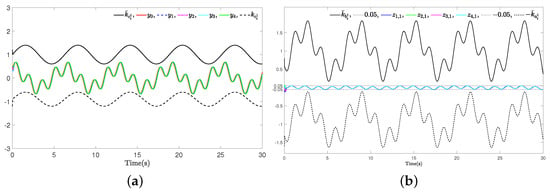
Figure 11. Example 2 (Case I): (a) Trajectories of leader $y_0$ and agents $y_i$; (b) The synchronization errors $z_{i,1}$.

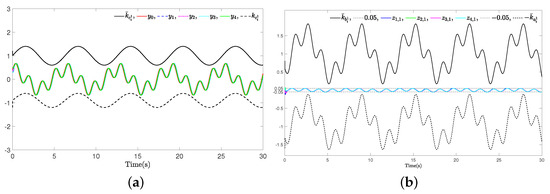
Figure 12. Example 2 (Case II): (a) Trajectories of leader $y_0$ and agents $y_i$; (b) The synchronization errors $z_{i,1}$.

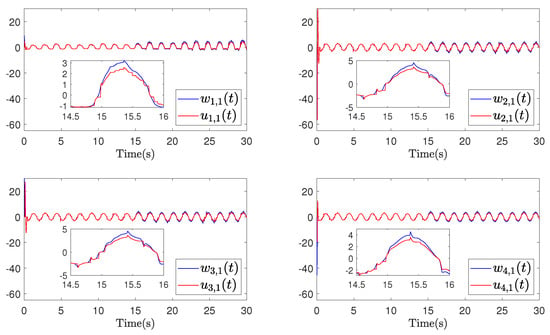
Figure 13. Example 2 (Case I): Trajectories of ${\omega }_{i,1}$ and $u_{i,1}$.

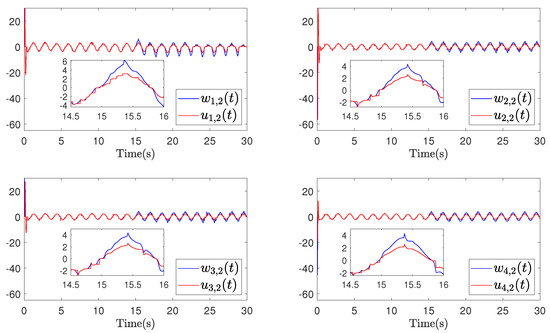
Figure 14. Example 2 (Case I): Trajectories of ${\omega }_{i,2}$ and $u_{i,2}$.

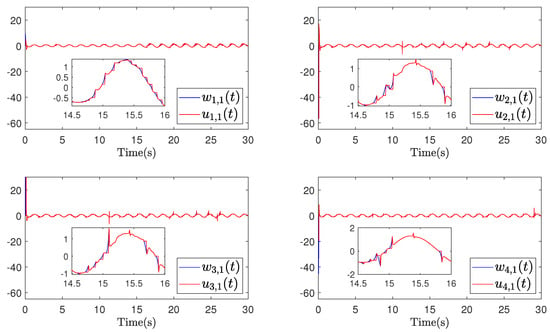
Figure 15. Example 2 (Case II): Trajectories of ${\omega }_{i,1}$ and $u_{i,1}$.

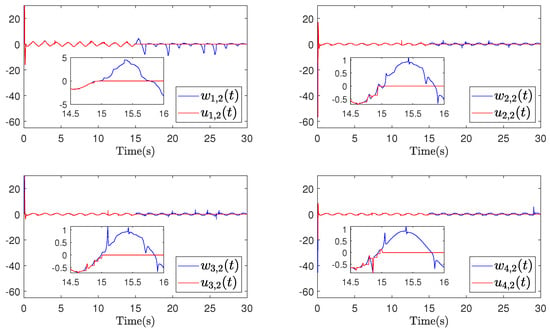
Figure 16. Example 2 (Case II): Trajectories of ${\omega }_{i,2}$ and $u_{i,2}$.

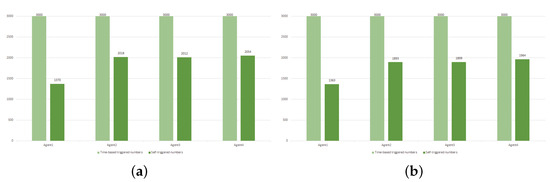
Figure 17. Example 2: (a) Comparison of trigger frequencies in Case I; (b) Comparison of trigger frequencies in Case II.

Table 5. The bandwidth saving rate of Example 2.

Case	Agent 1	Agent 2	Agent 3	Agent 4
Case I	54.33%	32.73%	32.93%	31.53%
Case II	54.57%	36.90%	36.70%	34.53%

5. Conclusions

Based on the STM, this work presents a fixed-time consensus control method, which tackles the challenges of actuator failures and time-varying constraints in MASs. The ABLFs and adaptive backstepping technique are employed to ensure system satisfaction for various types of full-state constraints (time-varying constraints, constant constraints, symmetric constraints, asymmetric constraints). Additionally, a fixed-time STM is constructed to achieve rapid MASs stabilization while alleviating communication pressure among the agents. From Example 2, it can be observed that, as the tracking signal becomes complex, the amount of communication resources saved by the STM decreases. In the future, we will further research and enhance it, aiming to maintain its high efficiency in various scenarios.