An Optimized Design of the Soft Bellow Actuator Based on the Box–Behnken Response Surface Design
Abstract
1. Introduction
- To study the parameters that influence the deformation response of the soft bellow actuator;
- To determine the optimized model of the soft bellow actuator and analyze the significant parameters using ANOVA;
- To propose a regression model to predict the deformation and stress response for this specific design of the soft bellow actuator;
- To validate the optimized design through experimental testing, assessing the deformation response and grasping performance using pulling force testing.
2. Materials and Methods
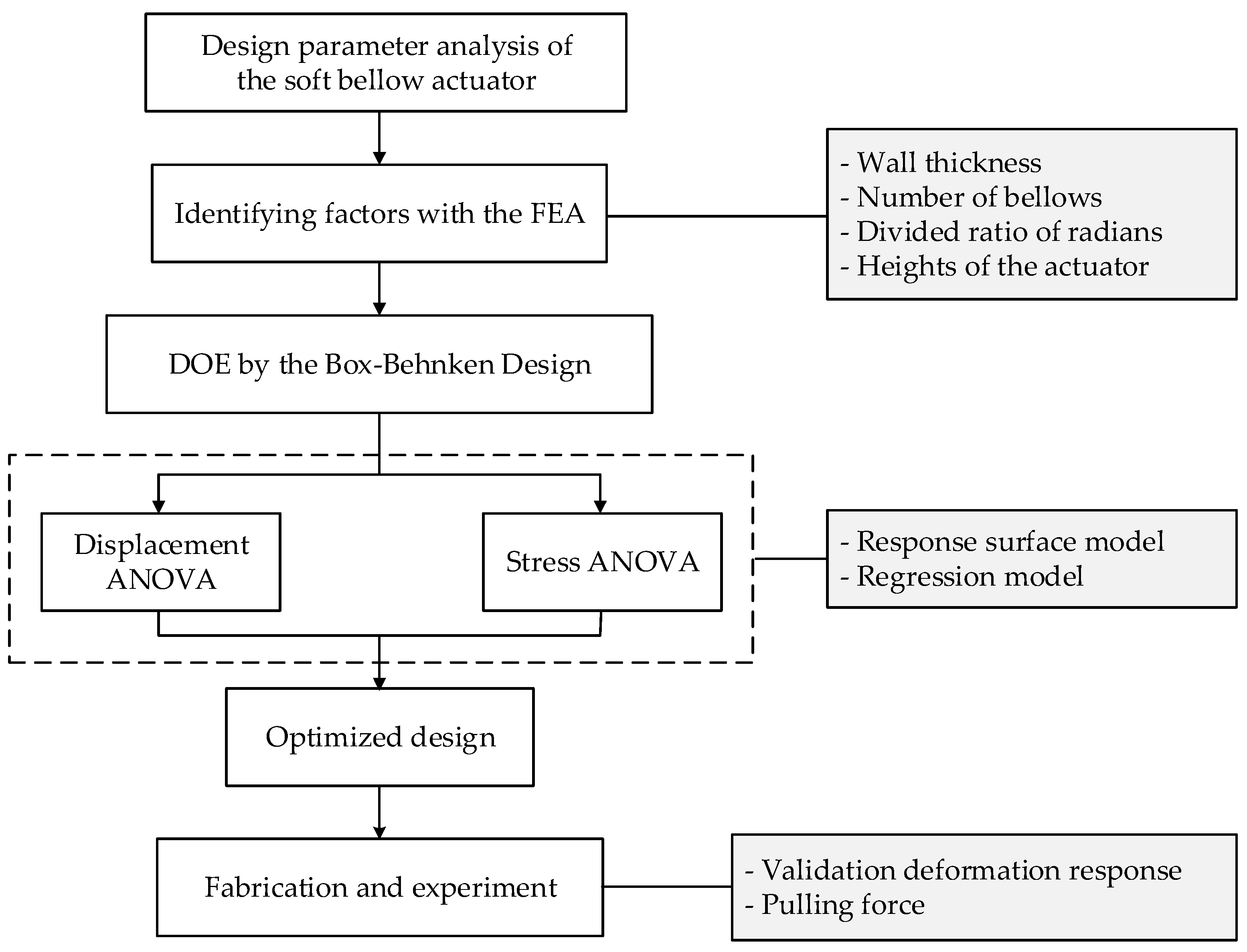
2.1. Workflow
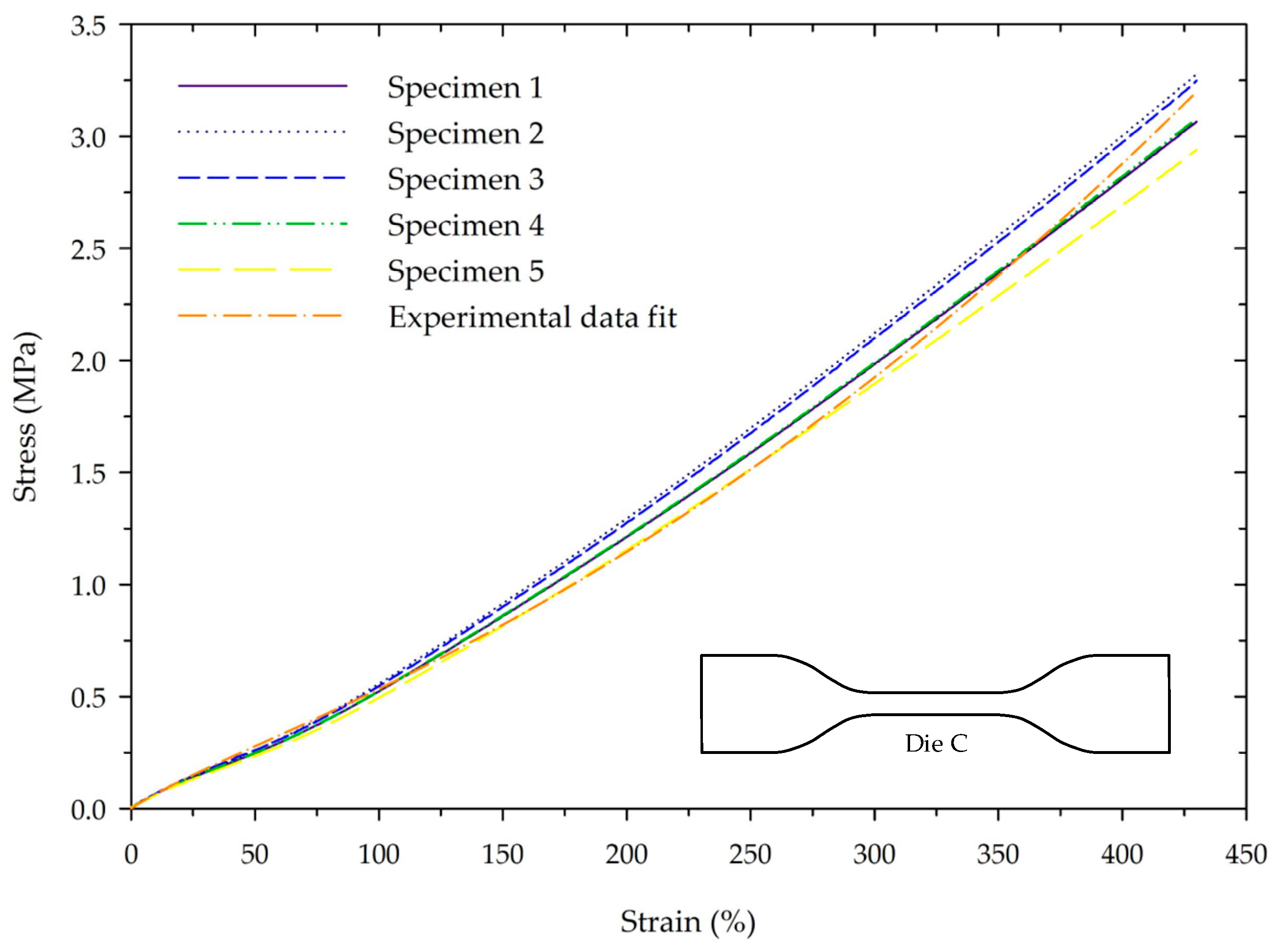
2.2. A Mathematical Model of Hyper-Elastic Materials
2.3. Design and Statistical Analysis of Experiments
3. Finite Element Analysis of Soft Bellow Design
3.1. Geometric Model of the Soft Bellow Actuator
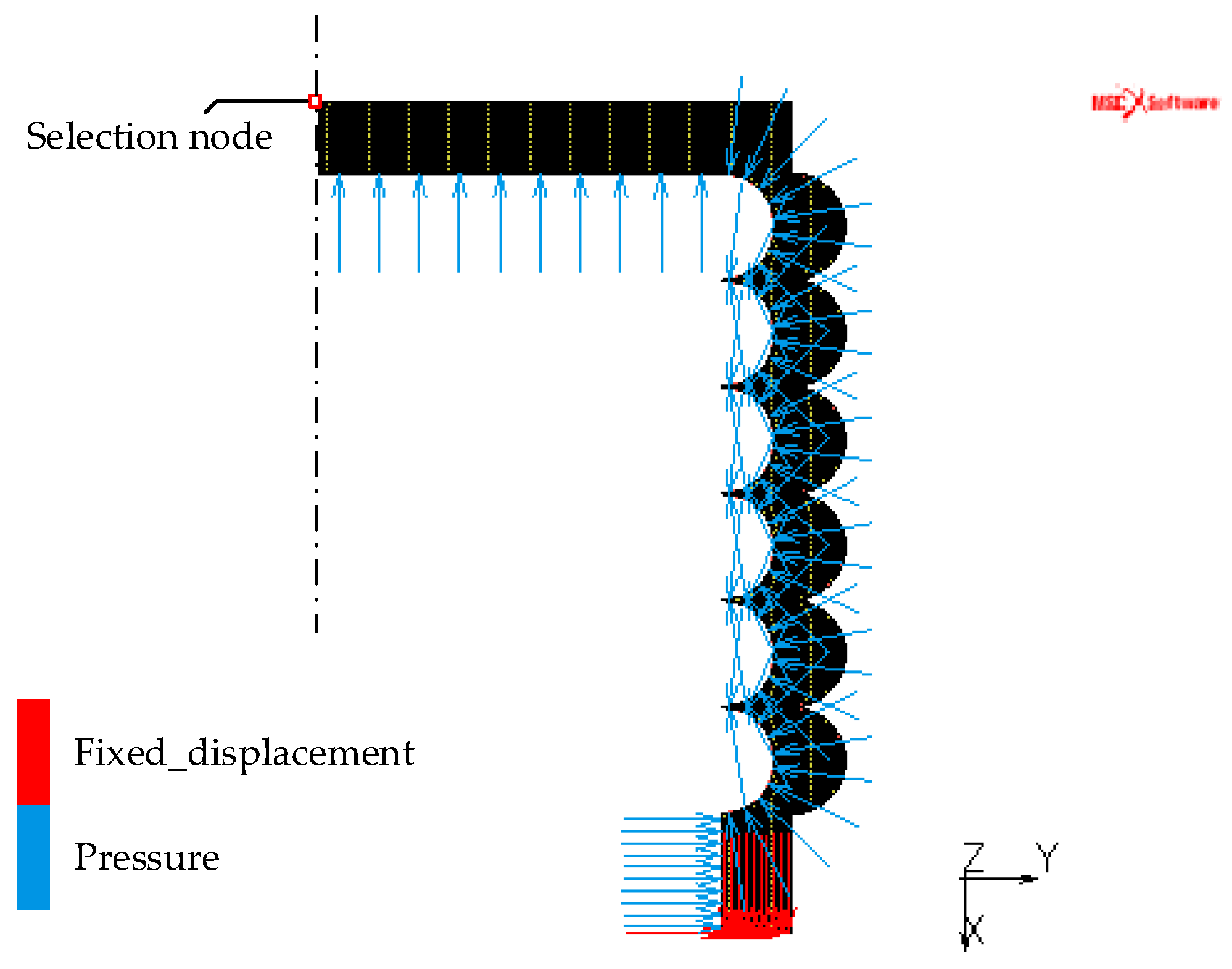
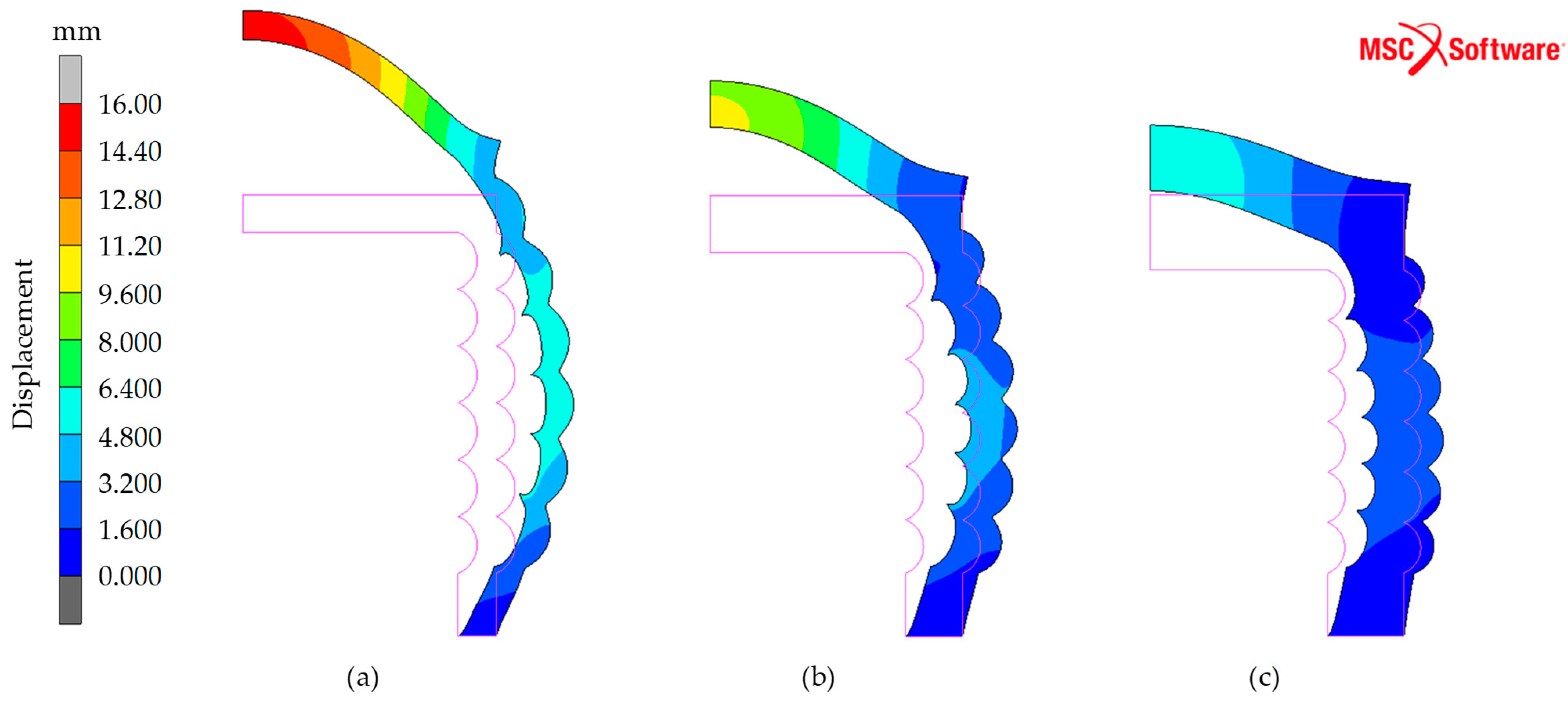
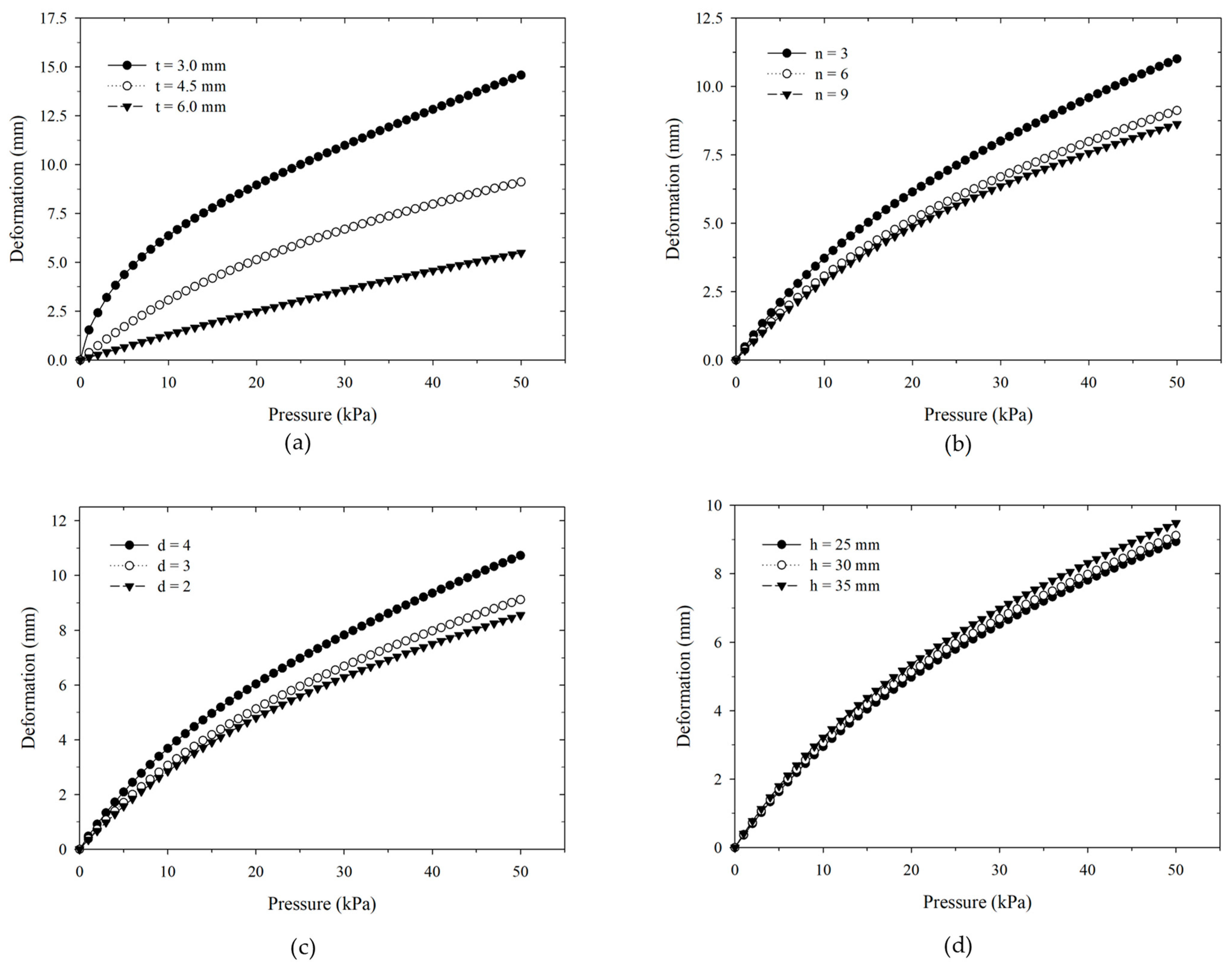
3.2. Simulation Analysis
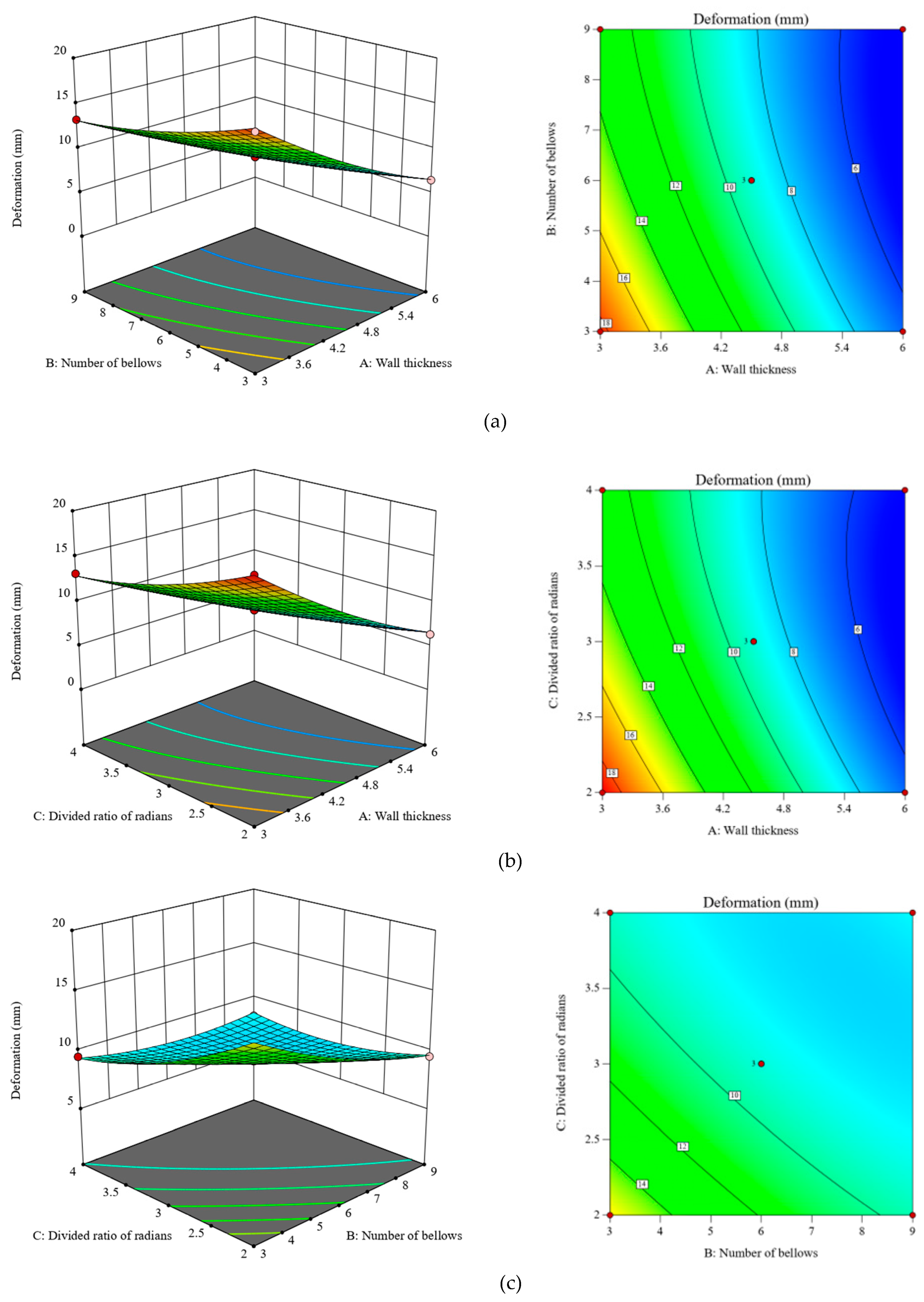
4. Box–Behnken Design
Analysis of Variance
5. Manufacturing and Assembly
6. Experiments and Results
6.1. Validation of the Deformation Response
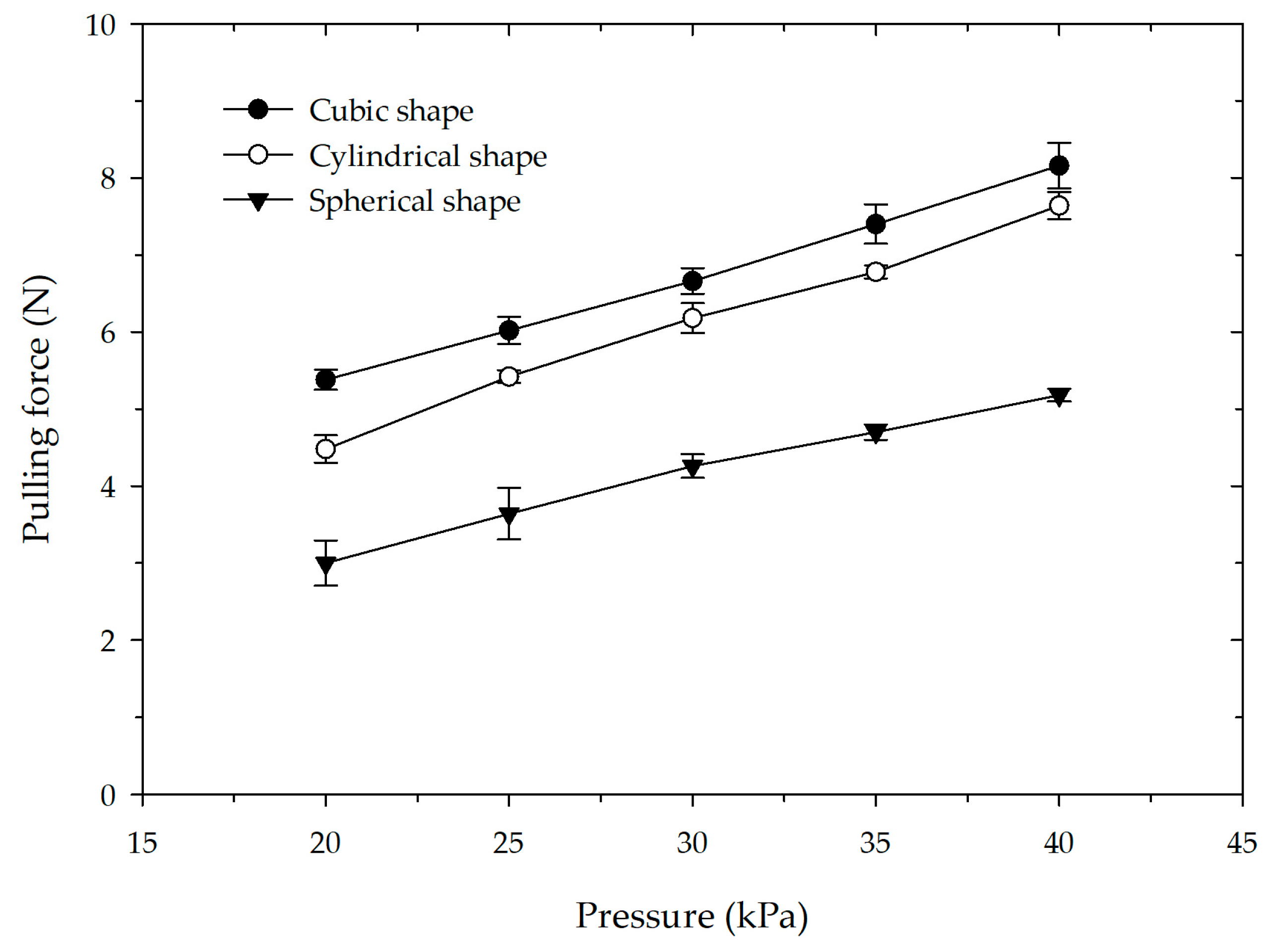
6.2. Pulling force Experiment
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Samadikhoshkho, Z.; Zareinia, K.; Janabi-Sharifi, F. A Brief Review on Robotic Grippers Classifications. In Proceedings of the 2019 IEEE Canadian Conference of Electrical and Computer Engineering (CCECE), Edmonton, AB, Canada, 5–8 May 2019; pp. 1–4. [Google Scholar]
- Li, M.; Pal, A.; Aghakhani, A.; Pena-Francesch, A.; Sitti, M. Soft Actuators for Real-World Applications. Nat. Rev. Mater. 2022, 7, 235–249. [Google Scholar] [CrossRef]
- Garcia Rubiales, F.J.; Ramon Soria, P.; Arrue, B.C.; Ollero, A. Soft-Tentacle Gripper for Pipe Crawling to Inspect Industrial Facilities Using Uavs. Sensors 2021, 21, 4142. [Google Scholar] [CrossRef] [PubMed]
- Morikage, O.; Wang, Z.; Hirai, S. Multi-Fingered Soft Gripper Driven by Bellows Actuator for Handling Food Materials. In Proceedings of the 2021 27th International Conference on Mechatronics and Machine Vision in Practice (M2VIP), Shanghai, China, 26–28 November 2021; pp. 363–368. [Google Scholar]
- Hu, Q.; Dong, E.; Sun, D. Soft Gripper Design Based on the Integration of Flat Dry Adhesive, Soft Actuator, and Microspine. IEEE Trans. Robot. 2021, 37, 1065–1080. [Google Scholar] [CrossRef]
- Pan, M.; Yuan, C.; Liang, X.; Dong, T.; Liu, T.; Zhang, J.; Zou, J.; Yang, H.; Bowen, C. Soft Actuators and Robotic Devices for Rehabilitation and Assistance. Adv. Intell. Syst. 2022, 4, 2100140. [Google Scholar] [CrossRef]
- Heung, H.L.; Tang, Z.Q.; Shi, X.Q.; Tong, K.Y.; Li, Z. Soft Rehabilitation Actuator with Integrated Post-Stroke Finger Spasticity Evaluation. Front. Bioeng. Biotechnol. 2020, 8, 111. [Google Scholar] [CrossRef]
- Sun, Z.; Guo, Z.; Tang, W. Design of Wearable Hand Rehabilitation Glove with Soft Hoop-Reinforced Pneumatic Actuator. J. Cent. South Univ. 2019, 26, 106–119. [Google Scholar] [CrossRef]
- Polygerinos, P.; Wang, Z.; Galloway, K.C.; Wood, R.J.; Walsh, C.J. Soft Robotic Glove for Combined Assistance and At-Home Rehabilitation. Robot. Auton. Syst. 2015, 73, 135–143. [Google Scholar] [CrossRef]
- Navas, E.; Fernández, R.; Armada, M.; Gonzalez-de-Santos, P. Diaphragm-Type Pneumatic-Driven Soft Grippers for Precision Harvesting. Agronomy 2021, 11, 1727. [Google Scholar] [CrossRef]
- Ranasinghe, H.N.; Kawshan, C.; Himaruwan, S.; Kulasekera, A.L.; Dassanayake, P. Soft Pneumatic Grippers for Reducing Fruit Damage During Strawberry Harvesting. In Proceedings of the 2022 Moratuwa Engineering Research Conference (MERCon), Moratuwa, Sri Lanka, 27–29 July 2022; pp. 1–6. [Google Scholar]
- Navas, E.; Dworak, V.; Weltzien, C.; Fernández, R.; Shokrian Zeini, M.; Käthner, J.; Shamshiri, R. An Approach to the Automation of Blueberry Harvesting Using Soft Robotics. 43. GIL-Jahrestag. Resiliente Agri-Food-Syst. 2023, pp. 435–440. Available online: https://dl.gi.de/server/api/core/bitstreams/9cf3b7f2-150d-4c51-951e-b8b40390d9f3/content (accessed on 10 June 2023).
- Zaidi, S.; Maselli, M.; Laschi, C.; Cianchetti, M. Actuation Technologies for Soft Robot Grippers and Manipulators: A Review. Curr. Robot. Rep. 2021, 2, 355–369. [Google Scholar] [CrossRef]
- Chen, R.; Zhang, C.; Sun, Y.; Yu, T.; Shen, X.-M.; Yuan, Z.-A.; Guo, J.-L. A Paper Fortune Teller-Inspired Reconfigurable Soft Pneumatic Gripper. Smart Mater. Struct. 2021, 30, 045002. [Google Scholar] [CrossRef]
- Walker, J.; Zidek, T.; Harbel, C.; Yoon, S.; Strickland, F.S.; Kumar, S.; Shin, M. Soft Robotics: A Review of Recent Developments of Pneumatic Soft Actuators. Actuators 2020, 9, 3. [Google Scholar] [CrossRef]
- Wang, Z.; Or, K.; Hirai, S. A Dual-Mode Soft Gripper for Food Packaging. Robot. Auton. Syst. 2020, 125, 103427. [Google Scholar] [CrossRef]
- Mosadegh, B.; Polygerinos, P.; Keplinger, C.; Wennstedt, S.; Shepherd, R.F.; Gupta, U.; Shim, J.; Bertoldi, K.; Walsh, C.J.; Whitesides, G.M. Pneumatic Networks for Soft Robotics That Actuate Rapidly. Adv. Funct. Mater. 2014, 24, 2163–2170. [Google Scholar] [CrossRef]
- Auysakul, J.; Vittayaphadung, N.; Gonsrang, S.; Smithmaitrie, P. Bending Angle Effect of TheCross-Section Ratio for a Soft Pneumatic Actuator. Int. J. Mech. Eng. Robot. Res. 2020, 9, 366–370. [Google Scholar] [CrossRef]
- Zhang, X.; Yu, S.; Dai, J.; Oseyemi, A.E.; Liu, L.; Du, N.; Lv, F. A Modular Soft Gripper with Combined Pneu-Net Actuators. Actuators 2023, 12, 172. [Google Scholar] [CrossRef]
- Cheng, P.; Ye, Y.; Yan, B.; Lu, Y.; Wu, C. Eccentric High-Force Soft Pneumatic Bending Actuator for Finger-Type Soft Grippers. J. Mech. Robot. 2022, 14, 060908. [Google Scholar] [CrossRef]
- Ye, Y.; Cheng, P.; Yan, B.; Lu, Y.; Wu, C. Design of a Novel Soft Pneumatic Gripper with Variable Gripping Size and Mode. J. Intell. Robot Syst. 2022, 106, 5. [Google Scholar] [CrossRef]
- Polygerinos, P.; Wang, Z.; Overvelde, J.T.; Galloway, K.C.; Wood, R.J.; Bertoldi, K.; Walsh, C.J. Modeling of Soft Fiber-Reinforced Bending Actuators. IEEE Trans. Robot. 2015, 31, 778–789. [Google Scholar] [CrossRef]
- Joseph, T.; Baldwin, S.; Guan, L.; Brett, J.; Howard, D. The Jamming Donut: A Free-Space Gripper Based on Granular Jamming. arXiv 2022, arXiv:2212.06485. [Google Scholar]
- Gao, G.; Chang, C.M.; Gerez, L.; Liarokapis, M. A Pneumatically Driven, Disposable, Soft Robotic Gripper Equipped with Multi-Stage, Retractable, Telescopic Fingers. IEEE Trans. Med. Robot. Bionics 2021, 3, 573–582. [Google Scholar] [CrossRef]
- Guo, N.; Sun, Z.; Wang, X.; Yeung, E.H.K.; To, M.K.T.; Li, X.; Hu, Y. Simulation Analysis for Optimal Design of Pneumatic Bellow Actuators for Soft-Robotic Glove. Biocybern. Biomed. Eng. 2020, 40, 1359–1368. [Google Scholar] [CrossRef]
- Cao, M.; Zhu, J.; Fu, H.; Loic, H.Y.F. Response Surface Design of Bellows Parameters with Negative Pressure Shrinkage Performance. Int. J. Interact. Des. Manuf. (IJIDeM) 2022, 16, 1041–1052. [Google Scholar] [CrossRef]
- Müller, D.; Sawodny, O. Modeling the Soft Bellows of the Bionic Soft Arm. IFAC-PapersOnLine 2022, 55, 229–234. [Google Scholar] [CrossRef]
- Dean, A.; Voss, D.; Draguljić, D. Response Surface Methodology. In Design and Analysis of Experiments; Dean, A., Voss, D., Draguljić, D., Eds.; Texts in Statistics; Springer International Publishing: Cham, Switzerland, 2017; pp. 565–614. ISBN 978-3-319-52250-0. [Google Scholar]
- Kleijnen, J.P.C. Response Surface Methodology. In Handbook of Simulation Optimization; Fu, M.C., Ed.; International Series in Operations Research & Management Science; Springer: New York, NY, USA, 2015; pp. 81–104. ISBN 978-1-4939-1384-8. [Google Scholar]
- Khuri, A.I.; Mukhopadhyay, S. Response Surface Methodology. WIREs Comput. Stat. 2010, 2, 128–149. [Google Scholar] [CrossRef]
- Honarpardaz, M. A Methodology for Design and Simulation of Soft Grippers. Simulation 2021, 97, 779–791. [Google Scholar] [CrossRef]
- Chen, F.; Xu, W.; Zhang, H.; Wang, Y.; Cao, J.; Wang, M.Y.; Ren, H.; Zhu, J.; Zhang, Y.F. Topology Optimized Design, Fabrication, and Characterization of a Soft Cable-Driven Gripper. IEEE Robot. Autom. Lett. 2018, 3, 2463–2470. [Google Scholar] [CrossRef]
- Tawk, C.; Alici, G. Finite Element Modeling in the Design Process of 3D Printed Pneumatic Soft Actuators and Sensors. Robotics 2020, 9, 52. [Google Scholar] [CrossRef]
- Guo, L.; Li, K.; Cheng, G.; Zhang, Z.; Xu, C.; Ding, J. Design and Experiments of Pneumatic Soft Actuators. Robotica 2021, 39, 1806–1815. [Google Scholar] [CrossRef]
- Marechal, L.; Balland, P.; Lindenroth, L.; Petrou, F.; Kontovounisios, C.; Bello, F. Toward a Common Framework and Database of Materials for Soft Robotics. Soft Robot. 2021, 8, 284–297. [Google Scholar] [CrossRef]
- Szurgott, P.; Jarzębski, Ł. Selection of a Hyper-Elastic Material Model-a Case Study for a Polyurethane Component. Lat. Am. J. Solids Struct. 2019, 16, 1–16. [Google Scholar] [CrossRef]
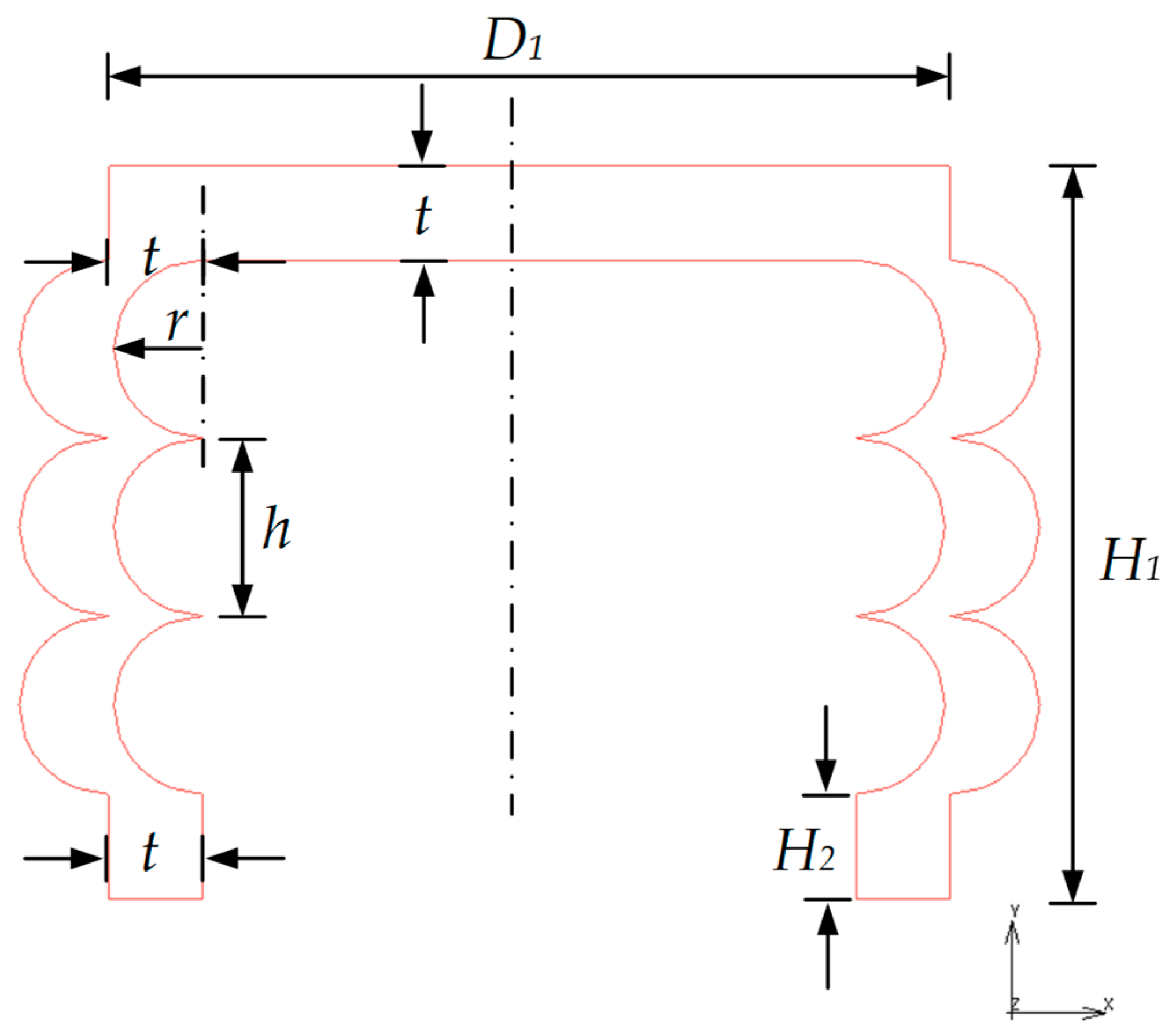







| Factor | Name | Low | Median | High |
|---|---|---|---|---|
| A | Wall thickness | 3 | 4.5 | 6 |
| B | Number of bellows | 3 | 6 | 9 |
| C | Divided ratio of radians | 2 | 3 | 4 |
| Standard Order | Running Order | Point Type | Blocks | A | B | C | D | E |
|---|---|---|---|---|---|---|---|---|
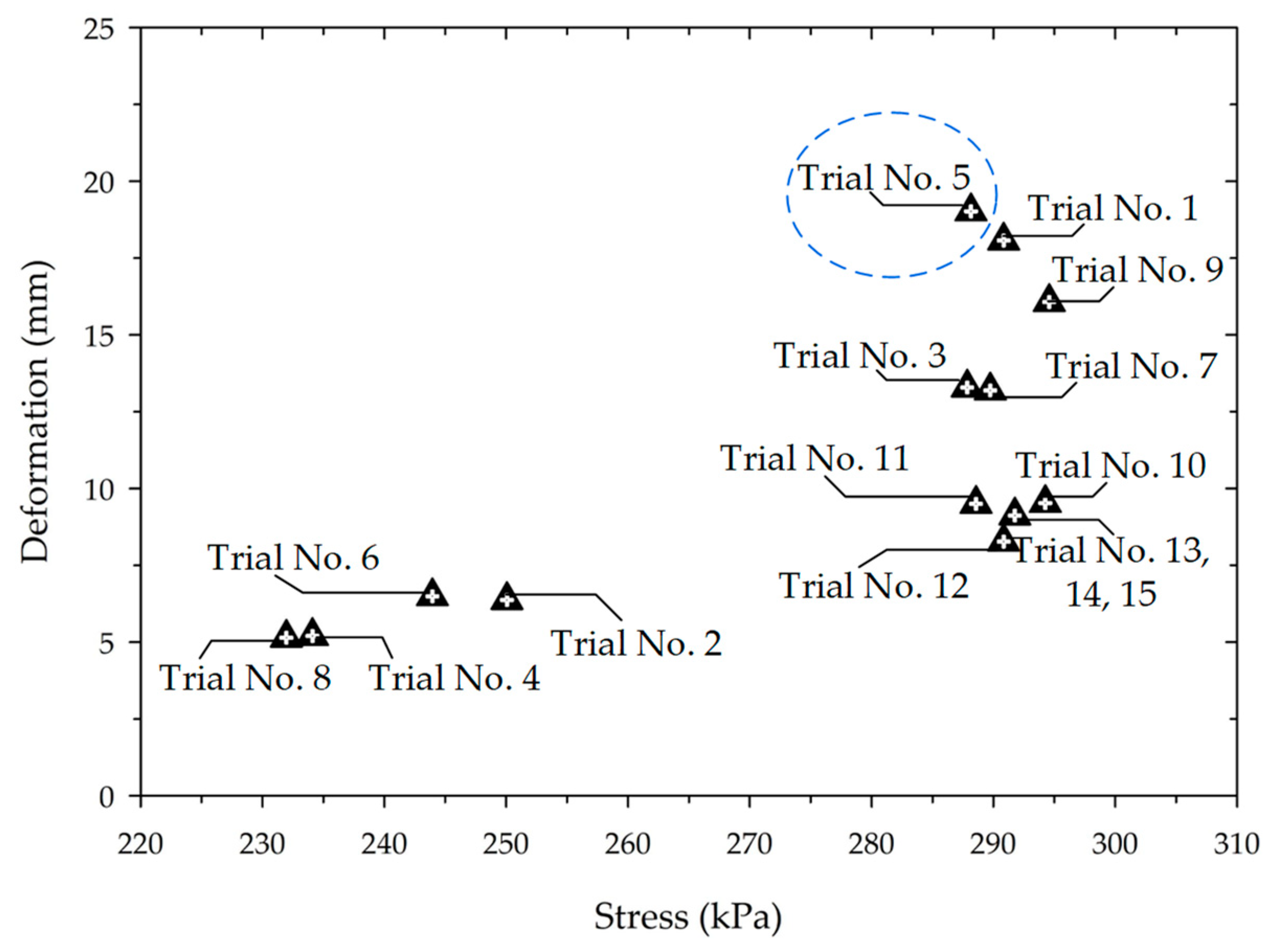
| 1 | 1 | 2 | 1 | 3 | 3 | 3 | 18.06 | 290.8 |
| 2 | 2 | 2 | 1 | 6 | 3 | 3 | 6.49 | 243.9 |
| 3 | 3 | 2 | 1 | 3 | 9 | 3 | 13.28 | 287.9 |
| 4 | 4 | 2 | 1 | 6 | 9 | 3 | 5.19 | 234.1 |
| 5 | 5 | 2 | 1 | 3 | 6 | 2 | 19.02 | 288.2 |
| 6 | 6 | 2 | 1 | 6 | 6 | 2 | 6.37 | 250.1 |
| 7 | 7 | 2 | 1 | 3 | 6 | 4 | 13.19 | 289.7 |
| 8 | 8 | 2 | 1 | 6 | 6 | 4 | 5.14 | 232.0 |
| 9 | 9 | 2 | 1 | 4.5 | 3 | 2 | 16.07 | 294.6 |
| 10 | 10 | 2 | 1 | 4.5 | 9 | 2 | 9.52 | 294.3 |
| 11 | 11 | 2 | 1 | 4.5 | 3 | 4 | 9.50 | 288.6 |
| 12 | 12 | 2 | 1 | 4.5 | 9 | 4 | 8.27 | 290.8 |
| 13 | 13 | 0 | 1 | 4.5 | 6 | 3 | 9.12 | 291.8 |
| 14 | 14 | 0 | 1 | 4.5 | 6 | 3 | 9.12 | 291.8 |
| 15 | 15 | 0 | 1 | 4.5 | 6 | 3 | 9.12 | 291.8 |
| Source | DF | Adj SS | Adj MS | F-Value | p-Value |
|---|---|---|---|---|---|
| Model | 9 | 277.84 | 30.87 | 273.89 | <0.0001 |
| Linear | |||||
| A | 1 | 203.59 | 203.59 | 1806.27 | <0.0001 |
| B | 1 | 23.97 | 23.97 | 212.64 | <0.0001 |
| C | 1 | 27.68 | 27.68 | 245.6 | <0.0001 |
| Square | |||||
| A× | 1 | 2.76 | 2.76 | 24.49 | 0.0043 |
| B×B | 1 | 2.22 | 2.22 | 19.66 | 0.0068 |
| C×C | 1 | 3.31 | 3.31 | 29.38 | 0.0029 |
| 2-way Interaction | |||||
| A×B | 1 | 3.05 | 3.05 | 27.02 | 0.0035 |
| A×C | 1 | 5.3 | 5.3 | 47.01 | 0.001 |
| B×C | 1 | 7.06 | 7.06 | 62.65 | 0.0005 |
| Error | 5 | 0.5636 | 0.1127 | ||
| Total | 14 | 278.4 | |||
| R2 = 0.998, adj-R2 = 0.9943, C.V.% = 3.2, and Adeq Precision = 51.55 | |||||
| Source | DF | Adj SS | Adj MS | F-Value | p-Value |
|---|---|---|---|---|---|
| Model | 9 | 7830.61 | 870.07 | 119.83 | <0.0001 |
| Linear | |||||
| A | 1 | 4827.23 | 4827.23 | 664.82 | <0.0001 |
| B | 1 | 14.86 | 14.86 | 2.05 | 0.212 |
| C | 1 | 84.18 | 84.18 | 11.59 | 0.0191 |
| Square | |||||
| A×A | 1 | 2757.63 | 2757.63 | 379.79 | <0.0001 |
| B×B | 1 | 0.2251 | 0.2251 | 0.031 | 0.8671 |
| C×C | 1 | 1.12 | 1.12 | 0.1541 | 0.7108 |
| 2-way Interaction | |||||
| A×B | 1 | 11.73 | 11.73 | 1.62 | 0.2597 |
| A×C | 1 | 96.82 | 96.82 | 13.33 | 0.0147 |
| B×C | 1 | 1.67 | 1.67 | 0.2299 | 0.6518 |
| Error | 5 | 36.3 | 7.26 | ||
| Total | 14 | 7866.92 | |||
| R2 = 0.9954 and adj-R2 = 0.9871, C.V.% = 0.9716, and Adeq Precision = 29.572 | |||||
| Pressure (kPa) | Deformation (mm) | Strain (%) | % Error of a Deformation | ||
|---|---|---|---|---|---|
| Experiment (Average) | Simulation | Experiment (Average) | Simulation | ||
| 5 | 1.22 | 5.37 | 0.035 | 0.153 | −77.29 |
| 10 | 4.452 | 7.81 | 0.127 | 0.223 | −42.99 |
| 15 | 6.672 | 9.66 | 0.191 | 0.276 | −30.92 |
| 20 | 8.864 | 11.26 | 0.253 | 0.322 | −21.29 |
| 25 | 10.224 | 12.73 | 0.292 | 0.364 | −19.68 |
| 30 | 11.76 | 14.11 | 0.336 | 0.403 | −16.63 |
| 35 | 13.124 | 15.41 | 0.375 | 0.440 | −14.85 |
| 40 | 14.544 | 16.66 | 0.416 | 0.476 | −12.72 |
| 45 | 15.74 | 17.86 | 0.450 | 0.510 | −11.89 |
| 50 | 16.84 | 19.02 | 0.481 | 0.543 | −11.46 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Auysakul, J.; Booranawong, A.; Vittayaphadung, N.; Smithmaitrie, P. An Optimized Design of the Soft Bellow Actuator Based on the Box–Behnken Response Surface Design. Actuators 2023, 12, 300. https://doi.org/10.3390/act12070300
Auysakul J, Booranawong A, Vittayaphadung N, Smithmaitrie P. An Optimized Design of the Soft Bellow Actuator Based on the Box–Behnken Response Surface Design. Actuators. 2023; 12(7):300. https://doi.org/10.3390/act12070300
Chicago/Turabian StyleAuysakul, Jutamanee, Apidet Booranawong, Nitipan Vittayaphadung, and Pruittikorn Smithmaitrie. 2023. "An Optimized Design of the Soft Bellow Actuator Based on the Box–Behnken Response Surface Design" Actuators 12, no. 7: 300. https://doi.org/10.3390/act12070300
APA StyleAuysakul, J., Booranawong, A., Vittayaphadung, N., & Smithmaitrie, P. (2023). An Optimized Design of the Soft Bellow Actuator Based on the Box–Behnken Response Surface Design. Actuators, 12(7), 300. https://doi.org/10.3390/act12070300






