Research on CNN-LSTM Brake Pad Wear Condition Monitoring Based on GTO Multi-Objective Optimization

Abstract

As the core component of the automobile braking system, brake pads have a complex structure and high failure rate. Their accurate and effective state monitoring can help to evaluate the safety performance of brake pads and avoid accidents caused by brake failure. The wear process of automobile brake pads is a gradual, nonlinear, and non-stationary time-varying system, and it is difficult to extract its features. Therefore, this paper proposes a CNN-LSTM brake pad wear state monitoring method. This method uses a Convolutional Neural Network (CNN) to complete the deep mining of brake pad wear characteristics and realize data dimensionality reduction, and a Long Short-Term Memory (LSTM) network to capture the time dependence of the brake pad wear sequence, so as to construct the nonlinear mapping relationship between brake pad wear characteristics and brake pad wear values. At the same time, the artificial Gorilla Troops Optimization (GTO) algorithm is used to perform multi-objective optimization of the network structure parameters in the CNN-LSTM model, and its powerful global search ability improves the monitoring effect of the brake pad wear status. The results show that the CNN-LSTM model based on GTO multi-objective optimization can effectively monitor the wear state of brake pads, and its coefficient of determination R2 value is 0.9944, the root mean square error RMSE value is 0.0023, and the mean absolute error MAE value is 0.0017. Compared with the BP model, CNN model, LSTM model, and CNN-LSTM model, the value of the coefficient of determination R2 is the closest to 1, which is increased by 8.29%, 5.52%, 4.47%, 3.30%, respectively, which can more effectively realize the monitoring and intelligent early warning of the brake pad wear state.

1. Introduction

The performance of the brake pads directly affects the safety and reliability of the whole braking system. When the remaining thickness of the brake pads exceeds the critical threshold, it will greatly reduce the braking effect of the car and even produce major braking accidents, which is undoubtedly a major safety hazard for civilian vehicles [1]. Therefore, it is necessary to carry out real-time monitoring and health management of the wear state of the brake pads, so that the management system can intelligently alarm according to the predicted results and guide the driver to replace the brake pads before they reach the end of their life cycle, which can greatly improve the passive safety of vehicle driving. At the same time, this has a certain practical significance for China′s automobile manufacturing industry and automobile maintenance industry in providing scientific support for the maintenance strategy and health management means.

The wear process of automobile brake pads has the characteristics of gradual change, nonlinearity, and instability, and there is no fixed life cycle. It is a great challenge to monitor the wear state of automobile brake pads. In its early stage, the research on brake pads focused on material performance analysis [2], experimental simulation [3] or simulation, and optimization of brake system control [4], and made certain achievements. Z. K. Li et al. [5] used the material characteristics of brake pads to construct a three-dimensional physical model, and they proposed a wear life prediction method for automobile brake pads based on the visual features of the image. The results indicated that the method had high detection accuracy and prediction reliability.

With the increasing demand for the reliability and safety of automobiles, the data-driven method combining sensor monitoring data with machine learning technology is widely used in the condition monitoring and fault diagnosis of brake systems. Its essence is to use computer vision technology to extract the characteristics that can characterize the degradation of a certain brake state. Machine learning technology can accurately simulate the whole process of brake performance degradation and compare it with historical data to complete the condition monitoring and fault diagnosis [6]. The most commonly used machine learning methods mainly include the BP neural network [7], artificial neural network (ANN) [8], support vector machine (SVM) [9], and so on.

S. Zhang et al. [10] used a BP neural network to construct a correlation prediction model between vehicle braking characteristics and braking deceleration. Through data verification, the accuracy and effectiveness of the model for vehicle deceleration prediction were confirmed. K. P. Babu et al. [11] used an artificial neural network (ANN) as a tool to control the anti-lock braking system to obtain the optimal braking pressure so as to minimize the stopping distance, the impact, and the final system stability. Compared with the hysteresis controller, the proposed model had obvious superiority. J. Liu et al. [12] proposed a support vector machine (SVM) model including feature vector selection, model construction, and decision boundary optimization and applied the model to the fault diagnosis of a high-speed train braking system. The results showed that the proposed model could better diagnose the braking system fault using several public unbalanced data sets. Although the use of machine learning technology has achieved certain results in the condition monitoring of the braking system, the generalization ability of the prediction model is insufficient, the prediction accuracy and accuracy are not high, and the model is more dependent on signal processing technology and expert experience.

A high-precision prediction model can very effectively improve the monitoring effect of the brake pad wear state, which is of great significance to realize intelligent early warning when the brake pad wear thickness is at the critical threshold. Therefore, a large number of experts and scholars have applied deep learning theory to the research on brake pad wear state monitoring, such as the Recurrent Neural Network (RNN) [13], Long Short-Term Memory (LSTM) network [14], Convolutional Neural Network (CNN) [15], etc., and its prediction effect is significantly higher than that of mechanical learning technology. Compared with machine learning methods, these prediction models have more powerful feature learning and mapping capabilities and can automatically mine deep features for prediction without prior knowledge or the help of human experts. Recently, tool life prediction based on a Long Short-Term Memory (LSTM) network was gradually carried out. J. Kang et al. [16] proposed a method to detect the abnormal braking system of metro vehicles based on a Long Short-Term Memory (LSTM) autoencoder. The formed subsequences were input into two LSTM modules to complete the diagnosis of the abnormal braking system. The results showed that the LSTM autoencoder could diagnose the anomaly in BOU data more effectively. However, for the samples with stronger nonlinearity and more prominent non-stationarity, the LSTM network can only mine the shallow features of the sample data owing to the defects in the network structure, which are difficult to effectively monitor and diagnose [17].

Compared with the Long Short-Term Memory (LSTM) network, the Convolutional Neural Network (CNN) can improve the ability to mine deep features of complex data in the prediction model by convolution and pooling operations [18]. However, the CNN network can only extract the spatial features of brake pad wear, avoid the temporal information, extract single features, and easily produce an overfitting phenomenon. It can be seen that it is difficult to achieve ideal results by using only one algorithm to construct a prediction model. Because of the limitations of a single algorithm prediction model, different algorithms are often fused and optimized to monitor the condition of complex systems in order to achieve higher prediction effects. Therefore, the combination of a Convolutional Neural Network (CNN) and Long Short-Term Memory (LSTM) network has become an inevitable trend. The CNN model is used to mine the deep features of the sample in space, and the LSTM model is used to capture the temporal information in time, so that the temporal and spatial features of the data are fully utilized.

Up to now, there has been little research on using the CNN-LSTM model to monitor the wear state of brake pads. However, R. D. Gabriel et al. [19] used a CNN-LSTM model to complete the remaining useful life monitoring of an electric vehicle bidirectional converter, and the model could fully mine the effective features of bidirectional converter data. The research results indicated that the CNN-LSTM model has higher robustness and prediction accuracy, which can improve the safety and reliability of the system, proving that it is also feasible to use the CNN-LSTM model to monitor the wear state of brake pads. In order to further improve the prediction effect of the model, it is necessary to optimize the hyperparameters in the CNN-LSTM model. In the early stage, the common hyperparameter optimization methods included random optimization, gradient-based optimization [20], genetic algorithm optimization [21], particle swarm optimization [22], Bayesian optimization [23], etc. However, the above methods were only suitable for the optimization of single or double objective hyperparameters in the prediction model, and it was difficult to obtain the optimal solution set for nonlinear, high-dimensional, and non-derivable multi-objective complex optimization problems. The artificial Gorilla Troops Optimization (GTO) algorithm is a new metaheuristic optimization algorithm proposed by Ben et al., 2021 [24], which can complete multi-objective optimization of multiple sets of solutions through a single learning. The algorithm is often used to solve multi-objective optimization problems (MOPs) with conflicting optimization objectives that need to be optimized at the same time. Its search performance and multi-objective optimization ability are better than other algorithms, and it has been widely used and studied by scholars in recent years [25].

Therefore, based on computer vision, deep learning, data-driven, and other technologies, this paper proposes a CNN-LSTM brake pad wear condition monitoring method based on multi-objective optimization of a GTO algorithm. The Convolutional Neural Network (CNN) is used as feature extractor in this method. The Long Short-Term Memory (LSTM) network is used as the trainer to predict the brake pad wear thickness in real time, and the GTO algorithm is used to perform multi-objective optimization on the network structure parameters in the model to achieve global optimization and improve the prediction effect of the model.

The rest of this paper is structured as follows. Section 2 mainly discusses the method and principle of brake pad wear state monitoring based on the CNN-LSTM-GTO model. Section 3 introduces the construction process of a brake pad wear sample data set and uses the method proposed in this paper for experimental testing and evaluation. Section 4 presents some important conclusions of this paper.

2. Brake Pad Wear Condition Monitoring Method

This section introduces the method of brake pad wear condition monitoring based on the CNN-LSTM-GTO model, mainly including the improved scheme, prediction process, and working principle of the CNN-LSTM-GTO model.

2.1. Improvement Scheme of the CNN-LSTM-GTO Model

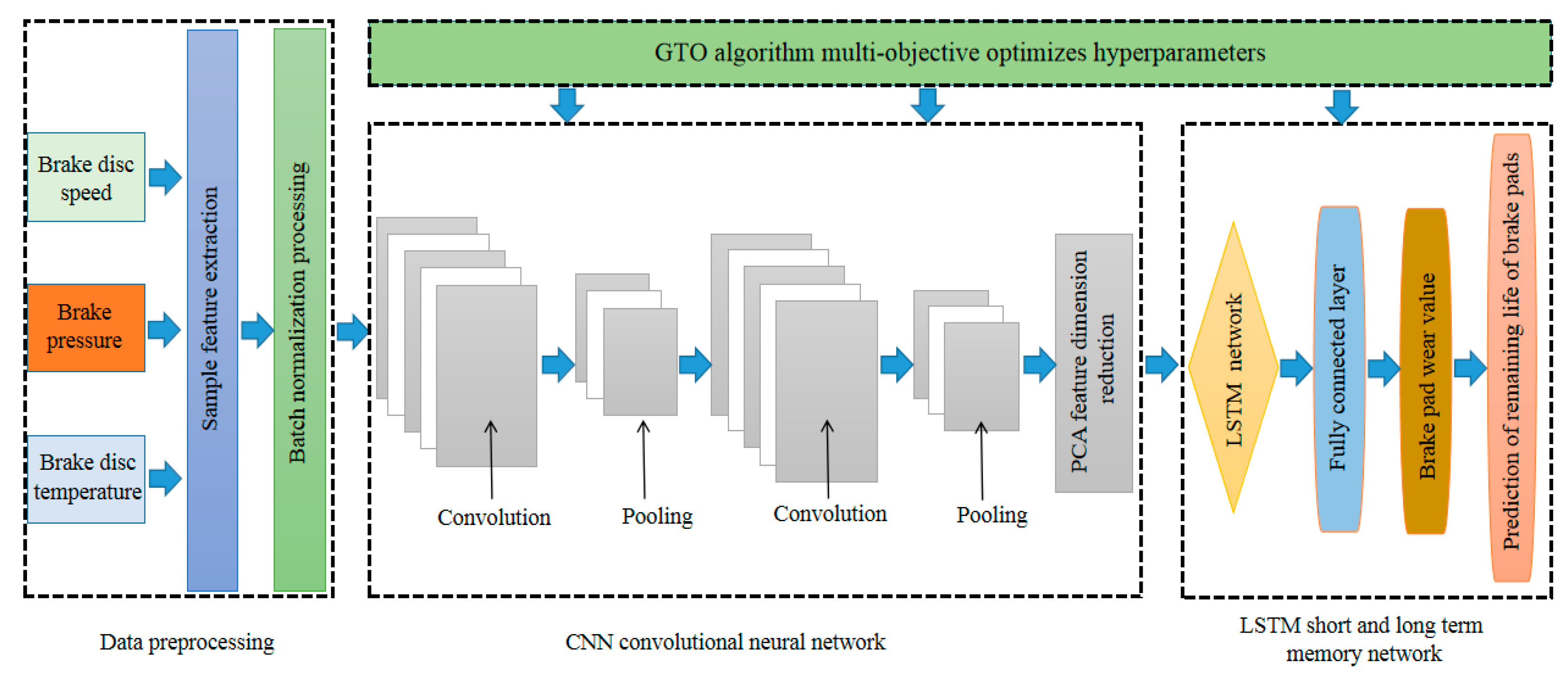
In order to improve the precision and accuracy of the brake pad wear condition monitoring model, this paper proposes a CNN-LSTM brake pad wear condition monitoring method based on multi-objective optimization of the GTO algorithm. This method can not only deeply mine the spatial features of brake disc speed, brake pressure, brake disc temperature, and other wear information, but also retains the effective information in the time dimension. A nonlinear mapping relationship is constructed with the wear thickness of the brake pads to output the wear thickness of the brake pads in real time, so as to calculate the residual thickness of the brake pads according to the initial thickness of the brake pads. When the residual thickness exceeds the wear threshold, a failure alarm will be generated. This monitoring method will have certain practical significance for realizing the predictive maintenance of automobile brake pads and improving the working reliability of brake pads. The improvements are as follows:

(1)

The detection of single wear information cannot contain all the wear characteristics of brake pads. Therefore, the data preprocessing part of the prediction model performs information fusion and batch normalization on the detected brake disc speed, brake pressure, and brake disc temperature, which improves the generalization ability of the model, avoids overfitting, and improves the convergence speed of the model.

(2)

The Convolutional Neural Network (CNN) is used as the feature learner of the condition monitoring model. The unique structure of the CNN model with local connection and weight sharing reduces the complexity of the network, and the spatial continuity of the sample features is maintained after convolution and pooling operations.

(3)

In order to capture the time series information in the process of brake pad wear, the Long Short-Term Memory (LSTM) network is used as the trainer. The Long Short-Term Memory (LSTM) network is a further optimization of the traditional RNN network, which can deal with longer time series data and avoid the phenomenon of gradient disappearance or gradient explosion.

(4)

The artificial Gorilla Troops Optimization (GTO) algorithm is used to optimize the network structure parameters in the CNN-LSTM model, which can automatically adjust the parameters while ensuring the training error is as small as possible, reduce the subjective influence of artificial selection parameters, and improve the prediction accuracy of the brake pad wear model. The CNN-LSTM hybrid prediction model based on GTO multi-objective optimization is shown in Figure 1.

2.2. Operation Process of CNN-LSTM-GTO Model

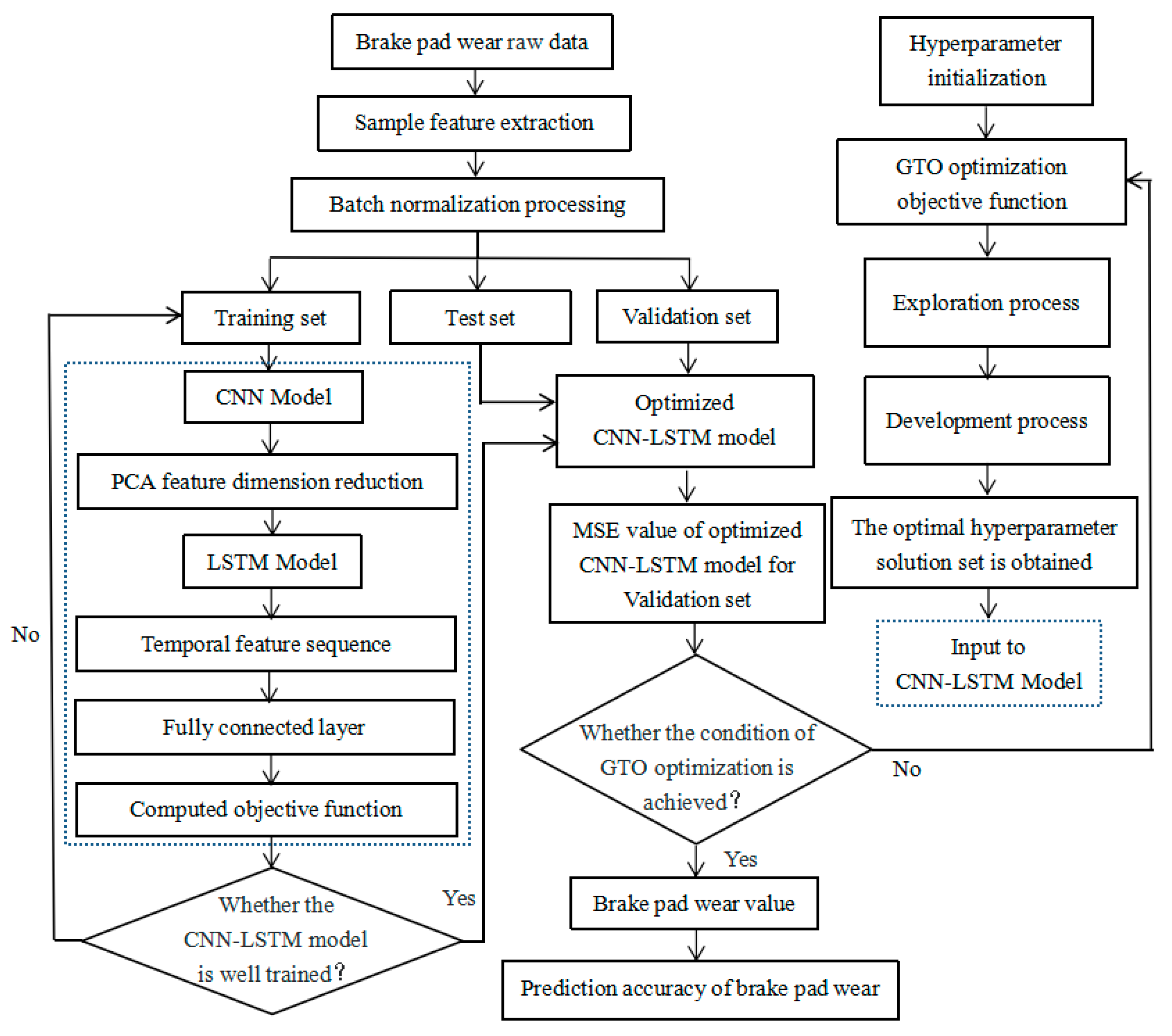
As shown in Figure 1, monitoring the wear state of brake pads mainly includes four main modules, which are the data preprocessing module, the artificial Gorilla Troops Optimization (GTO) algorithm multi-objective optimization module, the Convolutional Neural Network (CNN) module, and the Long Short-Term Memory (LSTM) network module. The brake pad wear prediction process of the CNN-LSTM-GTO model is shown in Figure 2, and the specific steps are as follows:

Step 1: The data preprocessing module performs information fusion and batch normalization on raw data such as the monitored brake disc speed, brake pressure, brake disc temperature, and the characterized brake disc wear values to form a spatiotemporal correlation sample data set.

Step 2: The GTO multi-objective optimization module is used to initialize the 11 hyperparameters to be optimized in the CNN-LSTM network structure, in order to prepare for finding the best hyperparameter solution set of the CNN-LSTM model.

Step 3: The brake pad wear sample data set formed in step 1 is divided into training set, validation set, and test set, and the division ratio is 7:1:2. At the same time, the initialized hyperparameters are input into the CNN-LSTM model.

Step 4: The training set is input into the CNN module for convolution and pooling operations, the deep features of the original data are extracted, and a compressed brake pad wear feature mapping vector after PCA dimension reduction is obtained.

Step 5: The compressed feature vector is input to the Long Short-Term Memory (LSTM) network module, and the LSTM network further captures the time-dependent characteristics of brake pad wear data.

Step 6: The 11 initial parameters provided in step 2 are used to train the CNN-LSTM network, and the fully connected layer and SoftMax layer are used to obtain the probability sequence and calculate the objective function. If the training termination condition is not reached, the above calculation is returned to step 4 until the maximum number of iterations is reached or the objective function converges.

Step 7: The validation set formed in step 3 is input into the trained CNN-LSTM model and the mean square error (MSE) between the predicted value and the actual value is calculated. If the termination condition is not reached, the GTO multi-objective optimization module iteratively updates the position of the population individuals through the exploration process and the development process until the optimal network structure parameter solution set is found.

Step 8: The test set formed in step 3 and the optimal network structure parameter solution set obtained in step 7 are input into the trained CNN-LSTM model for regression prediction of brake pad wear values, and then the prediction effect of the CNN-LSTM-GTO model proposed in this paper is evaluated.

2.3. Working Principle of CNN-LSTM-GTO Model

The CNN-LSTM hybrid model based on GTO multi-objective optimization combines the advantages of deep mining of the spatial features of the CNN network with the advantages of real-time capture of time series information of the LSTM network, and uses the GTO algorithm to perform multi-objective optimization on the network structure parameters in the model, so as to more accurately characterize the degradation trend of brake pad wear. The brake pad wear state monitoring model constructed in this paper has the characteristics of fast convergence, good stability, a repeatable training process, and high prediction accuracy. It can monitor the wear state of brake pads without prior knowledge or the help of human experts.

2.3.1. Convolution Neural Network (CNN)

With the explosive development of industrial big data, compared with traditional machine learning prediction methods, deep learning methods have shown more and more significant capabilities and advantages in dealing with nonlinear and large amounts of data [26]. As a typical representative of deep learning, the main difference between the Convolutional Neural Network (CNN) and other condition monitoring methods is the convolution operation and pooling operation, which can realize local connection and weight sharing and mine the deep features hidden in the sample [27]. Therefore, the pre-processing part of the condition monitoring model uses the CNN network to extract and fuse the spatial features of the sample data set, and its output is a one-dimensional sequence feature vector, which lays a foundation for using the LSTM network to monitor the wear state of brake pads. The principle of the model is as follows:

(1)

The sample data set after multi-channel feature fusion is input into the Convolutional Neural Network (CNN), and the convolutional layer convolved the data of the input layer with multiple convolution kernels to reduce the number of training parameters of the model. The weight value of each layer obtained by the convolution operation of the sample feature indirectly represents the local features of the sample. The higher the level is, the more detailed the local feature extraction is, and the spatial continuity of the sample can be maintained. The convolution operation is shown in Equation (1):

$$X_i^k={\displaystyle \sum _{j=1}^{\mathrm{n}}{W}_i^{kj}}\otimes X_{i-1}^j+{\mathrm{b}}_i^k$$

(1)

where $X_i^k$ represents the feature matrix of the kth neuron output by the ith layer, $W_i^{kj}$ represents the weight value of the kth neuron output by the ith layer, $\otimes$ represents the convolution operator, $X_{i-1}^j$ represents the feature matrix of the jth neuron output by the i − 1 layer, and ${\mathrm{b}}_i^k$ is the bias coefficient of the kth neuron output by the ith layer.

(2)

In order to improve the prediction accuracy of the brake pad wear condition monitoring model, the CNN network uses the Relu function for nonlinear activation, which has good unsaturated characteristics and avoids the phenomenon of gradient disappearance. The activation function is shown in Equation (2):

$$V_i^k=\mathrm{Re}lu\left(X_i^k\right)=\left\{\begin{array}{cc}0,& x_i^k<0\\ x_i^k,& x_i^k>0\end{array}\right.$$

(2)

where $x_i^k$ is each eigenvalue in the feature matrix.

Each tool wear feature datum is input into the pooling layer after the convolution operation, and the pooling type is selected as the maximum pooling, which can not only retain the original features but also reduce the size of the feature layer, simplify the complexity of the neural network, and improve the robustness of the sample features. The Max pooling is shown in Equation (3):

$$C_i^k\left(\begin{array}{cc}s,& t\end{array}\right)=\underset{\begin{array}{c}1+\left(s-1\right)Q\le d\le sQ\\ 1+\left(t-1\right)P\le h\le tP\end{array}}{Max}\left\{V_i^k\left(d,h\right)\right\}$$

(3)

where $V_i^k\left(d,h\right)$ is the eigenvalue of row d, column h of the ith feature matrix input by the pooling layer, $C_i^k\left(\begin{array}{cc}s,& t\end{array}\right)$ is the eigenvalue of row s, column t of the ith feature matrix obtained after the pooling process, P and Q are the length and width of the pooling region, respectively.

(3)

The n feature matrices with dimension S × T obtained from each row of the sample data set after two convolution and pooling operations are input into the global average pooling layer. The dimension of the pooling kernel of the global average pooling layer is consistent with the dimension of the feature matrix, and the dimension of the n feature matrices is reduced to reduce the collinearity of the sample features and avoid the influence of redundant features, thereby reducing the training time of the LSTM network. Therefore, the entire CNN model finally outputs a feature vector X_t = {x₁, x₂, …, x_i, …, x_j,} where xi is calculated as shown in Equation (4):

$$x_i=\frac{1}{ST}{\displaystyle \sum _{s=1}^S{\displaystyle \sum _{t=1}^T{C}_i^k}}\left(s,t\right)$$

(4)

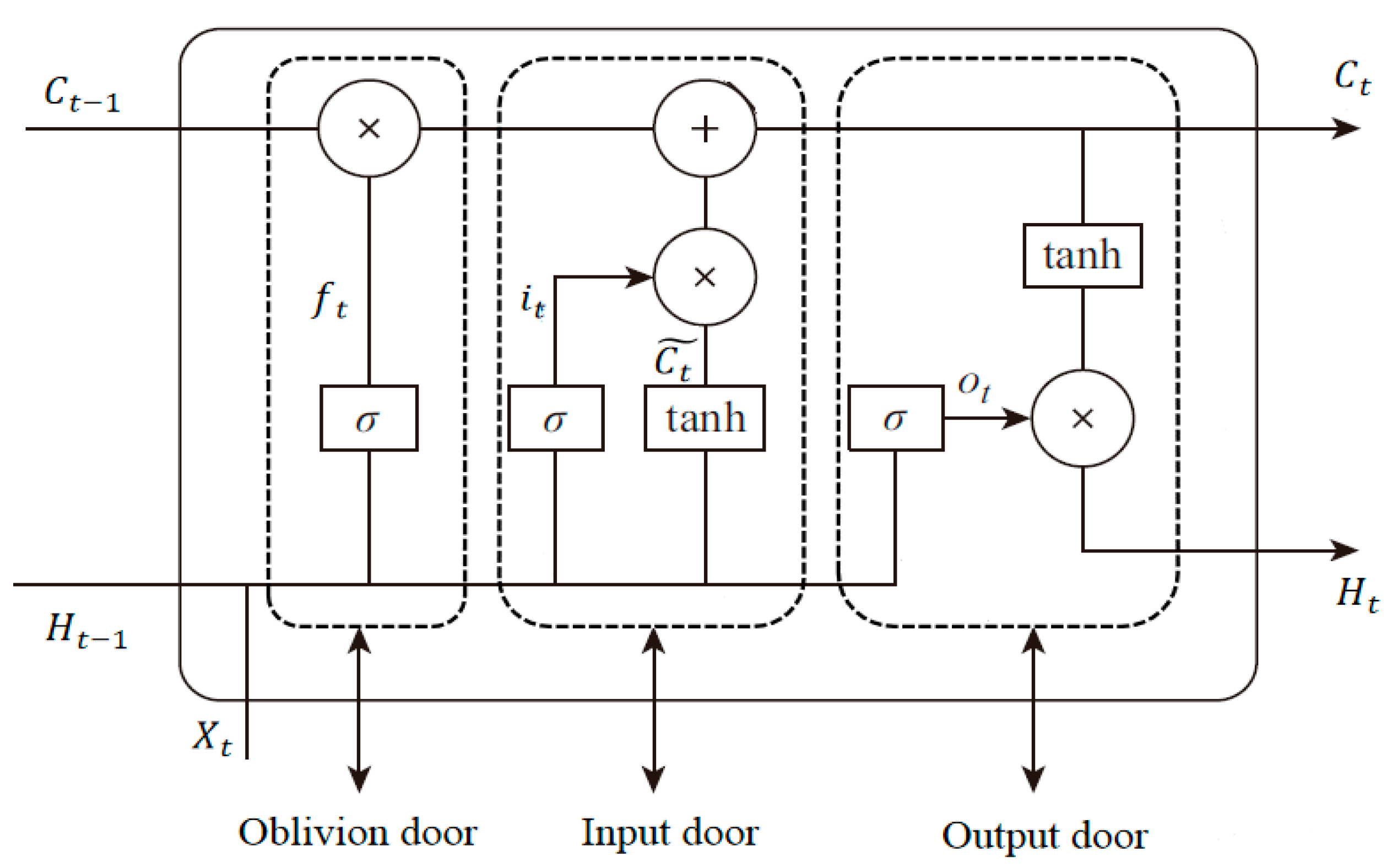
2.3.2. Long Short-Term Memory (LSTM) Neural Network

The CNN can mine the local spatial features related to brake pad wear, but it is difficult to extract longer time series data [28]. Therefore, this paper uses the LSTM network to further process the feature vector output by the CNN model and construct the relationship between the sample features and the time series. The LSTM network was proposed by Hochreiter and Schmidhuber in 1997, which was a further improvement of the traditional RNN network. In the input, output, and forget the past information, the memory cells are introduced to construct a new unit state to realize data transmission, and the logic operation is carried out through the input gate, output gate, and forget gate. It controls the path of data transmission so as to complete the processing of long time series data [29]. The LSTM network structure is shown in Figure 3.

In this paper, the LSTM network is used to extract the temporal features of the sample, and the specific principle is as follows:

(1)

The memory feature C_t−1 of the input of the previous layer unit is forgotten or memorized through the forget gate f_t. The calculation method of the forget gate f_t is shown in Equation (5):

$$f_t=\sigma \left(W_f\cdot \left[H_{t-1},X_t\right]+b_f\right)$$

(5)

where H_t−1 is the time series information output at the previous time, X_t is the sample feature input at this time, σ is the sigmoid function, W_f is the weight value of the forgetting gate training, and b_f is the bias coefficient of the forgetting gate training.

(2)

The input sample feature X_t is logically calculated through input gate i_t to update the memory of the whole system. The calculation method of input gate i_t is shown in Equation (6):

$$i_t=\sigma \left(W_i\cdot \left[H_{t-1},X_t\right]+b_i\right)$$

(6)

where W_i is the weight value of the input gate training, and b_i is the bias coefficient of the input gate training.

(3)

According to the path set by the system, a new memory feature C_t is generated. The calculation method of the new memory feature C_t constructed by the input gate and the forget gate is shown in Equation (7).

$$C_t=f_t\otimes C_{t-1}+i_t\otimes tanh\left(W_c\cdot \left[H_{t-1},X_t\right]+b_c\right)$$

(7)

where C_t−1 is the memory feature output at the last moment, tanh is the activation function, W_c is the weight value of the memory feature training, and b_c is the bias coefficient of the memory feature training.

(4)

The output gate o_t controls the memory feature C_t and outputs the timing feature H_t, which is transmitted to the next layer unit. The calculation methods of output gate ot and timing feature H_t are shown in Equations (8) and (9):

$$o_t=\sigma \left(W_o\cdot \left[H_{t-1},X_t\right]+b_o\right)$$

(8)

$$H_t=o_t\otimes tanh\left(C_t\right)$$

(9)

where W_o is the weight value of the output gate training, and b_o is the bias coefficient of the output gate training.

(5)

The brake pad wear feature vector M_t = {H₁, H₂, H₃…, H_t…, H_n} is constructed and input into the fully connected layer to predict the remaining life of the brake pads, and the wear value y_t of the brake pads is obtained. The calculation method is shown in Equation (10):

$$y_t=W_s{M}_t+b_s$$

(10)

where y_t is the predicted value of brake pad wear, W_s and b_s are the weight and bias value of the fully connected layer, respectively.

2.3.3. Artificial Gorilla Troops Optimization (GTO)

The CNN-LSTM model can monitor the wear state of brake pads, but it is prone to overfitting when dealing with data samples with many features [30]. It is necessary to use some optimization algorithms to determine the optimal hyperparameters of the CNN-LSTM model, so as to increase the nonlinear fitting performance and prediction accuracy of the model. The artificial Gorilla Troops Optimization (GTO) algorithm can effectively solve the problem of finding the global optimal solution set, has better applicability for solving large-scale nonlinear integer programming problems, and is widely used in multi-objective hyperparameter optimization [31]. The two core parts of the multi-objective optimization process of the GTO algorithm are the exploration process and the development process. In the exploration process, the optimal individual is selected by adjusting the migration position of the individual gorilla, and the development process completes the optimization of the multi-objective solution set by the two means of submission and competition. The specific principle is as follows:

(1)

In the first iteration of the GTO algorithm, the population is initialized first, and each individual gorilla in the initialized gorilla group is the network structure parameter to be optimized in the CNN-LSTM model. There are 11 hyperparameters to be optimized in this paper, and the mathematical model of population initialization is shown in Equation (11).

$$X_0=L_{\mathrm{b}}+rand(U_{\mathrm{b}}-L_{\mathrm{b}})$$

(11)

where L_b and U_b represent the minimum value and maximum value of a hyperparameter value range, respectively; rand () represents a random number in the range [0, U_b − L_b].

(2)

The exploration process of the GTO multi-objective optimization algorithm needs to set the probability coefficient P of the population reaching the final known position in each migration scheme, and its value range is [0, 1]; P is 0.03 in this paper. According to the relationship between the random number rand and the coefficient P, the gorillas′ migration schemes can be divided into three types, which are migration to unknown coordinates, migration to other gorillas′ position coordinates, and migration to known coordinates. When the obtained random number rand is less than the probability coefficient P, the first scheme is adopted, and the individual migrates toward the unknown coordinates. The mathematical model is shown in Equation (12):

$$GX(t+1)=(U_{\mathrm{b}}-L_{\mathrm{b}})\times r_1+L_{\mathrm{b}}$$

(12)

where GX(t + 1) is the candidate position coordinates of the individual gorilla in the next iteration; r₁ represents a random number, whose value range is [0, 1].

When the random number rand is greater than or equal to 0.5, the second scheme is adopted, and the relocation is carried out toward the location coordinates of the other gorillas. The mathematical model is shown in Equation (13):

$$GX(t+1)=(r_2-C)\times X_r(t)+L\times H$$

(13)

$$C=\left\{\cos (2\times r_3)+1\right\}\times (1-\frac{Iter}{Ite{r}_{\max }})$$

(14)

$$L=C\times rand(-1,1)$$

(15)

$$H=Z\times X(t)$$

(16)

where X(t) is the current position coordinate of the individual gorilla; X_r(t) represents the current position coordinate of the randomly selected gorilla individual; r₂ and r₃ represent two random numbers in the range [0, 1]; Iter represents the current iteration number; Iter_max is the set maximum number of iterations; Z is a random value in the range [−C,C] in the problem dimension.

When the random number rand is obtained between the coefficient P and 0.5, the third scheme is adopted, and the individuals migrate toward the known coordinates. In this paper, P is 0.03, and the mathematical model is shown in Equation (17):

$$GX(t+1)=X(t)-L\times \left\{L\times \left[X(t)-G{X}_{\mathrm{r}}(t)\right]+r_4\times \left[X(t)-G{X}_{\mathrm{r}}(t)\right]\right\}$$

(17)

where GX_r(t) represents the candidate position coordinates of a randomly selected individual gorilla; r₄ represents a random number whose value range is [0, 1].

In summary, the essence of the whole exploration process is to calculate the fitness value of each scheme GX individual. If GX(t) < X(t) is satisfied, the GX(t) individual replaces the X(t) individual to become the optimal individual, and the optimal individual is called silverback gorilla.

(1)

The development process of the GTO multi-objective optimization algorithm mainly includes two schemes: obeying silverback gorillas and competing for female mates. When C ≥ M, the development process of the GTO algorithm adopts the strategy of obeying the silverback gorilla in Scheme 1, and its mathematical model is shown in Equation (18):

$$GX(t+1)=L\times M\times \left[X(t)-X_{\mathrm{S}}\right]+X(t)$$

(18)

$$M={\left[{\left|\frac{1}{N}{\displaystyle \sum _{i=1}^{N}G{X}_i(t)}\right|}^g\right]}^{\frac{1}{g}}$$

(19)

$$g=2^L$$

(20)

where GX(t + 1) is the candidate position coordinate of the individual gorilla in the next iteration; X(t) is the current position coordinate of the individual gorilla; X_s represents the position coordinate of the silverback gorilla; N is the number of gorillas in the population.

When C < M, the development process of the GTO algorithm adopts the competitive female mate strategy of Scheme 2, and its mathematical model is shown in Equation (21):

$$GX(t)=X_{\mathrm{S}}-\left[X_{\mathrm{S}}\times Q-X(t)\times Q\right]\times A$$

(21)

$$Q=2\times r_5-1$$

(22)

$$A=\beta \times E$$

(23)

$$E=\left\{\begin{array}{l}{N}_1\begin{array}{cc}& \end{array}rand\ge 0.5\\ N_2\begin{array}{cc}& \end{array}rand<0.5\end{array}\right.$$

(24)

where Q is used to simulate the impact force; A is the coefficient vector of the violence level in the conflict; r₅ is a random number in the range [0, 1]. β represents a given coefficient, which is 3 in this paper; N₁ represents the normal distribution and random values in the scheme dimension; N₂ denotes a random value in a normal distribution.

At the end of the development process, a group optimization operation is carried out, in which the fitness values of all GX individuals are calculated again, and the relative size of the fitness value directly determines the result of this time to discard or cover the optimal individuals that were previously found. Through multiple iterations, the optimal hyperparameter solution set of the CNN-LSTM model is finally output.

3. Verification and Evaluation of Brake Pad Wear Condition Monitoring Experiment

This section mainly takes the constant speed friction and wear testing machine as the experimental platform, uses sensor technology to collect the raw data of brake pad wear in real time, constructs the sample data set after multi-channel data fusion, and inputs it into the hybrid model of CNN-LSTM-GTO proposed in this paper to complete the brake pad wear state monitoring experiment. It mainly includes the construction of a brake pad wear sample data set, the multi-objective optimization hyperparameter process of the GTO algorithm, and the verification and evaluation of the CNN-LSTM-GTO model.

3.1. Construction of the Sample Dataset

The experimental platform for brake pad wear condition monitoring used the JF150-S-II fixed-speed friction and wear test device, which includes three parts: power drive system, braking system, and measurement and control system. The construction of the brake pad wear sample data set mainly relied on the measurement and control system, which is mainly composed of sensors, data acquisition devices and computers, which can realize off-machine testing and automatic temperature control. The temperature control error was small and the precision was high. The experimental platform for brake pad wear state monitoring is shown in Figure 4.

The input of the sample data set in this paper mainly included three braking parameters: brake disc speed, brake pressure, and brake temperature. In order to simulate the real braking situation in the driving process of the car, the driving speed of the car was controlled between 40 and 120 km/h according to the national road safety regulations. The brake disc speed refers to the relative speed of sliding friction between the brake pads and the brake disc. Through calculation, it was determined that the brake disc speed control range was 354 to 1061 r/min. Brake pressure refers to the brake system to lock the brake pad pressure; this paper calculated the relevant requirements of automobile brake performance to control the brake pressure at 0.8 to 1.6 MPa, the measurement and control system through the pressure sensor to control the brake pressure. The brake temperature refers to the instantaneous temperature caused by the friction between the brake pads and the brake disc. The real-time temperature of the brake pads was extracted through the temperature sensor, and the extracted temperature range was 47.4 to 84.7 °C. The monitoring range of the three brake parameters is shown in

Table 1. Selection range of brake parameters.

Brake Parameters	Sensor	Parameter Range
Brake disc speed	Speed sensor	354 r/min to 1061 r/min
Brake pressure	Pressure sensor	0.8 MPa to 1.6 MPa
Brake disc temperature	Temperature sensor	47.4 °C to 84.7 °C

.

The original data of the above three braking parameters and the wear amount of the brake pads after braking were extracted. However, the wear amount of the brake pads after a single braking was very small and difficult to measure, so the extraction experiment for the braking characteristics was carried out every ∆t time. In this experiment, the number of braking times in ∆t time was 300, and each brake parameter was kept unchanged. Therefore, the three brake disc wear characteristics including brake disc speed, brake pressure, and brake disc temperature were obtained in each feature extraction experiment. Every 50 feature extractions in the experimental process were set as one group, that is, the brake pad reaching its life after 50 feature extraction experiments, and each group of experiments obtained a feature sample matrix of 50 × 3. At the same time, the thickness of the brake pads before and after braking in ∆t time was measured, and the wear amount of the brake pads after each braking was divided by the braking times, so a target sample matrix of 50 × 1 was obtained. The whole life process experiment of the brake pads was repeated three times, so three groups of sample data sets characterizing the wear state of the brake pads were obtained, with a dimension of 150 × 4.

In order to improve the generalization ability of the prediction model and determine the influence degree of the three brake parameters on brake pad wear, the first set of characteristic sample matrix and brake pad wear values were normalized, and the normalization processing method is shown in Formula (25):

$$X_{\mathrm{n}}=\frac{X-X_{\mathit{min}}}{X_{\mathit{max}}-X_{\mathit{min}}}$$

(25)

where X is the sample of each feature, X_min is the minimum value of the sample feature, and X_max is the maximum value of the sample feature.

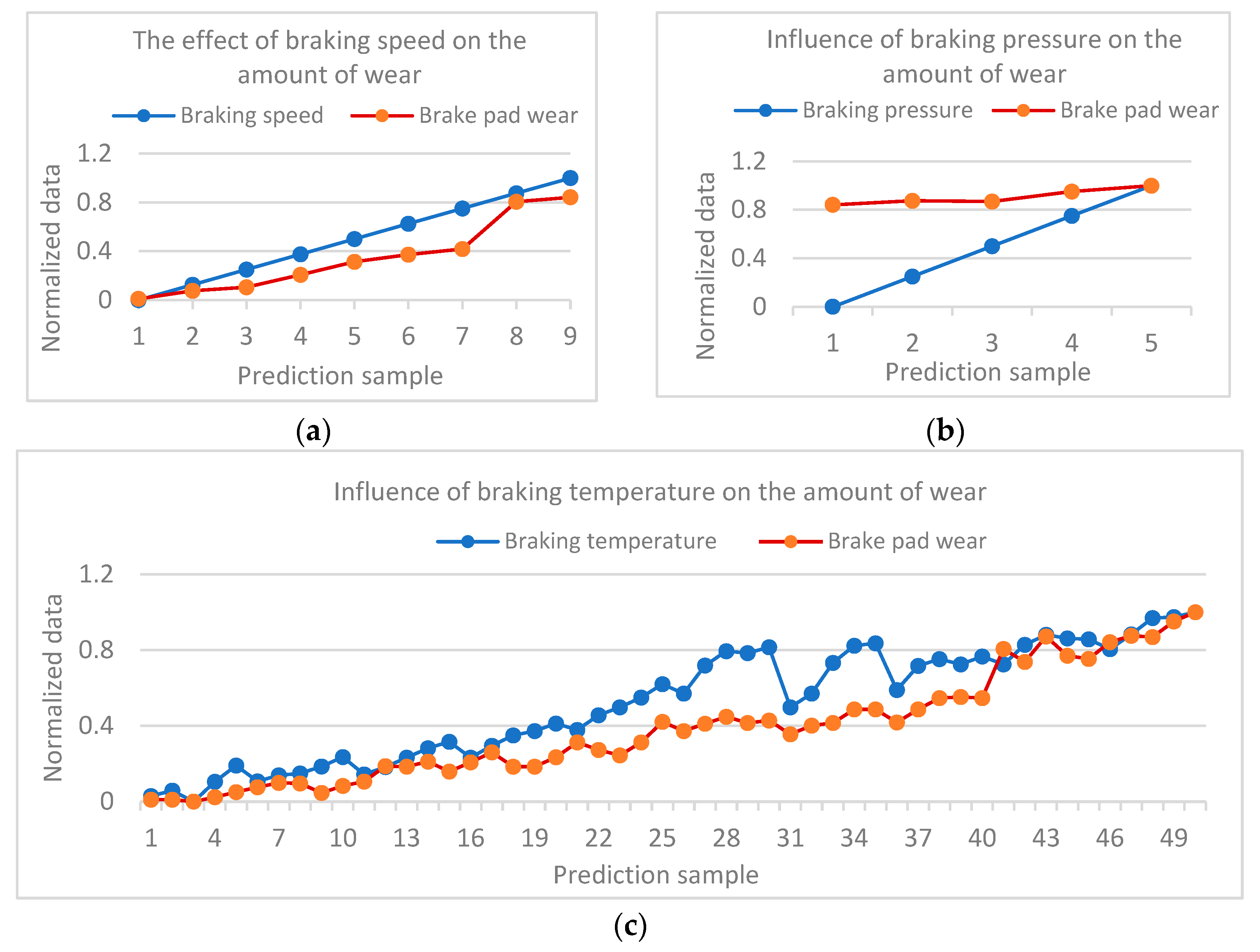
Figure 5 shows the influence of each brake parameter on brake pad wear after normalization. It can be seen from Figure 5 that, according to the above requirements, with the increase in brake disc speed, brake pressure, and brake temperature, there was an average increase trend of brake pad wear. However, the brake speed and temperature had a great influence on the brake pad wear, while the brake pressure had no significant influence on the brake pad wear. This was because with the increase in brake pressure, this will theoretically cause the brake pad wear to be more intense, but at the same time, it will also make the braking time relatively shorter, so the brake pressure has less impact on the brake pad wear for other parameters.

3.2. GTO Multi-Objective Optimization Hyperparameter Process

The essence of multi-objective optimization of artificial Gorilla Troops Optimization (GTO) algorithm is to find the maximum or minimum value of the fitness function. In this paper, the mean square error (MSE) between the predicted value and the actual value of the CNN-LSTM network was minimized as the fitness function; that is, a set of optimal hyperparameter solution sets were found to minimize the mean square error of the CNN-LSTM network. The process of multi-objective optimization of the CNN-LSTM network hyperparameters by the GTO algorithm consisted of three branches, which were the GTO algorithm, CNN-LSTM network, and sample data set.

First, the CNN-LSTM network decoded the input parameters of the GTO algorithm and initialized all the hyperparameters. Second, the sample data set was divided into training set and validation set, and the training set was used to complete the training of the CNN-LSTM network. Finally, the validation set was used to complete the prediction, and the mean square error between the actual value and the predicted value was obtained, and the mean square error value was returned to the GTO algorithm as the fitness value. The GTO algorithm optimized according to the fitness value, realized the iterative update of the individual gorilla candidate position coordinates, and finally output the optimal network structure parameter solution set. Figure 6 shows the fitness curve of the CNN-LSTM network optimized by the GTO algorithm. It was found that with the increase in the number of iterations, the mean square error (MSE) value of the CNN-LSTM network became smaller and smaller, and the globally optimal network structure parameter solution set appeared at the sixth iteration.

The 150 × 4 brake pad sample data set was input into the CNN-LSTM network, and the artificial Gorilla Troops Optimization (GTO) algorithm was used to complete the global optimization of the model hyperparameter set. The hyperparameter set contained a total of 11 parameters, which were the initial learning rate (Lr), training times (Epochs), the number of samples per batch (BatchSize), the number of kernels in convolutional layer 1 (Kernel_num), the number of kernels in convolutional layer 1 (Kernel_size), the number of kernels in pooling layer 1 (Pool1_size), the number of kernels in convolutional layer 2 (Kerne2_num), the number of kernels in convolutional layer 2 (Kerne2_size), the number of kernels in pooling layer 2 (Pool2_size), the number of nodes in the LSTM layer (Lstm_node) and the number of nodes in the fully connected hidden layer (Fc_node). The setting range of the hyperparameter set and the optimization results of the sixth iteration are shown in

Table 2. Hyperparameter results of the GTO multi-objective optimization CNN-LSTM model.

Sequence Number	Hyperparameters	Setting Range	Optimize Results
1	Lr	[1 × 10−4, 1 × 10−2]	0.0036
2	Epochs	[10, 100]	81
3	MiniBatchSize	[8, 64]	25
4	Kernel_num	[1, 20]	5
5	Kernel_size	[1, 10]	4
6	Pool1_size	[1, 5]	2
7	Kerne2_num	[1, 20]	10
8	Kerne2_size	[1, 10]	7
9	Pool2_size	[1, 5]	2
10	Lstm_node	[1, 50]	42
11	Fc_node	[1, 200]	90

.

3.3. Prediction Results of CNN-LSTM-GTO Model

The constant speed friction and wear test rig were used to carry out the experiment, and the 150 × 4 brake pad wear sample data set was input into the CNN-LSTM model based on GTO multi-objective optimization to complete the regression prediction of brake pad wear thickness by MATLAB software. The network structure of the CNN-LSTM-GTO model constructed parameter is shown in

Table 3. CNN-LSTM-GTO model constructed parameter.

Flow Chart	Network Structure	Parameter Settings
	Convolutional layer (conv1)	Activation function: RELU Initial Learn Rate: 0.0036 Kernel_num: 5 Kernel_size: 4
	Pooling layer (pool1)	Average pooling Pool1_size: 2
	Convolutional layer (conv2)	Activation function: RELU Initial Learn Rate: 0.0036 Kernel_num: 10 Kernel_size: 7
	Pooling layer (pool2)	Average pooling Pool1_size: 2
	LSTM layer (lstm)	Activation function: Sigmoid Number of hidden layer units: 42
	Fully connected layer (f)	Fc_node: 90

. Figure 7 shows the loss function curve of the brake pad wear state monitoring model. It can be seen that the loss value of this model showed a rapid decline trend in the first 60 iterations, and then the loss value tended to be stable, which means that the objective function could not be improved by continuing the iterative operation.

To quantify the prediction performance of the brake pad wear condition monitoring model, it was necessary to develop evaluation indicators. Three objective evaluation indicators were selected, which were the mean absolute error MAE, the root mean square error RMSE, and the coefficient of determination R². Among them, MAE obtains an evaluation value, but only through the comparison between the different models can it reflect the pros and pros of the model. Both mean square error RMSE and coefficient of determination R² directly characterize the quality of the model. The smaller the mean square error RMSE, the closer the value of the coefficient of determination R² is to 1, the higher [32] the precision and accuracy of the prediction model. The calculation formula of the three evaluation indicators is as follows:

$$MAE=\frac{{\displaystyle {\sum }_{t=1}^m\left|y_t-{\widehat{y}}_t\right|}}{m}$$

(26)

$$RMSE=\sqrt{\frac{{\displaystyle {\sum }_{t=1}^m{\left(y_t-{\widehat{y}}_t\right)}^2}}{m}}$$

(27)

$$R^2=1-\frac{{\displaystyle {\sum }_{t=1}^m{\left(y_t-{\widehat{y}}_t\right)}^2}}{{\displaystyle {\sum }_{t=1}^m{\left(y_t-{\overline{y}}_t\right)}^2}}$$

(28)

where m is the number of samples output by the fully connected layer, and the number of samples was 150; ${\widehat{y}}_t$ is the predicted value of tool wear; $y_t$ is the actual value of tool wear; ${\overline{y}}_t$ is the average value of tool wear.

The sample data set was divided into a training set, validation set, and test set, and the ratio was 7:1:2. The fitting effect of the test set is shown in Figure 8. The red line represents the equation y = x; it can be seen that the error between the true value and the predicted value was very small, which indicated that the CNN-LSTM model based on GTO multi-objective optimization had strong generalization ability and robustness. 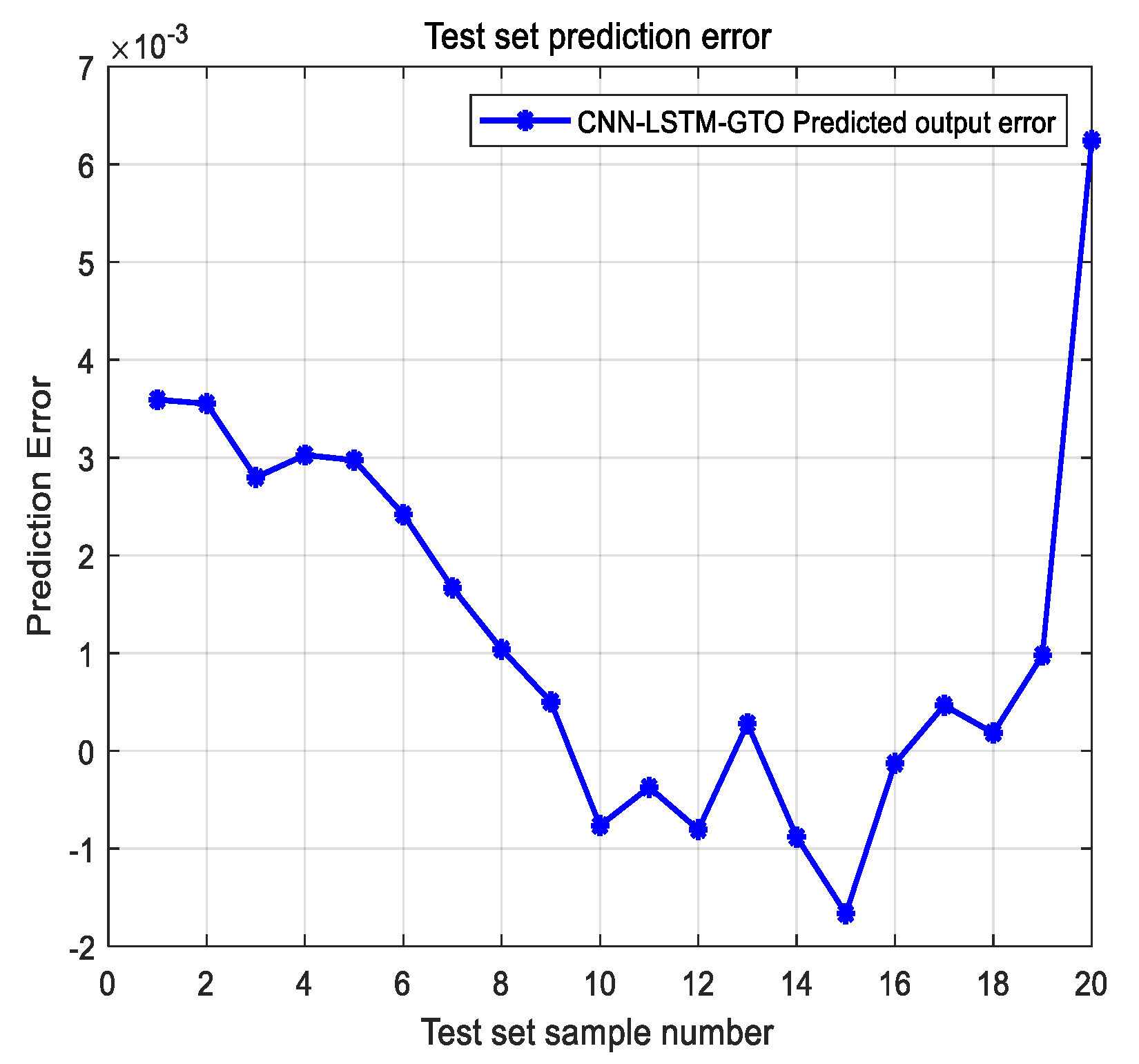Figure 9 shows the test errors of the CNN-LSTM-GTO model for 20 samples in the test set. It can be seen from the figure that the error values were controlled between −0.002 and 0.006, which indicated that it was safe and reliable to use this model to monitor the wear state of brake pads. Figure 10 shows the prediction results of the CNN-LSTM-GTO model for the test set. The determination coefficient R² value of the brake pad condition monitoring model was 0.9944, the root mean square error RMSE value was 0.0023, and the mean absolute error MAE value was 0.0017. In summary, the CNN-LSTM model based on multi-objective optimization of the GTO algorithm can effectively monitor the wear state of brake pads and achieve good results.

Figure 11 shows the comparison results of the CNN-LSTM model before and after optimization, where the blue curve is the prediction result of the CNN-LSTM model without optimization. The 11 hyperparameters in this model were manually selected, and their values were the median values of each value range. The green curve is the CNN-LSTM model optimized by the multi-objective GTO algorithm. It can be seen that the CNN-LSTM model optimized by the GTO algorithm had a better monitoring effect on brake pad wear condition, and the error curve between the predicted value and the real value of each sample had a lower fluctuation range and a higher degree of agreement. The CNN-LSTM model with manual selection of parameters had a wide fluctuation range and unstable prediction results, which was mainly because the GTO algorithm obtained a more accurate hyperparameter solution set after multi-objective optimization of the hyperparameters of the CNN-LSTM model, and found the most critical attribute that affected the accuracy of brake pad wear prediction, avoiding the blindness of setting parameters. Therefore, the prediction effect was improved.

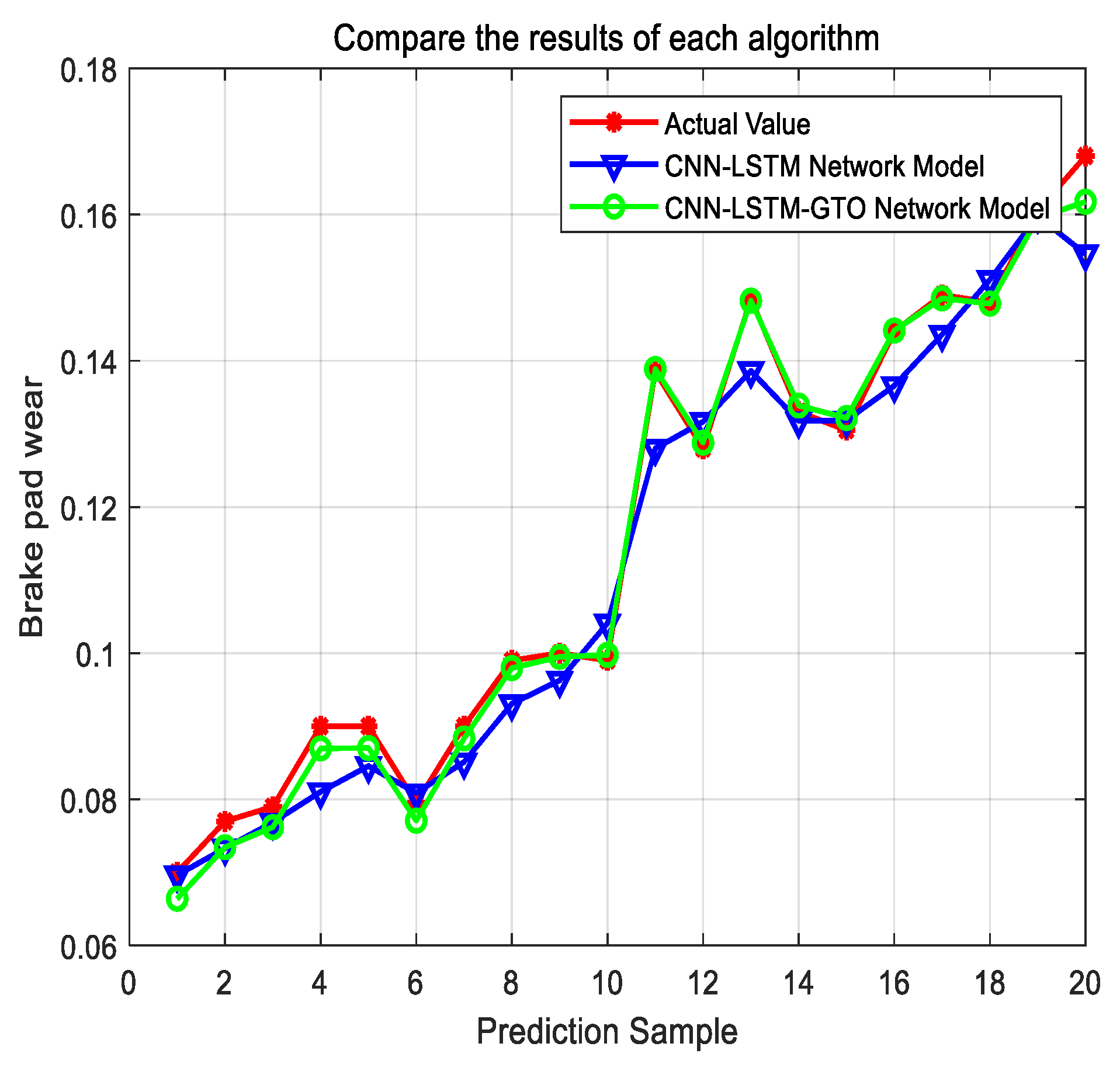
In order to further verify the prediction performance of the CNN-LSTM brake pad wear condition monitoring model based on GTO multi-objective optimization, it was compared with past traditional prediction models, such as the BP neural network, CNN model, LSTM model, and CNN-LSTM model. Figure 12 shows the comparison results of the four traditional condition monitoring models. It can be seen from Figure 10 and Figure 12 that the brake pad wear curve predicted by the CNN-LSTM model with GTO multi-objective optimization was closer to the real brake pad wear curve than the other four prediction models, and the fluctuation range of the error curve was the smallest. The prediction effects of the five brake pad condition monitoring models were CNN-LSTM-GTO > CNN-LSTM > LSTM > CNN > BP. It can be seen that the prediction performance of the CNN-LSTM brake pad wear condition monitoring model based on GTO multi-objective optimization proposed in this paper had certain advantages. This was because of the single algorithm of the BP neural network, CNN model, and LSTM model, incomplete feature extraction, and poor generalization ability. Although the prediction effect of the CNN-LSTM model was better than those of the BP neural network, CNN model, and LSTM model, the network structure parameters in the prediction model were not optimized by the GTO algorithm and were not the global optimal solution set, so it was still not as good as the prediction effect of the CNN-LSTM-GTO model proposed in this paper. This result once again proved the role of the artificial Gorilla Troops Optimization (GTO) algorithm in the process of brake pad wear condition monitoring.

Table 4. Comparison of the prediction performance results of the five models.

Algorithm	Test Set Prediction Results
	MAE	RMSE	R2
BP Neural Network	0.0071	0.0091	0.9121
CNN Network	0.0055	0.0076	0.9396
LSTM Network	0.0052	0.0069	0.9500
CNN-LSTM Network	0.0049	0.0060	0.9617
CNN-LSTM-GTO Network	0.0017	0.0023	0.9945

contains the calculation results of the five model evaluation indexes. Compared with other traditional prediction models, the mean absolute error MAE value of the CNN-LSTM-GTO brake pad wear condition monitoring model proposed in this paper was the smallest. Compared with the BP model, CNN model, LSTM model, and CNN-LSTM model, the MAE value of the proposed CNN-LSTM model was reduced by 76.1%, 69.1%, 67.3%, and 65.3%, respectively. The root mean square error (RMSE) value was the smallest, which was reduced by 74.7%, 69.7%, 66.7%, and 61.7% compared with the BP model, CNN model, LSTM model, and CNN-LSTM model, respectively. The value of determination coefficient R2 was closest to 1, which was 8.29%, 5.52%, 4.47%, and 3.30% higher than those of the BP model, CNN model, LSTM model, and CNN-LSTM model, respectively. These three results once again proved that the CNN-LSTM method based on GTO multi-objective optimization proposed in this paper had higher accuracy in predicting brake pad wear thickness and more effectively realized brake pad wear state monitoring and intelligent early warning. This was because this method could not only mine the deep spatial features, but also retained the effective features of the time series. At the same time, the model accurately found the best matching of the model hyperparameters after multi-objective optimization of the GTO algorithm, which made the generalization ability of the whole model stronger and further improved the accuracy of brake pad condition monitoring.

4. Conclusions

In this paper, the sensor technology was used to collect the original data of brake disc speed, brake pressure, and brake disc temperature that characterize the wear characteristics of brake pads, and the wear thickness of brake pads was measured at the same time. The brake disc wear sample data set was constructed after feature extraction and fusion. Then, a CNN-LSTM prediction model based on GTO multi-objective optimization was proposed to monitor the wear state of brake pads and, compared with other traditional prediction models, the results showed that:

(1)

With the increase in braking speed, braking pressure, and braking temperature, the average trend of brake pad wear was increasing; however, the brake speed and temperature had a great influence on the brake pad wear, and the brake pressure had no significant effect on the brake pad wear.

(2)

The global multi-objective optimization of 11 parameters of the CNN-LSTM model was completed by the artificial Gorilla Troops Optimization (GTO) algorithm, and a set of optimal hyper-parameter solution sets was finally obtained, which reduced the subjective influence of the artificial selection parameters, avoided the blindness of the parameter setting, and improved the prediction accuracy.

(3)

The CNN-LSTM-GTO model was used to regression predict the wear thickness of brake pads. The coefficient of determination R2 value was 0.9944, the root mean square error RMSE value was 0.0023, and the mean absolute error MAE value was 0.0017. This showed that the model effectively monitored the wear state of brake pads and achieved good results.

(4)

Compared with the BP model, CNN model, LSTM model, and CNN-LSTM model, the mean absolute error MAE and root mean square error RMSE values of the CNN-LSTM-GTO model proposed in this paper were reduced, and the determination coefficient R2 value was improved, which was closest to 1. This showed that the constructed brake pad life prediction model had fewer errors, better accuracy, and better effect.

In the future, the CNN-LSTM-GTO brake pad wear condition monitoring model can be widely used in automobile manufacturing and automobile maintenance. By real-time monitoring the brake disc speed, brake pressure, and brake disc temperature, the model outputs the wear amount of the brake pads after each braking and accumulates the wear amount after braking to calculate the residual thickness of the brake pads. When the residual thickness of the brake pads exceeds the wear threshold, a failure alarm prompt will be generated to avoid accidents caused by brake failure. The research on this method will play an important role in improving the level, safety, and reliability of the brake system in China′s automobile manufacturing industry and automobile maintenance industry and seize the strategic highland of the development of new science and technology in the international competition.