Abstract
Generating localized haptic feedback on touch displays has been a challenge in recent years. In this study, we introduce a haptic interface using transparent thin-film PVDF actuators to address this issue. The transparency feature can be used to mount the actuators at any location beneath the display, enabling localized haptic feedback as the generated vibration is primarily evident on the mounting area. Two different configurations are designed, simulated and prepared to explore the effectiveness of the proposed approach. The first configuration is used to characterize the haptic interface. Modal and forced-vibration analyses are performed to identify important design characteristics based on human factors. Subsequent 2AFC psychophysics experiments validate the characteristics. In the second configuration, eight actuators are attached to the touch surface in a 2 × 4 matrix formation and excited at different voltage amplitudes. Human experiments are conducted based on the results from corresponding forced-vibration analysis. The results show that subjects demonstrate an accuracy of 96% in identifying locations with haptic feedback when the actuators are excited with 232 Vpp. Overall, our study demonstrates the effectiveness of the proposed transparent haptic interface equipped with PVDF actuators in achieving localized haptic feedback on touch displays.
1. Introduction
With the prevalence of smartphones in the last decade, touch screens are everywhere in our daily life: mobile phones, kiosks, notebooks, tablet PCs, control interfaces of smart home appliances, etc. However, they mostly lack haptic feedback on their surface, which, as a supportive sensory channel, could have a high potential to improve task performance and usability [1,2]. Over the last decades, two main methods to obtain haptic feedback on touch screens have stood out: (1) electrostatic actuation and (2) electromechanical actuation. In the former method, a conductive transparent layer (i.e., indium tin oxide (ITO) films) embedded in the touch screen is excited with alternating voltages [2,3]. The latter is performed using different types of electromechanical actuators such as vibration motors, linear actuators, piezoelectric patches, and electroactive polymers, which are mechanically coupled to the touch screen [4,5].
Electrostatic actuation requires the relative movement of the user’s finger on the display at all times because it is mainly based on the change in friction force between the display surface and the finger. The electrostatic force, and hence the friction force, can be easily manipulated by varying the excitation voltage with a microcontroller. Moreover, touch interface systems that are actuated electrostatically do not include mechanically moving parts, which would reduce the lifespan of the appliance.
Typically, researchers employ the well-known surface capacitive touch sensor (Model: 3M SCT3250) to implement the electrostatic actuation method [1,6,7,8,9,10,11]. Here, the amplified excitation voltage is applied to the electrode embedded in the touch display, and the electric charges are evenly distributed on the entire conductive layer. Therefore, during a particular time period, only one haptic effect can be sensed by the contacting finger on a surface capacitive sensor. We refer to the finger of the current/different user by saying “natural stylus”. It is actually a tactile illusion that the user gets different feedback at different locations of the electrostatically actuated single-touch display. A second natural stylus would perceive the same haptic feedback, even if it contacted a different location simultaneously. At this point, one of the biggest drawbacks arises: there is actually no multi-haptic feedback in those studies. True multiple haptic effects, felt via several natural styli interacting with the touch display, can only be obtained by “partitioning” conductive surfaces. In a novel demo study, the ITO layer of a surface-capacitive touch sensor is partitioned by laser ablation method so that every “ITO-cell” can be excited individually [12]. Therefore, the haptic feedback is literally localized, and users perceive different haptic effects via each individual natural stylus. Similarly, in important studies, Haga et al. achieved localized haptic feedback on the electrodes of a commercially available projected capacitive touch sensor using beat phenomenon [13,14]. These sensors consisted of parallel electrodes partitioned for x–y coordinates and are commonly employed on the touch screens of smart devices.
A similar haptic localization issue applies to the second method (electromechanical actuation), since the actuators vibrate the entire surface to which they are attached. Moreover, in this method it is necessary to mount the actuators not beneath the display area, but rather under the peripheral edges (i.e., screen bezels or the surface borders, excluding the visual area), since they would obviously block the visual information coming from the display. So, focusing the produced vibration on the desired locations is a new research problem. Nevertheless, there are some signal-processing solutions that can overcome the problem of haptic feedback localization [15,16]. This technique is called time-reversal focusing, where the mechanical waves generated by multiple piezoelectric actuators are spatially and temporally focused. However, they are not easy to implement and might require considerable processing power.
One attractive alternative to localized haptic feedback might be the utilization of transparent actuators. Matysek et al. fabricated a 3 × 3 matrix array of multilayer dielectric elastomer actuators in their study [17]. In another work, conducted by Stubning et al., a design procedure for a transparent EAP-stack actuator with multiple layers was introduced [18]. However, neither of those actuators were implemented on a display interface. There were two more studies where researchers deployed transparent actuators to generate vibrotactile feedback. One of them involved the use of electroactive polymer (EAP) arrays and employed beat phenomena to render haptic effects [19]. The other one introduced transparent graphene-based stack actuators to generate bumps with high amplitudes on tactile displays [20]. Nevertheless, these studies have not investigated the localization problem. Another study introduced promising transparent dielectric elastomer actuators for utilization to generate localized tactile feedback [21]. Unfortunately, these should be prepared to demonstrate a predefined tactile pattern. Finally, an important contribution was made by Duong et al., who successfully developed a transparent relaxor ferroelectric polymer film vibrator capable of generating vibration amplitudes sufficient for haptic perception [22].
In this study, we propose a simple but effective method where transparent piezoelectric polymer (polyvinylidene fluoride (PVDF)) films can be utilized to generate localized haptic feedback on touch displays. Furthermore, the optical transparency feature of the film actuators provides design flexibility, since they can be mounted in any shape and at any location on the touch interface. To demonstrate this, we positioned 50 μm thin PVDF films beneath a transparent plastic plate that can be mounted on a display. Unlike when using a stack of actuators, this study achieved accurate localized haptic feedback using only single actuators. Indeed, stack actuators can have the disadvantage of reducing the transmittivity of light, thus affecting the visual quality of the display output. This drawback underscores the efficiency of the proposed method in delivering precise haptic sensations while simultaneously simplifying the overall design.
2. Methods
To test the proposed concept, two transparent touch interfaces were designed and constructed. They consist of transparent plastic plates and multiple transparent PVDF-film actuators (from PolyK Technologies, optical transparency > 90% at 300–1000 nm wavelength) attached beneath the touch surface. Two different configurations were examined using analytical and experimental methods: (a) First, the modal analysis was performed in order to identify the proper characteristic parameters such as actuation frequency and vibration amplitude considering human-factors principles. (b) Afterward, these findings were utilized to evaluate subjects’ performances via experimental studies.
2.1. Hardware
Multiple transparent PVDF-film actuators (20 × 20 × 0.05 mm) are attached to the bottom of a clear polyvinyl chloride (PVC) plastic layer (100 × 50 × 0.6 mm), which is constrained via a clamp mechanism along its rectangular perimeter. The PVDF films are ITO-coated on both surfaces. Coatings have a sheet resistance of about 200 Ω/sq, which means the thickness of an electrode is approximately 5 nm (the resistivity of ITO is ~10−4 Ω·cm). To ensure fixed boundary conditions, the plastic plate is clamped between two metal frames using several nuts and bolts on the sides. The structure stands on a 10-inch PC monitor, which is placed horizontally on a desk. Vibration isolation between the structure and the monitor is provided with a 1 cm thick foam rubber.
Unipolar analog input signals are generated by a 32-bit microcontroller (STM32F407G). An executable program is developed in Unity software to communicate with the microcontroller and convey indicators of the randomized signals. At the same time, the choice responses of the subjects are recorded via an interface. A custom-designed amplifier circuit with adjustable gain amplifies the unipolar signals and excites PVDF-film actuators. It hosts a high-pass filter stage to eliminate DC components originating from the microcontroller. Hence, pure sinusoidal high-voltage signals are obtained on the amplifier output. Finally, the excitation voltage is directed to the relevant actuators by a multi-channel relay module, which is controlled by the microcontroller board, as well. To ensure proper connection with transparent actuators, electrically conductive adhesive tapes are utilized. In case of incomplete connectivity silver paste is applied.
PVDF-film actuators are glued (clear epoxy adhesive) to the plate in such a way that the positive electrodes are positioned directly beneath the layer. Hence, to prove the safety of the interface, electrical breakdown for the utilized PVC plate must be investigated. The dielectric strength of the PVC material is about 25 kV/mm [23]:
breakdown voltage = dielectric strength × thickness = 25 kV/mm × 0.6 mm = 15 kV
Since operating excitation voltages are below 300 Vpp, the setup is safe to conduct human experiments.
For the experiments, two identical touch interfaces with different actuator configurations are prepared. In the first configuration, two actuators are mounted on the right and left sides, respectively. The second configuration consists of 8 actuators, which are mounted in a 2 × 4 array formation. Both configurations are arranged symmetrically with respect to the origin of the surface geometry (Figure 1).
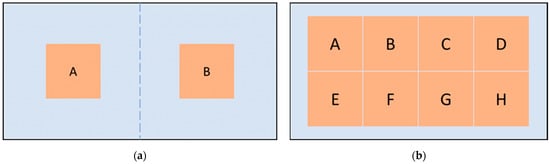
Figure 1.
Scaled versions of actuator configurations: (a) A/B configuration with 2 locations (A and B); (b) rray configuration with 8 locations (A–H).
2.2. Finite Element Analysis
2.2.1. General Information and Modal Analysis
To perform finite element analysis (FEA), the governing piezoelectric equations including the charge coefficients matrix are derived from various reliable sources [24,25,26,27,28,29,30], ensuring accurate representation in the program. In addition, the required coefficients of the elastic compliance matrix are obtained from experimental studies [23,26,28,31,32]. Consequently, the basic properties of the utilized PVDF material are given in Table 1.

Table 1.
Basic physical parameters used in the FEM analysis.
First, a modal analysis of the touch interface will be performed to determine the suitable frequency values, which will be used to validate the design experimentally. Then, a forced-vibration analysis will be performed to find the generated out-of-plane displacements and show the feedback localization.
The structures for A/B configuration and array configuration are built and simulated in a COMSOL Multiphysics finite-element analysis program. The only differences between the two configurations are the number and the arrangement of the PVDF actuators. Every actuator is attached beneath the PVC layer with their entire surface, and materials are assigned to geometries accordingly. After performing a modal analysis of the entire structure, the first natural frequencies were ωn1 = 451.2 Hz for the A/B configuration and ωn1 = 454.2 Hz for the array configuration, respectively (Figure 2). The slight variation in the values is because of the configuration difference.
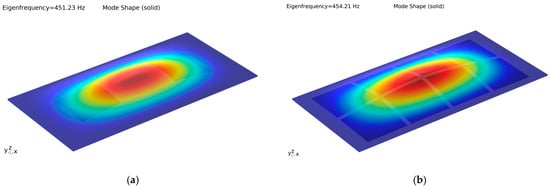
Figure 2.
First mode shape of the structure: (a) mode shape for the A/B configuration; (b) mode shape for the array configuration.
According to basic modal analysis principles, each of the natural frequency values corresponds to a definite and distinctive mode shape of the structure. Therefore, natural frequencies must be avoided in order to successfully generate localized vibrations at the desired locations. Thus, the frequency of the operating voltage must be far enough from the first natural frequency. In addition, it should also be situated in the perception interval for human skin, which can reach up to 800–1000 Hz [33,34]. Considering those design limitations, five frequency values will be selected. In coming sections of the study, these values will be used to determine the frequency at which the human fingertip is most sensitive to vibrotactile haptic cues.
The spacing between these frequency values should be at least as large as the Weber fraction to be able to convey significantly different stimuli to subjects. This difference between the frequency values is based on Weber’s rule, which states that as the intensity of a stimulus increases, the magnitude of the change needed to detect a difference increases proportionally [35]. In other words, the just noticeable difference (JND) between two stimuli is a constant fraction (Weber fraction) of the stimulus intensity. Weber’s rule can also be applied to vibration frequency and Weber fractions are mostly clustered around 15–30% [36,37]. Therefore, five equally spaced (30%) frequency values at the logarithmic scale were selected: 137, 178, 230, 300 and 390 Hz.
2.2.2. Forced-Vibration Analysis in the A/B Configuration
A forced-vibration analysis is performed to determine the response of a mechanical system to a time-varying input. Considering our case, this input is the periodically changing strain generated by the PVDF actuators and the response is out-of-plane displacement obtained on the plate surface. In order to compare the effect of frequency changes, it is necessary to normalize the displacement values at each frequency. This allows for a direct comparison of the impact of frequency in human experiments while eliminating the influence of other factors. Afterwards, the frequency value where the human fingertip exhibits the highest sensitivity and the detection threshold of the skin for vibrotactile cues will be identified.
In the first configuration, both actuators are excited with a pure sinusoidal signal of 100 V peak-to-peak amplitude and five selected frequencies. Individual excitation of the PVDF-based actuators provides the localization of the vibration, where the generated displacement amplitude reaches 0.36 μm, 0.37 μm, 0.39 μm, 0.45 μm and 0.63 μm, depending on signal frequencies, respectively (Figure 3). These displacement amplitudes are higher than the absolute detection threshold for the human fingertip reported in the literature [38,39]. Choi and Kuchenbecker reported the minimum threshold to be less than 0.1 μm [36]. Verrillo found that the absolute threshold for vibration detection is approximately 0.06 μm at around 250 Hz, which holds true for both men and women [37].
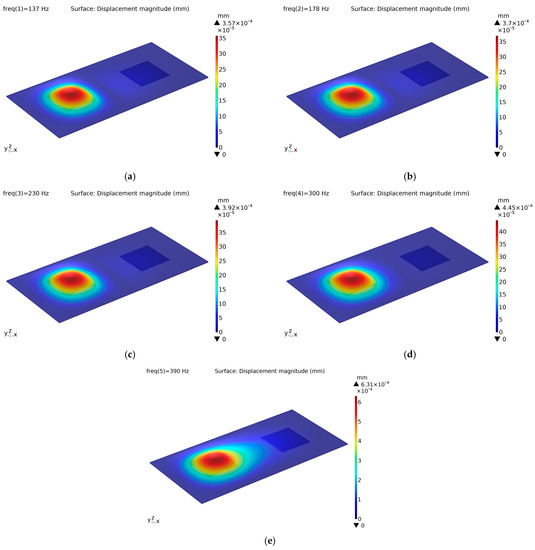
Figure 3.
Forced-vibration analysis outputs when only the left actuator is excited at: (a) 137 Hz; (b) 178 Hz; (c) 230 Hz; (d) 300 Hz; (e) 390 Hz.
Since the entire structure (the geometry and the positioning of the actuators) is symmetrical with respect to the origin, the vibration patterns observed when only actuator-B is excited are identical to those observed when only actuator-A is excited. Hence, they are omitted to save space. Additionally, it appears that the vibration pattern of the 390 Hz signal starts to become pervasive to some degree, likely due to its relative proximity to the first natural frequency (451 Hz, see Figure 2a), because, as stated earlier, mode shapes are vibration patterns occurring at natural frequencies. However, it can still be considered to be localized.
2.2.3. Forced-Vibration Analysis in the Array Configuration
In the second configuration, each actuator is activated individually with a 230 Hz sinusoidal signal (amplitude is 100 Vpp again). This frequency value, demonstrating the highest sensitivity for vibratory cues, was determined based on the results of the human experiment conducted in the A/B configuration. It lies in the range of 200–300 Hz, where the human fingertip is reported to be most perceptually sensitive to vibratory cues according to several studies [40,41,42,43]. Additionally, it is necessary to determine the displacement magnitudes, similar to the case for the A/B configuration.
As expected, the vibration maps formed by individually exciting actuators A, D, E, and H are almost identical in terms of shape and displacement magnitude (Figure 4). Likewise, the individual activation of the remaining actuators (B, C, F, and G) leads to the formation of similar vibration maps with increased displacement magnitudes. These equivalences among the corner-actuators and middle-actuators are based on the structural symmetry with respect to the origin. Obviously, the displacement magnitudes obtained in the array configuration are different from those in the A/B configuration since the positioning of the actuators has changed. Generally, the closer they are located to the boundaries, the lower the generated displacement.
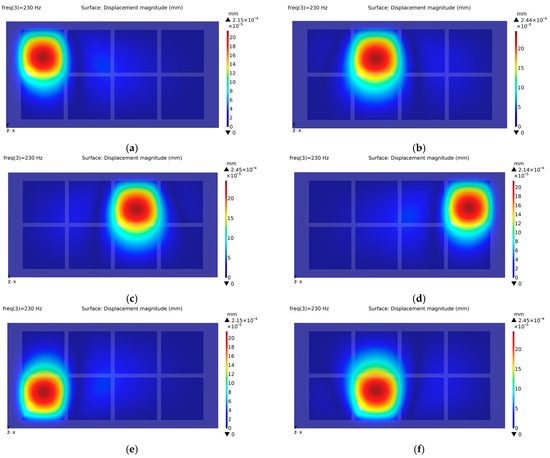
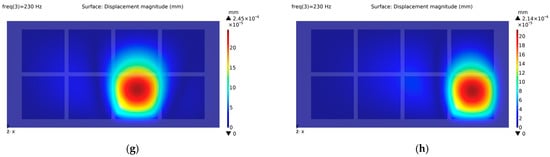
Figure 4.
Forced vibration analysis outputs show localized vibration patterns on corresponding locations only: (a) Actuator-A is excited; (b) Actuator-B is excited; (c) Actuator- C is excited; (d) Actuator-D is excited; (e) Actuator-E is excited; (f) Actuator-F is excited; (g) Actuator-G is excited; (h) Actuator-H is excited.
Here, it is important to state that forced-vibration analysis performed using FEA program provides convincing evidence of distinct and prominent vibration patterns on the corresponding actuators, solidly proving the effectiveness of achieving localized haptic feedback (Figure 4).
2.3. Experiments
2.3.1. A/B Configuration
The primary objective of the first experiment is to characterize the haptic interface by assessing and analyzing the key actuation parameters considering human factors: actuation frequency and detection threshold. For this, one of the classical psychophysical methods introduced by Fechner is used to estimate the absolute threshold value for detection: the repeated-measures, within-subject method of constant stimuli. This is accomplished with the one-interval, two-alternatives, forced-choice (1I-2AFC) paradigm, since it can provide more objective psychophysical procedures [35].
Here, one interval (1I) refers to the presentation of one detectable stimulus in each trial. In other words, both alternatives are presented concurrently in every single trial. Two alternatives (2A) means that two alternative stimuli are present in the experiment. The forced-choice (FC) paradigm is a commonly used method in psychophysics, wherein participants are presented with alternatives and required to choose the one where they perceive a detectable stimulus [35,44]. It is important to note that participants are not allowed to withhold their response or choose not to respond. The term 2AFC is often misused to describe a yes–no task, which involves randomly presenting a stimulus in some trials and not in others. In a yes–no task, the observer responds after each trial with either “yes” or “no.” However, the results of a yes–no task are more susceptible to various response biases compared to 2AFC tasks. For instance, in the case of extremely low tactile stimuli, a person may truthfully respond “no” (indicating that they did not perceive any vibration) on every trial, while the results of a 2AFC task would demonstrate the person’s ability to reliably determine the location (A-side or B-side) of the same extremely low-tactile stimulus.
In our study, the subjects are presented with two haptic stimuli: one generated by the actuator, the other having no stimulus at all. Their task is to determine which side, A or B, corresponds to the presence of haptic feedback.
Eight subjects (four female, four male) with a mean age of 28.9 years took part in the experiment. All of them were right-handed and used the index finger of their dominant hand in the experiment. They did not report any sensorimotor impairment.
After some preliminary observations, 50 V was predicted to be the required voltage amplitude at 230 Hz to produce vibratory feedback at the absolute detection threshold. Taking 50 V as the center value, 4 lower and 4 higher amplitudes of excitation voltage were added to the stimulus set, equally spaced on the logarithmic scale: 17 V, 22 V, 29 V, 38 V, 50 V, 65 V, 85 V, 110 V, 143 V. Considering Weber’s rule, the spacing between amplitude values was once again selected as 30%. This approach is explained in Section 2.2.1.
The simulation outputs of the forced-vibration analysis for the A/B configuration revealed that the excitation at each selected frequency produces similar vibration patterns, with different displacement amplitudes (Figure 3). Therefore, the activation voltages are adjusted to eliminate the frequency effect and equalize the displacement amplitudes using proper gain coefficients (Table 2).

Table 2.
Variation in vibration displacements with different frequencies.
For example, the amplitudes of the stimulus set are modified for 137 Hz:
1.08 × [17, 22, 29, 38, 50, 65, 85, 110, 143] = [18, 24, 31, 41, 54, 70, 92, 119, 154]
The designed touch interface has a rectangular shape since lateral motion is the most effective way to explore the surface properties [45]. Before the experiment, subjects were informed about their tasks and instructed to interact with the haptic interface as they would with a typical smart device equipped with a touch display. They were trained for approximately 3 min to become familiar with the haptic feedback effects generated by the touch-screen interface. In the training session, they were exposed to each stimulus twice (1 for each alternative side) at 230 Hz. In the experiment session, every subject conducted a set of 180 trials (9 stimuli) for each of 5 signal-frequency levels, a total of 900 trials. Hence, each stimulus appeared 20 times (10 times on A-side and 10 times on B-side). Those appearances were randomized block-wise: each stimulus was given once before any stimulus was given twice. This method helps to reduce the learning and carry-over effect and to increase statistical validity [46]. The subjects’ task was to determine the side with the haptic feedback and to select it with a mouse located next to the monitor (Figure 5a). To put this differently, they were exposed to the question: “where do you feel tactile feedback, A-side or B-side?”. When they made the selection, the next trial was immediately begun by the software. The experiment for one subject lasted about 70 min. The background image (Figure 5b) displayed on the monitor under the transparent haptic interface serves to demonstrate the optical transparency of the touch surface. Similarly, it is placed on a colored paper to emphasize optical transparency (Figure 6).
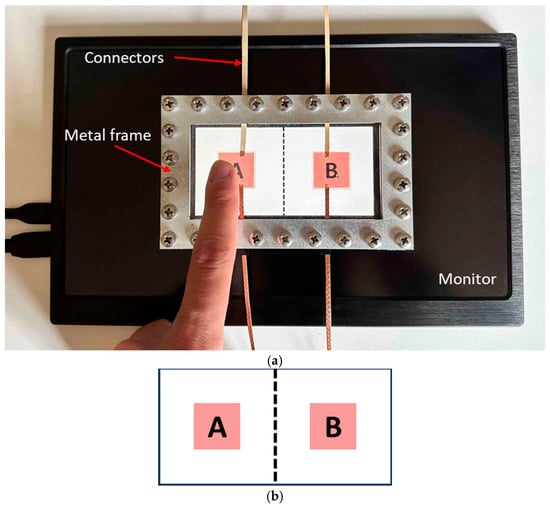
Figure 5.
(a) Experimental setup designed for the first experiment; (b) the original background image displayed on the monitor.

Figure 6.
The transparent interface on color paper in A/B configuration.
2.3.2. Array Configuration
In the second experiment, a multiple-choice procedure is designed to prove the ability of the touch-screen interface to provide localized haptic feedback. Here, the subjects try to detect the one with haptic feedback out of 8 locations: A, B, C, D, E, F, G, and H (Figure 7).

Figure 7.
(a) Experimental setup designed for the second experiment with 8 locations; (b) the original background image displayed on the monitor.
The operating frequency for the pure sine signal was set at 230 Hz. According to the results of the human experiments with the A/B configuration, this was the critical member of the frequency set where the participants’ fingertips are most sensitive to vibratory feedback. Two amplitudes were selected from the voltage stimuli set: one was the next greatest compared to the absolute detection threshold (65 V), and the other one was the highest level (143 V). Previous simulation results have shown that the generated displacement magnitude is higher when one of the actuators in the middle (B, C, F, or G) is actuated compared to the case when one of the actuators in the corners (A, D, E, or H) is actuated (Figure 4). To compensate for the difference caused by the location effect, the gain coefficient 2.45/2.15 = 1.13 was used to increase the excitation voltage of the corner actuators.
Additionally, the difference caused by the configuration of the actuators must also be eliminated. According to the finite-element analysis results, two different configurations led to maximum vibration magnitudes of 0.392 μm and 0.245 μm on the corresponding actuators, at 100 Vpp and 230 Hz, respectively (Figure 3 and Figure 4).
According to our findings in the FEA program, we observed a direct correlation between the excitation voltage and displacement amplitude of the generated vibration, which can be demonstrated as linear functions (Figure 8). Therefore, the maximum displacement amplitudes produced in A/B configuration at 65 V and 143 V are 0.25 μm and 0.56 μm, respectively. To obtain the same displacement amplitudes in the array configuration, the excitation signals with voltage amplitudes of 106 V and 232 V were used.
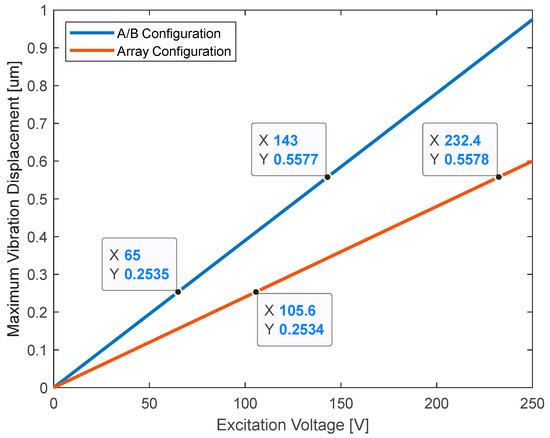
Figure 8.
Generated vibration displacements at 230 Hz with two different configurations.
Six subjects with a mean age of 27.5 years participated in the experiment, which was conducted over two sessions. Before the experiment, subjects underwent a 4 min training process. They were asked to explore the touch surface freely and to identify the specific location with the highest perceived haptic effect out of the eight available options using the mouse next to the monitor. In the training session, two different haptic cues (with amplitudes of 106 V and 232 V) appeared on each different location twice. In the experiment session, both signals were conveyed to each location 20 times. Therefore, the experiment consisted of a total of 320 trials per participant. After each trial, the subject’s response triggered the subsequent trial, in which haptic feedback stimuli were randomly delivered to different locations. Again, the stimuli were randomized block-wise. The multiple-choice experiment was completed approximately in 40 min.
3. Results
3.1. Results of the First Experiment
Success rates were averaged among eight subjects for each stimulus value (nine voltage levels), and the data points of psychometric functions for five different frequencies were obtained (Figure 9). The dashed curve indicates the ideal psychometric function in 2-AFC condition. Since there are two choices, it starts from the value of chance performance 0.5 and the threshold is defined as the point at which the participants achieve 75% correct responses. This threshold value is equivalent to a 50% threshold in a psychometric function derived from a yes/no detection experiment [35,46]. As depicted in the graph, the overall performance of the subjects improves as the stimuli amplitudes increase. However, the curve corresponding to 390 Hz exhibited an unexpected anomaly for the highest two stimuli, which can potentially be attributed to the pervasive behavior of the vibration pattern at that specific frequency. Participants appeared to encounter ambiguity during the decision-making process, particularly when the haptic effect was discernible not only on the intended target area but also close to the other side (Figure 3e). As anticipated, the participants’ performance yielded the most favorable outcomes at 230 Hz and at 300 Hz, respectively.
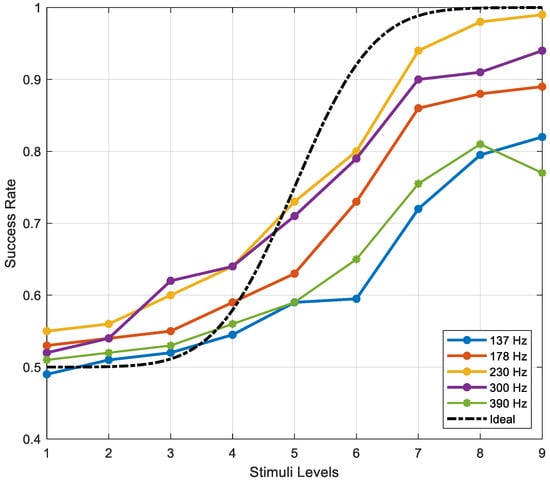
Figure 9.
Psychometric curves obtained in A/B configuration.
Absolute detection threshold results were analyzed using two-factor ANOVA with repeated measures. The null hypothesis of a significant effect was rejected when the resulting p-value was found to be less than the predefined significance level of α = 0.01. In our case, the null hypothesis states that the varying amplitude and frequency of the excitation signal did not affect the perception performance of the subjects. The results show that this is rejected (p < 0.01) for both factors, which means that amplitude and frequency have an independent significant effect on participants’ success rates. Moreover, there is no significant interaction effect between two factors (p > 0.01). In other words, the effect of one factor on the success rate does not depend on the levels of other factor, which is consistent with the parallel behavior observed in the psychometric curves for each frequency.
Ogive curves (Sigma-shaped or S-shaped curves) are fitted to the data points, with the threshold representing the stimulus level at which detection occurs in 75% of the total trials. If the threshold values fall between two stimuli, a simple linear interpolation process is employed. The excitation voltages to achieve vibration displacement amplitudes of detection threshold are calculated and given below (Table 3):

Table 3.
Variation in required voltages for detection thresholds with different frequencies.
The data tabulated above were plotted, and the obtained graph exhibits a U-shaped threshold characteristic, which aligns with the findings reported in the literature (Figure 10) [2,35,39,40,41,42,43,44,47]. This threshold characteristic verifies that the sensitivity of the human skin on the fingertip increases as the stimulus frequency increases up to approximately 200 Hz and diminishes as the stimulus frequency surpasses 300 Hz. Among the five different, equally spaced frequency values utilized in this study, we can observe that the skin’s detection threshold for vibratory cues is minimized at 230 Hz. Including additional frequency values would likely exhibit a consistent pattern with the trend depicted in the plotted graph.
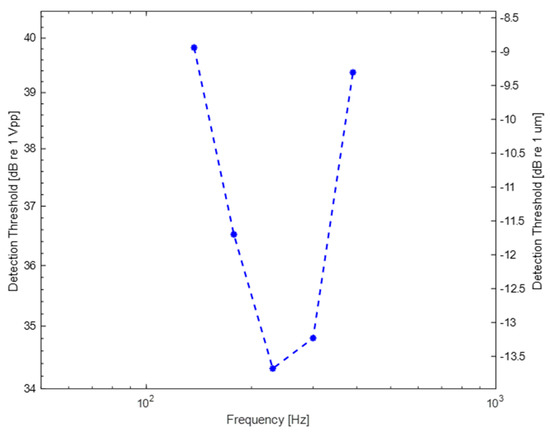
Figure 10.
Variation in mean detection thresholds with different frequencies.
3.2. Results of the Second Experiment
Success rates of the participants for each of the eight locations for two different voltage amplitudes are plotted in the bar charts below (Figure 11). These voltage amplitudes are represented by color bars: the blue bars correspond to low voltage (106 V) and the red bars correspond to high voltage (232 V). Bars start from a 50% success rate since the lowest one among all subjects is 55% (Subject 2 at location B). This proves that even the vibration displacement of 0.25 um is, to some extent, sufficient to perceive the haptic feedback, and the results are consistent with the findings reported in previous studies [38,39,47]. With only a few exceptions, every subject showed an improved performance across all eight locations when actuators are excited with higher voltage (232 V) compared to those activated with low voltage (106 V). Furthermore, two participants exhibited the best performance at a higher voltage, achieving 100% accuracy among all locations.
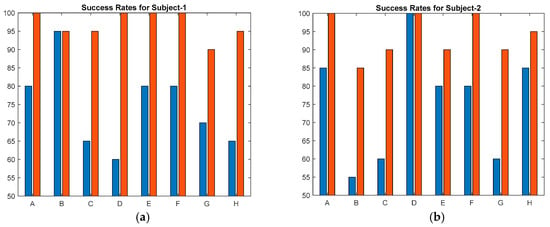
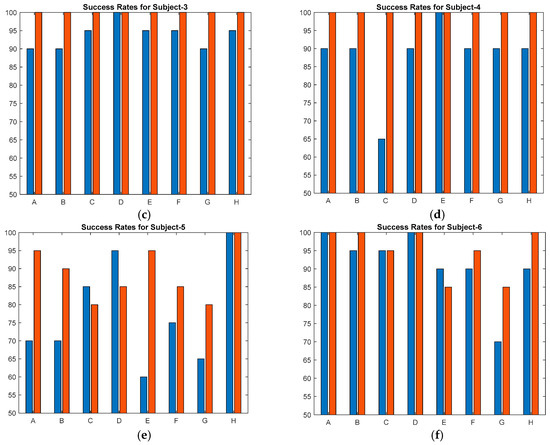
Figure 11.
Success rates on 8 locations (A-H) in array configuration at low voltage (blue bars) and at high voltage (red bars): (a) Subject-1; (b) Subject-2; (c) Subject-3; (d) Subject-4; (e) Subject-5; (f) Subject-6.
When the hit rates were averaged for each participant, it was observed that all of them exhibited a clear improvement in the success rate at a high voltage (Figure 12).
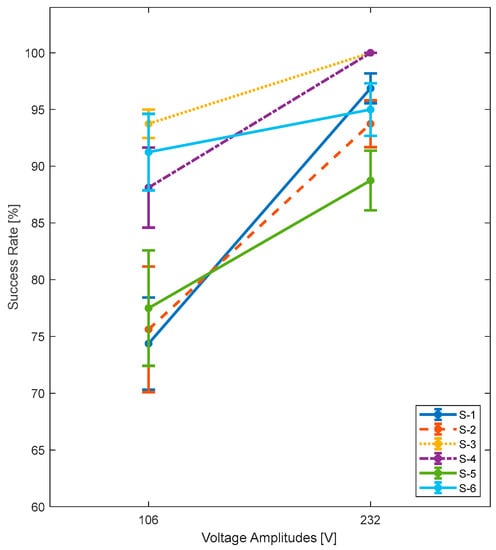
Figure 12.
Average values with standard error bars.
In addition to the performance metrics of the individuals, the general accuracy of location-based responses is also important. To demonstrate this, confusion matrices are plotted for both low- and high-voltage cases (Figure 13). The average performance of participants at a low voltage does not drop below 74% and reaches at least 82% when the two lowest performances are excluded. At high voltages, the average performance is significantly improved, reaching a success rate of 91% at the worst-performing location, location-G. Indeed, the average performance score at all locations for the entire touch interface is 95.8%. In both cases, the lowest performances are observed when the C- and G-actuators are actuated, which could be attributed to structural deficiencies such as the poorer coupling of the actuator to the surface or interference caused by neighbor actuators.
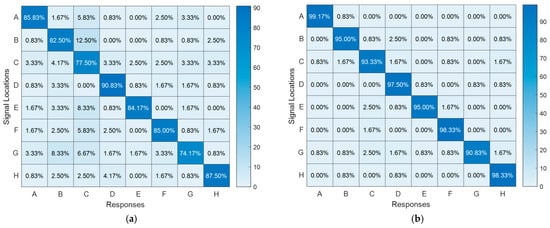
Figure 13.
Confusion matrices for 8 locations (A–H): (a) at low voltages; (b) at high voltages.
In addition, average success scores at the corner locations (A, D, E, H) consistently rank among the top 4 or 5 in both cases, because these actuators have fewer neighboring actuators that can potentially interfere with their haptic effects compared to the middle locations. Eventually, when the two lowest performances, at locations C and G, are excluded, the average performance at every location reaches a minimum accuracy of 95%, which can be considered a very good score.
4. Discussion and Conclusions
The concept of transparent localized haptics in this study is introduced via two different arrangements: A/B- and array configuration. In the first configuration, two actuators are mounted on the left and right sides of the rectangle plate. The finite element analysis method is employed to simulate the structure and obtain information about relevant design parameters, such as the frequency and amplitude of excitation signals and the generated amplitudes on the interface. Among the selected frequency set, 230 Hz is the frequency at which the detection threshold for vibrotactile cues is, at its minimum, 34.3 dB re 1 Vpp. As expected, the human fingertip sensitivity represents a U-shaped curve: amplitude thresholds increase when the frequency is lower or higher than 200–300 Hz because the skin on the human fingertip is most sensitive to vibratory feedback within the interval of 200–300 Hz. Similar findings have been reported in numerous previous studies [2,35,39,40,41,42,43,44,47].
The second configuration consists of eight actuators arranged in a 2 × 4 matrix formation and is designed to demonstrate the ability to generate localized haptic feedback on the desired locations. The actuation frequency of 230 Hz is chosen based on the supportive findings from the first experiment. Two excitation amplitudes, 106 and 232 volts, are selected: they generate maximum vibration displacements of 0.25 μm and 0.56 μm on the second setup, respectively. The success rates are averaged among six subjects and eight different locations, resulting in an accuracy of 83% at low voltages and 96% at high voltages.
Hence, the results, especially at higher voltages, strongly validate the localization process of the generated haptic feedback on touch displays, enhancing the overall user experience. Considering that the maximum amplitude used in this study is 232 V, it is evident that utilized transparent PVDF-based materials are suitable actuators for achieving localized and rich haptic effects, since they are able to handle excitation ranges of up to 5000 V. Here, it is worth mentioning that the touch interface is composed of a 0.6 mm thick PVC layer, and higher voltage levels would be necessary to generate comparable detectable haptic cues on a stiffer surface, such as glass. In addition, PVDF actuators allow for the possibility to increase the voltage to higher levels and to construct a stack (2–3 fold) of PVDF actuators without compromising much on transmittivity.
In addition, we employed an amperemeter with a resolution of 1 mA to estimate the power consumption of the proposed touch interface in array configuration. When applying a voltage amplitude of 70 Vrms at 230 Hz to all eight actuators simultaneously, the amperemeter consistently displayed zero current. This observation indicates that the current drawn by each individual actuator is less than 0.125 mA, resulting in an instantaneous power consumption of each actuator of less than 17.5 mW. It is important to note that a more sensitive measurement device capable of detecting microampere-level currents would result in a significantly lower power consumption being calculated. Our estimation aligns with the findings reported in a study published by D’Anniballe et al. [48]. In that study, they applied a sinusoidal electric field of 15 MV/m (f = 0.1 Hz) to a PVDF actuator with a size of 62 × 13 mm and a thickness of 50 μm. They observed a current draw of an amplitude of 2 μA, leading to an instantaneous power consumption of 1.88 mW.
Although the process of applying the actuators to touch surfaces poses challenges, this study serves as a good proof of concept. In the future, some microfabrication methods can be employed to produce touch interfaces with a higher haptic resolution. It is important to note that a comprehensive vibration analysis will always be necessary in order to effectively implement this in real-life applications.
Author Contributions
Conceptualization, E.S.E. and A.B.; methodology, E.S.E.; software, E.S.E.; validation, E.S.E.; formal analysis, E.S.E.; data curation, E.S.E.; writing—original draft preparation, E.S.E.; writing—review and editing, E.S.E. and A.B.; visualization, E.S.E.; supervision, A.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data available on request.
Conflicts of Interest
Both experiments reported in this study received approval from the Human Research Ethics Committee of Gebze Technical University.
References
- Prewett, M.S.; Elliott, L.R.; Walvoord, A.G.; Coovert, M.D. A Meta-Analysis of Vibrotactile and Visual Information Displays for Improving Task Performance. IEEE Trans. Syst. Man Cybern. 2012, 42, 123–132. [Google Scholar] [CrossRef]
- Bau, O.; Poupyrev, I.; Israr, A.; Harrison, C. TeslaTouch: Electrovibration for Touch Surfaces. In Proceedings of the 23nd Annual ACM Symp. on User Interface Software and Technology, New York, NY, USA, 3–6 October 2010; pp. 283–292. [Google Scholar]
- Ishizuka, H.; Hatada, R.; Cortes, C.; Miki, N. Development of a Fully Flexible Sheet-Type Tactile Display Based on Electrovibration Stimulus. Micromachines 2018, 9, 230. [Google Scholar] [CrossRef] [PubMed]
- Basdogan, C.; Giraud, F.; Levesque, V.; Choi, S. A Review of Surface Haptics: Enabling Tactile Effects on Touch Surfaces. IEEE Trans. Haptics 2020, 13, 450–470. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Teo, E.H.T.; Yao, K. Electromechanical Actuators for Haptic Feedback with Fingertip Contact. Actuators 2023, 12, 104. [Google Scholar] [CrossRef]
- Kim, H.; Kang, J.; Kim, K.; Lim, K.; Ryu, J. Method for Providing Electrovibration with Uniform Intensity. IEEE Trans. Haptics 2015, 8, 492–496. [Google Scholar] [CrossRef]
- Shultz, C.D.; Peshkin, M.A.; Colgate, J.E. Surface Haptics via Electroadhesion: Expanding Electrovibration with Johnsen and Rahbek. In Proceedings of the IEEE World Haptics Confenerce, Evanston, IL, USA, 22–26 June 2015. [Google Scholar]
- Zophoniasson, H.; Bolzmacher, C.; Anastassova, M.; Hafez, M. Electrovibration: Influence of the Applied Force on Tactile Perception Thresholds. In Proceedings of the Zooming Innovation in Consumer Electronics International Conference, Novi Sad, Serbia, 31 May–1 June 2017. [Google Scholar]
- Jiao, J.; Zhang, Y.; Wang, D.; Guo, X.; Sun, X. HapTex: A Database of Fabric Textures for Surface Tactile Display. In Proceedings of the IEEE World Haptics Conference, Tokyo, Japan, 9–12 July 2019. [Google Scholar]
- Isleyen, A.; Vardar, Y.; Basdogan, C. Tactile Roughness Perception of Virtual Gratings by Electrovibration. IEEE Trans. Haptics 2020, 13, 562–570. [Google Scholar] [CrossRef]
- Osgouei, R.H.; Kim, J.R.; Choi, S. Data-Driven Texture Modeling and Rendering on Electrovibration Display. IEEE Trans. Haptics 2020, 13, 298–311. [Google Scholar] [CrossRef]
- Emgin, S.; Ege, E.S.; Birer, O.; Basdogan, C. Localized Multi-Finger Electrostatic Haptic Display. In Proceedings of the IEEE World Haptics Conference Hardware Demonstration, Chicago, IL, USA, 22–25 June 2015. [Google Scholar]
- Haga, H.; Sugimoto, D.; Yang, Y.; Sasaki, H.; Asai, T.; Shigemura, K. Capacitive touchscreen-integrated electrostatic tactile display with localized sensation. J. Soc. Inf. Disp. 2019, 27, 59–71. [Google Scholar] [CrossRef]
- Haga, H.; Yoshinaga, K.; Yanase, J.; Sugimoto, D.; Takatori, K.; Asada, H. Electrostatic Tactile Display Using Beat Phenomenon for Stimulus Localization. IEICE Trans. Electron. 2015, 98, 1008–1014. [Google Scholar] [CrossRef]
- Bai, M.R.; Tsai, Y.K. Impact Localization Combined with Haptic Feedback for Touch Panel Applications Based on the Time-Reversal Approach. J. Acoust. Soc. Am. 2011, 129, 1297–1305. [Google Scholar] [CrossRef]
- Hudin, C.; Lozada, J.; Hayward, V. Localized Tactile Feedback on a Transparent Surface through Time-Reversal Wave Focusing. IEEE Trans. Haptics 2015, 8, 188–198. [Google Scholar] [CrossRef] [PubMed]
- Matysek, M.; Lotz, P.; Winterstein, T.; Schlaak, H.F. Dielectric Elastomer Actuators for Tactile Displays. In Proceedings of the World Haptics 2009—Third Joint EuroHaptics Conference and Symposium on Haptic Interfaces for Virtual Environment and Teleoperator Systems, Salt Lake City, UT, USA, 18–20 March 2009. [Google Scholar]
- Stubning, T.; Denes, I.; Beruscha, F. Design optimization of EAP-based haptic surfaces. In Proceedings of the IEEE 2nd International Conference on Dielectrics, Budapest, Hungary, 1–5 July 2018. [Google Scholar]
- Choi, D.S.; Kim, S.Y. Transparent Film-Type Vibrotactile Array and Its Haptic Rendering Using Beat Phenomenon. Sensors 2019, 19, 3490. [Google Scholar] [CrossRef] [PubMed]
- Kim, U.; Kang, J.; Lee, C.; Kwon, H.Y.; Hwang, S.; Moon, H.; Koo, J.C.; Nam, J.D.; Hong, B.H.; Choi, J.B.; et al. A transparent and stretchable graphene-based actuator for tactile display. Nanotechnology 2013, 24, 145501. [Google Scholar] [CrossRef] [PubMed]
- Ankit, N.T.; Rajput, M.; Chien, N.A.; Mathews, N. Highly transparent and integrable surface texture change device for localized tactile feedback. Small 2017, 14, 1702312. [Google Scholar] [CrossRef]
- Duong, Q.V.; Nguyen, V.P.; Dos Santos, F.D.; Choi, S.T. Localized Fretting-Vibrotactile Sensations for Large-Area Displays. ACS Appl. Mater. Interfaces 2019, 11, 33292–33301. [Google Scholar] [CrossRef]
- MatWeb. Available online: https://www.matweb.com/index.aspx (accessed on 1 May 2023).
- Piefort, V. Finite Element Modelling of Piezoelectric Active Structures. Ph.D. Thesis, Universite Libre de Bruxelles, Brussels, Belgium, 2001. [Google Scholar]
- Jalili, N. Piezoelectric-Based Vibration Control, from Macro to Micro/Nano Scale Systems, 1st ed.; Springer: New York, NY, USA, 2010; pp. 129–158. [Google Scholar]
- Holloway, F.C. Material Characterization of Poly(Vinylidene Fluoride): A Thin Film Piezoelectric Polymer. Master’s Thesis, Montana State University, Bozeman, Montana, 1997. [Google Scholar]
- Dahiya, R.S.; Valle, M. Robotic Tactile Sensing, 1st ed.; Springer: Dordrecht, Holland, 2013; pp. 195–210. [Google Scholar]
- Fukada, E.; Furukawa, T. Piezoelectricity and ferroelectricity in polyvinylidene fluoride. Ultrasonics 1981, 19, 31–39. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, Q.M.; Cross, L.E.; Sykes, A.O. Piezoelectric, dielectric, and elastic properties of poly(vinylidene fluoride/trifluoroethylene). J. Appl. Phys. 1993, 74, 3394–3398. [Google Scholar] [CrossRef]
- Ramanathan, A.K. Polyvinylindene Fluoride (PVDF) Films for Near-Static Measurement Applications. Ph.D. Thesis, The Ohio State University, Columbus, OH, USA, 2021. [Google Scholar]
- Zhao, J.M.; Song, X.X.; Liu, B. Standardized Compliance Matrices for General Anisotropic Materials and a Simple Measure of Anisotropy Degree Based on Shear-Extension Coupling Coefficient. Int. J. Appl. Mech. 2016, 8, 1650076. [Google Scholar] [CrossRef]
- Vazquez, M.; Petrearce, R.; Duran, J.; Acevedo, P. Simulation of a PVDF transducer array using the finite element method (FEM) to measure temperature gradients in a soft tissue. In Proceedings of the IEEE 9th IberoAmerican Congress on Sensors, Bogota, Colombia, 15–18 October 2014. [Google Scholar]
- Serhat, G.; Kuchenbecker, K.J. Free and Forced Vibration Modes of the Human Fingertip. Appl. Sci. 2021, 11, 5079. [Google Scholar] [CrossRef]
- Jones, L.A. Haptics, 1st ed.; The MIT Press: Cambridge, UK, 2018; pp. 1–55. [Google Scholar]
- Gescheider, A.G. Psychophysics: The Fundamentals, 3rd ed.; Lawrence Erlbaum Associates: Mahwah, NJ, USA, 1997; pp. 1–100. [Google Scholar]
- Choi, S.; Kuchenbecker, K.J. Vibrotactile Display: Perception, Technology, and Applications. Proc. IEEE 2013, 101, 2093–2104. [Google Scholar] [CrossRef]
- Israr, A.; Tan, H.Z.; Reed, C.M. Frequency and amplitude discrimination along the kinesthetic-cutaneous continuum in the presence of masking stimuli. J. Acoust. Soc. Am. 2006, 120, 2789–2800. [Google Scholar] [CrossRef] [PubMed]
- Verrillo, R.T. Comparison of vibrotactile threshold and suprathreshold responses in men and women. Percept. Psychophys. 1979, 26, 20–24. [Google Scholar] [CrossRef]
- Young, G.; Murphy, D.; Weeter, J. Audio-Tactile Glove. In Proceedings of the 16th International Conference on Digital Audio Effects, Maynooth, Ireland, 2–5 September 2013. [Google Scholar]
- Israr, A.; Choi, S.; Tan, H.Z. Detection Threshold and Mechanical Impedance of the Hand in a Pen-Hold Posture. In Proceedings of the 2006 IEEE/RSJ International Conference on Intelligent Robots and Systems, Beijing, China, 9–15 October 2006. [Google Scholar]
- Verrillo, R.T. Psychophysics of vibrotactile stimulation. J. Acoust. Soc. Am. 1985, 77, 225–232. [Google Scholar] [CrossRef]
- Jones, L.; Sarter, N. Tactile Displays: Guidance for Their Design and Application. J. Hum. Factors Ergon. Soc. 2008, 50, 90–111. [Google Scholar] [CrossRef]
- Gescheider, G.A.; Bolanowski, S.J.; Rope, J.V.; Verrillo, R.T. A four-channel analysis of the tactile sensitivity of the fingertip: Frequency selectivity, spatial summation, and temporal summation. Somatosens. Mot. Res. 2002, 19, 114–124. [Google Scholar] [CrossRef] [PubMed]
- Jones, L.A.; Tan, H.Z. Application of Psychophysical Techniques to Haptic Research. IEEE Trans. Haptics 2013, 6, 268–284. [Google Scholar] [CrossRef]
- Lederman, S.J. Tactile roughness of grooved surfaces: The touching process and effects of macro- and microsurface structure. Percept. Psychophys. 1974, 16, 385–395. [Google Scholar] [CrossRef]
- Cunningham, D.W.; Wallraven, C. Experimental Design: From User Studies to Psychophysics, 1st ed.; CRC Press: Boca Raton, FL, USA, 2012; pp. 101–120. [Google Scholar]
- Bolanowski, S.J.; Gescheider, G.A.; Verrillo, R.T.; Checkosky, C.M. Four channels mediate the mechanical aspects of touch. J. Acoust. Soc. Am. 1988, 84, 1680–1694. [Google Scholar] [CrossRef]
- D’Anniballe, R.; Zucchelli, A.; Carloni, R. The effect of morphology on poly(vinylidene fluoride-trifluoroethylene-chlorotrifluoroethylene)-based soft actuators: Films and electrospun aligned nanofiber mats. Sens. Actuators A Phys. 2021, 333, 113255. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).