Comfort-Oriented Semi-Active Suspension Configuration with Inerter-Based Network Synthesis
Abstract
1. Introduction
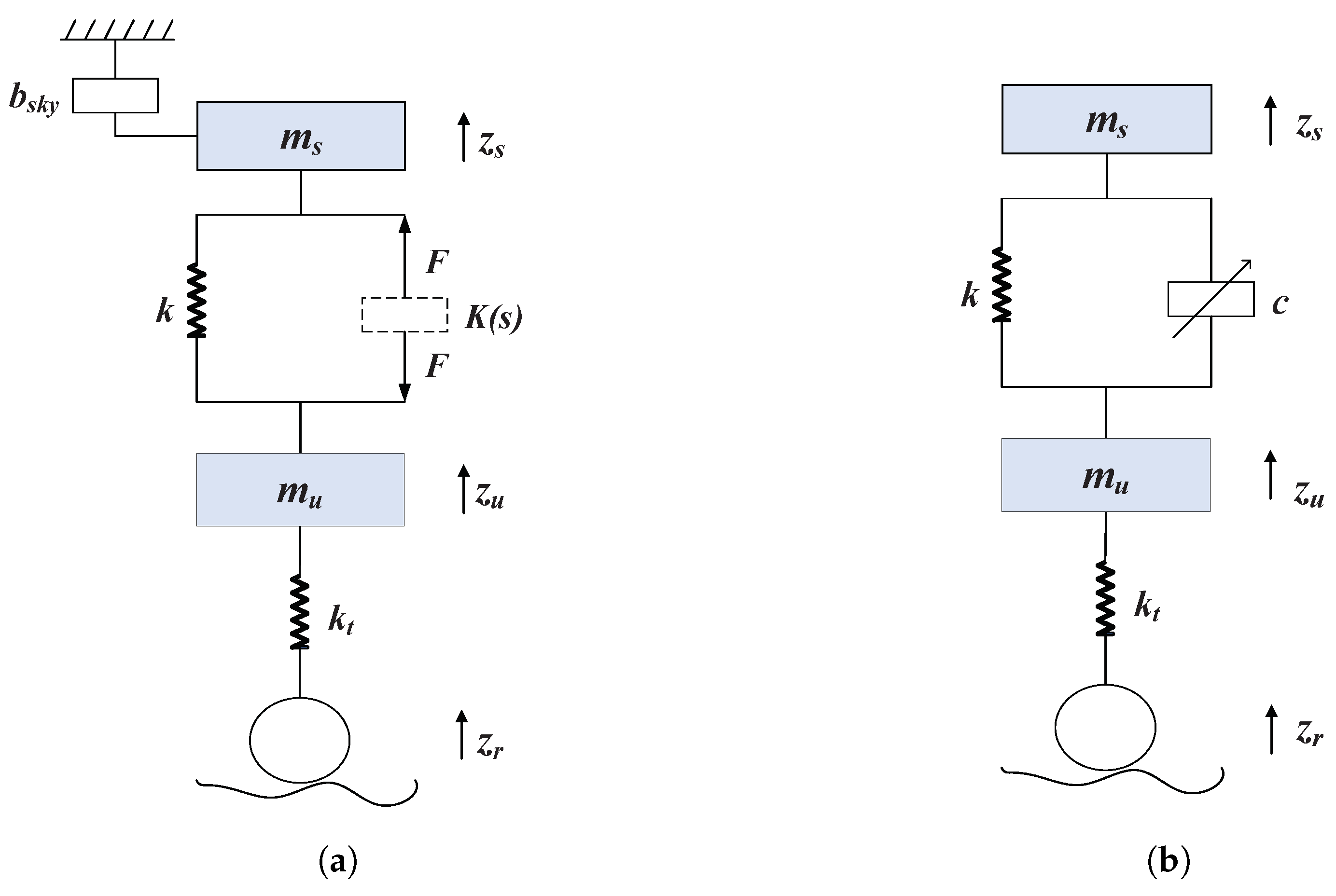
2. Models of Semi-Active ISD Suspension
2.1. Quarter Vehicle Suspension
2.2. Passive Network Synthesis
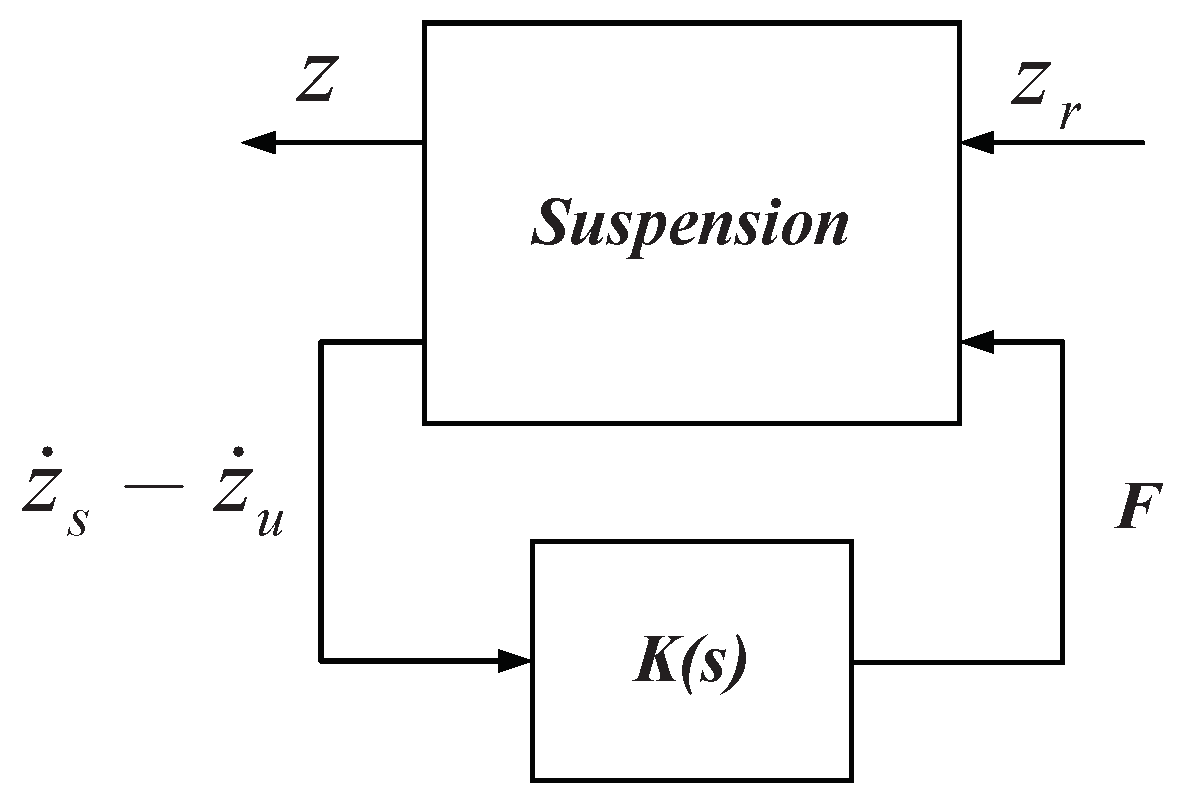
2.3. Design of Positive Real Controller
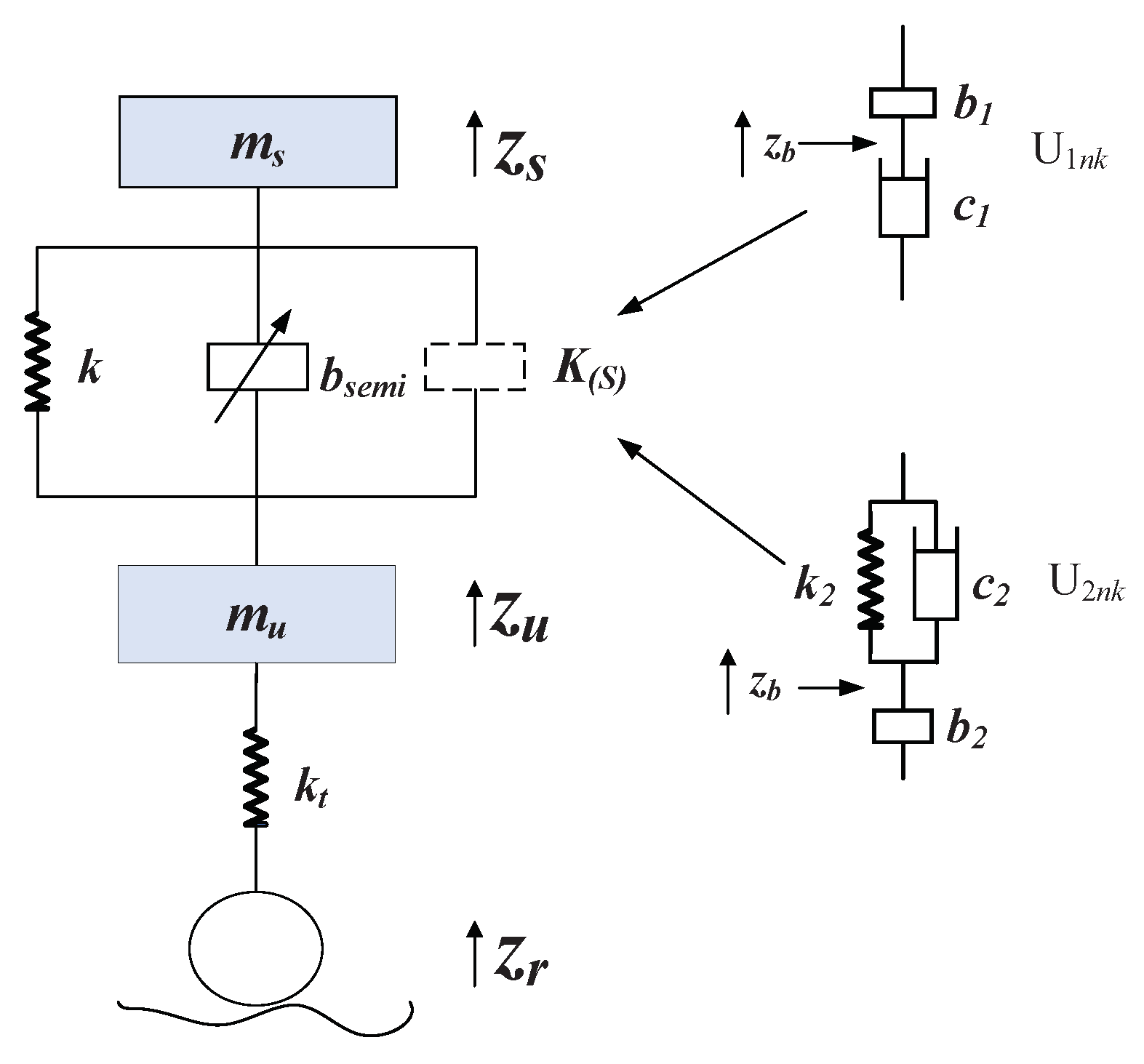
3. Network Synthesis of the Passive Part
3.1. Description of Suspension Performance
3.2. Solve BMI and Network Synthesis
4. Parameter Optimization for the Passive Part of the ISD Suspension
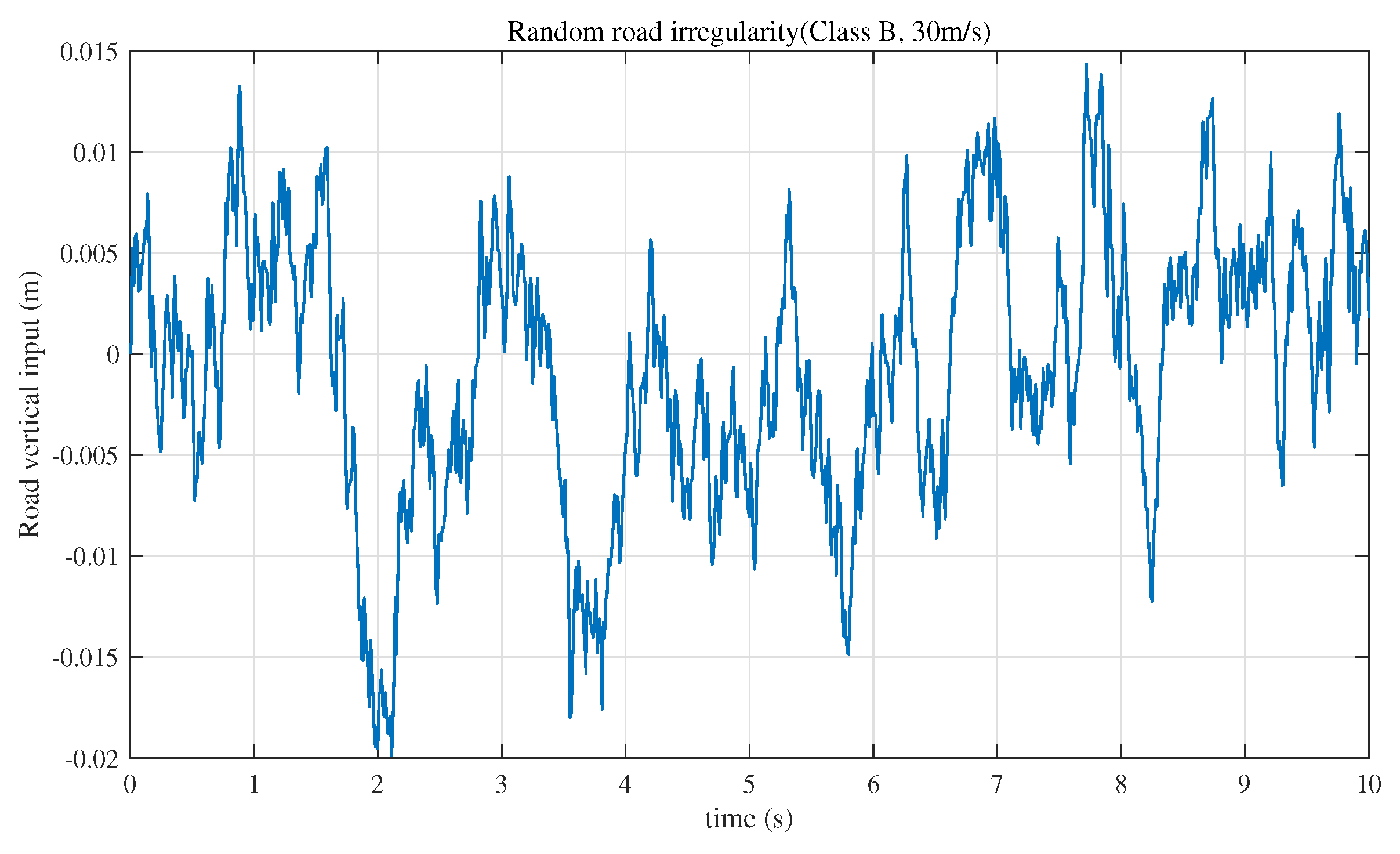
4.1. Random Road Input
4.2. Optimization Objectives and Optimization Methods
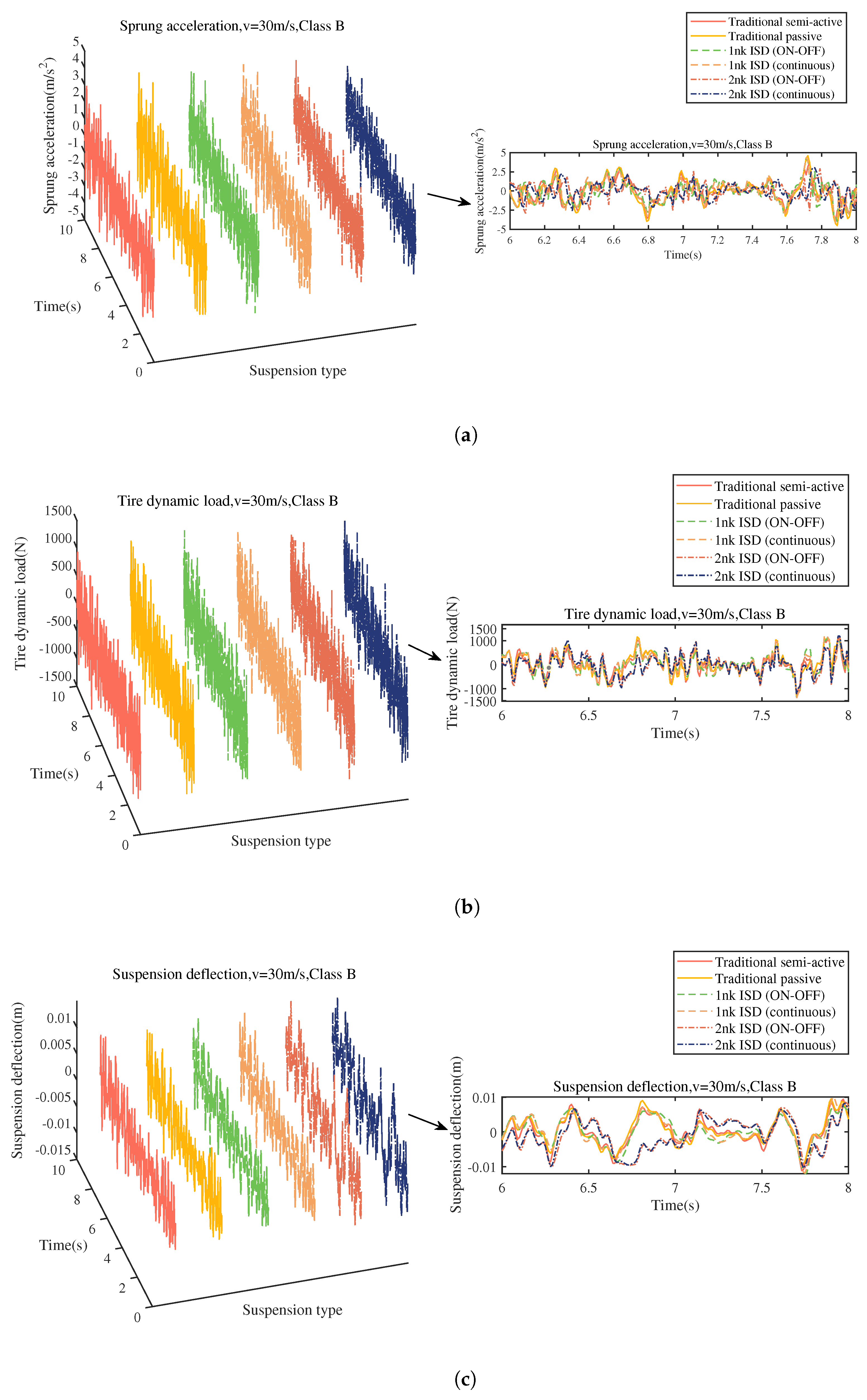
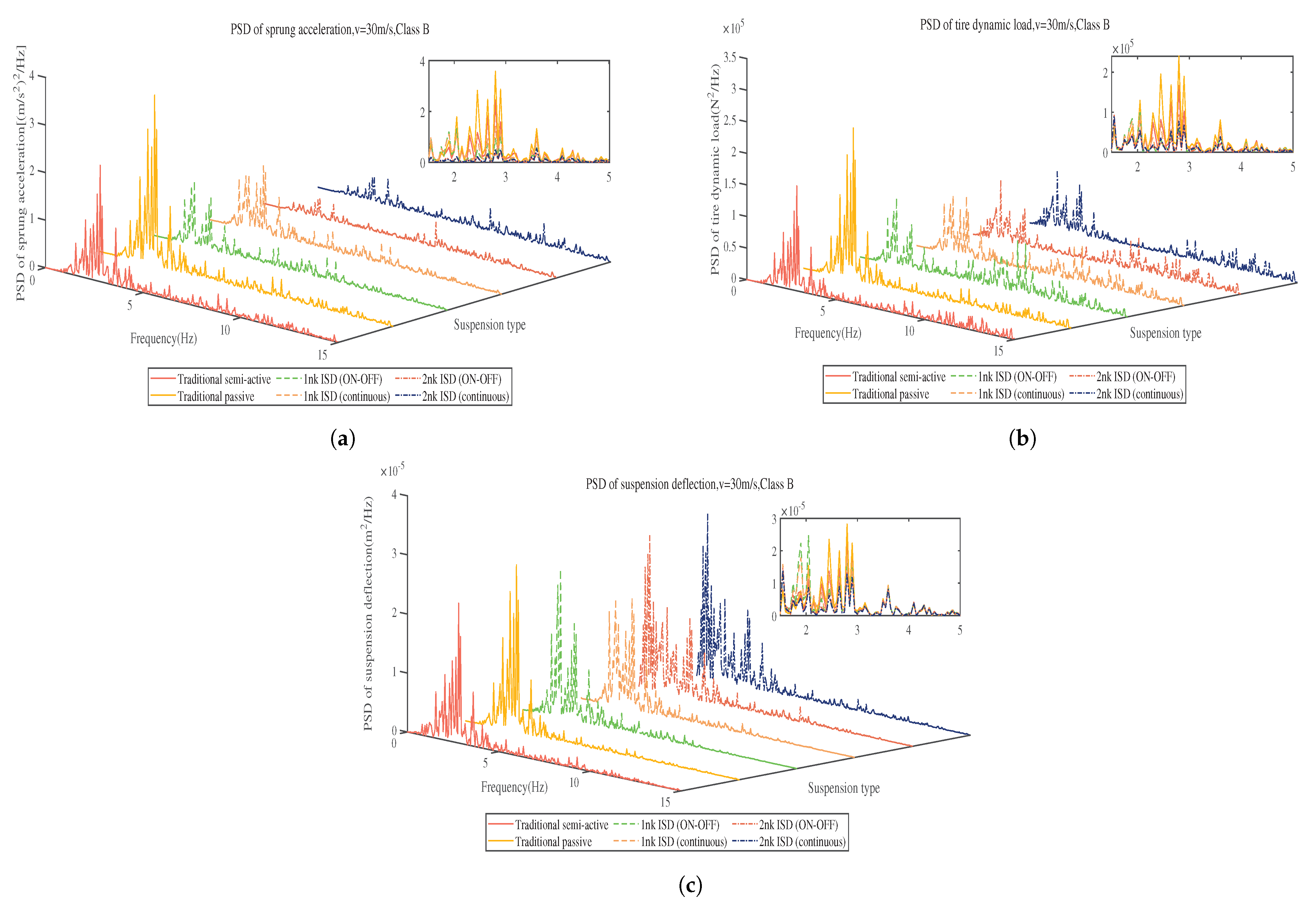
5. Performance Analysis and Discussion of Semi-Active ISD Suspensions
5.1. Semi-Active Realization of the Ideal Sky-Hook Inerter
5.2. Suspension Performance Analysis
6. Conclusions
- The network synthesis approach is implemented for the optimization of the suspension construction. The suspension can be realized physically by the network synthesis method, which is more targeted with suspension performance than the traditional structure method.
- The parameters of the obtained ideal Sky-hook ISD suspension are optimized using the PSO algorithm, and the performance of the obtained suspension structure can make further improvements to ride comfort while ensuring that the other performance does not deteriorate.
- Both the first-order and second-order semi-active ISD suspensions proposed in this paper can effectively suppress the sprung acceleration in the low frequency band, which improves the ride comfort of the vehicle. The second-order semi-active ISD suspensions show better overall performance in both time and frequency domain.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ghazaly, N.M.; Moaaz, A.O. The future development and analysis of vehicle active suspension system. Iosr J. Mech. Civ. Eng. 2014, 11, 19–25. [Google Scholar] [CrossRef]
- Savaresi, S.M.; Poussot-Vassal, C. Semi-Active Suspension Technologies and Models. In Active Suspension Technologies and Models; Elsevier: Oxford, UK, 2010; pp. 1–13. [Google Scholar]
- Priyandoko, G.; Mailah, M.; Jamaluddin, H. Direct voltage control of magnetorheological damper for vehicle suspensions. Smart Mater. Struct. 2013, 22, 105016. [Google Scholar]
- Chen, M.Z.Q.; Hu, Y.; Li, C.; Chen, G. Performance benefits of using inerter in semiactive suspensions. IEEE Trans. Control Syst. Technol. 2014, 23, 1571–1577. [Google Scholar] [CrossRef]
- Priyandoko, G.; Mailah, M.; Jamaluddin, H. Vehicle active suspension system using skyhook adaptive neuro active force control. Mech. Syst. Signal Proc. 2009, 23, 855–868. [Google Scholar] [CrossRef]
- Bitaraf, M.; Ozbulut, O.E.; Hurlebaus, S.; Barroso, L. Application of semi-active control strategies for seismic protection of buildings with MR dampers. Eng. Struct. 2010, 32, 3040–3047. [Google Scholar] [CrossRef]
- Yoon, D.S.; Kim, G.W.; Choi, S.B. Response time of magnetorheological dampers to current inputs in a semi-active suspension system: Modeling, control and sensitivity analysis. Mech. Syst. Signal Process. 2021, 146, 106999. [Google Scholar] [CrossRef]
- Pei, P.; Peng, Y.; Qiu, C. An improved semi-active structural control combining optimized fuzzy controller with inverse modeling technique of MR damper. Struct. Multidiscip. Optim. 2022, 55, 272. [Google Scholar] [CrossRef]
- Alonso, A.; Gimenez, J.G.; Nieto, J.; Vinolas, J. Air suspension characterisation and effectiveness of a variable area orifice. Veh. Syst. Dyn. 2010, 48, 271–286. [Google Scholar] [CrossRef]
- Ning, D.; Christie, M.D.; Sun, S.; Du, H.; Li, W.; Wang, Y. A controllable mechanical motion rectifier-based semi-active magnetorheological inerter for vibration control. Smart Mater. Struct. 2020, 29, 114005. [Google Scholar] [CrossRef]
- Chen, M.Z.Q.; Hu, Y. Semi-active Inerter and Adaptive Tuned Vibration Absorber. In Inerter and Its Application in Vibration Control Systems; Springer: Singapore, 2019; pp. 103–119. [Google Scholar]
- Smith, M.C. The inerter: A retrospective. Annu. Rev. Control Robot. Auton. Syst. 2020, 3, 361–391. [Google Scholar] [CrossRef]
- Smith, M.C. Synthesis of mechanical networks: The inerter. IEEE Trans. Autom. Control 2002, 47, 1648–1662. [Google Scholar] [CrossRef]
- Wang, K.; Chen, M.Z.Q. Passive mechanical realizations of bicubic impedances with no more than five elements for inerter-based control design. J. Frankl. Inst. 2021, 358, 5353–5385. [Google Scholar] [CrossRef]
- Papageorgiou, C.; Smith, M.C. Positive real synthesis using matrix inequalities for mechanical networks: Application to vehicle suspension. IEEE Trans. Control Syst. Technol. 2006, 14, 423–435. [Google Scholar] [CrossRef]
- Hu, Y.; Chen, M.Z.Q. Low-complexity passive vehicle suspension design based on element-number-restricted networks and low-order admittance networks. J. Dyn. Syst. Meas. Control 2018, 140, 101014. [Google Scholar] [CrossRef]
- Wang, K.; Chen, M.Z.Q.; Hu, Y. Synthesis of biquadratic impedances with at most four passive elements. J. Frankl. Inst. 2014, 351, 1251–1267. [Google Scholar] [CrossRef]
- Chen, L.; Liu, C.; Liu, W.; Nie, J.; Shen, Y.; Chen, G. Network synthesis and parameter optimization for vehicle suspension with inerter. Adv. Mech. Eng. 2016, 9. [Google Scholar] [CrossRef]
- Jiang, J.Z.; Smith, M.C. Regular positive-real functions and five-element network synthesis for electrical and mechanical networks. IEEE Trans. Autom. Control 2010, 56, 1275–1290. [Google Scholar] [CrossRef]
- Chen, M.Z.Q.; Li, Z.; Wang, H. Seismic response mitigation of a wind turbine via inerter-based structural control. Bull. Earthq. Eng. 2021, 21, 1361–1388. [Google Scholar] [CrossRef]
- He, H.; Li, Y.; Jiang, J.Z.; Burrow, S.; Neild, S.; Conn, A. Using an inerter to enhance an active-passive-combined vehicle suspension system. Int. J. Mech. Sci. 2021, 204, 106535. [Google Scholar] [CrossRef]
- Hu, Y.; Wang, K.; Chen, M.Z. Inerter-based semi-active suspensions with low-order mechanical admittance via network synthesis. Trans. Inst. Meas. Control 2018, 40, 4233–4245. [Google Scholar] [CrossRef]
- Tseng, H.E.; Hrovat, D. State of the art survey: Active and semi-active suspension control. Veh. Syst. Dyn. 2015, 57, 1034–1062. [Google Scholar] [CrossRef]
- Hu, Y.; Chen, M.Z.Q.; Xu, S.; Liu, Y. Semiactive Inerter and Its Application in Adaptive Tuned Vibration Absorbers. IEEE Trans. Control Syst. Technol. 2016, 25, 294–300. [Google Scholar] [CrossRef]
- Li, P.; Lam, J.; Cheung, K.C. Investigation on semi-active control of vehicle suspension using adaptive inerter. In Proceedings of the 21st International Congress on Sound and Vibration (ICSV 21), Beijing, China, 13–17 July 2014; pp. 3367–3374. [Google Scholar]
- Hu, Y.; Chen, M.Z.Q.; Sun, Y. Comfort-oriented vehicle suspension design with skyhook inerter configuration. J. Sound Vib. 2017, 405, 34–47. [Google Scholar] [CrossRef]
- Boyd, S.; El Ghaoui, L.; Feron, E.; Balakrishnan, V. Linear Matrix Inequalities in System and Control Theory; Society for Industrial and Applied Mathematics Philadelphia: Philadelphia, PA, USA, 1994. [Google Scholar]
- Smith, M.C.; Wang, F.C. Performance benefits in passive vehicle suspensions employing inerters. Veh. Syst. Dyn. 2004, 42, 235–257. [Google Scholar] [CrossRef]
- Katoch, S.; Chauhan, S.S.; Kumar, V. A review on genetic algorithm: Past, present, and future. Multimed. Tools Appl. 2021, 80, 8091–8126. [Google Scholar] [CrossRef] [PubMed]
- Kawanishi, M.; Ikuyama, Y. BMI optimization based on unimodal normal distribution crossover GA with relaxed LMI convex estimation. In Proceedings of the 2005, American Control Conference, Portland, OR, USA, 8–10 June 2005; pp. 2299–2304. [Google Scholar]
- Lofberg, J. YALMIP: A toolbox for modeling and optimization in MATLAB. In Proceedings of the 2004 IEEE International Conference on Robotics and Automation, Taipei, Taiwan, China, 2–4 September 2004; pp. 284–289. [Google Scholar]
- ISO 8608:2016; Mechanical Vibration–Road Surface Profiles–Reporting of Measured Data. ISO: Geneva, Switzerland, 2016. Available online: https://www.iso.org/standard/71202.html (accessed on 7 November 2022).
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95-International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; pp. 1942–1948. [Google Scholar]
- Marini, F.; Walczak, B. Particle swarm optimization (PSO). A tutorial. Chemom. Intell. Lab. Syst. 2015, 149, 153–165. [Google Scholar] [CrossRef]

| Parameter | Value |
|---|---|
| Sprung mass | 250 |
| Unsprung mass (kg) | 35 |
| Support spring stiffness k (N/m) | 80,000 |
| Tire stiffness (N/m) | 150,000 |
| Ideal Sky-hook inertance (kg) | 120 |
| Road Class | m |
|---|---|
| A (very good) | 16 |
| B (good) | 64 |
| C (average) | 256 |
| D (poor) | 1024 |
| E (very poor) | 4096 |
| Parameter Variable | Lower Limit | Upper Limit |
|---|---|---|
| Inertance (kg) | 100 | 1000 |
| Damping coefficient (N · s/m) | 1000 | 7000 |
| Inertance (kg) | 50 | 1000 |
| Damping coefficient (N · s/m) | 500 | 6000 |
| Spring stiffness (N/m) | 5000 | 20,000 |
| Parameter | Optimization Results |
|---|---|
| Inertance (kg) | 890.65 |
| Damping coefficient (N · s/m) | 2542.12 |
| Inertance (kg) | 996.13 |
| Damping coefficient (N · s/m) | 2005.21 |
| Spring stiffness (N/m) | 5002.92 |
| Conditions | Performance | Traditional Suspension | ISD Suspension (1 nk) | ISD Suspension (2 nk) | |||
|---|---|---|---|---|---|---|---|
| Index (RMS) | Passive | Semi-Active | ON-OFF | Continuous | ON–OFF | Continuous | |
| Sprung acceleration (m/s) | 0.7873 | 0.6825 | 0.6421 | 0.6378 | 0.4202 | 0.4338 | |
| Class A, 20 m/s | Tire dynamic load (N) | 218.7408 | 195.4778 | 195.7847 | 193.3658 | 174.3653 | 171.9115 |
| Suspension deflection (m) | 0.0021 | 0.0019 | 0.0021 | 0.0020 | 0.0027 | 0.0027 | |
| Sprung acceleration (m/s) | 0.9535 | 0.8281 | 0.7688 | 0.7721 | 0.5223 | 0.5306 | |
| Class A, 30 m/s | Tire dynamic load (N) | 365.1126 | 338.2103 | 361.4294 | 349.0471 | 337.0507 | 323.6969 |
| Suspension deflection (m) | 0.0033 | 0.0032 | 0.0034 | 0.0033 | 0.0042 | 0.0041 | |
| Sprung acceleration (m/s) | 1.2858 | 1.1300 | 1.1286 | 1.1035 | 0.8276 | 0.8531 | |
| Class B, 20 m/s | Tire dynamic load (N) | 265.1425 | 237.4449 | 237.2606 | 234.6618 | 210.9755 | 207.4685 |
| Suspension deflection (m) | 0.0025 | 0.0024 | 0.0025 | 0.0024 | 0.0030 | 0.0029 | |
| Sprung acceleration (m/s) | 1.5593 | 1.3679 | 1.3577 | 1.3373 | 1.0229 | 1.0399 | |
| Class B, 30 m/s | Tire dynamic load (N) | 443.2428 | 410.1071 | 435.5959 | 424.2941 | 409.5107 | 391.4729 |
| Suspension deflection (m) | 0.0039 | 0.0038 | 0.0039 | 0.0039 | 0.0047 | 0.0046 | |
| Vehicle | Performance | ISD Suspension (1 nk) | ISD Suspension (2 nk) | ||
|---|---|---|---|---|---|
| Speed | Index | ON-OFF | Continuous | ON-OFF | Continuous |
| Class A, 20 m/s | Ride comfort | 18.4% | 18.9% | 46.6% | 44.9% |
| Road-holding | 10.5% | 11.6% | 20.3% | 21.4% | |
| Class A, 30 m/s | Ride comfort | 19.4% | 19.1% | 45.2% | 44.4% |
| Road-holding | 10.5% | 11.5% | 20.4% | 21.8% | |
| Class B, 20 m/s | Ride comfort | 12.2% | 14.2% | 35.6% | 33.7% |
| Road-holding | 1.1% | 4.4% | 7.7% | 11.3% | |
| Class B, 30 m/s | Ride comfort | 13.1% | 14.2% | 34.4% | 33.3% |
| Road-holding | 1.8% | 4.3% | 7.6% | 11.7% | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Han, S.; Xiong, J.; Wang, W. Comfort-Oriented Semi-Active Suspension Configuration with Inerter-Based Network Synthesis. Actuators 2023, 12, 290. https://doi.org/10.3390/act12070290
Li Y, Han S, Xiong J, Wang W. Comfort-Oriented Semi-Active Suspension Configuration with Inerter-Based Network Synthesis. Actuators. 2023; 12(7):290. https://doi.org/10.3390/act12070290
Chicago/Turabian StyleLi, Yalin, Shichang Han, Junlin Xiong, and Wenbo Wang. 2023. "Comfort-Oriented Semi-Active Suspension Configuration with Inerter-Based Network Synthesis" Actuators 12, no. 7: 290. https://doi.org/10.3390/act12070290
APA StyleLi, Y., Han, S., Xiong, J., & Wang, W. (2023). Comfort-Oriented Semi-Active Suspension Configuration with Inerter-Based Network Synthesis. Actuators, 12(7), 290. https://doi.org/10.3390/act12070290






