A Back-Drivable Rotational Force Actuator for Adaptive Grasping
Abstract
1. Introduction
2. Design and Control Methods
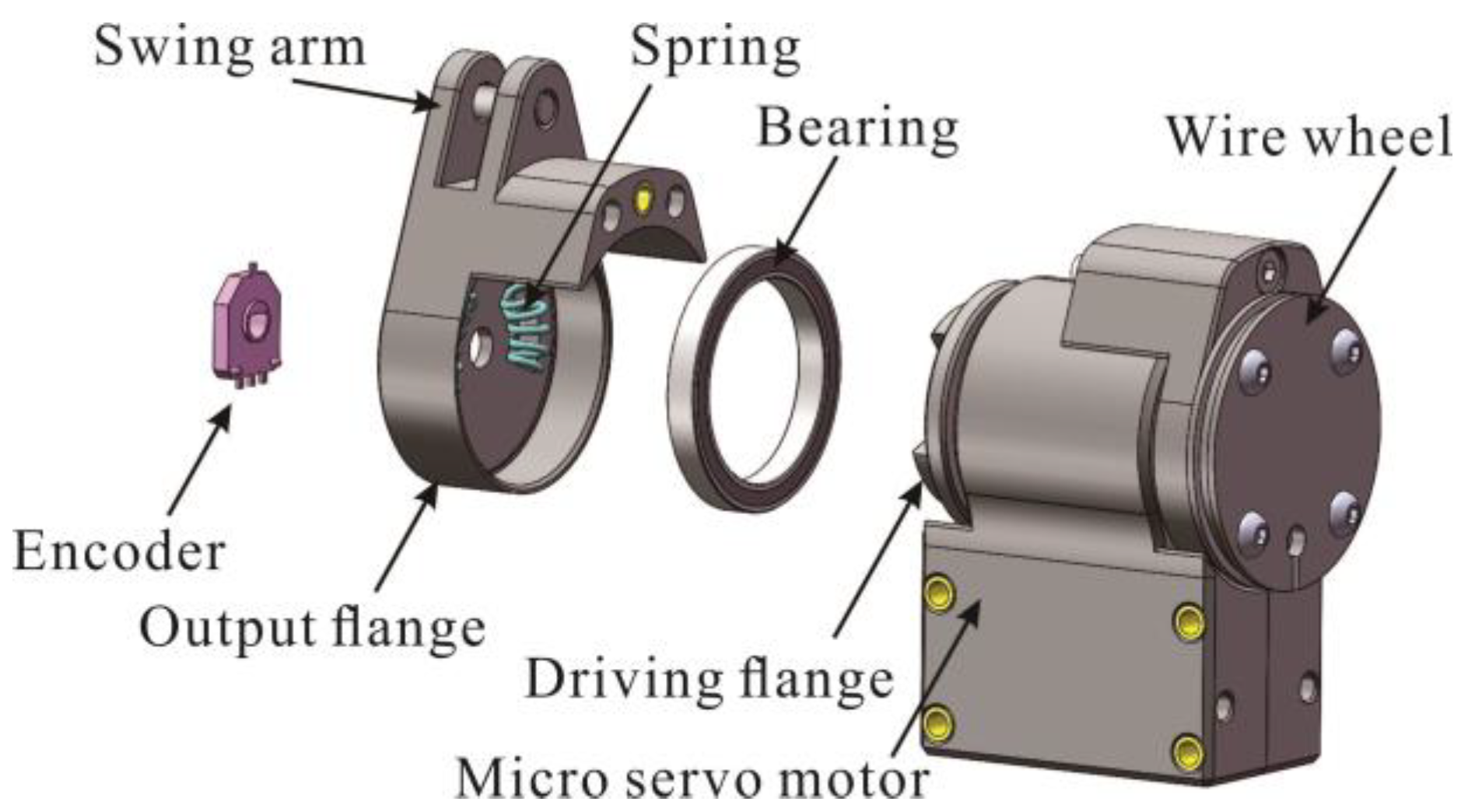
2.1. Mechanical Design
2.2. Model Identification and Control
3. Experimental Results and Discussion
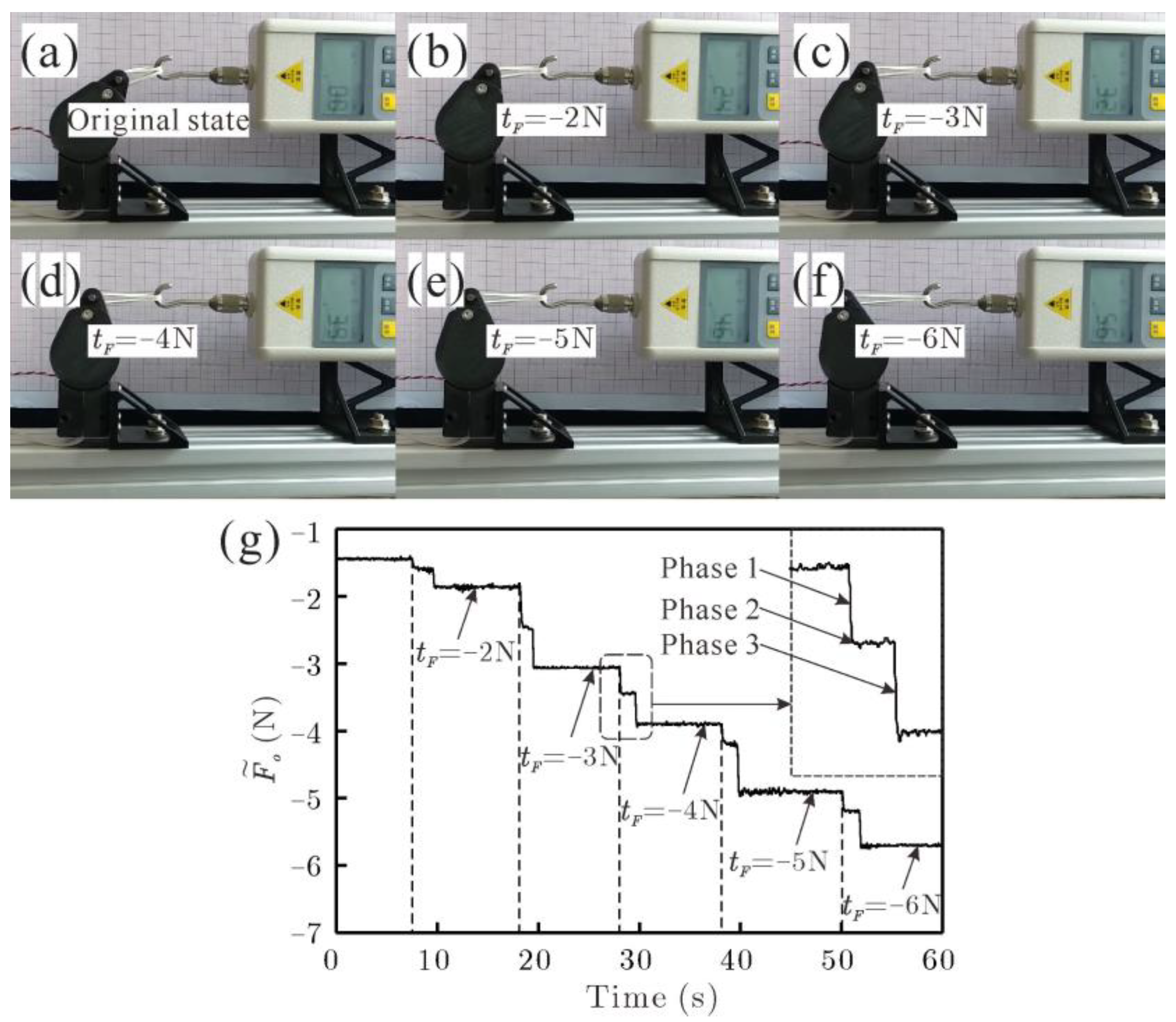
3.1. Step Response
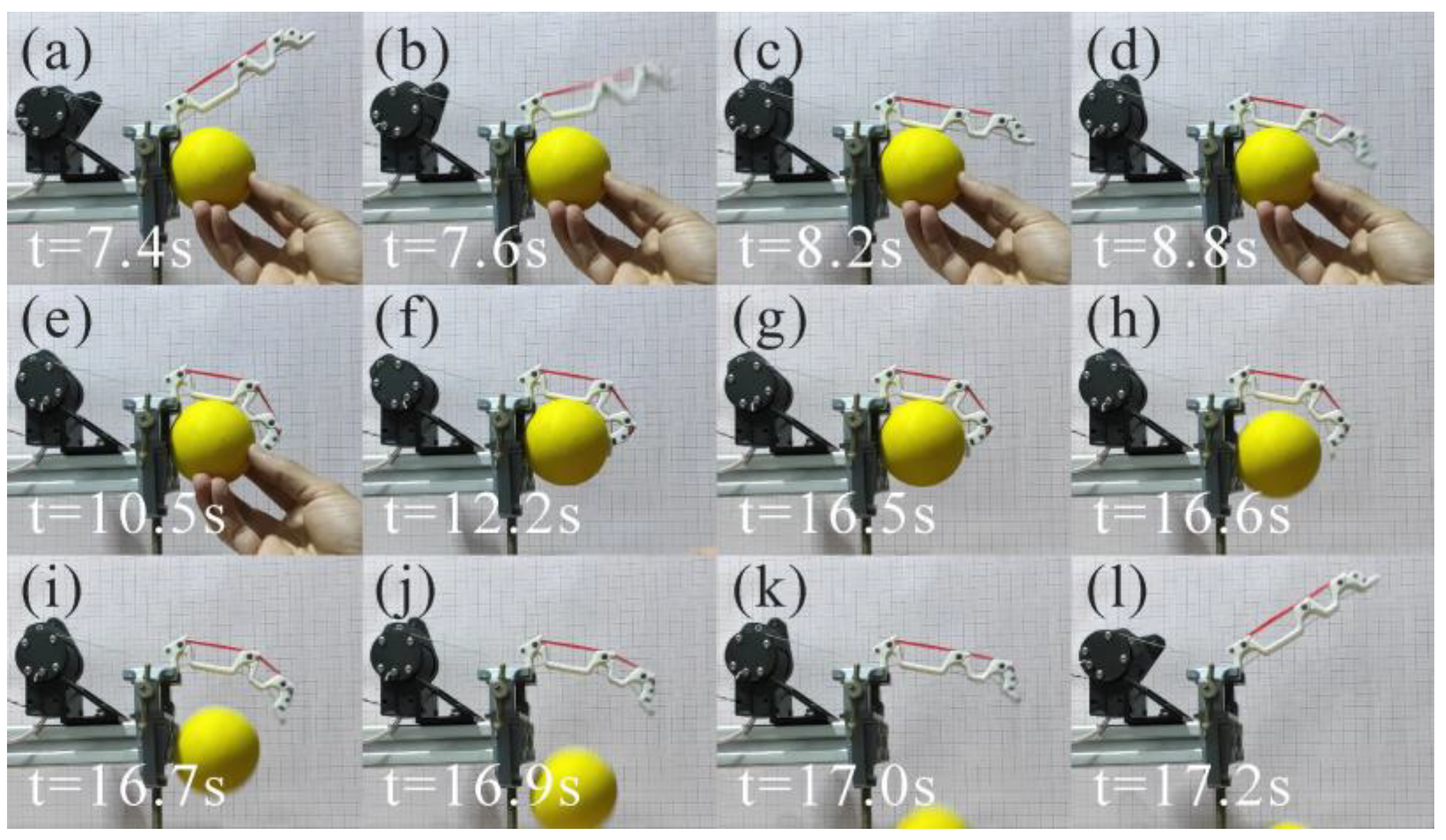
3.2. Adaptive Grasping Experiment
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Blanes, C.; Ortiz, C.; Mellado, M.; Beltrán, P. Assessment of eggplant firmness with accelerometers on a pneumatic robot gripper. Comput. Electron. Agric. 2015, 113, 44–50. [Google Scholar] [CrossRef]
- Ji, W.; Qian, Z.; Xu, B.; Chen, G.; Zhao, D. Apple viscoelastic complex model for bruise damage analysis in constant velocity grasping by gripper. Comput. Electron. Agric. 2019, 162, 907–920. [Google Scholar] [CrossRef]
- Xiong, Y.; Peng, C.; Grimstad, L.; From, P.J.; Isler, V. Development and field evaluation of a strawberry harvesting robot with a cable-driven gripper. Comput. Electron. Agric. 2019, 157, 392–402. [Google Scholar] [CrossRef]
- Endo, G.; Otomo, N. Development of a food handling gripper considering an appetizing presentation. In Proceedings of the 2016 IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 16–21 May 2016; pp. 4901–4906. [Google Scholar]
- Wang, Z.; Hirai, S. A Soft Gripper with Adjustable Stiffness and Variable Working Length for Handling Food Material. In Proceedings of the 2018 IEEE International Conference on Real-Time Computing and Robotics (RCAR), Kandima, Maldives, 1–5 August 2018; pp. 25–29. [Google Scholar]
- Kuriyama, Y.; Okino, Y.; Wang, Z.; Hirai, S. A Wrapping Gripper for Packaging Chopped and Granular Food Materials. In Proceedings of the 2019 2nd IEEE International Conference on Soft Robotics (RoboSoft), Seoul, Republic of Korea, 14–18 April 2019; pp. 114–119. [Google Scholar]
- Wang, Z.; Or, K.; Hirai, S. A dual-mode soft gripper for food packaging. Robot. Auton. Syst. 2020, 125, 103427. [Google Scholar] [CrossRef]
- Kim, U.; Seok, D.-Y.; Kim, Y.B.; Lee, D.-H.; Choi, H.R. Development of a grasping force-feedback user interface for surgical robot system. In Proceedings of the 2016 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Daejeon, Republic of Korea, 9–14 October 2016; pp. 845–850. [Google Scholar]
- Gerboni, G.; Brancadoro, M.; Tortora, G.; Diodato, A.; Cianchetti, M.; Menciassi, A. A novel linear elastic actuator for minimally invasive surgery: Development of a surgical gripper. Smart Mater. Struct. 2016, 25, 105025. [Google Scholar] [CrossRef]
- Guo, J.; Low, J.-H.; Liang, X.; Lee, J.S.; Wong, Y.-R.; Yeow, R.C.H. A Hybrid Soft Robotic Surgical Gripper System for Delicate Nerve Manipulation in Digital Nerve Repair Surgery. IEEE/ASME Trans. Mechatron. 2019, 24, 1440–1451. [Google Scholar] [CrossRef]
- Sun, Y.; Liu, Y.; Pancheri, F.; Lueth, T.C. Larg: A lightweight robotic gripper with 3-D topology optimized adaptive fingers. IEEE/ASME Trans. Mechatron. 2022, 27, 2026–2034. [Google Scholar] [CrossRef]
- Sun, Y.; Liu, Y.; Xu, L.; Zou, Y.; Faragasso, A.; Lueth, T.C. Automatic design of compliant surgical forceps with adaptive grasping functions. IEEE Robot. Autom. Lett. 2020, 5, 1095–1102. [Google Scholar] [CrossRef]
- Liu, C.-H.; Chiu, C.-H. Optimal design of a soft robotic gripper with high mechanical advantage for grasping irregular objects. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; pp. 2846–2851. [Google Scholar]
- Liu, C.-H.; Huang, G.-F.; Chiu, C.-H.; Chen, T.-L. Topology and size optimization of an adaptive compliant gripper to maximize the geometric advantage. In Proceedings of the 2016 IEEE International Conference on Advanced Intelligent Mechatronics (AIM), Banff, AB, Canada, 12–15 July 2016; pp. 1145–1150. [Google Scholar]
- Hua, H.; Song, J.; Zhao, J.; Liao, Z. Sensor-less Grasping Force Control of a Pneumatic Underactuated Robotic Gripper. J. Mech. Robot. 2023, 16, 031005. [Google Scholar] [CrossRef]
- Hua, H.; Liao, Z.; Zhao, J. Design, Analysis, and Experiment of an Underactuated Robotic Gripper Actuated by Linear Series Elastic Actuator. J. Mech. Robot. 2022, 15, 021002. [Google Scholar] [CrossRef]
- Hua, H.; Liao, Z.; Wu, X.; Chen, Y.; Feng, C. A Back-drivable Linear Force Actuator for Adaptive Grasping. J. Mech. Sci. Technol. 2022, 36, 4213–4220. [Google Scholar] [CrossRef]
- Odhner, L.U.; Jentoft, L.P.; Claffee, M.R.; Corson, N.; Tenzer, Y.; Ma, R.R.; Buehler, M.; Kohout, R.; Howe, R.D.; Dollar, A.M. A compliant, underactuated hand for robust manipulation. Int. J. Robot. Res. 2014, 33, 736–752. [Google Scholar] [CrossRef]
- Romeo, R.A.; Zocco, A.; Fiorio, L.; Pucci, D.; Maggiali, M. Force control with friction compensation in a pneumatic gripper. In Proceedings of the 2021 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Prague, Czech Republic, 27 September–1 October 2021; pp. 7231–7237. [Google Scholar]
- Romeo, R.A.; Fiorio, L.; L’Erario, G.; Maggiali, M.; Metta, G.; Pucci, D. Dynamic control of a rigid pneumatic gripper. IEEE Robot. Autom. Lett. 2020, 5, 2793–2800. [Google Scholar] [CrossRef]
- Zhang, T.; Jiang, L.; Wu, X.; Feng, W.; Zhou, D.; Liu, H. Fingertip three-axis tactile sensor for multifingered grasping. IEEE/ASME Trans. Mechatron. 2014, 20, 1875–1885. [Google Scholar] [CrossRef]
- Jentoft, L.P.; Dollar, A.M.; Wagner, C.R.; Howe, R.D. Intrinsic embedded sensors for polymeric mechatronics: Flexure and force sensing. Sensors 2014, 14, 3861–3870. [Google Scholar] [CrossRef]
- Kim, U.; Lee, D.; Yoon, W.J.; Hannaford, B.; Choi, H.R. Force sensor integrated surgical forceps for minimally invasive robotic surgery. IEEE Trans. Robot. 2015, 31, 1214–1224. [Google Scholar] [CrossRef]
- Li, Y.; Cao, Y.; Jia, F. A Neural Network Based Dynamic Control Method for Soft Pneumatic Actuator with Symmetrical Chambers. Actuators 2021, 10, 112. [Google Scholar] [CrossRef]
- Chavoshian, M.; Taghizadeh, M.; Mazare, M. Hybrid dynamic neural network and PID control of pneumatic artificial muscle using the PSO algorithm. Int. J. Autom. Comput. 2020, 17, 428–438. [Google Scholar] [CrossRef]
- Pratt, J.E.; Krupp, B.T. Series elastic actuators for legged robots: Unmanned Ground Vehicle Technology VI. In Proceedings of the Defense and Security, Orlando, FL, USA, 12–16 April 2004; pp. 135–144. [Google Scholar]
- Wensing, P.M.; Wang, A.; Seok, S.; Otten, D.; Lang, J.; Kim, S. Proprioceptive actuator design in the mit cheetah: Impact mitigation and high-bandwidth physical interaction for dynamic legged robots. IEEE Trans. Robot. 2017, 33, 509–522. [Google Scholar] [CrossRef]
- Tsagarakis, N.G.; Laffranchi, M.; Vanderborght, B.; Caldwell, D.G. A compact soft actuator unit for small scale human friendly robots. In Proceedings of the 2009 IEEE International Conference on Robotics and Automation, Kobe, Japan, 12–17 May 2009; pp. 4356–4362. [Google Scholar]
- Shi, Y.; Zhang, M.; Zhang, X.; Bai, F. Design and analysis of a rotary-type robot flexible joint. China Mech. Eng. 2016, 27, 2494. [Google Scholar]
- Kong, K.; Bae, J.; Tomizuka, M. Control of rotary series elastic actuator for ideal force-mode actuation in human–robot interaction applications. IEEE/ASME Trans. Mechatron. 2009, 14, 105–118. [Google Scholar] [CrossRef]
- Kong, K.; Bae, J.; Tomizuka, M. A Compact Rotary Series Elastic Actuator for Knee Joint Assistive System. In Proceedings of the IEEE International Conference on Robotics & Automation, Anchorage, AK, USA, 3–7 May 2010; pp. 2940–2945. [Google Scholar]
- Kong, K.; Bae, J.; Tomizuka, M. A Compact Rotary Series Elastic Actuator for Human Assistive Systems. IEEE/ASME Trans. Mechatron. 2012, 17, 288–297. [Google Scholar] [CrossRef]







| tF (N) | (%) | (%) | ||
|---|---|---|---|---|
| 2 | 2.4 | 20 | 2.0 | −16.7 |
| 3 | 3.0 | 3.3 | 2.8 | −6.7 |
| 4 | 3.9 | −2.5 | 3.8 | −2.6 |
| 5 | 4.5 | −10 | 4.6 | 2.2 |
| 6 | 5.6 | −6.7 | 5.5 | −1.8 |
| 7 | 7.1 | 1.4 | 6.8 | −4.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, X.; Hua, H.; Zhao, C.; Shi, N.; Wu, Z. A Back-Drivable Rotational Force Actuator for Adaptive Grasping. Actuators 2023, 12, 267. https://doi.org/10.3390/act12070267
Wu X, Hua H, Zhao C, Shi N, Wu Z. A Back-Drivable Rotational Force Actuator for Adaptive Grasping. Actuators. 2023; 12(7):267. https://doi.org/10.3390/act12070267
Chicago/Turabian StyleWu, Xiaofeng, Hongliang Hua, Che Zhao, Naiyu Shi, and Zhiwei Wu. 2023. "A Back-Drivable Rotational Force Actuator for Adaptive Grasping" Actuators 12, no. 7: 267. https://doi.org/10.3390/act12070267
APA StyleWu, X., Hua, H., Zhao, C., Shi, N., & Wu, Z. (2023). A Back-Drivable Rotational Force Actuator for Adaptive Grasping. Actuators, 12(7), 267. https://doi.org/10.3390/act12070267




