Modeling and Experimental Validation of the Performance of Electromechanical Height Adjustment Vehicle Suspension with Eccentric Mounted Screw System
Abstract
1. Introduction
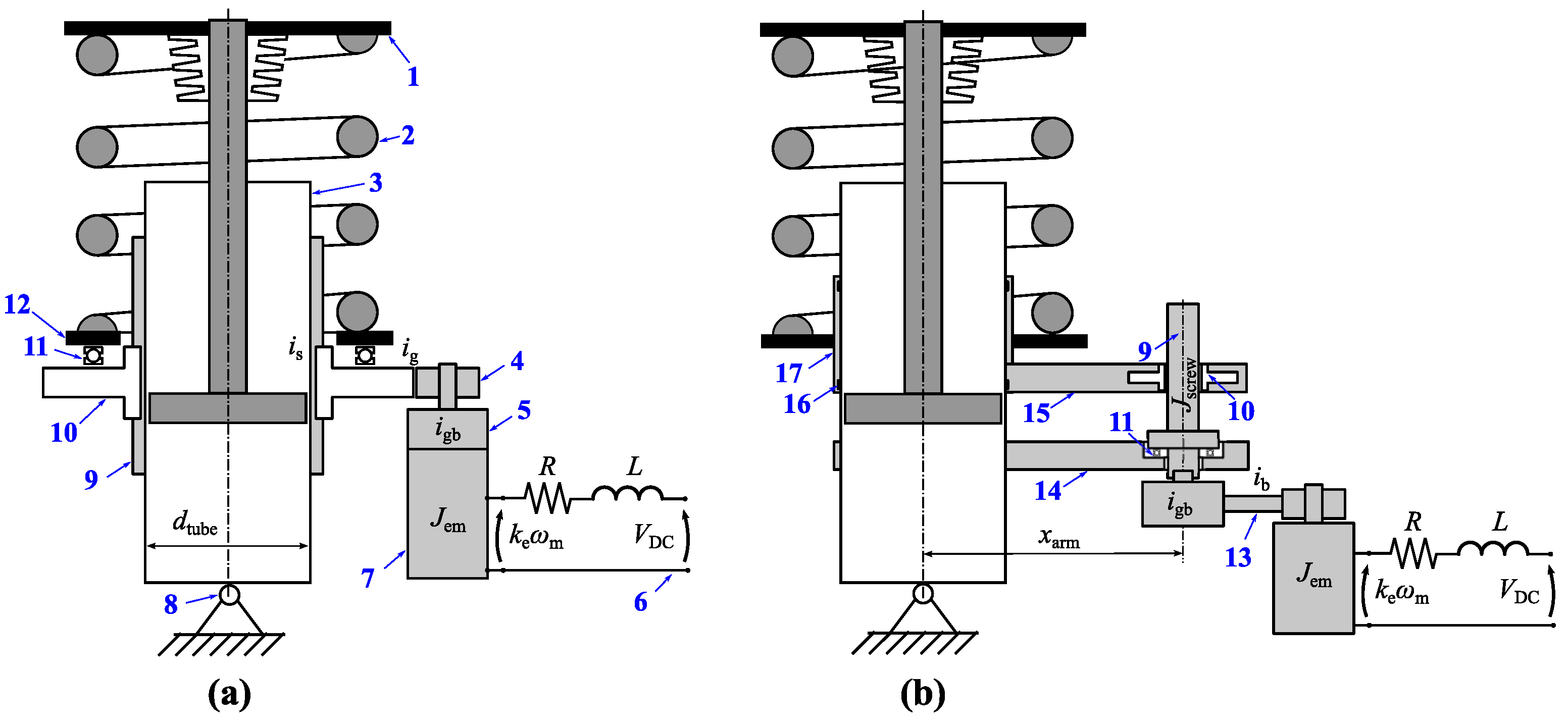
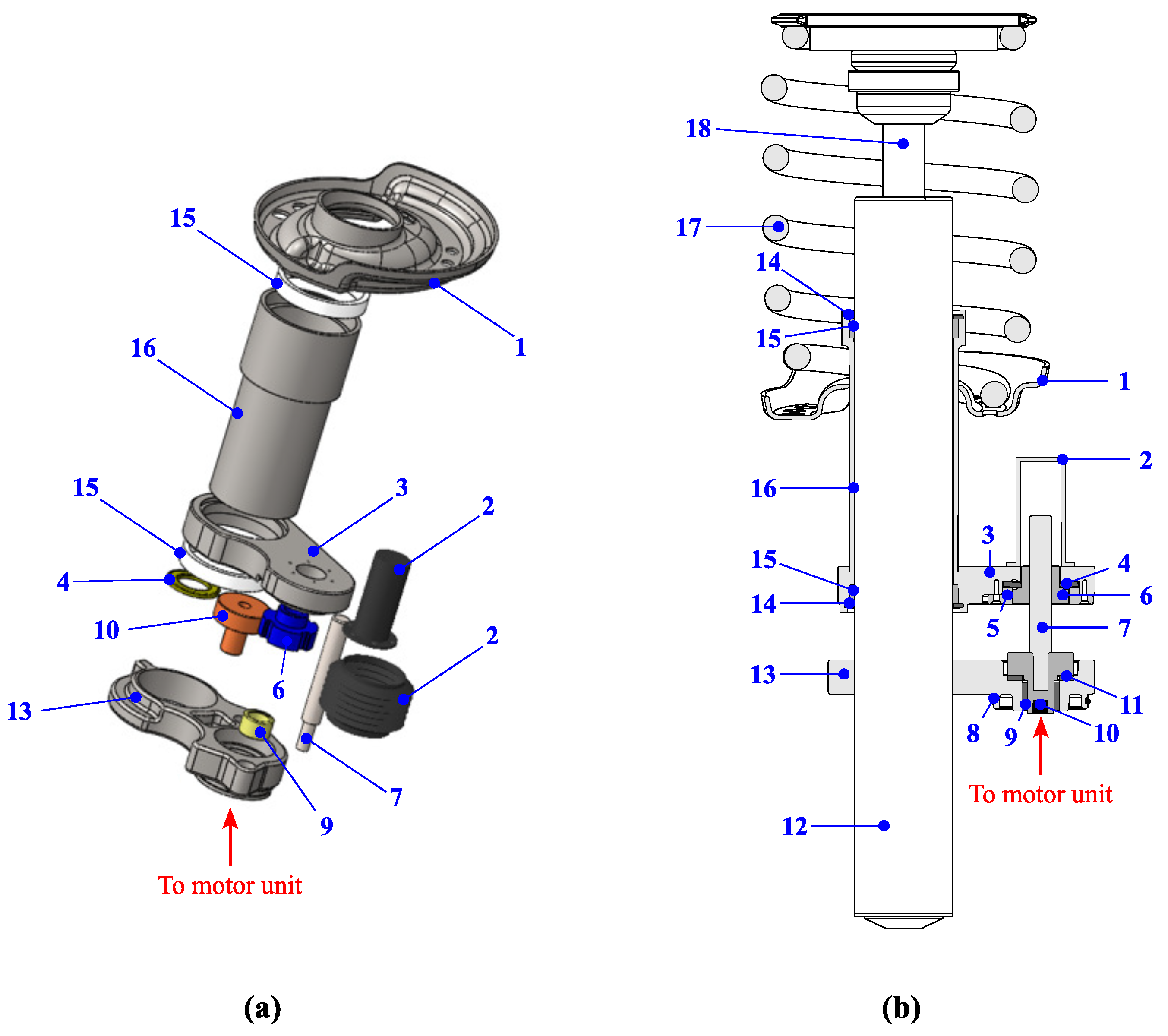
2. Description of the System
2.1. Working Principle
2.2. Component Sizing
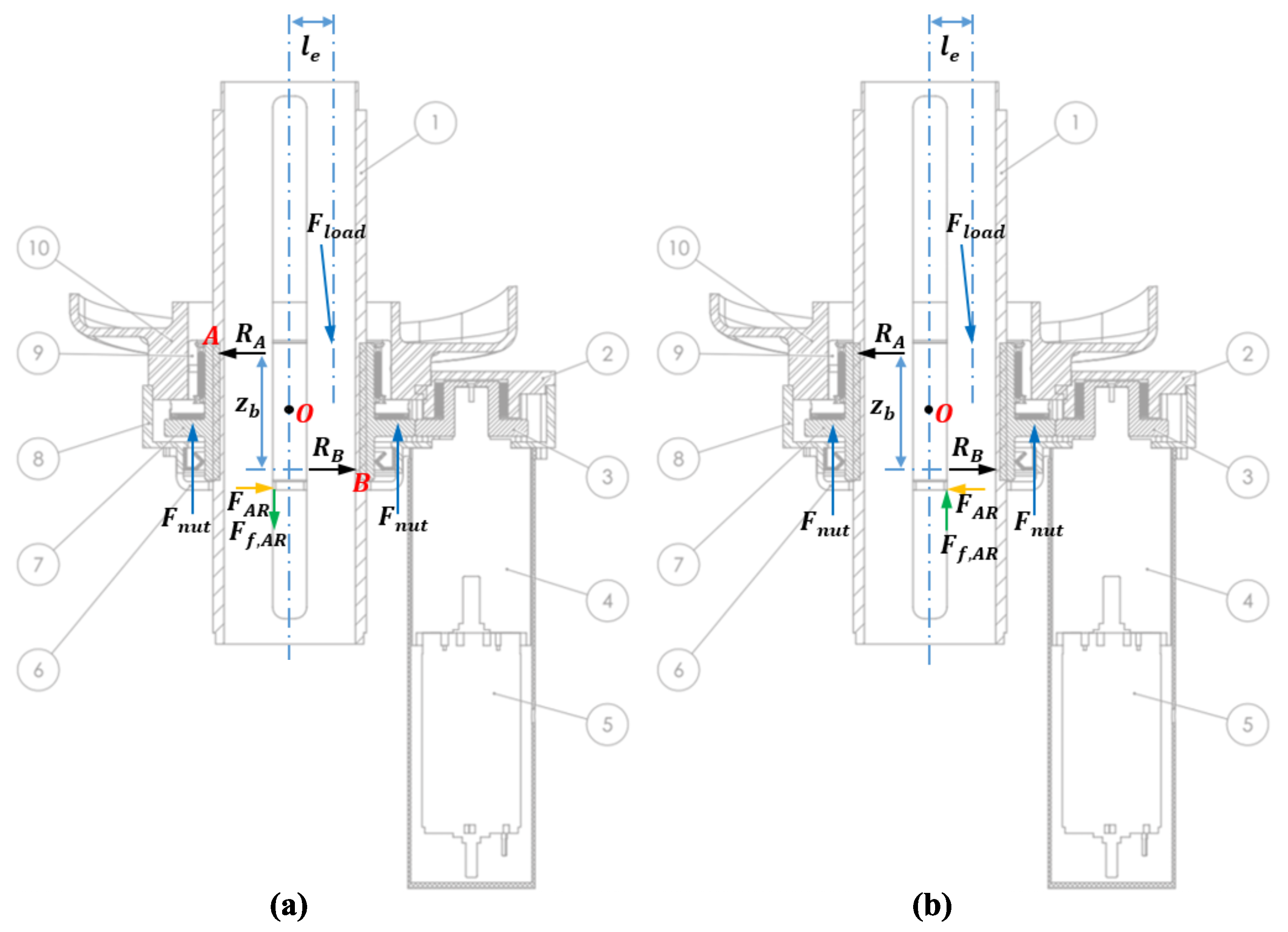
2.3. Eccentric Screw Actuator Prototype
- Smaller volume of the screw, which makes the substantial part of the system cost;
- The sliding surface of the shock absorber tube does not need a strict tolerance;
- Fewer and smaller bearings, replaceable by bronze bushings;
- Ease of maintenance.
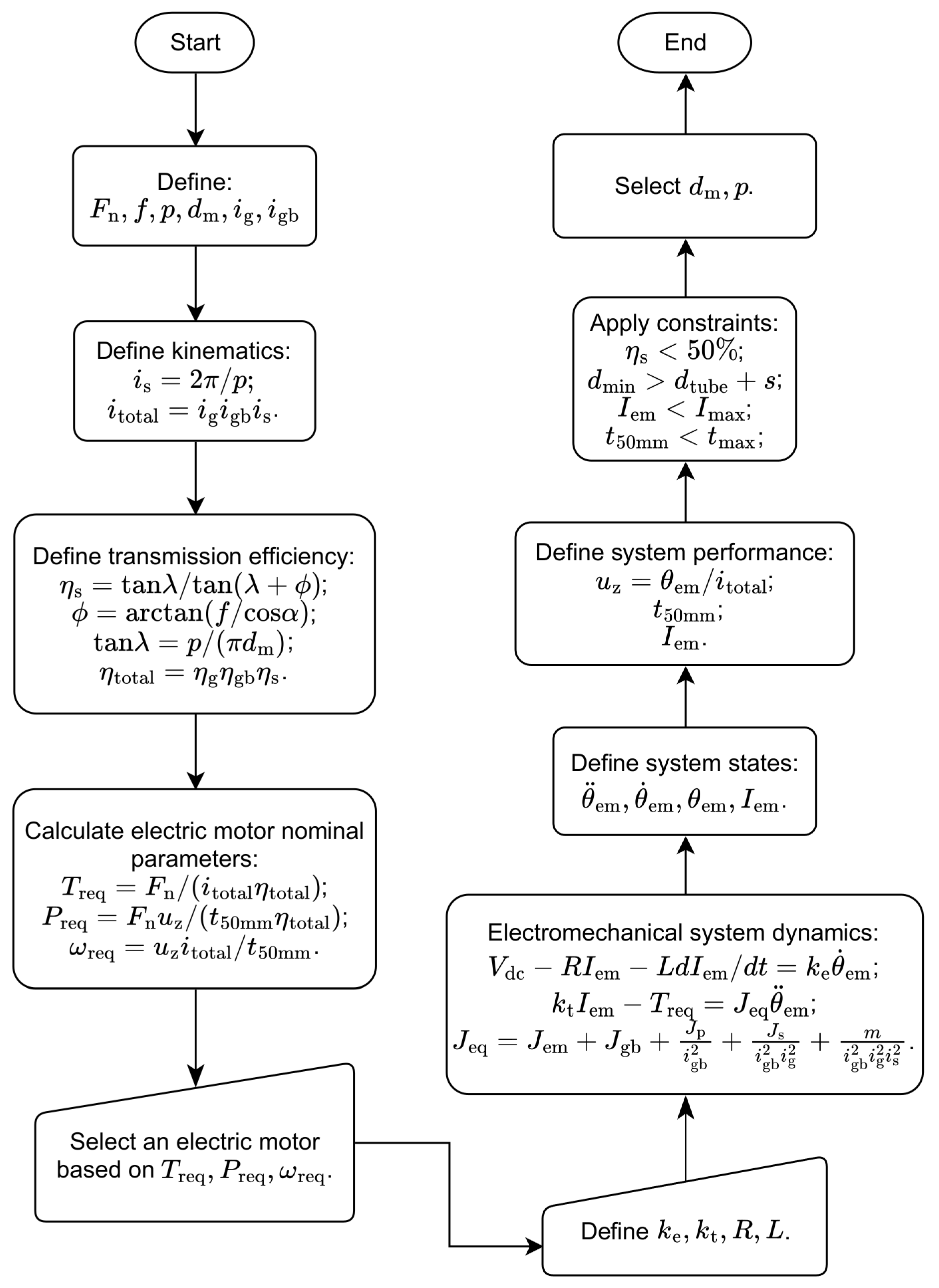
3. Numerical Modeling
- The shock absorber piston friction was neglected;
- The viscous force of the damper was not considered, as the actuation speed is small [29];
- The friction coefficients for the screw thread, collar, and anti-rotation elements were equal;
- The losses on the thrust bearings were not considered.
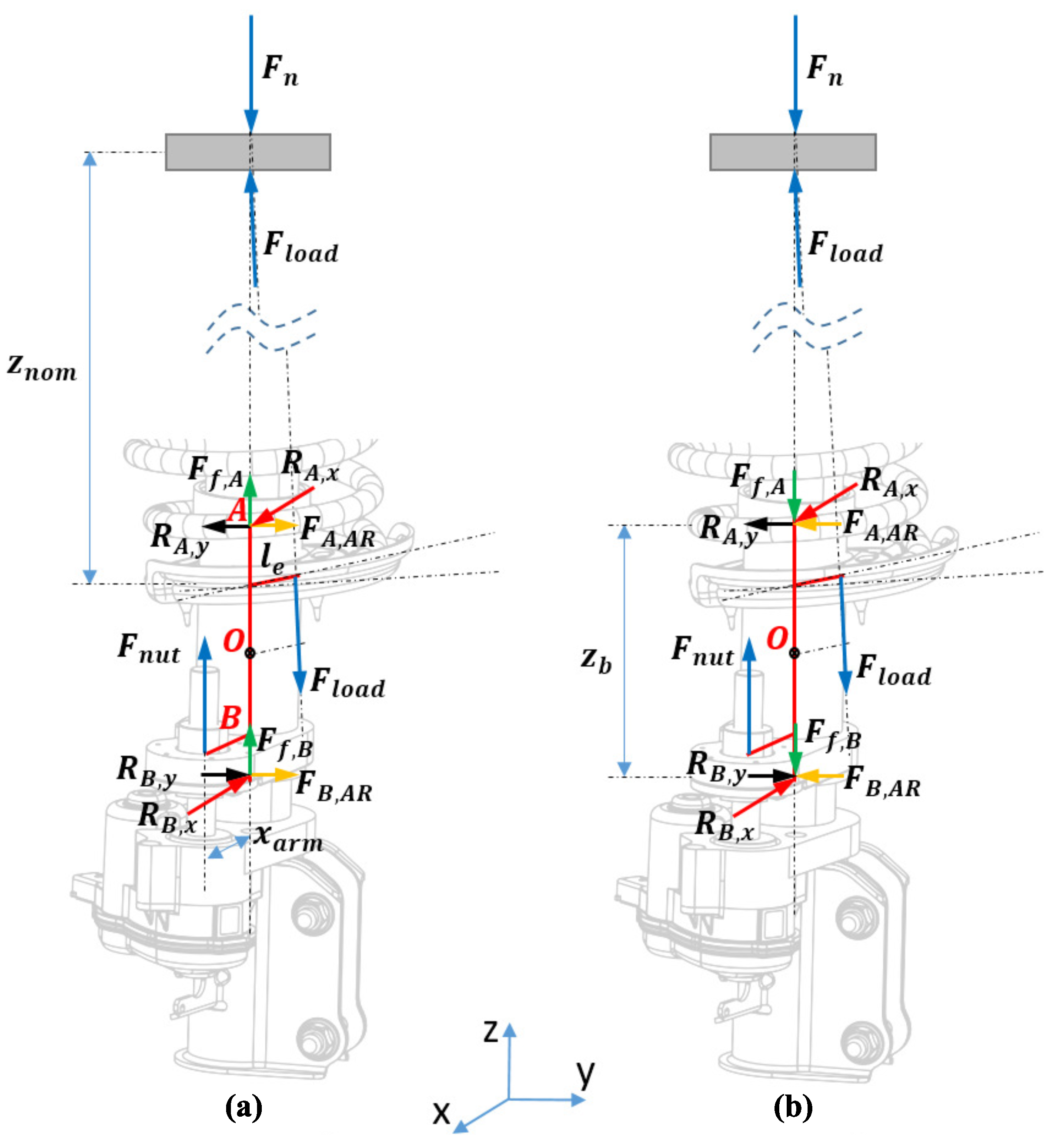
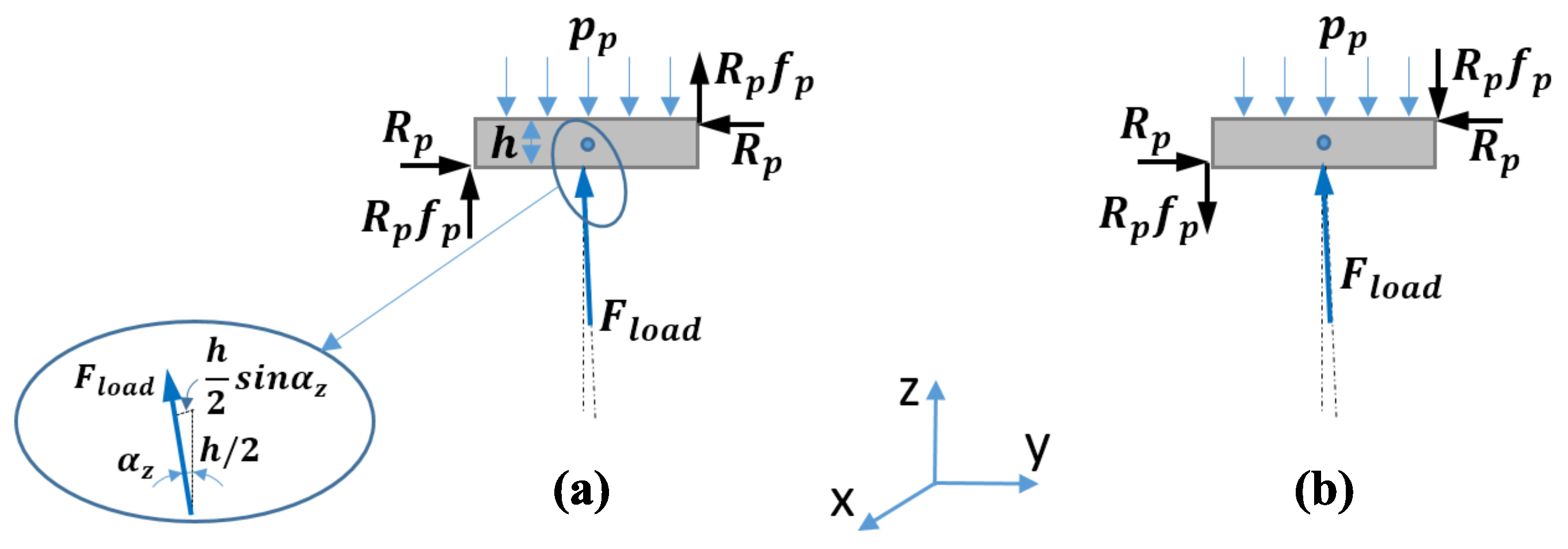
3.1. Eccentric Screw System Model
3.2. Concentric Screw System Model
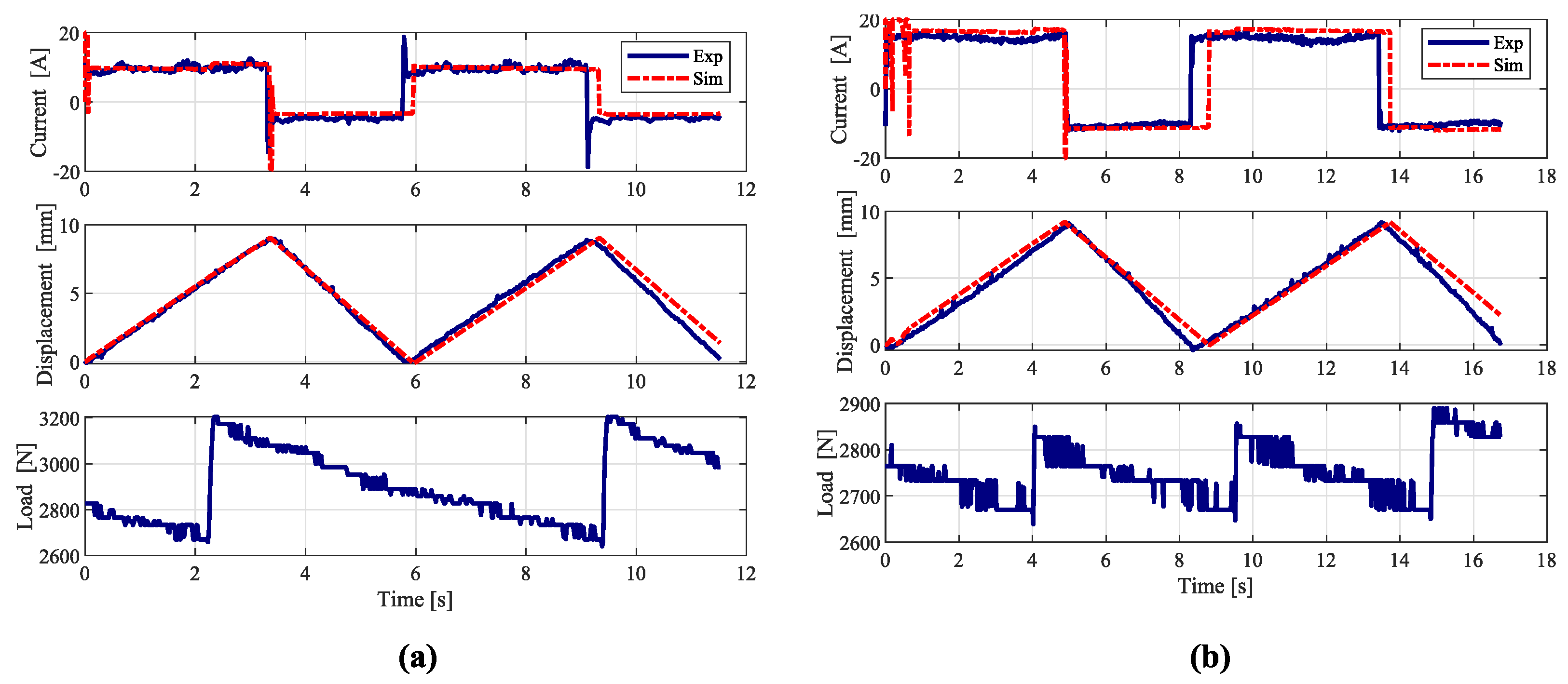
4. Experimental Results
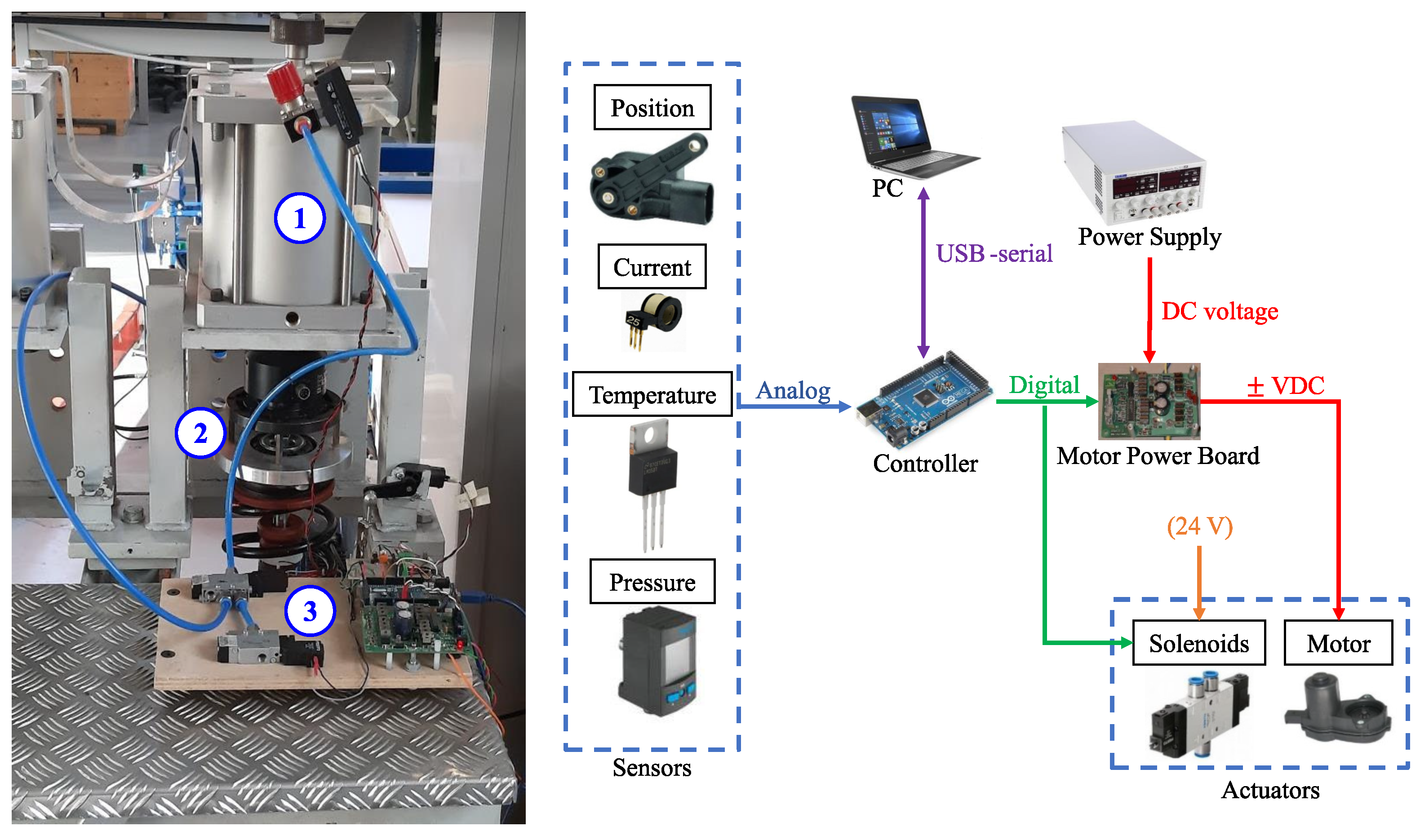
4.1. Experimental Setup
4.2. Experiments on Testbed
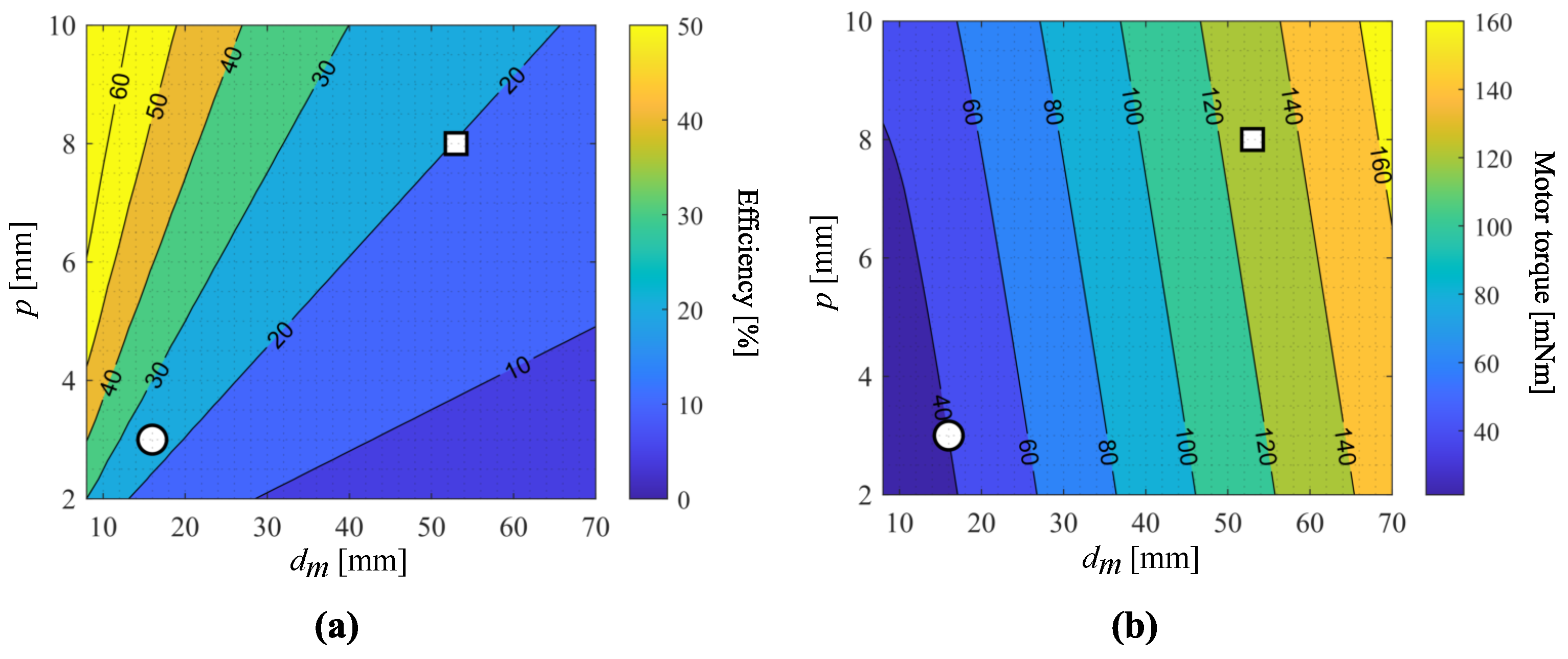
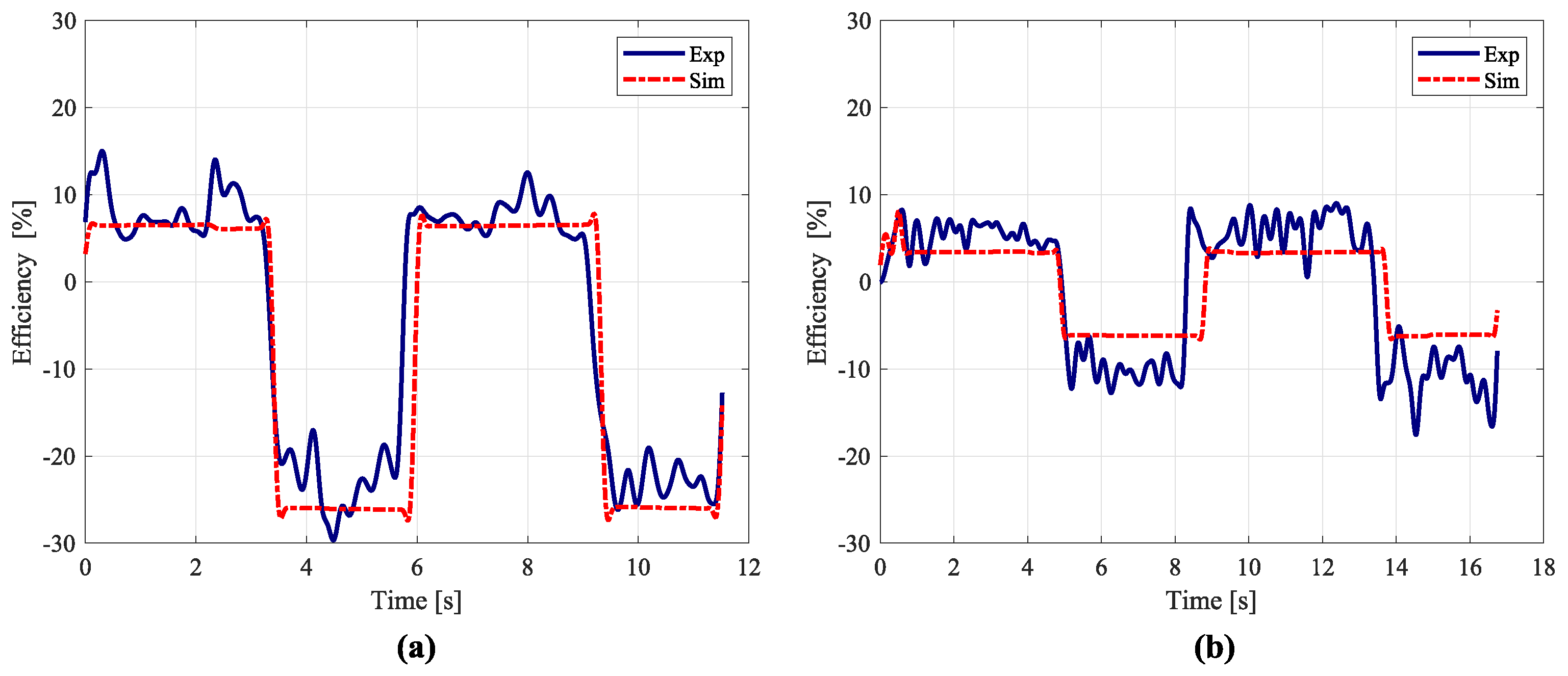
4.3. Efficiency Analysis
5. Vehicle Tests
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Carbon dioxide | |
| DC | Direct Current |
| SUV | Sport Utility Vehicle |
| GUI | Graphical User Interface |
Nomenclature
| Mean diameter of the screw | |
| Minor (root) diameter of the screw | |
| Diameter of the shock absorber tube | |
| Sliding friction coefficient on the bushings | |
| Sliding friction coefficient on the piston of the pneumatic cylinder | |
| Sliding friction coefficient on screw–nut surfaces | |
| Sliding friction coefficient on the anti-rotation system | |
| h | Height of the piston of the pneumatic cylinder |
| Speed reduction ratio of the parallel axis speed reducer | |
| Speed reduction ratio of the planetary gearbox | |
| Speed reduction ratio of the screw–nut mechanism | |
| Total speed reduction ratio of the parallel axis speed reducer, planetary gearbox | |
| and screw–nut mechanism | |
| Motor back EMF constant | |
| Motor torque constant | |
| Offset measured at the level of the lower spring holder | |
| p | Screw pitch |
| Pressure inside the pneumatic loading cylinder | |
| s | Diametric thickness of the power screw body |
| Time to cover 50 distance | |
| Maximum travel time requirement | |
| Spring holder vertical displacement | |
| Actuation speed of the load | |
| Distance between centers of the power screw and the shock absorber tube | |
| Vertical distance between two bushings | |
| Distance between mid-planes of upper and lower spring holders in nominal position | |
| Piston area of the pneumatic loading cylinder | |
| Friction force on the piston side surfaces | |
| Friction force on the anti-rotation system | |
| Load on the lower spring holder | |
| Static load due to the vehicle weight | |
| Load developed on the power screw | |
| Current to actuate the electric motor | |
| Maximum actuation current of the electric motor | |
| Steady state current absorption | |
| Moment of inertia of the electric motor’s rotating parts | |
| Equivalent moment of inertia of the rotating and translating elements | |
| Moment of inertia of the planetary gearbox | |
| Moment of inertia of the parallel axis speed reducer | |
| Moment of inertia of the screw | |
| L | Inductance of the motor winding |
| Nominal power of the electric motor | |
| Input electric power | |
| Output power from the height adjustment system | |
| Required power of the electric motor | |
| R | Resistance of the motor winding |
| Reaction force on the piston wall | |
| Reaction force in bushings at point A | |
| Reaction force in bushings in the XZ plane | |
| Reaction force in bushings in the YZ plane | |
| Reaction force in bushings at point B | |
| Torque on the electric motor shaft | |
| Nominal torque of the electric motor | |
| Friction torque due to bending | |
| Torque on the power screw required for actuation of the load | |
| Total torque required on the nut for actuation and to overcome frictions | |
| Required torque on the electric motor shaft | |
| Supply voltage of the vehicle battery | |
| Power screw thread angle | |
| Inclination angle of the load with respect to the Z (vertical) axis | |
| Angle between the arm and XZ plane | |
| Efficiency of the speed reducer or belt drive | |
| Efficiency of the planetary gearbox | |
| Efficiency of the overall conversion (from electric to mechanical actuation) | |
| Efficiency of the power screw | |
| Efficiency of the power screw in lifting phase | |
| Efficiency of the power screw in lowering phase | |
| Overall efficiency of the transmission path | |
| Power screw lead angle | |
| Angular speed of the electric motor shaft | |
| Angular speed of the electric motor shaft at nominal power | |
| Friction angle of the power screw | |
| Angular displacement of the electric motor shaft | |
| Angular velocity of the electric motor shaft | |
| Angular acceleration of the electric motor shaft | |
| Required angular velocity of the electric motor shaft |
References
- International Energy Agency. Key Trends in CO2 Emissions. Excerpt from: CO2 Emissions from Fuel Combustion (2015 Edition); IEA: Paris, France, 2015. [Google Scholar]
- Ott, T.; Onder, C.; Guzzella, L. Hybrid-electric vehicle with natural gas-diesel engine. Energies 2013, 6, 3571–3592. [Google Scholar] [CrossRef]
- Gabriel-Buenaventura, A.; Azzopardi, B. Energy recovery systems for retrofitting in internal combustion engine vehicles: A review of techniques. Renew. Sustain. Energy Rev. 2015, 41, 955–964. [Google Scholar] [CrossRef]
- Howell, J.; Sherwin, C.; Passmore, M.; Le Good, G. Aerodynamic Drag of a Compact SUV as Measured On-Road and in the Wind Tunnel. SAE Trans. 2002, 111, 583–590. [Google Scholar]
- Genta, G.; Morello, L. The Automotive Chassis: Volume 2: System Design; Springer Science & Business Media: Dordrecht, The Netherlands, 2009; pp. 146–149. [Google Scholar]
- CO2 Emission Standards for New Cars and Vans. Available online: https://www.europarl.europa.eu/RegData/etudes/BRIE/2022/698920/EPRS_BRI(2022)698920_EN.pdf (accessed on 26 May 2023).
- EU CO2 Emission Standards for Passenger Cars and Light-Commercial Vehicles. Available online: https://theicct.org/sites/default/files/publications/ICCTupdate_EU-95gram_jan2014.pdf (accessed on 26 May 2023).
- Faraj, J.; Harika, E.; Ramadan, M.; Ali, S.; Harambat, F.; Khaled, M. Effect of Underhood Architecture on Aerodynamic Drag—Suggestion of New Concepts for Fuel Consumption Reduction. Int. J. Automot. Technol. 2020, 21, 633–640. [Google Scholar] [CrossRef]
- Strassberger, M.; Guldner, J. BMW’s dynamic drive: An active stabilizer bar system. IEEE Control Syst. 2004, 24, 28–29. [Google Scholar]
- van der Westhuizen, S.F.; Els, P.S. Slow active suspension control for rollover prevention. J. Terramechanics 2013, 50, 29–36. [Google Scholar] [CrossRef]
- Amati, N.; Tonoli, A.; Castellazzi, L.; Ruzimov, S. Design of electromechanical height adjustable suspension. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2017, 232, 1253–1269. [Google Scholar] [CrossRef]
- Cogotti, A. A Parametric Study on the Ground Effect of a Simplified Car Model; SAE Technical Paper Series; SAE International: Warrendale, PA, USA, 1998. [Google Scholar] [CrossRef]
- Schuetz, T. Aerodynamics of Road Vehicles; SAE International: Warrendale, PA, USA, 2016. [Google Scholar]
- Semeraro, F.F.; Schito, P. Numerical Investigation of the Influence of Tire Deformation and Vehicle Ride Height on the Aerodynamics of Passenger Cars. Fluids 2022, 7, 47. [Google Scholar] [CrossRef]
- Dong, T.; Minelli, G.; Wang, J.; Liang, X.; Krajnović, S. The Effect of Ground Clearance on the Aerodynamics of a Generic High-Speed Train. J. Fluids Struct. 2020, 95, 102990. [Google Scholar] [CrossRef]
- Temporelli, R.; Micheau, P.; Boisvert, M. Control of an electromechanical clutch actuator by a parallel Adaptive Feedforward and Bang-Bang controller: Simulation and Experimental results. IFAC-PapersOnLine 2017, 50, 4787–4793. [Google Scholar] [CrossRef]
- Dong, G.; Wang, F.; Meng, D.; Chu, H.; Hong, J.; Gao, B. Modeling and control of ball-ramp electromechanical clutch actuator for in-wheel AMT of electric vehicles. Mech. Mach. Theory 2023, 180, 105129. [Google Scholar] [CrossRef]
- Jeong, S.-H.; Kim, K.-S. A 2-Speed Small Transmission Mechanism Based on Twisted String Actuation and a Dog Clutch. IEEE Robot. Autom. Lett. 2018, 3, 1338–1345. [Google Scholar] [CrossRef]
- Eskandary, P.K.; Angeles, J. The virtual screw: Concept, design and applications. Mech. Mach. Theory 2018, 128, 349–358. [Google Scholar] [CrossRef]
- Michel, W. Height Adjustment on a Wheel Suspension for Motor Vehicles. U.S. Patent US 7,784,800, 31 August 2010. [Google Scholar]
- Michel, W. Wheel Suspension for Motor Vehicles. U.S. Patent US 8,317,003, 27 November 2012. [Google Scholar]
- Bruno, W.; Conti, P.A.; Greco, G.; Amati, N.; Galluzzi, R.; Ruzimov, S.; Tonoli, A. Damper and Spring Unit for a Vehicle Suspension Provided with an Electro-Mechanical Adjustment Device for Adjusting the Vertical Position of the Spring. WIPO Patent WO2019097461, 23 May 2019. Available online: https://patentscope.wipo.int (accessed on 1 June 2023).
- Maxon Motor. Product Specifications. Available online: http://www.maxonmotor.com/maxon/view/product/273752 (accessed on 26 May 2023).
- Tonoli, A.; Amati, N.; Impinna, F.; Detoni, J.G.; Ruzimov, S.; Gasparin, E.; Abdivakhidov, K. Influence of dry friction on the irreversibility of cycloidal speed reducer. In Proceedings of the World tribology Congress, Torino, Italy, 8–13 September 2013. [Google Scholar]
- Meng, Y.; Wu, C.; Ling, L. Mathematical modeling of the transmission performance of 2K–H pin cycloid planetary mechanism. Mech. Mach. Theory 2007, 42, 776–790. [Google Scholar] [CrossRef]
- Raffone, E. An Electric Parking Brake Motor-On-Caliper actuator model for robust drive away control design. IFAC-PapersOnLine 2017, 50, 980–986. [Google Scholar] [CrossRef]
- Laus, L.P.; Simas, H.; Martins, D. Efficiency of gear trains determined using graph and screw theories. Mech. Mach. Theory 2012, 52, 296–325. [Google Scholar] [CrossRef]
- Budynas, R.G.; Nisbett, J.K. Shigley’s Mechanical Engineering Design, 8th ed.; McGraw Hill: New York, NY, USA, 2006; pp. 405–406. [Google Scholar]
- Körner, F.; Mayer, R. Analysis and characterization of the friction of vehicle body vibration dampers. Automot. Engine Technol. 2020, 5, 79–90. [Google Scholar] [CrossRef]
- Genta, G.; Morello, L. The Automotive Chassis: Volume 1: Component Design; Springer Science & Business Media: Dordrecht, The Netherlands, 2009; pp. 144–146. [Google Scholar]
- Rotation Angle Sensors. Available online: https://www.hella.com/resources-soe/assets/documents_global/1871_Brief_info_Angular_Sensors_HELLA_EN.pdf (accessed on 26 May 2023).
- AMP25 Open Loop Hall Effect Sensor. Available online: https://amploc.com/products/amp25-open-loop-hall-effect-sensor (accessed on 26 May 2023).
- Pressure Sensors SDE1, with Display. Available online: https://www.festo.com/cat/en-gb_gb/data/doc_ENUS/PDF/US/SDE1_ENUS.PDF (accessed on 26 May 2023).
- Air Solenoid Valve MEBH-3/2-1/8-B-230AC. Available online: https://us.rs-online.com/m/d/0b5bd1adfdc27e97aaf2970f6091f14a.pdf (accessed on 26 May 2023).
- LM35 Precision Centigrade Temperature Sensors. Available online: https://www.ti.com/lit/ds/symlink/lm35.pdf (accessed on 26 May 2023).
- ARDUINO MEGA 2560 REV3. Datasheet. Available online: https://docs.arduino.cc/static/b041a982c2b71c2b39349c223c58d72e/A000067-datasheet.pdf (accessed on 26 May 2023).
- Zuo, L.; Zhang, P.S. Energy Harvesting, Ride Comfort, and Road Handling of Regenerative Vehicle Suspensions. J. Vib. Acoust. 2013, 135, 011002. [Google Scholar] [CrossRef]
- Liu, J.; Liu, J.; Zhang, X.; Liu, B. Transmission and energy-harvesting study for a novel active suspension with simplified 2-DOF multi-link mechanism. Mech. Mach. Theory 2021, 160, 104286. [Google Scholar] [CrossRef]
- Micro-Epsilon Draw Wire Displacement Sensors. Available online: https://www.micro-epsilon.com/download/products/cat-wiresensor/dax--wireSENSOR-MK30--en-us.html (accessed on 26 May 2023).



| Feature | Symbol | Constraint |
|---|---|---|
| Static load | ≥3 kN | |
| Irreversibility limit | <50% | |
| Screw minor diameter | > | |
| Steady-state current | <15 A | |
| Time to travel 50 mm | <13 s |
| Category | Parameter | Symbol | Unit | Concentric | Eccentric |
|---|---|---|---|---|---|
| Screw | Thread angle (ACME) | 14.5 | 14.5 | ||
| Pitch | p | 8 | 3 | ||
| Mean diameter | 53 | 16 | |||
| Electric motor | Nominal power | 90 | 60 | ||
| Nominal torque | 73.1 | 37.5 | |||
| Nominal speed | 6500 | 8944 | |||
| Winding resistance | R | 0.314 | 0.378 | ||
| Winding inductance | L | − | 85 | 200 | |
| Torque constant | 0.0194 | 0.0097 | |||
| Back EMF constant | 0.0194 | 0.0097 | |||
| Supply voltage | 12 | 12 | |||
| Speed reducer | Gearbox ratio | - | 81:1 | 50:1 | |
| Gearbox efficiency | % | 72 | 75 | ||
| Final gear ratio | - | 2.22:1 | 3:1 | ||
| Final gear efficiency | % | 95 | 95 | ||
| Force application | Distance between spring holders | 220 | 266 | ||
| Distance between bushings | 48.5 | 142 | |||
| Lower arm length | - | 73 | |||
| Spring holder offset | 13 | 17 | |||
| Force inclination angle | 4.15 | 4.15 | |||
| Angle with respect to the plane | - | 42 | |||
| Friction coefficients | Anti-rotation | - | 0.25 | 0.25 | |
| Aluminum piston | - | 1.35 | 1.35 | ||
| Power screw and nut | - | 0.25 | 0.25 |
| Parameter | Unit | Concentric | Eccentric | ||
|---|---|---|---|---|---|
| Lowering | Lifting | Lowering | Lifting | ||
| Average current | 10 | 14.7 | 4.4 | 10 | |
| Average power | 120 | 176 | 53 | 120 | |
| Single-cycle energy | 0.123 | 0.27 | 0.04 | 0.124 | |
| Average efficiency | % | 6.2 | 3.4 | 26 | 6.5 |
| Average speed | 2.7 | 1.81 | 3.7 | 2.69 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ruzimov, S.; Castellanos Molina, L.M.; Galluzzi, R.; Manca, R.; Amati, N.; Tonoli, A. Modeling and Experimental Validation of the Performance of Electromechanical Height Adjustment Vehicle Suspension with Eccentric Mounted Screw System. Actuators 2023, 12, 264. https://doi.org/10.3390/act12070264
Ruzimov S, Castellanos Molina LM, Galluzzi R, Manca R, Amati N, Tonoli A. Modeling and Experimental Validation of the Performance of Electromechanical Height Adjustment Vehicle Suspension with Eccentric Mounted Screw System. Actuators. 2023; 12(7):264. https://doi.org/10.3390/act12070264
Chicago/Turabian StyleRuzimov, Sanjarbek, Luis M. Castellanos Molina, Renato Galluzzi, Raffaele Manca, Nicola Amati, and Andrea Tonoli. 2023. "Modeling and Experimental Validation of the Performance of Electromechanical Height Adjustment Vehicle Suspension with Eccentric Mounted Screw System" Actuators 12, no. 7: 264. https://doi.org/10.3390/act12070264
APA StyleRuzimov, S., Castellanos Molina, L. M., Galluzzi, R., Manca, R., Amati, N., & Tonoli, A. (2023). Modeling and Experimental Validation of the Performance of Electromechanical Height Adjustment Vehicle Suspension with Eccentric Mounted Screw System. Actuators, 12(7), 264. https://doi.org/10.3390/act12070264










