Robust Output Feedback Position Control of Hydraulic Support with Neural Network Compensator

Abstract

Hydraulic support is important equipment in the fully mechanized mining face, and the control performance of the hydraulic support multi-cylinder system directly affects the smooth progress of coal mining process, which is the basis for the continuous advancement of the coal face. However, the friction force of the hydraulic support in the process of pulling the frame is complex due to the underground environmental load. Moreover, the parameters of the moving cylinder are uncertain, and the state of the system cannot be fully measured, which increases the difficulty of control. A proportional-integral-derivative controller is usually used in electro-hydraulic closed-loop control systems because of its computational complexity, but its robustness is poorly adapted to variable load conditions in the coal mine. Therefore, a robust output feedback position controller is proposed in this paper to improve control accuracy and system robustness with only position signal. The multi-cylinder system of hydraulic support is modeled as a standard type, and then a high-order differentiator is proposed to estimate the immeasurable system states using the output position signal. A neural network compensator is applied to estimate and compensate for the external disturbance of the moving cylinder. Furthermore, the parameters of the ZY3200/08/18D hydraulic support are adopted to analyze the effectiveness of the designed controller in simulations. Finally, a real-time control system of hydraulic support is built, and the experimental results show that the novel robust output feedback controller has improved by 47.2% and 30.6% in tracking accuracy compared to PI controller.

1. Introduction

With the development of coal mine automation and intelligence, electro-hydraulic control technology is increasingly used in coal mining machinery, such as shearers and hydraulic supports [1,2]. Hydraulic transmission has higher power-to-weight ratio compared with mechanical transmission and electrical transmission, which is more adaptable to the environment of coal mines [3]. However, the electro-hydraulic system has strong nonlinearity, parameter uncertainty, modeling errors, and external disturbances resulting in low system control accuracy [4]. In addition, the hydraulic support group of the fully mechanized mining face is a typical multi-cylinder system, and only the position signal can be measured by displacement sensors, which increases the difficulty of position control of the hydraulic support moving cylinder [5]. Therefore, it is essential to find a suitable control method to improve the position control accuracy of the hydraulic support moving cylinder under coal mine conditions [6].

A hydraulic support moving cylinder system is essentially a typical valve-controlled single-rod hydraulic cylinder system. Due to the poor anti-interference capability of the traditional proportional-integral-derivative controller (PID), many scholars have proposed many advanced methods to improve its control performance [7,8]. Sliding mode control (SMC) was applied in many industrial systems due to its simple structure, suppressing external disturbances through robust terms. Furthermore, many novel control methods were applied into traditional sliding mode control to reduce the chattering, such as terminal and super-twisting sliding mode control [9,10]. Adaptive robust control (ARC) had both the advantages of adaptive control and robust control to achieve good control performance by adjusting model parameters and suppressing uncertain disturbances online [11,12]. Many scholars were led to optimize the structure of adaptive robust controller due to its excellent control performance [13,14]. In addition, disturbance observer (DO) could treat the uncertainty of internal parameters as lumped disturbances and then estimate and compensate for them to improve the anti-disturbance capability of the system [15,16]. The extended disturbance observer (EDO) and high-gain disturbance observer (HGDO) were used in the electro-hydraulic control system and a good tracking effect was obtained by accurately estimating the system disturbance [17,18]. The unknown dynamics estimator (UDE) was also an effective means to improve the control accuracy of the system with compensating the unknown dynamics of the hydraulic system [19].

While the aforementioned advanced methods have been proved to be useful in improving position control accuracy, these methods generally required to measure velocity, acceleration, and pressure, whereas, many industrial applications could only obtain output signals because of configuration cost constraints [20,21]. As a result, output feedback control has been extensively studied in recent years [22,23,24]. The proportional-integral observer (PIO) was proposed to estimate the system state for the differential cylinder position control system [25]. The high-order sliding mode observer (HSMO) was designed for hydraulic actuators to compensate for parameter uncertainty and model nonlinearity, which effectively improved the position tracking accuracy of hydraulic actuators [26]. The high-gain observer (HGO) was designed to improve position tracking accuracy for electro-hydraulic cylinder systems [27]. The extended state observer (ESO) was originally designed for the active disturbance rejection control method (ADRC), and then developed by combining with backstepping methods in electro-hydraulic control systems [28,29,30]. In addition, the differentiator is also an effective means for the output feedback control system. The extended differentiator (ED) was proposed for the hydraulic motor position tracking system with backstepping [31]. The Levant differentiator (LD) was used in electro-hydraulic systems to realize position control and force control with fast convergence property [32,33]. Compared with state feedback control methods, output feedback control only needs to measure the control signal, which saves the cost of system configuration and has the potential to replace PID controllers in industrial applications [34,35].

The contribution of the novel control method proposed in this paper can be summarized as follows:

(1)

A Multi-cylinder system for hydraulic support is introduced and modeled as a strict feedback format with lumped disturbance.

(2)

A higher-order differentiator (HOD) is presented to estimate the immeasurable system states of the moving cylinder with the only measurable output position signal.

(3)

A neural network compensator (NNC) is designed to estimate and compensate the lumped disturbances, mainly including external disturbance forces, unmodeled dynamics, and parameter uncertainties.

(4)

A robust output feedback controller (ROC) is proposed for the hydraulic support multi-cylinder system to improve control performance, combining the advantages of HOD and NNC.

2. Problem Formulation

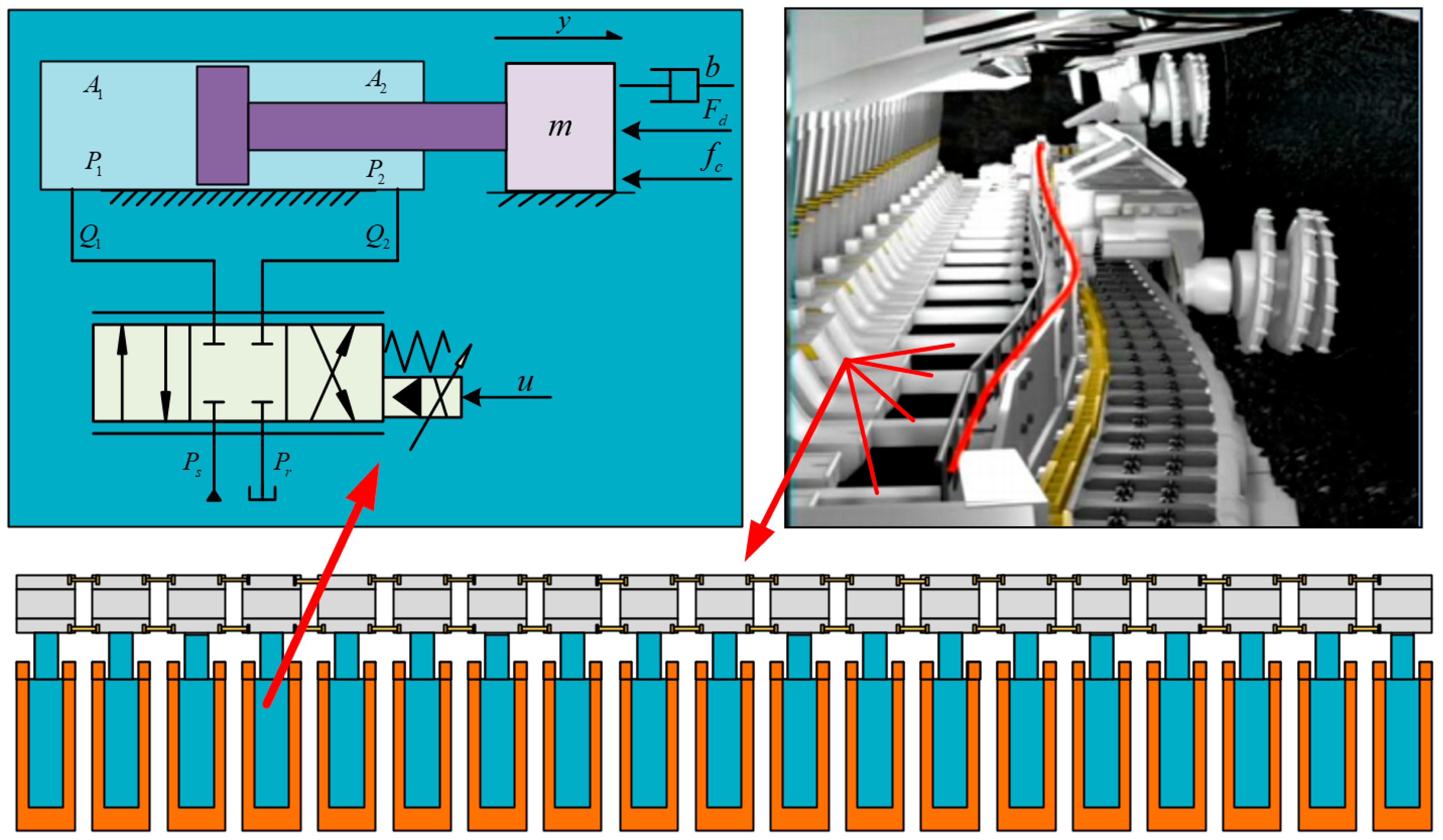
Figure 1 shows the multi-cylinder system of hydraulic support in a coal-mining face. Each single hydraulic support moving cylinder system is a typical valve-controlled single-rod cylinder system, where only the position signal can be measured by the displacement sensor [36]. However, multiple cylinders of the hydraulic support often move at the same time to meet the requirements of rapid mining, so it is necessary to improve the position accuracy and synchronization accuracy of the multi-cylinder system under disturbance conditions.

2.1. Convention Model

Taking one of the hydraulic support moving cylinders as an example, the load dynamics of the moving cylinder can be expressed as follows:

$$m\ddot{y}=(A_1{P}_1-A_2{P}_2)-b\dot{y}+F_d$$

(1)

The flow rates of the two chambers of the moving cylinder can be expressed as follows:

$$\begin{array}{l}{Q}_1=k_q{x}_v\sqrt{\frac{P_s}{2}+\mathrm{sign}(x_v)\left(\frac{P_s}{2}-P_1\right)}\\ Q_2=k_q{x}_v\sqrt{\frac{P_s}{2}+\mathrm{sign}(x_v)\left(P_2-\frac{P_s}{2}\right)}\end{array}$$

(2)

Since a hydraulic support moving system is typically a heavy-duty system, the hydraulic valve responds much faster than the whole system, so an approximation is designed: $x_v=k_v·u$.

Due to the development of sealing technology, external leakage is generally ignored [17]. Then, the pressure dynamic equation of the two chambers of the cylinder can be written as follows:

$$\begin{array}{l}{\dot{P}}_1=\frac{{\beta }_e}{V_{01}+A_{1}y}[Q_1-A_1\dot{y}-C_t(P_1-P_2)]+\Delta 1\\ {\dot{P}}_2=\frac{{\beta }_e}{V_{02}-A_{2}y}[-Q_2+A_2\dot{y}+C_t(P_1-P_2)]+\Delta 2\end{array}$$

(3)

Define the states as ${\left[x_1, x_2, x_3\right]}^T=\left[y_1, {\dot{y}}_1, (A_1{P}_1-A_2{P}_2\right)/m{]}^T$. Then the following state space equation holds.

$$\begin{array}{l}{\dot{x}}_1=x_2\\ {\dot{x}}_2=x_3-B{x}_2+d_1\\ {\dot{x}}_3=g_{1}u-g_2{x}_2-g_3(P_1-P_2)+d_2\end{array}$$

(4)

where

$$\left\{\begin{array}{c}B=\frac{b}{m},d_1=\frac{-F_d}{m},d_2=\frac{A_1\Delta 1-A_2\Delta 2}{m}\hfill \\ g_1=\frac{k_t{\beta }_e}{m}\left(\frac{A_1{R}_1}{V_1+A_{1}y}+\frac{A_2{R}_2}{V_2-A_{2}y}\right)\hfill \\ g_2=\frac{{\beta }_e}{m}\left(\frac{{A_1}^2}{V_1+A_{1}y}+\frac{{A_2}^2}{V_2-A_{2}y}\right)\hfill \\ g_3=\frac{{\beta }_e{C}_t}{m}\left(\frac{A_1}{V_1+A_{1}y}+\frac{A_2}{V_2-A_{2}y}\right)\hfill \\ R_1=\sqrt{\frac{P_s}{2}+\mathrm{sign}\left(u\right)\left(\frac{P_s}{2}-P_1\right)}\hfill \\ R_2=\sqrt{\frac{P_s}{2}+\mathrm{sign}\left(u\right)\left(P_2-\frac{P_s}{2}\right)}\hfill \end{array}\right.$$

(5)

2.2. Problem Formulation

Since only the position signal of the hydraulic support moving cylinder can be measured, new system state variables are defined as $z_1=x_1, z_2={\dot{z}}_1, z_3={\dot{z}}_2$. Then the new model of the moving cylinder is simplified into the following form:

$$\begin{array}{l}{z}_1=x_1\\ z_2=x_2\\ z_3=x_3-B{x}_2+d_1\end{array}$$

(6)

In the case of ignoring hydraulic cylinder leakage, the following equality is yielded:

$$\frac{Q_2}{Q_1}\approx \frac{A_2}{A_1}=n$$

(7)

The load pressure of the moving cylinder is defined as follows:

$$P_L=P_1-n{P}_2$$

(8)

Then, we have

$$P_1-P_2=\frac{1}{1+n^3}\left[\frac{\left(n^2+1\right)\left(n-1\right)}{2}{P}_s+\mathrm{sign}\left(u\right)\frac{\left(n^2-1\right)\left(n-1\right)}{2}{P}_s+\left(n^2+1\right)P_L\right]$$

(9)

Combining the above derived formulas, the controllable standard equation can be written as follows:

$$\begin{array}{l}{\dot{z}}_1=z_2\\ {\dot{z}}_2=z_3\\ {\dot{z}}_3=f_{1}u+f_2{z}_2+f_3{z}_3+H+D\end{array}$$

(10)

Among them, the expression of each item can be further expressed as follows:

$$\left\{\begin{array}{l}{f}_1=g_1\hfill \\ f_2=-g_2-g_3\frac{\left(n^2+1\right)mB}{\left(n^3+1\right)A_1}\hfill \\ f_3=-B-g_3\frac{\left(n^2+1\right)m}{\left(n^3+1\right)A_1}\hfill \\ H=-g_3\frac{\left(n^2+1\right)\left(n-1\right)}{2\left(n^3+1\right)}{P}_s-g_3\mathrm{sign}\left(u\right)\frac{\left(n^2-1\right)\left(n-1\right)}{2\left(n^3+1\right)}{P}_L\hfill \\ D=g_3\frac{\left(n^2+1\right)m}{\left(n^3+1\right)A_1}{d}_1+{\dot{d}}_1+d_2\hfill \end{array}\right.$$

(11)

Remark 1.

The model of the moving cylinder system is described in Brunovsky form, where only the system order and the control input coefficient are needed for system modeling. Moreover, the nonlinear function $D$ is a complex function and is regarded as a lumped disturbance mainly determined by unknown disturbances $d_1$, $d_2$.

Assumption 1.

The fixed physical parameters of each moving cylinder of hydraulic supports are the same, but the load force and unknown disturbance of different moving cylinders are different. Additionally, $P_1$ and $P_2$ are bounded by $P_s$ and $P_r$, where $0\le P_r<P_1,P_2<P_s$.

Assumption 2.

The force disturbance $d_1$ satisfies conditions $d_{1min}\le d_1\le d_{1max}$, and${\dot{d}}_{1min}\le {\dot{d}}_1\le {\dot{d}}_{1max}$, where $d_{1min}$ and $d_{1max}$ are the maximum and minimum value of $d_1$. Furthermore, ${\dot{d}}_{1min}$ and ${\dot{d}}_{1max}$ are the maximum and minimum value of ${\dot{d}}_1$, respectively. Similarly, pressure-flow disturbance $d_2$ is also bounded by $d_{2min}\le d_2\le d_{2max}$. Therefore, the unknown nonlinear function $D$ is bounded.

3. Controller Design

3.1. High-Order Differentiator Design

In this section, a high-order differentiator (HOD) is proposed to estimate the immeasurable states of each moving cylinder. For the standard Brunovsky model, the system states can be estimated by HOD if the system state has n-order derivatives with Lipschitz constant. Hence, the designed HOD can be written as follows:

$$\begin{array}{cc}\hfill {\dot{\hat{z}}}_1& =-{\lambda }_1{\left|{\hat{z}}_1-y\right|}^{\frac{n}{(n+1)}}sign({\hat{z}}_1-y)+{\hat{z}}_2\triangleq v_1\hfill \\ \hfill {\dot{\hat{z}}}_2& =-{\lambda }_2{\left|{\hat{z}}_2-v_1\right|}^{\frac{n-1}{n}}sign({\hat{z}}_2-v_1)+{\hat{z}}_3\triangleq v_2\hfill \\ & ⋮\hfill \\ \hfill {\dot{\hat{z}}}_i& =-{\lambda }_i{\left|{\hat{z}}_i-v_{i-1}\right|}^{\frac{(n-i+1)}{(n-i+2)}}sign({\hat{z}}_i-v_{i-1})+{\hat{z}}_{i+1}\triangleq v_i\hfill \\ & ⋮\hfill \\ \hfill {\dot{\hat{z}}}_n& =-{\lambda }_n{\left|{\hat{z}}_n-v_n\right|}^{\frac{1}{2}}sign({\hat{z}}_n-v_{n-1})+{\hat{z}}_{n+1}\triangleq v_n\hfill \\ \hfill {\dot{\hat{z}}}_{n+1}& =-{\lambda }_{n+1}sign({\hat{z}}_{n+1}-v_n)\hfill \end{array}$$

(12)

Assumption 3.

The measured noise of the position signal of the moving cylinder system is bounded by$\left|z_1-y\right|\le \epsilon$, where$\epsilon$is the maximal magnitude of measurement noise.

Therefore, the following inequalities are yielded in a finite time:

$$\begin{array}{cc}\hfill \left|z_i-{\hat{z}}_i\right|& \le {\mu }_i{\epsilon }^{(n-i+2)/(n+1)},i=1,2,\cdot \cdot \cdot n\hfill \\ \hfill \left|z_{i+1}-v_i\right|& \le {\rho }_i{\epsilon }^{(n-i+1)/(n+1)},i=1,2,\cdot \cdot \cdot n-1\hfill \end{array}$$

(13)

Remark 2.

The high-order differentiator meets the requirements of separation principle due to its fast convergence speed, so the output feedback controller and the state observer can be designed separately. Furthermore, the estimation errors of HOD are defined as ${\tilde{z}}_i=z_i-{\hat{z}}_i, i=1,2,\cdots n$. Then a positive constant $\sigma$ and a certain time $t_c$ exist to make the estimation errors bounded by $\left|{\tilde{z}}_i\right|\le \sigma$ when $t>t_c$, and $\sigma$ is determined by the control parameters ${\mu }_i$ and the maximal magnitude of measurement noise $\epsilon$.

3.2. Neural Network Compensator Design

To estimate and compensate the unknown nonlinear function $D$ of the moving system in time, a neural network compensator is designed in this section. Accordingly, the output of the radial basis function neural network for the moving cylinder can be expressed as follows:

$$\begin{array}{l}{h}_j=\exp \left(-\frac{{‖\lambda -c_j‖}^2}{b_j{}^2}\right)\\ \hat{D}={\hat{W}}^{T}H(\lambda )\end{array}$$

(14)

The nonlinear function $D$ of the system can be also expressed as follows:

$$D=W^{\ast }{}^{T}H(\lambda )+\delta$$

(15)

Remark 3.

Obviously, neural networks can approach any nonlinear function with the proper combination of linear Gaussian functions. The approximation error $\delta$ of a neural network can be ensured to be bounded by $\left|\delta \right|\le {\delta }_{max}$ if the optimal weight is chosen properly. Moreover, the error of estimation for the lumped disturbance $D$ can be expressed as $\tilde{D}=D-\hat{D}={\tilde{W}}^T+\delta$, where $\tilde{W}=W-\hat{W}$.

3.3. Robust Output Feedback Controller Design

Step 1: define the position tracking error of the moving cylinder as follows:

$${\dot{e}}_1=z_2-{\dot{y}}_d$$

(16)

Define a Lyapunov function $V_1$ as $V_1=e_1{}^2/2$; then the dynamic of $V_1$ can be written as follows:

$${\dot{V}}_1=e_1\left(z_2-{\dot{y}}_d\right)$$

(17)

To ensure ${\dot{V}}_{1j}\le 0$, the virtual control of $z_2$ is chosen as follows:

$${\alpha }_1=-k_1{e}_1+{\dot{y}}_d$$

(18)

Step 2: define the error between the actual input $z_2$ and its virtual input ${\alpha }_1$ as follows:

$$e_2=z_2-{\alpha }_1$$

(19)

The derivative of $e_2$ is written as follows:

$${\dot{e}}_2=z_3-{\dot{\alpha }}_1$$

(20)

Define the Lyapunov function as $V_2=V_1+e_2{}^2/2$, the dynamic of $V_2$ can be written as follows:

$${\dot{V}}_2={\dot{V}}_1+e_2\left(z_3-{\dot{\alpha }}_1\right)$$

(21)

Similar to Step 1, the virtual control of $z_3$ is designed as follows:

$${\alpha }_2=-e_1-k_2{e}_2+{\dot{\alpha }}_1$$

(22)

Step 3: define the error between the actual input $z_3$ and its virtual input ${\alpha }_2$ as follows:

$$e_3=z_3-{\alpha }_2$$

(23)

Taking the time derivative of (23), the following equation holds:

$${\dot{e}}_3=f_{1}u+f_2{z}_2+f_3{z}_3+H+D-{\dot{\alpha }}_2$$

(24)

Defining the Lyapunov function for Step 3 as $V_3=V_2+e_3{}^2/2$, the dynamic of $V_3$ can be written as follows:

$${\dot{V}}_3={\dot{V}}_2+e_3\left(f_{1}u+f_2{z}_2+f_3{z}_3+H+D-{\dot{\alpha }}_2\right)$$

(25)

The actual input of the moving cylinder system is designed as follows:

$$u=\frac{1}{f_1}\left(-f_2{z}_2-f_3{z}_3-H-\hat{D}+{\dot{\alpha }}_2-e_2-k_3{e}_3-{\epsilon }_N\mathrm{sign}\left(e_3\right)\right)$$

(26)

Define the Lyapunov function of the whole system as follows:

$$V=V_3+\frac{1}{2\gamma }{\tilde{\mathit{W}}}^2$$

(27)

The dynamic of $V$ can be expressed as follows:

$$\dot{V}=-k_1{e}_1{}^2-k_2{e}_2{}^2-k_3{e}_3{}^2+{\tilde{\mathit{W}}}^T\left(e_3\mathit{H}(\lambda )-\frac{1}{\gamma }\dot{\hat{\mathit{W}}}\right)+e_3\epsilon -{\epsilon }_N\left|e_3\right|$$

(28)

Moreover, the adaptive law of the neural network is designed as follows:

$$\dot{\hat{\mathit{W}}}=\gamma e_3\mathit{H}(\lambda )$$

(29)

In addition, we have

$$e_3\epsilon -{\epsilon }_N\left|e_3\right|\le 0$$

(30)

Combining (28), (29) and (30), the following inequality is obtained:

$$\dot{V}\le -k_1{e}_1{}^2-k_2{e}_2{}^2-k_3{e}_3{}^2\le 0$$

(31)

Remark 4.

According to (31), the Lyapunov function of this system is negative definite, which proves the whole system is stable. The new controller combining HOD and NNC solves the coupling problem between state estimation and disturbance estimation and obtains excellent control performance with the only available position signal. The controller takes into account not only its own position tracking, but also the velocity relationship with adjacent cylinders, which helps to improve synergy in multi-cylinder systems.

4. Simulation Results

To improve the moving speed of the hydraulic support, multiple moving cylinders will pull the frame at the same time, where the synchronization accuracy will become an important indicator that affects the straightness of the working surface. In this section, ZY3200/08/18D hydraulic support is taken as an example to verify the superiority of the designed controller. The fixed physical parameters of the hydraulic support moving cylinder are: $A_1=0.0154{ \mathrm{m}}^2$,$A_2=0.0083{ \mathrm{m}}^2$, $P_s=31.5 \mathrm{MPa}$, $P_r=0 \mathrm{Pa}$, ${\beta }_e=7\times {10}^8 \mathrm{Pa}$, $V_1=0.02{ \mathrm{m}}^3$, $V_2=0.02{ \mathrm{m}}^3$, $C_t=4\times {10}^{-13}{ \mathrm{m}}^3/\left(\mathrm{Pa}·\mathrm{s}\right)$, $b=1000 \mathrm{N}·\mathrm{s}/\mathrm{m}$, $m=12,000 \mathrm{kg}$. The expressions of the integration force of different moving cylinders are designed as $F_{d1}=10,000\times \tan \mathrm{h}\left(x_{21}/0.02\right)-3000\times \sin \left(\mathsf{\pi }\mathrm{t}\right)$, $F_{d2}=20,000\times \tan \mathrm{h}\left(x_{22}/0.02\right)-5000\times \sin \left(\mathsf{\pi }\mathrm{t}\right)$, where the first term is the basic friction force, and the second term is the set time-varying disturbance force. The control parameters of HOD are ${\lambda }_1=8$, ${\lambda }_2=5$, ${\lambda }_3=2$, ${\lambda }_4=1$. The basic coordinate vector of the Gaussian function of the neural network is selected as $c_j={\left[-1,-0.5, 0, 0.5, 1\right]}^T$, and the width chosen is $b_j=100$. The adaptation law coefficient is $\kappa =500$. Additionally, the control parameters of PI are $k_p=300$, $k_i=10$. The control parameters of ROC are $k_1=150$, $k_2=20$, $k_3=20$, $d_{2max}=10$.

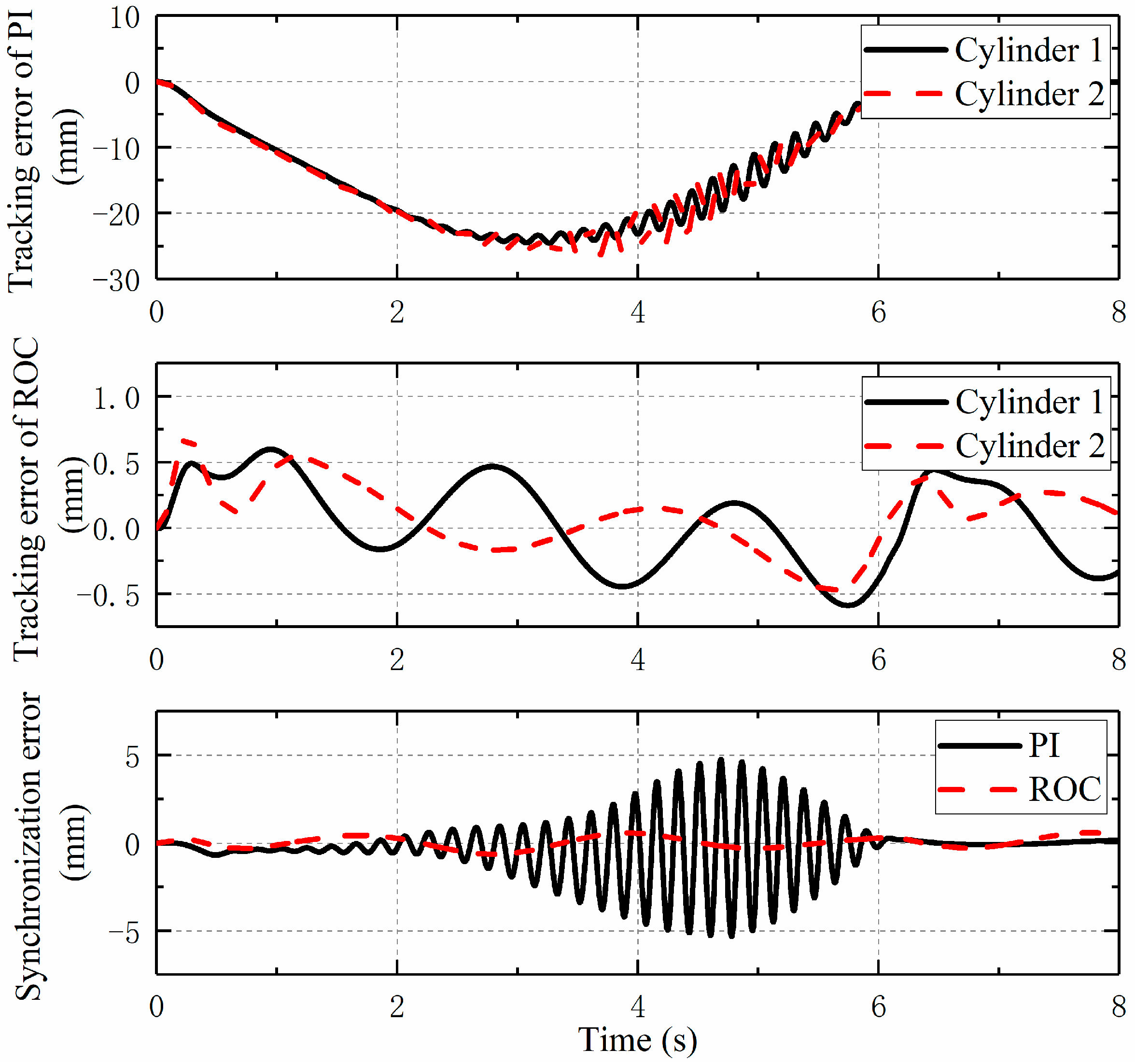
Taking the double moving cylinders of hydraulic support as an example, the performance of the output synchronization controller proposed in this paper is analyzed. The trajectory-tracking performance and tracking error are shown in Figure 2. It is clear that both Cylinder 1 and Cylinder 2 with PI controller have obvious lag in the tracking process, and the maximum lag is about 25 mm, which is caused by the large velocity of the expected trajectory at this stage. When the speed gradually slows down, the tracking error also decreases and fluctuates around zero. In addition, the error fluctuations of the two moving cylinders at similar positions are large, indicating that the tracking trajectory is not stable. However, the overall tracking performance of ROC controller is good and the tracking errors of both Cylinder 1 and Cylinder 2 fluctuate within the range of 0.5 mm, which is much smaller than that of the PI controller. Furthermore, it can be seen from the synchronization error diagram that the synchronization control accuracy of the double moving cylinders with PI control is about 5 mm, and there are large fluctuations especially in the stage of fast pulling. The synchronization accuracy of the ROC controller is higher, the maximum synchronization error is only about 0.8 mm, and the fluctuation is smaller, which help to achieve a higher straightness of the hydraulic support group after the movement. Compared with existing output feedback controllers, the ROC controller designed in this paper has a structure as simple as the PID controller, which only needs the order of the system to avoid the complex modeling process. Moreover, the self-learning ability of the neural network helps to estimate and compensate the unknown disturbance of the system to ensure the robustness of the system. To sum up, the ROC controller structure more easily meets the harsh working conditions in the mine and has the potential to replace the traditional PID controller compared with other output feedback controllers.

The estimation performances of HOD for moving cylinder states are displayed in Figure 3 and Figure 4. The estimated value of the position and velocity of the moving cylinder basically coincides with the actual value, indicating that the position and velocity estimated by HOD are very accurate. The estimated acceleration of the moving cylinder is consistent with the actual value in the overall trend, but there is a slight difference at the moment of starting and stopping the movement, which is caused by the instability of the neural network interference observer in the early stage of learning. Figure 5 presents the estimated performance of the designed NNC. According to Figure 5, the lumped disturbance $D$, including friction forces and uncertain parameters, can be estimated accurately by the designed NNC. As a whole, the estimated result of the NNC coincides with the given disturbance value, which shows that NNC can have accurate disturbance estimation even using estimated state of the HOD. Furthermore, the self-learning ability of the neural network can be used to predict various nonlinear functions with avoiding complex modeling processes, which has great significance for improving the computability and robustness of the hydraulic support system. Therefore, the novel output controller proposed in this paper has higher control precision and better control performance than the traditional PI controller, which means that the new controller has the potential to replace the PI controller.

5. Experimental Results

To verify the output controller designed in this paper and improve its practical applicability, a test bench for the hydraulic support multi-cylinder control system is built as shown in Figure 6. The fixed physical parameters of the multi-cylinder control system are given in

Table 1. Physical parameters of the electro-hydraulic asymmetric cylinder system.

Parameters	Values	Parameters	Values
$A_1\left({\mathrm{m}}^2\right)$	1.9625 × 10−3	$m\left(\mathrm{kg}\right)$	90
$A_2\left({\mathrm{m}}^2\right)$	1.000875 × 10−3	$b\left(\mathrm{N}·\mathrm{m}\right)$	4500
$P_s\left(\mathrm{Pa}\right)$	5 × 106	${\beta }_e\left(\mathrm{Pa}\right)$	7 × 108
$P_r\left(\mathrm{Pa}\right)$	0	$C_t\left({\mathrm{m}}^3/\mathrm{s}/\mathrm{Pa}\right)$	4 × 10−13
$V_{01}\left({\mathrm{m}}^3\right)$	3 × 10−3	$k_t\left({\mathrm{m}}^3/\mathrm{s}/\mathrm{V}/\sqrt{\mathrm{Pa}}\right)$	8.43 × 10−8
$V_{02}\left({\mathrm{m}}^3\right)$	3 × 10−3

[36].

The dimensions of the asymmetric cylinder are 35 mm/50 mm/300 mm. The servo valve is Atos DLHZO-TEB-SN-040, whose bandwidth is above 75 Hz with a ±10% signal, and rated flow is 40 L/min at 35 bar drop. The displacement sensor is Arspas CI6-6, whose accuracy is ±50 μm. The data acquisition card is National Instruments PCI-6229, with 16 bit A/D and 16 bit D/A converters. The control algorithm is applied in the MATLAB/Simulink real time environment with a target computer Advantech 610L and a host computer Dell Vostro 3460. The sampling rate is set to 200 Hz in this paper.

Generally, an overly complex controller may bring computational complexity which is unsuitable to the harsh environment in the coal mine. A PI controller is widely used because of its simple structure and easy parameter adjustment. Similarly, the designed controller also has the advantages of simple structure and easy adjustment of control parameters. Therefore, the experiment takes PID and ROC controllers as a comparative analysis in this paper. The control parameters of HOD are ${\lambda }_1=8$, ${\lambda }_2=5$, ${\lambda }_3=2$, ${\lambda }_4=1$. The basic parameters of the Gaussian function of NNC is selected as $c_j={\left[-1,-0.5, 0, 0.5, 1\right]}^T$, $b_j=5$ and $\gamma =20$. In addition, the control parameters of ROC are $k_1=100$, $k_2=60$, $k_3=60$ and of PI are $k_p=150$, $k_i=20$.

Figure 7 shows the position tracking performance of different controllers. It can be seen that the maximum tracking error of the moving cylinder with PI controller is about 7 mm, and the maximum tracking error of the double cylinders both appear at the place with the fastest movement speed. Due to the self-learning ability of the neural network, the tracking error of the twin cylinder under the ROC controller is relatively large in the initial stage of motion. With the increase of learning time and existing data, the tracking accuracies of the double cylinders are greatly improved and stabilized at about 1 mm. Compared with the PI controller, the synchronization accuracy of the ROC controller is lower in the initial stage, but with an increase in the movement time, the tracking accuracy of the ROC controller quickly reaches a higher value, and the synchronization accuracy of the dual cylinder is also greatly improved at this time. To make the comparison clearer, the average tracking error of the adjacent double cylinders for two controllers is calculated in

Table 2. Average tracking error of the adjacent double cylinders for two controllers.

Indexes	Cylinder1	Cylinder2	Synchronization
PI	3.07	3.53	0.63
ROC	1.62	2.45	1.24

. It can be seen that the tracking accuracy of the moving cylinders with ROC controller is improved by 47.2% and 30.6% compared with the PI controller, while the PI controller has the smaller absolute mean error with 0.63 mm. However, the maximum synchronization error of the PI controller in the later stage is 2.5 mm, while the synchronization accuracy of the ROC controller is basically stable at about 1 mm, which means that the ROC controller has a high straightness after motion. In other words, the ROC controller has the same simple structure as the PID controller, and it can estimate and compensate the unknown force disturbance and unmodeled dynamics of the system, which helps to have better robustness and control accuracy and meets the development demand of the intelligent hydraulic support.

Figure 8 and Figure 9 show the observation of the states of the moving cylinders by HOD. In the presence of noise, the influence of the measurement noise is often amplified when calculating the moving cylinder speed and acceleration, so the obtained velocity and acceleration will have a great impact value. In other words, the obtained signal shock will be larger as the derivative order increases, whereas when the designed HOD is used to estimate the system states, the negative impact of noise can be avoided. It can be seen from the figures that the observed velocity and acceleration curves of the double moving cylinders are smoother, which is helpful for the further design of the output feedback controller.

Figure 10 shows the estimation performance for the lumped disturbance of the double cylinders. It is clear that the disturbance estimation of the presented NNC to the two moving cylinders is consistent in the overall trend, but the two curves do not overlap. Due to the different load forces of the double cylinders and insufficient data and time of the neural network in the early stage, the fluctuation is slightly larger in the early moving stage. In the middle and later stages, with an increase in learning time, the neural network tends to be perfect, and the first estimate value becomes very stable and smooth. Therefore, the proposed NNC helps to improve the anti-disturbance capability and control accuracy of the hydraulic support moving cylinder system.

6. Conclusions

In this paper, a robust output feedback controller with neural network compensator is proposed for hydraulic support, which helps improve multi-cylinder synchronization accuracy and working surface straightness. The multi-cylinder system is represented as a standard feedback model, and the parameter uncertainties and external disturbances in the system are integrated as lumped disturbances. A higher-order differentiator is presented to estimate the unavailable states of the moving cylinder with the output signal, which can be applied directly in controller design due to the finite-time convergence property. A neural network compensator is designed to estimate and compensate for the external disturbances of the moving cylinder during the movement to improve the control accuracy and smoothness. Furthermore, the stability of the closed-loop system is proven by Lyapunov theory. Finally, simulations and experiments are carried out to demonstrate the effectiveness of the proposed controller, which shows the potential to completely replace the traditional PI controller.