Research on Fault Diagnosis of HVAC Systems Based on the ReliefF-RFECV-SVM Combined Model
Abstract
1. Introduction
- (1)
- Combining the ReliefF in the filter method and the recursive feature elimination method with cross-validation in the wrapper algorithm, a feature selection method based on ReliefF-RFECV is proposed. On the basis of effectively screening redundant features considering the correlation between features, the method aims to maximize the training speed and efficiently select the feature subset with minimal redundancy and strong relevance to the fault.
- (2)
- The task is to develop a simulation model of an air conditioner using Amesim software, simulate typical faults and normal states of the air conditioner under various operating conditions, and generate a simulation dataset. This dataset will include data from multiple operating conditions and can be used for fault detection and diagnosis.
- (3)
- The approach involves using an SVM model to diagnose faults using the selected optimal feature subset. This methodology aims to improve the accuracy of fault diagnosis.
- (4)
- The proposed method based on ReliefF-RFECV-SVM is validated using the ASHRAE 1043-RP experimental dataset and the simulation dataset. The results show that the proposed fault diagnosis method has high diagnosis accuracy and efficiency on both the chiller unit and the air conditioning system, and strong generalization ability.
2. ReliefF-RFECV-SVM Combined Model
- (1)
- Operating data from the HVAC system, including normal and fault conditions, are collected and pre-processed. The pre-processing involves removing non-stationary data and rejecting outliers using the Lajda criterion. The collected data are also normalized to eliminate the impact of data dimensionality.
- (2)
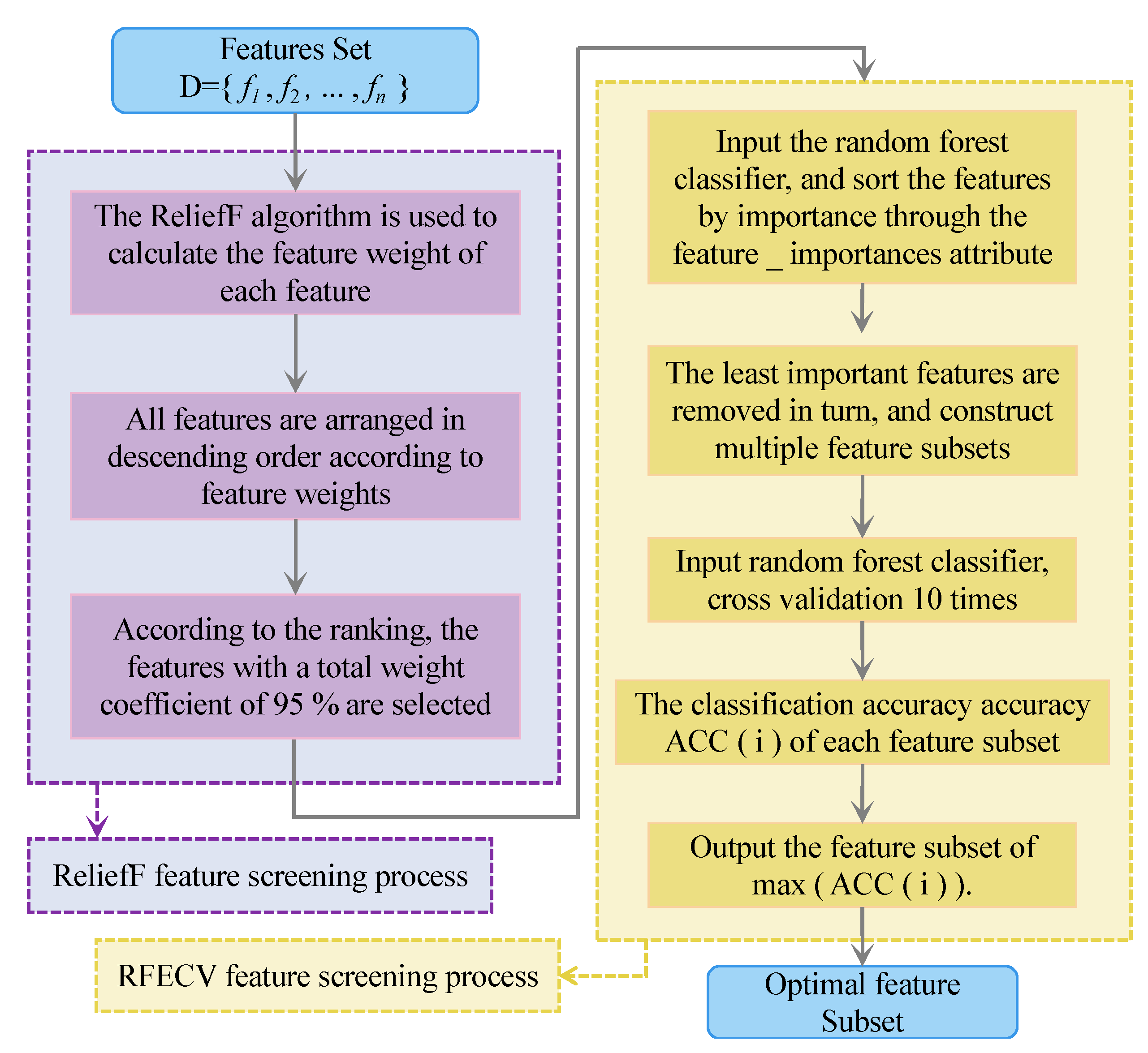
- The Relief-RFECV feature selection algorithm is used to filter the features of the dataset after data preprocessing. Firstly, the features with weights up to 95% of the total weights are filtered using the ReliefF method to form a feature subset, then the feature subset is screened again by the RFECV method, and the subset with the highest accuracy is selected as the optimal feature subset after constructing a random forest classifier for 10 times cross-validation.
- (3)
- A multi-classification SVM model is initialized and constructed, with 30% of the optimal feature subset randomly selected as the training set and the remaining 70% as the test set. The training set is used to train the multi-classification SVM model, with the model parameters optimized through grid search and cross-validation. The accuracy of the final fault diagnosis model is verified using the test set.
2.1. ReliefF-RFECV Feature Selection Method
2.1.1. Introduction of the ReliefF
2.1.2. Introduction of the RFECV
2.1.3. Introduction and Construction of the ReliefF-RFECV
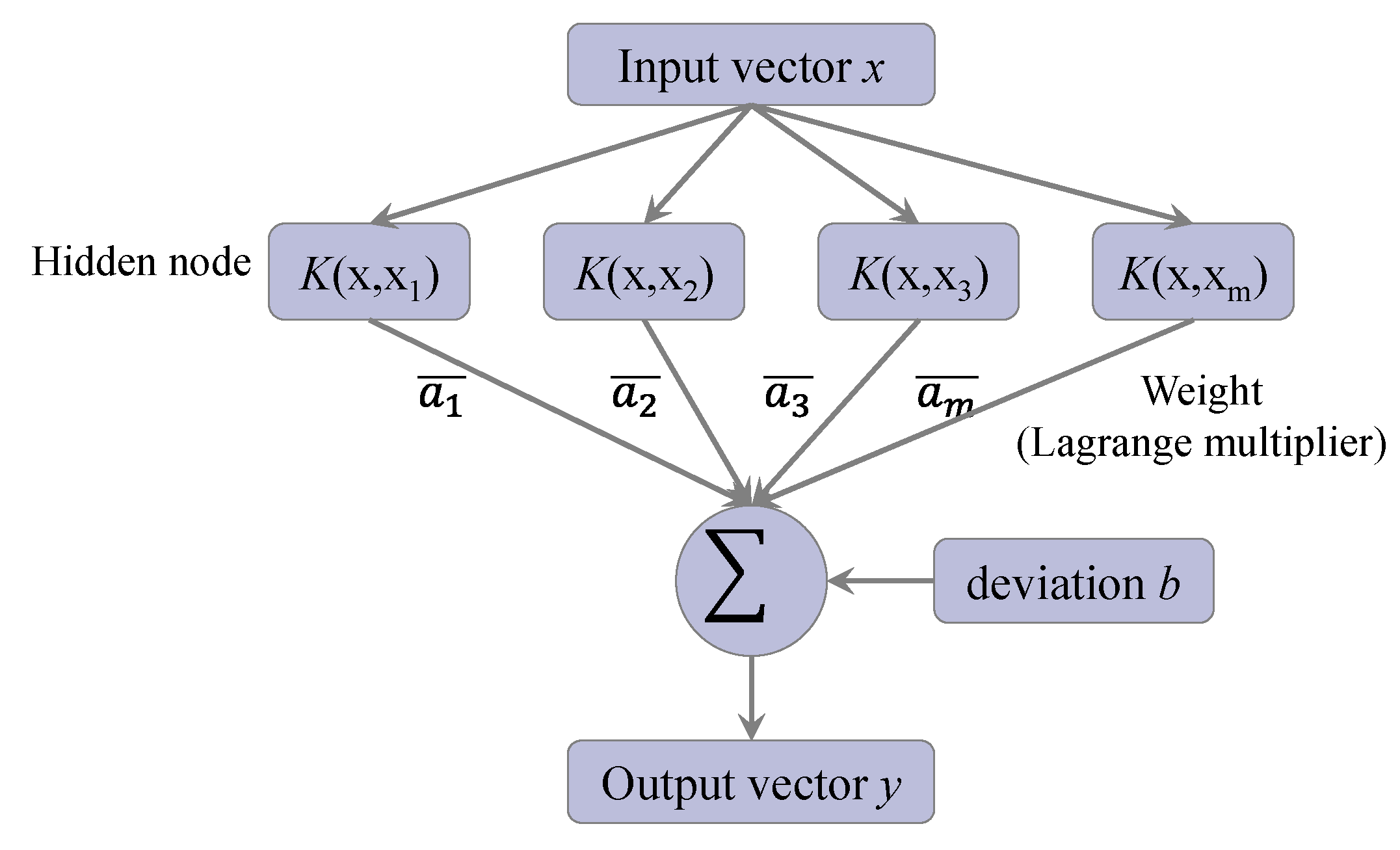
2.2. Multi-Classification Fault Diagnosis Method Based on SVM
3. Design of Fault Diagnosis
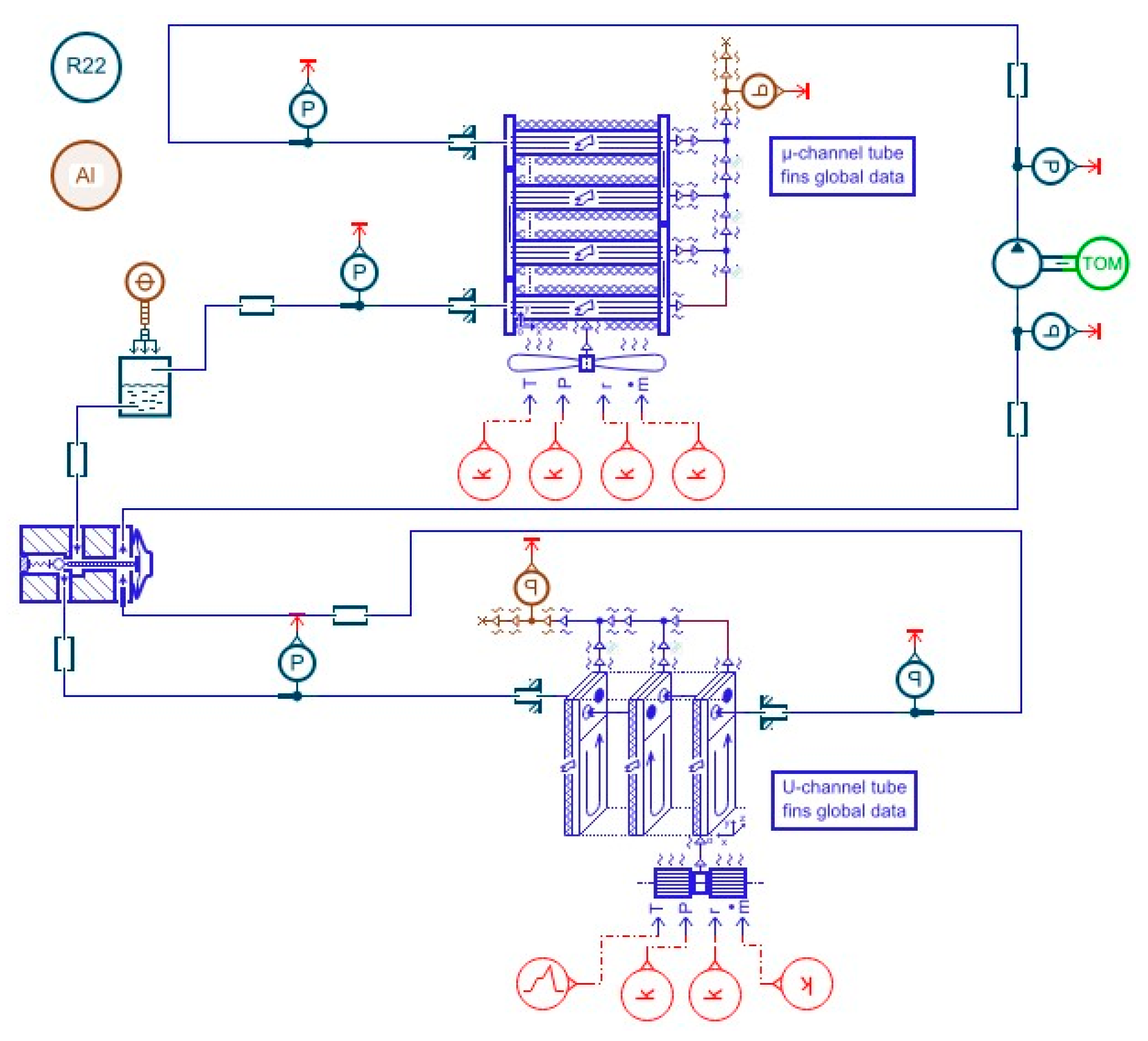
3.1. Data Description
3.2. Data Preprocessing
3.3. Feature Selection Based on the ReliefF-RFECV
3.4. Evaluation Metrics for Classification Performance
4. Analysis of Fault Diagnosis Results
4.1. Diagnostic Results on ASHRAE 1043-RP Dataset
4.2. Diagnosis Results of Simulation Dataset
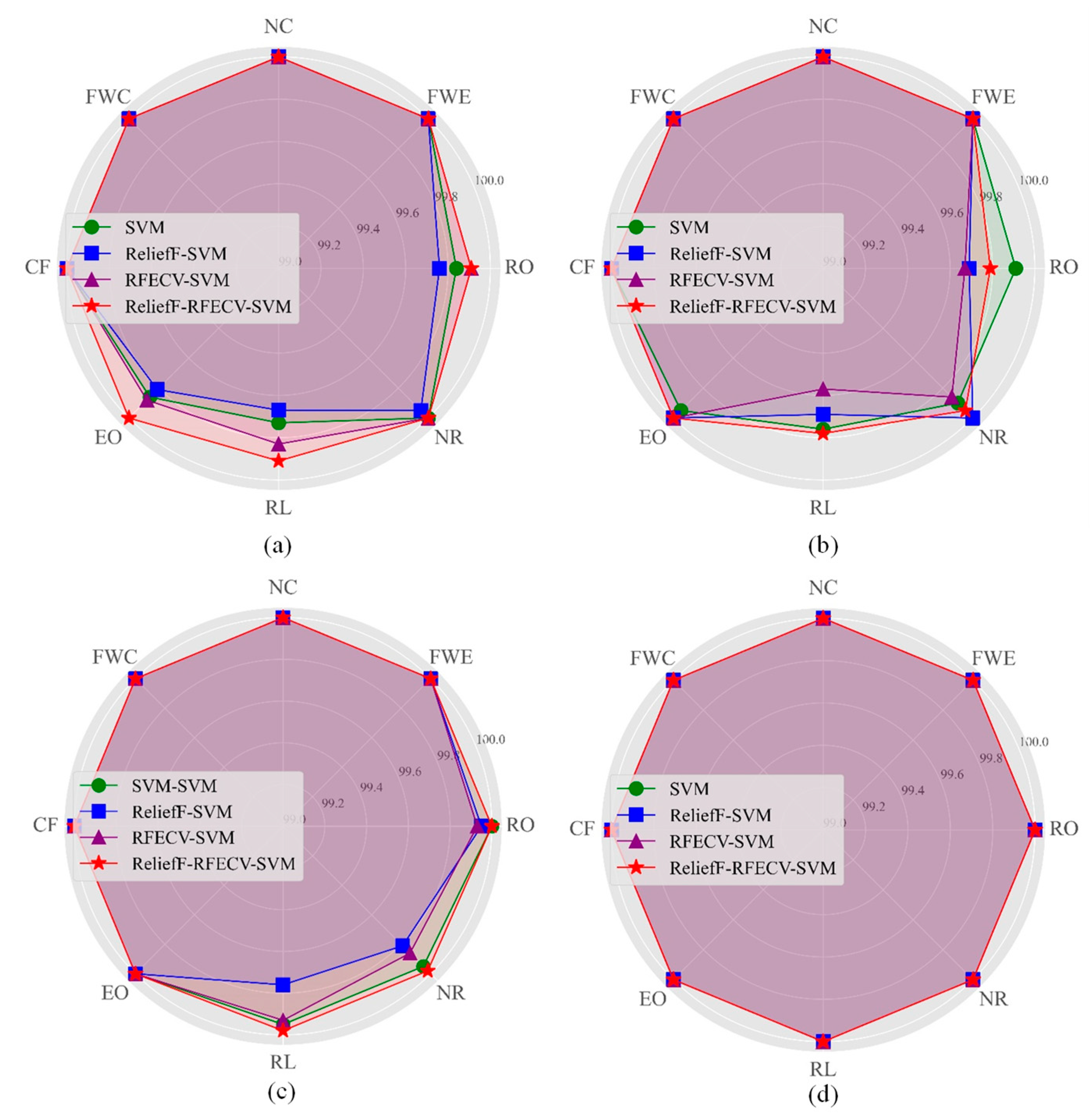
4.3. Analysis of Comparative Results
- (1)
- This method utilizes the RelifF-RFECV algorithm for feature selection and the SVM classifier for fault diagnosis, achieving fault diagnosis for typical faults in HVAC systems on both the ASHRAE 1043-RP dataset and the self-built Amesim simulation dataset.
- (2)
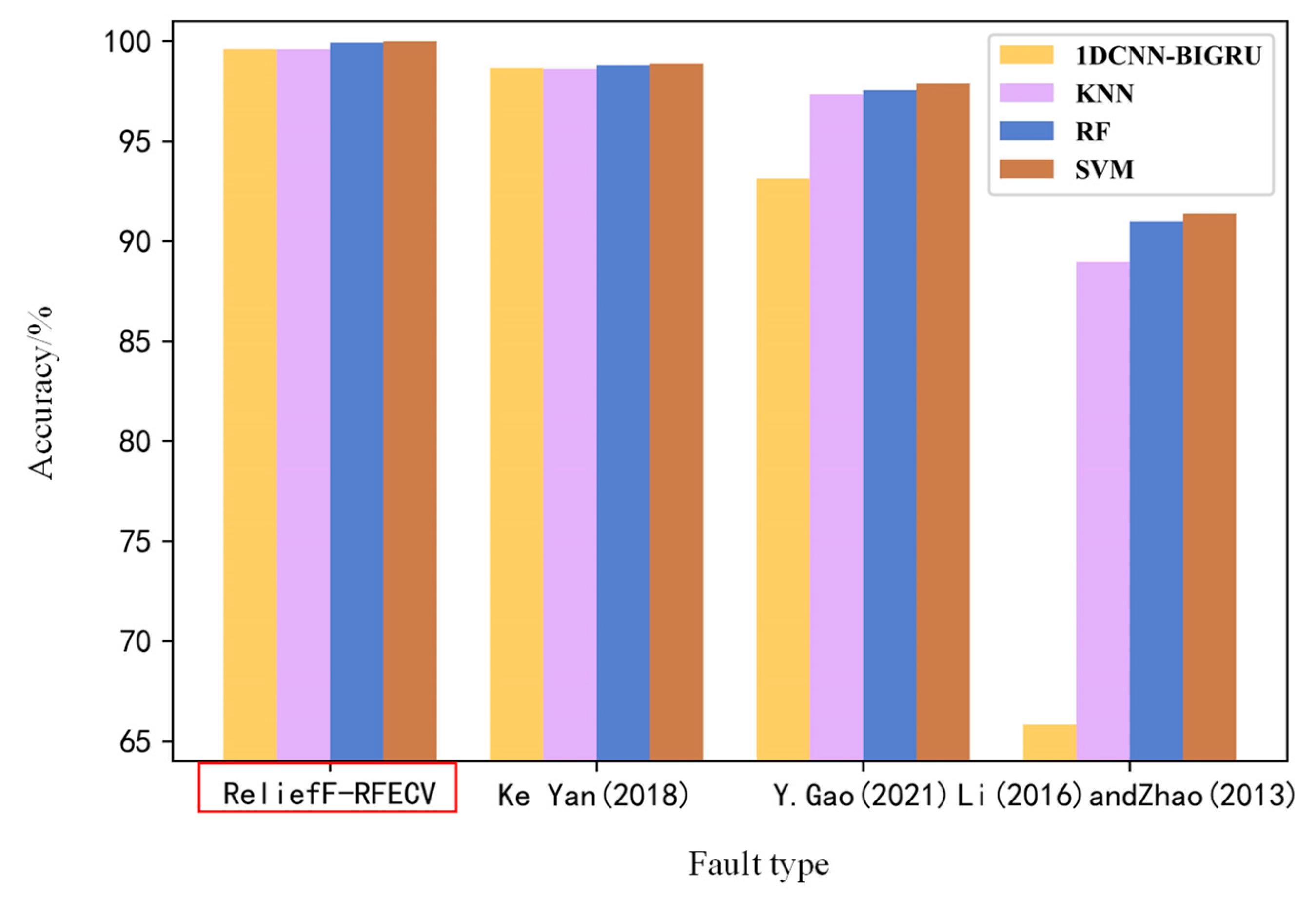
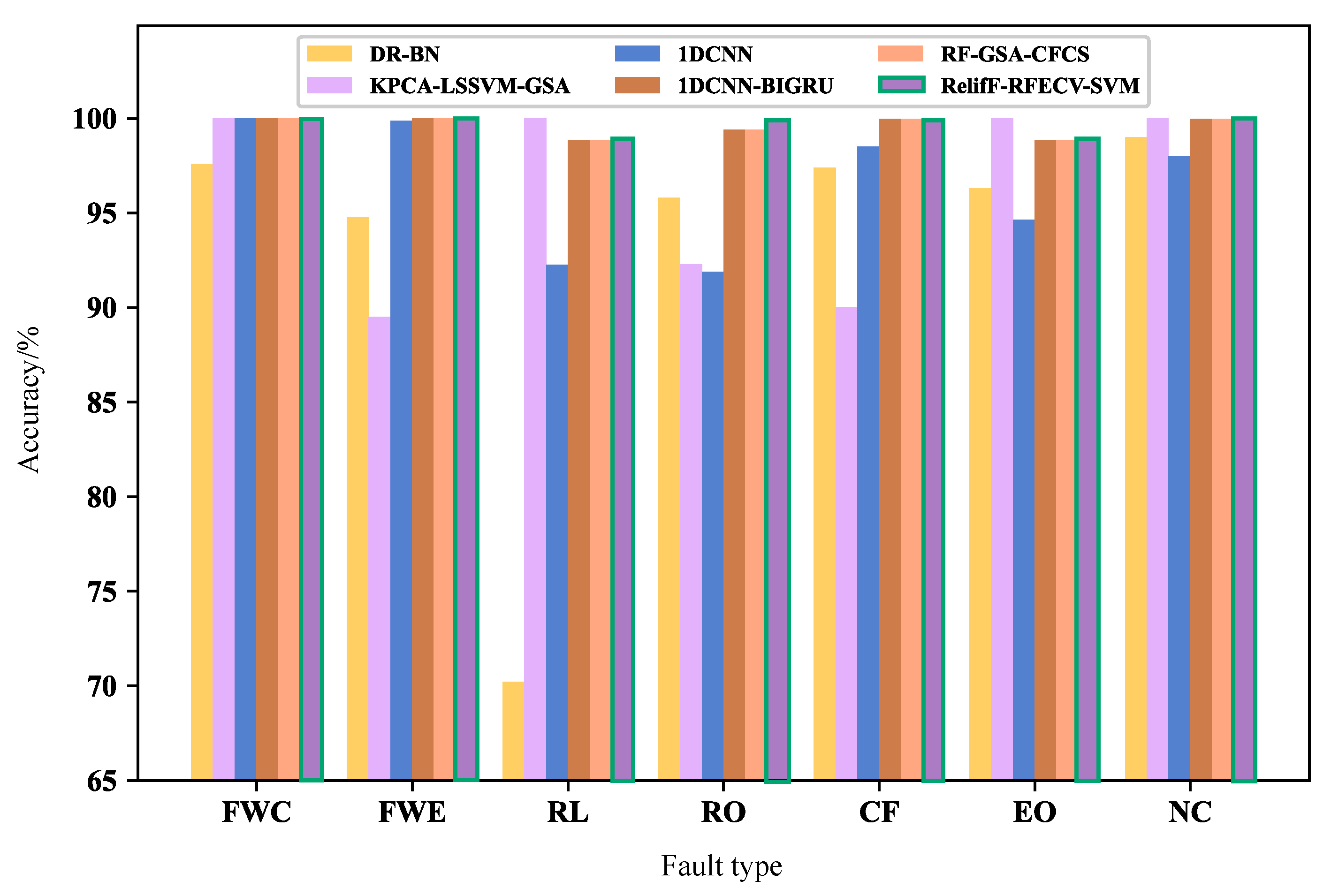
- On the ASHRAE 1043-RP dataset, the diagnostic accuracy at level 1 is enhanced from 99.94% to 99.98% compared to the original dataset. Similarly, on the simulation dataset, the diagnostic accuracy at level 1 is improved from 99.93% to 99.96% compared to the original dataset. This method outperforms other research methods in terms of diagnostic accuracy for all faults except for RO and EO faults, which have a slightly lower accuracy rate of 0.06% and 0.02%, respectively, compared to other methods. The overall accuracy rate of this method is as high as 99.98%.
- (3)
- The proposed RelifF-RFECV-SVM method reduces the diagnosis time by approximately 50% compared to the SVM method, while ensuring diagnostic accuracy. Similarly, in the fault diagnosis of self-built simulation data in Amesim, the time is reduced by about 60% to 70%.
- (4)
- This method exhibits strong generalization, achieving accurate fault diagnosis not only on the ASHRAE 1043-RP dataset but also on the self-built simulation dataset using Amesim.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Verhelst, J.; Van Ham, G.; Saelens, D.; Li, H. Model selection for continuous commissioning of HVAC-systems in office buildings: A review. Renew. Sustain. Energy Rev. 2017, 76, 673–686. [Google Scholar] [CrossRef]
- Beiter, P.; Elchinger, M.; Tian, T. Renewable Energy Data Book; National Renewable Energy Lab. (NREL): Golden, CO, USA, 2017. [Google Scholar]
- Yu, X.; Yan, D.; Sun, K.; Hong, T.; Zhu, D. Comparative study of the cooling energy performance of variable refrigerant flow systems and variable air volume systems in office buildings. Appl. Energy 2016, 183, 725–736. [Google Scholar] [CrossRef]
- Fan, Y.; Cui, X.; Han, H.; Lu, H. Chiller fault diagnosis with field sensors using the technology of imbalanced data. Appl. Therm. Eng. 2019, 159, 113933. [Google Scholar] [CrossRef]
- Yao, W.; Li, D.; Gao, L. Fault detection and diagnosis using tree-based ensemble learning methods and multivariate control charts for centrifugal chillers. J. Build. Eng. 2022, 51, 104243. [Google Scholar] [CrossRef]
- Tian, C.; Wang, Y.; Ma, X.; Chen, Z.; Xue, H. Chiller Fault Diagnosis Based on Automatic Machine Learning. Front. Energy Res. 2021, 9, 753732. [Google Scholar] [CrossRef]
- Han, S.; Shao, H.; Huo, Z.; Yang, X.; Cheng, J. End-to-end chiller fault diagnosis using fused attention mechanism and dynamic cross-entropy under imbalanced datasets. Build. Environ. 2022, 212, 108821. [Google Scholar] [CrossRef]
- Bai, X.; Zhang, M.; Jin, Z.; You, Y.; Liang, C. Fault detection and diagnosis for chiller based on feature-recognition model and kernel discriminant analysis. Sustain. Cities Soc. 2022, 79, 103708. [Google Scholar] [CrossRef]
- Gao, L.; Li, D.; Liu, X.; Liu, G. Enhanced chiller faults detection and isolation method based on independent component analysis and k-nearest neighbors classifier. Build. Environ. 2022, 216, 109010. [Google Scholar] [CrossRef]
- Huang, T.; Liang, C.; Bai, X.; Feng, Z.; Wang, F. Study on the feature-recognition-based modeling approach of chillers. Int. J. Refrig. 2019, 100, 326–334. [Google Scholar] [CrossRef]
- Yan, K.; Su, J.; Huang, J.; Mo, Y. Chiller fault diagnosis based on VAE-enabled generative adversarial networks. IEEE Trans. Autom. Sci. Eng. 2020, 19, 387–395. [Google Scholar] [CrossRef]
- Xiang, C.; Zhou, J.; Han, B.; Li, W.; Zhao, H. Fault Diagnosis of Rolling Bearing Based on a Priority Elimination Method. Sensors 2023, 23, 2320. [Google Scholar] [CrossRef]
- Wang, Z.; Luo, W.; Xu, S.; Yan, Y.; Huang, L.; Wang, J.; Hao, W.; Yang, Z. Electric Vehicle Lithium-Ion Battery Fault Diagnosis Based on Multi-Method Fusion of Big Data. Sustainability 2023, 15, 1120. [Google Scholar] [CrossRef]
- Jiusi, Z.; Ke, Z.; Yiyao, A.; Hao, L.; Shen, Y. An Integrated Multitasking Intelligent Bearing Fault Diagnosis Scheme Based on Representation Learning Under Imbalanced Sample Condition. IEEE Trans. Ind. Inform. 2023, 1, 1–12. [Google Scholar] [CrossRef]
- Jiusi, Z.; Congsheng, H.; Moyuen, C.; Xiang, L.; Jilun, T.; Hao, L.; Shen, Y.A. Data-model Interactive Remaining Useful Life Prediction Approach of Lithium-ion Batteries Based on PF-BiGRU-TSAM. IEEE Trans. Ind. Inform. 2023, 4, 1–12. [Google Scholar] [CrossRef]
- Zhu, X.; Chen, K.; Anduv, B.; Jin, X.; Du, Z. Transfer learning based methodology for migration and application of fault detection and diagnosis between building chillers for improving energy efficiency. Build. Environ. 2021, 200, 107957. [Google Scholar] [CrossRef]
- Chen, K.; Wang, Z.; Gu, X.; Wang, Z. Multicondition operation fault detection for chillers based on global density-weighted support vector data description. Appl. Soft Comput. 2021, 112, 107795. [Google Scholar] [CrossRef]
- Yan, K.; Zhou, X. Chiller faults detection and diagnosis with sensor network and adaptive 1DCNN. Digit. Commun. Netw. 2022, 8, 531–539. [Google Scholar] [CrossRef]
- Shen, C.; Zhang, H.; Meng, S.; Li, C. Augmented data driven self-attention deep learning method for imbalanced fault diagnosis of the HVAC chiller. Eng. Appl. Artif. Intell. 2023, 117, 105540. [Google Scholar] [CrossRef]
- Chandrashekar, G.; Sahin, F. A survey on feature selection methods. Comput. Electr. Eng. 2014, 40, 16–28. [Google Scholar] [CrossRef]
- Gao, Y.; Han, H.; Ren, Z.; Gao, J.; Jiang, S. Comprehensive study on sensitive parameters for chiller fault diagnosis. Energy Build. 2021, 251, 111318. [Google Scholar] [CrossRef]
- Zhou, X.; Xiong, Z.X.; Huang, X.F.; Yang, Y. Research on Fault Diagnosis Strategy of Chiller Based on Two-step Feature Selection and Lightgbm with Bayesian Optimization. Build. Sci. 2022, 38, 11. [Google Scholar]
- Dong, H.; Sun, J.; Li, T.; Ding, R.; Sun, X. A multi-objective algorithm for multi-label filter feature selection problem. Appl. Intell. 2020, 50, 3748–3774. [Google Scholar] [CrossRef]
- Ouadfel, S.; Abd Elaziz, M. Efficient high-dimension feature selection based on enhanced equilibrium optimizer. Expert Syst. Appl. 2022, 187, 115882. [Google Scholar] [CrossRef]
- Li, J.; Cheng, K.; Wang, S.; Lin, S. Feature selection: A data perspective. ACM Comput. Surv. (CSUR) 2017, 50, 1–45. [Google Scholar] [CrossRef]
- Shi, Y.; Dong, X.; Chen, B. The application of ReliefF algorithm in cement process fault diagnosis is improved. J. Mach. Des. 2022, 39, 40–45. [Google Scholar]
- Han, H.; Gu, B.; Wang, T.; Li, Z. Important sensors for chiller fault detection and diagnosis (FDD) from the perspective of feature selection and machine learning. Int. J. Refrig. 2011, 34, 586–599. [Google Scholar] [CrossRef]
- Yan, K.; Ma, L.; Dai, Y.; Shen, W.; Ji, Z.; Xie, D. Cost-sensitive and Sequential Feature Selection for Chiller Fault Detection and Diagnosis. Int. J. Refrig. 2018, 86, 401–409. [Google Scholar] [CrossRef]
- Xu, L.L.; Chi, D.X. Machine learning classification strategies for unbalanced data sets. Comput. Eng. Appl. 2020, 56, 12–27. [Google Scholar]
- Kononenko, I. Estimating attributes: Analysis and extensions of RELIEF. In Proceedings of the European Conference on Machine Learning on Machine Learning, Catania, Italy, 6 April 1994; Springer: Berlin/Heidelberg, Germany, 1994. [Google Scholar]
- Fu, C.; Zhou, S.; Zhang, D.; Chen, L. Relative Density-Based Intuitionistic Fuzzy SVM for Class Imbalance Learning. Entropy 2023, 25, 34. [Google Scholar] [CrossRef]
- Wang, J.; Wang, X.; Li, X.; Yi, J. A Hybrid Particle Swarm Optimization Algorithm with Dynamic Adjustment of Inertia Weight Based on a New Feature Selection Method to Optimize SVM Parameters. Entropy 2023, 25, 531. [Google Scholar] [CrossRef]
- Mangkunegara, L.S.; Purwono, P. Analysis of DNA Sequence Classification Using SVM Model with Hyperparameter Tuning Grid Search CV. In Proceedings of the 2022 IEEE International Conference on Cybernetics and Computational Intelligence, Malang, Indonesia, 16–18 June 2022; pp. 427–432. [Google Scholar]
- Kiruthika, N.S.; Thailambal, G. Dynamic Light Weight Recommendation System for Social Networking Analysis Using a Hybrid LSTM-SVM Classifier Algorithm. Opt. Mem. Neural Netw. 2022, 31, 59–75. [Google Scholar] [CrossRef]
- Comstock, M.C.; Braun, J.E. Development of Analysis Tools for the Evaluation of Fault Detection and Diagnostics for Chillers; ASHRAE Research Project 1043-RP, HL 99-20, Report #4036-3; Purdue University: West Lafayette, IN, USA, 1999. [Google Scholar]
- Liu, Y.C.; Fan, C.; Liu, X.Y.; Lin, L. Deep recurrent neural network-based Strategy for chiller fault detection and diagnosis. Build. Sci. 2022, 8, 38. [Google Scholar]
- Li, P.; Anduv, B.; Zhu, X.; Jin, X.; Du, Z. Across working conditions fault diagnosis for chillers based on IoT intelligent agent with deep learning model. Energy Build. 2022, 268, 112188. [Google Scholar] [CrossRef]
- Li, G.; Hu, Y.; Chen, H.; Shen, L.; Li, H.; Hu, M.; Liu, J.; Sun, K. An improved fault detection method for incipient centrifugal chiller faults using the PCA-R-SVDD algorithm. Energy Build. 2016, 116, 104–113. [Google Scholar] [CrossRef]
- Zhao, Y.; Wang, S.; Xiao, F. Pattern recognition-based chillers fault detection method using Support Vector Data Description (SVDD). Appl. Energy 2013, 112, 1041–1048. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, Z.; Gu, X.; He, S.; Yan, Z. Feature selection based on Bayesian network for chiller fault diagnosis from the perspective of field applications. Appl. Therm. Eng. Des. Process. Equip. Econ. 2018, 129, 674–683. [Google Scholar] [CrossRef]
- Xia, Y.; Zhao, J.; Ding, Q.; Liu, J. Incipient Chiller Fault Diagnosis Using an Optimized Least Squares Support Vector Machine with Gravitational Search Algorithm. Front. Energy Res. 2021, 9, 755649. [Google Scholar] [CrossRef]
- Zengren, P.; Yanhui, L.; Zhiwei, L.; Qiwen, X.; Ying, W. 1DCNN-BiGRU network for surface roughness level detection. Surf. Topogr.-Metrol. Prop. 2022, 10, 44005. [Google Scholar]




| Num. | Fault Type | SL1 | SL2 | SL3 | SL4 |
|---|---|---|---|---|---|
| 1 | Flow water of condenser Insufficient (FWC) | −10% | −20% | −30% | −40% |
| 2 | Flow water of evaporator Insufficient (FWE) | −10% | −20% | −30% | −40% |
| 3 | Refrigerant leak (RL) | −10% | −20% | −30% | −40% |
| 4 | Refrigerant over (RO) | +10% | +20% | +30% | +40% |
| 5 | Condenser fouling (CF) | −12% | −20% | −30% | −45% |
| 6 | Excessive over (EO) | +14% | +32% | +50% | +68% |
| 7 | Non-condensable gas contained (NC) | +1% | +2% | +3% | +5% |
| Num. | Fault Type | Fault Introduction Method | SL1 | SL2 | SL3 | SL4 |
|---|---|---|---|---|---|---|
| 1 | Condenser Fouling (CF) | Adjust the air mass flow through the condenser | −10% | −20% | −30% | −40% |
| 2 | Compressor Wear (CW) | Change the speed of the compressor | −10% | −20% | −30% | −40% |
| 3 | Evaporator Scaling (ES) | Adjust the air mass flow through the evaporator | −10% | −20% | −30% | −40% |
| Num. | Name | Features | Num. | Name | Features |
|---|---|---|---|---|---|
| 1 | Lto | Exhaust temperature of condenser | 13 | Zto | Evaporator exhaust temperature |
| 2 | Lpo | Exhaust pressure of condenser | 14 | Zpo | Evaporator exhaust pressure |
| 3 | Lti | Condenser suction temperature | 15 | Zti | Evaporator suction temperature |
| 4 | Lpi | Condenser suction pressure | 16 | Zpi | Evaporator suction pressure |
| 5 | LWc | Condenser outlet humidity | 17 | ZWc | Evaporator outlet humidity |
| 6 | LTc | Condenser outlet temperature | 18 | ZTc | Evaporator outlet temperature |
| 7 | TRC | Refrigerant temperature in condenser | 19 | TRE | Refrigerant temperature in evaporator |
| 8 | PRC | Refrigerant pressure in condenser | 20 | PRE | Refrigerant pressure in evaporator |
| 9 | Yto | Exhaust temperature of compressor | 21 | FPc | Expansion valve outlet pressure |
| 10 | Ypo | Compressor delivery pressure | 22 | Fpi | Expansion valve inlet pressure |
| 11 | Yti | Compressor suction temperature | 23 | Qc | Specific refrigerating effect |
| 12 | Ypi | Compressor suction pressure | 24 | SH | Degree of superheat |
| Num. | Features | Description |
|---|---|---|
| 1 | TWI | Temperature of City Water In |
| 2 | FWE | Flow Rate of Evaporator Water |
| 3 | PO_feed | Pressure of Oil Feed |
| 4 | PO_net | Oil Feed minus Oil Vent Pressure |
| 5 | FWC | Flow Rate of Condenser Water |
| 6 | VC | Condenser Valve Position |
| 7 | TCA | Condenser Approach Temperature |
| 8 | TRC_sub | Liquid-line Refrigerant Subcooling from Condenser |
| 9 | TO_sump | Temperature of Oil in Sump |
| 10 | TO_feed | Temperature of Oil Feed |
| 11 | TR_dis | Refrigerant Discharge Temperature |
| 12 | THI | Temperature of Hot Water In |
| 13 | THO | Temperature of Hot Water Out |
| 14 | TRE | Saturated Refrigerant Temperature in Evaporator |
| 15 | PRE | Pressure of Refrigerant in Evaporator |
| 16 | T_suc | Refrigerant Suction Temperature |
| 17 | TWO | Temperature of City Water Out |
| 18 | TWED | Evaporator Water Temperature Delta |
| 19 | TEO | Temperature of Evaporator Water Out |
| 20 | Evap Tons | Calculated Evaporator Cooling Rate |
| 21 | TCO | Temperature of Condenser Water Out |
| 22 | TSI | Temperature of Shared HX Water In (in Condenser Water Loop) |
| 23 | TCI | Temperature of Condenser Water In |
| 24 | TSO | Temperature of Shared HX Water Out (in Condenser Water Loop) |
| 25 | TEI | Temperature of Evaporator Water In |
| 26 | TWEI | Temperature of Evaporator Water In |
| 27 | TWEO | Temperature of Evaporator Water Out |
| 28 | TWCI | Temperature of Condenser Water In |
| 29 | TWCO | Temperature of Condenser Water Out |
| 30 | TBI | Temperature of Building Water In (in Evaporator Water Loop) |
| 31 | TBO | Temperature of Building Water Out (in Evaporator Water Loop) |
| 32 | Cond Tons | Calculated Condenser Heat Rejection Rate |
| 33 | Cooling Tons | Calculated City Water Cooling Rate |
| 34 | Shared Cond Tons | Calculated Shared HX Heat Transfer (only valid with no water bypass) |
| 35 | Cond Energy Balance | Calculated 1st Law Energy Balance for Condenser Water Loop (only valid with no water bypass) |
| 36 | Shared Evap Tons | Calculated Shared HX Heat Transfer (should equal Shared Cond Tons with no water bypass) |
| 37 | Building Tons | Calculated Steam Heating Load |
| 38 | kW | Watt Transducer Measuring Instantaneous Compressor Power |
| 39 | COP | Calculated Coefficient of Performance |
| 40 | TEA | Evaporator Approach Temperature |
| 41 | TRC | Saturated Refrigerant Temperature in Condenser |
| 42 | PRC | Pressure of Refrigerant in Condenser |
| 43 | Tsh_suc | Refrigerant Suction Superheat Temperature |
| 44 | Tsh_dis | Refrigerant Discharge Superheat Temperature |
| 45 | P_lift | Pressure Lift Across Compressor |
| 46 | Amps | Current Draw Across One Leg of Motor Input |
| 47 | RLA% | Percent of Maximum Rated Load Amps |
| 48 | Tolerance% | Calculated Heat Balance Tolerance According to ARI 550 |
| 49 | TWCD | Condenser Water Temperature Delta |
| 50 | VSS | Small Steam Valve Position |
| 51 | VM | 3-way Mixing Valve Position |
| 52 | VW | City Water Valve Position |
| 53 | FWW | Calculated City Water Flow Rate |
| 54 | FWB | Calculated Condenser Water Bypass Flow Rate |
| Number | Name | Feature |
|---|---|---|
| 1 | Lti | Condenser suction temperature |
| 2 | Yto | exhaust temperature of compressor |
| 3 | LWc | Condenser outlet humidity |
| 4 | ZWc | Evaporator outlet humidity |
| 5 | Qc | specific refrigerating effect |
| 6 | SH | degree of superheat |
| True Label | |||
|---|---|---|---|
| Predict label | 0 | 1 | |
| 0 | TP | FP | |
| 1 | FN | TN | |
| Fault Diagnosis Method | Level 1 | Level 2 | Level 3 | Level 4 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| AC | F1 | Time | AC | F1 | Time | AC | F1 | Time | AC | F1 | Time | |
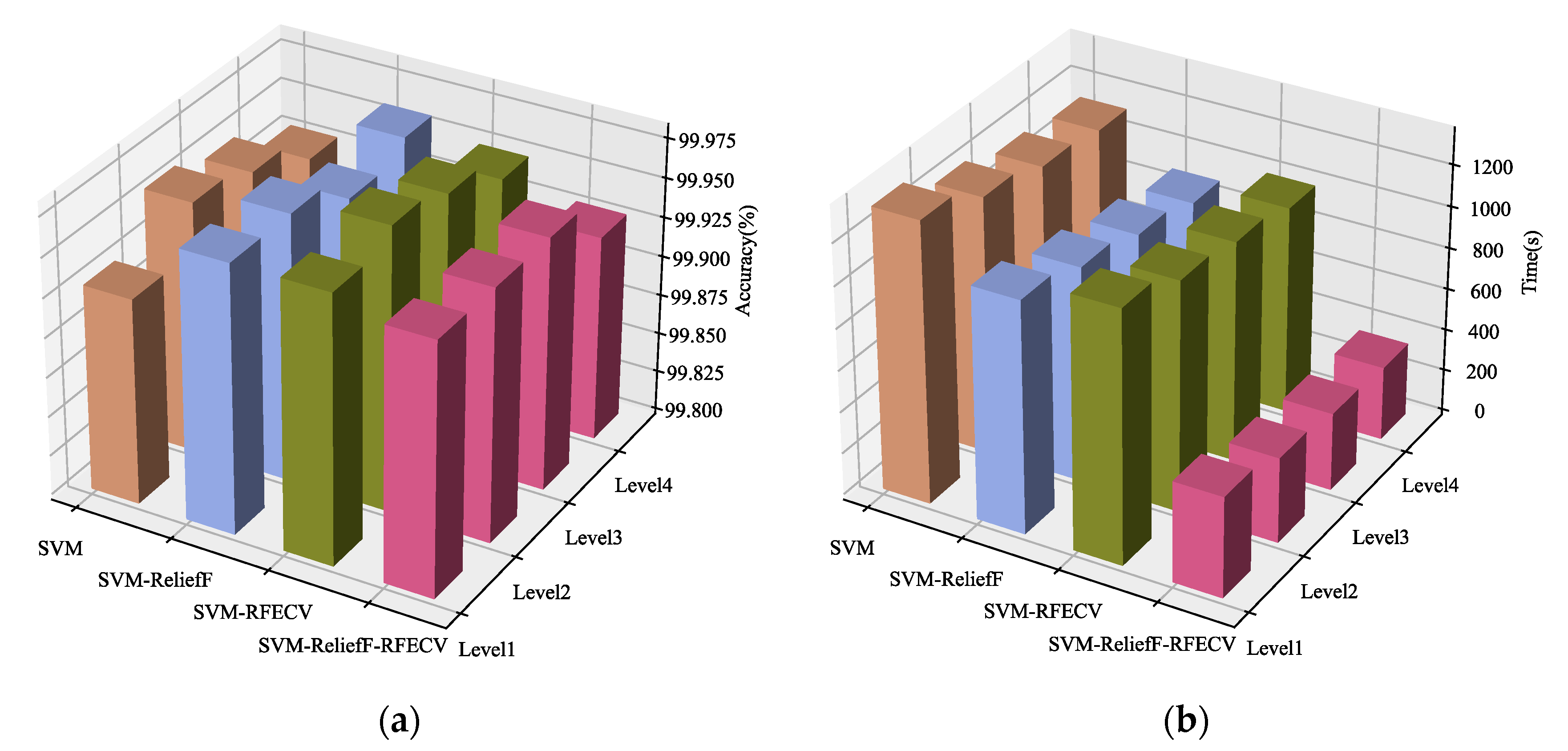
| SVM | 99.93 | 99.93 | 1256.08 | 99.94 | 99.94 | 1166.40 | 99.99 | 99.99 | 1087.98 | 100 | 100 | 1027.04 |
| SVM-ReliefF | 99.90 | 99.90 | 1094.64 | 99.92 | 99.92 | 1006.09 | 99.94 | 99.94 | 947.71 | 99.98 | 99.98 | 872.39 |
| SVM-RFECV | 99.95 | 99.95 | 557.62 | 99.89 | 99.89 | 512.55 | 99.99 | 99.97 | 479.27 | 100 | 100 | 445.08 |
| SVM-ReliefF-RFECV | 99.98 | 99.98 | 602.14 | 99.94 | 99.94 | 552.72 | 99.99 | 99.99 | 517.74 | 100 | 100 | 476.82 |
| Fault Diagnosis Method | Level 1 | Level 2 | Level 3 | Level 4 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| AC | F1 | Time | AC | F1 | Time | AC | F1 | Time | AC | F1 | Time | |
| SVM | 99.93 | 99.93 | 1256.08 | 99.94 | 99.94 | 1166.40 | 99.99 | 99.99 | 1087.98 | 100 | 100 | 1027.04 |
| SVM-ReliefF-RFECV | 99.98 | 99.98 | 602.14 | 99.94 | 99.94 | 552.72 | 99.99 | 99.99 | 517.74 | 100 | 100 | 476.82 |
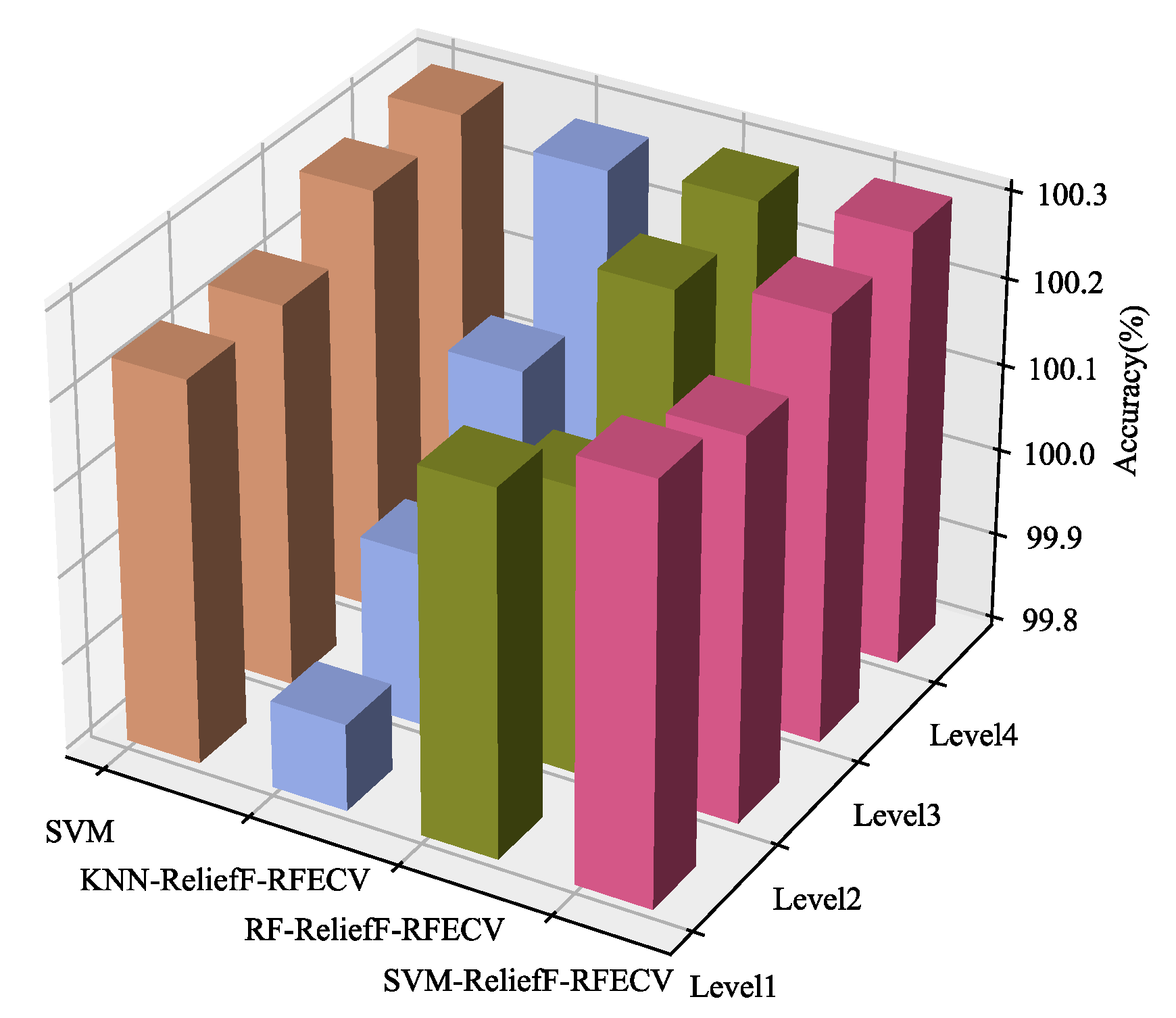
| RF | 99.80 | 99.80 | 536.95 | 99.83 | 99.83 | 533.20 | 99.95 | 99.95 | 512.28 | 99.99 | 99.99 | 495.89 |
| RF-ReliefF-RFECV | 99.92 | 99.92 | 388.81 | 99.83 | 99.83 | 378.87 | 99.97 | 99.97 | 370.70 | 99.99 | 99.99 | 354.31 |
| KNN | 98.71 | 98.72 | 29.07 | 98.96 | 98.96 | 25.65 | 99.51 | 99.50 | 24.55 | 99.76 | 99.76 | 24.36 |
| KNN-ReliefF-RFECV | 99.60 | 99.60 | 13.38 | 99.70 | 99.70 | 11.79 | 99.83 | 99.84 | 13.61 | 99.98 | 99.98 | 10.55 |
| Fault Diagnosis Method | Level 1 | Level 2 | Level 3 | Level 4 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| AC | F1 | Time | AC | F1 | Time | AC | F1 | Time | AC | F1 | Time | |
| SVM | 99.94 | 99.94 | 1346.83 | 99.96 | 99.95 | 1234.07 | 99.95 | 99.95 | 1163.28 | 99.93 | 99.94 | 1127.35 |
| SVM-ReliefF | 99.97 | 99.97 | 1112.47 | 99.97 | 99.97 | 1035.18 | 99.95 | 99.93 | 964.28 | 99.96 | 99.96 | 896.71 |
| SVM-RFECV | 99.97 | 99.97 | 1209.91 | 99.98 | 99.98 | 1105.44 | 99.97 | 99.97 | 1058.14 | 99.95 | 99.95 | 998.14 |
| SVM-ReliefF-RFECV | 99.96 | 99.96 | 483.29 | 99.96 | 99.96 | 410.04 | 99.96 | 99.96 | 372.12 | 99.93 | 99.93 | 353.36 |
| Fault Diagnosis Method | Level1 | Level2 | Level3 | Level4 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| AC | F1 | Time | AC | F1 | Time | AC | F1 | Time | AC | F1 | Time | |
| SVM | 99.94 | 99.94 | 1346.83 | 99.96 | 99.95 | 1234.07 | 99.95 | 99.95 | 1163.28 | 99.93 | 99.94 | 1127.35 |
| SVM-ReliefF-RFECV | 99.96 | 99.96 | 483.29 | 99.96 | 99.96 | 410.04 | 99.96 | 99.96 | 372.12 | 99.93 | 99.93 | 353.36 |
| RF | 99.81 | 99.92 | 627.01 | 99.90 | 99.91 | 554.48 | 99.92 | 99.92 | 581.07 | 99.88 | 99.89 | 593.86 |
| RF-ReliefF-RFECV | 99.92 | 99.93 | 452.85 | 99.92 | 99.92 | 432.69 | 99.92 | 99.92 | 433.29 | 99.91 | 99.91 | 400.17 |
| KNN | 99.81 | 99.81 | 14.90 | 99.88 | 99.88 | 15.72 | 99.90 | 99.91 | 15.61 | 99.87 | 99.87 | 15.97 |
| KNN-ReliefF-RFECV | 99.82 | 99.82 | 9.49 | 99.84 | 99.85 | 9.49 | 99.88 | 99.88 | 9.37 | 99.88 | 99.88 | 9.80 |
| Fault Diagnosis Method | The Diagnostic Accuracy of Each Fault | Overall Accuracy | ||||||
|---|---|---|---|---|---|---|---|---|
| FWC | FWE | RL | RO | CF | EO | NC | ||
| DR-BN | 97.6 | 94.8 | 70.2 | 95.8 | 97.4 | 96.3 | 99 | 93.01 |
| KPCA-LSSVM-GSA | 100.0 | 89.5 | 100.0 | 92.3 | 90 | 100.0 | 100.0 | 95.97 |
| 1DCNN | 100.0 | 99.88 | 92.25 | 91.88 | 98.5 | 94.63 | 98.00 | 96.45 |
| 1DCNN-BIGRU | 100.0 | 100.0 | 98.69 | 99.06 | 99.98 | 98.77 | 99.98 | 99.50 |
| RF-GSA-CFCS | 100.0 | 100.0 | 99.01 | 100.0 | 100.0 | 99.0 | 100.0 | 99.71 |
| ReliefF-RFECV-SVM | 100.0 | 100.0 | 99.94 | 99.93 | 100.0 | 99.98 | 100.0 | 99.98 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nie, L.; Wu, R.; Ren, Y.; Tan, M. Research on Fault Diagnosis of HVAC Systems Based on the ReliefF-RFECV-SVM Combined Model. Actuators 2023, 12, 242. https://doi.org/10.3390/act12060242
Nie L, Wu R, Ren Y, Tan M. Research on Fault Diagnosis of HVAC Systems Based on the ReliefF-RFECV-SVM Combined Model. Actuators. 2023; 12(6):242. https://doi.org/10.3390/act12060242
Chicago/Turabian StyleNie, Lei, Rouhui Wu, Yizhu Ren, and Mengying Tan. 2023. "Research on Fault Diagnosis of HVAC Systems Based on the ReliefF-RFECV-SVM Combined Model" Actuators 12, no. 6: 242. https://doi.org/10.3390/act12060242
APA StyleNie, L., Wu, R., Ren, Y., & Tan, M. (2023). Research on Fault Diagnosis of HVAC Systems Based on the ReliefF-RFECV-SVM Combined Model. Actuators, 12(6), 242. https://doi.org/10.3390/act12060242





