Evaluation of Spiral Pneumatic Rubber Actuator Using Finite Element Analysis for Radial Transportation
Abstract
1. Introduction
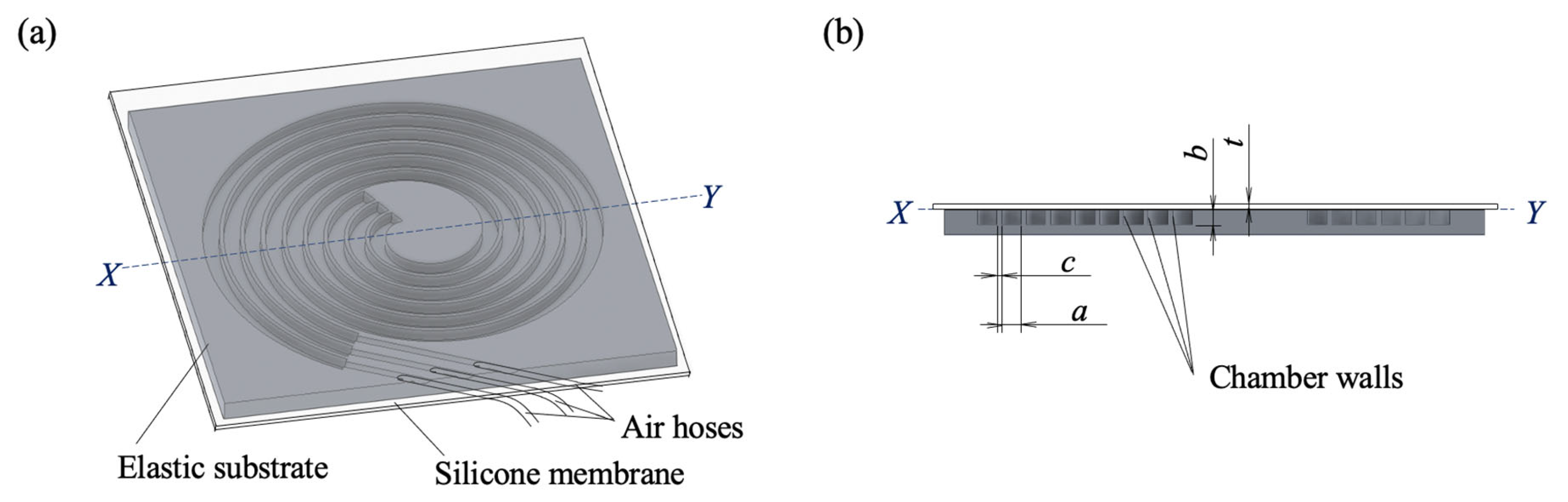
2. Design and Fabrication
2.1. Structural Design
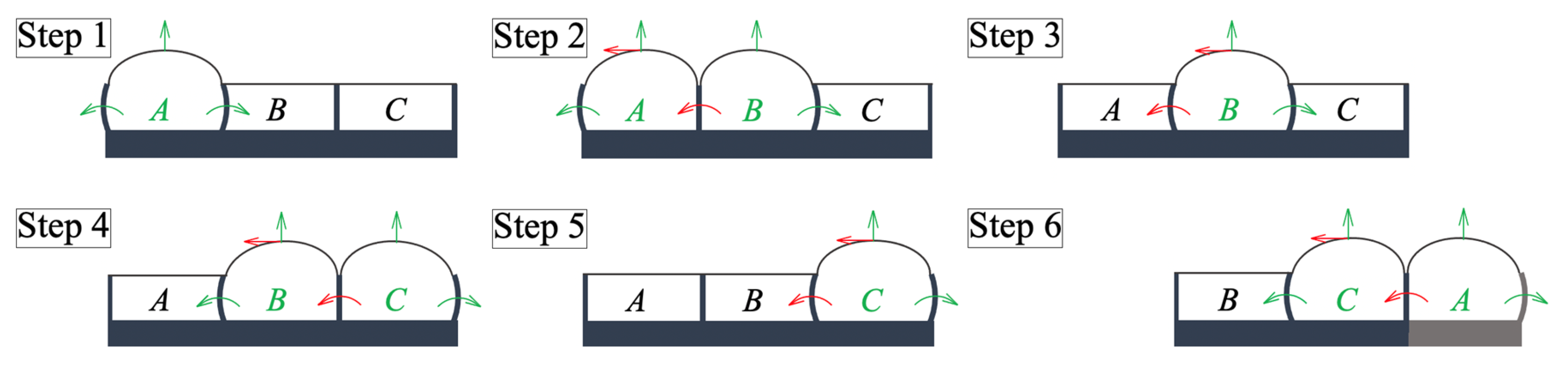
2.2. Actuator Principle
2.3. Fabrication
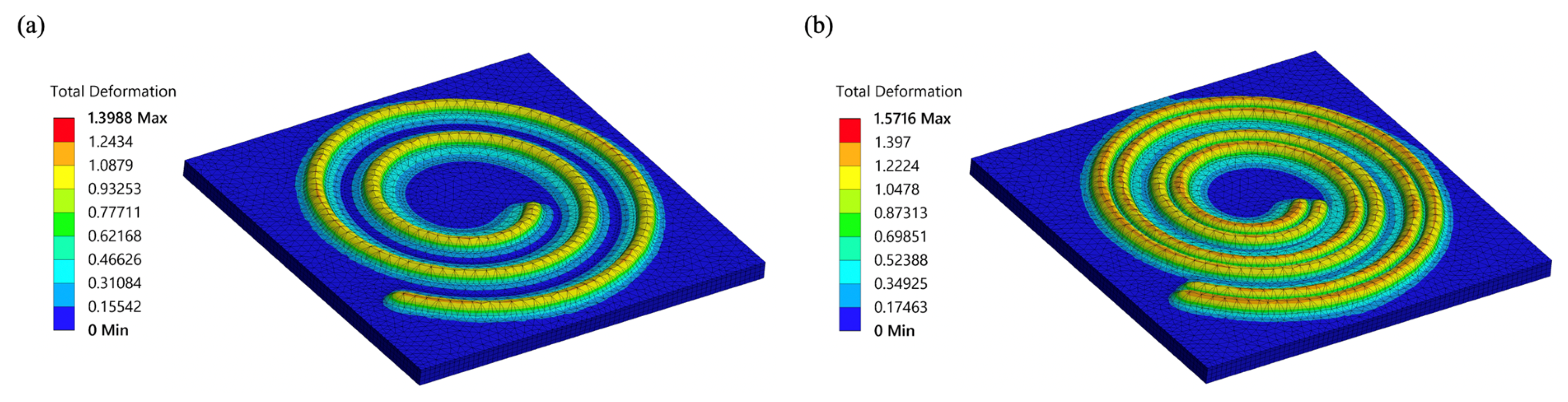
3. Finite Element Simulations
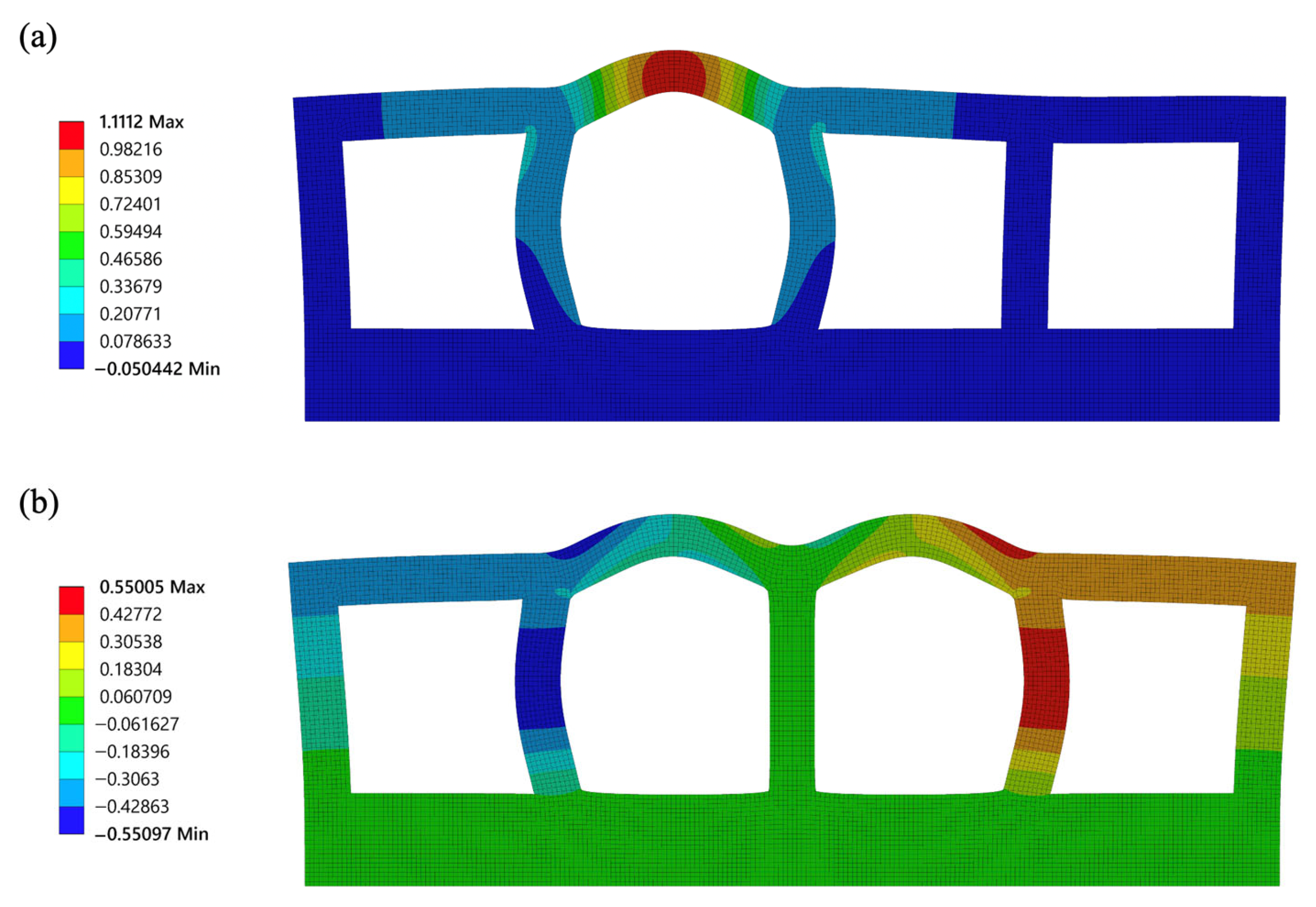
3.1. FEA Model of Spiral Actuator
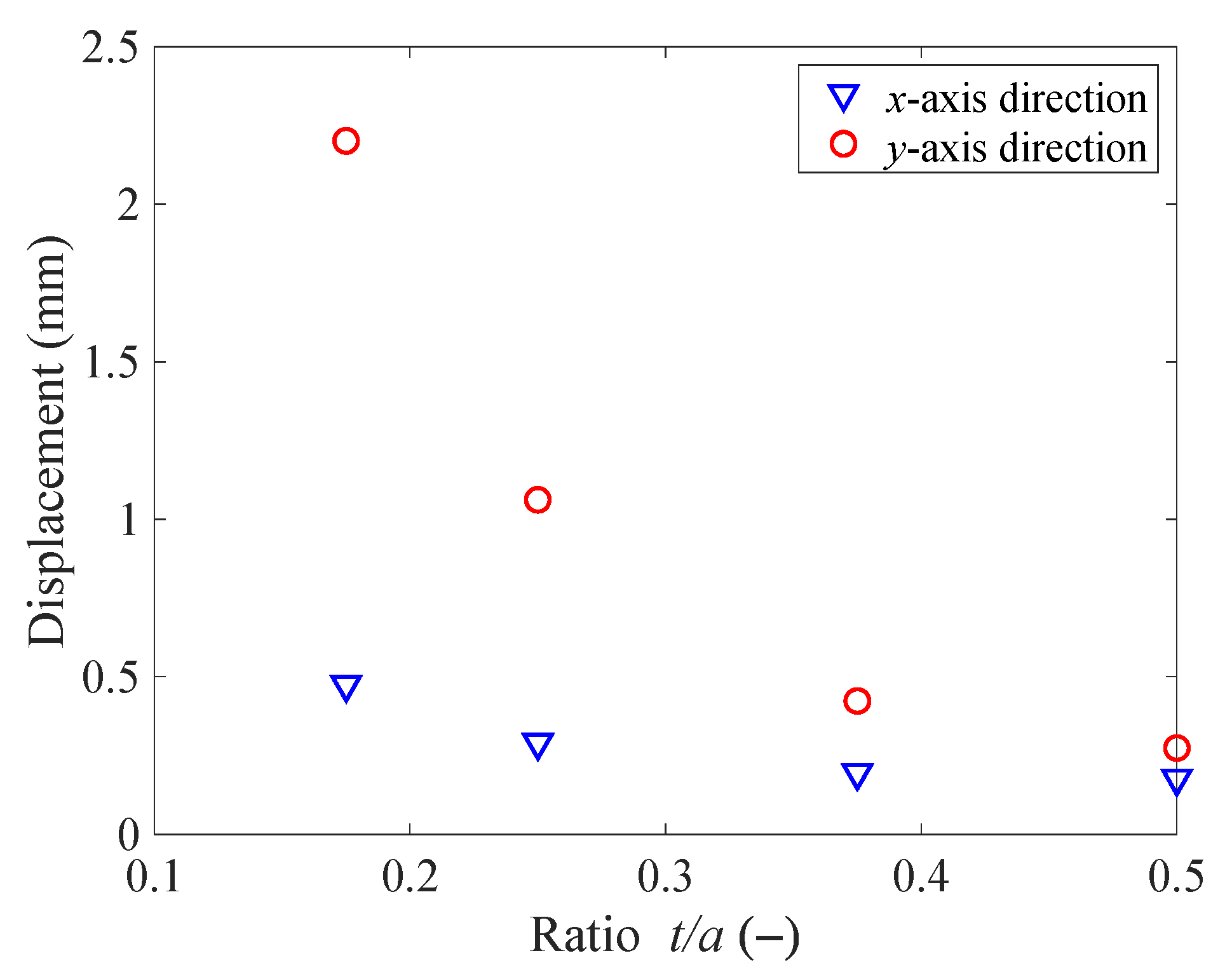
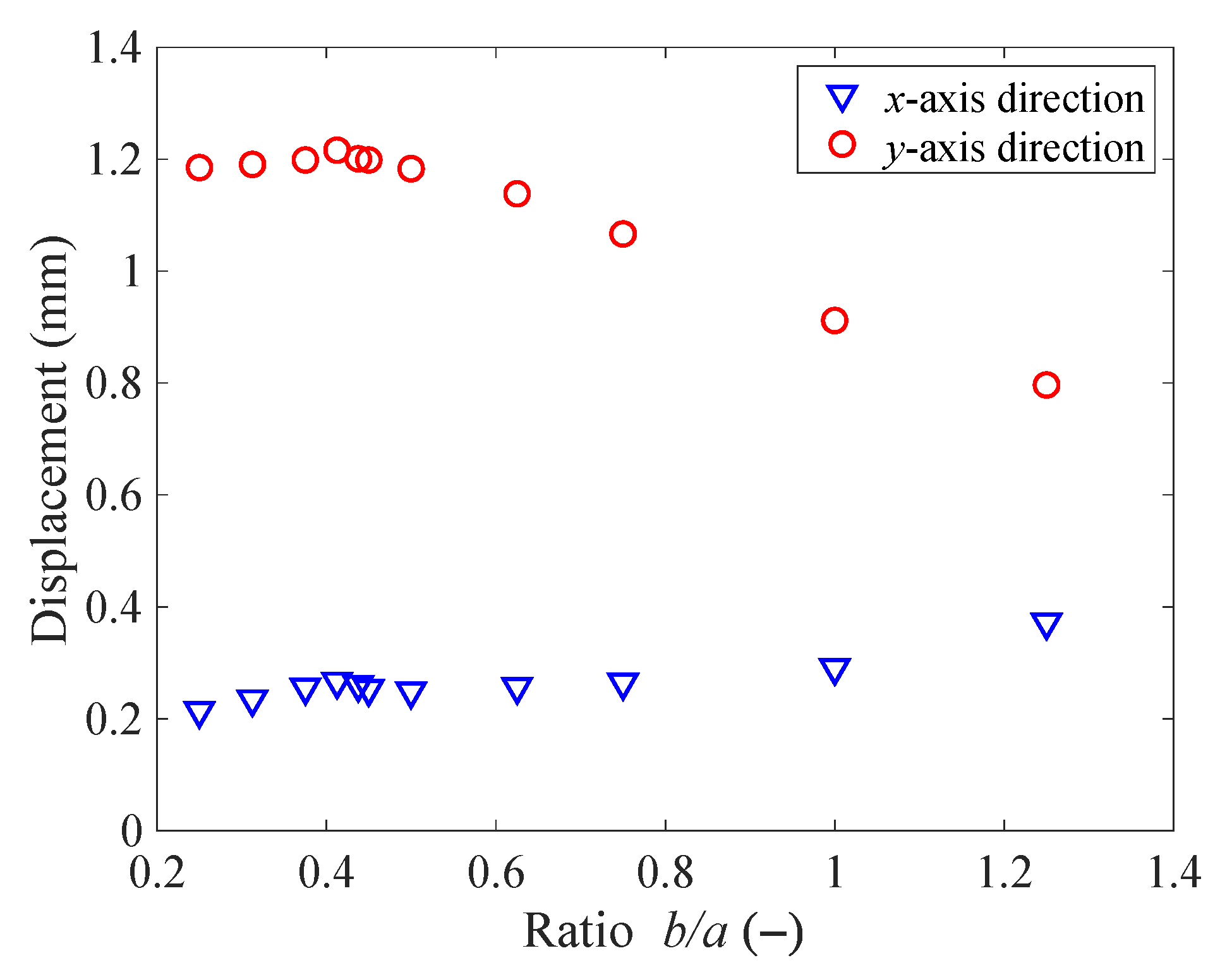
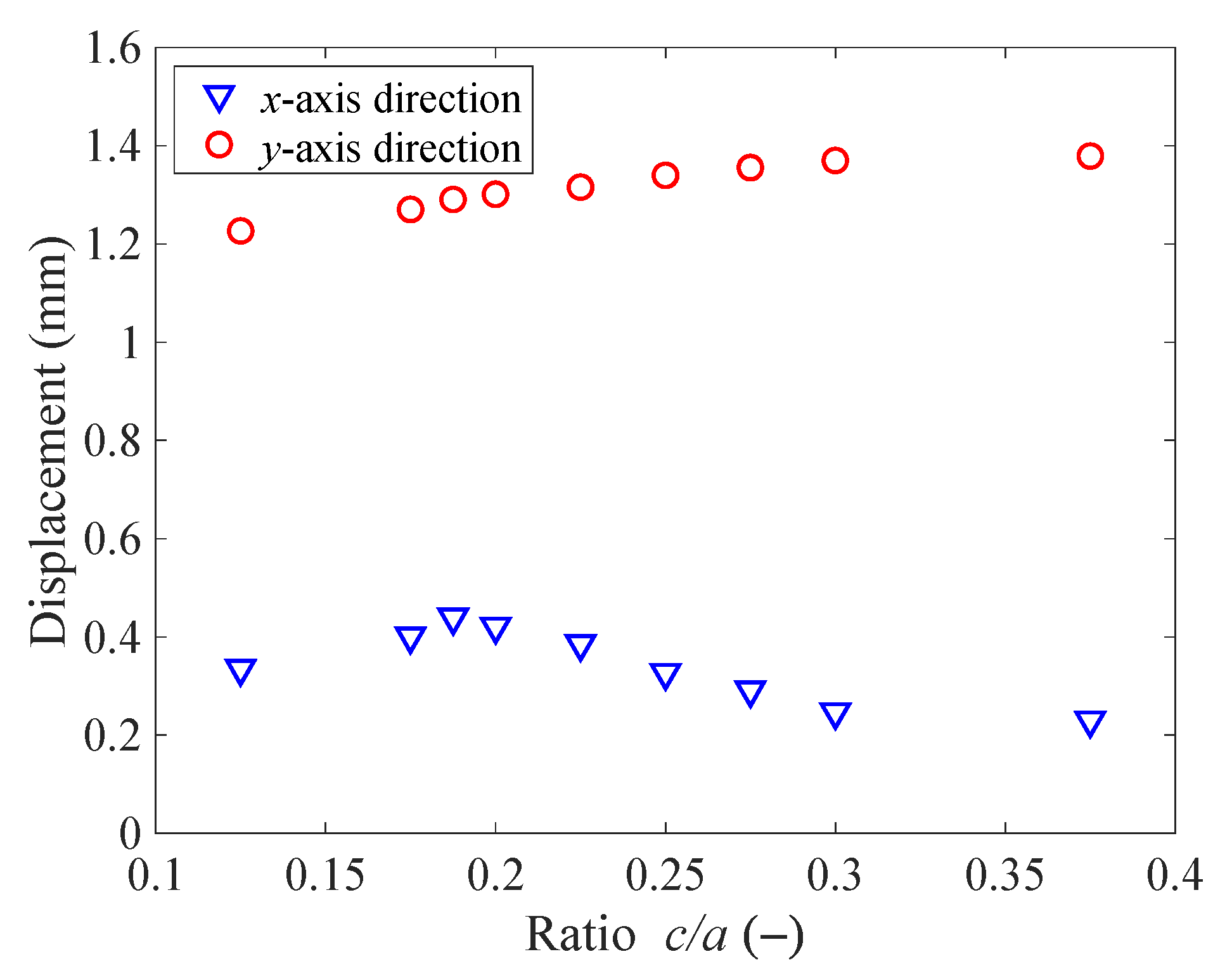
3.2. Effect of Structural Parameters
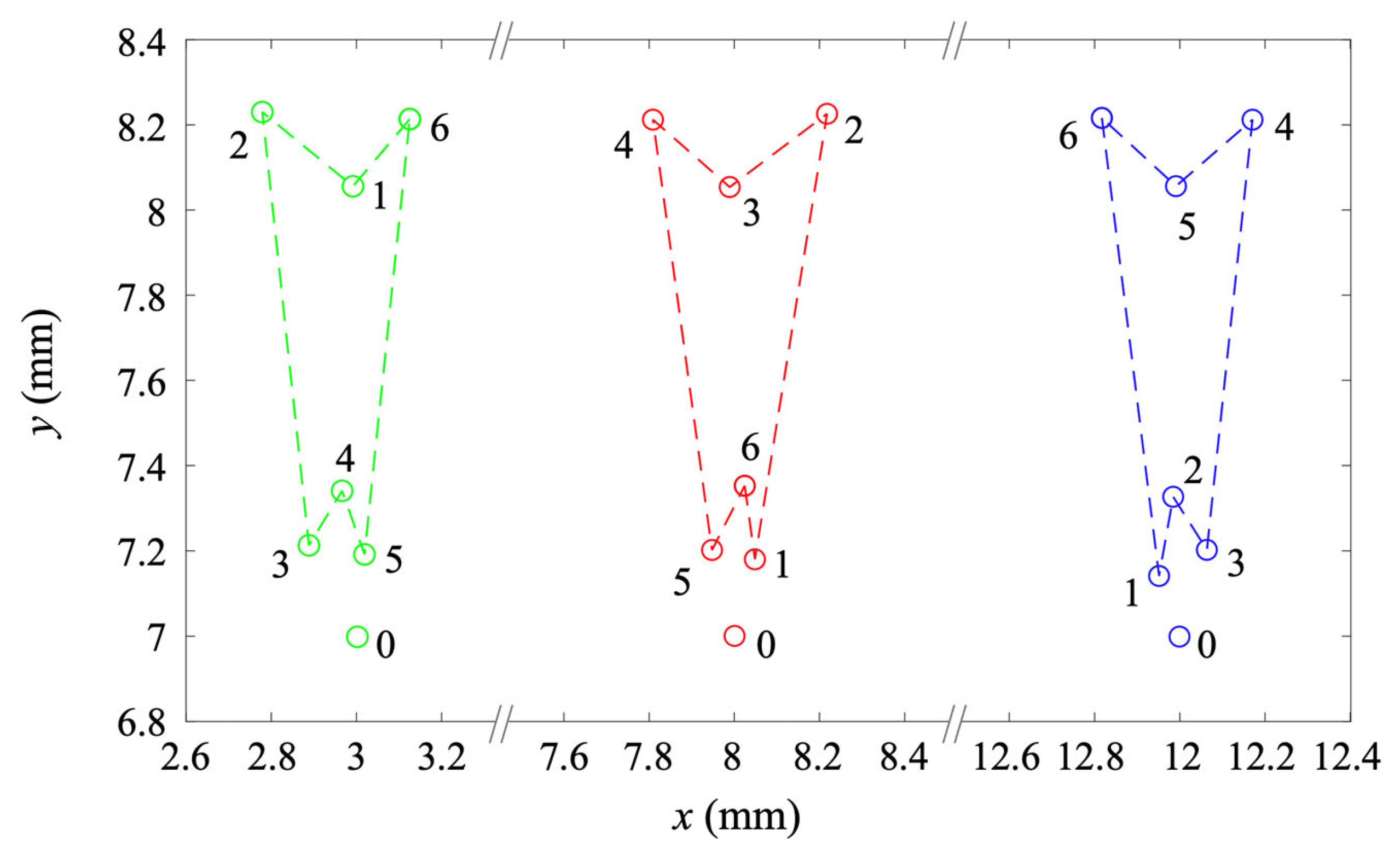
4. Experiments and Discussions
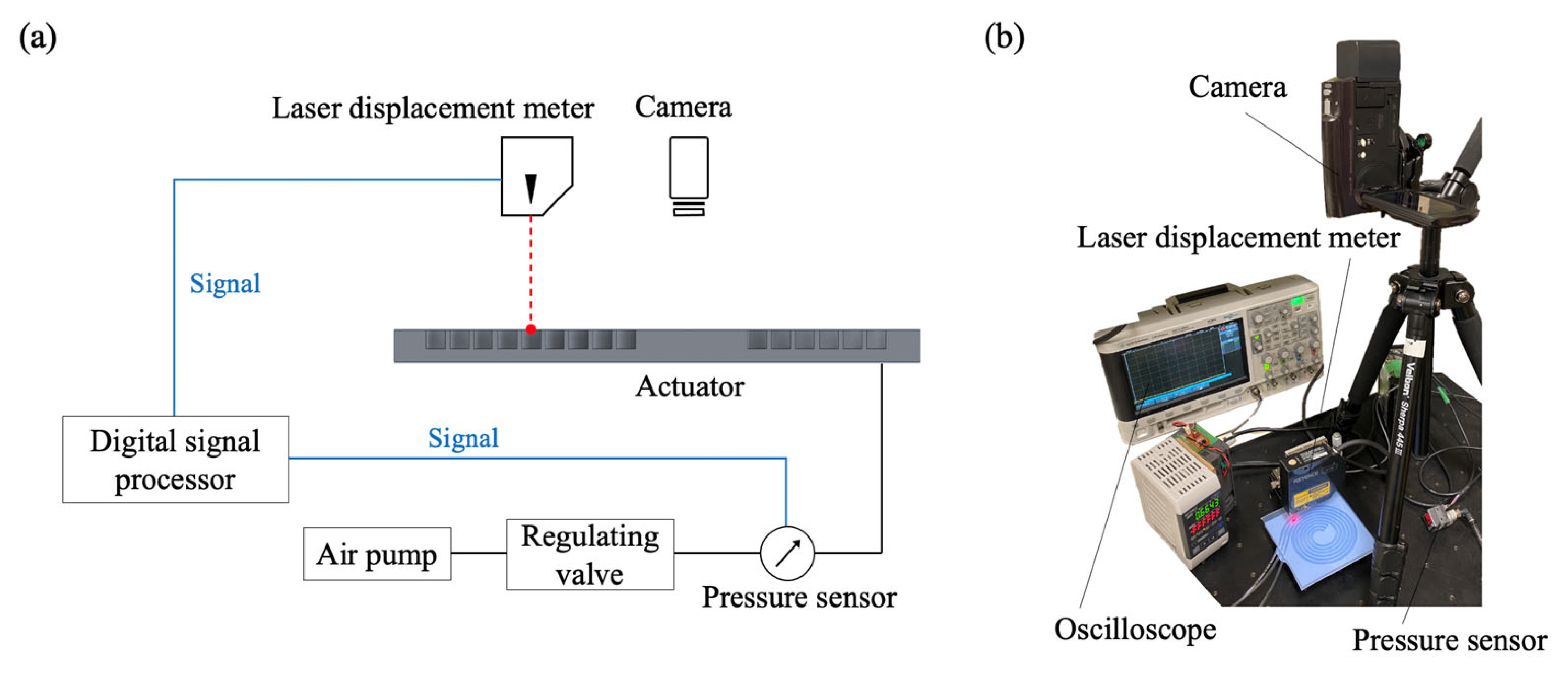
4.1. Experimental Apparatus and Method
4.2. Experimental Validation
4.3. Transportation Experiments
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Nurzaman, S.G.; Iida, F.; Margheri, L.; Laschi, C. Soft robotics on the move: Scientific networks, activities, and future challenges. Soft Robot. 2014, 1, 154–158. [Google Scholar] [CrossRef]
- Suzumori, K.; Asaad, S. A Novel Pneumatic Rubber Actuator for Mobile Robot Bases. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS ‘96), Osaka, Japan, 8 November 1996; pp. 1001–1006. [Google Scholar] [CrossRef]
- Jung, K.; Koo, J.C.; Nam, J.; Lee, Y.K.; Choi, H.Y. Artificial annelid robot driven by soft actuators. Bioinspiration Biomim. 2007, 2, S42. [Google Scholar] [CrossRef] [PubMed]
- Lotz, P.; Matysek, M.; Schlaak, H.F. Peristaltic pump made of dielectric elastomer actuators. In Proceedings of the SPIE Smart Structures and Materials + Nondestructive Evaluation and Health Monitoring, San Diego, CA, USA, 6 April 2009; p. 72872D. [Google Scholar] [CrossRef]
- Xu, L.; Chen, H.-Q.; Zou, J.; Dong, W.-T.; Gu, G.-Y.; Zhu, L.-M.; Zhu, X.-Y. Bio-inspired annelid robot: A dielectric elastomer actuated soft robot. Bioinspiration Biomim. 2017, 12, 025003. [Google Scholar] [CrossRef] [PubMed]
- Suleman, A.; Burns, S.; Waechter, D. Design and modeling of an electrostrictive inchworm actuator. Mechatronics 2004, 14, 567–586. [Google Scholar] [CrossRef]
- Poole, A.D.; Booker, J.D.; Wishart, C.L.; McNeill, N.; Mellor, P.H. Performance of a Prototype Traveling-wave Actuator Made from a Dielectric Elastomer. IEEE/ASME Trans. Mechatron. 2012, 17, 525–533. [Google Scholar] [CrossRef]
- Qi, X.; Shi, H.; Pinto, T.; Tan, X. A Novel Pneumatic Soft Snake Robot Using Traveling-wave Locomotion in Constrained Environments. IEEE Robot. Autom. Lett. 2020, 5, 1610–1617. [Google Scholar] [CrossRef]
- Jang, Y.; Nabae, H.; Endo, G.; Suzumori, K. Analysis of the multi-balloon dielectric elastomer actuator for traveling wave motion. Sens. Actuators A Phys. 2022, 333, 113243. [Google Scholar] [CrossRef]
- Suzumori, K. Pneumatic Rubber Actuator Driven by Elastic Traveling Waves. JSME Int. J. C-Mech. Syst. Mach. Elem. Manuf. 1999, 42, 398–403. [Google Scholar] [CrossRef]
- Miyaki, Y.; Tsukagoshi, H. Self-Excited Vibration Valve That Induces Traveling Waves in Pneumatic Soft Mobile Robots. IEEE Robot. Autom. Lett. 2020, 3, 4133–4139. [Google Scholar] [CrossRef]
- Connolly, F.; Polygerinos, P.; Walsh, C.J.; Bertoldi, K. Mechanical Programming of Soft Actuators by Varying Fiber Angle. Soft Robot. 2015, 2, 26–32. [Google Scholar] [CrossRef]
- Smith, M.; Cacucciolo, V.; Shea, H. Fiber pumps for wearable fluidic systems. Science 2023, 379, 1327–1332. [Google Scholar] [CrossRef] [PubMed]
- Ran, L.; Zhou, W.; He, J.; Zhan, L.; Chen, Q.; Yu, H.; Peng, B. A novel three-dimensional contact model of piezoelectric traveling wave ultrasonic micromotor. Smart Mater. Struct. 2020, 29, 075016. [Google Scholar] [CrossRef]
- Bieze, T.M.; Largilliere, F.; Kruszewski, A.; Zhang, Z.; Merzouki, R.; Duriez, C. Finite element methods-based kinematics and closed-loop control of soft, continuum manipulators. Soft Robot. 2018, 5, 348–364. [Google Scholar] [CrossRef] [PubMed]
- Sun, Y.; Zhang, D.; Liu, Y.; Lueth, T.C. FEM-Based Mechanics Modeling of Bio-Inspired Compliant Mechanisms for Medical Applications. IEEE Trans. Med. Robot. Bionics 2020, 2, 364–373. [Google Scholar] [CrossRef]
- Webster, R.J., III; Jones, B.A. Design and kinematic modeling of constant curvature continuum robots: A review. Int. J. Robot. Res. 2010, 29, 1661–1683. [Google Scholar] [CrossRef]
- Huang, S.; Meng, D.; She, Y.; Wang, X.; Liang, B.; Yuan, B. Statics of continuum space manipulators with nonconstant curvature via pseudorigid-body 3R model. IEEE Access 2018, 6, 70854–70865. [Google Scholar] [CrossRef]
- Holland, H.C. The Archimedes Spiral. Nature 1957, 179, 432–433. [Google Scholar] [CrossRef]
- Henke, E.-F.M.; Wilson, K.E.; Anderson, I.A. Entirely soft dielectric elastomer robots. In Proceedings of the SPIE Smart Structures and Materials + Nondestructive Evaluation and Health Monitoring (EAPAD), Portland, OR, USA, 25–29 March 2017; p. 101631N. [Google Scholar] [CrossRef]
- Holzapfel, G.A. Nonlinear Solid Mechanics: A Continuum Approach for Engineering; Wiley: Chichester, UK, 2010; ISBN 978-0-471-82319-3. [Google Scholar]

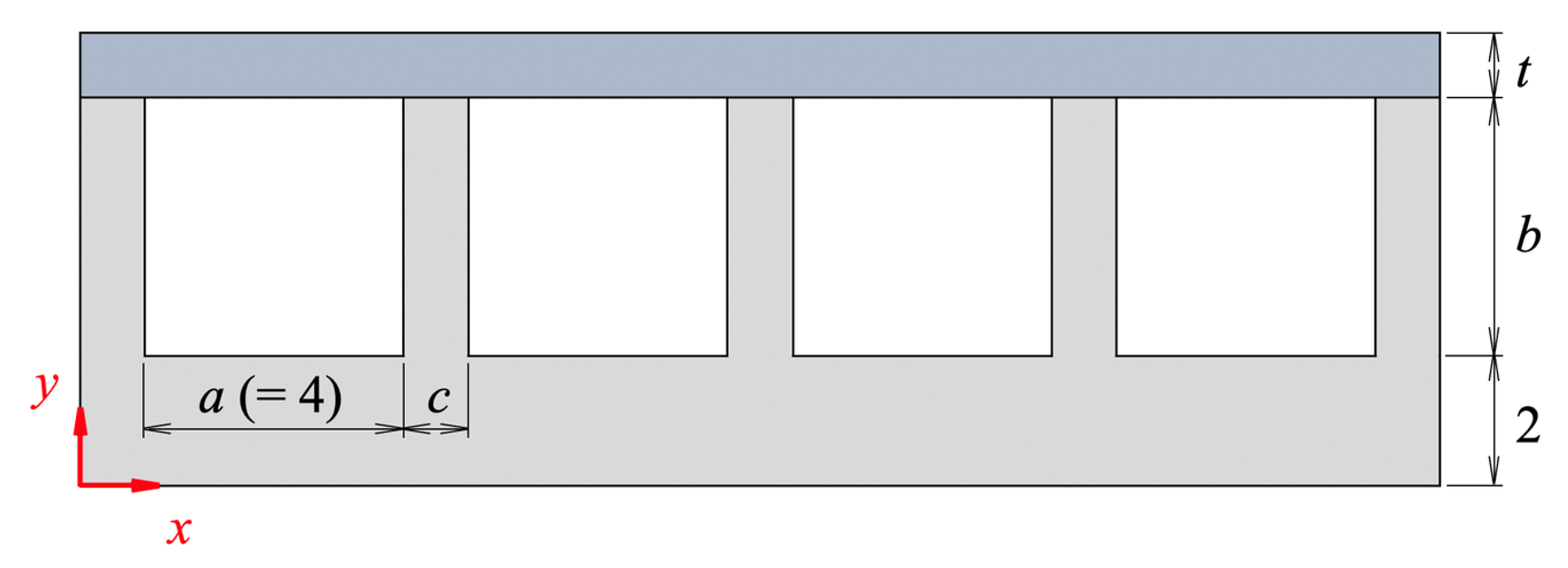




| Parameter | Value (mm) |
|---|---|
| Air chamber width, a | 4.0 |
| Membrane thickness, t | 0.5–2.0 |
| Air chamber depth, b | 1.0–5.0 |
| Wall thickness, c | 0.5–2.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jang, Y.; Nabae, H.; Suzumori, K. Evaluation of Spiral Pneumatic Rubber Actuator Using Finite Element Analysis for Radial Transportation. Actuators 2023, 12, 205. https://doi.org/10.3390/act12050205
Jang Y, Nabae H, Suzumori K. Evaluation of Spiral Pneumatic Rubber Actuator Using Finite Element Analysis for Radial Transportation. Actuators. 2023; 12(5):205. https://doi.org/10.3390/act12050205
Chicago/Turabian StyleJang, Yujin, Hiroyuki Nabae, and Koichi Suzumori. 2023. "Evaluation of Spiral Pneumatic Rubber Actuator Using Finite Element Analysis for Radial Transportation" Actuators 12, no. 5: 205. https://doi.org/10.3390/act12050205
APA StyleJang, Y., Nabae, H., & Suzumori, K. (2023). Evaluation of Spiral Pneumatic Rubber Actuator Using Finite Element Analysis for Radial Transportation. Actuators, 12(5), 205. https://doi.org/10.3390/act12050205








