Multi-Objective Optimal Design of μ–Controller for Active Magnetic Bearing in High-Speed Motor

Abstract

In this paper, a control strategy based on the inverse system decoupling method and μ-synthesis is proposed to control vibration in a rigid rotor system with active magnetic bearings that are built into high-speed motors. First, the decoupling method is used to decouple the four-degrees-of-freedom state equation of the electromagnetic bearing rigid rotor system; the strongly coupled and nonlinear rotor system is thus decoupled into four independent subsystems, and the eigenvalues of the subsystems are then configured. The uncertain parametric perturbation method is used to model the subsystem, and the multi-objective ant colony algorithm is then used to optimize the sensitivity function and the pole positions to obtain the optimal μ-controller. The closed-loop system thus has the fastest possible response, the strongest internal stability, and the best disturbance rejection capability. Then, the unbalanced force compensation algorithm is used to compensate for the high-frequency eccentric vibration; this algorithm can attenuate the unbalanced eccentric vibration of the rotor to the greatest extent and improve the robust stability of the rotor system. Finally, simulations and experiments show that the proposed control strategy can allow the rotor to be suspended stably and suppress its low-frequency and high-frequency vibrations effectively, providing excellent internal and external stability.

1. Introduction

High-speed motors have advantages that include high efficiency, low volume, and high power density, and they can be connected directly to high-speed mechanical equipment without an additional gearbox, which improves efficiency and reduces the overall size of the machine. These motors are thus widely used in turbo boosters, air compressors, grinders, and flywheel energy storage devices [1].

An active magnetic bearing (AMB) has notable features such as an absence of mechanical friction, zero lubrication, a long service life, and controllable dynamic behavior, compared with traditional mechanical bearings. Therefore, an AMB has an irreplaceable position in the application of high-speed rotor systems and has become the most important rotor support unit for high-speed rotating machinery [2].

Because the air gap between the AMB stator and the rotor is very small, the controller of the AMB rotor system must be stable enough to withstand vibrations and maintain system operation. Therefore, when designing this controller, it is necessary not only to meet the basic requirement of providing a stable rotor system, but also to optimize the controller as much as possible to achieve high dynamic performance for the rotor system. The design of this controller thus becomes a key step in AMB engineering design practice.

However, the high-speed motor rotor system is still a strongly coupled system. As the system’s rotational speed increases, the gyroscopic torque that is coupled between the system’s four degrees of freedom (4-DOF) will not only destroy the applied control action, but may even affect the overall stability of the AMB rotor system [3]. Gong [4] used a polarity switch tracking filter and a disturbance observer to achieve the active control of a magnetically levitated rotor system over its full rotational speed range; however, the core of this method was still based on use of a proportional–integral–derivative (PID) controller, which has low robustness and stability, and coupling still occurred between the degrees of freedom of the rotor system, meaning that the closed-loop system could not achieve accurate decoupling control in the higher speed range. Therefore, to realize high-precision control at higher speeds, more sophisticated control strategies must be developed. Zhao [5] used the feedforward decoupling method and a time-optimal tracking differentiator to realize decoupling of the rotor system at the cost of a minimum calculation amount, but this method will cause the decoupling subsystem to be not entirely symmetrical, and this is not conducive to controller design for high-precision control. Chen [6] used a combined strategy involving the feedback decoupling method and a 2-DOF PID controller to realize radial displacement control in the higher speed range. This method can also realize complete decoupling of the rotor system, but the 2-DOF PID controller shows a weakly robust performance, and it cannot overcome relatively strong external disturbance forces.

At present, PID controllers are widely used in AMB rotor systems to provide a mature control algorithm. Usually, a PID controller can allow the rotor to run stably at certain speeds, but when the plant parameters change or when the disturbance factors are uncertain, it is difficult to obtain good control performance, and the system may even become unstable. To solve the problems described above, Zhang [7] designed an H_∞ robust controller that showed a strong ability to suppress external disturbances and effectively attenuated a fluid surge disturbance force acting on the impeller of a centrifugal compressor. However, this method cannot measure and stabilize uncertain parametric perturbations of the control system itself. Kuseyri [8] modeled the rotor’s eccentric unbalanced disturbance force and the uncertain parametric perturbation structure of the AMB system and then synthesized an H_∞ controller using a linear matrix inequality (LMI) method, which achieved exciting experimental results. This method suppressed more than 95% of the unbalanced disturbance vibrations, but it is essentially an empirical selection method without the multi-objective optimization process. As a rising star of the robust control family, the μ-controller provides an effective way to solve these problems. The μ-controller can model an uncertain parametric perturbation structure when it is synthesized, and the μ-analysis can even measure the stability margin for the uncertain parametric perturbation system to ensure that the entire closed-loop system remains stable with respect to the bounded parametric perturbation. At the same time, because of the fast response time of the μ-controller, the adjustment time required after multi-objective optimization can be less than 10 ms, and the controller also has a strong ability to suppress disturbances. When the rotor is disturbed by an external force, the controller will then generate a compensation force to offset the disturbance, and the bounded disturbance will be attenuated completely to zero within 10 ms. Therefore, the μ-controller performs particularly rigidly during the experiments, and regardless of the disturbance or even after a collision with the rotor from the exterior, the rotor remains perfectly centered. In contrast, the suspension force of the PID-controlled AMB has a “soft” characteristic, and the anti-interference performance of the rotor system is weak. Because the “P” parameter that represents rigidity in PID control cannot be increased without limit, too large a value of “P” will lead to system instability.

In this paper, the major contributions are as follows:

(1)

An inverse system decoupling method is used to decompose the radial 4-DOF state equation of the nonlinear AMB-rigid rotor system into four double-integrator subsystems to eliminate the gyroscopic effects that are coupled at high speeds. Pole reconfiguration of the subsystem is performed to overcome the limitations of the μ-synthesis DK iteration method. The subsystem is modeled using an uncertain parametric perturbation method, and the μ-controller is synthesized via a 6-DK iterative method. Then, a closed-loop robust system is designed that is not overly conservative at the expense of its performance.

(2)

To avoid the frequent use of trial-and-error to find a suitable weighting function, this paper introduces a multi-objective ant colony algorithm to search automatically for the optimal sensitivity function and pole position. The controller obtained using this method thus has the fastest response speed possible, the highest stability margin, and the strongest external disturbance attenuation.

(3)

To eliminate the unbalanced eccentric disturbance force that occurs during high-speed operation, this paper also proposes an unbalanced compensation module that is added to the current channels of the AMBs. This module searches for the eccentric position in four directions with high efficiency and can completely compensate for the unbalanced eccentric vibration.

2. Dynamic Model of Rotor System

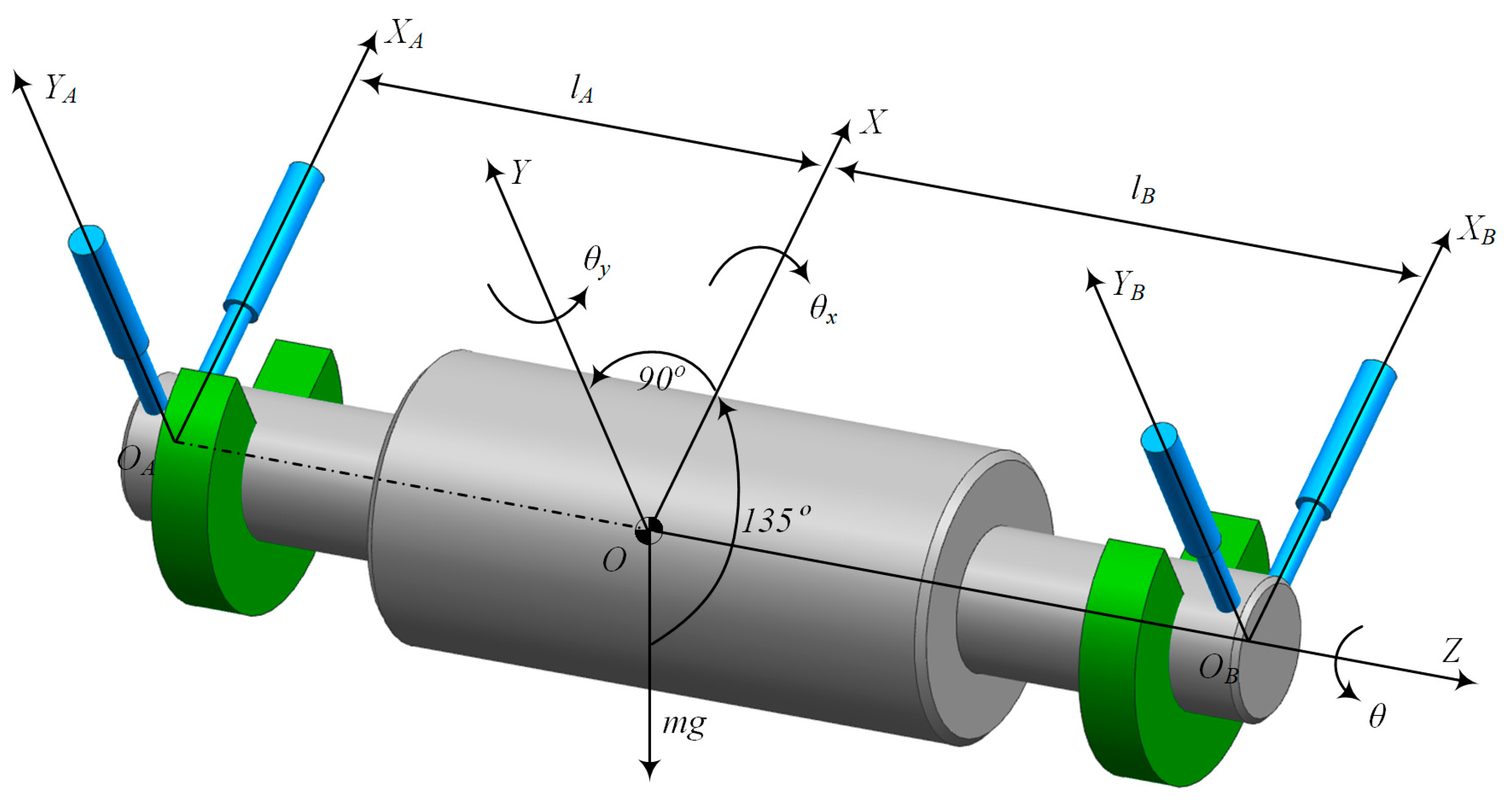
As shown in Figure 1, the magnetically levitated high-speed motor studied in this paper is a horizontal structure. The rotor is supported by two AMBs (AMB-A and AMB-B). The rotor’s radial positions are measured using a total of four eddy current displacement sensors on the left and right.

The dynamic model of the high-speed motor rotor system is depicted in Figure 2. In order to analyze it rigorously, some assumptions are set: due to the rotor’s first-order bending speed being much higher than its rated speed, the AMB rotor can be regarded as a rigid rotor; the left and right AMBs are installed at the same axial positions as the corresponding sensors; the magnetic coupling interaction between the radial and axial coordinates is ignored. The origin O is the geometric center of the rotor, and the right-handed spiral stator coordinate system O-XYZ is established. The Z axis is on the line connecting the two radial AMB geometric centers O_A and O_B. In addition, the radial plane AMB stator coordinate systems O_AX_AY_A and O_BX_BY_B are established to describe the operating state of the rotor at the positions where AMBs are located. The distances from the left and right radial AMB planes to the origin point are l_A and l_B, respectively.

During operation, the rotor’s spatial position is described using the translational displacements x and y of the mass center O along the X- and Y-axes and the rotation angles θ_x and θ_y around the X- and Y-axes. The positive directions for θ_x and θ_y are shown in Figure 2.

Based on the rotor dynamics, the equation for the radial 4-DOF horizontal AMB-rigid rotor system can be given as:

$$M\ddot{Z}+G\dot{Z}=LF+f_u$$

(1)

where Z = [θ_y x θ_x y]^T, and M and G are the mass matrix and the gyroscopic effect matrix of the rotor, respectively. L and F are the arm coefficient matrix of the rotor and the electromagnetic force vector, respectively, and f_u is the unbalanced eccentric force vector; these parameters are:

$$M=\left[\begin{array}{cccc}J& 0& 0& 0\\ 0& m& 0& 0\\ 0& 0& J& 0\\ 0& 0& 0& m\end{array}\right],G=\left[\begin{array}{cccc}0& 0& -J_z\omega & 0\\ 0& 0& 0& 0\\ J_z\omega & 0& 0& 0\\ 0& 0& 0& 0\end{array}\right],F=\left[\begin{array}{c}{f}_{xA}\\ f_{xB}\\ f_{yA}\\ f_{yB}\end{array}\right],L=\left[\begin{array}{cccc}{l}_A& -l_B& 0& 0\\ 1& 1& 0& 0\\ 0& 0& -l_A& l_B\\ 0& 0& 1& 1\end{array}\right],f_u=\left[\begin{array}{c}m{u}_z\epsilon ({\omega }^2\cos \theta +\dot{\omega }\sin \theta )\\ m\epsilon ({\omega }^2\cos \theta +\dot{\omega }\sin \theta )-\frac{\sqrt{2}}{2}mg\\ m{u}_z\epsilon (\dot{\omega }\cos \theta -{\omega }^2\sin \theta )\\ m\epsilon ({\omega }^2\sin \theta -\dot{\omega }\cos \theta )-\frac{\sqrt{2}}{2}mg\end{array}\right]$$

where m is the rotor mass; J is the transverse inertia moment of the rotor; J_z is the polar inertia moment of the rotor; f_xA, f_xB, f_yA, and f_yB are the electromagnetic forces generated by the radial AMB-A and AMB-B in the x and y directions, respectively; θ is the rotation angle; θ = ωt + φ, where ω is the angular velocity; φ is the initial angle; g is the acceleration due to gravity; ε is the projection of the distance between the mass center and the geometric center on the OXY surface; and u_z is the projection of the distance between the mass center and the geometric center on the OZ axis.

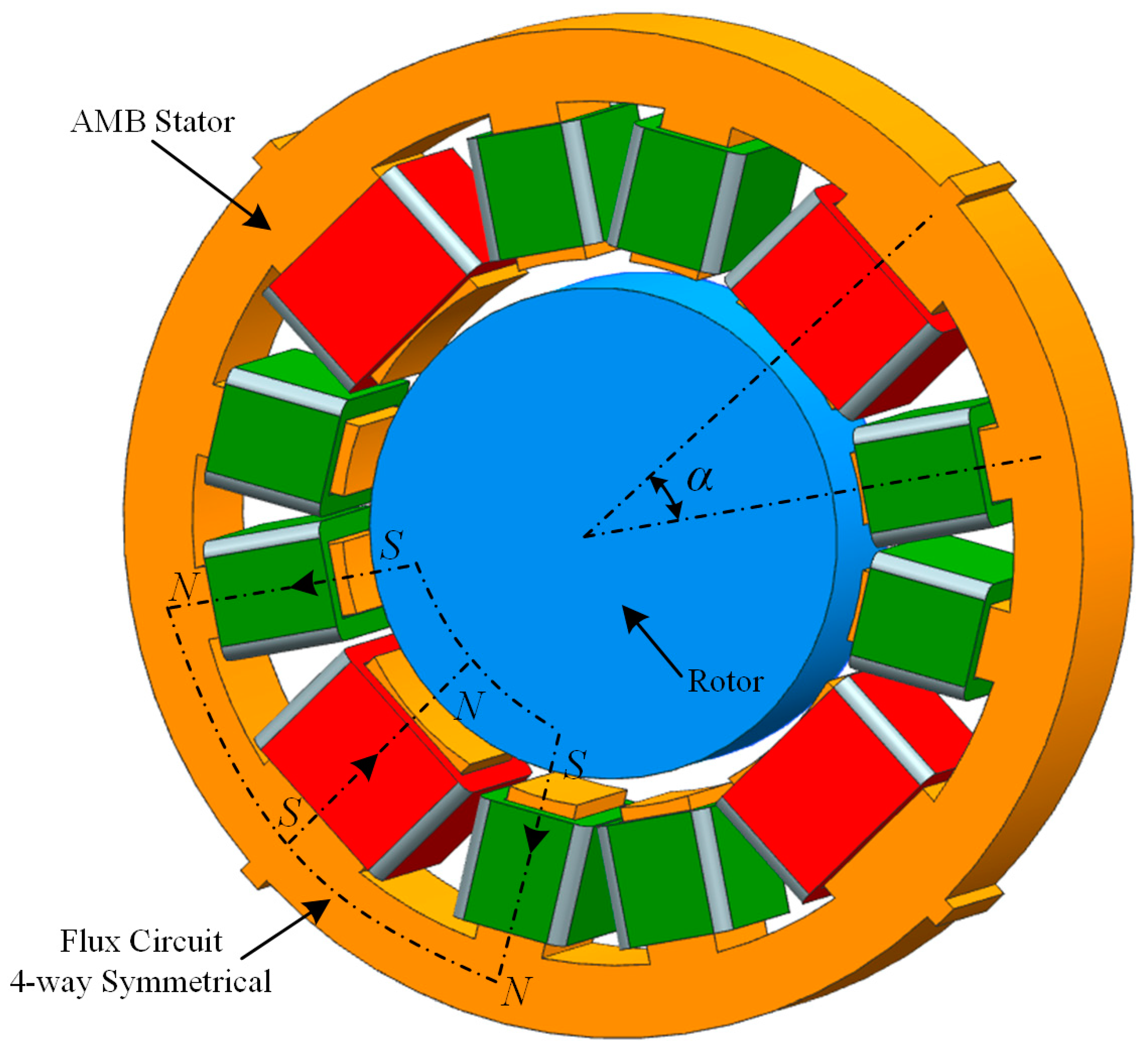
As shown in Figure 3, the AMB stator uses a novel 12-pole coil structure. When compared with the traditional eight-pole coil structure, its magnetic force distribution is more uniform, thus producing less electromagnetic noise and vibration, and the maximum magnetic levitation capacity is improved significantly.

There are a total of four magnetic poles built into the 12-pole AMB stator, where each magnetic pole includes a main pole yoke and two secondary pole yokes, and the opposing pairs of magnetic poles constitute a radial channel. In theory, the four radial channels are independent of each other; the electromagnetic force for each channel is generated by a differential current, and the related differential equations are

$$\{\begin{array}{c}{f}_{xA}={\mu }_{0}A{N}^2\left(\frac{{(I_0+i_{xA})}^2}{{(\delta -x_a\cos \alpha )}^2}-\frac{{(I_0-i_{xA})}^2}{{(\delta +x_a\cos \alpha )}^2}\right)\cos \alpha +{\mu }_{0}A{N}^2\left(\frac{{(I_0+i_{xA})}^2}{{(\delta -x_a)}^2}-\frac{{(I_0-i_{xA})}^2}{{(\delta +x_a)}^2}\right)\\ f_{xB}={\mu }_{0}A{N}^2\left(\frac{{(I_0+i_{xB})}^2}{{(\delta -x_b\cos \alpha )}^2}-\frac{{(I_0-i_{xB})}^2}{{(\delta +x_b\cos \alpha )}^2}\right)\cos \alpha +{\mu }_{0}A{N}^2\left(\frac{{(I_0+i_{xB})}^2}{{(\delta -x_b)}^2}-\frac{{(I_0-i_{xB})}^2}{{(\delta +x_b)}^2}\right)\\ f_{yA}={\mu }_{0}A{N}^2\left(\frac{{(I_0+i_{yA})}^2}{{(\delta -y_a\cos \alpha )}^2}-\frac{{(I_0-i_{yA})}^2}{{(\delta +y_a\cos \alpha )}^2}\right)\cos \alpha +{\mu }_{0}A{N}^2\left(\frac{{(I_0+i_{yA})}^2}{{(\delta -y_a)}^2}-\frac{{(I_0-i_{yA})}^2}{{(\delta +y_a)}^2}\right)\\ f_{yB}={\mu }_{0}A{N}^2\left(\frac{{(I_0+i_{yB})}^2}{{(\delta -y_b\cos \alpha )}^2}-\frac{{(I_0-i_{yB})}^2}{{(\delta +y_b\cos \alpha )}^2}\right)\cos \alpha +{\mu }_{0}A{N}^2\left(\frac{{(I_0+i_{yB})}^2}{{(\delta -y_b)}^2}-\frac{{(I_0-i_{yB})}^2}{{(\delta +y_b)}^2}\right)\end{array}$$

(2)

where μ₀ is the free-space permeability; A is the cross-sectional area of the secondary magnetic pole; N is the number of turns of the coil; I₀ is the bias current; δ is the AMB air gap length; and i_xA, i_xB, i_yA, and i_yB are the control currents of AMB-A and AMB-B in the x and y channels, respectively.

Let Y and U be the radial displacement vector and the control current vector of the AMBs, respectively:

$$Y={\left[\begin{array}{cccc}{x}_a& x_b& y_a& y_b\end{array}\right]}^T,U={\left[\begin{array}{cccc}{i}_{xA}& i_{xB}& i_{yA}& i_{yB}\end{array}\right]}^T$$

The relationship between Y and Z is

$$Y=L^{T}Z$$

(3)

The electromagnetic force is linearized around the operating point (I₀, i_x0, i_y0, x_a = x_b = y_a = y_b = 0) to give

$$\{\begin{array}{c}\begin{array}{l}{k}_x=4{\mu }_{0}A{N}^2\frac{I_0^2+i_{x0}^2}{{\delta }^3}(1+{\cos }^2\alpha )\\ k_y=4{\mu }_{0}A{N}^2\frac{I_0^2+i_{y0}^2}{{\delta }^3}(1+{\cos }^2\alpha )\end{array}\\ k_i=4{\mu }_{0}A{N}^2\frac{I_0}{{\delta }^2}(1+\cos \alpha )\end{array}$$

(4)

where k_x and k_y are the displacement stiffness coefficients of the x and y channels, respectively; i_x0 and i_y0 are the compensation currents of the x and y channels to cancel the gravity, respectively; and k_i is the current stiffness coefficient of the x and y channels.

The linearized electromagnetic force can then be expressed as

$$F=K_{s}Y+K_{i}U$$

(5)

where K_s and K_i are the force–displacement matrix and force–current matrix of the AMB, respectively, and are

$$K_s=\left[\begin{array}{cccc}{k}_{sxA}& 0& 0& 0\\ 0& k_{sxB}& 0& 0\\ 0& 0& k_{syA}& 0\\ 0& 0& 0& k_{syB}\end{array}\right],K_i=\left[\begin{array}{cccc}{k}_{ixA}& 0& 0& 0\\ 0& k_{ixB}& 0& 0\\ 0& 0& k_{iyA}& 0\\ 0& 0& 0& k_{iyB}\end{array}\right]$$

where k_sxA = k_sxB = k_x; k_syA = k_syB = k_y; and k_ixA = k_ixB = k_iyA = k_iyB = k_i.

3. Inverse Decoupling Method and Eigenvalue Assignment

By combining (1), (3) and (5), the following can be obtained:

$$M{(L^T)}^{-1}\ddot{Y}+G{(L^T)}^{-1}\dot{Y}=LF+f_u$$

(6)

The following can be obtained by converting from (6):

$$\ddot{Y}=-L^T{M}^{-1}G\dot{Z}+L^T{M}^{-1}LF+L^T{M}^{-1}{f}_u$$

(7)

When only considering the coupling relationship inside the system, the external disturbance f_u can be removed first; then, after the expansion of (7), it can be found that:

$$\ddot{Y}=\left[\begin{array}{l}{\ddot{Y}}_1\\ {\ddot{Y}}_2\\ {\ddot{Y}}_3\\ {\ddot{Y}}_4\end{array}\right]=\left[\begin{array}{l}\frac{l_A{J}_z\omega {\dot{\theta }}_x}{J}+(\frac{1}{m}+\frac{{l_A}^2}{J})f_{xA}+(\frac{1}{m}-\frac{l_A{l}_B}{J})f_{xB}\\ -\frac{l_B{J}_z\omega {\dot{\theta }}_x}{J}+(\frac{1}{m}+\frac{{l_B}^2}{J})f_{xB}+(\frac{1}{m}-\frac{l_A{l}_B}{J})f_{xA}\\ \frac{l_A{J}_z\omega {\dot{\theta }}_y}{J}+(\frac{1}{m}+\frac{{l_A}^2}{J})f_{yA}+(\frac{1}{m}-\frac{l_A{l}_B}{J})f_{yB}\\ -\frac{l_B{J}_z\omega {\dot{\theta }}_y}{J}+(\frac{1}{m}+\frac{{l_B}^2}{J})f_{yB}+(\frac{1}{m}-\frac{l_A{l}_B}{J})f_{yA}\end{array}\right]$$

(8)

Because F is a function of U, $\ddot{Y}$ can be written as a function of U. Then, the question is whether U can be written as a function of $\ddot{Y}$ inversely, i.e., $\ddot{Y}$ also exists if U exists. The reversibility of (8) is now derived as follows:

Let

$$D=\frac{\partial \ddot{Y}}{\partial U}=\left[\begin{array}{cccc}\frac{\partial {\ddot{Y}}_1}{\partial U_1}& \frac{\partial {\ddot{Y}}_1}{\partial U_2}& \frac{\partial {\ddot{Y}}_1}{\partial U_3}& \frac{\partial {\ddot{Y}}_1}{\partial U_4}\\ \frac{\partial {\ddot{Y}}_2}{\partial U_1}& \frac{\partial {\ddot{Y}}_2}{\partial U_2}& \frac{\partial {\ddot{Y}}_2}{\partial U_3}& \frac{\partial {\ddot{Y}}_2}{\partial U_4}\\ \frac{\partial {\ddot{Y}}_3}{\partial U_1}& \frac{\partial {\ddot{Y}}_3}{\partial U_2}& \frac{\partial {\ddot{Y}}_3}{\partial U_3}& \frac{\partial {\ddot{Y}}_3}{\partial U_4}\\ \frac{\partial {\ddot{Y}}_4}{\partial U_1}& \frac{\partial {\ddot{Y}}_4}{\partial U_2}& \frac{\partial {\ddot{Y}}_4}{\partial U_3}& \frac{\partial {\ddot{Y}}_4}{\partial U_4}\end{array}\right]=\left[\begin{array}{cccc}{k}_{ixA}(\frac{1}{m}+\frac{l_A^2}{J})& k_{ixB}(\frac{1}{m}-\frac{l_A{l}_B}{J})& 0& 0\\ k_{ixA}(\frac{1}{m}-\frac{l_A{l}_B}{J})& k_{ixB}(\frac{1}{m}+\frac{l_B^2}{J})& 0& 0\\ 0& 0& k_{iyA}(\frac{1}{m}+\frac{l_A^2}{J})& k_{iyB}(\frac{1}{m}-\frac{l_A{l}_B}{J})\\ 0& 0& k_{iyA}(\frac{1}{m}-\frac{l_A{l}_B}{J})& k_{iyB}(\frac{1}{m}+\frac{l_B^2}{J})\end{array}\right]$$

(9)

It can be concluded from the above that

$$\det (D)=\frac{k_{ixA}{k}_{ixB}{k}_{iyA}{k}_{iyB}{(l_A+l_B)}^4}{m^2{J}^2}\ne 0$$

(10)

The relative order of the system is α = (α1, α2, α3, α4) = (2, 2, 2, 2), which satisfies α1 + α2 + α3 + α4 = 8 ≤ n, where n is the number of state variables. According to inverse system theory [9], the system is invertible.

Introducing a new variable V = [V₁ V₂ V₃ V₄]^T, the new variable and the second derivative of the output variable are made to satisfy the following relationship:

$$V_1={\ddot{Y}}_1,V_2={\ddot{Y}}_2,V_3={\ddot{Y}}_3,V_4={\ddot{Y}}_4$$

(11)

Then, the transfer function from V to Y is given by

$$\frac{Y_i}{V_i}=\frac{1}{s^2},i=1,2,3,4$$

(12)

Equation (12) shows that the nonlinear and strongly coupled AMB-rigid rotor system is decoupled via the inverse decoupling method, the radial 4-DOF rotor system is decomposed into four translational radial degrees of freedom, and on each degree of freedom is a pseudo-linear subsystem with a transfer function of 1/s².

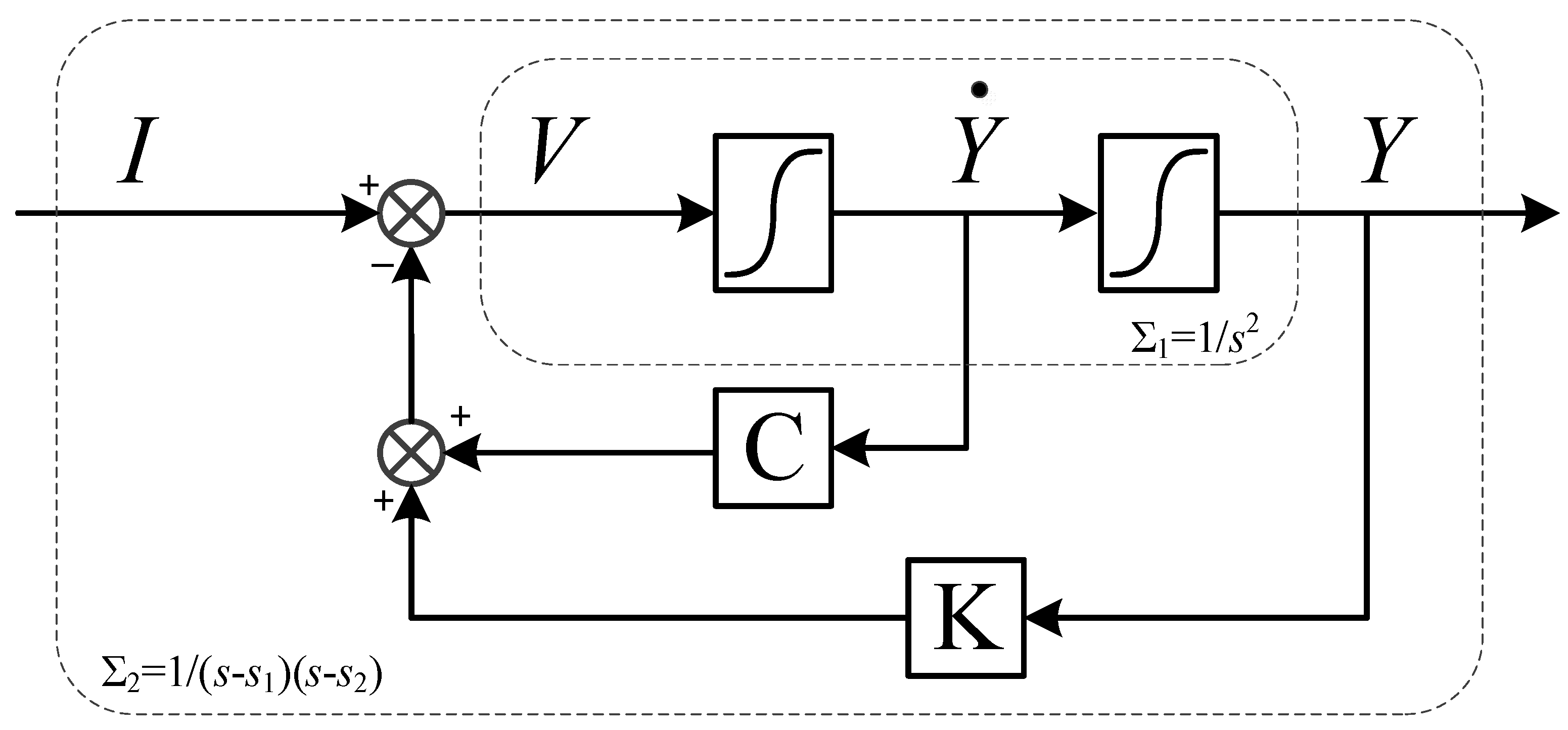
When designing the controller for the subsystem, the D-K iterations method will indicate that the μ-controller cannot be synthesized because the plant contains two zero eigenvalues located on the imaginary axis. To overcome this limitation, it is necessary to configure the subsystem poles. As shown in Figure 4, the closed-loop negative state feedback is adopted. Let the configured poles be s₁ and s₂, and the characteristic equation be D(s) = (s − s₁)(s − s₂); then, the coefficients of the state feedback are

$$c=-(s_1+s_2),k=s_1\cdot s_2$$

(13)

4. Uncertainties Model and μ-Synthesis Method

Because the motion equations of the four radial channels of the AMB-rigid rotor system when decoupled using the inverse system method are symmetrical and are independent of each other, only the subsystem structure attributed to a single channel is studied here. The designed μ-controller can be distributed symmetrically for each channel. The motion equation for one single-channel subsystem after pole configuration can be given as

$$\ddot{Y}+c\dot{Y}+kY=I$$

(14)

During actual operation, and especially during high-speed operation, the AMB-rigid rotor system has a high-amplitude sinusoidal noise signal in the output from the displacement sensors, which is attributed to the unbalanced eccentric vibration. This signal will affect the stability of the decoupled subsystem; equivalently, it can also be regarded as the main source of the uncertain parametric perturbation structure of the subsystem.

Suppose that during high-speed operation, there is an unbalanced vibration in one radial channel given by $\overline{d}(t)=\overline{r}\sin (\omega t)=p_k{\delta }_k\overline{Y}$, where $\overline{r}$ is the vibration amplitude, which is generally less than 0.05 mm over the full rotational speed range, and the radial displacement amplitude $\overline{Y}$ is less than 0.5 mm of the bearing air gap; thus, we set p_k = 10% and −1 ≤ δ_k ≤ 1. By introducing the vibration displacement $Y=\overline{Y}+\overline{d}$, we find that

$$(1+p_m{\delta }_m)\ddot{\overline{Y}}+c(1+p_c{\delta }_c)\dot{\overline{Y}}+k(1+p_k{\delta }_k)\overline{Y}=I$$

(15)

where $\overline{Y}$ is the ideal displacement variable when the vibration signal $\overline{d}$ is not considered in the total radial displacement Y, p_m = p_c = p_k = 10% and −1 ≤ δ_m, δ_c, δ_k ≤ 1.

Equation (15) can be represented by the upper linear fractional transform (LFT) with M_m, M_c, M_k, δ_m, δ_c, and δ_k, and its state equation is

$$\{\begin{array}{c}\left[\begin{array}{c}{y}_m\\ \ddot{\overline{Y}}\end{array}\right]=M_m\left[\begin{array}{c}{u}_m\\ I-v_c-v_k\end{array}\right],u_m={\delta }_m{y}_m\\ \left[\begin{array}{c}{y}_c\\ v_c\end{array}\right]=M_c\left[\begin{array}{c}{u}_c\\ \dot{\overline{Y}}\end{array}\right],u_c={\delta }_c{y}_c\\ \left[\begin{array}{c}{y}_k\\ v_k\end{array}\right]=M_k\left[\begin{array}{c}{u}_k\\ \overline{Y}\end{array}\right],u_k={\delta }_k{y}_k\end{array}$$

(16)

where $M_m=\left[\begin{array}{cc}-p_m& 1\\ -p_m& 1\end{array}\right],M_c=\left[\begin{array}{cc}0& c\\ p_c& c\end{array}\right],M_k=\left[\begin{array}{cc}0& k\\ p_k& k\end{array}\right]$

The subsystem structure with uncertainties can be described as shown in Figure 5.

From Figure 5, the state equation for the subsystem with structured uncertainty can be derived, and by eliminating variables v_c and v_k, the system matrix S, which describes the dynamic characteristics of the subsystem, is

$$\begin{array}{c}\left[\begin{array}{c}\dot{y}\\ \ddot{y}\\ y_m\\ y_c\\ y_k\\ y\end{array}\right]=\left[\begin{array}{cccccc}0& 1& 0& 0& 0& 0\\ -k& -c& -p_m& -p_c& -p_k& 1\\ -k& -c& -p_m& -p_c& -p_k& 1\\ 0& c& 0& 0& 0& 0\\ k& 0& 0& 0& 0& 0\\ 1& 0& 0& 0& 0& 0\end{array}\right]\left[\begin{array}{c}y\\ \dot{y}\\ u_m\\ u_c\\ u_k\\ I\end{array}\right],\left[\begin{array}{c}{u}_m\\ u_c\\ u_k\end{array}\right]=\left[\begin{array}{ccc}{\delta }_m& 0& 0\\ 0& {\delta }_c& 0\\ 0& 0& {\delta }_k\end{array}\right]\left[\begin{array}{c}{y}_m\\ y_c\\ y_k\end{array}\right]\\ \end{array}$$

(17)

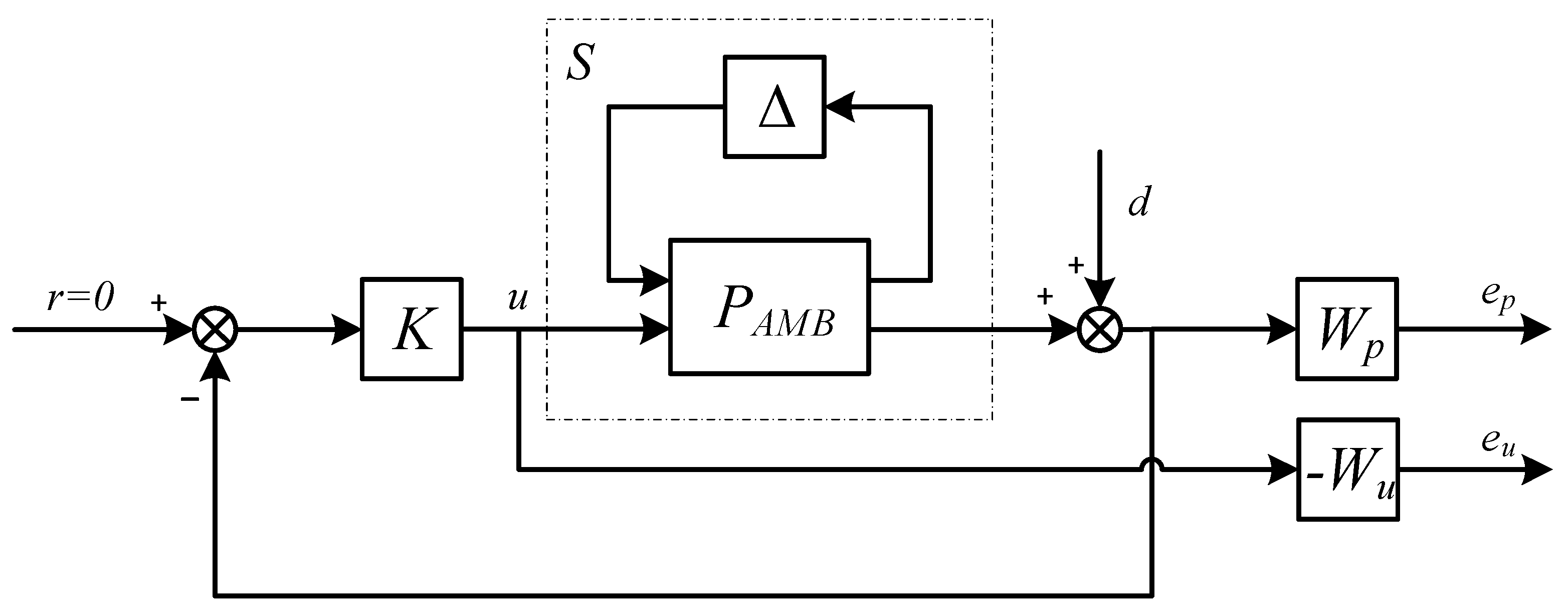
The block diagram of the closed-loop system that shows the feedback structure and includes elements reflecting the model uncertainty and performance requirements obtained at this stage is as shown in Figure 6, where P is the plant, K is the controller, and Δ is the uncertainty matrix. In addition, W_p is the performance weighting function, and W_u is the control weighting function.

The μ-synthesis method was proposed to assort systems with structured uncertainties. The uncertain behavior of the original system can be described by the LFT representation, and the controller synthesis is performed with an uncertain closed-loop system model using the structured singular value μ and the LFT framework. 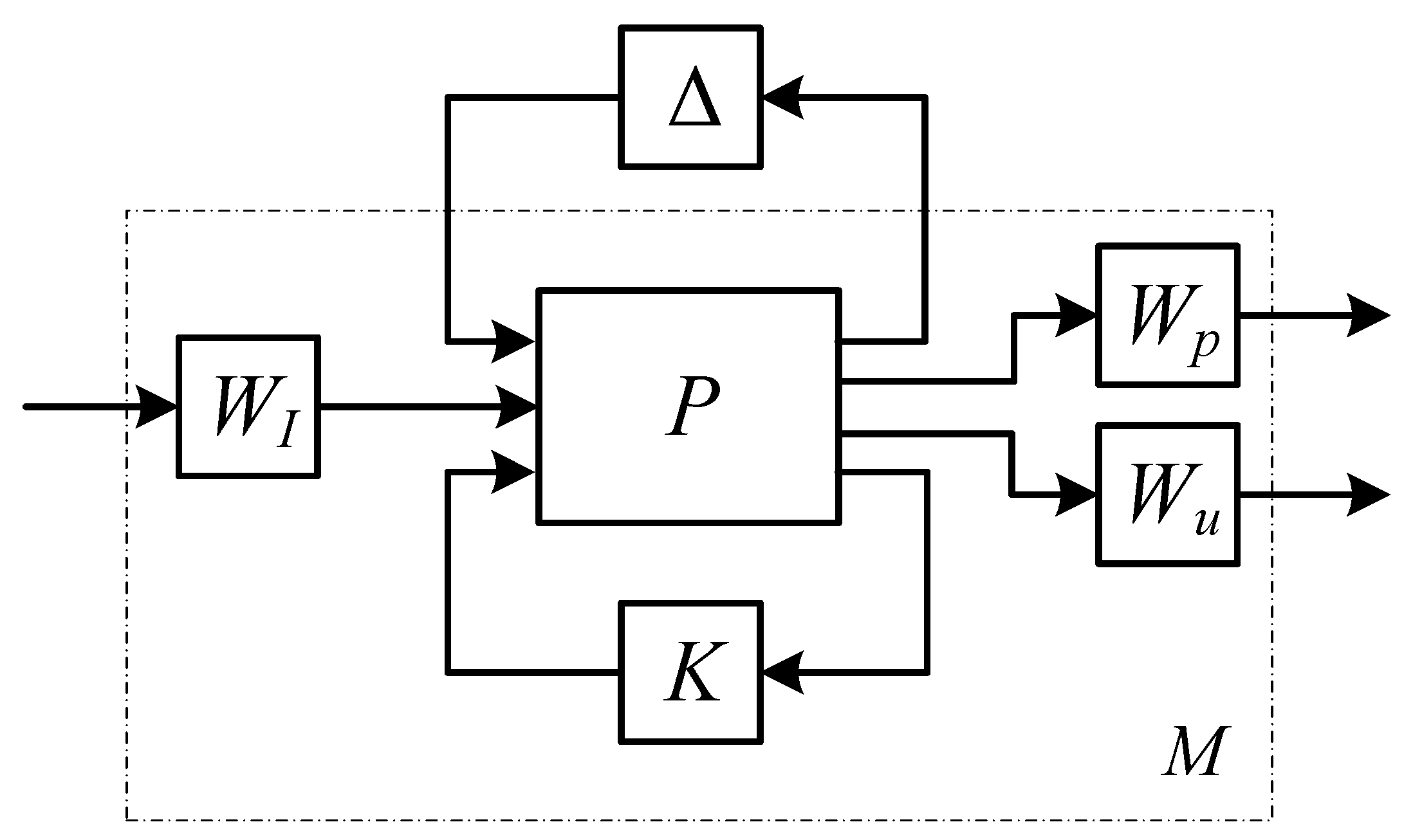As a result, a μ-control closed-loop system can be designed that is not excessively conservative at the expense of performance [10]. The diagram of the μ-control framework for the AMB-rotor system is shown in Figure 7.

The structure of the matrix Δ is the result of the locations at which each parametric uncertainty occurs in the system model. The weighting functions W_p and W_u are selected to constrain the frequency-based performance requirements in closed-loop systems. The matrix M is the lower LFT of the plant P and the controller K.

$$M=F_{\mathrm{l}}(P,K)$$

(18)

The μ-synthesis framework can be represented by the upper LFT of the weighted closed-loop system M and the uncertain perturbation matrix Δ, which maps disturbance input w to performance response z.

$$z=F_u({\rm M},\mathsf{\Delta })w$$

(19)

The defined structure Δ destabilized the system M, and the stability of the entire system can be evaluated using the maximum singular value μ.

$${\mu }_{\mathsf{\Delta }}^{-1}(M)=\underset{\mathsf{\Delta }\in \mathsf{\Delta }}{\min }\{\overline{\sigma }(\mathsf{\Delta }):\det (I-M\mathsf{\Delta })=0\}$$

(20)

If the structured singular value is less than unity, this indicates that a greater perturbation than the set uncertain perturbation is required to destabilize the system. Therefore, the closed-loop system with the synthesized controller is stable and robust with respect to the bounded uncertainties [11].

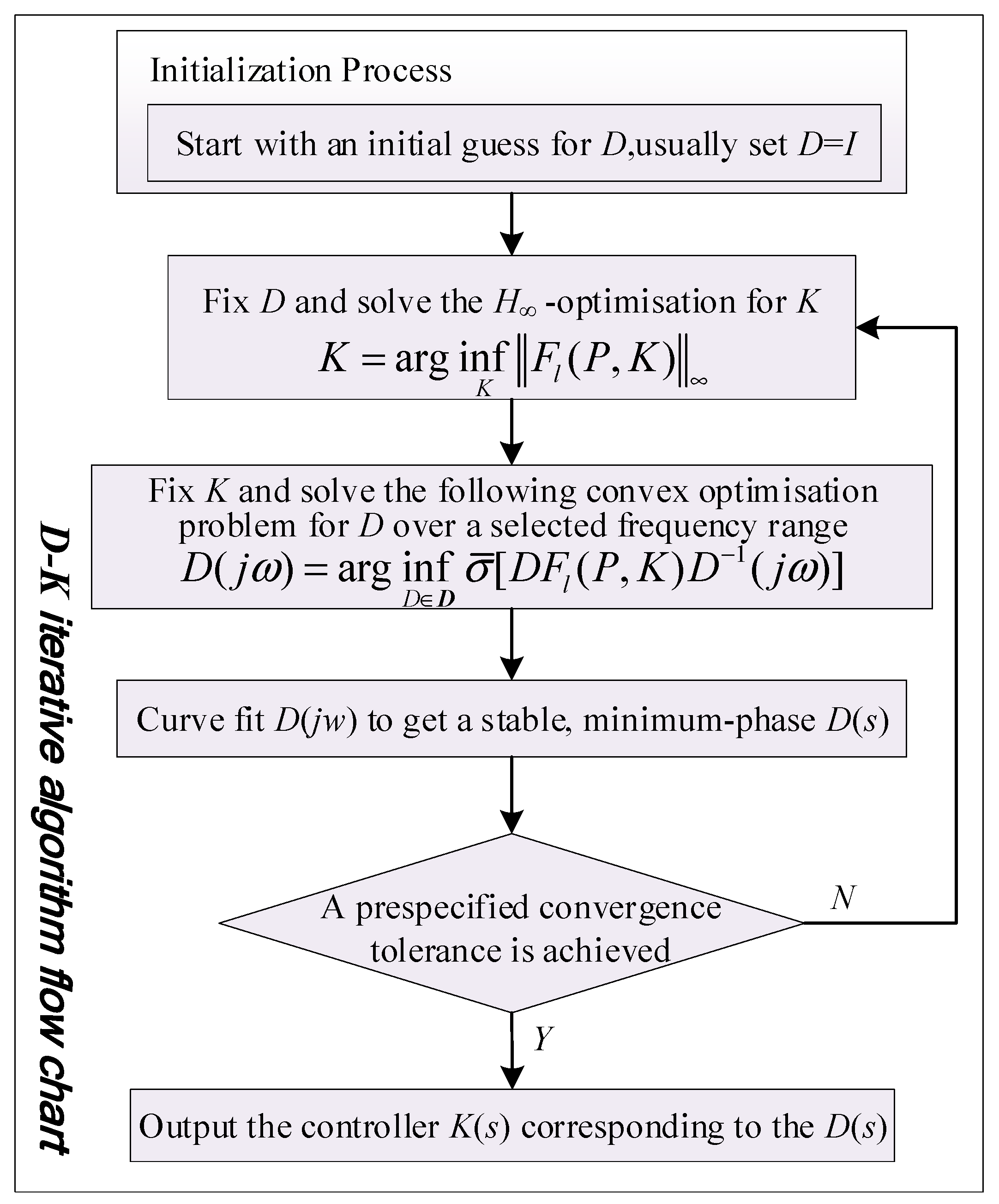
Finding appropriate weighting functions is a critical step in robust controller design and usually requires many trials. For complex systems, significant effort is thus required. Therefore, a multi-objective ant colony algorithm is introduced to search automatically for the optimal sensitivity function. The μ-controller is synthesized using the dksyn tool integrated in the MATLAB Robust Control Toolbox. In this tool, a 6-DK iterative algorithm [12] is used. The flow chart of the algorithm is shown in Figure 8.

5. Multi-Objective Optimization of μ-Controller

5.1. Multi-Objective Function

When optimizing the μ-controller, it requires the explicit definition of some targets to optimize the general performance of the controller. The response time, the tracking error, and the disturbance attenuation of the controller can be used as one objective function. The multi-objective optimization process frequently calls several objective functions simultaneously. The results of using these single objective functions are usually contradictory, hence they cannot be simply compared as being superior or inferior. Generally, the better result for one target will be the worse result for the other target, and enhancement to any objective value will deteriorate at least another objective value. One such result is called the Pareto solution [13].

The multi-objective function for μ-controller optimization used in this paper is defined as:

$$f=a\cdot (R_{\max }-R)/(R_{\max }-R_{\min })+b\cdot (S-S_{\min })/(S_{\max }-S_{\min })+c\cdot (D_{\max }-D)/(D_{\max }-D_{\min }),a+b+c=1$$

(21)

where a, b, and c are weight factors that represent the importance of the relevant objectives, and different ratios will have different effects on the controller performance. R, R_min, and R_max are the settling time of the closed-loop system to a step input and the minimum and maximum values of this settling time, respectively; S, S_min, and S_max are the stability margin of the closed-loop system and the minimum and maximum values of this stability margin, respectively. D, D_min, and D_max are the disturbance attenuation of the closed-loop system and the minimum and maximum values of this attenuation, respectively.

This function includes the step input reference response performance, the robust stability, and the robust performance of the μ-controller multiplied by their respective weighting factors. The essential feature of the ant colony algorithm is that it maximizes the evaluation value of the objective function. Equation (21) thus shows that the optimization objectives are the shortest response time, the largest stability margin, and the strongest disturbance attenuation. In addition, according to ISO standard 14839-3, the penalty constraint set for the optimization algorithm is that the maximum magnitude of the sensitivity function for the closed-loop control system should be less than 9.5 dB [14].

5.2. Variable Constraints

It can easily be determined from Figure 6 that:

$$\left[\begin{array}{c}{e}_p\\ e_u\end{array}\right]=\left[\begin{array}{c}{W}_p{(I+SK)}^{-1}\\ W_{u}K{(I+SK)}^{-1}\end{array}\right]d$$

(22)

Therefore, the design criterion for robust performance is that all transfer functions from d to e_p and e_u should be small in the sense of H_∞ for all possible uncertain transfer matrices Δ.

$${\Vert \left[\begin{array}{c}{W}_p{(I+SK)}^{-1}\\ W_{u}K{(I+SK)}^{-1}\end{array}\right]\Vert }_{\infty }<\gamma$$

(23)

The weighting functions W_p and W_u are used to reflect the relative significance of the performance requirements over the different frequency ranges. The performance weighting function W_p is selected to have a second-order form as follows:

$$W_p(s)=x_1\cdot \frac{s^2+x_{2}s+x_3}{s^2+x_{4}s+x_5}$$

(24)

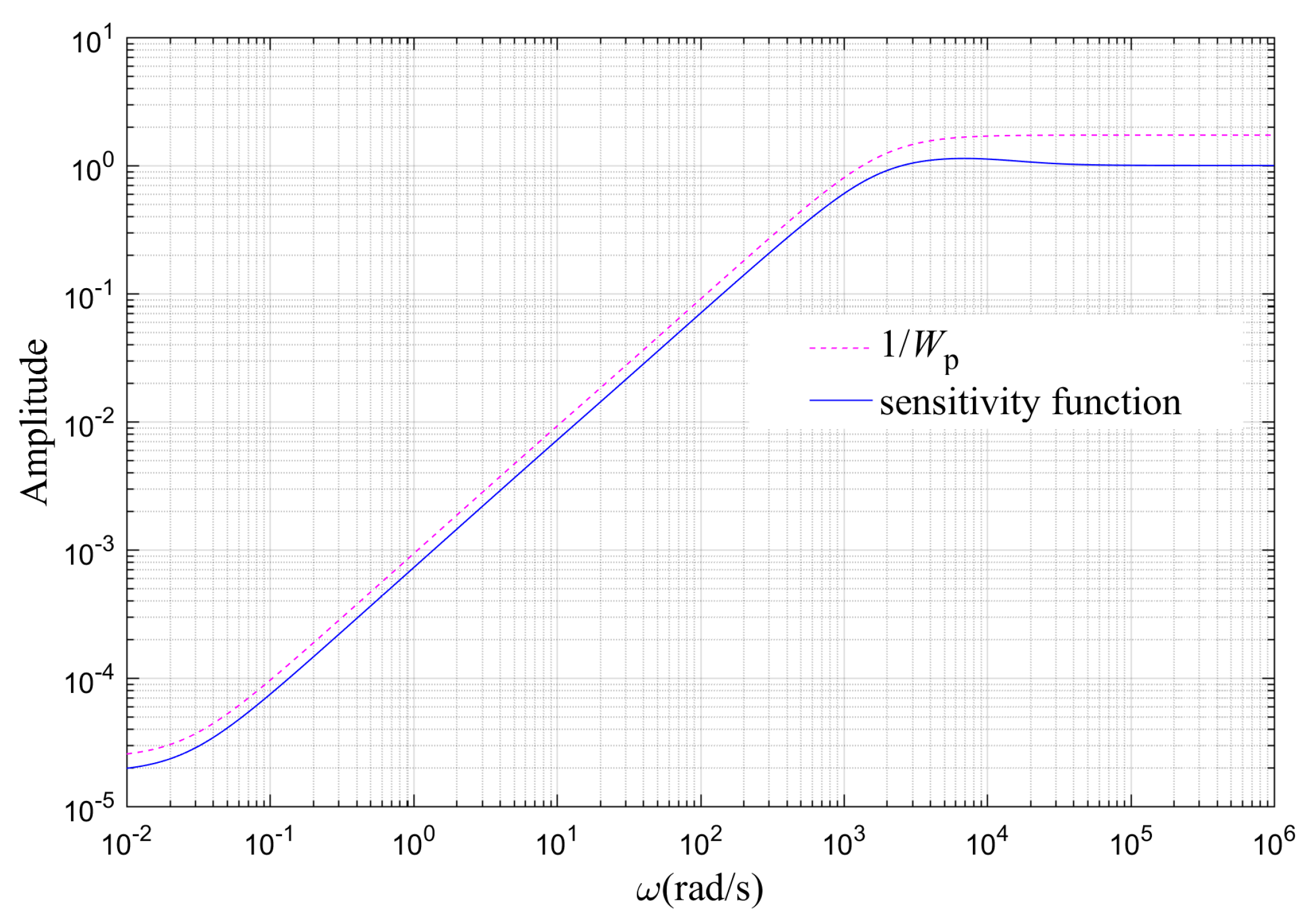
The value of x₁ shows a strong relationship with the response speed and the quality of the waveform of the closed-loop system relative to the reference input. Both x₂ and x₄ affect the turning frequency of the weighting function W_p and thus indirectly and slightly affect some of the closed-loop system performance characteristics. Equation (24) shows that in the low frequency range, the reciprocal of W_p tends toward x₅/x₃, and the designed controller sensitivity function will be below the 1/W_p curve; this means that the value of x₅/x₃ is related to the disturbance attenuation and the steady-state tracking error. Therefore, x₅/x₃ is usually set to be equal to 0.001 or less to meet the performance requirements.

The control weighting function W_u is selected simply as the scalar form:

$$W_u(s)=x_6$$

(25)

Equation (13) shows that the subsystem poles affect the damping c and the stiffness k of the controlled plant. A low level of system damping will accelerate the controller’s response. Greater system stiffness leads to a greater bearing control force and a better active control effect, but the required controller is not easy to synthesize. Therefore, it is necessary to use a multi-objective optimization algorithm to search for the best parametric combination. The multi-objective algorithm uses eight variables, as listed in

Table 1. Ant variables and bounds.

Variable	Description	Lower Bound	Upper Bound
x1	proportional term of Wp	0.01	1.0
x2	first-order term of the Wp numerator	0.5 × 103	2 × 103
x3	constant term of the Wp numerator	1.5 × 104	3 × 104
x4	first-order term of the Wp denominator	10	20
x5	constant term of the Wp denominator	0.1	0.5
x6	proportional term of Wu	1 × 10−8	12 × 10−8
x7	positive real pole	450	550
x8	negative real pole	−550	−450

, with upper and lower bounds that are selected carefully for the optimization process.

5.3. Ant Colony Algorithm and Optimization

The artificial ant colony algorithm, which simulates an ant colony’s intelligence, has features that include distributed computation, positive feedback, and heuristic searching. The ant colony algorithm has shown many good performance aspects through use of its inherent pheromone search mechanism. Its positive feedback and synergy make it suitable for use in distributed systems, and its implicit parallelism offers strong development potential. The problems that it can solve have gradually expanded to include some constrained problems and multi-objective problems [15,16,17]. When the ant colony algorithm was initially proposed, it was used for discrete domain optimization problems. Therefore, the μ-synthesis problem, which is a continuous domain optimization problem, requires the original ant colony algorithm to be modified.

In this paper, a grid scaling method is used for the continuous domain ant colony algorithm. Each grid point corresponds to a variable space state, and each ant crawls between the grid points and leaves certain amounts of pheromone information to influence the action of future generations of ants. When all ants in one generation have finished crawling, for grid points that satisfy the constraints, the objective function values are compared, the optimal individual is recorded, and the pheromone matrix is updated. Then, at the beginning of the next generation, the variable range near the grid point is scaled down by a ratio r (0.5–0.9), and the new generation of ants is placed to start crawling. By repeating the above process, until the grid spacing is below the given precision.

When each variable range is divided into N parts, there are N + 1 nodes, and n variables have (N + 1)ⁿ grid points. The calculations of these grid points can become an n-level decision process. In the decision process, the calculation of ant transition probability can use the following formula:

$$p_{ij}^k(t)=\frac{{\left[{\tau }_{ij}(t)\right]}^{\alpha }{\left[{\eta }_{ij}(t)\right]}^{\beta }}{{\displaystyle \sum _{k\subset A_k}{\left[{\tau }_{is}(t)\right]}^{\alpha }{\left[{\eta }_{is}(t)\right]}^{\beta }}},ifj\in A_k$$

(26)

where p^k_ij(t) is ant k’s transition probability from the ith to jth node, A_k is the node collection that ant k can reach, τ_ij(t) is determined using the pheromone matrix, and η_ij(t) is determined using the heuristic matrix, i.e., η_ij(t) is set as a constant (1.5).

The equation to update the pheromone matrix component is:

$${\tau }_{ij}(t+1)=(1-\rho )\cdot {\tau }_{ij}(t)+\mathsf{\Delta }{\tau }_{ij}(t)$$

(27)

where ρ is the evaporation rate, and Δτ_ij(t) is determined by the pheromone increment matrix.

The equation to update the pheromone increments is:

$$\mathsf{\Delta }{\tau }_{ij}(t)={\displaystyle \sum _{k=1}^m\mathsf{\Delta }{\tau }_{ij}^k(t)}+Q\cdot f$$

(28)

where Q is set as a constant (0.05), and f is the multiple objective function as in (21).

5.4. Optimization Solution

Figure 9 shows that the multi-objective ant colony algorithm converges fully after 16 iterations, which confirms the high efficiency of the algorithm sufficiently.

After the closed-loop system is modeled and the optimization objectives are defined, it is interesting to observe the results of optimization algorithm execution. Figure 10 depicts the individual sampling process and the iterative evolution of the three targets. It is known that the optimization objectives are the settling time of the step response of the closed-loop system, the stability margin of the uncertain perturbation structure, and the controller design index γ. The settling time can be measured directly using the stepinfo function. The stability margin is obtained via the frequency sweep method, where the starp function is used first to connect the controller to form a closed-loop system; then, the frequency sweep function, frsp, is used to obtain the frequency response of the closed-loop system; finally, the pkvnorm function is used to obtain the upper bound of the μ function of the perturbation structure, and the reciprocal of this bound is the lower bound of the stability margin. This means that at least the stability margin times of the perturbation can be tolerated to ensure that the closed-loop system is robust and stable. The frequency sweep method is conservative to an extent but can be regarded as a fast and stable evaluation method.

Smaller settling times give faster control system responses, and a larger stability margin indicates stronger system robustness to the structured uncertainty. The γ value is an important index for controller design. A larger γ value means that the controller is more difficult to synthesize. When the γ value exceeds 1, it means that a stable closed-loop controller cannot be synthesized. As the value of γ decreases, it becomes easier to design the controller, and a smaller sensitivity function amplitude for the closed-loop system indicates stronger system attenuation of external disturbances. The optimization results show clear consistency between the response speed and the stability margin, and there is also a clear contradiction between the response speed and γ or between the stability margin and γ. It is easy to understand that when the controller is faster, it is then more stable, but it is also more difficult to synthesize.

Finally, the compromise solution that was calculated after the comparison of the object values is shown in the lower left corner of Figure 10. This solution should provide a comprehensive optimal performance, and its variables and performance parameters are listed in

Table 2. Optimized ant solutions.

x1	x2	x3	x4	x5	x6	x7	x8	Settling Time	Stability Margin	γ	Object Value
0.5791	1923.5	2.607 × 104	14.076	0.3603	1.3977 × 10−8	452.151	−471.994	8.45 ms	5.1108	0.8821	0.8887

.

6. Unbalanced Eccentric Vibration Compensation Method

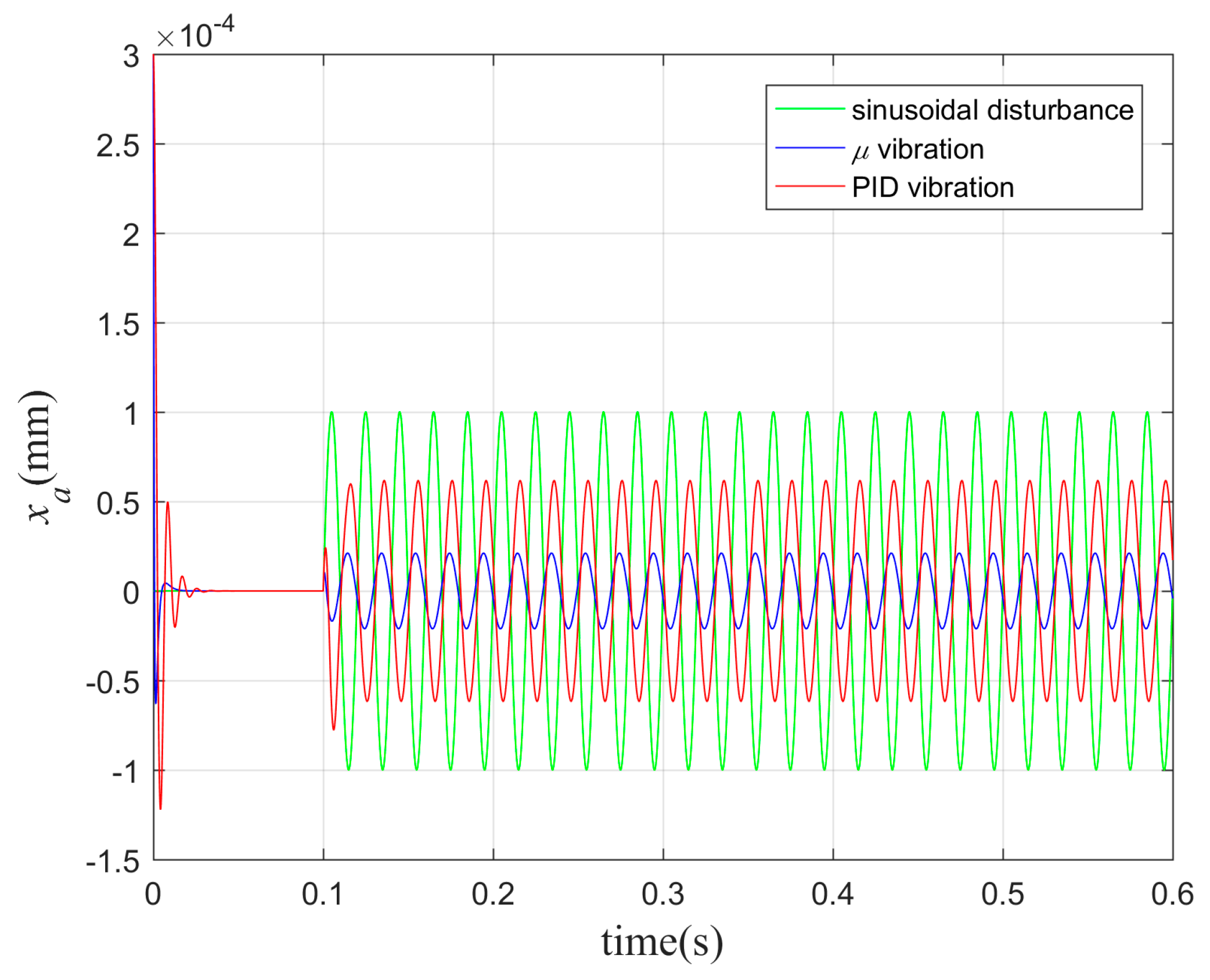
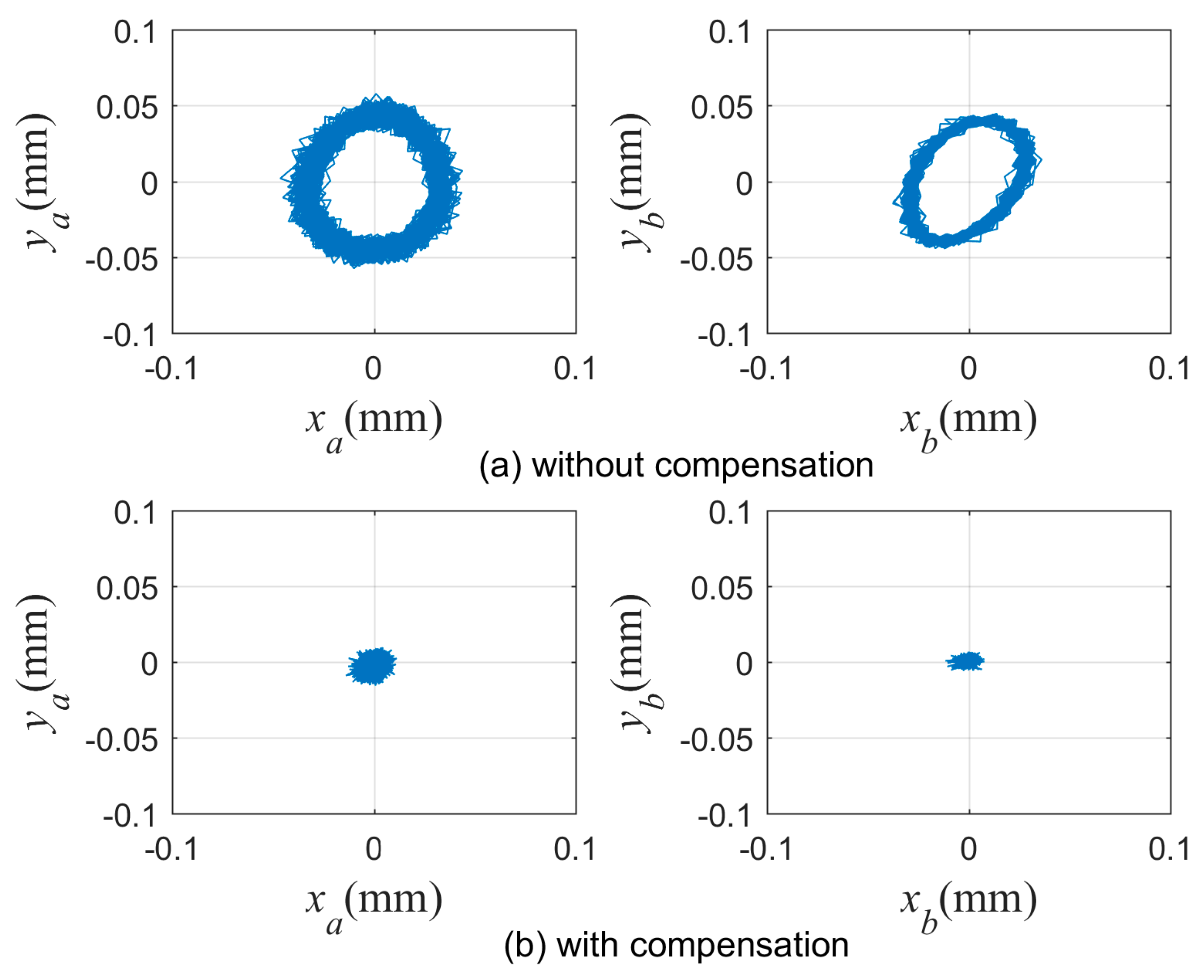
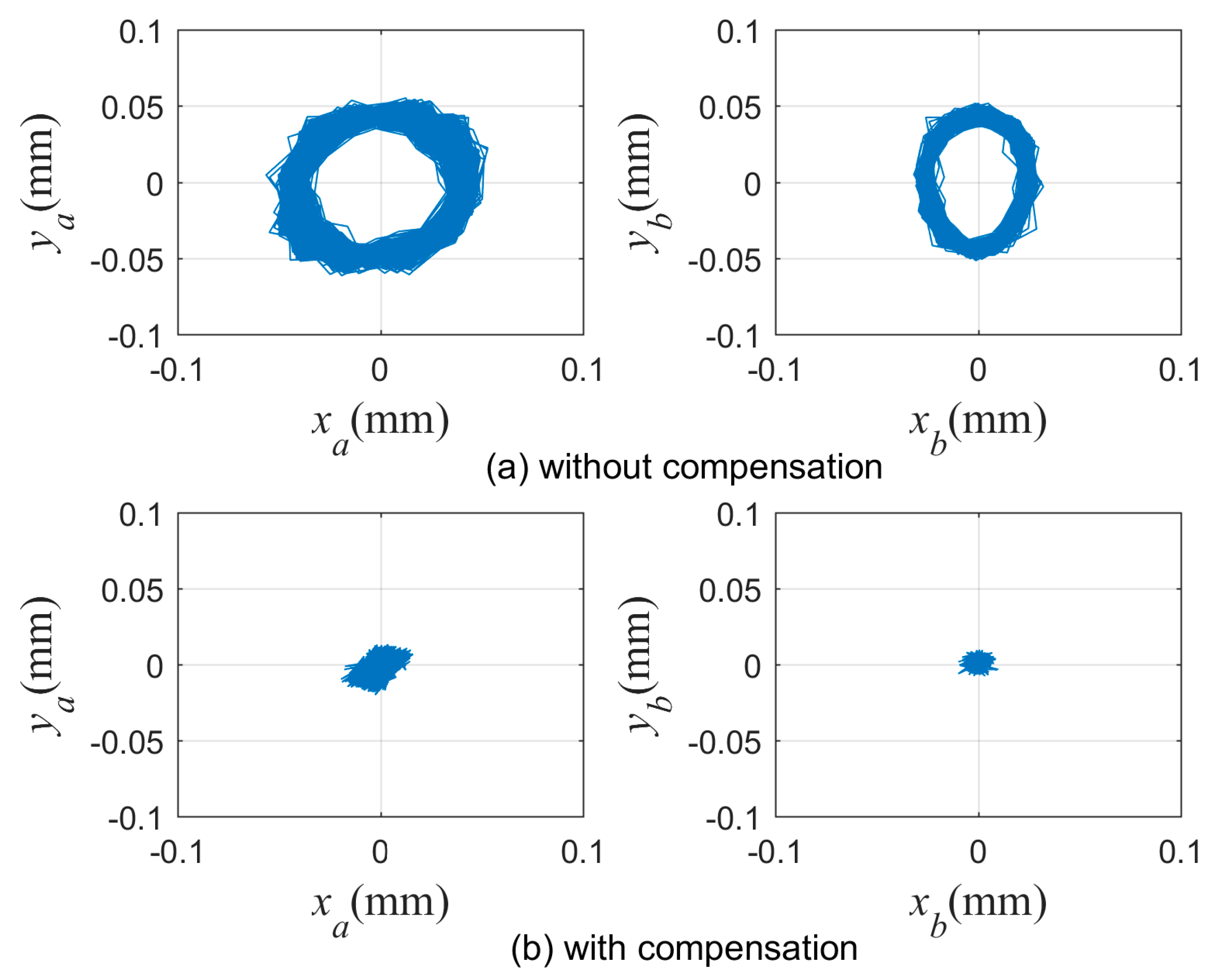
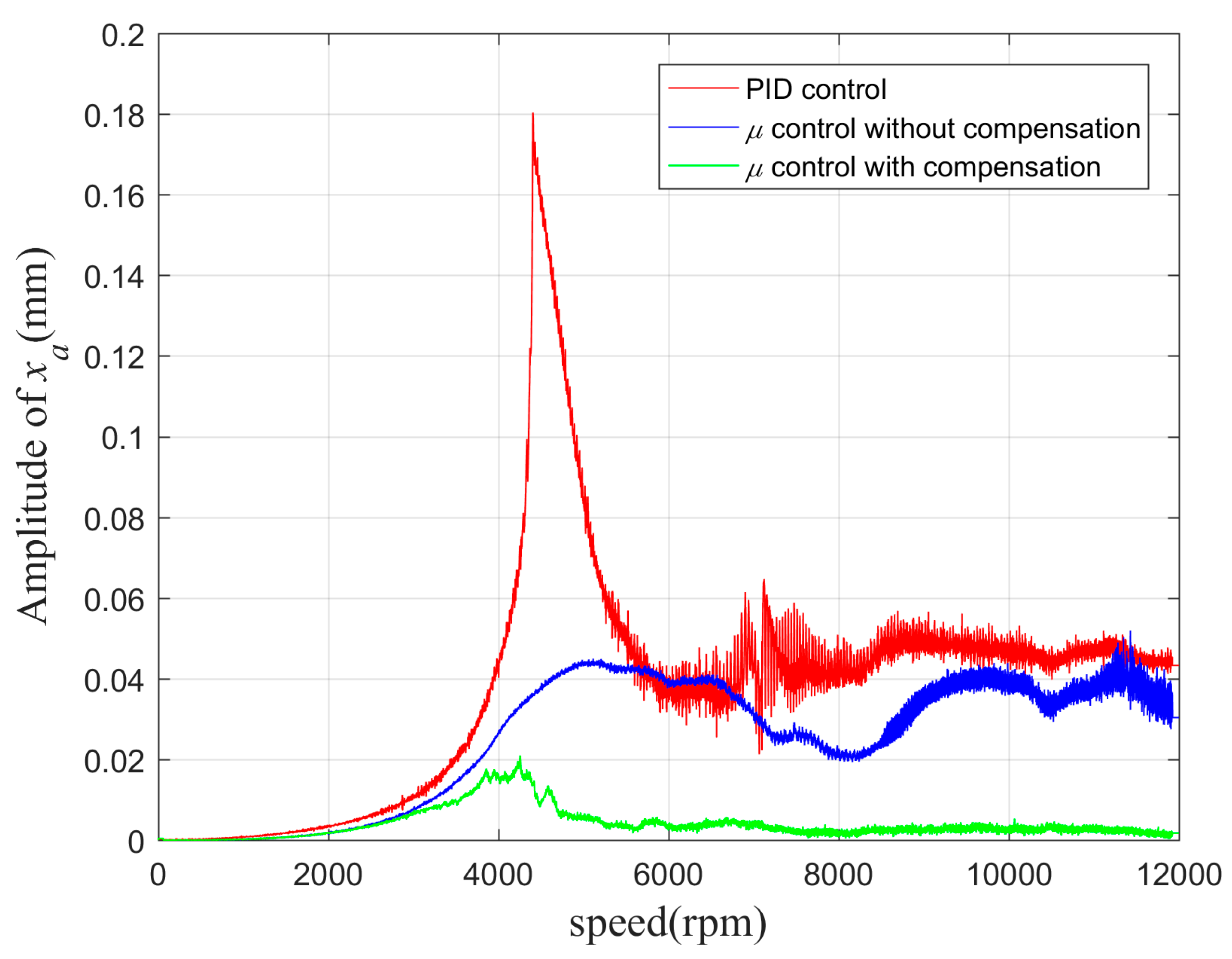
Because of machining technology limitations and assembly tolerances, the mass center of a rigid rotor is not consistent with its geometric center. During high-speed operation, unbalanced vibration will be generated by the centrifugal force. The frequency of this unbalanced vibration is the same as the rotational speed, and the excitation force is proportional to the square of the rotational speed. When the rotational speed increases, the frequency of this excitation force also increases. Figure 14 (see Section 7.1) shows that when the frequency exceeds 100 Hz (6000 rpm), the disturbance suppression force of the robust controller gradually decreases. This results in saturation of the controller’s control force, causing the rotor vibration force to increase sharply, and this seriously affects the operational stability of the high-speed motor rotor system. Therefore, it is necessary to compensate for this unbalanced force.

6.1. Principle of Unbalanced Vibration Compensation Method

The basic principle of the compensation method proposed in this paper is to extract the same frequency vibration signal from the rotor, from which a compensation signal can be generated and injected into the output channel of the controller; then, a compensation force that is equal and opposite to the rotor’s centrifugal force is generated by the AMB to compensate for the centrifugal force, and the rotor is forced to rotate around its geometric axis. The aim of this method is to minimize the rotor vibration amplitude, and it begins by identifying the position of the rotor mass center. Here, a correlation method in the signal processing technique is applied that can extract the amplitude of the fundamental frequency of the vibration signal accurately from the radial channels of the AMBs.

The displacement vibration signal of the radial AMB channel can be given as

$$f(t)=a_1\cos \omega t+b_1\sin \omega t+a_2\cos 2\omega t+b_2\sin 2\omega t+\cdots$$

(29)

when only the fundamental frequency vibration is considered, and the following can be obtained by performing a Fourier series expansion:

$$\{\begin{array}{c}{a}_1=\frac{\omega }{\pi }{\displaystyle {\int }_0^{\frac{2\pi }{\omega }}f(t)\cos \omega tdt}\\ b_1=\frac{\omega }{\pi }{\displaystyle {\int }_0^{\frac{2\pi }{\omega }}f(t)\sin \omega tdt}\end{array}$$

(30)

Then, according to digital signal processing theory, the sampling period is set as T_s, and the Fourier coefficient of the same frequency vibration signal at this time is:

$$\{\begin{array}{c}{a}_x=\frac{\omega }{\pi }{\displaystyle \sum _{k=1}^{\frac{2\pi }{\omega T_s}}f(k{T}_s)\cos (k\omega T_s)T_s}\\ b_x=\frac{\omega }{\pi }{\displaystyle \sum _{k=1}^{\frac{2\pi }{\omega T_s}}f(k{T}_s)\sin (k\omega T_s)T_s}\end{array}$$

(31)

The vibration signal amplitude at the rotor A end can be defined as $E_a=\sqrt{a_x^2+b_x^2}$, which represents the intensity of the vibration at the rotor A end at the current sampling time.

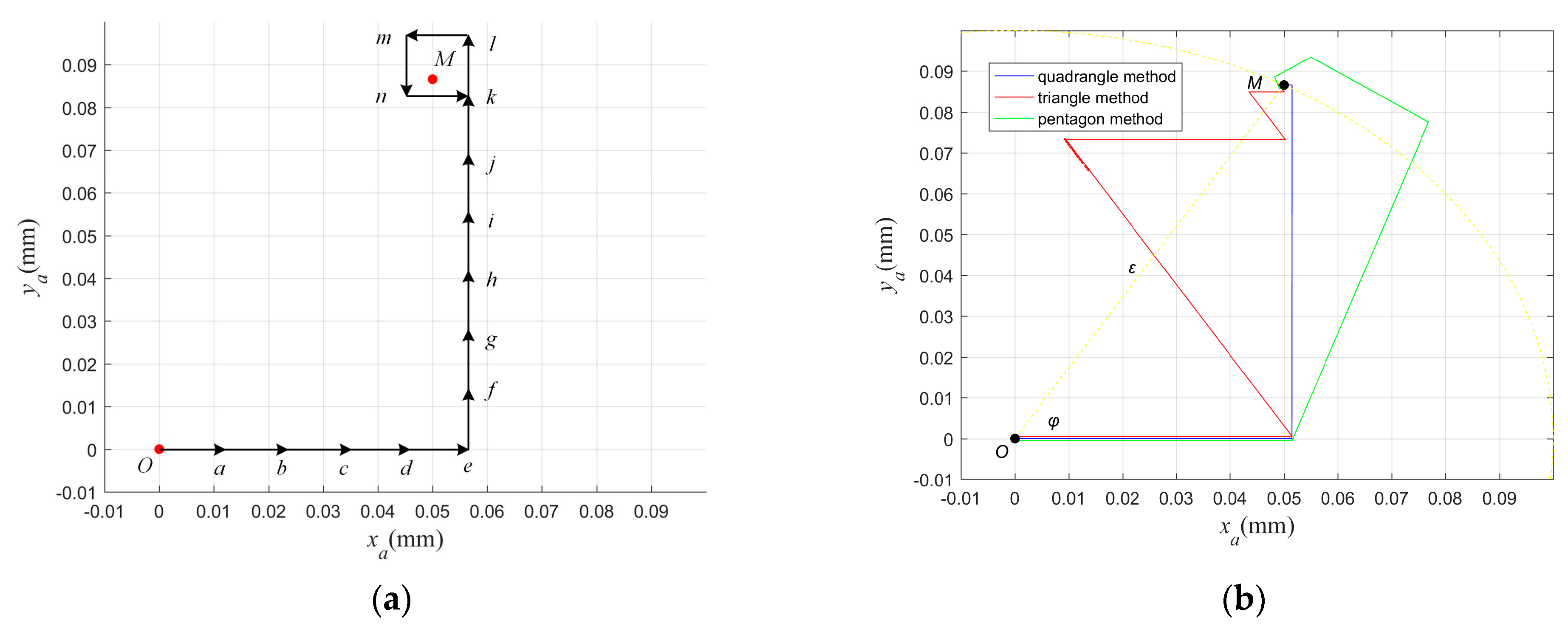
As illustrated in Figure 11a, the detailed steps for the quadrangle search method for the unbalanced mass center position are as follows:

(1)

Randomly define a search starting point, usually by selecting the origin point (α,β)₀ = (0,0), r₀ = R∠0, where α = εcosφ and β = εsinφ;

(2)

The kth step, r_k−1 = R∠ψ_k−1, (α,β)_k = (α,β)_k−1 + r_k−1;

(3)

$\{\begin{array}{c}{\psi }_k={\psi }_{k-1},r_k=R\angle {\psi }_k,if(E_a(k)\le E_a(k-1))\\ {\psi }_k={\psi }_{k-1}+\frac{\pi }{2},r_k=R\angle {\psi }_k,if(E_a(k)>E_a(k-1))\end{array}$;

(4)

$\{\begin{array}{c}\mathrm{Output} \mathrm{the} \mathrm{search} \mathrm{result}{(\alpha ,\beta )}_k,if(E_a(k)<E_t),\\ \mathrm{Return} \mathrm{to} \mathrm{step} 2, \mathrm{continue} \mathrm{search},k=k+1,if(E_a(k)\ge E_t)\end{array}$.

Figure 11. Diagrams of fixed and variable step size search processes. (a) Fixed step size search. (b) Variable step size search.

Figure 11. Diagrams of fixed and variable step size search processes. (a) Fixed step size search. (b) Variable step size search.

Iterative searching with a fixed step size can be used to identify unbalanced parameters, but the identification precision of the algorithm is only R (i.e., one step size). To improve the algorithm’s convergence precision, the size of R must be reduced, but a reduction in R will increase the search time. Therefore, the precision and speed of the convergence of the unbalanced search method with the fixed step size are contradictory. To solve this problem, a variable step size algorithm is used in this work. In the initial stage of the search, a large step size is used, and the step size is then reduced gradually. Finally, the target position is approached with an infinitely small error to ensure high convergence precision.

The core variable step size algorithm Is

$$R(k)=R(0)E_a(k)$$

(32)

The actual effect of this algorithm is illustrated in Figure 11b. The simulation shows that the search path of the quadrangle method is more direct and more efficient than those of other search methods such as the triangle and pentagon methods. If the starting threshold is set to zero, it converges fully to obtain the exact unbalanced parameters.

6.2. Realization of Unbalanced Vibration Compensation

From (7) and the inverse system decoupling method, it can be found that

$$\ddot{Y}+c\dot{Y}+kY=I+K_i^{-1}{L}^{-1}{f}_u$$

(33)

It is only necessary to inject the compensation current I_u = −K_i⁻¹L⁻¹f_u into the current channels, and then, precise compensation of the unbalanced vibration can be achieved.

7. Simulation and Experiments

7.1. Simulation with Simulink

7.1.1. Response Performance Testing of Closed-Loop System

When the AMB-rigid rotor system uses closed-loop control, each radial independent channel adopts a μ-controller that is tuned using the multi-objective optimal method. When simulating a rotor that is statically suspended (i.e., n = 0 rpm) at the working point, square wave signals with amplitudes of 0.1 mm are added to the input of each channel, and the transient time response at the output of each channel is shown in Figure 12. The simulation results show that the transient time response to the reference input is relatively fast: the rise time is less than 1 ms, the settling time is less than 10 ms, and the tracking error is almost zero. Hence, the target of high-precision control is realized.

7.1.2. Robust Performance Testing of Closed-Loop System

When the rotor is suspended stably in the center position and rotates at its rated speed (n = 3000 rpm), a sinusoidal signal with a frequency of 50 Hz and eccentricity ε of 1 × 10⁻⁴ m is injected into the control system at t = 0.1 s to test the anti-disturbance performance of the rotor system. The corresponding output signal waveform is shown in Figure 13. The green line represents the equivalent vibration caused by the eccentric force at the system’s output end, which has an amplitude of 0.1 mm; the red line is the output waveform of the decentralized PID controller. The design and adjustment of this controller were achieved by defining the equivalent stiffness and equivalent damping of the AMB and by analyzing the influences of bias currents on them and on the critical speed of the rotor system. Then, numerical simulations and experiments were carefully carried out to tune the PID parameters for this test rig (P = 6500, I = 1000, D = 4.5) [18,19]; the blue line is the output waveform from the μ-controller. These results show that the μ-controller has a strong disturbance suppression capability, with a disturbance attenuation rate of 0.21, and its displacement vibration peak value is 65.8% smaller than that of the PID controller.

In Figure 14, the singular value curve of the optimal μ-controller shows that the μ-controller has a strong suppression force relative to the external disturbance below a frequency of 50 Hz, and stronger suppression occurs as the frequency decreases.

7.2. Experimental Results

The magnetically levitated high-speed motor rig is shown in Figure 15. The motor is a 75 kW permanent magnet synchronous motor, where the rotor is supported by two AMBs in the radial direction and by a pair of permanent magnet bearings in the axial direction. The rig control system consists of a dSPACE controller, a two-level switching power amplifier, four non-contact eddy current sensors, and a host computer. The parameters used in the experiments are given in

Table 3. Parameters of the experimental platform.

Symbol	Description	Value
VDC	DC-link voltage	100 V
I0	maximum bias current	2.5 A
Pt	total available power	500 VA
m	mass of rotor	18.09 kg
δ	nominal air gap length	0.5 mm
J	transverse moment of inertia	0.2 kg·m2
Jz	polar moment of inertia	0.0223 kg·m2
lA	distance between the AMB-A and geometric center	140 mm
lB	distance between the AMB-B and geometric center	120 mm
kx, ky	displacement stiffness	542,464 N/m
ki	current stiffness	256.872 N/A

.

7.2.1. Static Suspension Test

When the rotor is actually suspended in the central position on the rig (n = 0 rpm), the transient response of x_a is as shown in Figure 16. In the figure, the red line represents the response waveform of the decentralized PID controller, and the blue line represents the response waveform of the optimal μ-controller. The figure shows that the overshoot of the μ-controller is smaller, its settling time is shorter, there is no floating transition time, and its overall performance is thus better.

7.2.2. Decoupling Performance Test

At 6000 rpm, the reference input of x_a stepped up from 0 to 0.1 mm. The radial displacements of the AMB-rigid rotor system in this case are as shown in Figure 17. These results demonstrate that the step change in the radial displacement x_a does not lead to variations in the other three radial displacements, i.e., the four radial displacements of the control system are decoupled completely. These experimental results are consistent with the theoretical analysis, and thus, the expected goal of the control system design has been realized.

7.2.3. Active Vibration Control of the AMB-Rigid Rotor System

After decoupling via the inverse system method, the gyro coupling effect in the radial channels of the closed-loop rotor system is eliminated completely, and there is only the eccentric disturbance vibration with the same frequency as the speed. As Figure 18 and Figure 19 show, the rotor vibration amplitudes before compensation were slightly less than 0.05 mm and slightly greater than 0.05 mm at 6000 rpm and 10,000 rpm, respectively.

Figure 18 shows that as a result of the anti-disturbance effect of the μ-controller and the effect of the compensation algorithm, the unbalanced vibration is effectively suppressed at 6000 rpm, and thus, the rotor motion trajectory after compensation is very small. Figure 19 also shows that even at a higher rotational speed, the unbalanced vibration can largely be controlled, and active displacement vibration control is achieved.

To test the effectiveness of the proposed compensation algorithm over the full rotational speed range, uniform acceleration running testing of the AMB-rigid rotor system was performed. During the test, the motor accelerated from 0 rpm to 12,000 rpm with a constant acceleration of 2π rad/s², and the results are shown in Figure 20.

As Figure 20 shows, μ-control does not have a first-order vibration peak like that of PID control, and the acceleration curve is both continuous and smooth. With the application of the compensation algorithm, the rotor vibration is greatly suppressed to within 0.02 mm and is later close to zero. As the speed continues to increase beyond 12,000 rpm, the vibration displacement of the rotor tends to show a constant amplitude; this is called the “self-centering” effect. The rotor rotates around its inertial axis and operates in a true force-free state. The high-speed motor rotor system has thus achieved active vibration control over its full rotational speed range.

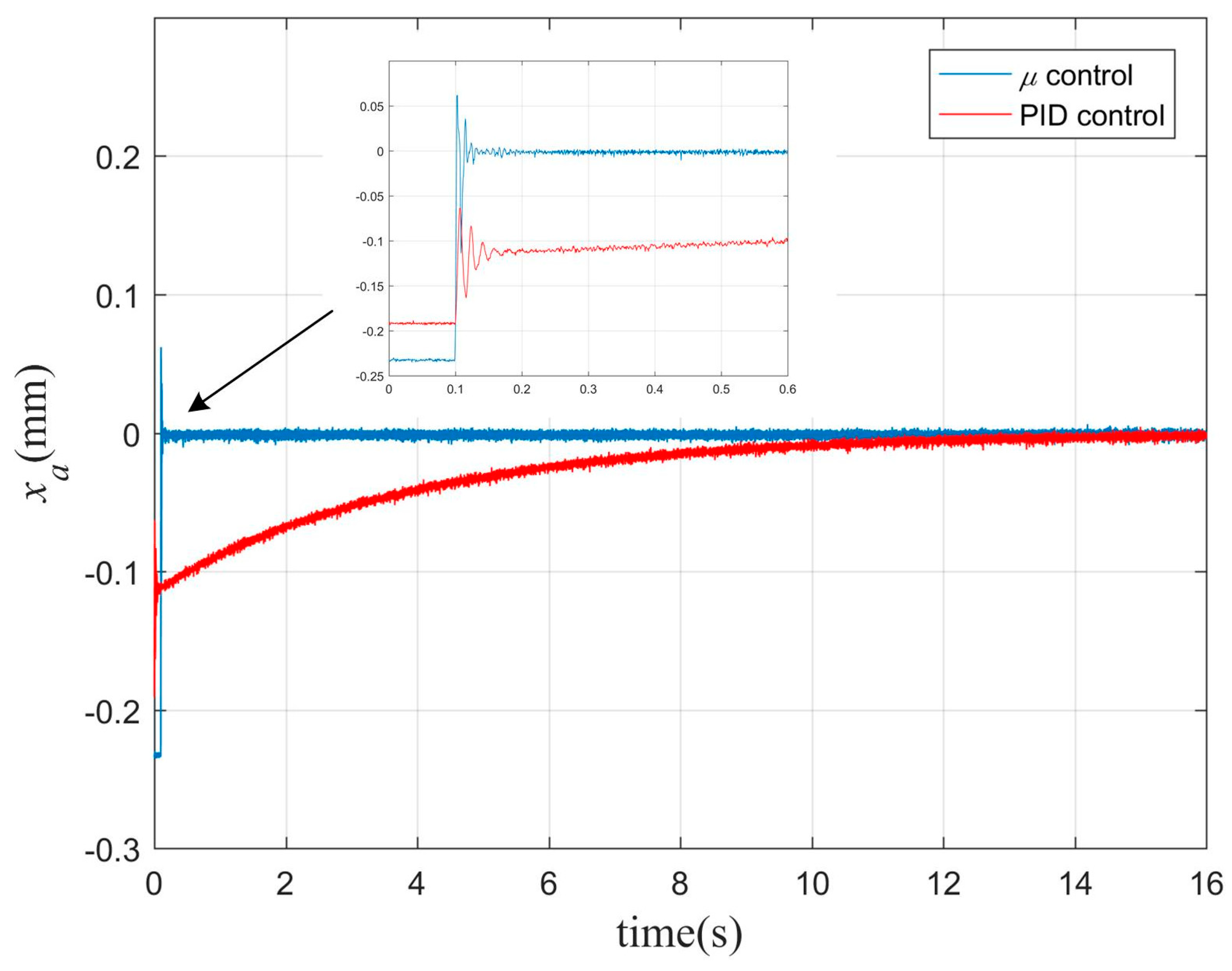
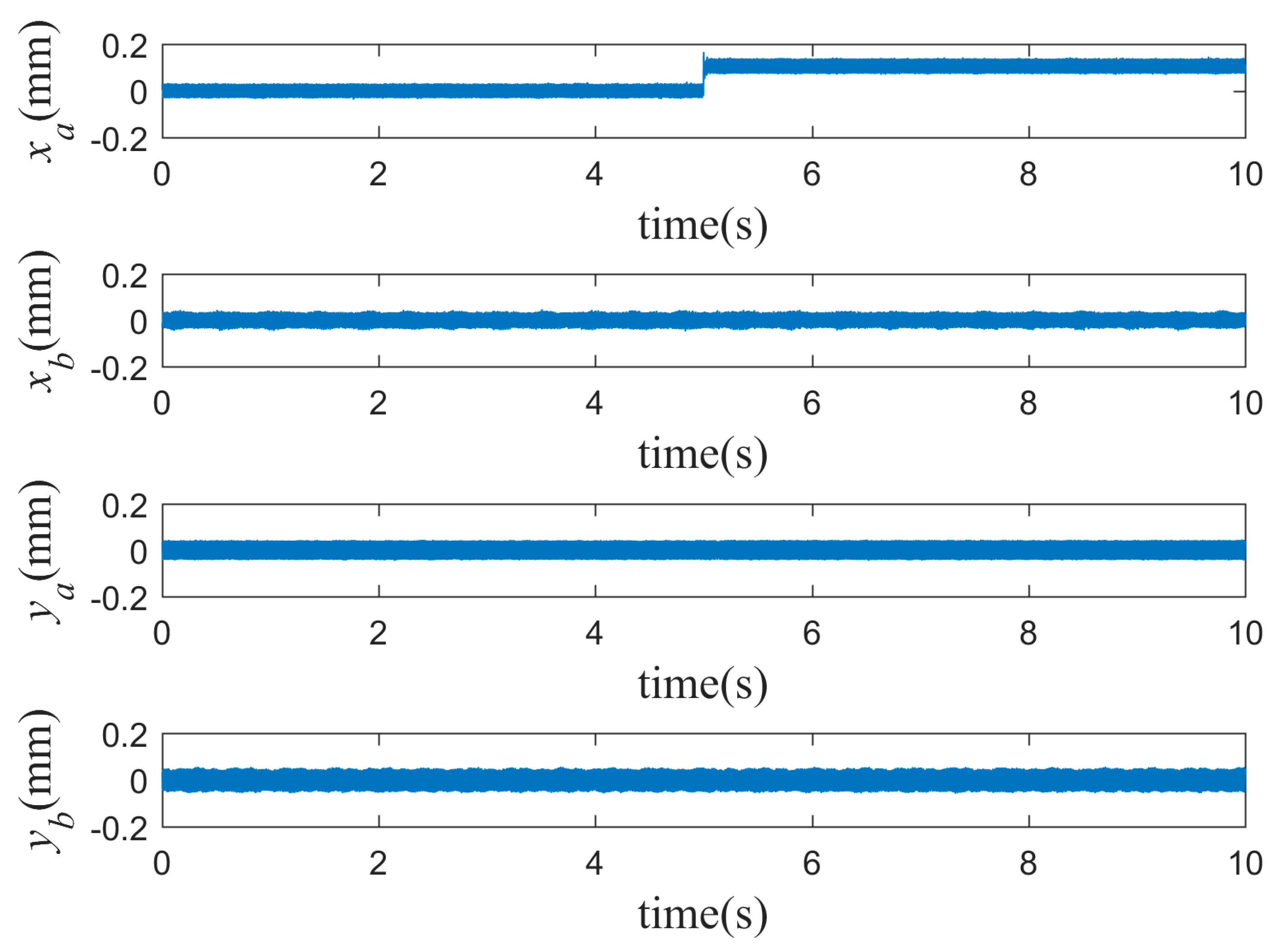
8. Conclusions

In this paper, a μ-synthesis strategy for AMBs in a high-speed motor is proposed. The determination of the appropriate weight functions W_p and W_u represents a key step in the μ-control scheme. By defining a second-order weighting function W_p with higher degrees of freedom, a multi-objective ant colony algorithm based on this function can be used to search for the optimal sensitivity function to achieve the fastest possible response speed, the highest stability margin, and the strongest external disturbance attenuation for the closed-loop system under study. By using the perturbation method for uncertain parameters, it is theoretically guaranteed that the control system will be robust and stable up to its rated speed (n = 12,000 rpm), and the stability margin is 5.11 times (i.e., it is stable within a vibration amplitude of 0.25 mm). The simulation results also show that the optimal μ-controller has an excellent disturbance suppression ability, which weakens the unbalanced disturbance vibration of the rotor system at low speeds by as much as 65.8% when compared with the classical PID controller. At higher rotational speeds, a compensation algorithm based on real-time variable step size iterative searching for eccentric positions is applied to enhance the disturbance rejection of the controller. Further experiments show that the algorithm can realize unbalanced displacement vibration compensation over the full rotational speed range. The entire control strategy can not only ensure stable rotor suspension but also can suppress the disturbance vibration strongly. The μ-controller’s response performance is also greatly improved when compared with the PID. The μ-control strategy performs excellently in both static and dynamic conditions and is the preferred choice to replace PID. The realization of an optimal μ-controller also provides effective information and a reference for AMB engineering design practice.