Abstract
The application of control systems in precision irrigation is critical to ensure the accurate distribution of water in crops under various uncertainties. Shifts in the loading of the water supply on the control valve can be a significant uncertainty. Changes in weather and the uncertainty of the water level in the reservoir are also challenging issues. Sliding Mode Control (SMC) is a robust control technique that is simple to apply to deal with uncertainty, while Fast Terminal Sliding Mode Control (FTSMC) has the benefit of the rapid convergence. The DC electric motor, which is a common component of electric control valves, can be employed in designing control techniques for precision irrigation applications. This study aims to design a proposed experimental-based method, namely FTSMC for valve regulation under water load uncertainty for precision irrigation application. Modification of the signum function should be used to eliminate the chattering effect in real experiments.The results of experiments showed that the proposed method was superior to the conventional Proportional Integral Derivative (PID) and traditional SMC techniques in terms of overshoot, convergence rate and error. Because of those reasons, the FTSMC approach should be implemented on control valves against load uncertainty in precision irrigation applications.
1. Introduction
Automation and control systems play an important role in precision irrigation to ensure the accurate distribution of water to crops [1,2]. Moreover, water allocation needs to be channelled appropriately according to various plant conditions, such as plant types, land area, and soil conditions. A closed-loop control system and smart water management platform techniques have been developed to realize precision irrigation [3,4]. Suitable automation techniques will support advanced monitoring and management systems, enhancing sustainability in precision irrigation [5,6]. However, there are also challenges and opportunities [7,8], primarily uncertainty in the application of precision irrigation, specifically related to using actuators of control valves. One of the primary sources of uncertainty is the shift in the loading of the water supply on the control valve, especially variations in the water level. Weather changes have become a fundamental uncertainty in the field; when it is hot, the water will evaporate, while when it rains, it may increase the water supply in the reservoir. Therefore, it is necessary to design the proper control technique to control the valve according to the needs of precision irrigation, mainly for water load uncertainty.
Robust control is one approach in control theory to design controllers whose primary concern is reliability at dealing with uncertainty [9]. The H-infinity method is a type of robust control that synthesizes a controller to guarantee stability against uncertainty [10], while robust repetitive control has been developed to deal with uncertainty in periodic signals [11]. Another robust control method often used is the sliding mode control (SMC) technique, which forces the system to slide along a cross-section of the system’s normal behavior [12]. The SMC method is simpler to apply and has robustness to uncertainty, so this technology has become popular today. However, the SMC method has many variations that can be investigated for their potential in applying precision irrigation [13]. One type of this developing technique is fast terminal sliding mode control (FTSMC) because it has a quick convergence speed [14,15]. Therefore, the FTSMC method offers a challenging study to deal with uncertainties in applying precision irrigation in valve control.
A predictive controller model using discrete Laguerre networks and machine learning has been developed for precision irrigation [16]. The nonsingular fast terminal sliding mode control technique is used for pneumatic cylinder servo systems [17] and attitude control of a quadrotor [18]. However, they have not focused on valve control applications. A study of a fast terminal sliding mode controller method has been carried out on the pneumatic actuator [19]. Research on automotive electronic throttle systems with robust sliding mode control methods has been invented [20,21]. Because of those reasons, studies that emphasize valve control objects in precision irrigation applications are still lacking. Moreover, experimental validation studies are crucial for direct application in agricultural fields, although theoretical studies and simulations are also critical in upstream research. As the main component widely used by electric valves, the DC motor can be used for experimental validation to bring the design results closer to the actual application in precision irrigation. The purpose of this research is to develop a proposed experimental-based method, which is robust FTSMC to control valves to deal with water load uncertainty for precision irrigation applications. The lack of studies on an excellent robust SMC in plant valve control with an experimental guarantee for precision irrigation applications is an exciting research gap explored in this paper. The following are some of the contributions and novelties from this research, summarized as follows:
- Experimental validation using a DC motor plant, the central component of the electrical valve control, adding load experiments so that the design results will be closer to reality in the field.
- Proposing the FTSMC method for solving problems in precision irrigation applications.
- An in-depth investigation of the accuracy comparison of the proposed method compared to conventional control techniques, namely error, overshoot, and signal response rate.
- Detailed experimental design and stability analysis of the proposed method.
This research is required to support the program of the Ministry of Agriculture, the Republic of Indonesia for the farmer, specifically the activities of watering potato seeds in Garut, West Java, watering shallots in Sumenep, East Java, and agricultural irrigation in Jeneponto, South Sulawesi. Research related to the automation of electric control valves is vital to support precision irrigation and the smart farming agenda in Jeneponto, South Sulawesi, which still uses manual valve control, see Figure 1.

Figure 1.
Manual valve regulation for agricultural irrigation in Jeneponto, South Sulawesi, Indonesia.
The rest of this paper is structured as follows. Section 2 explains the problem statement and the design underlying a water load uncertainty issue, valve control model and fast terminal sliding mode control strategy. Section 3 presents the experimental validation under the change of the load mass. A comparison study with other methods is also discussed in this section. Finally, the conclusion is illustrated in Section 4.
2. Problem Statement and Design
2.1. Uncertainty Issue
Shifts in the height of the water level h in the reservoir will be the primary source of uncertainty in the loading of water F on the control valve according to hydrostatic pressure; notably, the higher the water level, the heavier the load on the control valve [22,23]. On the other hand, changing the load on the electric motor in the control valve will change the plant model. The following figure can investigate uncertainties in the application of precision irrigation in the field.
Figure 2 portrays the uncertainty of the water level difference in the reservoir causing a distinction in the water weight in the control valve according to the influence of gravity g in Equation (1) below.
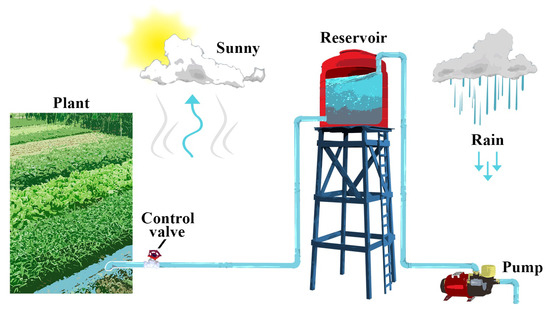
Figure 2.
Uncertainty analysis of valve control for precision irrigation in the field.
A decrease in water level on reservoir area A due to use during crop spraying and evaporation and also water filling by pumps and rainwater [24,25] may result in uncertainty in water level changes. The uncertainty of the water level in (2) will affect the uncertainty of the loading of the hydrostatic force on the control valve [26,27].
Differences in water density due to shifts in temperature due to weather changes can also cause uncertainty in the water load on the control valve in (3). Moreover, hot weather or dark cloudy rain may affect the reservoir’s irrigation water density in outdoor conditions [28].
2.2. Valve Control Model
The control valve design is fundamental to optimising and improving the plant in the future [29]. We will operate an electric valve with a DC voltage source of 12 volts as a control valve in a precision irrigation application so that we can use a DC motor facility, Quanser’s Qube servo 2 [30], in the laboratory in modelling experiments and for testing the performance of our proposed method with the matlab-simulink software, which is described in Figure 3.

Figure 3.
Instrument of DC motor as experimental design facility.
The value of the motor torque T is proportional to the armature current i according to a constant and can be described referring to Newton’s second law of the moment of inertia J and the constant of viscous motor friction b.
Electrical energy through electromotive voltage (back-emf) E is converted into motion energy in the form of angle speed [31,32]. is the constant to convert back-emf to angle speed .
Kirchhoff’s second law applies a closed electrical circuit, which has properties of voltage source V, resistance R and inductance L, shown in Figure 4, to develop the formula of (7) as follows.
E is substituted by Equation (6) to be (8).
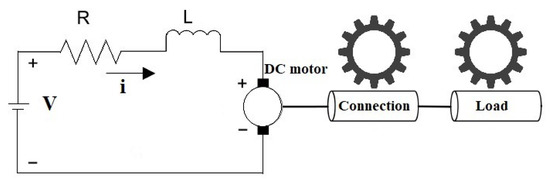
Figure 4.
Diagram of DC motor parameters.
We can utilise K to define the motor torque and back emf constant since the motor torque constant and the back emf are in the same SI unit, . Then we can apply the Laplace transform to the modelling Equations (5) and (8) so that it can be expressed in the Laplace variable s as follows. Variables of i and are changed to capital, I, and , respectively, in the complex frequency domain.
The control valve model compares the valve position angle as the output with the voltage signal as the system input [33,34].
The model in (11) indicates that the DC motor components as valve drivers such as affect the plant properties. However, we can directly use the input voltage and output angle data from the DC motor platform in Figure 3 with identification techniques [35,36]. In general, we can develop a proposed method with a mathematical model of control systems, which can be in the form of a transfer function or state space. In this study, we will use the transfer function obtained from the identification system technique.
2.3. Fast Terminal Sliding Mode Control Design
The foremost step in designing the sliding mode controller [38] is defining the tracking error, which is the difference between the measured and desired angle and its derivation.
Traditional SMC has a sliding surface s which is linear and then selected.
where c > 0. On the other hand, FTSMC can be developed to boost the convergence rate of the basic SMC as follows.
where and are two positive coefficients. The sign function is described in (19).
Further, let us determine the Lyapunov function V as follows.
Remark 1.
Note that a standard quadratic Lyapunov function is used to show the stability of sliding surface s. A different function, such as the non-quadratic Lyapunov function discussed in [39,40], can also be considered to both ensure the stability and enhance the tracking performance.
The derivative of the Lyapunov function in (20) must be less than zero so that it can guarantee its stability.
Therefore, the sliding surface of FTSMC in (18) can be derived as follows.
We substitute the second derivative of error in (16) for the derivative of the sliding surface in (23).
The transfer function of the control valve modelling in the second derivative of the angular position in (13) is inserted into (24).
The sliding surface in (18) and its derivatives in (25) are substituted in the Lyapunov function derivatives in (22) to be (26).
We can design the input control of voltage, v in (27), to guarantee its stability when the motion on sliding surface () occurs in this circumstance. The value of gain, G, is positive.
Next, we can develop the block diagram for the proposed control method in Figure 5 from (14)–(18), while the structure inside the red rectangle represents the unique diagram of FTSMC in (18).
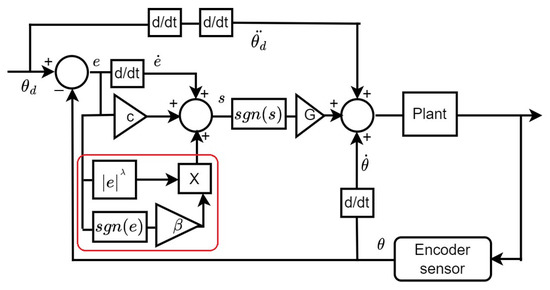
Figure 5.
Block diagram of the proposed control structure.
The diagram indicates that the reference angle, measured angle, and error contribute to the proposed controller design. The gain design procedure can be carried out by referring to Lyapunov stability in (22) so that the values can be simulated in advance according to the identification model in the (11) operating software of simulink-matlab. However, the gain values () may change slightly in the experiment due to the limitations of the amplifier in Figure 3 in supplying electric power as input control. The following is a summary of determining the gain in the proposed controller.
- Simulate the gain value using the software concerning the convergence of the Lyapunov stability guarantee.
- Adjust the gain value referring to the simulation results with the amplifier capability in the experimental validator device.
3. Results and Discussion
The design of the input control of voltage in (27) was implemented as a controller in the DC motor experiment in Figure 6.

Figure 6.
Experimental validation with DC motor.
The following were the experimental results of angular position control on a DC motor in Figure 7. Destructive events happen with poor results due to the chattering effect being interrupted in the experiment [41,42].
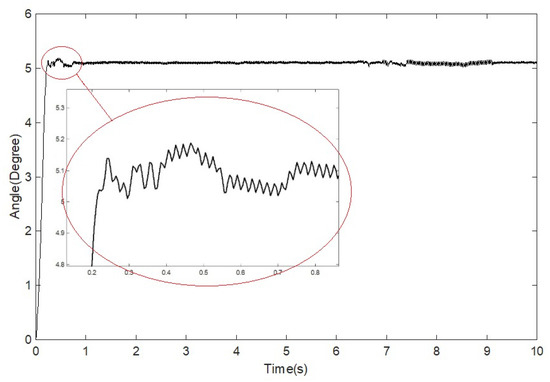
Figure 7.
Chattering problem in experiment results.
Several recent studies have successfully reduced chattering effects using the extended Kalman filter [43], Genetic Algorithm [42], and Neural Network [44] strategies. However, we preferred to adjust the signum function for reasons of convenience in this study. We could modify the signum function in (19) to minimize the chattering impact that appeared in the actual experiment to (28) by a positive boundary layer ().
Interestingly, the equation of (28) succeeded in eliminating the chattering problem in the response signal of the measured angle in the experiment. We need to compare the experimental results of our proposed method (FTSMC) with the Proportional–Integral–Derivative (PID) controller and common SMC in (17) to be more convincing. We design the PID control traditionally in the following formulation of (29) by determining the proportional (), integral (), and derivative () gains by manually testing with their values. The comparison results of them are shown in Figure 8.
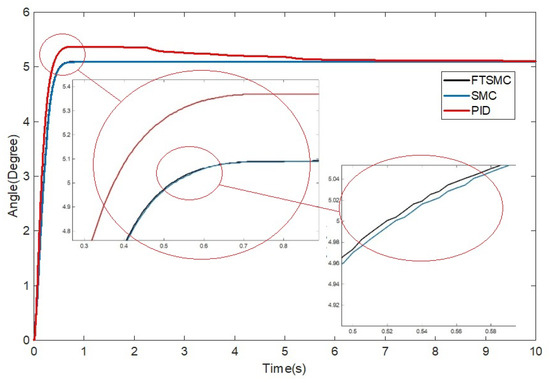
Figure 8.
Experiment yields.
Remark 2.
Note that we apply a traditional setting for the PID controller in this study. Optimisation [45,46] of the PID controller has a possibility of better results.
Although all methods achieved asymptotic stability, with errors approaching zero over time (), PID had a significant overshoot of about 5.36 degrees. On the other hand, the FTSMC and SMC step response values almost coincided, but the proposed method had a slightly faster response. This study proves that the SMC theory achieved excellent measurement results that construct a perfect robust control signal without overshoot. The load shift uncertainty on the electric control valve in (1)–(3) could be analogized to the change in the load mass on the DC motor so that a load of 1 kg was added to the plan shown in Figure 9.

Figure 9.
The addition of a load of 1 kg to the experimental tool of the DC motor.
The following were the experiments’ outcomes (See Figure 10) when adding a mass load of 1 kg to the plant.
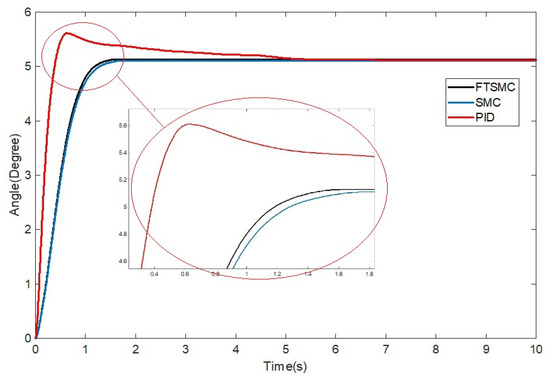
Figure 10.
Experiment results under mass load change.
Shifts in the load on the plant resulted in the PID technique having a larger overshoot at 5.61 degrees. Fascinatingly, the proposed method had a more rapid response—approximately 0.1 degrees—to convergence than the traditional SMC technique, which was more clearly visible in increasing the load on the DC motor. However, it had a longer settling time at 1.6 s than the no-load plant at 0.7 s. The error values from the results of all experiments could be investigated as follows.
We should employ the statistical root-mean-square error (RMSE) method in (14) to compare the difference quantitatively in error between FTSMC and SMC with the following equation in (30). The PID controller is undoubtedly seen to have its own distinctions, particularly the overshoot phenomenon, while our proposed method and common SMC have almost the same signal, so it needs to be investigated utilizing the RMSE approach.
The following RMSE calculation in (30) results was from Figure 11, which compared the proposed (FTSMC) and general SMC techniques in Table 1.
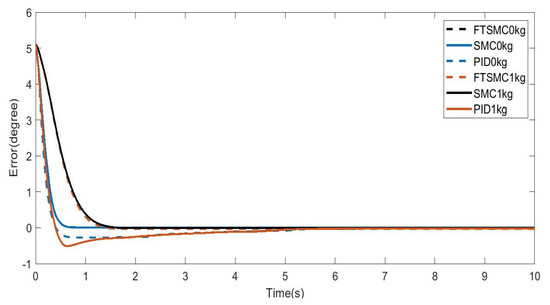
Figure 11.
Error values.

Table 1.
RMSE investigation.
The proposed method had a smaller rms value than the common SMC. On the one hand, the difference in rmse was obviously observable in the 1 kg load treatment (See Figure 11), with 0.011 degrees between an FTSMC and SMC of 0.906 and 0.917 degrees, respectively. On the other hand, the no-load plant had a slighter rmse dissimilarity of 0.003 degrees between FTSMC at 0.571 degrees and SMC at 0.574 degrees so that the response signal of both in Figure 8 appeared extremely close.
The overshoot constraint on the PID method on valve control for precision irrigation applications could cause inaccuracies in watering plants and waste the water supply [47]. Moreover, certain types of plants could rot due to excess water [48,49]. The experimental design in the laboratory showed that the proposed method did not have an overshoot like the conventional PID method, even though the response signal was faster than the common SMC technique, so the FTSMC approach was recommended to be implemented in control valves for irrigation applications. Nevertheless, PID optimization may achieve better yields than manual tuning in (29). We claim that our proposed method is better than the general PID technique, which is designed manually, especially regarding the overshoot problem. In addition, the error value, primarily the minimalist rmse in the proposed method, actually supports the precision irrigation program against water load uncertainty.
Measurement accuracy is critical in precision agriculture, so the slight difference in error (rmse) between the proposed method and traditional SMC is significant. The small dissimilarity in error will considerably impact the long term. For illustration, an error of 1 mL of irrigation fluid per plant watering will cause an error of 2 mL per day if watering is accomplished twice in the morning and evening. Therefore, a month can cause an inefficiency of 60 mL or 720 mL annually. Fascinatingly, an increment in loading leads to striking differences between FTSMC and common SMC, which are the highlight of the results of this study. This experimental achievement can strengthen the theory of FTSMC, which has a more rapid convergence rate against load uncertainty than traditional SMC, and then it will inspire other researchers to implement FTSMC knowledge in other applications.
4. Conclusions
The design of a control valve for precision irrigation applications with the proposed FTSMC method has been successfully performed in the laboratory by employing an experimental tool of the DC motor. One of the main problems in applying the SMC technique in experiments was the chattering event which can be solved by modifying the signum function. The measurement results showed that FTSMC was superior to the conventional PID method in terms of overshoot weaknesses. Moreover, the additional load on the plant increased the overshoot on the PID. This study proved that the robust SMC theory built an ideal robustness response signal without overshoot phenomena in experiments so that it can inspire other researchers to implement modern control system science in real applications. Experimental validation indicated that traditional SMC had a slower convergent signal response than the proposed method. Additionally, FTSMC achieved more accurate results due to the minor RMSE analysis in the higher load. Therefore, the FTSMC technique can be recommended for electric control valves under load uncertainty in agricultural irrigation applications.
Author Contributions
Conceptualization, J.A.P., P.P., E.K.; methodology, J.A.P., E.K. and S.W.; software, P.P. and T.M.; validation, J.A.P. and E.B.P.; formal analysis, E.K.; investigation, E.B.P. and P.P.; resources, S.W.; data curation, J.A.P. and D.R.; writing—original draft preparation, J.A.P.; writing —review and editing, S.W. and E.K.; visualization, D.R.; supervision, P.P. and S.W.; project administration, T.M. and R.R.; funding acquisition, P.P., R.R. and T.M. All authors have read and agreed to the published version of the manuscript.
Funding
The authors received financial support for publication from the UPLAND Project, with the support of IsDB and IFAD, which focus on increasing smallholders’ agriculture productivity, incomes, livelihoods, and resilience in the targeted area.
Data Availability Statement
Not applicable.
Acknowledgments
The team of authors is grateful to the management of the Research Center for Photonics, Rumah Program Sains Fundamental Molekuler-Organisasi Riset Nanoteknologi dan Material(ORMN), National Research and Innovation Agency (BRIN) of Republic Indonesia for supporting this research. Thank you to the Ministry of Agriculture, Republic of Indonesia, for funding this work.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| FTSMC | Fast Terminal Sliding Mode Control |
| SMC | Sliding Mode Control |
| RMSE | Root Mean Square Error |
| PID | Proportional Integral Derivative |
| DC | Direct Current |
References
- Abioye, E.A.; Abidin, M.S.Z.; Mahmud, M.S.A.; Buyamin, S.; Ishak, M.H.I.; Abd Rahman, M.K.I.; Otuoze, A.O.; Onotu, P.; Ramli, M.S.A. A review on monitoring and advanced control strategies for precision irrigation. Comput. Electron. Agric. 2020, 173, 105441. [Google Scholar] [CrossRef]
- Liang, Z.; Liu, X.; Xiong, J.; Xiao, J. Water allocation and integrative management of precision irrigation: A systematic review. Water 2020, 12, 3135. [Google Scholar] [CrossRef]
- Klein, L.J.; Hamann, H.F.; Hinds, N.; Guha, S.; Sanchez, L.; Sams, B.; Dokoozlian, N. Closed loop controlled precision irrigation sensor network. IEEE Internet Things J. 2018, 5, 4580–4588. [Google Scholar] [CrossRef]
- Kamienski, C.; Soininen, J.P.; Taumberger, M.; Dantas, R.; Toscano, A.; Salmon Cinotti, T.; Filev Maia, R.; Torre Neto, A. Smart water management platform: IoT-based precision irrigation for agriculture. Sensors 2019, 19, 276. [Google Scholar] [CrossRef] [PubMed]
- Adeyemi, O.; Grove, I.; Peets, S.; Norton, T. Advanced monitoring and management systems for improving sustainability in precision irrigation. Sustainability 2017, 9, 353. [Google Scholar] [CrossRef]
- Capraro, F.; Tosetti, S.; Rossomando, F.; Mut, V.; Vita Serman, F. Web-based system for the remote monitoring and management of precision irrigation: A case study in an arid region of Argentina. Sensors 2018, 18, 3847. [Google Scholar] [CrossRef]
- Zhang, J.; Guan, K.; Peng, B.; Jiang, C.; Zhou, W.; Yang, Y.; Pan, M.; Franz, T.E.; Heeren, D.M.; Rudnick, D.R.; et al. Challenges and opportunities in precision irrigation decision-support systems for center pivots. Environ. Res. Lett. 2021, 16, 053003. [Google Scholar] [CrossRef]
- Bodkhe, U.; Tanwar, S.; Bhattacharya, P.; Kumar, N. Blockchain for precision irrigation: Opportunities and challenges. Trans. Emerg. Telecommun. Technol. 2020, 33, e4059. [Google Scholar] [CrossRef]
- Mahmoud, M.S. Robust Control and Filtering for Time-Delay Systems; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Prakosa, J.A.; Gusrialdi, A.; Kurniawan, E.; Stotckaia, A.D.; Adinanta, H.; Suryadi. Experimentally robustness improvement of DC motor speed control optimization by H-infinity of mixed-sensitivity synthesis. Int. J. Dyn. Control 2022, 10, 1968–1980. [Google Scholar] [CrossRef]
- Kurniawan, E.; Wang, H.; Sirenden, B.H.; Prakosa, J.A.; Adinanta, H.; Suryadi, S. Discrete-time modified repetitive sliding mode control for uncertain linear systems. Int. J. Adapt. Control Signal Process. 2021, 35, 2245–2258. [Google Scholar] [CrossRef]
- Mohd Zaihidee, F.; Mekhilef, S.; Mubin, M. Robust speed control of PMSM using sliding mode control (SMC)—A review. Energies 2019, 12, 1669. [Google Scholar] [CrossRef]
- Yu, X.; Feng, Y.; Man, Z. Terminal sliding mode control—An overview. IEEE Open J. Ind. Electron. Soc. 2020, 2, 36–52. [Google Scholar] [CrossRef]
- Amirkhani, S.; Mobayen, S.; Iliaee, N.; Boubaker, O.; Hosseinnia, S.H. Fast terminal sliding mode tracking control of nonlinear uncertain mass–spring system with experimental verifications. Int. J. Adv. Robot. Syst. 2019, 16, 1729881419828176. [Google Scholar] [CrossRef]
- Du, H.; Chen, X.; Wen, G.; Yu, X.; Lü, J. Discrete-time fast terminal sliding mode control for permanent magnet linear motor. IEEE Trans. Ind. Electron. 2018, 65, 9916–9927. [Google Scholar] [CrossRef]
- Abioye, E.A.; Abidin, M.S.Z.; Aman, M.N.; Mahmud, M.S.A.; Buyamin, S. A model predictive controller for precision irrigation using discrete lagurre networks. Comput. Electron. Agric. 2021, 181, 105953. [Google Scholar] [CrossRef]
- Zhao, L.; Xia, Y.; Yang, H.; Zhang, J. Nonsingular Fast Terminal Sliding Mode Control. In Pneumatic Servo Systems Analysis; Springer: Berlin/Heidelberg, Germany, 2022; pp. 227–244. [Google Scholar]
- Lian, S.; Meng, W.; Lin, Z.; Shao, K.; Zheng, J.; Li, H.; Lu, R. Adaptive attitude control of a quadrotor using fast nonsingular terminal sliding mode. IEEE Trans. Ind. Electron. 2021, 69, 1597–1607. [Google Scholar] [CrossRef]
- Nguyen, H.T.; Trinh, V.C.; Le, T.D. An adaptive fast terminal sliding mode controller of exercise-assisted robotic arm for elbow joint rehabilitation featuring pneumatic artificial muscle actuator. Actuators 2020, 9, 118. [Google Scholar] [CrossRef]
- Hu, Y.; Wang, H.; Yazdani, A.; Man, Z. Adaptive full order sliding mode control for electronic throttle valve system with fixed time convergence using extreme learning machine. Neural Comput. Appl. 2022, 34, 5241–5253. [Google Scholar] [CrossRef]
- Hu, Y.; Wang, H. Robust tracking control for vehicle electronic throttle using adaptive dynamic sliding mode and extended state observer. Mech. Syst. Signal Process. 2020, 135, 106375. [Google Scholar] [CrossRef]
- Žvanut, P. 3D Finite Element Analysis of a Concrete Dam Behavior under Changing Hydrostatic Load: A Case Study. Materials 2022, 15, 921. [Google Scholar] [CrossRef]
- Carrera, F.F.; Sanchez, H.S.; Garcia-Orellana, Y.; Chadrina, O. A System for Measuring Water Levels in Open-Air Irrigation Canals. In Proceedings of the EPJ Web of Conferences, Madrid, Spain, 20–24 September 2021; Volume 248, p. 02011. [Google Scholar]
- Sun, M.; Gao, X.; Zhang, Y.; Song, X.; Zhao, X. A new solution of high-efficiency rainwater irrigation mode for water management in apple plantation: Design and application. Agric. Water Manag. 2022, 259, 107243. [Google Scholar] [CrossRef]
- Maftukhah, T.; Wijonarko, S.; Rustandi, D.; Sirenden, B.H.; Prakosa, J.A. Design and Implementation of Three Application Software Employed in Web Based Rain Gauge Calibrators. In Proceedings of the 2021 8th International Conference on Information Technology, Computer and Electrical Engineering (ICITACEE), Semarang, Indonesia, 23–24 September 2021; pp. 107–112. [Google Scholar]
- Cassan, L.; Dellinger, G.; Maussion, P.; Dellinger, N. Hydrostatic pressure wheel for regulation of open channel networks and for the energy supply of isolated sites. Sustainability 2021, 13, 9532. [Google Scholar] [CrossRef]
- Parwanti, A.; Wahyudi, S.; Ni’am, M. Barrier knock-down weir as an alternative technology for irrigation. In Proceedings of the IOP Conference Series: Earth and Environmental Science; IOP Publishing: Bristol, UK, 2022; Volume 955, p. 012004. [Google Scholar]
- Wijonarko, S.; Maftukhah, T.; Rustandi, D.; Widiyatmoko, B.; Bayuwati, D.; Sirenden, B.H.; Prakosa, J.A.; Hidayat, A.R.; Mandaris, D.; Firdaus, H.; et al. Empirical Formulas Between Outdoor Temperature And Humidity. In Proceedings of the 2021 7th International Conference on Electrical, Electronics and Information Engineering (ICEEIE), Malang, Indonesia, 2 October 2021; pp. 1–6. [Google Scholar]
- Prakosa, J.A.; Kozlova, L.P. Design and simulation of automatic control valve for gas flow meter calibrator of bell prover. In Proceedings of the 2018 IEEE Conference of Russian Young Researchers in Electrical and Electronic Engineering (EIConRus), St. Petersburg, Russia, 29 January–1 February 2018; pp. 966–969. [Google Scholar]
- Govind, A.; Selva Kumar, S. A comparative study of controllers for QUANSER QUBE Servo 2 rotary inverted pendulum system. In Advances in Electrical and Computer Technologies; Springer: Berlin/Heidelberg, Germany, 2020; pp. 1401–1414. [Google Scholar]
- Barkas, D.A.; Ioannidis, G.C.; Psomopoulos, C.S.; Kaminaris, S.D.; Vokas, G.A. Brushed DC Motor Drives for Industrial and Automobile Applications with Emphasis on Control Techniques: A Comprehensive Review. Electronics 2020, 9, 887. [Google Scholar] [CrossRef]
- Prakosa, J.A.; Kurniawan, E.; Sirenden, B.H.; Adinanta, H.; Afandi, M.I.; Ula, R.K.; Pratomo, H. Synthesis Method of Mixed Sensitivity for H-infinity Robust Control Optimization on DC Motor of Mechatronics Model. In Proceedings of the 2021 International Conference on Radar, Antenna, Microwave, Electronics, and Telecommunications (ICRAMET), Bandung, Indonesia, 23–24 November 2021; pp. 68–73. [Google Scholar]
- Kumar, S.; Tewari, V.K.; Bharti, C.K.; Ranjan, A. Modeling, simulation and experimental validation of flow rate of electro-hydraulic hitch control valve of agricultural tractor. Flow Meas. Instrum. 2021, 82, 102070. [Google Scholar] [CrossRef]
- Mu, H.; Wang, Y.; Teng, H.; Jin, Y.; Zhao, X.; Zhang, X. Cooling system based on double-ball motor control valve. Adv. Mech. Eng. 2021, 13, 16878140211011280. [Google Scholar] [CrossRef]
- Chiuso, A.; Pillonetto, G. System identification: A machine learning perspective. Annu. Rev. Control Robot. Auton. Syst. 2019, 2, 281–304. [Google Scholar] [CrossRef]
- Prakosa, J.A.; Kurniawan, E.; Adinanta, H.; Suryadi, S.; Purwowibowo, P. Experimental based identification model of low fluid flow rate control systems. In Proceedings of the 2020 International Conference on Radar, Antenna, Microwave, Electronics, and Telecommunications (ICRAMET), Tangerang, Indonesia, 18–20 November 2020; pp. 200–205. [Google Scholar]
- Ma’arif, A.; Çakan, A. Simulation and arduino hardware implementation of dc motor control using sliding mode controller. J. Robot. Control 2021, 2, 582–587. [Google Scholar]
- Zirkohi, M.M. Fast terminal sliding mode control design for position control of induction motors using adaptive quantum neural networks. Appl. Soft Comput. 2022, 115, 108268. [Google Scholar] [CrossRef]
- Hosseinzadeh, M.; Yazdanpanah, M.J. Performance enhanced model reference adaptive control through switching non-quadratic Lyapunov functions. Syst. Control Lett. 2015, 76, 47–55. [Google Scholar] [CrossRef]
- Tao, G. Model reference adaptive control with L 1+ α tracking. Int. J. Control 1996, 64, 859–870. [Google Scholar] [CrossRef]
- Oliveira, T.R.; Hsu, L.; Nunes, E.V.L. Smooth sliding control to overcome chattering arising in classical SMC and super-twisting algorithm in the presence of unmodeled dynamics. J. Frankl. Inst. 2022, 359, 1235–1256. [Google Scholar] [CrossRef]
- Ye, M.; Wang, H. A Robust Adaptive Chattering-Free Sliding Mode Control Strategy for Automotive Electronic Throttle System via Genetic Algorithm. IEEE Access 2020, 8, 68–80. [Google Scholar] [CrossRef]
- Cheng, X.; Liu, H.; Lu, W. Chattering-Suppressed Sliding Mode Control for Flexible-Joint Robot Manipulators. Actuators 2021, 10, 288. [Google Scholar] [CrossRef]
- Xiong, P.Y.; Jahanshahi, H.; Alcaraz, R.; Chu, Y.M.; Gómez-Aguilar, J.; Alsaadi, F.E. Spectral Entropy Analysis and Synchronization of a Multi-Stable Fractional-Order Chaotic System using a Novel Neural Network-Based Chattering-Free Sliding Mode Technique. Chaos Solitons Fractals 2021, 144, 110576. [Google Scholar] [CrossRef]
- Guo, B.; Zhuang, Z.; Pan, J.S.; Chu, S.C. Optimal Design and Simulation for PID Controller Using Fractional-Order Fish Migration Optimization Algorithm. IEEE Access 2021, 9, 8808–8819. [Google Scholar] [CrossRef]
- Rahayu, E.S.; Ma’arif, A.; Çakan, A. Particle Swarm Optimization (PSO) Tuning of PID Control on DC Motor. Int. J. Robot. Control Syst. 2022, 2, 435–447. [Google Scholar] [CrossRef]
- Querejeta, J.I.; Ren, W.; Prieto, I. Vertical decoupling of soil nutrients and water under climate warming reduces plant cumulative nutrient uptake, water-use efficiency and productivity. New Phytol. 2021, 230, 1378–1393. [Google Scholar] [CrossRef]
- Wagg, C.; Hann, S.; Kupriyanovich, Y.; Li, S. Timing of short period water stress determines potato plant growth, yield and tuber quality. Agric. Water Manag. 2021, 247, 106731. [Google Scholar] [CrossRef]
- Langenfeld, N.J.; Pinto, D.F.; Faust, J.E.; Heins, R.; Bugbee, B. Principles of nutrient and water management for indoor agriculture. Sustainability 2022, 14, 10204. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).