Abstract
The vibration performance is critical to the suspension control and the torque precision of the magnetically suspended momentum flywheel (MSMW). The translational and torsional vibration of the MSMW are investigated in this article, and the damping regulation method is proposed to improve the anti-vibration performance of the MSMW. Firstly, the modellings of the MSMW, including the dynamic models and the displacement coordinate, are developed, and the comprehensive damping characteristics of the MSMW are investigated. Moreover, the transfer functions of the translational and the torsional vibrations are established using the dimensionless model, and the relationship between the dynamic response and the stiffness/damping coefficient is studied. Furthermore, the numerical simulations of the dynamic response of the translational and torsional vibration are conducted. Finally, the experiments are designed to verify the vibration characteristics of the MSMW, and the dynamic displacements are measured to analyze the anti-vibration performance of the proposed damping regulation method. The results indicate that the displacement deflection of the translational vibration is reduced by 68.8%, and the angle deflection of the torsional vibration is mitigated by 71.2% by regulating the damping coefficient.
1. Introduction
The reaction wheel, as a kind of the inertial actuator, is widely used in satellites and spacecraft to realize the attitude control [1,2]. The reaction moment could be outputted by regulating the rotating speed around the axial axis of the flywheel rotor in the reaction wheel, and the support precision of the flywheel rotor is thus a critical factor affecting the control precision of the reaction moment [3,4]. For the mechanical reaction wheel with the mechanical bearings, the support accuracy of the flywheel rotor could be easily disturbed by the external disturbance and the self-excited vibration [5,6]. Therefore, the magnetic suspension technique was tried to suspend the flywheel rotor in the reaction wheel, and the five degrees of freedom (DoF) position and displacements of the flywheel rotor are controlled by the active magnetic bearing (AMB) [7,8,9]. Compared to the normal reaction wheel using the mechanical bearing, the magnetically suspended momentum flywheel (MSMW) has advantages such as non-contact suspension, no lubrication system, and active controllability.
Moreover, the vibration characteristics of the 5-DoF MSMW system are the foundation of the vibration control of the flywheel rotor suspended by the magnetic forces [10,11], and the stiffness and damping coefficients could be regulated to suppress the vibration magnitudes of the 5-DoF MSMW system [12]. The resonant vibration performance of the nonlinear AMB-rotor system was studied in [13], and a combination control model, including the proportional-derivative control model, the integral resonant control model, and the positive position feedback control model, was used to suppress the resonant vibration of the nonlinear rotor. For the magnetically suspended flywheel (MSFW) used in the energy storage system [14], the dynamic behavior and the suspension stability of the flywheel rotor on five DoFs were analyzed. For the magnetically levitated turbo molecular pump [15], the static/dynamic unbalance vibration performances of the rotor part suspended by the magnetic forces were researched, and the displacement deflections caused by the synchronous vibration were measured and analyzed. In reference [16,17], the vibration performances of the great-weight flywheel rotor were investigated, and the simulation and experimental results verified that the translational magnitude of the flywheel rotor could be effectively mitigated by regulating the damping coefficient. In [18], Cole and Fakkaew studied the dynamic characteristics of a thin-walled rotor suspended by the magnetic forces, and the coupling level of the magnetically levitated rotor was minimized. However, the abovementioned publications only investigated the translational vibration characteristics of the magnetically levitated rotor system, so the characteristics of the torsional vibration around the radial axis were not explored.
Furthermore, the vibration suppressing methods, including the auxiliary control devices [19,20] and the control methods [21], were also proposed to suppress the vibration magnitude of the MSFW system. On the one hand, to suppress the harmonic vibration of the magnetically suspended rotor, the supplementary vibration control devices were designed to mitigate the vibration magnitude of the magnetically suspended rotor in [19,20], and the results indicated that the displacement deflections were reduced greatly. However, the supplementary vibration control devices need the additional space so that the structure becomes more complex. On the other hand, the control methods were also used to minimize the vibration response of the magnetically suspended rotor. The decoupling method was applied to the vibration reduction of the magnetically suspended rotor [22,23], and the vibration amplitude of the rotor part was reduced by 55% by measuring the dynamic displacements. In reference [24,25], the notch filter was designed to suppress the harmonic vibration of the AMB-rotor system, and the experiments were conducted on a Lorentz-force type magnetic bearing and a magnetically suspended rotor, respectively. The variable angle compensator was used to control the synchronous vibration of the magnetically suspended rigid rotor [26], and the experimental results showed that the dynamic displacement of the rigid rotor was reduced from 0.025 mm to 0.015 mm. In those control methods, most researchers tried to analyze and suppress translational vibration of the magnetically suspended rotor on three translational DoFs, and the torsional vibrations of the magnetically suspended rotor around the two torsional DoFs were not researched in detail.
Above all, the research on the magnetically suspended rotor was focused on the analysis and control of the translational vibration, but the torsional vibration of the flywheel rotor also disturbs the suspension precision and the moment precision of the MSMW system. Therefore, the vibration characteristics of a 5-DoF MSMW system are fully analyzed in this article, and the translational and torsional vibration of the flywheel rotor suspended by the magnetic forces are investigated. Moreover, the damping regulation method is proposed to mitigate the translational and torsional vibration of the MSMW.
In this article, the force characteristics and the displacement coordinate of the 5-DoF.
MSMW are studied in Section 2. The translational vibration model of the flywheel rotor is established in Section 3, and the torsional vibration model of the flywheel rotor is devel-oped in Section 4. Furthermore, in Section 5, the numerical simulation of the dynamic response of the translational and torsional vibrations is conducted. The experiments and measurements about the dynamic displacements of the 5-DoF MSMW are performed in Section 6. Finally, the conclusions about the vibration characteristics and the anti-vibration performance are summarized in Section 7.
2. Force Modelling of 5-DoF MSMW
2.1. System View of 5-DoF MSMW
The structure of the 5-DoF MSMW system is shown in Figure 1a. The axial 3-DoF AMB unit at the lower end and the upper end of the stator base could control the axial displacements of the flywheel rotor, and the resultant torques could control the deflection angles of the flywheel rotor around the two radial axes. The radial 2-DoF AMB unit could generate the magnetic forces to control the radial displacements of the flywheel rotor. Therefore, the 5-DoF active position control of the flywheel rotor is accomplished by the axial 3-DoF AMB unit and the radial 2-DoF AMB unit. Moreover, the protective bearings at the lower end and the upper end of the stator base could protect the flywheel rotor when the axial 3-DoF AMB unit and the radial 2-DoF AMB unit fail to provide the magnetic forces. The coreless brushless DC motor (BLDCM) could realize the speed regulation of the flywheel rotor around the axial principal axis. Furthermore, the displacement coordinate of the 5-DoF MSFW controlled by the axial 3-DoF AMB and the 2-DoF radial AMB is defined in Figure 1b. The translational displacements of the flywheel rotor on three DoFs are defined as [x, y, z]. The torsional angles of the flywheel rotor around two DoFs are defined as [β, −α], the β is the torsional angle of the flywheel rotor around the y-axis, and the α is the torsional angle of the flywheel rotor around the x-axis. For the 5-DoF displacements of the MSWM, there are coupling terms caused by the dynamic coupling and the gyroscopic effect, but the coupling effect among 5-DoF displacements is not considered and analyzed in this article. Moreover, the 1-DoF rotation of the flywheel rotor around the z-axis is controlled by the BLDCM, and the rotating speed of the flywheel rotor is defined as Ω. The torque arm of the axial 3-DoF AMB is la, and the span distance of the axial displacement sensor is ls.

Figure 1.
The system view of the 5-DoF MSFW. (a) The main components of the 5-DoF MSMW; (b) the displacement terms of the 5-DoF MSMW.
2.2. Displacement and Force Coordinates of 5-DoF MSMW
The displacement terms of the flywheel rotor on five DoFs are controlled by the axial 3-DoF AMB and the radial 2-DoF AMB. As shown in Figure 2a, the EM windings at the negative and positive directions of the x-axis and the y-axis could generate the magnetic forces to realize the difference control of the flywheel rotor. Thus, for the 2-DoF suspension of the flywheel rotor along the radial directions, the attractive magnetic forces fr = [fy+, fy−, fx+, fx−] generated by the radial 2-DoF AMB could control the radial displacements of the flywheel rotor along the y-axis and the x-axis.

Figure 2.
The structure and force models of the 2−DoF radial AMB. (a) The top view of the 2−DoF radial AMB; (b) the force distributions of the 2−DoF radial AMB.
In Figure 3a, the eight EM windings at the upper and lower ends of the stator base could generate the magnetic force to control the axial suspension of the flywheel rotor. Moreover, in Figure 3b, the EM windings at the lower and upper ends of the stator base could also generate the deflection torques to control the torsion of the flywheel rotor around the radial axes. For the one DoF axial suspension of the flywheel rotor, the resultant attractive force of the magnetic forces [fuz1, fuz2, fuz3, fuz4, flz1, flz2, flz3, flz4] could control the axial displacement of the flywheel rotor in the z-axis. Moreover, the deflection torques Ta= [Tα, Tβ] are generated to control the torsions of the flywheel rotor around the y-axis and the x-axis, so the deflection torques could be expressed as
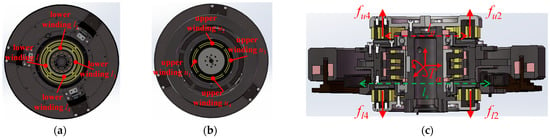
Figure 3.
The structure and force models of the 3-DoF axial AMB. (a) The upper end of the 3-DoF axial AMB; (b) the force distributions of the 3-DoF axial AMB; (c) the force distributions of the 3-DoF axial AMB.
Based on the suspension model and the torsional model shown in Figure 2a and Figure 3c, the dynamic models of the flywheel rotor with the magnetic forces are written into
Therefore, the attractive magnetic forces of the axial 3-DoF AMB and the radial 2-DoF AMB could be regulated to realize the stable suspension and the vibration suppression of the 5-DoF MSMW when the disturbance forces and torques are imposed on it.
Furthermore, according to the displacement coordinate of the 5-DoF MSMW in Figure 1b, the displacement terms could be obtained by the differential signals of the displacement sensors in the radial and axial axes, so the translational displacements of the flywheel rotor on three DoFs could be expressed as
The torsional angles of the flywheel rotor on two DoFs could be written into
Thus, the displacement terms of the 5-DoF MSMW could be obtained by the axial and radial displacement sensors, and the axial displacement z and the torsional angle α are measured and analyzed to investigate the vibration characteristics of the 5-DoF MSMW in following simulations and experiments.
2.3. Translational Stiffness and Damping Characteristics of 5-DoF MSMW
The attractive magnetic forces generated by the axial 3-DoF AMB and the radial 2-DoF AMB could be approximately expressed as the linear functions about the displacement term and the control current, and there are
Because the flywheel rotor suspended by the axial 3-DoF AMB and the radial 2-DoF AMB is not a self-stabilizing system, the displacement feedback model in Figure 4 is designed to realize the stable suspension control of the 5-DoF MSMW. The reference displacements are chosen as the system input of the feedback control model, and then the errors between the reference displacements and the outputted displacements are used as the input of the stiffness/damping regulator to generate the control voltages. Furthermore, the control voltages are converted to the control currents of the electromagnetic windings by the power amplification units. Finally, based on the dynamic models of the 5-DoF MSMW and the feedback control loop, the suspension displacements of the rotor could be actively controlled. The bandwidth of the AMB is 10 kHz, and the damping regulation based on the feedback control causes a little influence on the bandwidth of the AMB.

Figure 4.
The feedback model used in the displacement control of the 5-DoF MSMW.
In detail, considering the proportional-derivative model is used to regulate the stiffness/damping coefficients, it could be expressed as
For the power amplification unit of realizing the conversion between the control voltage and the control current, it could be designed as
Based on (2), the dynamic model of the flywheel rotor with the magnetic force could be written to
In addition, the displacement sensitivity of the eddy-current sensor is defined as ks. The closed-loop transfer function from the reference displacement to the outputted displacement could be written to
Furthermore, the equivalent damping and stiffness coefficients of the axial 3-DoF AMB and the radial 2-DoF AMB could be obtained as follows
Therefore, based on the closed-loop feedback control and the stiffness/damping regulator, the magnetic forces generated by the axial 3-DoF AMB and the radial 2-DoF AMB could be controlled to realize the stable suspension and the active vibration suppression of the flywheel rotor on five DoFs. In detail, based on Equation (10), the comprehensive damping and stiffness could be regulated, and then the dynamic response could be tuned, too, based on Equation (10).
2.4. Torsional Stiffness and Damping Characteristics of 5-DoF MSMW
The deflection torques generated by the axial 3-DoF AMB unit could be used to control the torsion motions of the flywheel rotor around the radial axis, and the torsional stiffness and damping characteristics could be also obtained to regulate the deflection torques in (1).
Similarly, the equivalent damping and stiffness coefficients of the deflection torques could be, respectively, expressed as
So, the comprehensive damping and stiffness coefficients of the axial 3-DoF AMB unit could also be regulated to improve the anti-vibration performance of the 5-DoF MSMW.
3. Translational Vibration Modelling of 5-DoF MSMW
3.1. Translational Vibration Model of 5-DoF MSMW
During the operation process of the 5-DoF MSMW, by regulating the rotating speed of the momentum wheel, the vibration displacement of the momentum wheel could affect the stability of the 5-DoF MSMW, and the vibration model should be established. The equivalent vibration models of the 5-DoF MSMW are shown in Figure 5 when it is mounted on the shacking table. In detail, the equivalent translational vibration is illustrated in Figure 5a, and the equivalent torsional vibration model is shown in Figure 5b. For the axial displacement of the 5-DoF MSMW, the axial displacement of the stator base is defended as zs, and the axial displacement of the flywheel rotor is defined as zr. For the radial displacement of the 5-DoF MSMW, the radial displacement of the flywheel rotor is defined as xr during the torsional state, and the torsional angle of the flywheel rotor is chosen as β. For the stiffness and damping coefficients of the whole system, the stiffness and damping parameters of the connection joint between the stator base of the 5-DoF MSMW and the shacking table are defined as Kj and Cj. For the axial 3-DoF AMB unit, the translational stiffness and damping coefficients are Ka and Ca, respectively. The torsional stiffness and damping coefficients unit are Kta and Cat, separately.
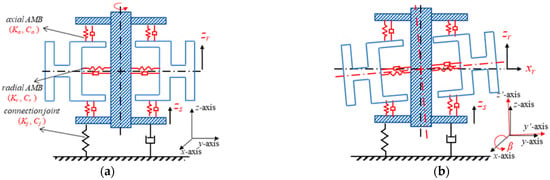
Figure 5.
The force models of the 5-DoF MSMW on the shacking table. (a) The equivalent translational vibration model of the 5-DoF MSMW; (b) the equivalent torsional vibration model of the 5-DoF MSMW.
For the translation vibration of the 5-DoF MSMW shown in Figure 5a, the dynamic models in the axial direction could be expressed as
where ms is the mass of the stator base, and mr is the mass of the flywheel rotor. fs is the excitation force acting on the stator base, and it is usually expressed as .
Furthermore, Equation (12) could be rewritten into
where Zr and Zs are both the complex numbers indicating the displacement variations.
By bring the displacement terms with Zr and Zs together, there are
For the displacement term Zr of the FW rotor, we get the following function
The dynamic displacements of the FW rotor and then stator in the 5-DoF MSMW could be solved as follows:
The vibration transfer functions of the stator base and the flywheel rotor in the axial direction could be written into
Moreover, the frequency response function of the stator base is expressed as
The frequency response function of the flywheel rotor could be written to
where the natural vibration frequency of the stator base is , and the natural vibration frequency of the flywheel rotor is . The frequency ratios of the stator base and the flywheel rotor are and , respectively. The equivalent damping coefficients of the stator base and the flywheel rotor are and . The mass ratio between the stator base and flywheel rotor is .
Given that mass ratio νm is a constant value, by simplifying the transfer functions of the translational vibration models, (18) and (19) could be further written to
where the system coefficients are
Finally, the vibration magnitudes of the stator base and the flywheel rotor are
Therefore, the vibration amplitudes of the stator base and the flywheel rotor in the axial direction could be evaluated by the above Equations.
3.2. Translational Vibration Model of 5-DoF MSMW with Active Controllable Stiffness and Damping
For the 5-DoF MSMW system, the stiffness and the damping coefficients could be regulated by tuning the control current of the axial 3-DoF AMB. When the damping coefficient of the axial AMB is tuned to a low value, the axial 3-DoF AMB could be considered as a pure mass suspension model, and comprehensive damping could be expressed as
Thus, the vibration models of the flywheel rotor could be regarded as a pure mass term mounted on the stator base. Equations (18) and (19) could be simplified into
When the stiffness coefficients of the axial 3-DoF AMB are tuned to a low term, the natural frequency decided by the comprehensive stiffness could be expressed as
Furthermore, the vibration equations could be expressed to
Therefore, in this case, the natural vibration frequency is decreased when the stiffness coefficient of the axial 3-DoF AMB is tuned to a low value, and the suspension model of the axial 3-DoF AMB could be simplified to a pure damper system.
4. Torsional Vibration Modelling of 5-DoF MSMW
4.1. Torsional Vibration Model of 5-DoF MSMW
As shown in Figure 5b, the disturbances acting on the flywheel rotor could also lead to the torsional vibration along the radial axes. The disturbance forces on the flywheel rotor could be transferred to the disturbance torques Ts, and the torsional angle of the flywheel rotor around the x-axis is β. For the deflection torque generated by the axial 3-DoF AMB to control the torsional motion of the flywheel rotor, the stiffness coefficient could be defined as Kta, and the damping coefficient is Cta. For the connection joint between the 5-DoF MSMW and the shacking table, the torsional stiffness coefficient is Ktj, and the torsional damping coefficient is Ctj. Therefore, the torsional vibration models of the flywheel rotor and the stator base could be written to
The transfer functions of the torsional vibrations are expressed as
The dimensionless transfer functions of the torsional vibrations could be furthermore written to
where the natural frequency of the stator base’s torsional vibration is , and the natural frequency of the flywheel rotor’s torsional vibration is . The torsional frequency ratios of the stator base and the flywheel rotor between the rotating frequency are and , respectively. The equivalent damping coefficients of the torsional vibration are and . The moment of inertial ratio between the stator base and the flywheel rotor is .
Given the moment of inertial ratio νj is a fixed value, the torsional functions in (31) could be further simplified to
where the system coefficients of the torsional vibration are
Finally, the response magnitudes of the torsional vibration are
Therefore, the torsional vibrations of the stator base and the flywheel rotor around the radial axes could be evaluated by the above equations, and the response magnitude could be regulated by tuning the damping coefficients.
4.2. Torsional Vibration Model of 5-DoF MSMW with Active Controllable Stiffness and Damping
For the torsional vibration of the 5-DoF MSMW, the stiffness and the damping coefficients could be regulated by tuning the control current of the axial 3-DoF AMB unit. When the damping coefficient of the axial 3-DoF AMB unit is tuned to a low value, the comprehensive damping of the axial 3-DoF AMB unit could be expressed as
Thus, the torsional vibration models of the flywheel rotor could be regarded as a pure mass block mounted on the stator base and the shock machine. The dynamic equations of the torsional vibration could be further written to
When the stiffness coefficients of the axial 3-DoF AMB unit is tuned to a low value, and the natural frequency of the torsional vibration is
Furthermore, the transfer equations of the torsional vibration could be expressed to
The natural frequency of the torsional vibration is decreased when the stiffness coefficient of the axial 3-DoF AMB unit is tuned to a low term, and the torsional model could be simplified to a pure damper system.
5. Numerical Simulation
In order to verify the vibration characteristics and the analysis results of the 5-DoF MSMW in the above sections, the simulations are conducted to analyze the translational and torsional vibrations of the 5-DoF MSMW. The response magnitude of the transfer function is used to the evaluate the vibration characteristics of the translation and torsion. The parameters of the 5-DoF MSMW are shown in Table 1, and the corresponding stiffness and damping coefficients of the axial 3-DoF AMB unit and the radial 2-DoF AMB unit used in the simulation are introduced in the following sections.

Table 1.
The system parameters of the 5-DoF MSMW.
5.1. Translational Vibration of 5-DoF MSMW
Firstly, based on the analysis results in Section 4, the vibration characteristics of the 5-DoF MSMW along the axial direction are simulated and analyzed. When the stiffness coefficient of the axial 3-DoF AMB unit is defined as Ka = 500, the response magnitudes of the translational vibration with different damping coefficients are plotted in Figure 6a. In detail, as shown by the red line, the maximum magnitude of the translational vibration is about 26.08 dB at the frequency 87.25 Hz when the damping coefficient is Ca = 0.04. When the damping coefficient is increased to Ca = 0.10, the maximum magnitude of the translational vibration is reduced to 9.34 dB. Therefore, the damping coefficient of the axial 3-DoF AMB unit could suppress the response magnitude of the translational vibration. Moreover, when the damping coefficient of the axial 3-DoF AMB unit is chosen as the fixed value Ca = 0.06, the response magnitudes of the translational vibration at different stiffness coefficients are shown in Figure 6b. The response magnitude is marked by the red line when the stiffness coefficient is Ka = 200, and the maximum response magnitude is 18.31 dB when the response frequency is at 86.5 Hz. The maximum value of the response magnitude is about 24 dB at 84.5 Hz when the stiffness coefficient is increased to Ka = 800. According to the response curves, the variation of the stiffness coefficient causes little influence on the response magnitude, but it could change the natural response frequency of the translational vibration.
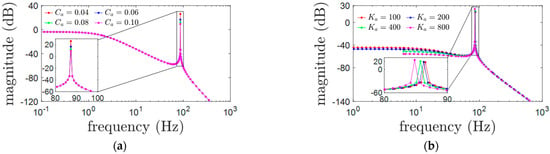
Figure 6.
The translational vibration of the flywheel rotor along the axial direction. (a) The translational vibration amplitudes of the flywheel rotor with different damping coefficients; (b) the translational vibration amplitudes of the flywheel rotor with different stiffness coefficients.
5.2. Torsional Vibration of 5-DoF MSMW
According to the analysis results in Section 3.1, the torsional vibration of the 5-DoF MSMW around the radial axis is simulated and analyzed. For the connection joint in the simulation, the torsional stiffness coefficient is defined as Kjt = 58, and the torsional damping coefficient is chosen as Cjt = 0.025. For the flywheel rotor, the response curves of the torsional vibration are plotted in Figure 7 when the stiffness coefficient and the damping coefficient of the axial 3-DoF AMB unit are chosen as different values. As shown in Figure 7a, the stiffness coefficient of the axial 3-DoF AMB unit is defined as Kat = 5, and the vibration magnitude of the torsional vibration is −33.52 dB at the 475 Hz when the damping coefficient is chosen as Cat = 0.4. The vibration magnitude of the torsional vibration is reduced to 41.1 dB when the damping coefficient is increased to Cat = 1.0. Thus, the response magnitude of the torsional vibration could be mitigated by the damping coefficient of the axial 3-DoF AMB unit. The frequency of the torsional vibration could also be regulated by the stiffness coefficient, and the resonant vibration of the torsion could be avoidable. As illustrated in Figure 7b, the vibration magnitude of the torsional vibration is 8.58 dB when the stiffness coefficient is defined as Kat = 4, and it is changed to 26.9 dB when the stiffness coefficient is increased to 32. Therefore, for the torsional vibration of the 5-DoF MSMW, the damping coefficient of the axial 3-DoF AMB unit could effectively control the vibration magnitude, and then the stiffness coefficient could change the natural frequency of the torsional vibration.
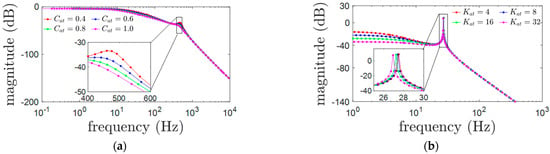
Figure 7.
The torsional vibration of the flywheel rotor along the axial direction. (a) The torsional vibration amplitudes of the flywheel rotor with different damping coefficients. (b) The torsional vibration amplitudes of the flywheel rotor with different stiffness coefficients.
6. Experimental Validation
6.1. Vibration Measurement System of 5-DoF MSMW
To evaluate the vibration performances of the 5-DoF MSMW, the experiments are conducted on the shock table in Figure 8. For the translational vibration measurement in Figure 8a, the 5-DoF MSMW is located on the shock table. The excitation forces generated by the shock machine are imposed on the 5-DoF MSMW and the connection joint in the z-axis. For the torsional vibration measurement, the 5-DoF MSMW is mounted on the connection joint, and the torsional disturbances outputted by the shock machine are imposed on the 5-DoF MSMW around the x-axis. Moreover, the displacement sensors mounted on the stator part of the 5-DoF MSMW could detect the dynamic displacements of the flywheel rotor in radial and axial directions. Those displacement signals are also fed back to the control system of the axial 3-DoF AMB units, and then the magnetic forces along the axial and radial directions could be regulated to suppress the vibration disturbance. In the meantime, the accelerators mounted on the shock table could also measure the dynamic vibration signals of the 5-DoF MSMW suffering the disturbances of the shock machine. The other important parameters are listed in Table 1. For the 5-DoF MSMW, the mass is 12.5 kg, the equatorial moment of inertia is 0.29 kgm2, and the polar moment of inertia 0.15 kgm2. For the axial 3-DoF AMB unit, the current stiffness is 128 N/A, and the displacement stiffness is −132.7 N/mm. For the radial 2-DoF AMB unit, the current stiffness is 132.26 N/A, and the displacement stiffness is −352 N/mm.

Figure 8.
The vibration experimental systems of the 5-DoF MSMW. (a) The translational vibration system of the 5-DoF MSMW. (b) The torsional vibration system of the 5-DoF MSMW.
In the experiment, the 5-DoF MSMW is located on the shock table along the z-axis, and then the impulse and random disturbances generated by the shock table could be imposed on the MSMW. In order to make the momentum wheel stably suspended at the equilibrium position, the stiffness and damping coefficients could be regulated to generate the magnetic forces according to Equations (10) and (11), and then the disturbance imposed on the MSMW could be actively suppressed.
6.2. Translational Vibration Experiment of 5-DoF MSMW
For the translational vibration of the 5-DoF MSMW, the vibration characteristics along the radial axes are similar to the vibrations along the axial axis, so the vibration characteristics of the MSMW along the axial axis is chosen as the example in the experiment. In the translational vibration experiment of 5-DoF MSMW in Figure 8a, the impulse disturbance, the harmonic disturbance, and the random disturbance in Table 2 generated by the shock table are respectively imposed on the 5-DoF MSMW. When the impulse disturbance with 10 N is imposed on the 5-DoF MSMW along the axial direction, the axial displacement curves of the 5-DoF MSMW using different damping coefficient of the 3-DoF axial AMB unit are plotted in Figure 9a. As marked by the blue line, the displacement deflection in the axial direction is −0.45 μm when the damping coefficient of the axial AMB unit is Ca = 0.06. The displacement deflection plotted by the red line is reduced to −0.14 μm when the damping coefficient is increased to Ca = 0.10. Moreover, the random disturbance is imposed on the 5-DoF MSMW along the axial direction, and the displacement curves of the flywheel rotor are plotted in Figure 9b. The root mean square (RMS) value is used to evaluate the axial displacement of the flywheel rotor. As plotted by the green line, the RMS is 0.063 μm when the damping coefficient is Ca = 0.06. The RMS of axial displacement is mitigated to 0.015 μm when the damping coefficient is increased to Ca = 0.10.

Table 2.
The sine−swept vibration source.
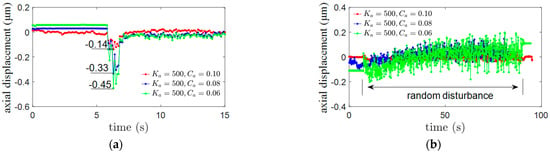
Figure 9.
The translational displacements of the 5−DoF MSMW with different types of disturbances. (a) The axial translational displacements of the flywheel rotor suffering the impulse disturbance with different damping coefficients. (b) The axial translational displacements of the flywheel rotor suffering the random disturbance with different damping coefficients.
Meanwhile, the axial displacements of the flywheel rotor at different excitation frequencies are plotted in Figure 10 when the sine-swept vibration source (in T) is imposed on the 5-DoF MSMW along the axial direction. The maximum displacement deflection of the axial vibration occurs at the 85 Hz, and the displacement deflection of the flywheel rotor in the axial direction is mitigated by the damping coefficient. The maximum deflection of the axial displacement (shown by the green line) is 0.54 μm when the damping coefficient is Ca = 0.06. When the damping coefficient is increased to 0.10, the maximum deflection of the axial displacement shown by the red line is 0.06 μm.
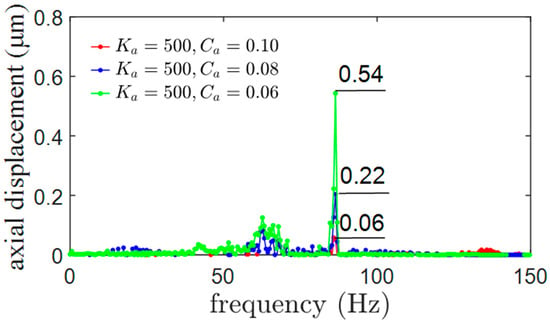
Figure 10.
The translational displacements of the 5-DoF MSMW at different excitation frequencies.
Therefore, based on the displacement measurement of the 5-DoF MSMW along the axial direction, the increase in the damping coefficient could effectively control the vibration magnitude of the 5-DoF MSMW.
6.3. Torsional Vibration Experiment of 5-DoF MSMW
As illustrated in Figure 8b, the torsion measurements of the 5-DoF MSMW suffering the different types of disturbances conducted as well as the torsional angle of the flywheel rotor could be obtained by measuring the axial displacements around the radial axes. Firstly, the torsional angles of the flywheel rotor suffering the impulse disturbance are plotted in Figure 11a. The torsional angle of the flywheel rotor is −0.80° shown by the green line when the torsional damping is Cat = 0.6 and it is reduced to −0.23°, shown by the red line when the torsional damping is increased to Cat = 1.0. In addition, the torsional angles of the flywheel rotor suffering the random disturbance are illustrated in Figure 11b, the root mean square (RMS) value of the torsional angle is 0.060° with the torsional damping Cat = 0.6, and then the RMS value of the flywheel rotor’s torsional angle is reduced to 0.032° when the torsional damping is increased to Cat = 1.0.
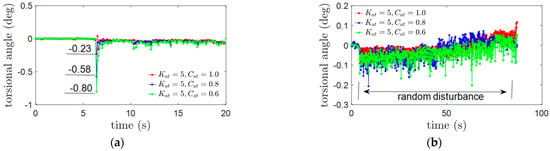
Figure 11.
The torsional angles of the 5−DoF MSMW with different types of disturbances. (a) The torsional angles of the flywheel rotor suffering the impulse disturbance with different damping coefficients; (b) The torsional angles of the flywheel rotor suffering the random disturbance with different damping coefficients.
Moreover, the radial displacements of the flywheel rotor at 2000 rpm are measured to analyze the vibration characteristics of the s5-DoF MSMW with different damping coefficients, and the radial displacements and the power spectrum diagram are plotted in Figure 11. The maximum deflection value of the radial displacement is 0.12 μm when the torsional damping is chosen as Cat = 0.6. The maximum deflection of the radial displacement is mitigated to 0.05 μm at the damping coefficient Cat = 1.0. In addition, as shown in Figure 12b, the power spectrum density of the radial displacement is also reduced by increasing the damping coefficients.
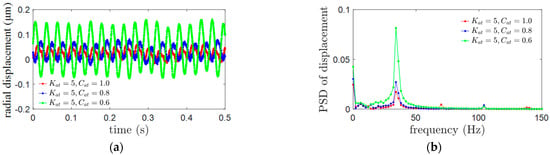
Figure 12.
The vibration characteristics of the 5−DoF MSMW when the rotating speed is 2000 rpm. (a) The radial displacement of the flywheel rotor at 2000 rpm. (b) The power spectrum density of the radial displacement at 2000 rpm.
Thus, the torsion experiments of the 5-DoF MSMW verify that the damping coefficient of the axial 3-DoF AMB unit may control the torsional vibration of the flywheel rotor.
7. Conclusions
The suspension stability and position precision of the 5-DoF MSMW are important to guarantee the output precision of the reaction torque, so the vibration characteristics and the anti-vibration ability of the 5-DoF MSMW are investigated in this article. In the theoretical analysis about the vibration characteristics of the 5-DoF MSMW, the vibration models of the 5-DoF MSMW including the translation and the torsion are developed, and the response functions indicate that the vibration magnitude could be mitigated by regulating the comprehensive damping coefficients. Moreover, the simulations and experiments are conducted to analyze the vibration characteristics of the 5-DoF MSMW. The simulation results show that the vibration magnitudes of the translation and torsion are suppressed by increasing the comprehensive damping coefficient. The experimental results present that the displacement deflection in the axial direction is reduced by 68.8% and the torsional angle around the radial axis could be mitigated by 71.2% by increasing the damping coefficient.
To further regulate the translational and torsional displacements of the MSMW, the optimization methods about the stiffness and damping coefficients could be considered in future work. Moreover, the stability control of the 5-DoF MSMW could be investigated considering the gyro effect at high rotating speed.
Author Contributions
Conceptualization, B.X. and H.L.; methodology, B.X. and H.L.; software, B.X. and H.L.; validation, B.X. and H.L.; formal analysis, H.L.; investigation, H.L.; resources, H.L.; data curation, B.X.; writing—original draft preparation, B.X. and H.L.; writing—review and editing, B.X. and H.L.; visualization, B.X. and H.L.; supervision, B.X. and H.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Mahfouz, A.; Pritykin, D.; Biggs, J. Hybrid Attitude Control for Nano-Spacecraft: Reaction Wheel Failure and Singularity Handling. J. Guid. Control. Dyn. 2021, 44, 548–558. [Google Scholar] [CrossRef]
- Ismail, Z.; Varatharajoo, R. A study of reaction wheel configurations for a 3-axis satellite attitude control. Adv. Space Res. 2009, 45, 750–759. [Google Scholar] [CrossRef]
- Kumar, K.D.; Godard; Abreu, N.; Sinha, M. Fault-tolerant attitude control of miniature satellites using reaction wheels. Acta Astronaut. 2018, 151, 206–216. [Google Scholar] [CrossRef]
- Abd-Elhay, A.-E.R.; Murtada, W.A.; Yosof, M.I. A high accuracy modeling scheme for dynamic systems: Spacecraft reaction wheel model. J. Eng. Appl. Sci. 2022, 69, 1–22. [Google Scholar] [CrossRef]
- Fu, C.; Sinou, J.-J.; Zhu, W.; Lu, K.; Yang, Y. A state-of-the-art review on uncertainty analysis of rotor systems. Mech. Syst. Signal Process. 2023, 183, 109619. [Google Scholar] [CrossRef]
- Jia, Q.; Li, H.; Chen, X.; Zhang, Y. Observer-based reaction wheel fault reconstruction for spacecraft attitude control systems. Aircr. Eng. Aerosp. Technol. 2019, 91, 1268–1277. [Google Scholar] [CrossRef]
- Tuysuz, A.; Achtnich, T.; Zwyssig, C.; Kolar, J.W. A 300 000-r/min Magnetically Levitated Reaction Wheel Demonstrator. IEEE Trans. Ind. Electron. 2018, 66, 6404–6407. [Google Scholar] [CrossRef]
- Xiang, B.; Liu, H.; Yu, Y. Gimbal effect of magnetically suspended flywheel with active deflection of Lorentz-force magnetic bearing. Mech. Syst. Signal Process. 2022, 173, 109081. [Google Scholar] [CrossRef]
- Zhai, L.; Han, B.; Liu, X.; Zhao, J. Losses estimation, thermal-structure coupled simulation analysis of a magnetic-bearing reaction wheel. Int. J. Appl. Electromagn. Mech. 2019, 60, 33–53. [Google Scholar] [CrossRef]
- Xiang, B.; Wen, T.; Liu, Z. Vibration analysis, measurement and balancing of flywheel rotor suspended by active magnetic bearing. Measurement 2022, 197, 111305. [Google Scholar] [CrossRef]
- Dagnaes-Hansen, N.A.; Santos, I.F. Magnetically suspended flywheel in gimbal mount-Test bench design and experimental validation. J. Sound Vib. 2019, 448, 197–210. [Google Scholar] [CrossRef]
- Dagnaes-Hansen, N.A.; Santos, I.F. Magnetically suspended flywheel in gimbal mount–Nonlinear modelling and simulation. J. Sound Vib. 2018, 432, 327–350. [Google Scholar] [CrossRef]
- Saeed, N.A.; El-Shourbagy, S.M.; Kamel, M.; Raslan, K.R.; Awrejcewicz, J.; Gepreel, K.A. On the Resonant Vibrations Control of the Nonlinear Rotor Active Magnetic Bearing Systems. Appl. Sci. 2022, 12, 8300. [Google Scholar] [CrossRef]
- Soni, T.; Dutt, J.K.; Das, A. Dynamic behavior and stability of energy efficient electro-magnetic suspension of rotors involving time delay. Energy 2021, 231, 120906. [Google Scholar] [CrossRef]
- Zheng, S.; Wang, C. Rotor Balancing for Magnetically Levitated TMPs Integrated With Vibration Self-Sensing of Magnetic Bearings. IEEE/ASME Trans. Mechatron. 2021, 26, 3031–3039. [Google Scholar] [CrossRef]
- Li, X.; Dietz, D.; An, J.; Erd, N.; Gemeinder, Y.; Binder, A. Manufacture and Testing of a Magnetically Suspended 0.5 kWh-Flywheel Energy Storage System. IEEE Trans. Ind. Appl. 2022, 58, 1–11. [Google Scholar] [CrossRef]
- Li, X.; Palazzolo, A.; Wang, Z. A Combination 5-DOF Active Magnetic Bearing for Energy Storage Flywheels. IEEE Trans. Transp. Electrif. 2021, 7, 2344–2355. [Google Scholar] [CrossRef]
- Cole, M.O.T.; Fakkaew, W. An Active Magnetic Bearing for Thin-Walled Rotors: Vibrational Dynamics and Stabilizing Control. IEEE/ASME Trans. Mechatron. 2018, 23, 2859–2869. [Google Scholar] [CrossRef]
- Xiang, B.; Wong, W. Electromagnetic vibration absorber for torsional vibration in high speed rotational machine. Mech. Syst. Signal Process. 2020, 140, 106639. [Google Scholar] [CrossRef]
- Lusty, C.; Keogh, P. Active Vibration Control of a Flexible Rotor by Flexibly Mounted Internal-Stator Magnetic Actuators. IEEE/ASME Trans. Mechatron. 2018, 23, 2870–2880. [Google Scholar] [CrossRef]
- Hutterer, M.; Wimmer, D.; Schrödl, M. Control of magnetically levitated rotors using stabilizing effects of gyroscopes. Mech. Syst. Signal Process. 2021, 166, 108431. [Google Scholar] [CrossRef]
- Numanoy, N.; Srisertpol, J. Vibration Reduction of an Overhung Rotor Supported by an Active Magnetic Bearing Using a Decoupling Control System. Machines 2019, 7, 73. [Google Scholar] [CrossRef]
- Xiang, B.; Wong, W. Decoupling control of magnetically suspended motor rotor with heavy self-weight and great moment of inertia based on internal model control. J. Vib. Control 2021, 28, 1591–1604. [Google Scholar] [CrossRef]
- Gallego, G.B.; Rossini, L.; Achtnich, T.; Araujo, D.M.; Perriard, Y. Novel Generalized Notch Filter for Harmonic Vibration Suppression in Magnetic Bearing Systems. IEEE Trans. Ind. Appl. 2021, 57, 6977–6987. [Google Scholar] [CrossRef]
- Peng, C.; He, J.; Deng, Z.; Liu, Q. Parallel mode notch filters for vibration control of magnetically suspended flywheel in the full speed range. IET Electr. Power Appl. 2020, 14, 1672–1678. [Google Scholar] [CrossRef]
- Gong, L.; Zhu, C. Synchronous Vibration Control for Magnetically Suspended Rotor System Using a Variable Angle Compensation Algorithm. IEEE Trans. Ind. Electron. 2020, 68, 6547–6559. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).