Analysis and Structure Optimization of Scissor-Type Micro-Stirrer with the Most Effective Output Performance for Thrombus Dissolution in Interventional Therapy
Abstract
1. Introduction
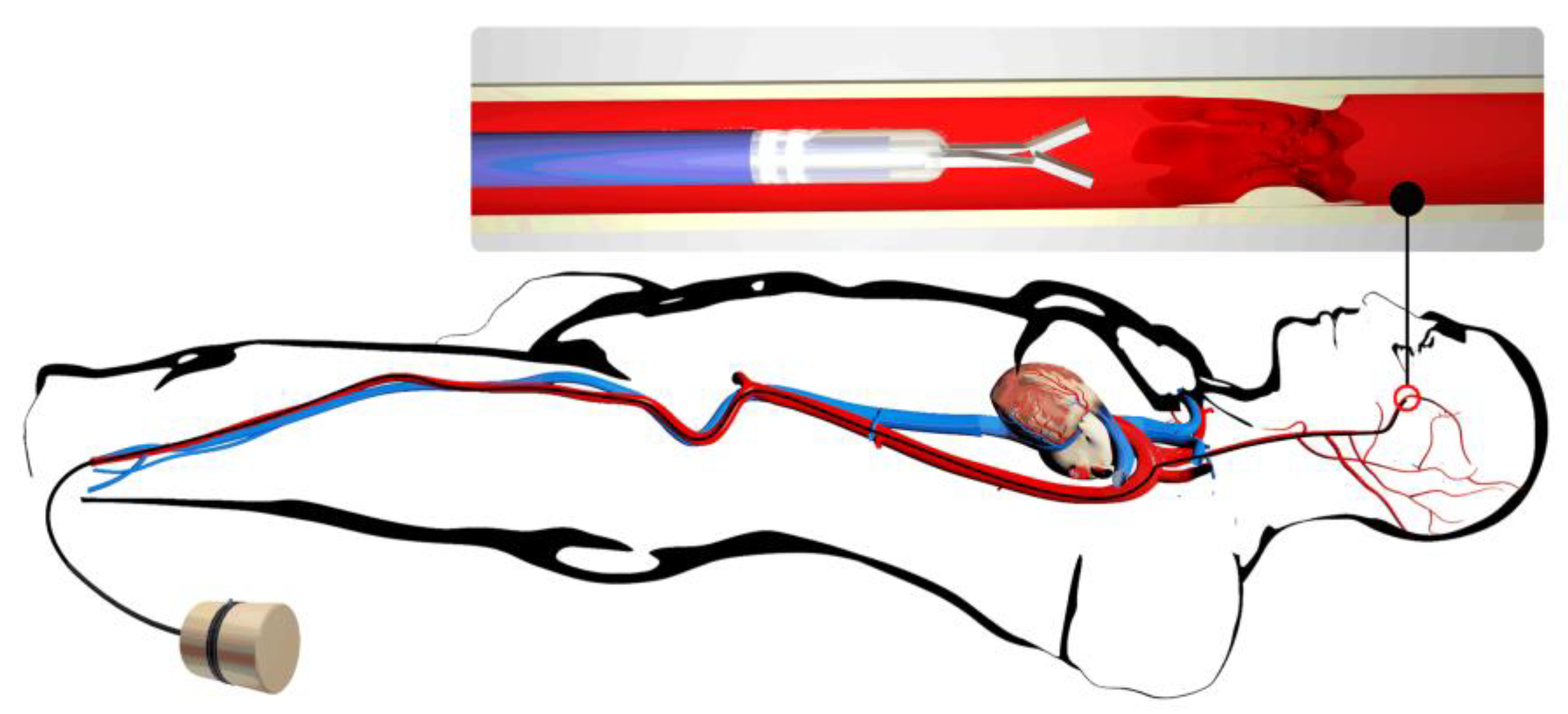
2. Design Concept and Evaluation
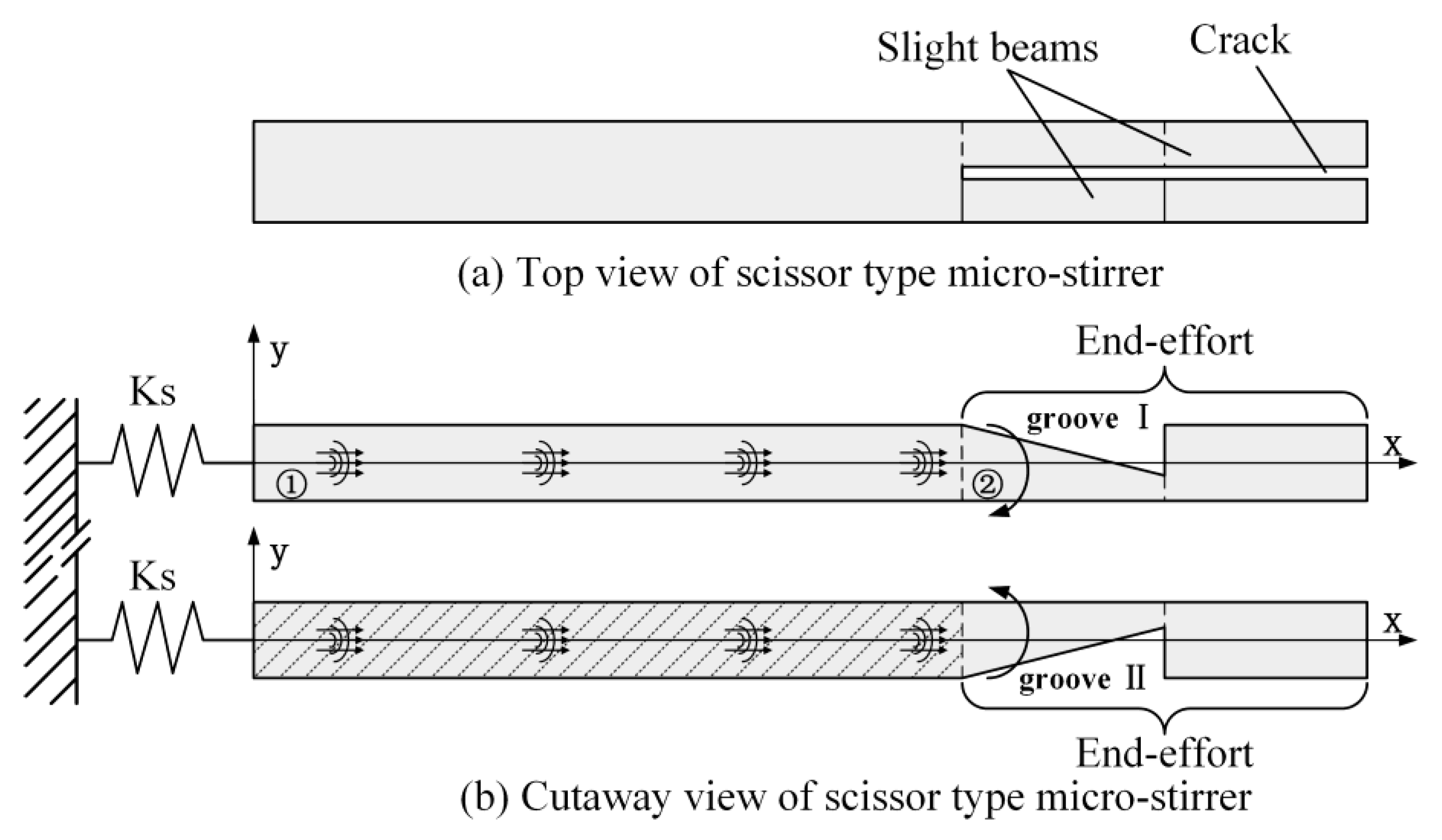
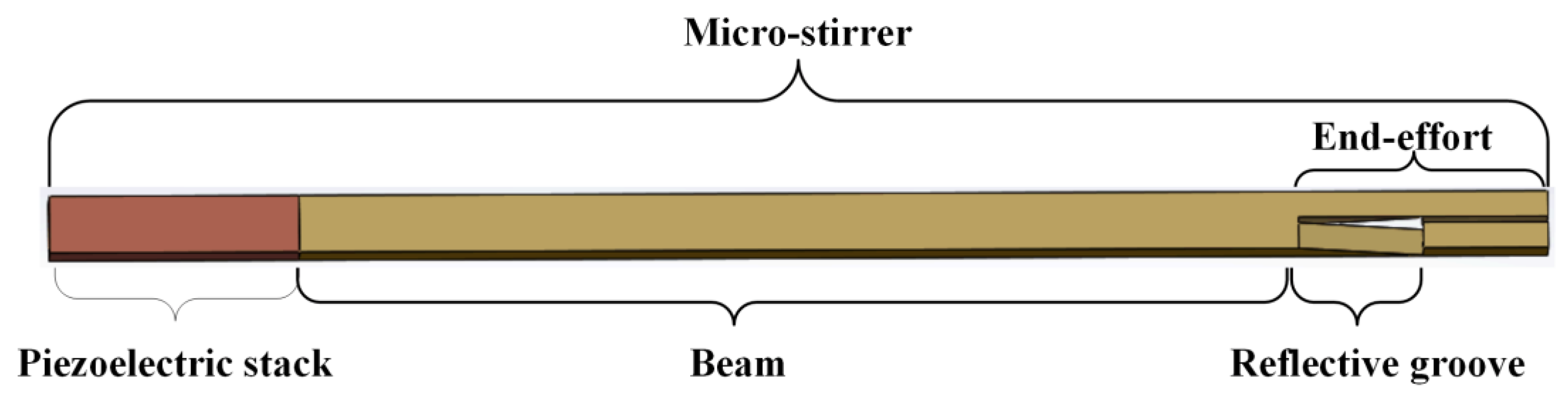
2.1. Concept of Structure Design
2.2. Evaluation of Stirrer Design
3. Structure Modeling and Optimization
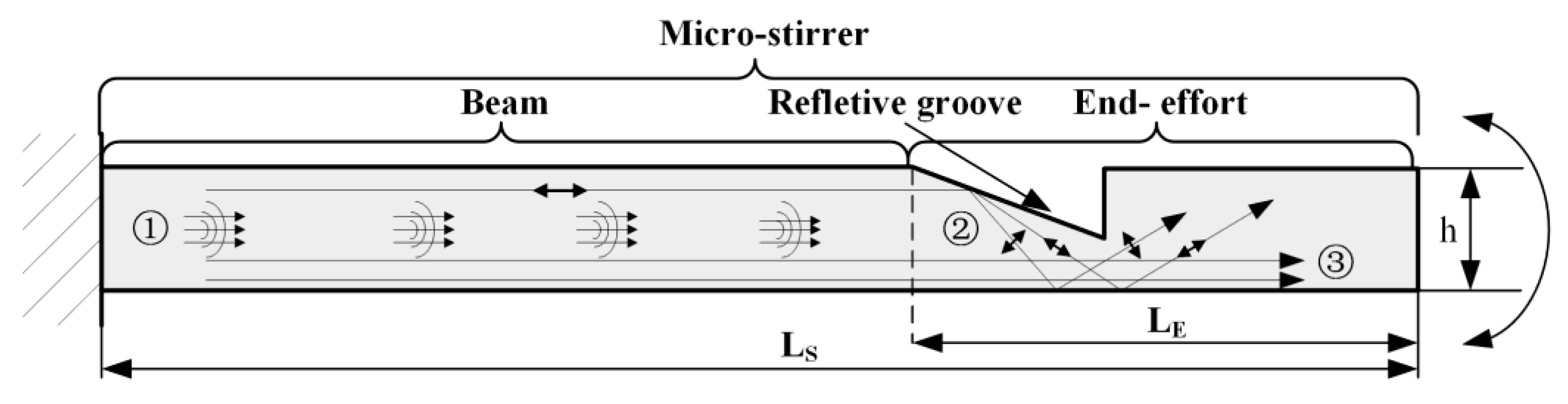
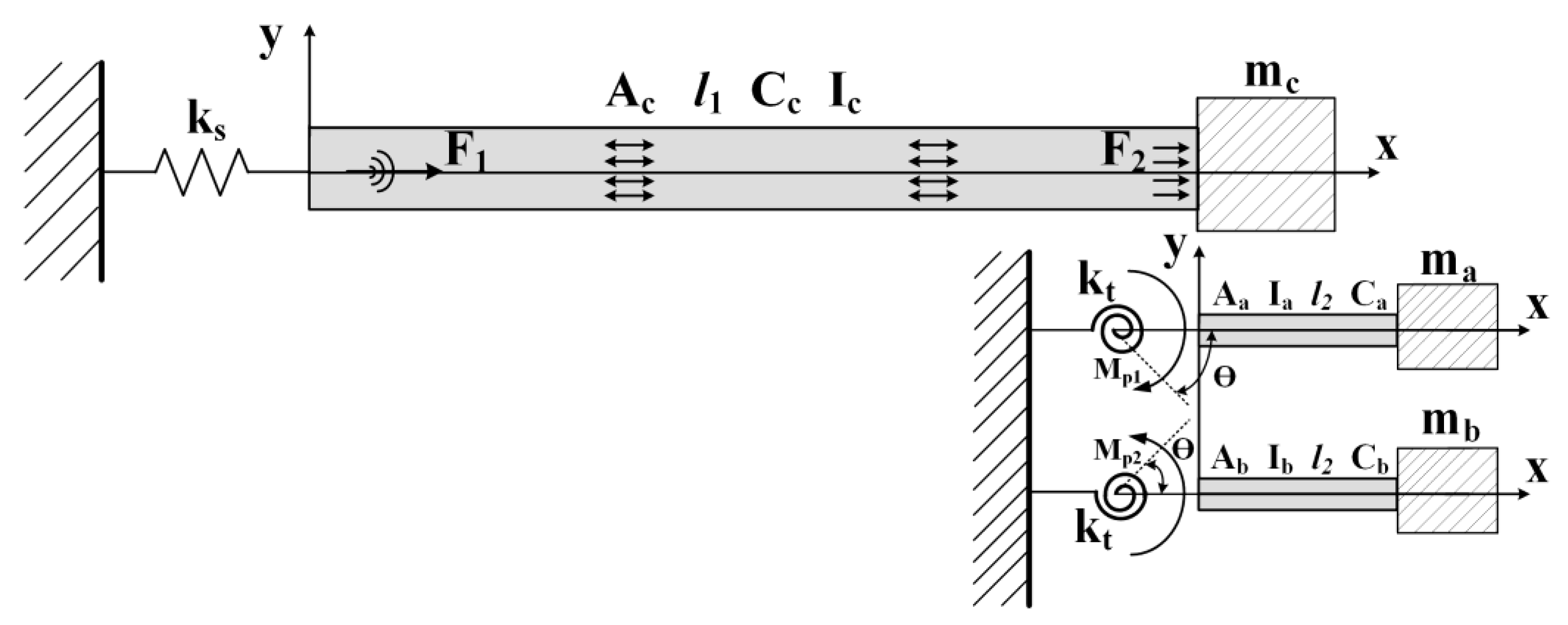
3.1. Mathematical Modeling
3.2. Structure Parameters Optimization
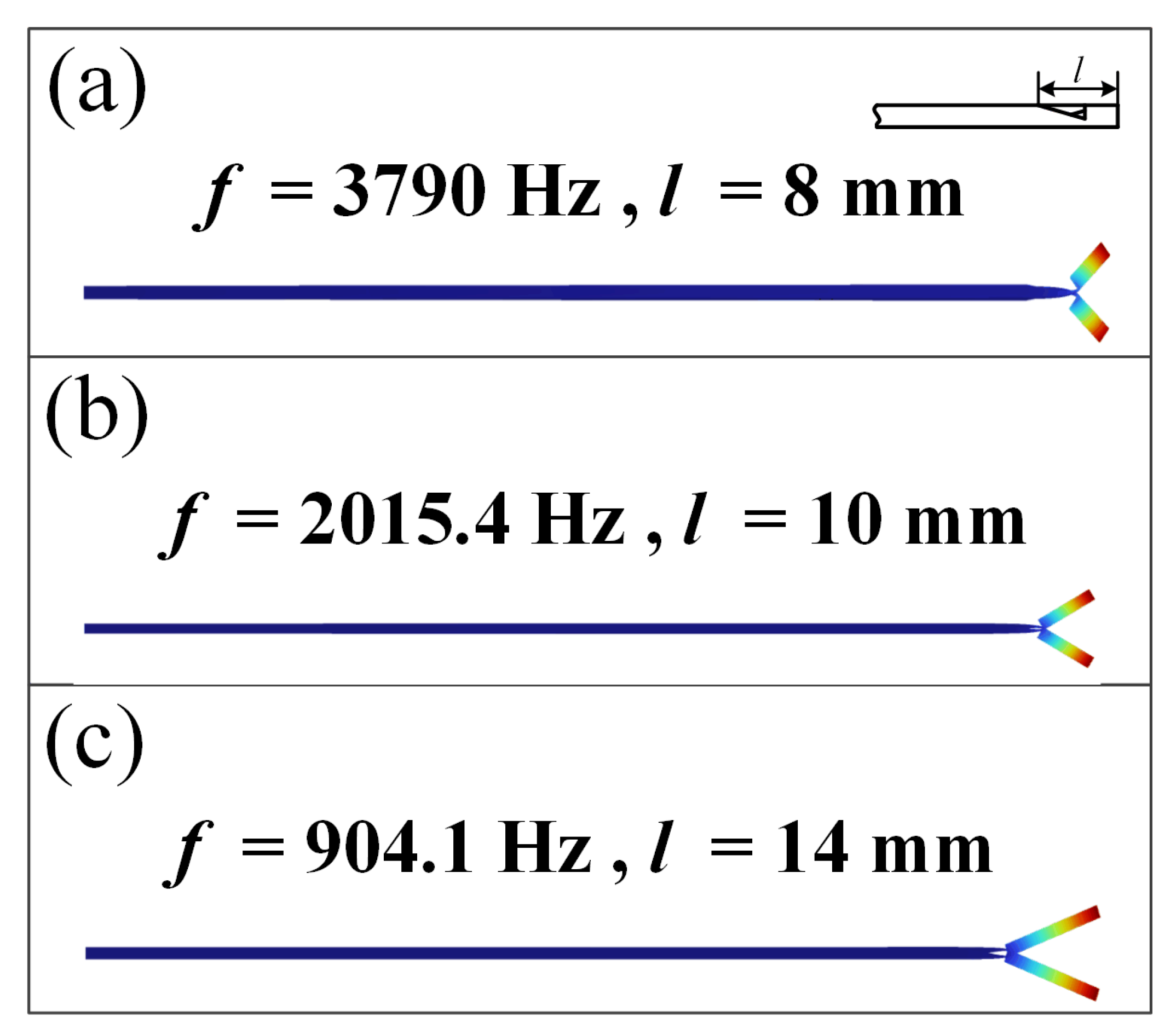
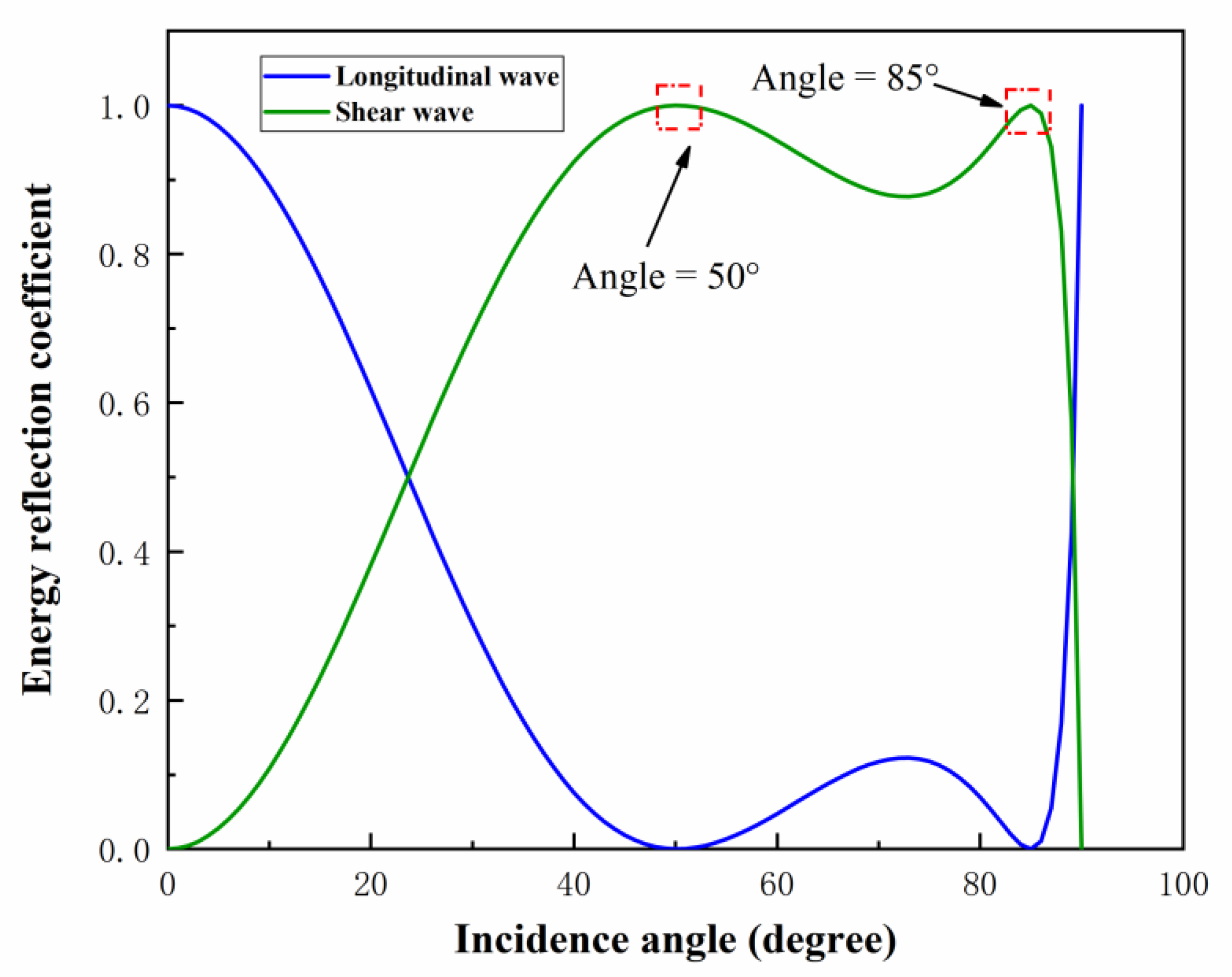
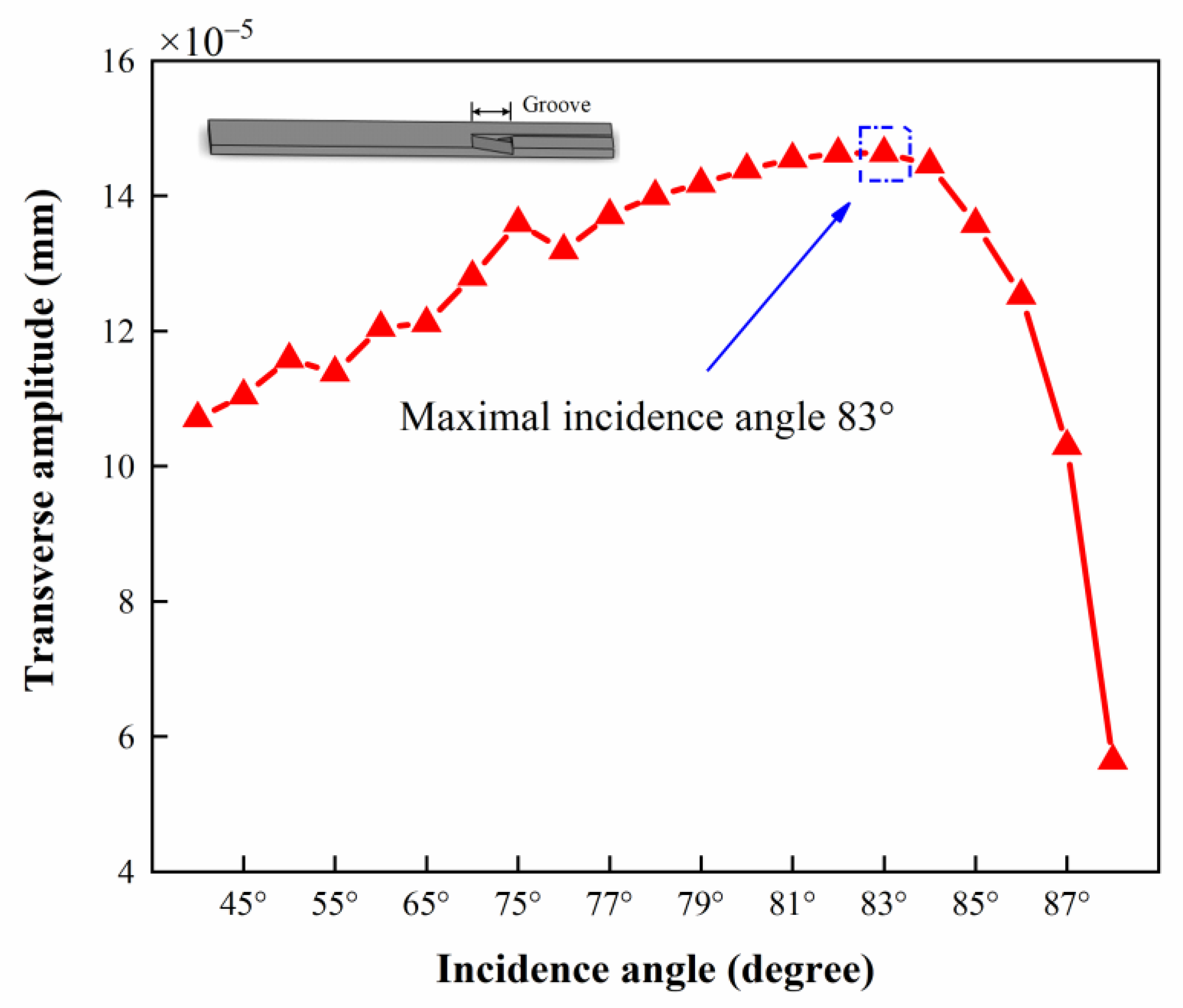
3.2.1. Incident Angle
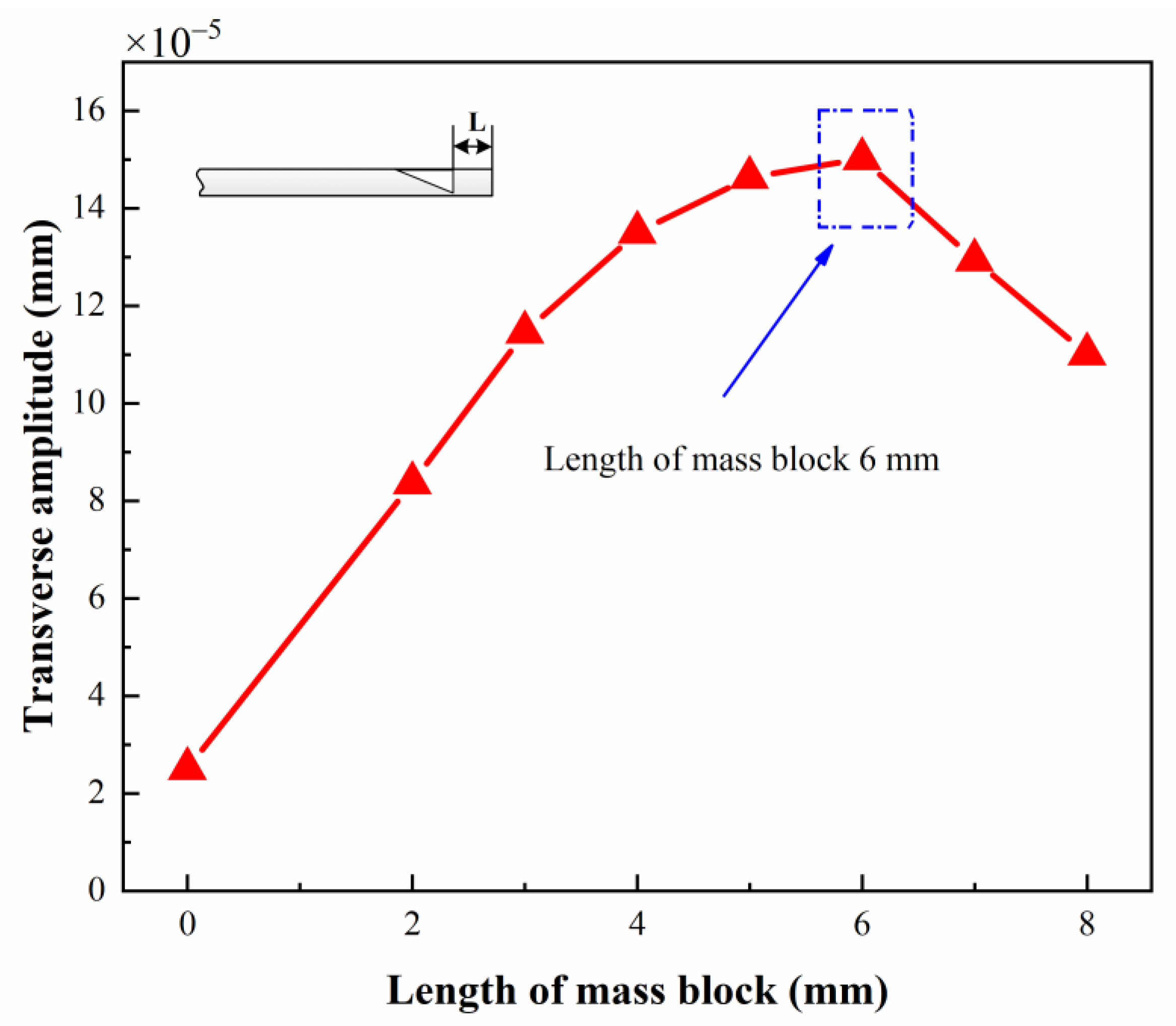
3.2.2. Inertia Mass
3.2.3. Stiffness
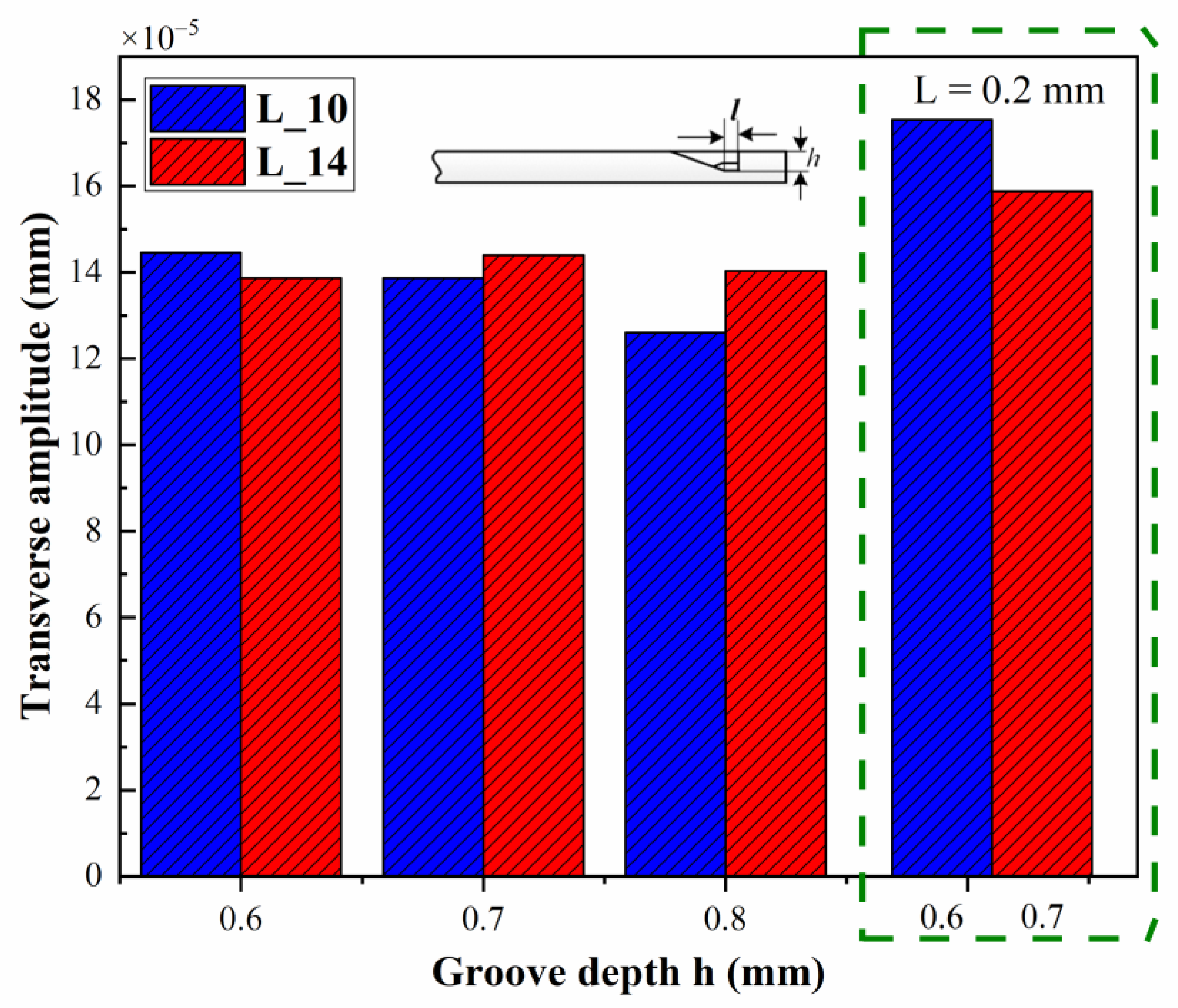
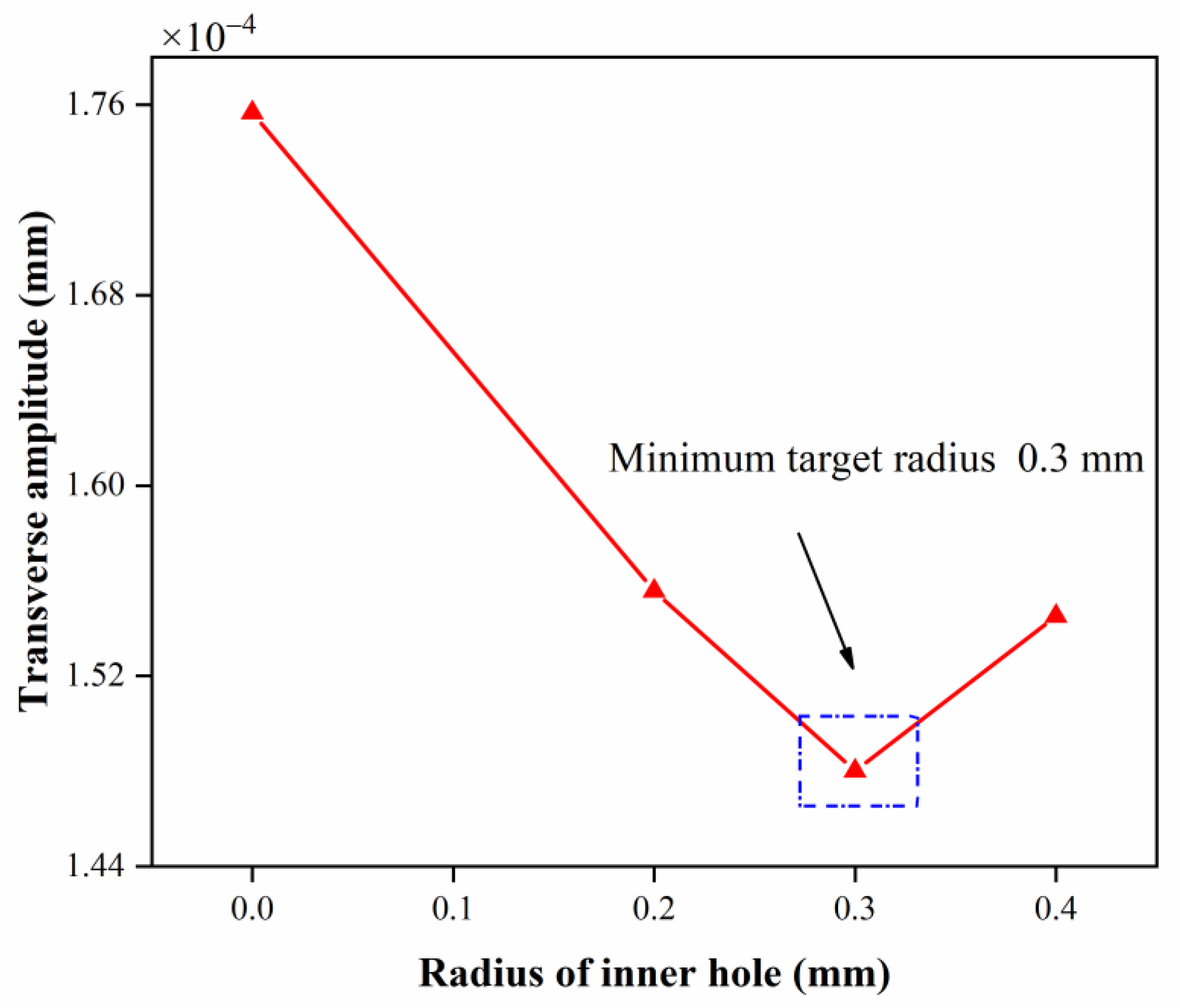
3.2.4. Inner Hole
4. Evaluation and Discussion
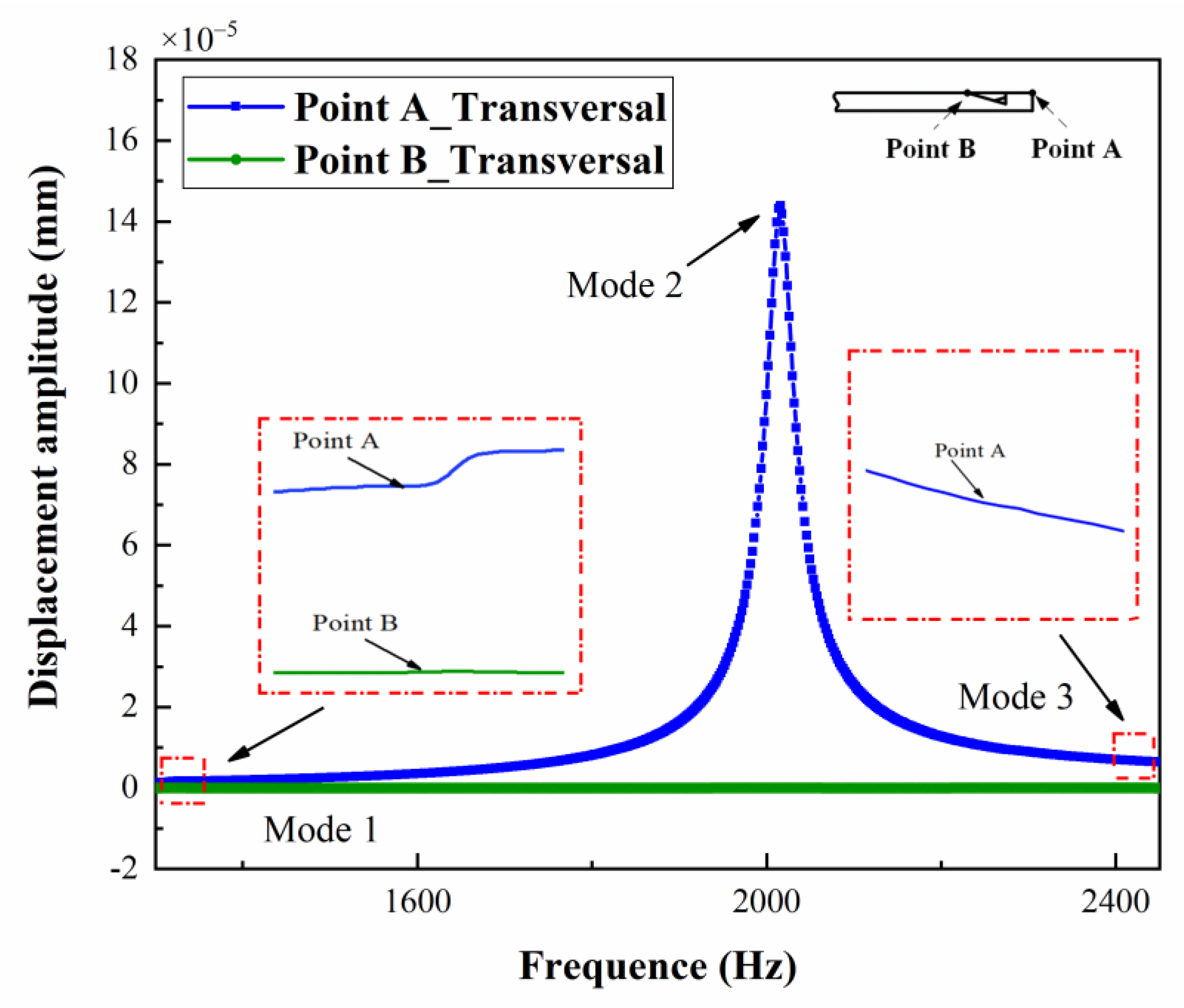
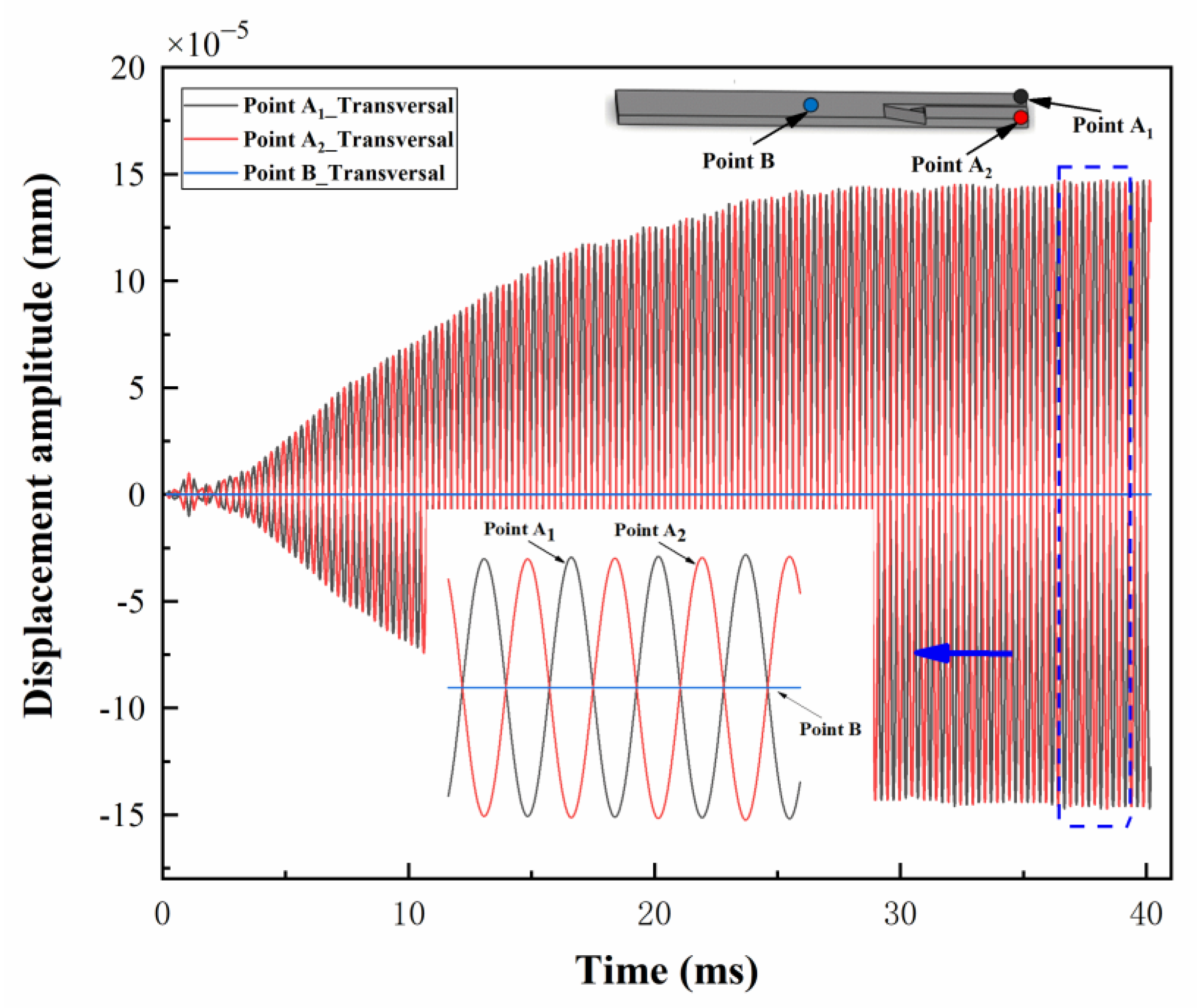
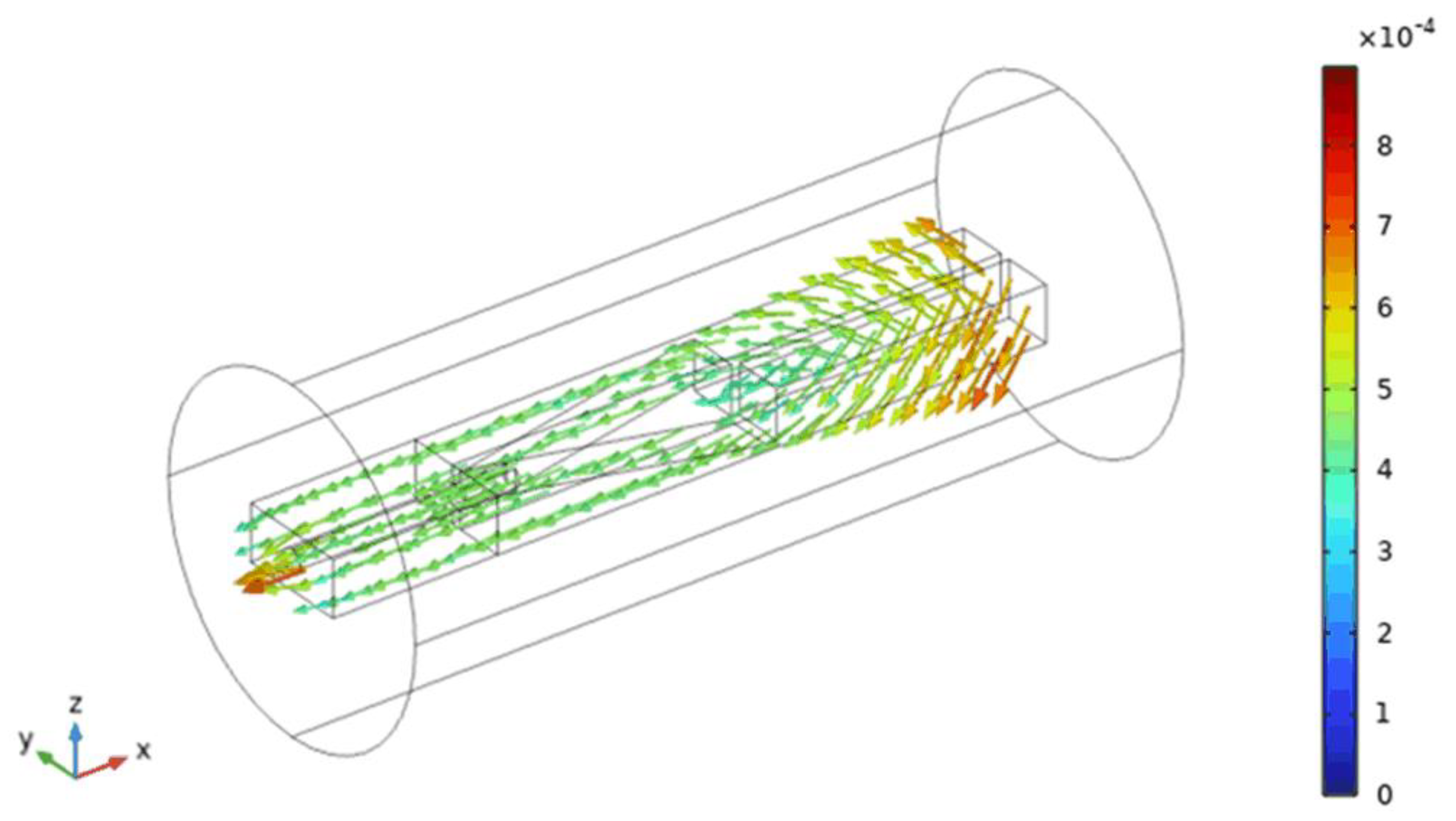
4.1. Fluid-Structure Interaction Simulation
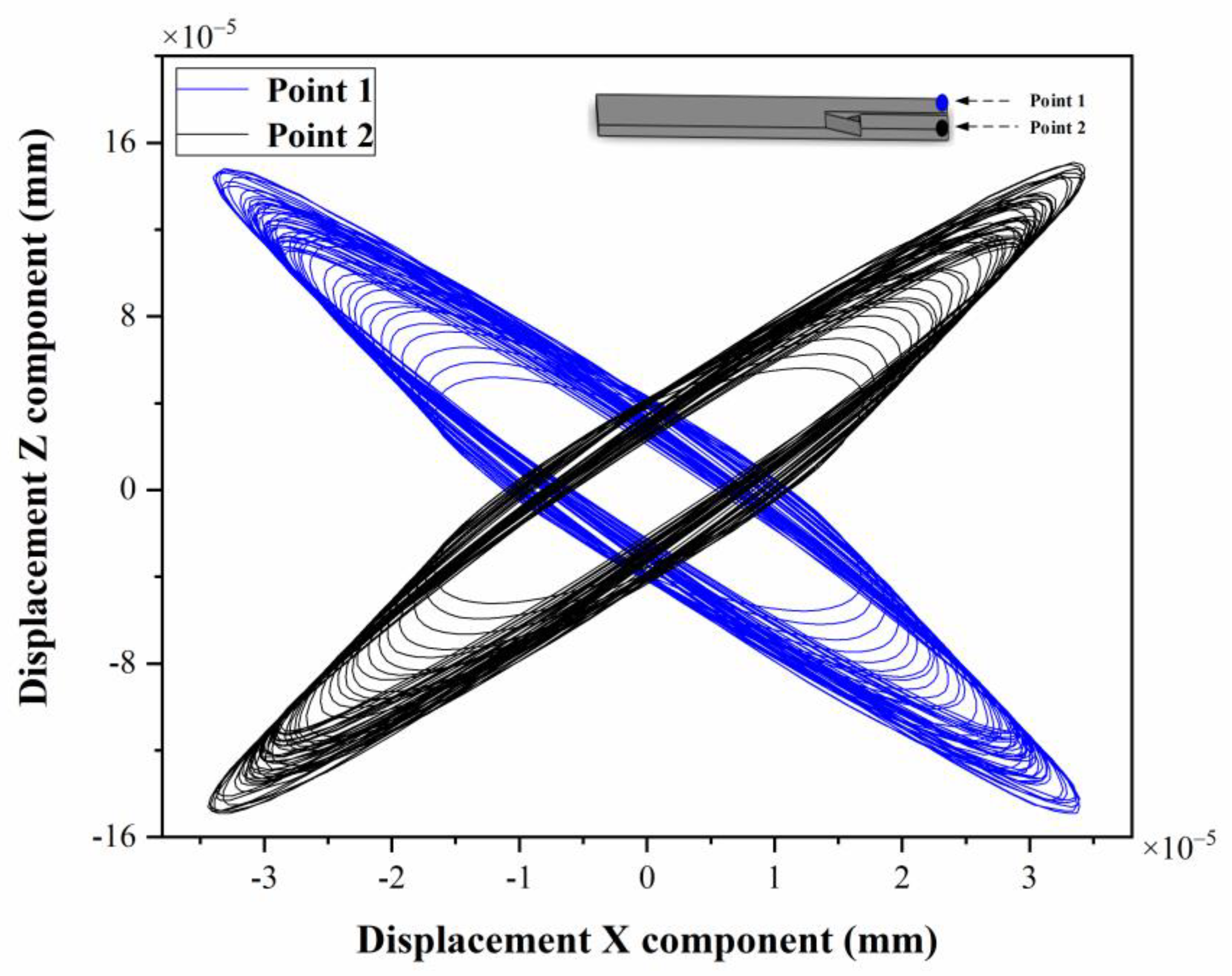
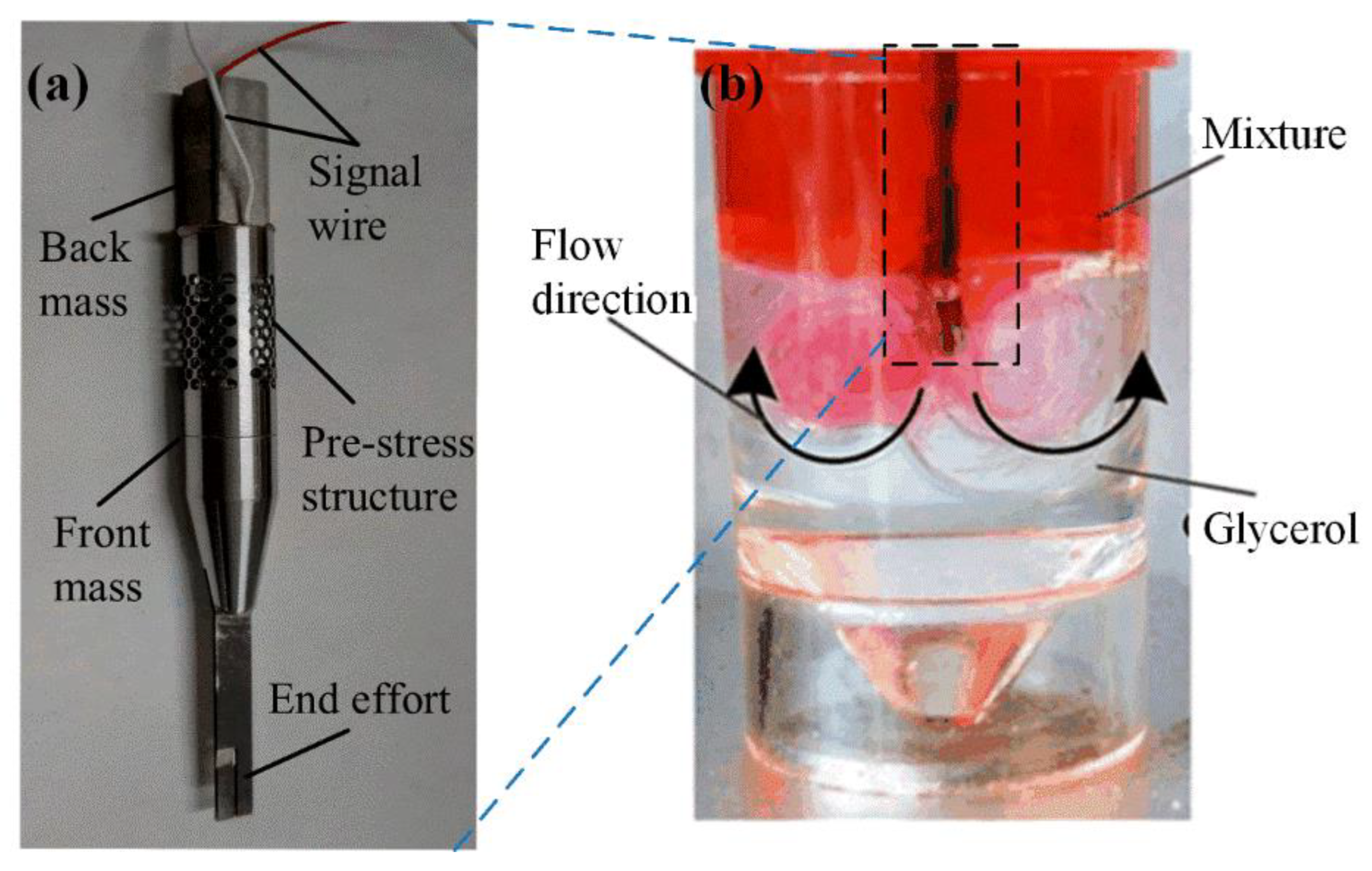
4.2. Experiment Analysis
4.3. Discussion of Advantages and Limitations
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Vos, T.; Lim, S.S.; Abbafati, C.; Abbas, K.M.; Abbasi, M.; Abbasifard, M.; Abbasi-Kangevari, M.; Abbastabar, H.; Abd-Allah, F.; Abdelalim, A.; et al. Global burden of 369 diseases and injuries in 204 countries and territories, 1990–2019: A systematic analysis for the Global Burden of Disease Study 2019. Lancet 2020, 396, 1204–1222. [Google Scholar] [CrossRef] [PubMed]
- Lindsay, M.P.; Norrving, B.; Sacco, R.L.; Brainin, M.; Hacke, W.; Martins, S.; Pandian, J.; Feigin, V. World stroke organization (WSO): Global stroke fact sheet 2019. Int. J. Stroke. 2019, 14, 806–817. [Google Scholar] [CrossRef] [PubMed]
- Mira, K.; Andreas, L. Global burden of stroke. Semin. Neurol. 2018, 38, 208–211. [Google Scholar]
- Paul, S.; Candelario-Jalil, E. Emerging neuroprotective strategies for the treatment of ischemic stroke: An overview of clinical and preclinical studies. Exp. Neurol. 2021, 335, 113518. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Q.; Shan, W.; Liu, L.; Fu, X.; Liu, P.; Hu, Y. Predictors of functional outcome and hemorrhagic complications in acute ischemic stroke patients treated with intravenous thrombolysis—A retrospective analysis. Int. J. Clin. Pharm. Ther. 2017, 55, 893–900. [Google Scholar] [CrossRef]
- Wang, R.; Zeng, J.; Wang, F.; Zhuang, X.; Chen, X.; Miao, J. Risk factors of hemorrhagic transformation after intravenous thrombolysis with rt-PA in acute cerebral infarction. QJM Int. J. Med. 2019, 112, 323–326. [Google Scholar] [CrossRef]
- Gill, D.; Baheerathan, A.; Aravind, A.; Veltkamp, R.; Kar, A. Severe Hemorrhagic Transformation after Thrombolysis for Acute Ischemic Stroke Prevents Early Neurological Improvement. J. Stroke. Cerebrovasc. 2016, 25, 2232–2236. [Google Scholar] [CrossRef]
- Park, T.H.; Lee, J.S.; Park, S.S.; Ko, Y.; Lee, S.J.; Lee, K.B.; Lee, J.; Kang, K.; Park, J.M.; Choi, J.C.; et al. Safety and Efficacy of Intravenous Recombinant Tissue Plasminogen Activator Administered in the 3 to 4.5 Hour Window in Korea. J. Stroke. Cerebrovasc. 2014, 23, 1805–1812. [Google Scholar] [CrossRef]
- Clark, W.M.; Madden, K.P. Keep the Three Hour TPA Window: The Lost Study of Atlantis. J. Stroke. Cerebrovasc. 2009, 18, 170. [Google Scholar] [CrossRef]
- Davis, S.M.; Donnan, G.A. 4.5 hours: The new time window for tissue plasminogen activator in stroke. Stroke 2009, 40, 2266–2267. [Google Scholar] [CrossRef]
- Leys, D.; Deplanque, D. Thrombolysis beyond the three-hour time window. Clin. Exp. Hypertens. 2006, 28, 313–316. [Google Scholar] [CrossRef] [PubMed]
- Katz, J.M.; Gobin, Y.P. Merci (R) retriever in acute stroke treatment. Expert. Rev. Med. Devic. 2006, 3, 273–280. [Google Scholar] [CrossRef] [PubMed]
- Alshekhlee, A.; Pandya, D.J.; English, J.; Zaidat, O.O.; Mueller, N.; Gupta, R.; Nogueira, R.G. Merci mechanical thrombectomy retriever for acute ischemic stroke therapy: Literature review. Neurology 2012, 79, S126–S134. [Google Scholar] [CrossRef] [PubMed]
- Son, S.; Choi, D.S.; Oh, M.K.; Hong, J.; Kim, S.K.; Kang, H.; Park, K.J.; Choi, N.C.; Kwon, O.Y.; Lim, B.H. Comparison of solitaire thrombectomy and penumbra suction thrombectomy in patients with acute ischemic stroke caused by basilar artery occlusion. J. Neurointerv. Surg. 2016, 8, 13–18. [Google Scholar] [CrossRef] [PubMed]
- Nogueira, R.G.; Frei, D.; Kirmani, J.F.; Zaidat, O.; Lopes, D.; Turk, A.S.; Heck, D.; Mason, B.; Haussen, D.C.; Levy, E.I. Safety and efficacy of a 3 -Dimensional stent retriever with aspiration-based thrombectomy vs. aspiration -based thrombectomy alone in acute ischemic stroke intervention: A randomized clinical trial. JAMA Neurolog. 2018, 75, 304–311. [Google Scholar] [CrossRef]
- Pereira, V.M.; Yilmaz, H.; Pellaton, A.; Slater, L.A.; Krings, T.; Lovblad, K.O. Current Status of Mechanical Thrombectomy for Acute Stroke Treatment. J. Neuroradiol. 2015, 42, 12–20. [Google Scholar] [CrossRef]
- Arai, D.; Ishii, A.; Chihara, H.; Ikeda, H.; Miyamoto, S. Histological Examination of Vascular Damage Caused by Stent Retriever Thrombectomy Devices. J. Neurointerv. Surg. 2016, 8, 992–995. [Google Scholar] [CrossRef]
- Mechanical Thrombolysis in Acute Stroke. Available online: http://emedicine.medscape.com/article/1163240-overview#a1 (accessed on 8 May 2017).
- Jiang, Z.W.; Liu, Z.H.; Kato, S.; Suzuki, M. Fundamental Study on a Novel Method for Dissolution of Cerebral Thrombus by Micro Piezo-stirrer. In Proceedings of the JSME-IIP/ASME-ISPS Joint Conference on Micromechatronics for Information and Precision Equipment, Yokohama, Japan, 16–18 June 2003. [Google Scholar]
- Jiang, Z.W.; Morita, M.; Watanabe, T.; Kato, S.; Suzuki, M. Study on In-vivo measurement of solubility for cerebral thrombus dissolution. Int. J. Appl. Electrom. 2006, 24, 225–234. [Google Scholar] [CrossRef]
- Yang, J.J.; Morita, M.; Jiang, Z.W. Design of a novel scissoring micro-stirrer for blood clot dissolution. Sens. Actuator. A Phys. 2016, 248, 130–137. [Google Scholar]
- Morita, M.; Yang, J.J.; Fujioka, Y.; Jiang, Z.W. A novel mechanical thrombectomy device based on complex longitudinal-torsional vibration. J. Adv. Mech. Des. Syst. 2018, 12, JAMDSM0086. [Google Scholar] [CrossRef]
- Ajoudanian, M.; Jiang, Z.W.; Morita, M. Study on a new type micro-stirrer excited by longitudinal elastic wave for thrombus dissolution. Int. J. Appl. Electrom. 2011, 37, 67–77. [Google Scholar] [CrossRef]
- Ajoudanian, M.; Jiang, Z.W.; Morita, M. Design of a novel type micro-stirrer excited by longitudinal elastic wave for thrombus dissolution. J. Biomech. Sci. Eng. 2011, 6, 262–269. [Google Scholar]
- Jen, C.; Kobayashi, M. Ultrasonic and Advanced Methods for Nondestructive Testing and Material Characterization, 1st ed.; Chen, C.H., Ed.; World Scientific Publisher: Singapore, 2007; Volume 1, pp. 33–40. [Google Scholar]
- Yang, J.J.; Xu, T.J. A novel phacoemulsification needle with scissor-like motion end effector for reducing heat generation at cornea incision. Sens. Actuator. A Phys. 2019, 288, 92–100. [Google Scholar] [CrossRef]




| Parameters | Value | Unit |
|---|---|---|
| Material | Titanium | — |
| Young’s modulus (E) | 115.7 | GPa |
| Density (ρ) | 4540 | Kg/m3 |
| Poisson’s ratio (ν) | 0.32 | — |
| Length of stirrer | 90 | mm |
| Length of end-effort | 10 | mm |
| Length of groove | 5 | mm |
| Length of PZT | 10 | mm |
| Width | 2 | mm |
| Thickness | 1 | mm |
| Groove angle | 80 | degree |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, J.; Rong, B.; Wang, L.; Morita, M.; Deng, G.; Jiang, Y.; Qian, J. Analysis and Structure Optimization of Scissor-Type Micro-Stirrer with the Most Effective Output Performance for Thrombus Dissolution in Interventional Therapy. Actuators 2023, 12, 60. https://doi.org/10.3390/act12020060
Yang J, Rong B, Wang L, Morita M, Deng G, Jiang Y, Qian J. Analysis and Structure Optimization of Scissor-Type Micro-Stirrer with the Most Effective Output Performance for Thrombus Dissolution in Interventional Therapy. Actuators. 2023; 12(2):60. https://doi.org/10.3390/act12020060
Chicago/Turabian StyleYang, Jingjing, Benyang Rong, Lei Wang, Minoru Morita, Guifang Deng, Yifan Jiang, and Junbing Qian. 2023. "Analysis and Structure Optimization of Scissor-Type Micro-Stirrer with the Most Effective Output Performance for Thrombus Dissolution in Interventional Therapy" Actuators 12, no. 2: 60. https://doi.org/10.3390/act12020060
APA StyleYang, J., Rong, B., Wang, L., Morita, M., Deng, G., Jiang, Y., & Qian, J. (2023). Analysis and Structure Optimization of Scissor-Type Micro-Stirrer with the Most Effective Output Performance for Thrombus Dissolution in Interventional Therapy. Actuators, 12(2), 60. https://doi.org/10.3390/act12020060





