Abstract
The article presents a comparison of the methods of modeling the underactuated ball and beam system. This study was carried out to select a model suitable for the development of a control system using the model-based design methodology. Firstly, the approach commonly used in research was verified. It was also examined whether it is important to take into account the eccentric fixation in these models. An original model taking into account friction resistance was also proposed. The considered models were simulated in Matlab/Simulink software environments and verified in reality. The obtained results were compared and analyzed.
1. Introduction
An underactuated system is interpreted as a mechanical system with more degrees of freedom than controlling inputs. One of the main reasons of underactuation is the presence of elastic or nonholonomic binds in the system. Dynamics of underactuated systems are usually non-linear, which makes their analysis using methods of classical control theory more difficult [1]. Research regarding effective controlling methods is still a current issue that is developed in many scientific facilities. Underactuated systems appear in many fields of industry and robotics; examples of this are industrial manipulators, walking robots, airplanes, watercrafts or rehabilitation equipment [2,3,4,5,6,7].
One of the most well-known examples of an underactuated mechanical system is a device called ‘ball and beam’. It consists of a straight beam (which can be turned along the horizontal axis) and a ball which lies on the beam and can roll to the left or right due to a tilt of the beam. By means of a review of construction solutions, one can notice that enforcing a tilt of the beam can be performed in a number of ways, e.g., by a band mechanism, in a system of hinged quadrangle or by a direct connection of the beam with an engine whereas the location of the ball is dependent on the dynamics of the entire set and cannot be directly controlled [8,9]. This system is thus insufficiently prompted and highly non-linear.
The first papers regarding the control of the ‘ball and beam’ system [10] go back as far as the end of the 1970s. In the following years, many papers were published covering various problems, including global stability or using newer and newer control algorithms, including fuzzy logic, neural networks or optimal control [11,12,13,14]. Most papers concern stabilizing the ball in a defined point of the beam. This problem is a popular example in control theory and it is well researched. Moving the ball from its initial location to another can be realized in an optimal way, by tilting the beam solely in the acceleration phase and decelerating the ball before the point of destination, without unnecessary beam oscillations. A similar issue is the problem of trajectory tracking, which is the basic challenge in controlling uncontrolled systems [15,16,17,18]. Designing such control systems and the selection of their retables can be led using simulation research. Suitable numerical models are needed for this and most mathematical models and is used while using control with compensation of the dynamics of the passive part [19].
A mathematical model is by definition a simplification of a real object and its accuracy and complexity should be adjusted to the considered problem. That is why, while modeling a typical ‘ball and beam’ system, a simplified model is most often used, similar to the dynamics of a ball on an inclined plane. At the stage of modeling, it is assumed that the eccentric fixation of the beam had a negligible influence on the behavior of the ball. There is no doubt that this is undisputable in devices where the axis of turning of the beam is near the edge on which the ball rolls. One can, however, notice that in some construction solutions this distance amounts to several dozen millimeters, which can influence the functioning of the system.
Thus far, no publication was found in which the influence of an eccentric fixation of the beam on the equations of the movement of the ball was analyzed. The aim of this paper is thus to verify if such an assumption is legitimate. The analysis of this problem is thus a novelty of this paper. The mathematical model for a system where the eccentric fixation is taken into account is described in the article.
The second issue considered in the publication was the inclusion of friction forces in the modelling. In the literature review, it was noted that the frictional forces are omitted in the form of a simplifying assumption. The authors were unable to find a paper in which the mathematical model of the ball-beam system took into account friction forces. It is also difficult to find works that show the correlation between the numerical model and the experimental setup (despite the fact that this arrangement is a commonly used academic example). However, we can find papers on the validation of simulation models for other underactuated mechanical systems, in which a very good correlation with experimental data was achieved. An example can be the work [20] with the Furuta Pendulum and Inertia Wheel Pendulum identification, where a complete generalized description of the identification process is given.
The motivation to undertake such research was the observation of the movement of the ball in the device, the construction form of which is shown in Figure 1. In this system, a steel bearing ball (1) rolls on the U-shaped aluminum profile (2). The device works in real-time mode using the RT-DAC/USB2 card (3) connected to PC with MATLAB Simulink software (4). An incremental encoder 1024 P/R—SparkFun COM-11102 (5) was used in the research. The displacement of the ball was recorded using a laser sensor Panasonic HG-C1400-P (6). As an actuator the motor Power HD WH-40KG Waterproof Titanium Gear Digital Servo (7) was used.

Figure 1.
The ball and beam system used in the research.
The mechanism enforcing the tilting of the beam in it operates based in the principle of a hinged quadrangle. The turning of the beam in it is realized by using a bearing of a roller screwed to a channel section on which the ball rolls. This way of placing the beam causes the system to differ from a classic inclined plane.
Designing advanced control algorithms is more and more often carried out using the model-based design methodology, where the settings of the control system are selected in numerical simulations using optimization methods. For this approach to be effective, it is necessary to have a numerical model as close as possible to the real system. This methodology is extremely useful in the design of complex dynamical systems. An example here may be uncontrolled systems, such as the considered ball and beam system, where optimal control requires the use of complex algorithms compensating the energy of the passive module, and the selection of settings of such regulators using the experimental method is very difficult [21,22,23,24]. Having an accurate numerical model therefore allows you to tune the control system in a way that is close to optimal. Properly correlated models can also be used as reliable reference plants, to learn about phenomena occurring in systems or as the increasingly popular digital twins [25,26,27].
2. Ball and Beam System Modeling
The task undertaken by the authors was to examine the effectiveness of various methods of modeling the ball-beam system, and to verify whether taking into account the friction forces and the eccentric bearing of the beam has a significant influence on the accuracy of the numerical model.
This paper describes three approaches to modeling such systems. In the first case, a simplified but also the most widely used model was used. Within the second approach equations of movement of the ball were derived while taking into account the turning of the beam along the axis moved from the plane of the ball’s movement. The third model was developed taking into account the friction forces in the contact between the ball and the beam.
Previous publications provide various approaches to modeling the ball and beam system. When it comes to running a numerical simulation and examining its dynamics, devising a model in the convention of multibody systems is sufficient, using, e.g., such programs like Simscape or Adams. Such modeling methodology allows performing simulation research, but the user does not have access to movement equations describing the behavior of an object. A mathematical model of the system may, however, be necessary in a situation where the user would like to apply an advanced controlling system, e.g., with a compensation function. That is when it is necessary to formulate the equations of motion [28].
The following three subsections present: The equations of motion for the model most often used in the literature, the mathematical model of the ball and beam system taking into account the eccentric attachment of the beam, and the model, including friction force acting on the ball.
In the general case, the equations of motion of underactuated mechanical systems can be expressed in vector form:
where is the inertia matrix, is the centrifugal and Coriolis matrix, is the gravity term, is a non-square matrix of external forces, is the actuator input vector and denotes the configuration vector, which, for the analysed ball and beam system, is:
These simple Lagrangian mechanical systems (1) may represent both an underactuated mechanical system as well as fully-actuated systems, according to the column rank of matrix [29]. In the ball and beam system, the angle of the inclination of the beam is controlled, and the displacement of the ball depends on this angle.
Due to the fact that, in mechatronic systems, servomotors are more and more often used where there is a velocity or position mode and only the equations of the ball movement were given. The analysis does not include the equations of the rotary movement of the beam. This assumption is also due to the fact that the beam dynamics equation depends on the design of the device and makes direct comparison impossible.
In the form of an introduction to the part discussing mathematical models, a scheme of the model illustrating the device used in conducted analysis has been presented in Figure 2.
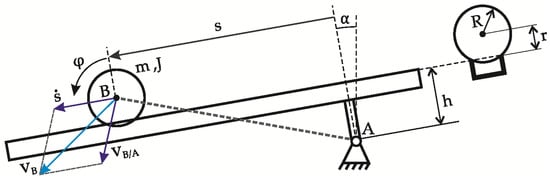
Figure 2.
Scheme of the ball and beam system.
In each of the following mathematical models, the same symbols are used:
- —ball displacement,
- —rotation angle of the ball
- —angle of beam deflection,
- —mass of ball,
- —ball’s moment of inertia,
- —ball radius,
- —rolling radius,
- —eccentricity,
- —gravity acceleration
2.1. Commonly Used Model
Withing the realization of this research, a review of publications regarding the ball and beam system has been performed. It has been noticed that the approach in which the equations of the movement of the ball on the beam have been compared to the equation of the movement of the ball rolling on an inclined plane is most often used. These equations, aside from inertia parameters, only include the angle of the inclination of the beam. Among others, the radius of the ball is omitted and it is assumed that the axis of rotation of the beam intersects the plane on which the ball rolls [30,31,32,33]. A mathematical model allowing a derivation of the linear acceleration of the rolling ball has been shown in Equation (3) and in the further part of the work it was called the “CUM Model”.
This equation can also be linearized around the operating point for small , when . It gives us the following linear approximation of the system:
2.2. Model with Eccentric Fixation
While attempting to derive the movement equations for the device elaborated by the authors, it was decided to verify what influence the off-centered bearing of the beam has on the dynamics of the ball and beam system. This model corresponds exactly to the scheme in Figure 2. Thus, in the mathematical model, both the radius and the distance of the axis of rotation of the beam from the plane on which the ball rolls have been taken into account. A similar approach to the modeling of the ball-beam system can be found in papers [34,35] while the authors only take into account the influence of the radius of the ball on the kinetic energy of the system. In the further part of this work, this model was called the “CAM model”.
In the considered case, the kinetic energy is expressed by:
where
The potential energy is described by the following equation:
Calculating the successive derivatives needed in the Lagrange equation of the second kind we have:
The equation of motion derived using the Langrage method of the second order have the following form:
2.3. Model with the Friction Forces Included
The third of the compared approaches to modeling the ball-beam system assumed the use of the CUM model (3) and the incorporation of the resistance forces occurring during the rolling of the ball on the beam. During the validation, various friction modeling methods were verified [36]. In this publication, a model was proposed in which velocity-dependent friction was used, and the friction force was determined using the modified approach proposed by Specker et al. [37,38]. In the proposed model, the sign function is approximated by the hyperbolic tangent function with the transition velocity , which defines the slope of the force in the static. This parameter should be estimated as well as the value of the damping coefficient . Thus, the friction force was taken as:
and then the ball equation of motion has the form:
After performing mathematical transformations, the formula for the acceleration of the ball was obtained in the form:
3. Validation of Computational Models
In order to compare the compliance of individual methods of modeling the ball-beam system with the behavior of the real object, a series of experimental studies was carried out. The publication presents one of the cases considered to be the most representative. During the experiment the beam was deflected from its equilibrium position in such a way that the ball could move in both directions. The graph of the beam deflection angle as a function of time, which was set during the test, is shown in Figure 3.
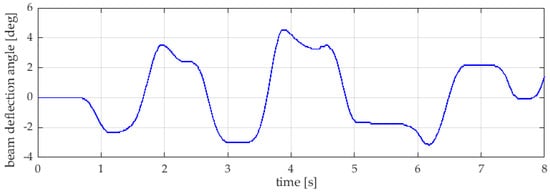
Figure 3.
Measured beam deflection angle as a function of time.
At the initial moment, the position of the ball was approx. 0.36 m. During the test, the angle of the beam deflection was measured using an encoder, and this signal was used as a set angle in numerical models. The first experimental tests for the model showed significant differences between the measurements and numerically calculated displacements of the ball, as shown in Figure 4.
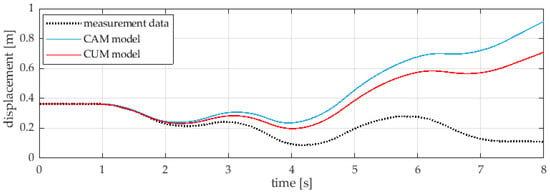
Figure 4.
Ball displacement as a function of time and comparison of waveforms from experimental data with CAM and CUM numerical models.
Due to these large discrepancies between the recorded data and the simulation results, in the CUM and CAM models the initial deflection of the beam was taken into account, which may have resulted from a beam leveling error. This parameter was estimated in further calculations and the considered mathematical models (4) and (14) took the form:
The estimated parameter was also the coefficient of friction . The value of the transition velocity was estimated once and assumed as a constant value. The estimation process was carried out using optimization methods, where the minimized objective function was the square of the difference between the displacement measured experimentally and calculated numerically. In the simulation studies, those parameters that could be measured experimentally or calculated were assumed as constants. The parameter values used in the simulation studies are summarized in Table 1.

Table 1.
List of parameters used in numerical calculations.
In order to validate the numerical models of the ball-beam system, the differences between the position of the ball measured during the experiment and determined in the simulations using the three considered numerical models were first verified. The results of these tests are summarized in Figure 5. Figure 6 shows the absolute errors of displacement as a function of time for each of the models.
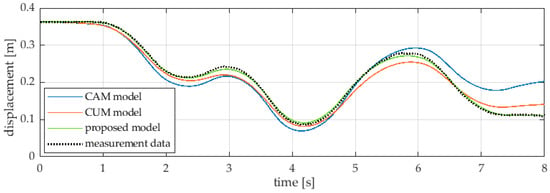
Figure 5.
Ball displacement as a function of time and comparison of waveforms from experimental data and numerical models.
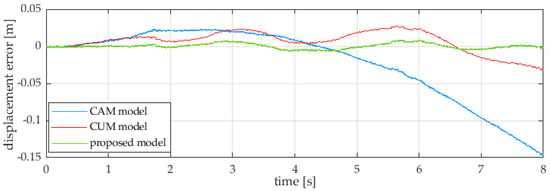
Figure 6.
Absolute errors of ball displacement as a function of time for the considered numerical models.
Subsequently, an analogous comparison was made for velocity (Figure 7). Figure 8 lists the absolute velocity errors as a function of time for each of the models, and the visible noise results from the quality of the experimentally measured signal.
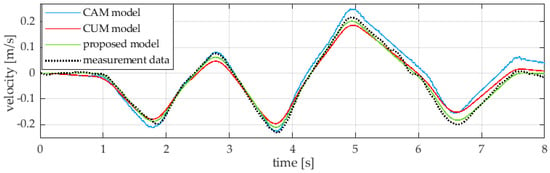
Figure 7.
Ball velocity as a function of time and comparison of waveforms from experimental data and numerical models.
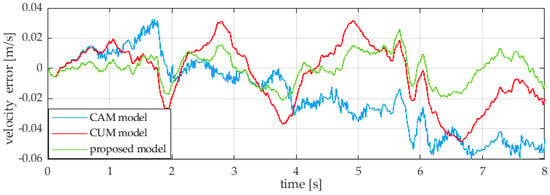
Figure 8.
Absolute errors of ball velocity as a function of time for the considered numerical models.
In order to better systematize the obtained results, quality indicators were additionally determined regarding the absolute errors of displacement and velocity . These indicators were calculated as integrals:
A summary of the obtained values for the adopted quality indicators of model convergence and maximum errors is presented in Table 2.

Table 2.
Summary of quality indicators for numerical models validation.
4. Discussion and Conclusions
The analysis of the results from the validation of the numerical models of the ball-beam system allowed us to notice interesting effects. As can be seen in Figure 3 and Figure 4, the difference in the ball displacement between the measurement data and the results from the model commonly used in the literature is surprisingly large. Despite the fact that the ball’s total range of motion during the test was about 0.25 m, the maximum difference in displacement was reached. Including the eccentric mechanism in the mathematical model had a rather negative effect on the results (at least in the presented case). During the analysis of the whole series of measurement data, it was noticed that the CAM and CUM models are very sensitive to beam leveling errors. In the real system, due to micro-deformations and rolling friction, the ball remains in equilibrium within a certain range of the beam deflection. Although these angles are small, they significantly affect the behavior of the object. Not including them in the first two compared models drastically worsened the correlation of results.
The verification tests described in the publication were carried out in the context of future work on the control algorithm for the underactuated ball and beam system, using the digital twin as a reference model [39] instead of using filters for noise reduction [40,41], so as to eliminate the unfavorable effects associated with the calculation of derivatives from measurement signals [42,43]. The results of the research showed that the use of models commonly used in the literature in such a task may be insufficient. These models, even with small errors in the measurement of the angle of rotation of the beam, generate large discrepancies. The looseness occurring in the real object may therefore affect the insufficient correlation, which may temporarily be very large.
It is also unjustified to complicate the models by taking into account the exact location of the axis of rotation of the beam. Taking into account the eccentricity of the axis of rotation does not solve the problems described earlier.
The next part of the paper presents the model of the ball-beam system proposed by the authors, taking into account the friction force. The developed model allowed to obtain a good correlation with the results of experimental measurements. Importantly, the model did not take into account the beam leveling error, and only the estimation of the friction force coefficient for the assumed transposition speed was carried out. The accuracy of the obtained results can be further improved by taking into account and estimating the leveling error.
The results of the conducted analyzes indicated that building accurate models of the ball and beam system should therefore be focused on taking into account the resistance forces of the ball movement.
The results of the conducted analyzes indicated that accurate models of the ball and beam system (which are to be used, for example, to optimize the settings of control systems) should take into account the resistance forces of the ball’s movement. The analysis of the ball’s initial moment of motion also shows that in order to further improve the convergence of the model with the real system, it is worth considering even more accurate modeling of the resistance forces and taking into account the two-point method of supporting the ball on the beam, taking into account the components of the resistance forces (rolling friction and sliding friction) [20] or experimentally identifying the resistance forces that occur during rolling [44].
Author Contributions
Conceptualization, G.G.; methodology, G.G., P.D. and K.L.; software, P.D. and K.L.; validation, G.G., P.D. and K.L.; formal analysis, G.G.; writing—original draft preparation, P.D. and K.L; writing—review and editing, G.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The readers can access the data reported in this paper from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zhang, Z.; Suh, C.S. Underactuated Mechanical Systems—A Review of Control Design. J. Vib. Test. Syst. Dyn. 2022, 6, 21–51. [Google Scholar] [CrossRef]
- Li, L.; Tokuda, I.; Asano, F. Energy-Efficient Locomotion Generation and Theoretical Analysis of a Quasi-Passive Dynamic Walker. IEEE Robot. Autom. Lett. 2020, 5, 4305–4312. [Google Scholar] [CrossRef]
- Wu, J.; Ye, W.; Wang, Y.; Su, C.-Y. A General Position Control Method for Planar Underactuated Manipulators with Second-Order Nonholonomic Constraints. IEEE Trans. Cybern. 2021, 51, 4733–4742. [Google Scholar] [CrossRef] [PubMed]
- Deng, K.; Miao, J.; Sun, X. Robust Path-Following Control of Underactuated AUVs with Multiple Uncertainties and State Constraints. J. Phys. Conf. Ser. 2021, 2121, 012042. [Google Scholar] [CrossRef]
- Tian, J.; Wei, C.; Luo, M.; Wang, N.; Tan, C.; Zhao, Y. Parametric Research on Underactuated Tendon-Driven Grasping Mechanism for Space Capture Operation. Int. J. Precis. Eng. Manuf. 2019, 21, 237–247. [Google Scholar] [CrossRef]
- Moradi, R.; Alikhani, A.; Fathi Jegarkandi, M. Ultimate State Boundedness of Underactuated Spacecraft Subject to an Unmatched Disturbance. J. Theor. Appl. Mech. 2017, 55, 1055. [Google Scholar] [CrossRef]
- Zhu, X.; He, B. Underactuated Rehabilitation Robotics for Hand Function. J. Robot. Control (JRC) 2021, 2, 337–341. [Google Scholar] [CrossRef]
- Muftah, M.N.; Faudzi, A.A.M.; Sahlan, S.; Mohamaddan, S. Intelligent Position Control for Intelligent Pneumatic Actuator with Ball-Beam (IPABB) System. Appl. Sci. 2022, 12, 11089. [Google Scholar] [CrossRef]
- Niro, L.; Kaneko, E.H.; Mollon, M.F.; Chaves, W.D.S.; Montezuma, M.A.F. Control of a Modified Ball and Beam System Using Tracking System in Real Time with a DC Motor as an Actuator. Int. J. Adv. Eng. Res. Sci. 2017, 4, 99–107. [Google Scholar] [CrossRef]
- Wellstead, P.E.; Chrimes, V.; Fletcher, P.R.; Moody, R.; Robins, A.J. The Ball and Beam Control Experiment. Int. J. Electr. Eng. Educ. 1978, 15, 21–39. [Google Scholar] [CrossRef]
- Srivastava, A.; Pratap, B. Nonlinear Observer-Based Robust Controller Design for Ball and Beam System: An LMI-Based Approach. Int. J. Nonlinear Dyn. Control 2018, 1, 211. [Google Scholar] [CrossRef]
- Howimanporn, S.; Chookaew, S.; Silawatchananai, C. Monitoring and Controlling of a Real-Time Ball Beam Fuzzy Predicting Based on PLC Network and Information Technologies. J. Adv. Inf. Technol. 2022, 13, 1–8. [Google Scholar] [CrossRef]
- Ali, S.S. Position Control of Ball and Beam System Using Robust H∞ Loop Shaping Controller. Indones. J. Electr. Eng. Comput. Sci. 2020, 19, 91–98. [Google Scholar] [CrossRef]
- Kharola, A.; Patil, P.P. Neural Fuzzy Control of Ball and Beam System. Int. J. Energy Optim. Eng. 2017, 6, 64–78. [Google Scholar] [CrossRef]
- Danilo Montoya, O.; Gil-González, W.; Ramírez-Vanegas, C. Discrete-Inverse Optimal Control Applied to the Ball and Beam Dynamical System: A Passivity-Based Control Approach. Symmetry 2020, 12, 1359. [Google Scholar] [CrossRef]
- Moreno–Valenzuela, J.; Montoya–Cháirez, J.; Santibáñez, V. Robust Trajectory Tracking Control of an Underactuated Control Moment Gyroscope via Neural Network–Based Feedback Linearization. Neurocomputing 2020, 403, 314–324. [Google Scholar] [CrossRef]
- Okafor, E.; Udekwe, D.; Ibrahim, Y.; Bashir Mu’azu, M.; Okafor, E.G. Heuristic and deep reinforcement learning-based PID control of trajectory tracking in a ball-and-plate system. J. Inf. Telecommun. 2021, 5, 179–196. [Google Scholar] [CrossRef]
- Singh, R.; Bhushan, B. Real-Time Control of Ball Balancer Using Neural Integrated Fuzzy Controller. Artif. Intell. Rev. 2020, 53, 351–368. [Google Scholar] [CrossRef]
- Mehedi, I.M.; Al-Saggaf, U.M.; Mansouri, R.; Bettayeb, M. Two Degrees of Freedom Fractional Controller Design: Application to the Ball and Beam System. Measurement 2019, 135, 13–22. [Google Scholar] [CrossRef]
- Moreno-Valenzuela, J.; Aguilar-Avelar, C. Identification of Underactuated Mechanical Systems. Intell. Syst. Control Autom. Sci. Eng. 2017, 88, 27–49. [Google Scholar] [CrossRef]
- Dalla Libera, A.; Romeres, D.; Jha, D.K.; Yerazunis, B.; Nikovski, D. Model-Based Reinforcement Learning for Physical Systems without Velocity and Acceleration Measurements. IEEE Robot. Autom. Lett. 2020, 5, 3548–3555. [Google Scholar] [CrossRef]
- Gao, S.; Liu, C.; Tuo, Y.; Chen, K.; Zhang, T. Augmented Model-Based Dynamic Positioning Predictive Control for Underactuated Unmanned Surface Vessels with Dual-Propellers. Ocean Eng. 2022, 266, 112885. [Google Scholar] [CrossRef]
- Mombaur, K.; Henning Koch, K.; Felis, M. Model-Based Optimization for Robotics. J. Robot. Soc. Jpn. 2014, 32, 492–498. [Google Scholar] [CrossRef]
- Burghardt, A.; Gierlak, P.; Skwarek, W. Modeling of Dynamics of Cooperating Wheeled Mobile Robots. J. Theor. Appl. Mech. 2021, 59, 649–659. [Google Scholar] [CrossRef]
- Najva, N.; Saleem, A. Model Reference Controller Approach for Robot Arm Tracking Using Neural Networks. Indian J. Sci. Technol. 2019, 12, 39. [Google Scholar] [CrossRef]
- Sławski, S.; Kaczmarczyk, J.; Szymiczek, M.; Pakieła, W. Numerical Studies on the Influence of a Reinforcing Material on the Energy Absorption in a Multilayered Composite during Impacts. Mech. Compos. Mater. 2021, 57, 309–320. [Google Scholar] [CrossRef]
- Hyatt, P.; Johnson, C.C.; Killpack, M.D. Model Reference Predictive Adaptive Control for Large-Scale Soft Robots. Front. Robot. AI 2020, 7, 558027. [Google Scholar] [CrossRef]
- Gembalczyk, G.; Gierlak, P.; Duda, S. Control System Design of an Underactuated Dynamic Body Weight Support System Using Its Stability. Sensors 2021, 21, 5051. [Google Scholar] [CrossRef]
- Liu, Y.; Yu, H. A Survey of Underactuated Mechanical Systems. IET Control Theory Appl. 2013, 7, 921–935. [Google Scholar] [CrossRef]
- Keshmiri, M.; Jahromi, A.F.; Mohebbi, A.; Hadi Amoozgar, M.; Xie, W.-F. Modeling and Control of Ball and Beam System Using Model Based and Non-Model Based Control Approaches. Int. J. Smart Sens. Intell. Syst. 2012, 5, 14–35. [Google Scholar] [CrossRef]
- Sehgal, K. Modelling and Control of Dynamical Ball and Beam System Using SA Tuned PIDA and PIaD Controllers. In Proceedings of the 2021 IEEE International Conference on Electronics, Computing and Communication Technologies (CONECCT), Bangalore, India, 9–11 July 2021; pp. 1–6. [Google Scholar]
- Latif, S.; Muhammad, E.; Naeem, U. Implementation of Ball and Beam System Using Classical and Advanced Control Techniques. In Proceedings of the 2019 International Conference on Applied and Engineering Mathematics (ICAEM), Taxila, Pakistan, 27–29 August 2019. [Google Scholar] [CrossRef]
- Nguyen, C.X.; Phan, H.N.; Hoang, L.D.; Tran, H.N. The Design of a Quasi-Time Optimal Cascade Controller for Ball and Beam System. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1029, 012022. [Google Scholar] [CrossRef]
- Zaare, S.; Soltanpour, M.R. The Position Control of the Ball and Beam System Using State-Disturbance Observe-Based Adaptive Fuzzy Sliding Mode Control in Presence of Matched and Mismatched Uncertainties. Mech. Syst. Signal Process. 2021, 150, 107243. [Google Scholar] [CrossRef]
- Burghardt, A.; Giergiel, J. Modelling and Control of a Underactuated Sphere and Beam System. Commun. Nonlinear Sci. Numer. Simul. 2011, 16, 2350–2354. [Google Scholar] [CrossRef]
- Flores, P. Contact Mechanics for Dynamical Systems: A Comprehensive Review. Multibody Syst. Dyn. 2021, 54, 127–177. [Google Scholar] [CrossRef]
- Specker, T.; Buchholz, M.; Dietmayer, K. A New Approach of Dynamic Friction Modelling for Simulation and Observation. IFAC Proc. Vol. 2014, 47, 4523–4528. [Google Scholar] [CrossRef]
- Specker, T.; Buchholz, M.; Dietmayer, K. Dynamical Modeling of Constraints with Friction in Mechanical Systems. IFAC-PapersOnLine 2015, 48, 514–519. [Google Scholar] [CrossRef]
- Liu, X.; Jiang, D.; Tao, B.; Jiang, G.; Sun, Y.; Kong, J.; Tong, X.; Zhao, G.; Chen, B. Genetic Algorithm-Based Trajectory Optimization for Digital Twin Robots. Front. Bioeng. Biotechnol. 2022, 9, 1433. [Google Scholar] [CrossRef]
- Saków, M.; Marchelek, K. Design and Optimisation of Regression-Type Small Phase Shift FIR Filters and FIR-Based Differentiators with Optimal Local Response in LS-Sense. Mech. Syst. Signal Process. 2021, 152, 107408. [Google Scholar] [CrossRef]
- Paszkowski, W. Modeling of Vibroacoustic Phenomena Using the Method of Parameterizing the Audio Signa. Eksploat. I Niezawodn.—Maint. Reliab. 2020, 22, 501–507. [Google Scholar] [CrossRef]
- Sahib, M.A. A Novel Optimal PID plus Second Order Derivative Controller for AVR System. Eng. Sci. Technol. Int. J. 2015, 18, 194–206. [Google Scholar] [CrossRef]
- Veinović, S.; Stojić, D.; Ivanović, L. Optimized PIDD2 Controller for AVR Systems Regarding Robustness. Int. J. Electr. Power Energy Syst. 2023, 145, 108646. [Google Scholar] [CrossRef]
- Czapla, T.; Fice, M.; Niestrój, R. Experimental Identification of Wheel-Surface Model Parameters: Various Terrain Conditions. Sci. Rep. 2022, 12, 16015. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).