Semi-Supervised Blade Icing Detection Method Based on Tri-XGBoost

Abstract

Blade icing caused by low-temperature environments results in the degradation of wind turbine power performance. As there is no obvious influence on the performance of wind turbines in the early stage of blade icing, it is difficult to detect the early icing state, so there will be inaccurate labels in the process of data collection. To address these challenges, this paper proposes a novel semi-supervised blade icing detection method based on a tri-training algorithm. In the proposed method, extreme gradient boosting tree (XGBoost) is used as the base classifier. A tri-training algorithm is used to integrate three base classifiers and the integrated model generates a pseudo-label for unlabeled data. In addition, we introduce Focal Loss as the loss of the base classifier in the proposed model, which solves the problem of class imbalance caused by the fact that the wind turbine is operating under normal conditions in most cases. In order to verify the effectiveness of the proposed blade icing detection method, experiments are implemented on the collected Supervisory Control and Data Acquisition (SCADA) data. The experimental results show that the proposed method effectively improves the ability to identify blade icing. Compared with other methods, it has better classification performance, robustness, and generalization.

1. Introduction

According to the latest statistics released by the International Renewable Energy Agency (IRENA), the global cumulative installed renewable energy capacity reached 3064 GW in 2021. In China, the cumulative installed renewable energy capacity reached 1063 GW in 2021, accounting for 31.9% of the global installed capacity. In particular, the global cumulative installed wind energy capacity is about 732 GW, while China is in a leading position globally with a cumulative installed wind energy capacity of 282 GW, accounting for 38.5% [1]. In the predictable future, the development of wind energy will go further and become a more important part of energy consumption. The wind speed increases by 0.1 m/s per 100 m of altitude below 1000 m. Wind energy is often abundant in cold regions or high-altitude areas [2]. Air density is higher in cold regions at high altitudes due to the fact that cold air is denser than warm air. Consequentially, the potential wind energy is 10% higher in cold regions than otherwise [3]. Therefore, most wind farms are located in these regions. During the winter, these regions are more prone to the occurrence of blade icing [4]. The process of ice accumulation on the blades is very slow. In fact, many environmental variables, including air humidity, wind speed, and ambient temperature, are associated with blade icing [5]. The lift force and drag force of the blade will decrease and increase, respectively, when it is icing, which will increase blade weight, and even lead to blade fracture [6]. Blade icing operation most commonly affects the actual output of the wind turbine for power production [7]. Regions with extremely cold climates can reduce annual power production by 20% to 50% [8]. Early diagnosis of blade icing helps to reduce power loss and improve the security of wind turbine operation [9]. Figure 1 shows a wind turbine blade that has accumulated ice due to the cold climate.

Wind turbine blade icing detection is an emerging research field. At present, many scholars are engaged in research in this field [10]. Current blade icing detection techniques include two main directions, model-based approaches and data-driven approaches [11]. Based on an object’s internal workings, accurate mathematical models are known as model-based approaches [12], which construct a multi-resolution analysis method to extract the current frequency components of wind turbines. Then, based on the fact that the wind turbine inertia gradually increases due to the blade icing, the wavelet analysis method is used to analyze the change in the current frequency component to detect whether the blade is icing. Three methods for creating power threshold curves are proposed to distinguish the icing production cycle from the non-icing production cycle, and they are applied to the wind turbines of four wind farms. The effectiveness of the methods is verified by comparative analysis [13]. In the literature [14], early detection of blade icing is achieved using controlled acoustic waves propagating in a wind turbine blade. The ice observations are analyzed using three metrics: fast Fourier transform (FFT), amplitude attenuation, and root-mean-square relative error (RMS). It is quite challenging to build a model-based approach because of the unstable operating environment of the wind turbine and the complicated structure of the components [15].

At present, due to the remote location of wind farms, SCADA systems are widely used in wind farms [16]. These systems allow technicians to collect and analyze real-time data remotely and monitor the status of the wind turbine operation based on the acquired data. The collection of real-time data provides the basis for a data-driven approach [17]. Thus, the data-driven approach is widely used in the field of blade icing detection.

The data-driven approach builds an intelligent model by using information from a significant number of data samples and mining the potential sample features in the data. As a main data-driven method, supervised learning has been widely used in the field of blade icing detection. In the literature [18], after feature extraction using recursive feature elimination methods, an integrated learning approach combined with Random Forest (RF) and Support Vector Machine (SVM) is used to improve the accuracy of the model. The literature [19] proposes an MBK-SMOTE algorithm that combines the MiniBatchK-means clustering algorithm and the SMOTE algorithm, aiming to solve the severe class imbalance problem in blade icing. An end-to-end CNN-LSTM model is suggested in the literature [20] to convert SCADA data into multivariate time series for automatic feature extraction. Deep autoencoders are used in the literature [21] to extract multi-level fault features from SCADA data and utilize ensemble learning methods to build icing detection models. In the literature [22], the short-term and long-term features affecting blade icing are extracted according to the icing physics, and the hybrid features formed by the combination of short-term and long-term are fully considered. These features are used to build the Stacked-XGBoost algorithm. A multi-level convolutional recurrent neural network (MCRNN) is proposed in the literature [23] for blade icing detection. A parallel structure combining LSTM branches and CNN branches is established for feature extraction using discrete wavelet decomposition to extract multilevel features in the time and frequency domains. A temporal attention-based convolutional neural network (TACNN) is proposed in the literature [24]. Discriminative features in the original data are automatically identified by the temporal attention module. Compared with the model-based method, the supervised learning method reduces the need for long-term knowledge of experts and solves the complexity and challenge of blade icing physical modeling. However, such methods are more dependent on data quality as well as label quality [25]. It is impossible to rely on human observation to gather substantial volumes of labeled data in the actual setting of wind turbine operation [26]. Manually annotated labels frequently contain errors. Therefore, supervised learning methods are difficult to effectively apply to wind turbine blade icing detection due to the large amount of inaccurate labeled data included in practical applications.

In order to solve the problems of less blade icing time, imbalance of classes, and inaccurate manually labeled data, this paper proposes a tri-XGBoost method that combines the tri-training [27] semi-supervised learning algorithm on the basis of the XGBoost [28] algorithm. As an important semi-supervised learning algorithm, tri-training can be applied to many real-world scenarios because it does not require special learning algorithms. The tri-training algorithm uses three classifiers, which are not required for different supervised learning algorithms. Such a setting determines how to pseudo-label the unlabeled data. With a limited number of labels, the tri-training algorithm greatly improves the classification ability of the algorithm. Overall, the proposed method makes use of the incorrectly labeled data and develops new features based on the original features using domain knowledge. Then, Pearson correlation coefficients are used for feature selection [29]. Focal loss [30] is chosen as the loss function for the iterative update of the classifier. The proposed method provides a new solution to the issues of inaccurate labeling and class imbalance in blade icing.

The contributions of this study are shown as follows. The tri-training algorithm is used for the first time to detect icing on wind turbine blades. It can fully exploit the potential information of unlabeled samples to help the model identify icing. It is useful for maintaining the safe operation of wind turbines and improving the efficiency of power generation. This is because it is difficult to obtain a large number of labeled icing samples when the turbine is generating electricity. The proposed method effectively combines feature standardization, cost-sensitive learning, the XGBoost algorithm, and the tri-training semi-supervised learning algorithm to enhance the performance of the model to identify icing. It not only solves the class imbalance problem of labeled samples but also converts incorrectly labeled samples into usable data, which greatly reduces label dependence.

The rest of the paper is organized as follows. Section 2 briefly describes the theoretical background of the proposed method. Section 3 describes how the proposed blade icing detection method is implemented. Section 4 describes a case study of the proposed method in real data. The experimental results of the case study are discussed and analyzed in Section 5. Finally, Section 6 summarizes the work.

2. Theoretical Background

2.1. XGBoost Algorithm

XGBoost [28] is not only a type of Boosting model that belongs to the ensemble machine learning but also an improved gradient boosted decision tree (GBDT) algorithm [31]. XGBoost introduces the second-order Taylor expansion based on GBDT, which increases the model accuracy while providing XGBoost with the ability to customize the loss function. XGBoost adds the complexity of the tree model as a regular term in the objective function, which helps to avoid model overfitting.

Equation (1) is the objective function of XGBoost, where $l\left(y_i,{\widehat{y}}_i^{\left(t-1\right)}+f_t\left(x_i\right)\right)$ is the loss function of the model. $x_i$ denotes the i-th instance of the input, and the complexity of the model is expressed by $\mathsf{\Omega }\left(f_t\right)$. As XGBoost is a kind of Boosting model, the prediction of the model for the i-th instance $x_i$ is presented as ${\widehat{y}}_i^{\left(t\right)}={\widehat{y}}_i^{\left(t-1\right)}+f_t\left(x_i\right)$, where $t$ denotes the number of iterations of the training process.

$${\mathcal{L}}^{\left(t\right)}={\displaystyle \sum }_{i=1}^{n}l\left(y_i,{\widehat{y}}_i^{\left(t-1\right)}+f_t\left(x_i\right)\right)+\mathsf{\Omega }\left(f_t\right)$$

(1)

In order to solve for $f_t$ at the minimum of Equation (1), the objective function becomes Equation (2) after the second-order Taylor expansion of the loss function according to the Taylor formula.

$${\mathcal{L}}^{\left(t\right)}={\displaystyle \sum }_{i=1}^n\left[g_i{f}_t\left(x_i\right)+\frac{1}{2}{h}_i{f}_t^2\left(x_i\right)\right]+\mathsf{\Omega }\left(f_t\right)$$

(2)

where $g_i=\frac{\partial l\left(y_i,{\widehat{y}}_i^{\left(t-1\right)}\right)}{\partial {\widehat{y}}_i^{\left(t-1\right)}}$ is the first-order gradient statistics on the loss function and $h_i=\frac{{\partial }^{2}l\left(y_i,{\widehat{y}}_i^{\left(t-1\right)}\right)}{\partial {\left({\widehat{y}}_i^{\left(t-1\right)}\right)}^2}$ is the second-order gradient statistics on the loss function. The complexity of the model $\mathsf{\Omega }\left(f_t\right)$ is defined as Equation (3).

$$\mathsf{\Omega }\left(f_t\right)=\gamma T+\frac{1}{2}\lambda {\displaystyle \sum }_{j=1}^T{w}_j^2$$

(3)

In Equation (3), $\gamma$ and $\lambda$ are the hyperparameters of the model, $T$ is the number of leaves in the tree, and $w_j$ is the weight of the current leaf. To further simplify the objective function, define $G_j={{\displaystyle \sum }}_{i\in I_j}{g}_i,$ $H_j={{\displaystyle \sum }}_{i\in I_j}{h}_i$, where $I_j=\left\{i|q\left({\mathrm{x}}_i\right)=j\right\}$ is defined as the j-th leaf of the instance set. Equation (4) rewrites the objective function as a quadraticfunction on the weight of the j-th leaf.

$${\mathcal{L}}^{\left(t\right)}={\displaystyle \sum }_{j=1}^T\left[G_j{w}_j+\frac{1}{2}\left(H_j+\lambda \right)w_j^2\right]+\gamma T$$

(4)

To minimize the objective function, the solution yields the optimal $w$ and the objective function ${\mathcal{L}}^{\left(t\right)}$ as Equation (5) and Equation (6), respectively.

$$w_j^{*}=-\frac{G_j}{H_j+\lambda }$$

(5)

$${\mathcal{L}}^{\left(t\right)}=-\frac{1}{2}{\displaystyle \sum }_{j=1}^T\frac{G_j^2}{H_j+\lambda }+\gamma T$$

(6)

The optimal tree structure is solved when the value of Equation (6) is minimized.

2.2. Focal Loss

The weighted cross-entropy loss for the binary classification is presented as follows.

$$L_w=-{\displaystyle \sum }_{i=1}^m\left(\alpha y_i\log \left({\widehat{y}}_i\right)+\left(1-y_i\right)\log \left(1-{\widehat{y}}_i\right)\right)$$

(7)

where $m$ is the amount of the instance, ${\widehat{y}}_i$ denotes the estimated probability of predicting the i-th instance for the class with label = 1, and $y_i$ is the true label of the i-th instance. $\alpha$ is a hyperparameter to adjust the class weights, which is used to rebalance the distribution of the loss function and address the problem of positive and negative class imbalance. According to the literature [32], the binary Focal Loss is defined as follows.

$$L_F=\left\{\begin{array}{c}-\alpha {(1-\widehat{y})}^{\gamma }\log \widehat{y},y=1\\ -\left(1-\alpha \right){\widehat{y}}^{\gamma }\log \left(1-\widehat{y}\right),y=0\end{array}\right.$$

(8)

Focal Loss improves on the cross-entropy loss to address the challenge that different examples in the dataset have different levels of classification difficulty. $\mathsf{\gamma }$ is a hyperparameter that reshapes the weight of the loss function for easy examples and hard examples. Down-weighting easy examples, thus focusing the training on hard examples, helps to improve the accuracy of classification for hard examples.

2.3. Generalized Tri-Training Algorithm

Traditional supervised learning methods rely on a large number of labeled samples, while in industry, especially in fields such as fault diagnosis, assigning labels to data is often labor-intensive. The labeling quality of the data is not guaranteed, as the start time of the failure is unknown, resulting in label noise. Therefore, it is necessary to introduce semi-supervised learning algorithms that allow the learner to make full use of unlabeled data to assist labeled data for training. In the literature [27], a tri-training method is proposed. Tri-training is a semi-supervised learning method based on disagreement (i.e., difference) [33]. Tri-training uses the same learning algorithm to generate three learners, and there is no specific requirement for the learning algorithm. To make the learners meet the diversity requirement, Bootstrap sampling of the original labeled data [34] is required to obtain three labeled training sets. Tri-training first trains the three classifiers using the labeled data and then generates pseudo-labels of the unlabeled data based on the trained classifiers. The pseudo-labeled data and the original labeled data are used to iteratively update the classifiers until they no longer change. Note that in each iteration, the pseudo-labeled samples from the previous round are reprocessed as unlabeled samples. Finally, using a straightforward voting strategy, three classifiers are combined into one strong classifier.

3. Proposed Wind Turbine Blade Ice Detection Algorithm

3.1. Tri-XGBoost Algorithm

In order to solve the problem of inaccurate labels and class imbalance in SCADA data, a tri-XGBoost based on the wind turbine blade icing detection method is constructed in this paper. The proposed method combines the XGBoost machine learning algorithm and tri-training semi-supervised learning algorithm. On the one hand, using Focal Loss for class imbalance learning focuses training on a sparse set of hard samples. On the other hand, samples with low label reliability are considered as unlabeled samples and their pseudo-labels are generated by the tri-training algorithm. Hence, the icing detection model can make full use of unlabeled data and reduce the reliance on labeled data. It can still achieve a better training performance with fewer minority class labels.

The pseudo-code of the proposed tri-XGBoost algorithm in this paper is shown in Algorithm 1. First, Bootstrap sampling is performed on the original labeled data to obtain three labeled training sets. Then, three base classifiers $XG{B}_1$, $XG{B}_2$, and $XG{B}_3$ are initially trained using these three labeled training sets. Unlabeled samples will be fed into these initially trained base classifiers. Next, these initially three base classifiers generate pseudo-labels for the unlabeled samples. In each round of tri-training, the newly labeled samples obtained by a single classifier $XG{B}_i$ are provided by the remaining two classifiers in collaboration. If the remaining two classifiers both agree on the labeling of the same unlabeled sample, that sample can be added to the labeled training set of $XG{B}_i$. Namely, it is considered to have a high confidence. Finally, the number of samples selected to be added to the labeled training set varies in each round, so $L^t$ and $L^{t-1}$ denote the set of samples added to the training set of classifier $XG{B}_i$ in rounds $t$ and $t-1$, respectively. In each round of iteration, $L^{t-1}$ is put back into the unlabeled dataset $U$ for reprocessing.

Algorithm 1: tri-XGBoost algorithm
Input: Labeled datasets $L$, Unlabeled datasets $U$, Classifiers $XGB$
Output: $\mathrm{A} \mathrm{strong} \mathrm{learner} \mathrm{combined} \mathrm{by} XG{B}_i\left(i\in \left\{1,2,3\right\}\right)$ using the voting method
1.	for $i \in \left\{1,2,3\right\}$ do
2.	$D_i\leftarrow BootstrapSample\left(L\right)$
3.	$XG{B}_i\leftarrow XGB\left(D_i\right)$
4.	${\tilde{e}}_i^0\leftarrow 0.5$$; L_i^0\leftarrow 0$$; t\leftarrow 0$
5.	end for
6.	repeat until$\mathrm{none} \mathrm{of} {\widehat{y}}_i changes$
7.	$\mathbf{for} i \in \left\{1,2,3\right\}$ do
8.	$L_i\leftarrow \varnothing ,updat{e}_i\leftarrow FALSE$
9.	$\mathrm{Calculate} \mathrm{the} \mathrm{classification} \mathrm{error} \mathrm{rate} \mathrm{of} XG{B}_j\&XG{B}_k \left(j,k\ne i\right)$
10.	$\mathbf{for} \mathrm{every} x\in U$ do
11.	$\mathbf{if} XG{B}_j=XG{B}_k\left(j,k\ne i\right)$ then
12.	$L_i^t\leftarrow L_i^t\bigcup \left\{\left(x,XG{B}_j\left(x\right)\right)\right\}$
13.	end if
14.	end for
15.	$\mathbf{if} 0<\frac{{\tilde{e}}_i^t}{{\tilde{e}}_i^{t-1}}<\frac{\left|L_i^{t-1}\right|}{\left|L_i^t\right|}<1$ then
16.	$updat{e}_i\leftarrow TRUE$
17.	else
18.	$\mathbf{if} \left|L_i^{t-1}\right|>\frac{{\tilde{e}}_i^t}{{\tilde{e}}_i^{t-1}-{\tilde{e}}_i^t}$ then
19.	$\mathrm{Remove} \left|L_i^t\right|-\lceil \frac{{\tilde{e}}_i^{t-1}\left|L_i^{t-1}\right|}{{\tilde{e}}_i^t}-1\rceil$$\mathrm{samples} \mathrm{randomly} \mathrm{from} L_i^t$
20.	$updat{e}_i\leftarrow TRUE$
21.	end if
22.	end if
23.	$\mathbf{if} updat{e}_i=TRUE$ then
24.	$\mathrm{retrain} XG{B}_i using L\bigcup L_i^t$
25.	end if
26.	end for
27.	$t\leftarrow t+1$
28.	end repeat

However, if the remaining two classifiers predict the sample incorrectly, a sample with a noisy label is obtained. After the samples with noisy label are added to the training set of classifier $XG{B}_i$, it will have a negative impact on the classification performance of the classifier. Based on [27], the negative impact of noisy labels can be compensated if the number of newly labeled training samples is large enough and satisfies certain conditions. Therefore, the new samples added to the training set of classifier $XG{B}_i$ need to satisfy the following condition:

$$0<\frac{{\tilde{e}}_i^t}{{\tilde{e}}_i^{t-1}}<\frac{\left|L_i^{t-1}\right|}{\left|L_i^t\right|}<1$$

(9)

In Equation (9), ${\tilde{e}}_i^t$ denotes the upper bound of the classification error rate of the remaining two classifiers. If the new samples added to the training set do not satisfy Equation (9), random under-sampling of $L_i^t$ is performed to remove $\left|L_i^t\right|-\lceil \frac{{\tilde{e}}_i^{t-1}\left|L_i^{t-1}\right|}{{\tilde{e}}_i^t}-1\rceil$ number of samples. $L_i^{t-1}$ should satisfy Equation (10) such that the size of the training set $L_i^t$ is still larger than $\left|L_i^{t-1}\right|$ after under-sampling.

$$\left|L_i^{t-1}\right|>\frac{{\tilde{e}}_i^t}{{\tilde{e}}_i^{t-1}-{\tilde{e}}_i^t}$$

(10)

As mentioned above, we set the initial classification error rate threshold ${\tilde{e}}_i^0$ to 0.5, the number of new sample sets $L_i^0$ added to the training set of classifier $XG{B}_i$ to 0, and the number of iterative rounds initialized to 0.

3.2. Modeling Method for Blade Ice Detection

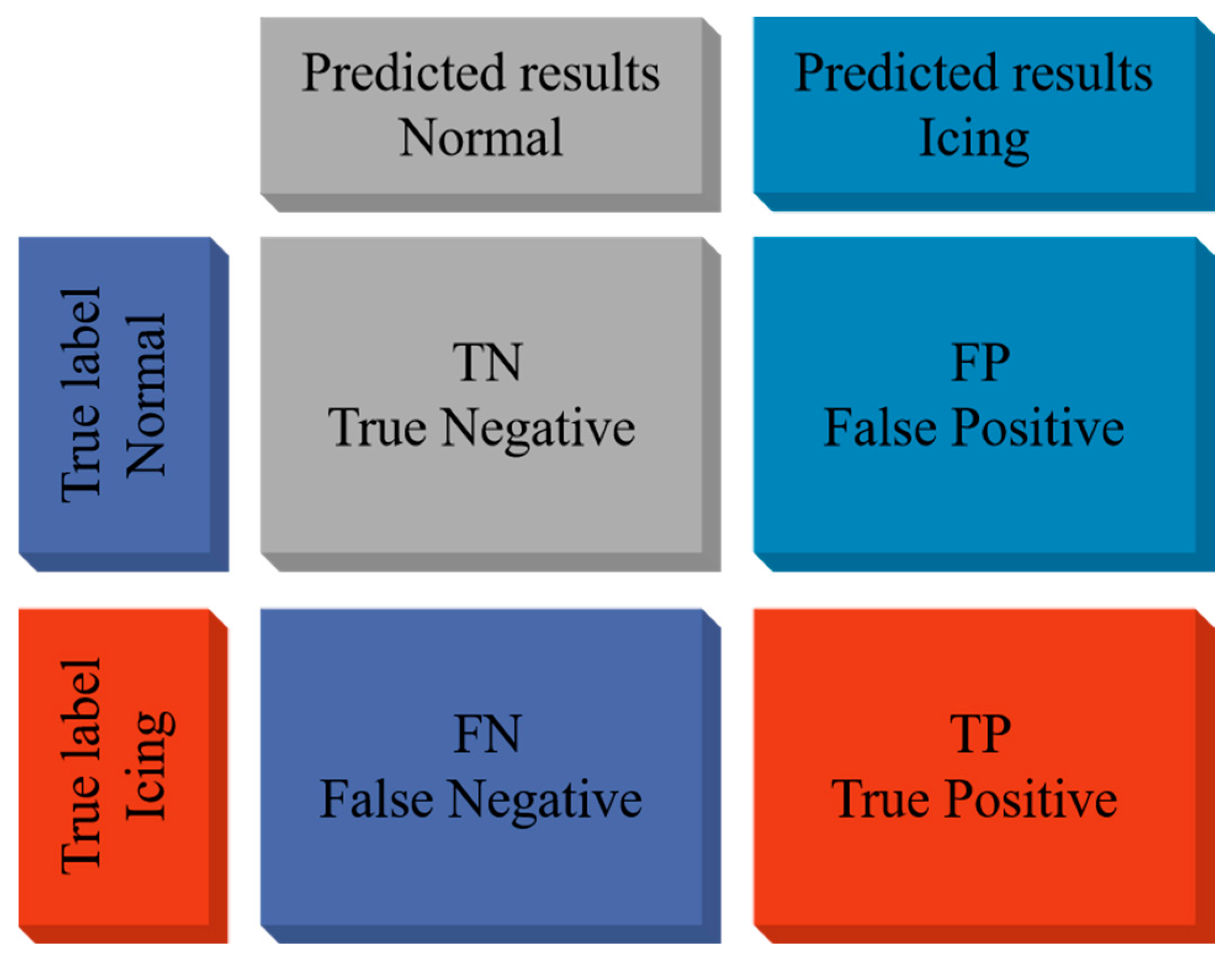
In this paper, we use the data collected from the wind turbine SCADA system to build a model for blade icing detection based on a data-driven approach. The collected data include 18 continuous type variables such as wind speed, active power, generator speed, and pitch angle. Blade icing detection is abstracted as a binary classification task. The tri-XGBoost algorithm is proposed for the problems of inaccurate labeling and class imbalance of SCADA data. The general flow chart of the modeling of blade icing detection based on tri-XGBoost is shown in Figure 2.

Data-driven modeling for blade icing detection generally consists of several components: icing cause analysis, data pre-processing, feature processing, class imbalance learning, and model evaluation. The specific modeling steps are as follows.

Step 1 Training set construction and data pre-processing. As mentioned before, the ice accumulates on the blades slowly and over time. The labeling information of blade icing is obtained by professional observation. Early icing samples may be mislabeled as normal due to untimely observations. These mislabeled samples used for model training will have a negative impact on the accuracy and generalization ability of the model. In this paper, based on the above tri-XGBoost algorithm, the original SCADA dataset is divided into a labeled dataset and unlabeled dataset.

Blade icing can lead to power limiting operation of the turbine. According to expert’s knowledge, there are several other causes of turbine-limiting power operation as follows: One reason is the electrical grid scheduling power limit; it is difficult to store the power that is transmitted from the wind farm to the grid when the wind speed is too high. Another reason is that due to problems with the main components of the turbine, the turbine needs to operate with limited power to avoid accidents. A further reason is that some wind farms are close to residential areas; during the night to avoid excessive noise, turbines should be in limiting power operation. We found that the non-icing causes of limiting power operation of the turbine can be filtered based on two features: the pitch angle and the active power of the turbine. Therefore, in order to improve the accuracy and generalization performance of the model, these samples with non-icing causes for the limiting power operation of the wind turbine are eliminated in the data pre-processing stage.

Step 2 Feature processing. During the blade icing period, the wind speed, power, and generator speed of the wind turbine deviate significantly from the normal operating conditions. For a given wind speed, it manifests with lower power and generator speed with respect to the normal. In this paper, the existing features of the original data are combined to create three new features to be input into the model. Pearson correlation coefficients are used to reduce the dimensionality of the features, and screen the features with too high a correlation and eliminate them. After feature extraction, to eliminate the effect of unit and scale differences between features, we use the standardization method for feature scaling of the data.

Step 3 Class imbalance learning and model training. The methods for dealing with class imbalance can be divided into three main categories, namely, under-sampling, over-sampling, and cost-sensitive learning. In order to retain the original data as much as possible, this paper selects the cost-sensitive learning method and introduces the Focal Loss to replace the original loss function of the XGBoost algorithm. This method does not change the original distribution of the data compared to data resampling when dealing with class imbalance, which greatly reduces the possibility of model overfitting. In the training process of the model, different examples are classified with different degrees of difficulty. Focal Loss focuses the learning on which examples are more difficult to classify and reduces the weights of which examples are easily classified. The improvement of class weighting is also introduced into Focal Loss. Thus, Focal Loss focuses on both hard examples as well as minority class examples.

The labeled and unlabeled data are input into the tri-XGBoost model for collaborative training. After initializing the base classifier using the labeled data, the pseudo-label of the unlabeled data is generated according to the trained base classifier. The base classifiers are iteratively updated until none of the base classifiers change anymore. The final classification model is obtained using the majority voting.

Step 4 Parameter optimization and model evaluation. The methods of parameter optimization include grid search, random search, and Bayesian optimization. In this paper, the grid search algorithm is chosen to determine the optimal hyperparameters. Grid search traverses the given parameter spaces and finds the parameter with the highest accuracy on the test set from all parameters by exhaustive enumeration. The test set is subjected to the same data pre-processing and feature engineering to ensure the same feature dimensionality. Model evaluation is performed with the processed test set to validate the model classification performance.

4. Case Study

4.1. Data Description and Data Pre-Processing

Experimental data are collected from three wind turbines at a wind farm in Guizhou Province, China. The annual average air density at the wind farm location is 0.945 kg/m³ and the altitude ranges from 2000 to 2300 m. In this paper, SCADA data from 1 October 2020 to 29 April 2021 are used for data analysis and icing detection modeling. Data from the SCADA system are sampled once every minute. A large number of invalid samples were generated in the original data due to turbine shutdown and SCADA system communication interruptions. To avoid affecting the classification performance of the model, the invalid samples should be dropped. As mentioned in Section 3.2, in some scenarios other than blade icing, the turbine may also operate with limited power. Therefore, these samples (i.e., those that are operating at limited power due to the other three reasons described in Section 3.2) need to be eliminated. The method adopted in this study is to screen the data of normal operating conditions, which is with pitch angle greater than 1.5° and active power less than 1500 kW, and then eliminate them. After data pre-processing, three turbines are left with 177,619, 173,451, and 170,014 samples.

The process of ice accumulation on the blades usually involves several stages. There are three main types of blade icing, glaze ice, rime ice, and “mixed” (i.e., a combination of two types of icing) [35]. During the time period in which ice accumulates on the blades, the power generated by the wind turbine will be reduced to varying degrees as a result. As shown in Figure 3a demonstrates the case of data with high label reliability. On the contrary, Figure 3b demonstrates the case of data with low label reliability, which is the subject of this paper. What can be noticed in Figure 3b is that a large number of samples in limiting power operation are still labeled as normal. It cannot be ruled out that there are other reasons for limiting power operation, but it is clear that most of the icing samples were indeed mislabeled. The data in Figure 3 have been normalized and the values of the axes have no practical significance.

4.2. Feature Processing

As shown in

Table 1. Original feature description of the data.

No.	Variable Name	Description
1	windSpeed	Short-filtered wind speed
2	power	Active power
3	externalTemperature	Nacelle external temperature
4	generatorSpeed	Generator Speed
5	positionDeviation	Nacelle position deviation
6	position	Nacelle position
7	pitch1Angle	Angle of pitch 1
8	pitch2Angle	Angle of pitch 2
9	pitch3Angle	Angle of pitch 3
10	pitch1Speed	Speed of pitch 1
11	pitch2Speed	Speed of pitch 2
12	pitch3Speed	Speed of pitch 3
13	accelerationX	Tower drive direction acceleration
14	accelerationY	Tower non-drive direction acceleration
15	internalTemperature	Nacelle internal temperature
16	internalTemperature2	Nacelle another measurement point temperature
17	gridPower	Active power exported to the grid
18	yawSpeed	Yaw speed

, the original features of the data are mainly 18 operational parameters such as short-filtered wind speed, active power, pitch angle, nacelle external temperature, and generator speed. As the values of power and gridPower are almost the same, in this paper, we use power rather than gridPower for blade icing detection. Based on expert knowledge and data analysis [36], three new features are created:

$$k_{wp}={\left(\frac{windSpeed+w{s}_{Q3}}{power+w{s}_{Q3}}\right)}^2-1$$

(11)

$$k_{wg}={\left(\frac{windSpeed+w{s}_{Q3}}{generatorSpeed+w{s}_{Q3}}\right)}^2-1$$

(12)

$$k_{wpg}={\left[\frac{{\left(windSpeed+w{s}_{Q3}\right)}^2}{\left(power+w{s}_{Q3}\right)\times \left(generatorSpeed+w{s}_{Q3}\right)}\right]}^2-1$$

(13)

where $windSpeed$ denotes the short-filtered wind speed, $w{s}_{Q3}$ denotes the third quartile of the short-filtered wind speed, $power$ denotes the active power, and $generatorSpeed$ denotes the generator speed.

As shown in Figure 4, the values of the three new features created show a more significant increase in the time range where the label is 1 (i.e., icing). Pearson correlation analysis is performed on the original features of the data and the newly constructed features. Features with Pearson correlation coefficients over 0.9 are excluded to avoid the degradation of model classification accuracy and generalization performance due to feature redundancy.

After feature extraction, we apply a feature scaling technique to the features with the aim of eliminating the effect of magnitude between data features so that there can be comparability between different features. The most commonly used methods of feature scaling are normalization and standardization. Normalization, or Min-Max Scaling, is a linear transformation of the original data that maps the data to the range [0,1]. This study uses standardization, also called the Z-Score normalization method, which maps the data to a distribution with a mean of 0 and a standard deviation of 1. The formula is as follows.

$$z=\frac{x-\mu }{\sigma }$$

(14)

$x$ denotes the feature value of the original data, $\mu$ denotes the mean value of the features of the original data, and $\sigma$ denotes the standard deviation of the feature values of the original data.

4.3. Evaluation Metrics

In this paper, blade icing detection is abstracted as a binary classification task that can be evaluated using the model evaluation criterion for machine learning classification problems. The confusion matrix is one of the most intuitive and effective ways to evaluate binary classification models. As shown in Figure 5, TP indicates that the sample’s true label is icing and the classification result of the prediction model is also icing. TN indicates that the sample’s true label is normal and the classification result of the prediction model is also normal. FP indicates that the sample’s true label is normal and the predicted classification result is icing. FN indicates that the sample’s true label is icing and the predicted classification result is normal.

Considering the existence of class imbalance in the blade icing data, the following five evaluation metrics calculated from the confusion matrix are selected to evaluate the model performance: Accuracy (Acc), Precision (Pre), Recall (Rec), F1-score (F1), and Matthews correlation coefficient (MCC).

$$Acc=\frac{TP+TN}{TP+TN+FP+FN}$$

(15)

$$Pre=\frac{TP}{TP+FP}$$

(16)

$$Rec=\frac{TP}{TP+FN}$$

(17)

$$F1=2\times \frac{Pre\times Rec}{Pre+Rec}$$

(18)

$$MCC=\frac{TP\times TN-FP\times FN}{\sqrt{\left(TP+FN\right)\left(TP+FP\right)\left(TN+FP\right)\left(TN+FN\right)}}$$

(19)

Rec, F1, and MCC are more important metrics for the problem addressed by the proposed approach in this paper. The higher the value of Rec, the less the icing condition of the blade is missed. F1 is a statistic used to evaluate the generalization performance of the model and is the weighted average of Pre and Rec. In the case of the class imbalance dataset, the performance of the model can be well evaluated. The higher the value of F1, the better the performance of the classifier. The closeness of the value of MCC to 1 represents the robustness of the model. For binary classification problems, the MCC is the most intuitive and simple of the confusion-matrix-based evaluation criteria in the application scenario where the classes are unbalanced. Acc is prone to be misleading in this case [37].

4.4. Experimental Setup

This experiment is set-up as follows. As the labels of the data are obtained from human observations, the labels for icing tend to be for severely iced samples, and the reliability of the labels for samples from the time before the known icing period is low. Data with low label reliability in this study are data from the period before the original data labeled as icing conditions. Consequently, the normal labeled samples within 1 h before the time point when icing was found are considered as unreliable samples, and the rest of the samples are considered as reliable samples. The reliable samples are randomly divided into training and test sets in the ratio of 7:3, and the unreliable samples are added to the training set. To illustrate that the proposed method effectively reduces the dependence on labeled data, the data in the training set are tested according to different labeled rates R. The selected value of R is increased from 0.1 to 0.9. In order to eliminate the contingencies of experimental results, both the proposed method and the selected comparison method are repeated 10 times with any labeled rate R. The average of the experiment results of 10 times is taken as the final result of the experiment.

The hyperparameters of the base classifier XGBoost model are tuned by traversing a given combination of parameters. The base classifier XGboost uses a grid search method to optimize the model hyperparameters, and the results of the grid search are shown in

Table 2. Grid search results of the base classifier XGBoost.

Hyper-Parameter	Searching Result	Searching Range
Learning_rate	0.01	[0.001, 0.01, 0.02, 0.03, 0.1]
N_estimators	1000	[100, 500, 1000, 1500, 2000]
Max_depth	4	[3–7]
Subsample	0.8	[0.6, 0.7, 0.8, 0.9, 1]
Colsample_bytree	0.8	[0.6, 0.7, 0.8, 0.9, 1]

. All the models mentioned in this experiment are tested in the same environment as follows: a PC with Intel Core i7-10710U @ 1.10 GHz, 16 GB of RAM, Python 3.8.5, and Scikit-learn 0.23.2, manufactured by Lenovo Ltd. in Beijing, China.

5. Discussion of Results

In order to verify the effectiveness of the feature processing method proposed in this paper, data before feature processing and data after feature processing are used for comparison experiments. Figure 6 shows the test results of the two kinds of data input to the model after training at R = 0.5. As shown in the figure, after the feature processing, all the metrics of the model improve substantially. Specifically, Acc improves by 7.2%, Pre improves by 29.6%, Rec improves by 16.3%, F1 improves by 22.7%, and MCC improves by 31%. The results show that the proposed feature processing method effectively improves the performance of model classification.

In order to verify the superiority of the tri-XGBoost method proposed in this study, we compare supervised XGBoost with the semi-supervised learning method proposed in this study. In this experiment, we select the three most representative labeled rates R. The values of R are taken as 0.2, 0.5, and 0.8. As shown in

Table 3. Comparison of supervised and semi-supervised classification models.

Method		Acc	Pre	Rec	F1	MCC
Supervised XGBoost	R = 0.2	0.836	0.688	0.540	0.605	0.509
	R = 0.5	0.928	0.861	0.785	0.821	0.777
	R = 0.8	0.919	0.832	0.766	0.798	0.748
Semi-supervised (this paper)	R = 0.2	0.857	0.678	0.677	0.675	0.583
	R = 0.5	0.959	0.941	0.870	0.904	0.879
	R = 0.8	0.969	0.930	0.919	0.925	0.905

, with R = 0.2, supervised XGBoost and the proposed model perform almost identically in Acc and Pre. However, there is already a large gap in Rec, F1, and MCC, which are quite important for blade icing detection. With R = 0.5, the proposed method significantly outperforms the supervised XGBoost method in all metrics, where Pre reaches the highest value of 0.941 in this experiment. With R = 0.8, our model improves 20% in Rec, 15.9% in F1, and 21% in MCC compared to the supervised XGBoost method. It can be observed that the performance of supervised XGBoost at R = 0.8 decreases compared to R = 0.5, which may be due to the presence of inaccurately labeled samples in the labeled data, resulting in noise within the model. The results show that the proposed method is less affected by labeling inaccuracies. Overall, with extremely limited labels, the proposed method still shows a large improvement in three metrics, Rec, F1, and MCC. Compared with Acc and Pre, the significant improvement of these three metrics can better represent the help of the proposed method for blade icing detection.

The proposed method in this study modifies the loss function of the base classifier XGboost to Focal Loss, and we compare XGboost with Focal Loss and XGboost with Logistic loss. The application scenario of this study suffers from class imbalance and inaccurate labeling, and the problem of hard samples arises when the tri-training method is applied to generate pseudo-labels. In this experiment, we select three most illustrative labeled rates R. The chosen values of R are 0.1, 0.2 and 0.3.

As shown in

Table 4. Effect of different loss functions on model performance.

Loss Function		Acc	Pre	Rec	F1	MCC	Train Time (s)
Logistic Loss	R = 0.1	0.746	0.434	0.385	0.408	0.248	47.185
	R = 0.2	0.821	0.605	0.569	0.586	0.473	55.723
	R = 0.3	0.885	0.793	0.688	0.736	0.666	61.849
Focal Loss	R = 0.1	0.754	0.476	0.424	0.449	0.292	40.267
	R = 0.2	0.857	0.678	0.677	0.675	0.583	50.142
	R = 0.3	0.931	0.867	0.809	0.837	0.794	57.513

, in the case of insufficient labeled data, the loss function of choosing Focal Loss as the base classifier is effectively improved in all metrics compared to Logistic Loss. It can be observed that the training time of the model is also relatively reduced when there is the same amount of labeled data. The less the amount of labeled data, the more training time is saved by the proposed method in this study. For the labeled rate R = 0.1, 0.2, and 0.3, the training time is saved by 14.7%, 10%, and 7%, respectively. Focal Loss shows the ability to speed up the model fitting and effectively improves the model classification. For the class imbalance problem of the binary classification task, Focal Loss demonstrates good rebalancing ability. However, if future studies go further into the prediction of blade icing degrees, the performance of Focal Loss may need to be reconsidered.

The self-training algorithm [38] is often compared to the tri-training algorithm as a type of semi-supervised learning algorithm. The self-training algorithm uses the same base classifier as the tri-training algorithm. Unlike the tri-training algorithm, in each round, each classifier generates pseudo-labels for itself for unlabeled samples instead of labeling the samples by the other two classifiers. With the base classifier uniformly set to XGBoost with Focal Loss, we carry out a comparative analysis of two classical semi-supervised strategies.

Table 5. Comparison of self-training and tri-training semi-supervised learning strategies.

Semi-Supervised Strategy		Acc	Pre	Rec	F1	MCC
self-training	R = 0.2	0.826	0.634	0.566	0.599	0.489
	R = 0.4	0.918	0.822	0.791	0.806	0.755
	R = 0.6	0.941	0.873	0.835	0.854	0.817
	R = 0.8	0.962	0.933	0.880	0.905	0.882
tri-training	R = 0.2	0.857	0.678	0.677	0.675	0.583
	R = 0.4	0.946	0.881	0.869	0.875	0.840
	R = 0.6	0.974	0.940	0.933	0.937	0.920
	R = 0.8	0.969	0.930	0.919	0.925	0.905

shows the results of detecting blade icing using two different semi-supervised learning strategies when the labeled rate R is chosen to be 0.2, 0.4, 0.6, and 0.8. With R = 0.2, the tri-training algorithm improves 19.6% in Rec, 12.7% in F1, and 19.2% in MCC compared to the self-training algorithm. With R = 0.4, the tri-training algorithm improves 9.9% in Rec, 8.6% in F1, and 11.3% in MCC compared to the self-training algorithm. With R = 0.6, the tri-training algorithm improves 11.7% in Rec, 9.7% in F1, and 12.6% in MCC compared to the self-training algorithm. With R = 0.8, the tri-training algorithm improves 4.4% in Rec, 2.2% in F1, and 12.6% in MCC compared to the self-training algorithm. The classification performance of the tri-training algorithm is generally improved over that of the self-training algorithm regardless of the chosen labeled rate. The only exception is that when the labeled rate R = 0.8, the Pre value of the model with the tri-training algorithm decreases slightly. It is worth noting that the improvement in the tri-training semi-supervised strategy compared to the self-training semi-supervised strategy for the ability of the model to detect blade icing gradually diminishes as the labeled rate increases.

The base classifier XGBoost is replaced with other base classifiers under the same experimental setup for comparison. The performance of the proposed method is tested against the commonly used classification algorithms such as SVM, K Nearest Neighbor (KNN), RF, and LightGBM, all of which are trained using the tri-training method. The test results are shown in Figure 7. In this experiment, the values of the labeled rate R are taken from 0.1 to 0.9.

As shown in Figure 7, the proposed model in this study achieves the best performance on all five different evaluation metrics when the labeled rate R is greater than 0.3. The results show that the performance of the models improves with the increase in the labeled rate R, except for the case where the base classifier is a KNN. When the labeled rate R is less than 0.3, KNN performs even better than all base classifiers. However, because the value is still low, it cannot effectively detect blade icing in real-world scenarios. SVM will be particularly vulnerable to false detection in the blade icing detection process as its Rec value is at the same level as other base classifiers and its Pre value is quite low. When the labeled rate R is greater than 0.3, RF and LightGBM have a large gap with the proposed model in Recall, F1, and MCC. It is notable that RF, LightGBM, and XGboost show similar growth trends as the labeled rate R increases. All three algorithms mentioned above are one of the decision-tree-based ensemble methods, and XGBoost shows better classification performance in blade icing detection. It can be concluded that the proposed model works well with a limited number of labels.

In summary, the proposed blade icing detection method in this paper effectively extracts the features characterizing blade icing and reduces the dependence of machine learning models on labeled data. For hard samples, the proposed method demonstrates good generalization ability. By penalizing hard samples more than easy samples, the algorithm performs better. XGBoost is compared with other base classifiers, such as SVM, KNN, RF, and LightGBM. With a good detection rate and low false alarm rate, XGBoost is well-suited as a base classifier for blade icing detection.

6. Conclusions

In this paper, a semi-supervised learning algorithm based on tri-XGBoost is proposed to address the problems of inaccurate labeling and class imbalance of SCADA data in wind turbine blade icing detection. Specifically, we implement a tri-training algorithm. The tri-training algorithm presented effectively and rationally utilizes the inaccurately labeled samples and significantly improves the classification performance of the model. In addition, the original features are fused to obtain the most differentiating information. The features are normalized to eliminate the effect of feature magnitude on model learning. The cost-sensitive learning approach is used to deal with the class imbalance problem, in which Focal Loss is introduced to improve the XGBoost algorithm. By comparing the proposed method with other classification algorithms in experiments, it is verified that the proposed method in this paper has better classification performance. Experimental results also show that the proposed tri-XGBoost algorithm can achieve great classification performance even when there are only a small number of labeled samples. It is of practical significance for wind turbines to reduce the loss of power generation, avoid the risk of blade breakage during the cold period, and improve the safety of operation.

The classification performance of the model may be affected when the same model is applied to different wind farms or different types of wind turbines. As part of our ongoing research, we will apply transfer learning to blade icing detection to enhance the model’s generalization capability.