Abstract
A suspension flux internal model control method is proposed to address the problem of the strong coupling of a single-winding bearingless flux-switching permanent magnet motor leading to a significant ripple of the rotor radial displacement. Firstly, based on air-gap magnetic field modulation theory, the stator flux equation considering rotor dynamic eccentricity is established to reveal the relationship between the eccentric rotor and the magnetic field. Secondly, according to the dynamic characteristics of the motor and the variation law of the air-gap magnetic field, the suspension-plane flux is substituted into the rotor dynamic model, and the suspension flux-dynamics internal model and corresponding output are constructed, respectively. Finally, a complete control strategy is established, and the rotor is stably suspended by PWM control. The simulation and experimental results show that the proposed method has better steady-state and dynamic performance than traditional PID control, and the maximum radial displacement ripples of the rotor are reduced by 53% and 50% in steady-state and dynamic operation.
1. Introduction
The magnetic bearing has several advantages, such as high precision, a long life, no friction, and no need for lubrication. The bearingless motor wraps the windings of the magnetic bearing around the stator of the rotating motor, and the suspension mechanism of the magnetic bearing can be replaced by an air-gap bias magnetic field, which effectively improves the integration, efficiency, and power density of the motor. It has broad application prospects in the fields of multi-electric ship and aerostatic propulsion, CNC machine tool spindle, centrifugal unit, etc. [1,2,3]. The bearingless flux-switching permanent magnet motor (BFSPMM) lasts for the flux-switching motor characteristics of easy heat dissipation and high torque density in permanent magnets (PMs). Using the advantage of multi-phase motors with multiple degrees of freedom, the multi-phase single-winding BFSPMM adopts only one set of the stator winding current to independently control the rotor suspension and rotation [4,5]. It demonstrates heightened levels of integration, degrees of freedom, power density, and winding utilization efficiency [6,7].
Owing to the uneven mass distribution of the rotor, manufacturing process errors, unbalanced magnetic forces, etc., an excitation force with the same frequency as the rotational speed exists during operation. This leads to a lack of overlap between the geometric central axis and the inertial axis of the rotor, resulting in ripples in rotor displacement and torque. The vibrational signal will introduce interference to torque control, capturing a periodic current signal within the winding and inducing periodic radial electromagnet pull. Especially, the torque and suspension force of a single-winding bearingless motor has strong coupling, the control method is more complicated, and it is more difficult to suppress the radial displacement and speed ripples of the rotor during operation. In ref. [8], a hybrid active–passive actuation approach is introduced to solve the problem of destabilizing stiffness produced by the PMs. However, the controllable performance of the supporting parameters is reduced. At present, high-performance control methods of the bearingless motor are mainly aimed at the dual-winding structure, and the primary emphasis in the investigation of single-winding PM-stator bearingless motors lies in the development of topology designs and the examination of electromagnetic characteristics, whereas it is less on the control methods [9,10]. Therefore, it is necessary to study the high-performance suspension control method of single-winding BFSPMM. The existing bearingless motor control methods can be divided into (1) traditional proportion-integration-differentiation (PID) control and its improvements; (2) inverse systems and their intelligent methods; and (3) control methods based on advanced control theories.
In ref. [11], a suspension force model based on finite element simulation and the Maxwell tensor method is established, combined with a dynamic coupling observer and a coupled suspension force regulator to dynamically compensate the PID controller, which improves the stability and robustness of the system. In refs. [12,13], a winding MMF interference and the output of the disturbance observer were added to the PID closed loop as feedforward compensation to reduce the control ring disturbance of the rotor radial displacement, respectively. Although the PID controller can effectively manage steady-state errors and achieve fundamental motor suspension operations, it is unable to attenuate the oscillations stemming from dynamic disturbances.
With the development of the control methods, many advanced control methods can be applied to the control system of the bearingless motor. By establishing the model inverse system, the dynamic decoupling performance of the suspension and rotation control of the bearingless motor can be effectively realized [14]. The internal model control (IMC) can be combined with the inverse system method to optimize the decoupling effect of the PID controller in the traditional inverse system control strategy [15]. Due to the complex construction process of the inverse system model, relevant studies mostly focus on the optimization methods of the inverse system model construction and intelligent methods are usually used to assist in the establishment of the inverse system model [16,17]. In addition, suspension systems need positioning sensors and control algorithms to maintain stable levitation. However, these systems often encounter feedback noise, which requires the use of filters to reduce the noise. When there is excessive noise in the feedback, it becomes difficult to estimate velocity and disturbance force, especially for high-bandwidth scenarios. In such cases, state observers can assist in enhancing the performance of control algorithms [18].
At present, the research results of high-performance control strategies for bearingless motors focus on the design and application of advanced control theories. In ref. [19], based on the differential geometry control method and sliding mode control principle, the strongly coupled system in the suspension/rotation control part was linearized and decomposed into independent subsystems for control. For high-speed applications, the traditional methods are not in effect in suspension control of the rotor owing to inherent parameter variations and external suspension loads. In ref. [20], a suspension current predictive control strategy is designed by calculating the given value of the optimal suspension current within the sampling period based on the fuzzy dynamic objective function. Furthermore, in modeling the global sliding-mode switching surface, additional fast-decaying nonlinear functions and rotor-tracking error functions have been incorporated [21]. In ref. [22], the repetitive control theory is combined with a fractional delay filter to suppress the rotor vibration caused by mass imbalance, manufacturing process error, or unbalanced magnetic pull.
The active disturbance rejection controller (ADRC) can increase the overall robustness of the control system to disturbances of different natures, but it is not able to compensate for radial load disturbances [23]. To further improve the controller bandwidth, the flux linkage model with the rotor dynamics model is used to construct an integral series standard model suitable for an ADRC controller [24]. To further optimize the dynamic effect and robustness of the ADRC, a fuzzy controller and genetic algorithm were introduced in refs. [25,26], respectively, to adjust the observer bandwidth online.
As mentioned above, most of the existing methods are the direct application of advanced observers/controllers, whereas few involve an optimal control aiming to the own characteristics of the bearingless motor. Therefore, this paper attempts to obtain the dynamic model of the rotor dynamic eccentric by mathematical modeling and proposes a suspension flux internal model control method to address the problem of the strong coupling of a single-winding bearingless flux-switching permanent magnet motor leading to a significant ripple of the rotor radial displacement. IMC, as a controller design strategy based on a process mathematical model, can intuitively analyze the physical meanings of the control variables and effectively improve the motor suspension performance by combining the strong regularity and periodicity of the rotor suspension operation state of the bearingless motor.
Herein, a suspension flux internal mode control strategy for single-winding BFSPMM is proposed. The topology and mathematical model of the motor are introduced, and the decoupling control method of the six-phase single-winding bearingless motor is analyzed. Then, based on the air-gap magnetic field modulation theory, the suspension flux equation considering the dynamic eccentricity is established, and the effect of rotor radial displacement on the magnetic field can be analyzed by the equation. According to the theoretical deduction, the internal model and controller are established, and the outputs of the controller in the x- and y-directions are derived by feedback linearization theory. Finally, a high-performance suspension operation is realized by the PWM controller. Simulation and experimental results show that the proposed method has better steady-state and dynamic performance than traditional PID control.
This paper is organized as follows: In Section 2, the mathematical model of the researched motor is established. In Section 3, the principle of suspension flux internal model control strategy is introduced. In Section 4, the simulation and experimental results are provided. Finally, in Section 5 and Section 6, the strategy is discussed and summarized, respectively.
2. Topology and Mathematical Model of BFSPMM
2.1. Topology
The topology of the BFSPMM is shown in Figure 1. The structure of the stator and rotor is the same as the 12/10 pole mechanical-bearing FSPMM. Each phase winding is composed of k1-k2-k3-k4 in series, k = A-F. The current iA-iF flows through the phase winding A-F, respectively. They contain the torque current components iAT-iFT that control the motor’s rotation and the suspension current components iAS-iFS that control the motor’s suspension, and iAS = iDS, iES = iBS, iCS = iFS, iAT = −iDT, iET = −iBT, and iCT = −iFT. Through the suspension current, which is spatially symmetrical and in the same direction, the suspension force in three directions with a spatial difference of 120° can be generated to produce a controlled suspension operation. While the suspension current which is spatially symmetrical and in the opposite direction can be regarded as a three-phase FSPMM, which can generate stable electromagnetic torque. This current mode allows for the decoupling of rotation and suspension control.
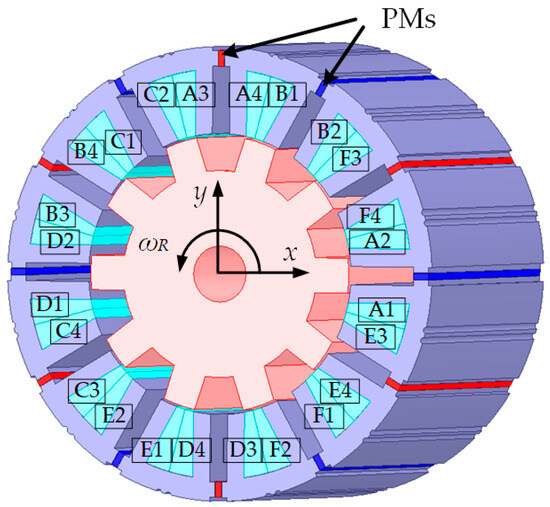
Figure 1.
Topology of BFSPMM.
It is defined that the radial displacement of the rotor is divided into x- and y-directions. The mechanical angular frequency of the rotor is ꞷR, the mechanical angle is θR, and the electrical angle is θr = 10 θR.
To control the motor’s rotation and suspension independently, the six-phase current can be decomposed into the torque-plane current components iαTiβT, suspension-plane current components iαSiβS, and zero-sequence currents io1io2 by constant power transformation matrix T6 [6]:
where
The torque-plane current components can be transformed to the synchronous rotation dq coordinate system, and the torque can be controlled by the strategy of idT = 0. Thus, the electromagnetic torque is:
where |ψf| is the amplitude of the PM flux linkage, and iqT and idT can be obtained by the following transformation:
The motor rotation can be stably controlled according to (3). To effectively control the rotor suspension, rotor dynamics need to be analyzed.
2.2. Rotor Dynamics Model of BFSPMM
The research object in this paper is a two-degree-of-freedom bearingless motor, and its coordinate system of the rotor motion is shown in Figure 2. The xyz-axis is defined as the stationary coordinate system, and the irjrkr-axis as the synchronous rotating coordinate system. Due to the unbalanced moment NxNy, there is precession along the z-axis when the rotor rotates tangentially along the kr-axis. The angles of inclination of the kr-axis to the y- and x-axes are θx and θy, respectively. As the inclination of the shaft is very small, θx and θy are proportional to the x- and y-direction displacements of the rotor.
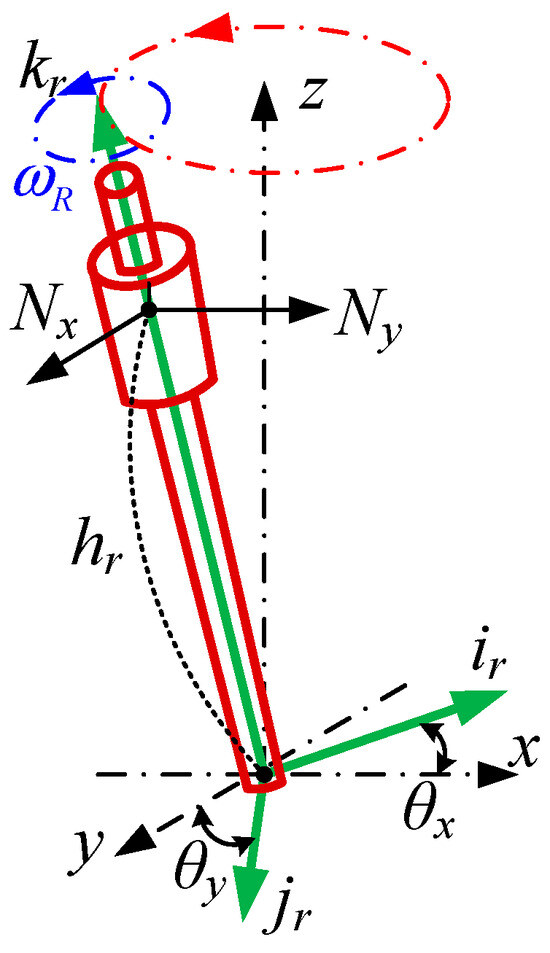
Figure 2.
Rotor-motion coordinate system of BFSPMM.
We assume G, hr, and lr to be the gravity of the rotor, the height of the mass center, and the axis length, respectively. Ir and IR are the moment of inertia of the rotor radial and tangential, respectively. According to the moment formula, the rotor dynamics model can be written as follows:
where Fx and Fy are the radial electromagnetic pulls in the x-and y-directions, respectively. According to [10], the linear relationships between FxFy and suspension current components idSiqS are as follows:
where kPM and kqT are the amplitude of the fundamental component of the suspension force generated by the coactions of unit suspension current with the PMs’ MMF and iqT, respectively. The suspension current idSiqS can be obtained by the following equation:
where
2.3. Suspension Force-Flux Mathematical Model
To effectively control radial electromagnetic force by flux linkage, it is necessary to establish the relationship between suspension force and suspension-plane flux linkage.
By matrix T6, the stator flux of the stationary coordinate system can be deduced as follows:
where
where Lii(i = A~F) represents the self-inductance of phase winding i, Mij(i = A~F, j = A~F, I ≠ j) represents the mutual inductance of phase winding i and j, and ψfi(i = A~F) represents the PM flux of phase winding i.
2.3.1. Expression of No-Load PM Flux
To accurately express the stator flux under the rotor dynamic eccentricity, the flux equation of each phase winding is established based on the air-gap field modulation theory [27,28]. The PMs, stator, rotor, and armature windings can be combined into three cascade elements, i.e., excitation source–modulator–filter, as shown in Figure 3. FPM represents the MMF of the PMs, MS represents the stator modulation function, MR Represents the rotor modulation function, and Wi (i = A~F) represents the winding function.
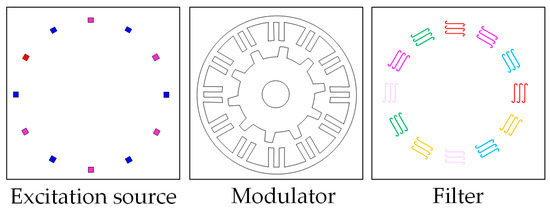
Figure 3.
Cascade model of air-gap magnetic field modulation theory.
Figure 4 is the schematic diagram of the BFSPMM modulation function, and θ represents the circumference angle of the air gap. Taking phase winding A as an example, the no-load flux linkage without rotor eccentricity can be expressed as:
where rg is the air-gap radius, μ0 is the air permeability, and Δg is the air-gap length. WA represents the winding function of phase A, and it is generated by that conductor distribution function Ci(θ) modulated by stator modulation function Ms(θ), i.e., WA = Ms·CA. As the winding of each phase is made up of two coils with symmetrical spatial axes in series, CA = CA1 + CA2, CA1, and CA2 are conductor distribution functions of coils A1-A2 and coils A3-A4, respectively, whose Fourier series expansion is as follows:
where Nw is the number of coil turns,
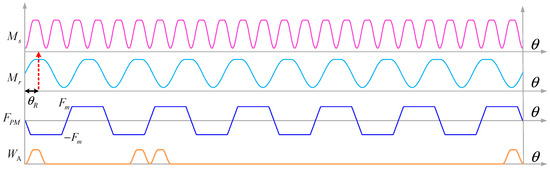
Figure 4.
Modulation function diagram of BFSPMM.
In (13), MS = MSW·MSF, MSW is the modulation function of the tooth slot at windings, MSF is the modulation function of the tooth slot at PMs, and the Fourier series expansion is as follows:
where
where lts is the distance from the center of each U-core of the stator, lsp is the width of the PM, and as and bs are constants.
In (13), the Fourier series expansion of the modulation function of the rotor MR is as follows:
where
where ltr and lsr are the widths of the tooth and slot of the rotor, respectively. ar and br are constants.
In (13), the Fourier series expansion of the MMF of the PMs is as follows:
where Fm is the amplitude of the MMF, and af is a Fourier series.
Substituting (14)~(20) into (13), the PM flux without the rotor eccentricity of the phase winding A can be obtained as follows:
where am is a constant. bm1, bm2, and bnm are Fourier series.
Similarly, it can be deduced that the no-load PM flux of phase winding i is:
where k = 0~5 corresponds to phase winding i = A~F.
The expression of the flux linkage under the dynamically eccentric rotor can be constructed as a flux linkage without rotor eccentricity pluses a modulated flux change by the rotor eccentricity modulation operator Me. The modulation operator Me is a sinusoidal function with the eccentric angle φ as the positive direction, i.e.,
where e is the eccentric distance. The modulated flux change in phase winding i can be deduced as
where ψem = ψfm·me, me is a constant.
2.3.2. Inductance Expression
When a unit current flows through the winding, whose winding function is Wi(θ), and the flux induced by another winding, whose winding function is Wj(θ), the mutual inductance between the phase winding is represented by i and j. Thus, the mutual inductance expression without rotor eccentricity is as follows:
where Mji is the self-inductance of phase winding i when i = j, denoted as Lii0. Taking phase winding A as an example, and substituting (14)~(19) into (25), it is deduced that the self-inductance of phase winding A without rotor eccentricity is:
where L0~L4 are constants, and L0 >> L2 > L3 > L1 > L4. Thus, it can be obtained that Lii0 ≈ L0.
The same as the no-load PM flux, the inductance of single-winding BFSPMM is an inductance without rotor eccentricity pluses a modulated inductance change by the rotor eccentricity modulation operator Me. The inductance changes in phase winding i can be deduced as
where Le = L0·le, and le is a constant.
According to (25)~(27), the mutual inductance of phase winding i and j with the rotor eccentricity is as follows:
where, when i ≠ j, Mji0 is the DC component of the mutual inductance between phase winding i and j without the rotor eccentricity, and Mjie is the change in the mutual inductance caused by the eccentric rotor. When i = j, Mji = Lii. According to [29], there is a fixed proportional coefficient of the mutual inductance and self-inductance of single-winding BFSPMM. Thus, (28) can be rewritten as
2.3.3. Mathematical Model of Suspension Flux
According to (22), (24), and (28), the mathematical model of the flux linkage ψA~ψF can be obtained. By substituting (22), (24), and (29) into (9), the suspension-plane flux of the stationary coordinate system αSβS can be deduced as
where
where v1~v3 are constants.
By the rotation transformation, the suspension-plane flux ψαSψβS of the stationary coordinate system can be transformed into a dSqS coordinate system, and the flux in the dSqS coordinate system is as follows:
where
In (32), the first term is the controllable flux component generated by the suspension current component idS and iqS, and the latter two terms can be regarded as the disturbance components ψdSd and ψqSd.
Substituting idS and iqS in (32) into (6), the linear relationships between FxFy and suspension-plane flux ψdSψqS are as follows:
3. Suspension Flux Internal Model Control Strategy
3.1. Suspension Flux-Dynamics Internal Model of BFSPMM
Assuming , according to (5), (32), and (34), the suspension flux-dynamics internal model of BFSPMM can be established as follows:
Taking the x-direction as an example to analyze the controller output. The error between actual output and internal model output is defined as
A second-order low-pass filter is used to reduce the high-frequency harmonic signal in the error:
where ꞷn is the natural oscillation frequency, and ζF is the damping coefficient of the filter.
To make x track a given signal x*, an auxiliary function is defined as follows:
According to (38), when ≈ = x − , xf ≈ x − x*. Thus, the control problem that rotor radial displacement tracks a given signal becomes the control problem that xf = 0. Similarly, the derivation of the y-direction is not detailed here.
3.2. Feedback Linearization of Auxiliary Function
To make the xf = 0, setting , it can be deduced that
According to feedback linearization theory [30], Equation (39) can be linearized as follows:
Substituting the second line of (32) and (40) into (39), and considering x* = 0, it can be deduced that the output of the internal model controller in the x-direction is as follows:
Similarly, the output of the internal model controller in the y-direction is as follows:
3.3. Control Block Diagram
The control block diagram of the control strategy proposed in this paper is shown in Figure 5. Substituting the suspension flux ψdSψqS into equation (34), the internal model value of the rotor radial displacement is obtained. The internal model parameters are shown in Table 1. The given value ux*uy* of the output of the internal model controller is calculated according to (36)~(42), and the following equation calculates the suspension-plane flux error:
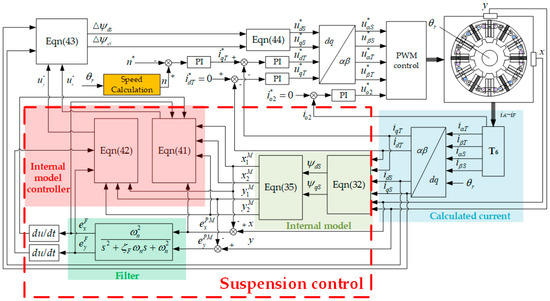
Figure 5.
Control strategy.

Table 1.
Parameters of internal model.
According to (43), the suspension-plane expected voltage vector can be calculated as follows:
where Rs is the winding resistance, and Ts is the control period.
The rotation of BFSPMM can be controlled by idT = 0, according to (3)~(4). The zero-sequence current component io2 is controlled to zero by a PI controller. Thus, the torque-plane expected voltage vector udT*uqT*, which controls the motor rotation, the suspension-plane expected voltage vector udS*uqS*, which controls the motor suspension, and the zero-sequence-plane expected voltage vector uo2* can be obtained. Finally, the control strategy proposed in this paper can be realized by PWM control.
4. Verification
4.1. Test Platform
The prototype unit of the motor studied in this paper is shown in Figure 6a. The horizontal direction of the test prototype is the y-direction, and the vertical direction is the x-direction. The prototype is connected with the DC motor and magnetic powder brake through an elastic coupling. The DC motor is used as gearing of the tangential load gearing. The load side of the BFSPMM shaft is equipped with auxiliary bearings that limit the radial displacement of the rotor to within 0.3 mm. The experimental platform is composed of an RTU-BOX 206® controller(Nanjing Rtunit Information Technology Co., Ltd., Nanjing, China) with TMS320F28377D as the core, a building block power module, and a high-power density power, as shown in Figure 6b.
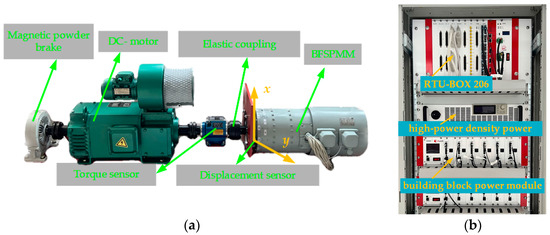
Figure 6.
Experimental tests: (a) BFSPMM unit; (b) Controller and driver.
4.2. Simulation Results
A complete control model based on Figure 5 is built-in MATLAB/Simulink. The simulation study started the suspension operation under the condition of 2 N·m load at 1000 r/min. As shown in Figure 7a, the rotor starts suspension under a PID controller at zero time. After 200 ms, the fundamental component of the rotor radial displacement ripple stabilizes to near the given displacement 0, but the high-frequency pulsation related to the rotational speed is still large, with an amplitude of 0.08 mm. The corresponding suspension current is shown in Figure 7b. When the rotor is stably suspended, the suspension current maintains a stable fundamental component related to the high-frequency ripple of the radial displacement of the rotor. When the method proposed in this paper is used for the suspension control, it is shown in Figure 7c. Evidently, the proposed strategy has better suspension performance. The fundamental component of the radial displacement of the rotor is stabilized at a given value in only 100 ms, and the amplitude of the high-frequency harmonic component is reduced to less than 0.35 mm. The corresponding suspension current is shown in Figure 7d. The suspension current of the strategy has more high-frequency components, which will bring more losses.
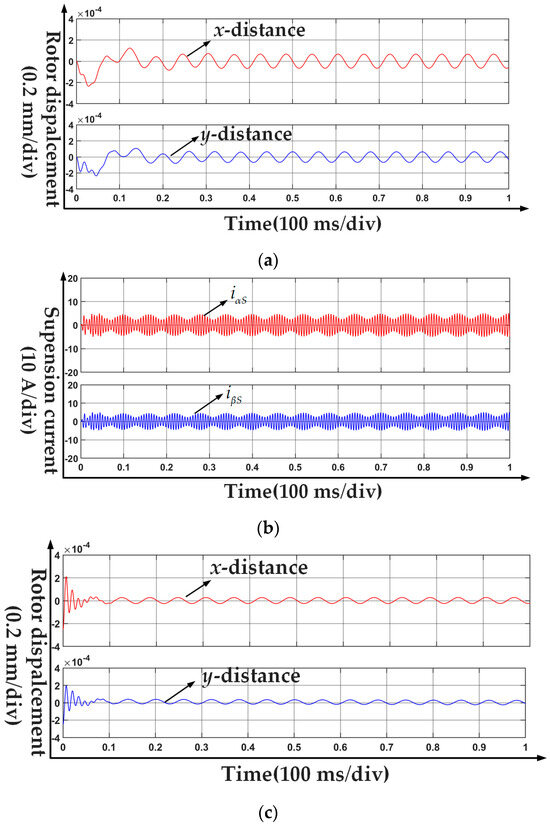
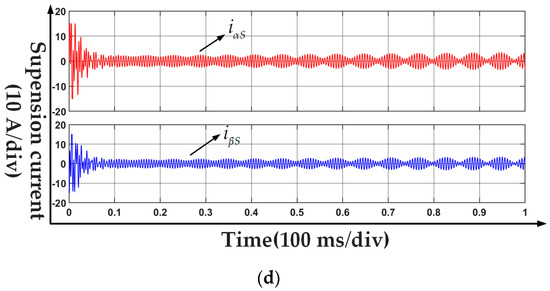
Figure 7.
Simulation results: (a) Rotor displacement under PID control; (b) Suspension current under PID control; (c) Rotor displacement under proposed control; (d) Suspension current under proposed control.
4.3. Steady-State Experiment
The proposed method is compared with the traditional PID method under no-load conditions at 500 r/min, as shown in Figure 8a,b. The rotor has an evident gyroscopic effect under PID control, and the maximum radial displacement ripple of the rotor is 0.15 mm, whereas the rotor is controlled at the geometric center of the motor by the method proposed in this paper, and the maximum radial displacement ripple of the rotor is 0.07 mm. Therefore, the proposed method can effectively reduce the radial displacement ripple of the rotor and has better control accuracy.
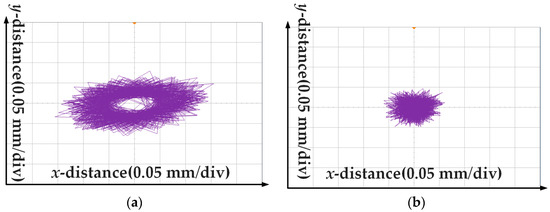
Figure 8.
Comparison of the steady-state experiment: (a) Traditional PID method; (b) Proposed method.
4.4. Dynamic-State Experiment
A speed step test of 2 N·m load at 0–1000 r/min is carried out on the test prototype, as shown in Figure 9. In the process of the speed step, the radial displacement of the rotor increases due to mechanical coupling. The rotor suspension controlled by PID always has the radial displacement ripple at the same frequency as the rotating speed, and the maximum displacement is ±0.2 mm, as shown in Figure 9a. The suspension current under PID control is shown in Figure 9b. The suspension current contains significant harmonic components during the speed step. In a steady state, the fundamental component of the suspension current has an evident ripple related to the radial displacement of the rotor. When the rotor suspension is controlled by the proposed method, the radial displacement pulsation is evidently reduced, and the maximum displacement is no more than ±0.1 mm, as shown in Figure 9c. The corresponding suspension current is shown in Figure 9d. The suspension current obtained by the method proposed in this paper contains a high harmonic component, which is very abundant even in the steady state. The reason is that the controller generates a more controllable radial electromagnetic pull to suppress the radial displacement ripple of the rotor.
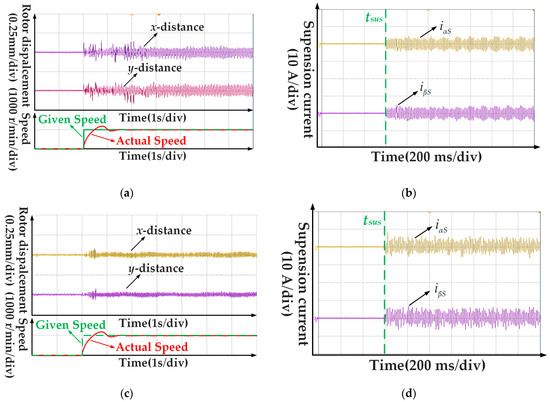
Figure 9.
Comparison of the dynamic-state experiment: (a) Rotor displacement under PID control; (b) Suspension current under PID control; (c) Rotor displacement under proposed control; (d) Suspension current under proposed control.
5. Discussion
As a general controller, the traditional PID method is widely used in various industrial control fields, almost applicable to all controlled objects. Therefore, in many kinds of literature, the proposed novelty control methods would be compared with the traditional PID method. In this paper, a suspension flux internal model control strategy for single-winding BFSPMM is proposed, and it has better steady-state and dynamic performance than traditional PID control, as shown in Table 2.

Table 2.
Control strategy comparison.
As the controller output in (41), at an ideal steady-state operation, the suspension force coupling between the x- and y-directions can be ignored, and ≈ = x − = 0. In this case, the internal mode controller output is as follows:
The above equation can be rewritten as follows:
where KP is a proportional coefficient, KD is a differential coefficient, and
Therefore, the output of the internal model controller can be considered as a combination of proportional-differential control and feedforward compensation. Furthermore, the internal model controller output can be rewritten as follows:
where
Therefore, the internal model controller can be written in the form of a linear active disturbance rejection controller (LADRC), as shown in Figure 10. According to the conclusion of [19], it can be reasoned that the proposed method and PID have the same stability margin in the low-frequency stage. During the middle- and high-frequency stages, the presented approach exhibits superior high-frequency disturbance suppression. Furthermore, the disturbance compensation demonstrates robust estimation capabilities when dealing with the overall system perturbations. By integrating the known model perturbation information within an internal model controller, an expansion of the controller bandwidth becomes feasible. Consequently, the method introduced here exhibits enhanced disturbance rejection performance and effectively mitigates radial displacement ripples of the rotor.

Figure 10.
The connection between the proposed method and LADRC.
In the proposed method, the change mechanism of rotor radial displacement can be analyzed based on the air-gap magnetic field modulation theory, and direct control of radial electromagnetic pull by air-gap magnetic field can effectively improve the suspension operation capability of the rotor. However, the internal model controller output depends on the accuracy of the parameters. This control strategy provides a kind of controller design way, which is weak in universality to bearingless motors of different structures. In addition, compared with the traditional PID controller, this strategy needs more complex signal processing, and the control strategy proposed in this paper makes the output peak of the inverter increase, which will increase the motor loss. These weaknesses currents are areas that need further improvement in the future.
6. Conclusions
The suspension force in the rotor dynamics is replaced by the suspension-plane flux in this paper, and the suspension flux-dynamics internal model of a single-winding BFSPMM is constructed. The output of the internal model controller can be equivalent to the form of a LADRC, and the conclusion is as follows:
- (1)
- The high-performance decoupling control of a single-winding BFSPMM is realized, and the radial displacement of the rotor is always suspended with a small radial displacement in the geometric center axis.
- (2)
- Compared with the traditional PID control, the proposed method has better steady-state performance, and the maximum radial displacement ripple of the rotor is reduced by 53%, which effectively improves the antijamming and robustness of the system.
- (3)
- Compared with the traditional PID control, the proposed method has better dynamic-state performance and reduces the radial vibration of the rotor in the process of speed regulation under the load-speed step condition.
Author Contributions
Methodology, validation, and writing, Y.C.; project administration and funding acquisition, W.Y.; software, R.Y.; conceptualization and supervision, B.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China, Grant 52171308, the Natural Science Foundation of Fujian Province, Grant 2021J01843, 2022J01811, and the Research Launch Funding of Jimei University, Grant ZQ2023002.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Chen, J.; Zhu, J.; Severson, E.L. Review of Bearingless Motor Technology for Significant Power Applications. IEEE Trans. Ind. Appl. 2020, 56, 1377–1388. [Google Scholar] [CrossRef]
- Sun, X.; Chen, L.; Yang, Z. Overview of Bearingless Permanent-Magnet Synchronous Motors. IEEE Trans. Ind. Electron. 2012, 60, 5528–5538. [Google Scholar] [CrossRef]
- Asama, J. Development of Slotless Single-Drive Bearingless Permanent Magnet Motor With Aerostatic Bearings for High-Speed Applications. IEEE Trans. Ind. Appl. 2023, 59, 4076–4082. [Google Scholar] [CrossRef]
- Sala, G.; Valente, G.; Di Nardo, M.; Degano, M.; Zanchetta, P.; Gerada, C. Power-Sharing Control in Bearingless Multi-Sector and Multi-Three-Phase Permanent Magnet Machines. IEEE Trans. Ind. Electron. 2021, 68, 9070–9080. [Google Scholar] [CrossRef]
- Khamitov, A.; Gruber, W.; Bramerdorfer, G.; Severson, E.L. Comparison of Combined Winding Strategies for Radial Nonsalient Bearingless Machines. IEEE Trans. Ind. Appl. 2021, 57, 6856–6869. [Google Scholar] [CrossRef]
- Chen, Y.; Wu, X.; Zhou, Y. Fault-Tolerant Operation Control Strategy for Combined Winding Bearingless Flux-Switching Permanent Magnet Motor Drive System with One Opened Phase. IEEE Trans. Energy Convers. 2021, 36, 2861–2871. [Google Scholar] [CrossRef]
- Jurdana, V.; Bulic, N.; Gruber, W. Topology Choice and Optimization of a Bearingless Flux-Switching Motor with a Combined Winding Set. Machines 2018, 6, 57. [Google Scholar] [CrossRef]
- Van Verdeghem, J.; Severson, E.L.; Dehez, B. Hybrid Active–Passive Actuation Approach of Passively Levitated Thrust Self-Bearing Machines. IEEE Trans. Ind. Appl. 2021, 57, 7035–7045. [Google Scholar] [CrossRef]
- Asama, J.; Chiba, A. Three-Coil Combined Winding Configuration for a 2-DOF Actively Controlled Bearingless Permanent Magnet Motor. IEEE Trans. Ind. Appl. 2021, 57, 6765–6773. [Google Scholar] [CrossRef]
- HNguyen, H.P.; Nguyen, X.B.; Bui, T.T.; Ueno, S.; Nguyen, Q.D. Analysis and Control of Slotless Self-Bearing Motor. Actuators 2019, 8, 57. [Google Scholar]
- Yang, F.; Yuan, Y.; Sun, Y.; Ding, S.; Yan, L.; Xu, J. Coupling Suspension Force Regulator Considering Time-Varying Characteristic for a Bearingless Switched Reluctance Motor. IEEE Trans. Ind. Electron. 2023, 70, 6632–6641. [Google Scholar] [CrossRef]
- Yang, Z.; Sun, C.; Sun, X.; Sun, Y. An Improved Dynamic Model for Bearingless Induction Motor Considering Rotor Eccentricity and Load Change. IEEE Trans. Ind. Electron. 2022, 69, 3439–3448. [Google Scholar] [CrossRef]
- He, X.; Yao, Y. An Improved Hybrid Control Scheme of a Switched Reluctance Motor for Torque Ripple Reduction. Appl. Sci. 2022, 12, 12283. [Google Scholar] [CrossRef]
- Nguyen, Q.D.; Giap, V.N.; Huang, S.-C. Inversed Model-Based Disturbance Observer Base on Adaptive Fast Convergent Sliding Mode Control and Fixed-Time State Observer for Slotless Self-Bearing Motor. Symmetry 2022, 14, 1206. [Google Scholar] [CrossRef]
- Sun, X.; Shi, Z.; Chen, L.; Yang, Z. Internal Model Control for a Bearingless Permanent Magnet Synchronous Motor Based on Inverse System Method. IEEE Trans. Energy Convers. 2016, 31, 1539–1548. [Google Scholar] [CrossRef]
- Xu, B.; Zhu, H.; Wang, X. Decoupling Control of Outer Rotor Coreless Bearingless Permanent Magnet Synchronous Motor Based on Least Squares Support Vector Machine Generalized Inverse Optimized by Improved Genetic Algorithm. IEEE Trans. Ind. Electron. 2022, 69, 12182–12190. [Google Scholar] [CrossRef]
- Sun, X.; Chen, L.; Jiang, H.; Yang, Z.; Chen, J.; Zhang, W. High-Performance Control for a Bearingless Permanent-Magnet Synchronous Motor Using Neural Network Inverse Scheme Plus Internal Model Controllers. IEEE Trans. Ind. Electron. 2016, 63, 3479–3488. [Google Scholar] [CrossRef]
- Petersen, N.; Slininger, T.; Severson, E.L. State Observers and Run-Out Reduction for Magnetically Levitated Motor Systems. IEEE Trans. Ind. Appl. 2023, 59, 1812–1823. [Google Scholar] [CrossRef]
- Yuvapriya, T.; Lakshmi, P. Design of Fractional Order Sliding Mode Controller for Semi Active Suspension System. In Proceedings of the 2019 IEEE International Systems Conference (SysCon), Orlando, FL, USA, 8–11 April 2019; pp. 1–5. [Google Scholar]
- Yang, Z.; Wu, J.; Lu, C.; Wang, D. Predictive current control of a bearingless induction motor model based on fuzzy dynamic objective function. Trans. Inst. Meas. Control 2020, 42, 3183–3195. [Google Scholar] [CrossRef]
- Rao, P.N.; Devarapalli, R.; Márquez, F.P.G.; Malik, H. Global Sliding-Mode Suspension Control of Bearingless Switched Reluctance Motor under Eccentric Faults to Increase Reliability of Motor. Energies 2020, 13, 5485. [Google Scholar] [CrossRef]
- Ye, X.; Yang, Z.; Sun, X. Improved Repetitive Control for Bearingless Induction Motor. Proc. CSEE 2019, 39, 6104–6112. [Google Scholar]
- Teixeira, R.d.A.; da Silva, W.L.A.; Amaral, A.E.S.; Rodrigues, W.M.; Salazar, A.O.; Villarreal, E.R.L. Application of Active Disturbance Rejection in a Bearingless Machine with Split-Winding. Energies 2023, 16, 3100. [Google Scholar] [CrossRef]
- Chen, Y.; Zhou, Y. Active Disturbance Rejection and Ripple Suppression Control Strategy with Model Compensation of Single-Winding Bearingless Flux-Switching Permanent Magnet Motor. IEEE Trans. Ind. Electron. 2022, 69, 7708–7719. [Google Scholar] [CrossRef]
- Yang, Z.; Jia, J.; Sun, X.; Xu, T. A Fuzzy-ELADRC Method for a Bearingless Induction Motor. IEEE Trans. Power Electron. 2022, 37, 11803. [Google Scholar] [CrossRef]
- Wang, X.; Zhu, H. Active Disturbance Rejection Control of Bearingless Permanent Magnet Synchronous Motor Based on Genetic Algorithm and Neural Network Parameters Dynamic Adjustment Method. Electronics 2023, 12, 1455. [Google Scholar] [CrossRef]
- Chen, Y.; Zhou, Y. Radial Displacement Sensorless Control in Full Speed Range of Single-Winding Bearingless Flux-Switching Permanent Magnet Motor. IEEE Trans. Energy Convers. 2022, 38, 599–610. [Google Scholar] [CrossRef]
- Cheng, M.; Han, P.; Hua, W. General Airgap Field Modulation Theory for Electrical Machines. IEEE Trans. Ind. Electron. 2017, 64, 6063–6074. [Google Scholar] [CrossRef]
- Chen, Y.; Zhou, Y. Radial Displacement Sensorless Control of Bearingless Flux-Switching Permanent Magnet Machines Based on Difference of Symmetric-Winding Flux Linkages. IEEE Trans. Ind. Electron. 2021, 68, 7793–7803. [Google Scholar] [CrossRef]
- Pathak, K.; Franch, J.; Agrawal, S. Velocity and position control of a wheeled inverted pendulum by partial feedback linearization. IEEE Trans. Robot. 2005, 21, 505–513. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).