Electrohydraulic and Electromechanical Buoyancy Change Device Unified Vertical Motion Model
Abstract
:1. Introduction
2. Dynamic Model of the Vertical Motion of a VBS Actuated Device
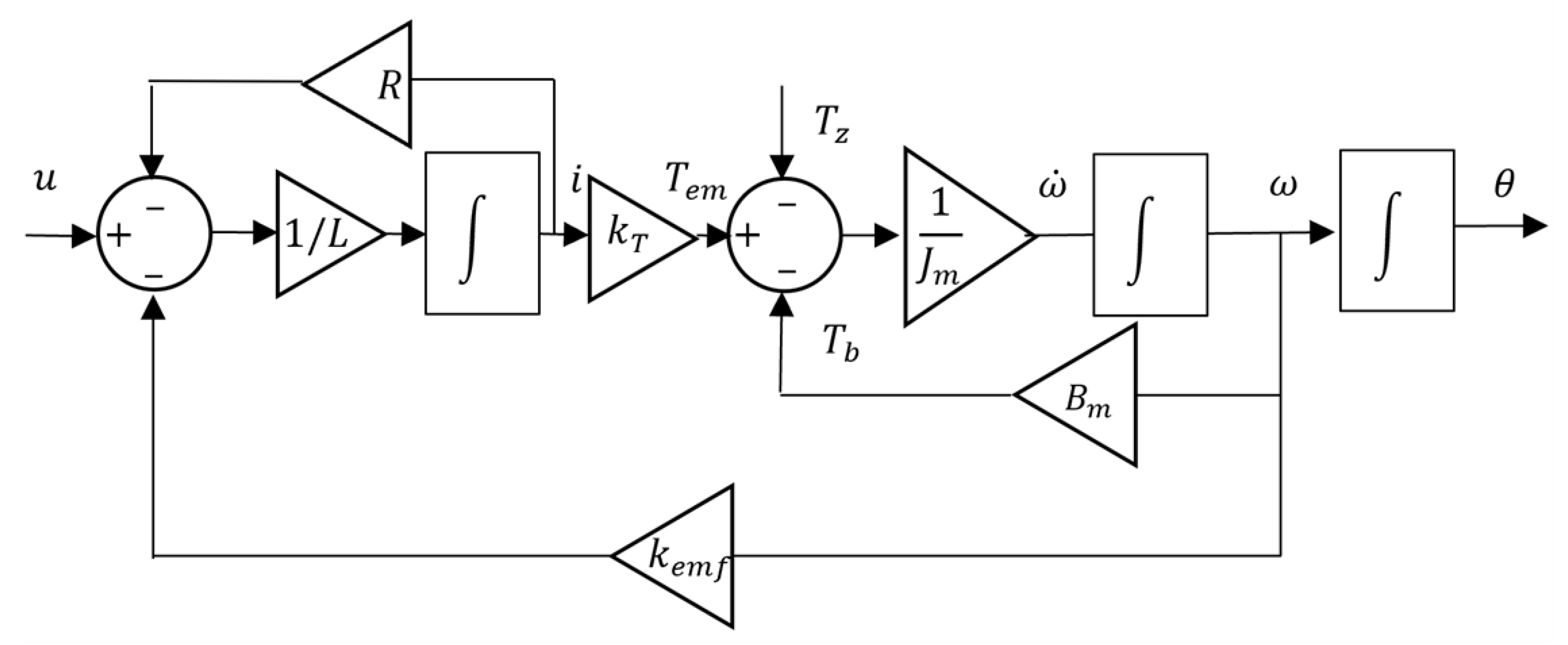
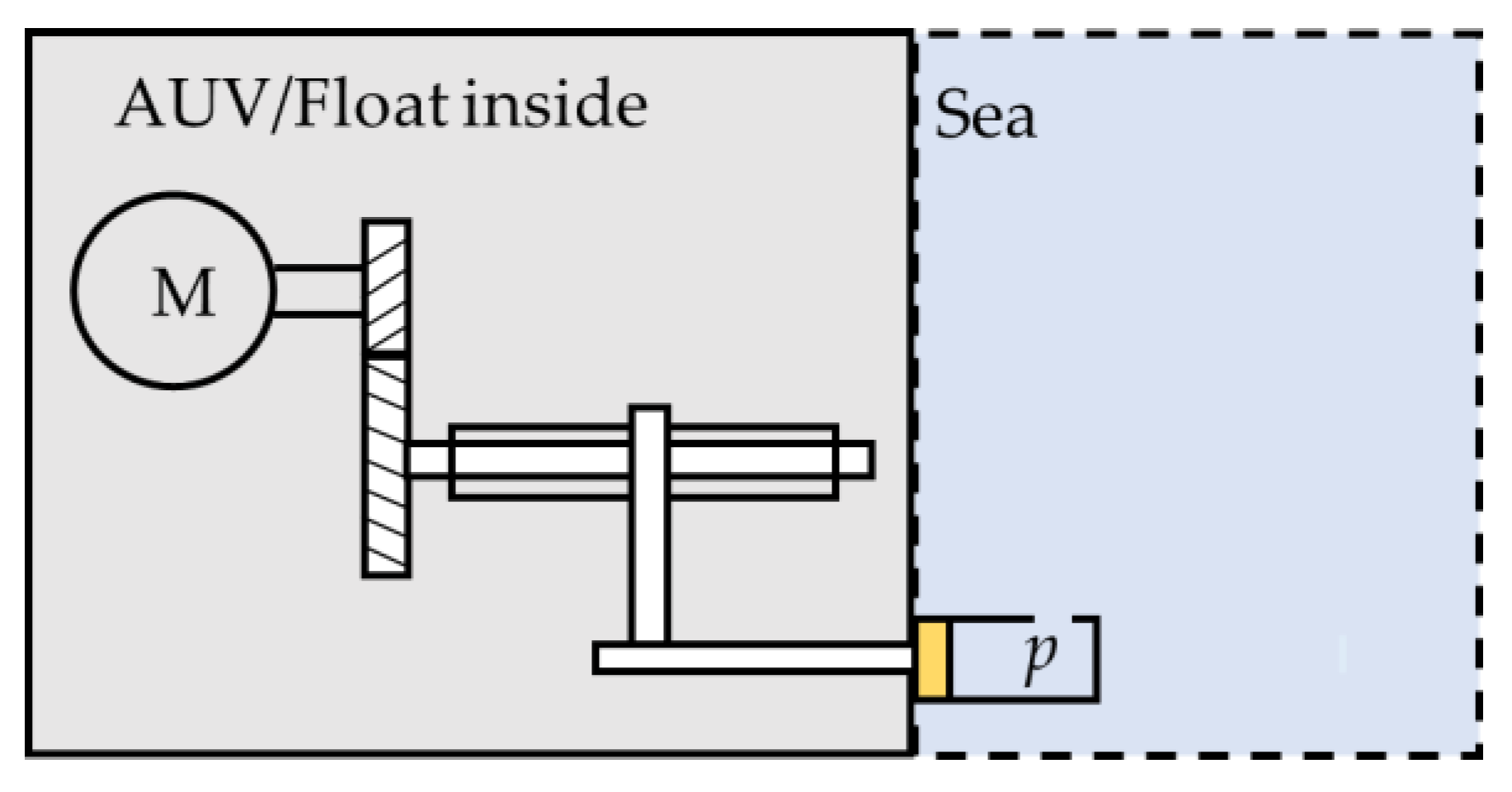
2.1. Actuation System Model
2.1.1. Motor Model
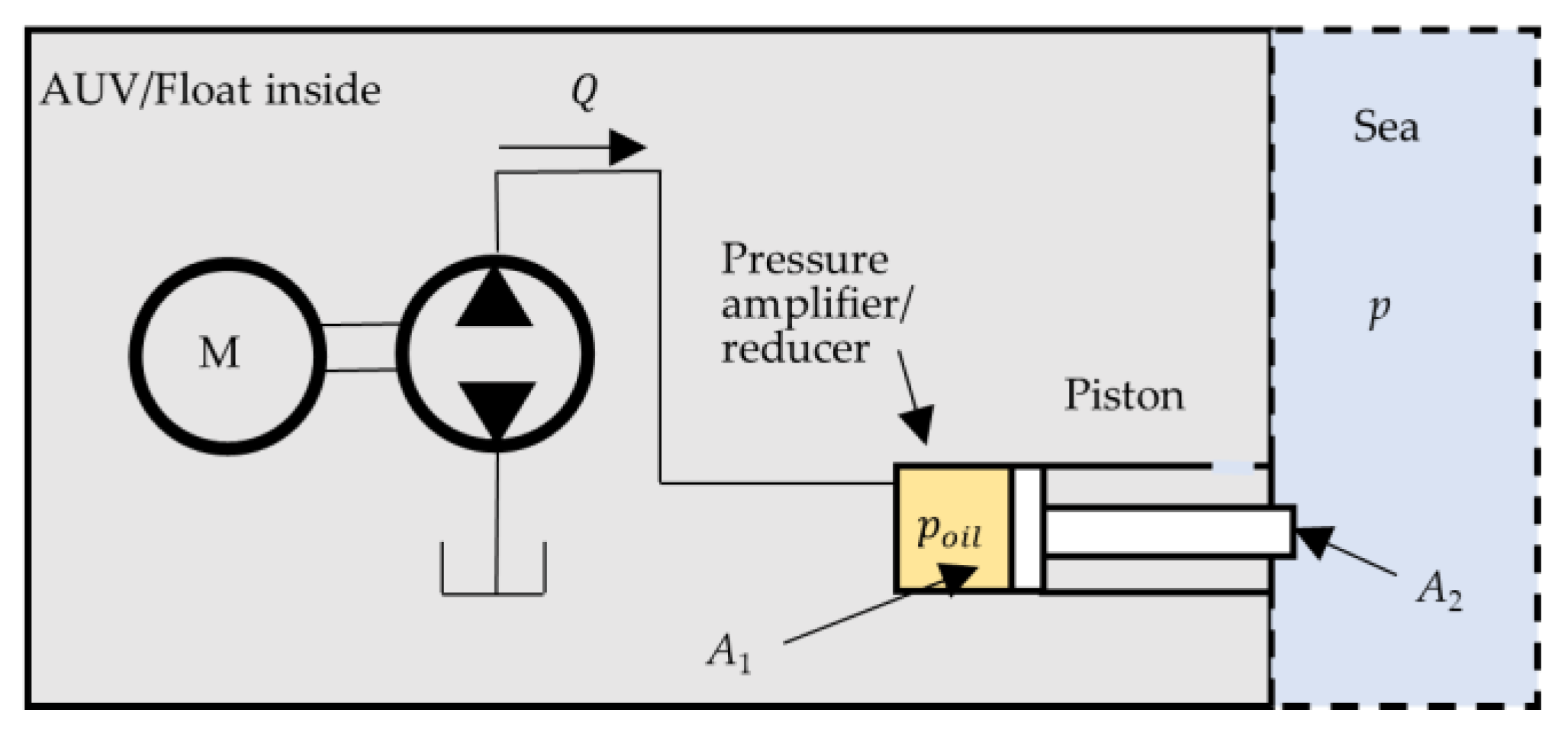
2.1.2. Electrohydraulic Solution Model
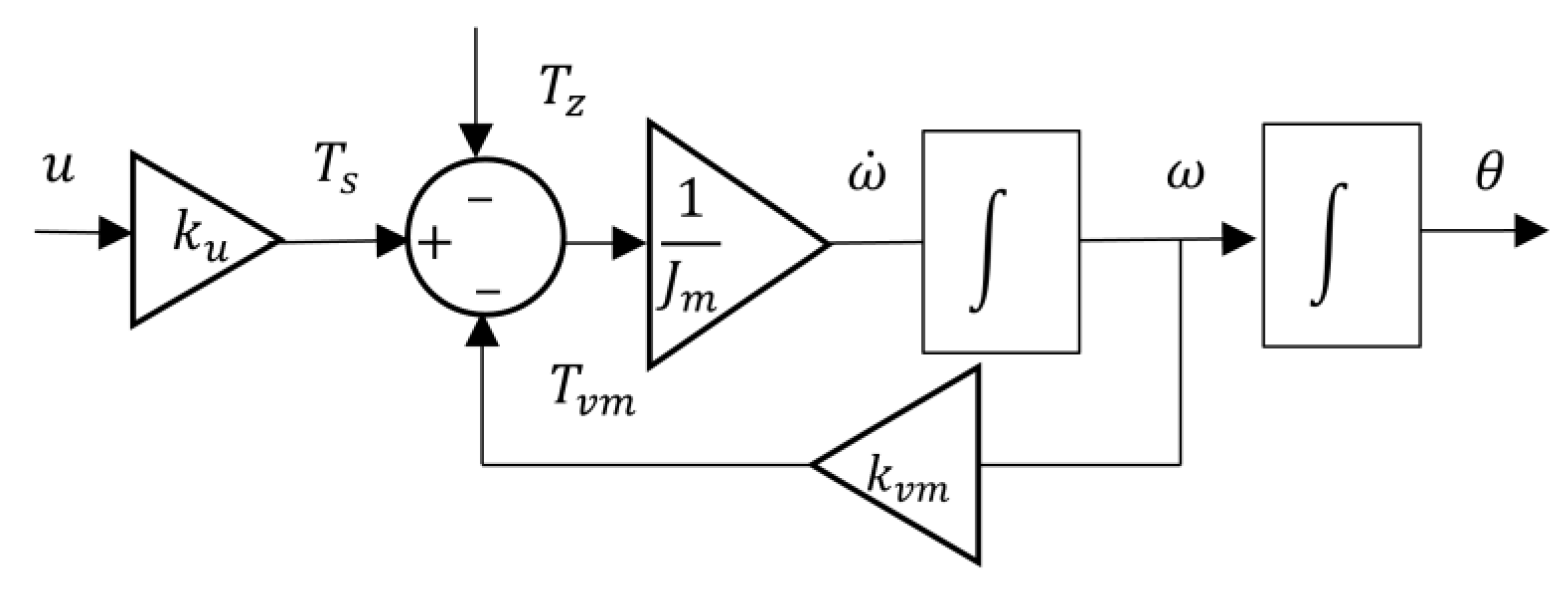
2.1.3. Electromechanical Solution Model
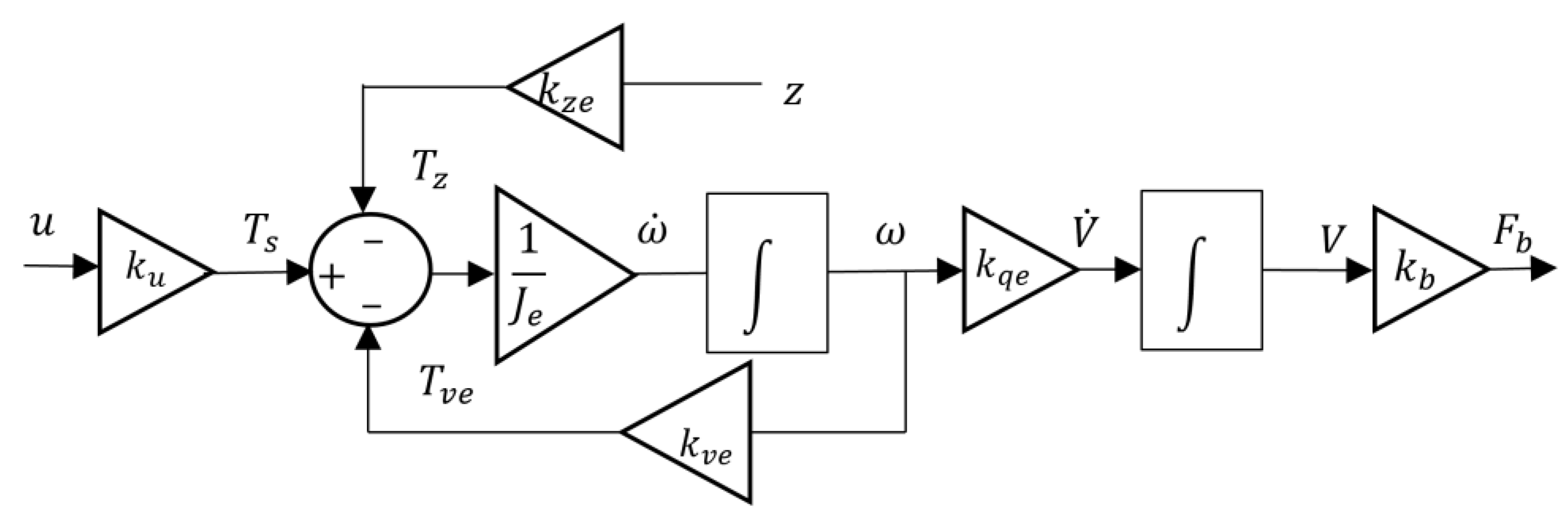
2.1.4. Unified Model for the Actuation System of the VBS
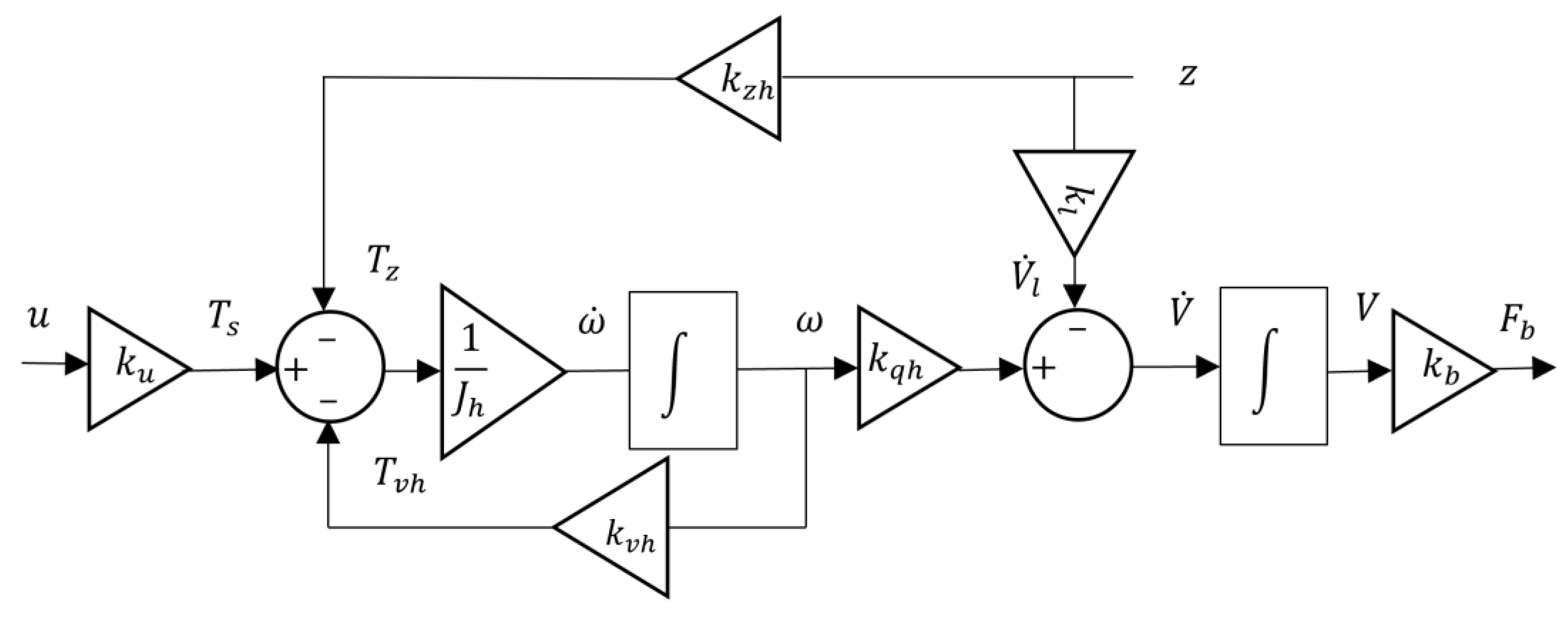
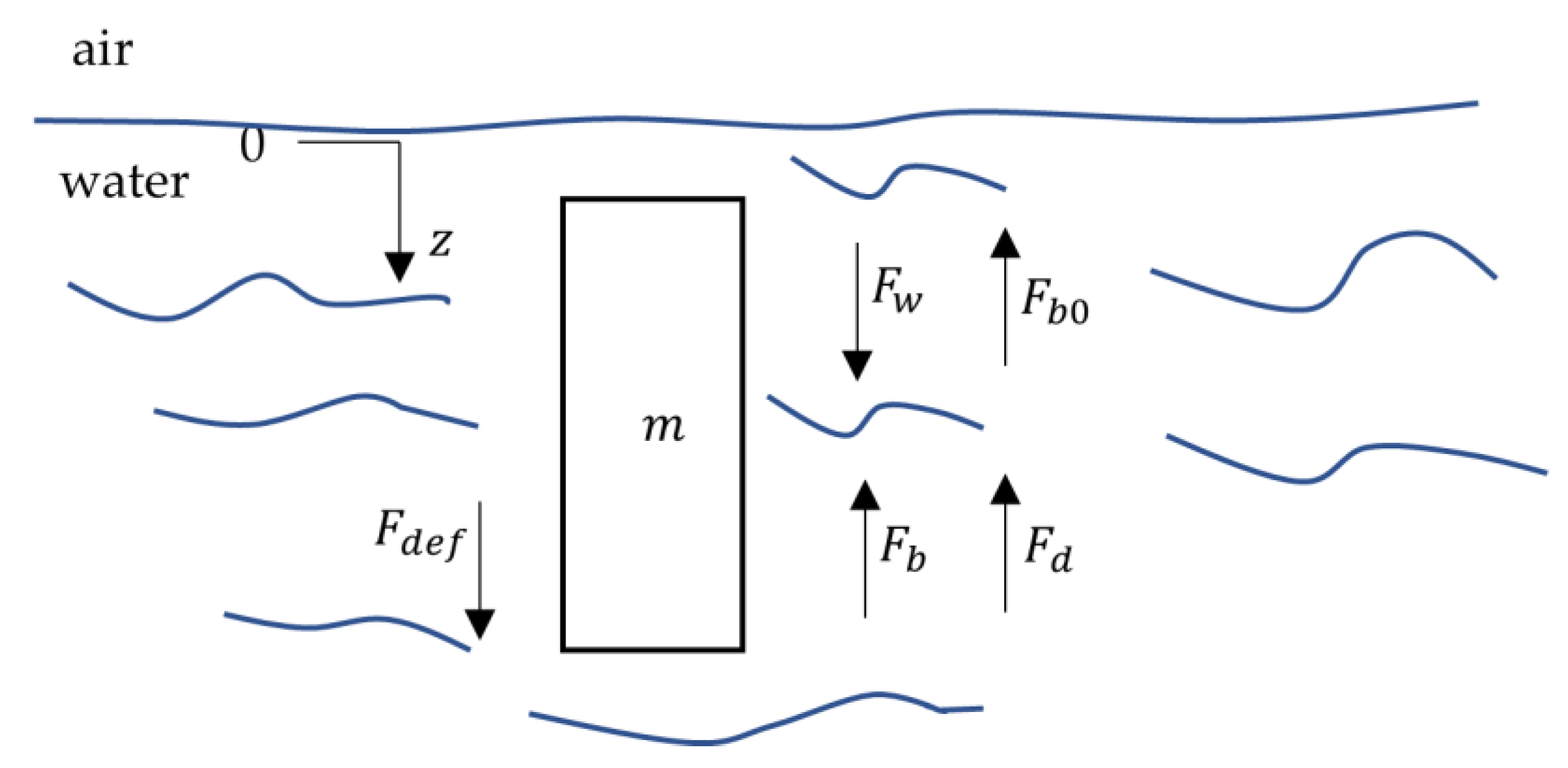
2.2. Overall Vertical Motion Model of the VBS Actuated Device
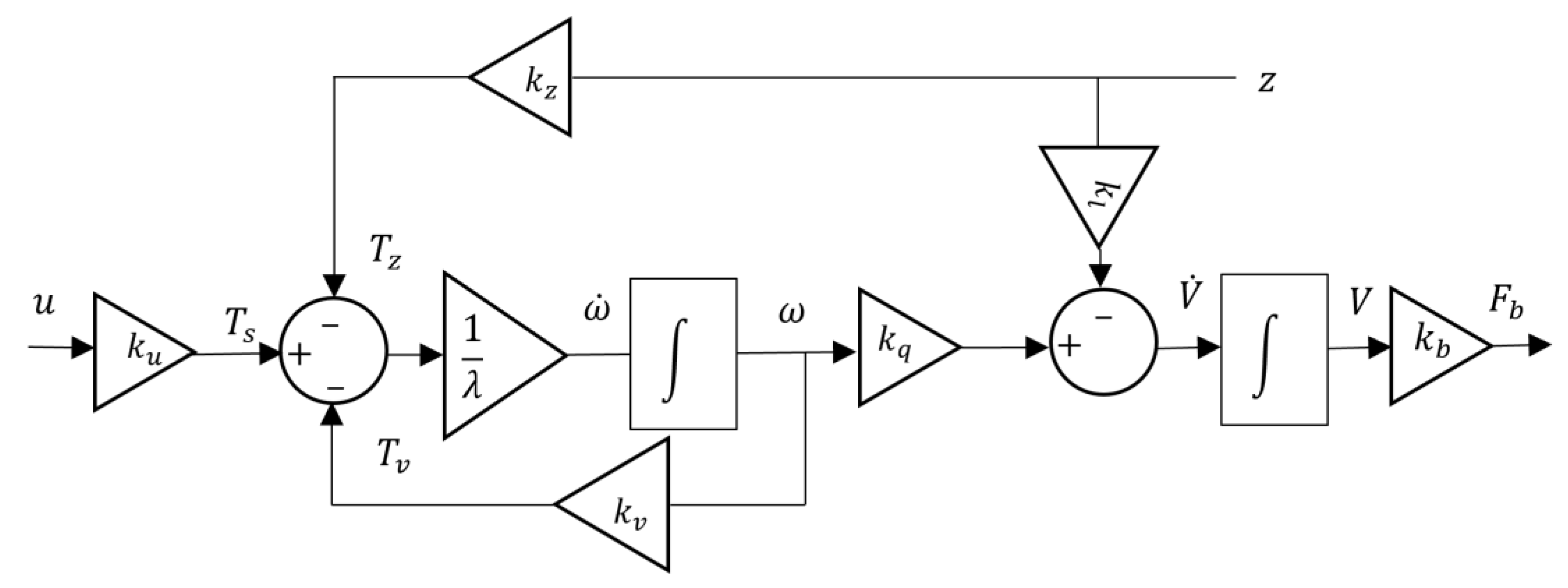
2.3. Simplified Model for Parameter Identification in Shallow Water
2.4. Overall Vertical Motion Model with Identification Parameters
2.5. Open-Loop Stability Analysis
- , which is expected in the electromechanical solution, and might be acceptable if a high volumetric efficient pump is used in the electrohydraulic solution;
- , by assuming that the device structure compressibility is exactly counterbalanced with the increase in water density with pressure;
- , by assuming that the outside pressure does not influence the velocity and position of the actuator (for instance, if the controller is able to fully reject the disturbance caused by the VBS depth in Equation (33)).
3. Experimental Results
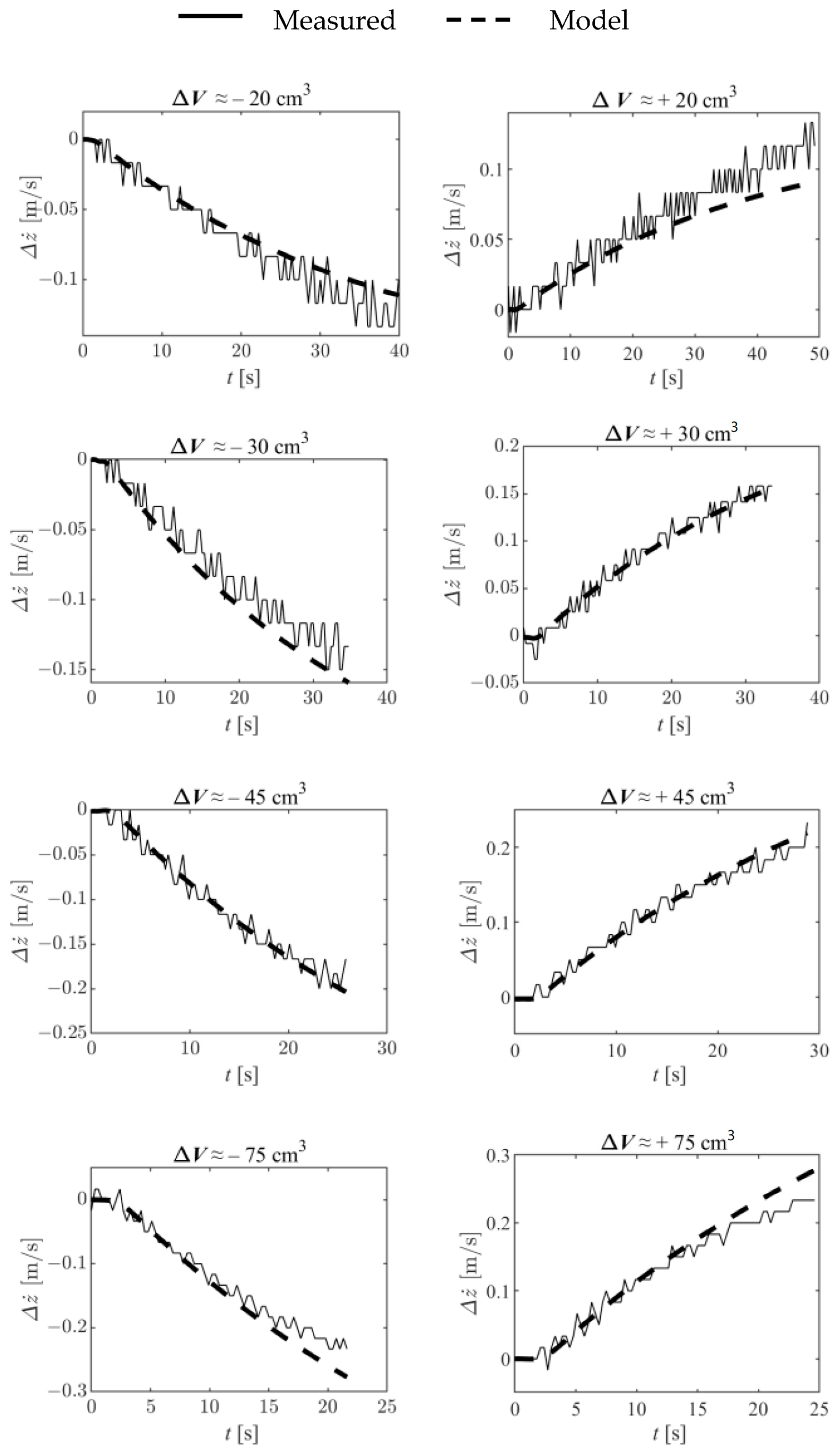
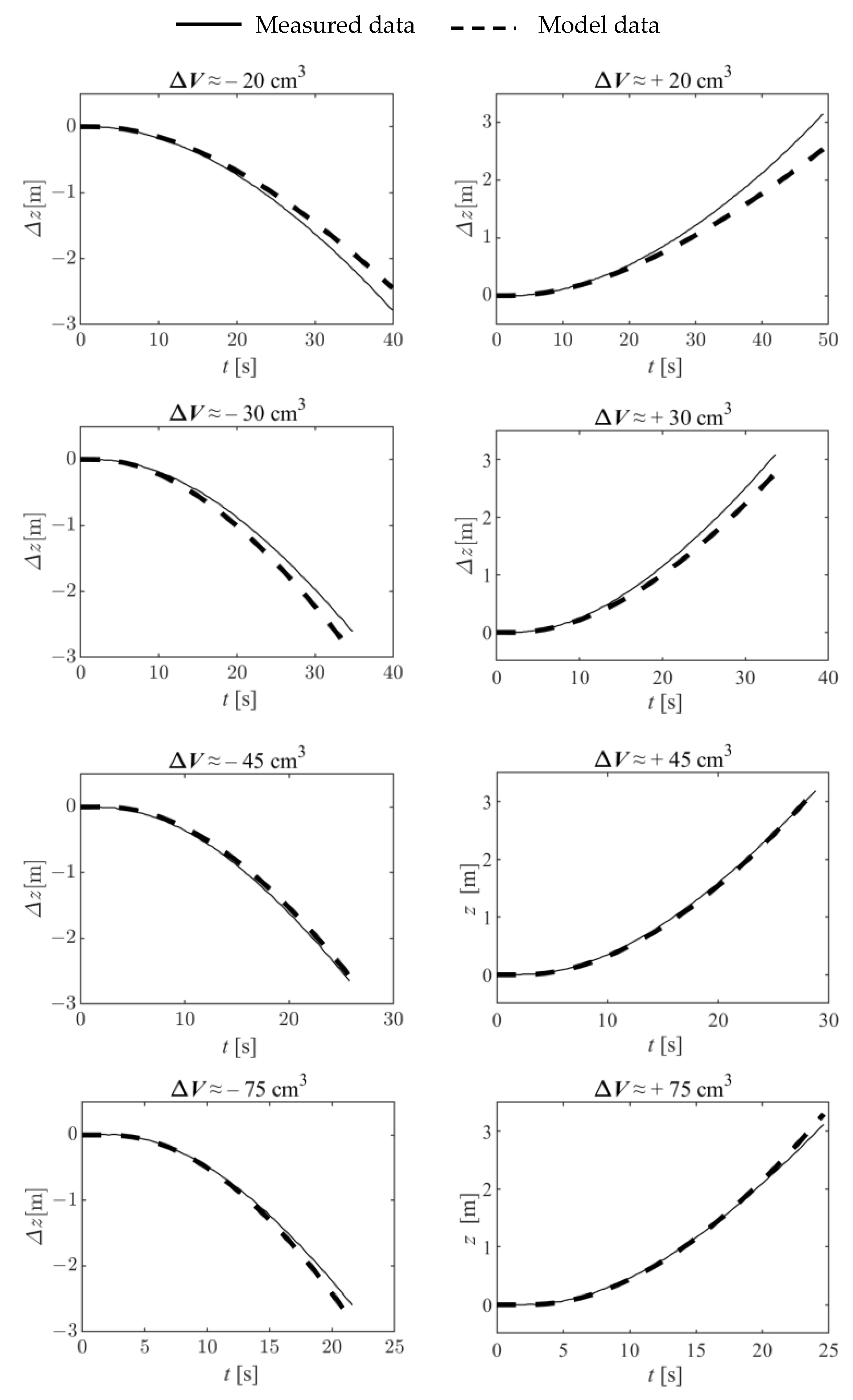
3.1. Model Identification Results
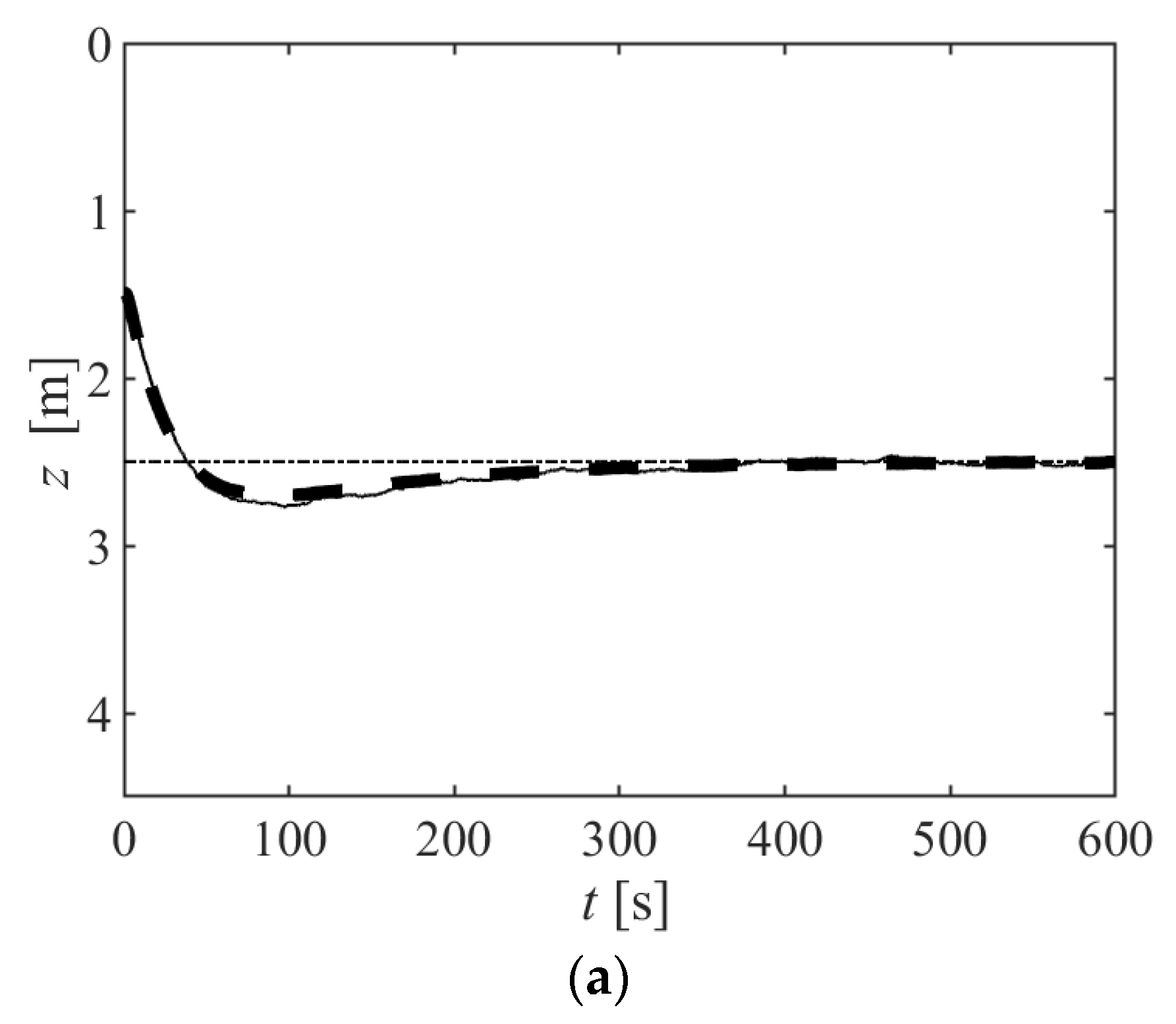
- Starting from the bottom, and using closed-loop control, control the depth of the vehicle until it reaches nearly zero velocity around , where should be conveniently chosen, according to the vehicle length, in order to ensure that it is neither touching the bottom nor partially emerged (see step (d) below). When this happens, the vehicle is at its zero-buoyancy setting. Please notice that the dynamic and steady state closed-loop characteristics obtained with the controller used at this stage (and at stage (c)) are essentially irrelevant, as the only purpose is to make the vehicle reach a nearly zero velocity. For this reason, the controller to be used in this step can have a coarse tuning;
- Stop closed-loop control, and increase the buoyancy by a factor of . In the particular case of the prototype presented in Figure 11, this is equivalent to increasing the piston position by a constant value . This was made in an open loop, by using the information provided by the manufacturer regarding the steady state relation between applied voltage and actuator speed. Having that information, the time that a given voltage should be applied to reach a desired position can be easily calculated. Wait until the vehicle reaches the bottom while recording the value of its depth z;
- Using closed-loop control, control the depth of the vehicle until it reaches nearly zero velocity around When this happens, the vehicle is at its zero buoyancy setting;
- Stop closed-loop control, and decrease the buoyancy by a factor of . Again, in the particular case of the prototype presented in Figure 11, this is equivalent to decreasing the piston position by a constant value, . Wait until the vehicle reaches the bottom, while recording the value of its depth z.
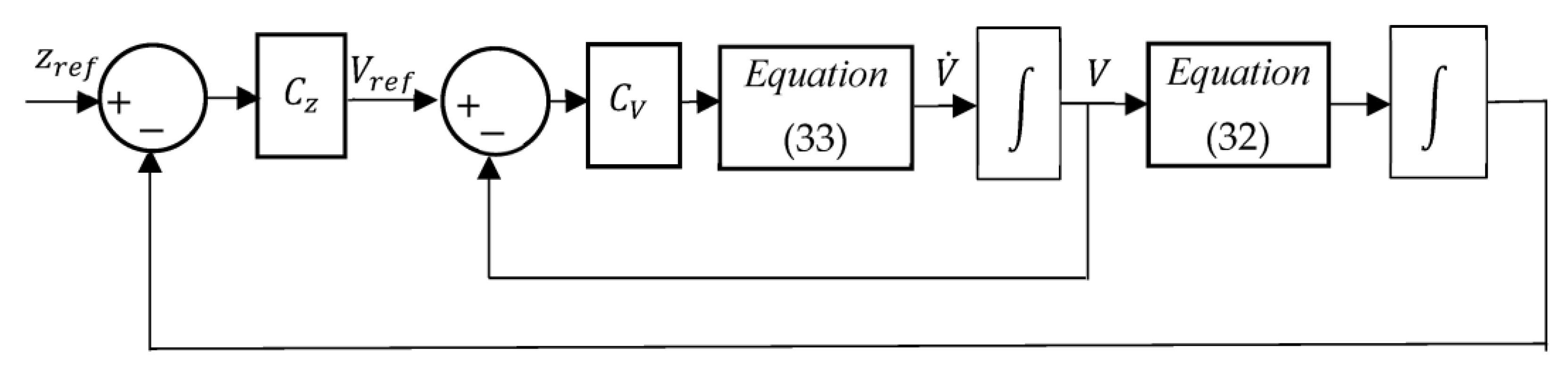
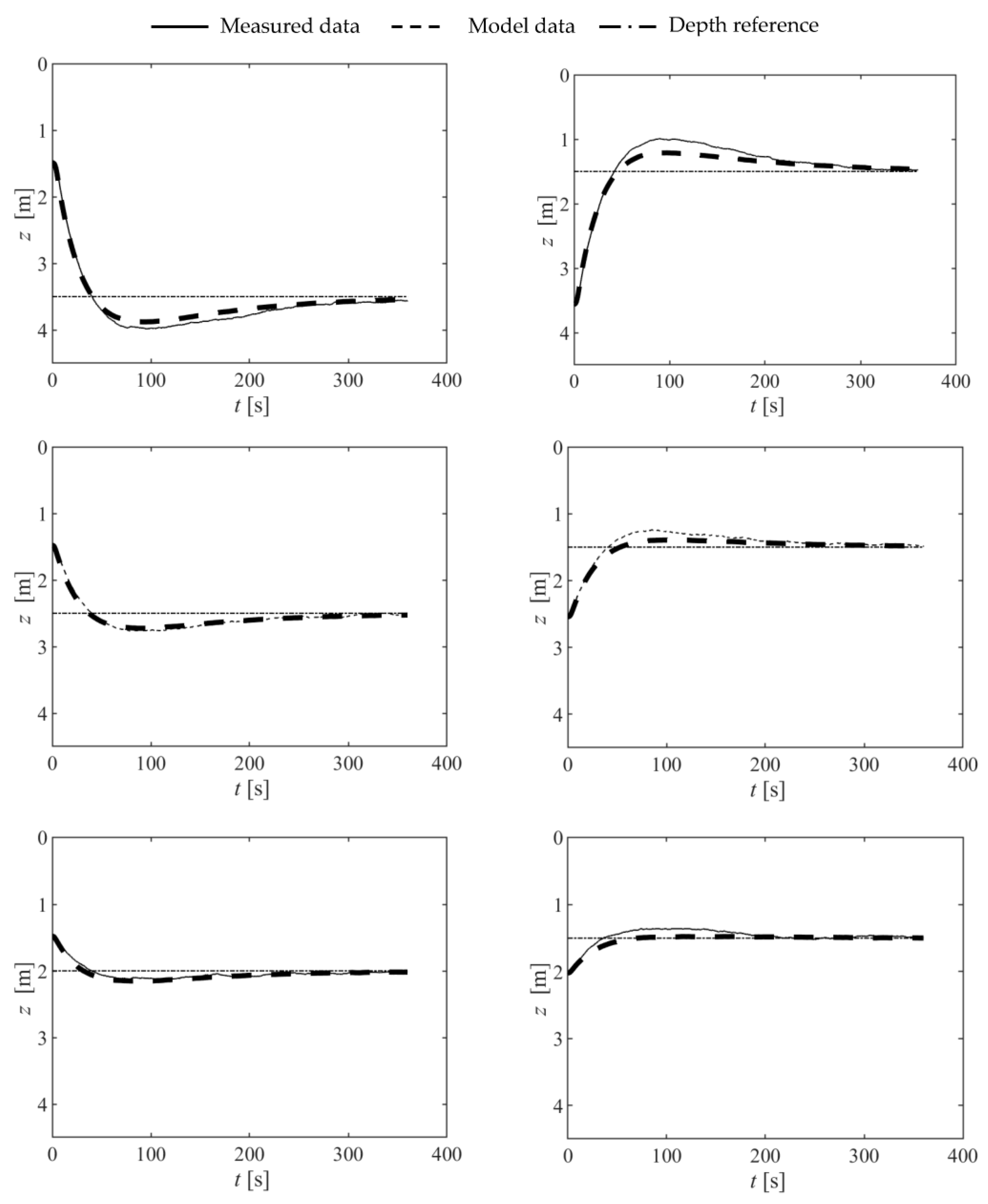
3.2. Control Results
4. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yuh, J. Design and develop of an autonomous underwater vehicle: A survey. Auton. Robot 2000, 8, 7–24. [Google Scholar] [CrossRef]
- Toro, N.; Robles, P.; Jeldres, R. Seabed mineral resources, an alternative for the future of renewable energy: A critical review. Ore Geol. Rev. 2020, 126, 103699. [Google Scholar] [CrossRef]
- Sahoo, A.; Dwivedy, S.K.; Robi, P.S. Advancements in the field of autonomous underwater vehicle. Ocean Eng. 2019, 181, 145–160. [Google Scholar] [CrossRef]
- Katzschmann, R.K.; DelPreto, J.; MacCurdy, R.; Rus, D. Exploration of underwater life with an acoustically controlled soft robotic fish. Sci. Robot. 2018, 3, eaar3449. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, N.-D.; Choi, H.-S.; Tran, N.-H.; Kim, S.-K. Development of Ray-Type Underwater Glider. In Proceedings of the AETA 2017—Recent Advances in Electrical Engineering and Related Sciences: Theory and Application, Ho Chi Minh, Vietnam, 7–9 December 2018; pp. 677–685. [Google Scholar]
- Sun, C.; Song, B.; Wang, P.; Wang, X. Shape optimization of blended-wing-body underwater glider by using gliding range as the optimization target. Int. J. Nav. Archit. Ocean Eng. 2017, 9, 693–704. [Google Scholar] [CrossRef]
- Alam, K.; Ray, T.; Anavatti, S.G. Design and construction of an autonomous underwater vehicle. Neurocomputing 2014, 142, 16–29. [Google Scholar] [CrossRef]
- Oubei, H.M.; Shen, C.; Kammoun, A.; Zedini, E.; Park, K.-H.; Sun, X.; Liu, G.; Kang, C.H.; Ng, T.K.; Alouini, M.-S.; et al. Light based underwater wireless communications. Jpn. J. Appl. Phys. 2018, 57, 08PA06. [Google Scholar] [CrossRef]
- Sharifzadeh, M.; Ahmadirad, M. Performance analysis of underwater wireless optical communication systems over a wide range of optical turbulence. Opt. Commun. 2018, 427, 609–616. [Google Scholar] [CrossRef]
- Soomro, M.; Azar, S.N.; Gurbuz, O.; Onat, A. Work-in-Progress: Networked Control of Autonomous Underwater Vehicles with Acoustic and Radio Frequency Hybrid Communication. In Proceedings of the 2017 IEEE Real-Time Systems Symposium (RTSS), Paris, France, 5–8 December 2017; pp. 366–368. [Google Scholar]
- Lin, Y.-H.; Shou, K.-P.; Huang, L.-J. The initial study of LLS-based binocular stereo-vision system on underwater 3D image reconstruction in the laboratory. J. Mar. Sci. Technol. 2017, 22, 513–532. [Google Scholar] [CrossRef]
- Hildebrandt, M.; Kirchner, F. IMU-aided stereo visual odometry for ground-tracking AUV applications. In Proceedings of the OCEANS’10 IEEE SYDNEY, Sydney, NSW, Australia, 24–27 May 2010; pp. 1–8. [Google Scholar]
- Sukvichai, K.; Wongsuwan, K.; Kaewnark, N.; Wisanuvej, P. Implementation of visual odometry estimation for underwater robot on ROS by using RaspberryPi 2. In Proceedings of the 2016 International Conference on Electronics, Information, and Communications (ICEIC), Danang, Vietnam, 27–30 January 2016; pp. 1–4. [Google Scholar]
- Vo, T.Q.; Kim, H.S.; Lee, B.R. A study on turning motion control of a 3-joint fish robot using sliding mode based controllers. In Proceedings of the ICCAS 2010, Gyeonggi, Republic of Korea, 27–30 October 2010; pp. 1556–1561. [Google Scholar]
- Kato, N.; Ito, Y.; Kojima, J.; Takagi, S.; Asakawa, K.; Shirasaki, Y. Control performance of autonomous underwater vehicle “AQUA EXPLORER 1000” for inspection of underwater cables. In Proceedings of the Proceedings of OCEANS’94, Brest, France, 13–16 September 1994; Volume 131, pp. I/135–I/140. [Google Scholar]
- Wang, Z.; Guo, S.; Shi, L.; Pan, S.; He, Y. The application of PID control in motion control of the spherical amphibious robot. In Proceedings of the 2014 IEEE International Conference on Mechatronics and Automation, Tianjin, China, 3–6 August 2014; pp. 1901–1906. [Google Scholar]
- Li, J.H.; Lee, P.M. A neural network adaptive controller design for free-pitch-angle diving behavior of an autonomous underwater vehicle. Robot. Auton. Syst. 2005, 52, 132–147. [Google Scholar] [CrossRef]
- Falcão Carneiro, J.; Bravo Pinto, J.; Gomes de Almeida, F.; Cruz, N.A. Design and Experimental Tests of a Buoyancy Change Module for Autonomous Underwater Vehicles. Actuators 2022, 11, 254. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, B.; Wang, L. Autonomous underwater vehicle depth control based on an improved active disturbance rejection controller. Int. J. Adv. Robot. Syst. 2019, 16, 1729881419891536. [Google Scholar] [CrossRef]
- Carneiro, J.F.; Pinto, J.B.; Almeida, F.G.; Cruz, N.A. Variable Buoyancy or Propeller-Based Systems for Hovering Capable Vehicles: An Energetic Comparison. IEEE J. Ocean. Eng. 2020, 46, 414–433. [Google Scholar] [CrossRef]
- Love, T.; Toal, D.; Flanagan, C. Buoyancy Control for an Autonomous Underwater Vehicle. IFAC Proc. Vol. 2003, 36, 199–204. [Google Scholar] [CrossRef]
- Huang, H.; Zhang, C.; Ding, W.; Zhu, X.; Sun, G.; Wang, H. Design of the Depth Controller for a Floating Ocean Seismograph. J. Mar. Sci. Eng. 2020, 8, 166. [Google Scholar] [CrossRef]
- Qi, Y.; Wu, X.; Zhang, G.; Sun, Y. Energy-Saving Depth Control of an Autonomous Underwater Vehicle Using an Event-Triggered Sliding Mode Controller. J. Mar. Sci. Eng. 2022, 10, 1888. [Google Scholar] [CrossRef]
- Bai, Y.; Hu, R.; Bi, Y.; Liu, C.; Zeng, Z.; Lian, L. Design and Depth Control of a Buoyancy-Driven Profiling Float. Sensors 2022, 22, 2505. [Google Scholar] [CrossRef]
- Qiu, Z.; Wang, Q.; Li, H.; Yang, S.; Li, X. Depth Control for a Deep-Sea Self-Holding Intelligent Buoy Under Ocean Current Disturbances Based on Finite-Time Boundedness Method. IEEE Access 2019, 77, 114670–114684. [Google Scholar] [CrossRef]
- Ranganathan, T.; Singh, V.; Thondiyath, A. Theoretical and Experimental Investigations on the Design of a Hybrid Depth Controller for a Standalone Variable Buoyancy System—vBuoy. IEEE J. Ocean. Eng. 2018, 45, 414–429. [Google Scholar] [CrossRef]
- Mezo, T.; Maillot, G.; Ropert, T.; Jaulin, L.; Ponte, A.; Zerr, B. Design and control of a low-cost autonomous profiling float. Mech. Ind. 2020, 21, 512. [Google Scholar] [CrossRef]
- Hu, R.; Lu, D.; Xiong, C.; Lyu, C.; Zhou, H.; Jin, Y.; Wei, T.; Yu, C.; Zeng, Z.; Lian, L. Modeling, characterization and control of a piston-driven buoyancy system for a hybrid aerial underwater vehicle. Appl. Ocean Res. 2022, 120, 102925. [Google Scholar] [CrossRef]
- Carneiro, J.F.; Pinto, J.B.; Almeida, F.G.d.; Cruz, N.A. Model Identification and Control of a Buoyancy Change Device. Actuators 2023, 12, 180. [Google Scholar] [CrossRef]
- Moritz, F.G. Electromechanical Motion Systems—Design and Simulation; John Wiley & Sons: Hoboken, NJ, USA, 2014. [Google Scholar]
- Merritt, H. Hydraulic Control Systems; John Wiley & Sons: New York, NY, USA, 1967. [Google Scholar]
- Murrenhoff, H. Fundamentals of Fluid Power. Part 1: Hydraulics, 8th ed.; IFAS Institute fur Fluidtechnische Antriebe and Steuerungen: Aachen, Germany, 2016. [Google Scholar]
- Ogata, K. Modern Control Engineering, 5th ed.; Pearson: London, UK, 2009. [Google Scholar]

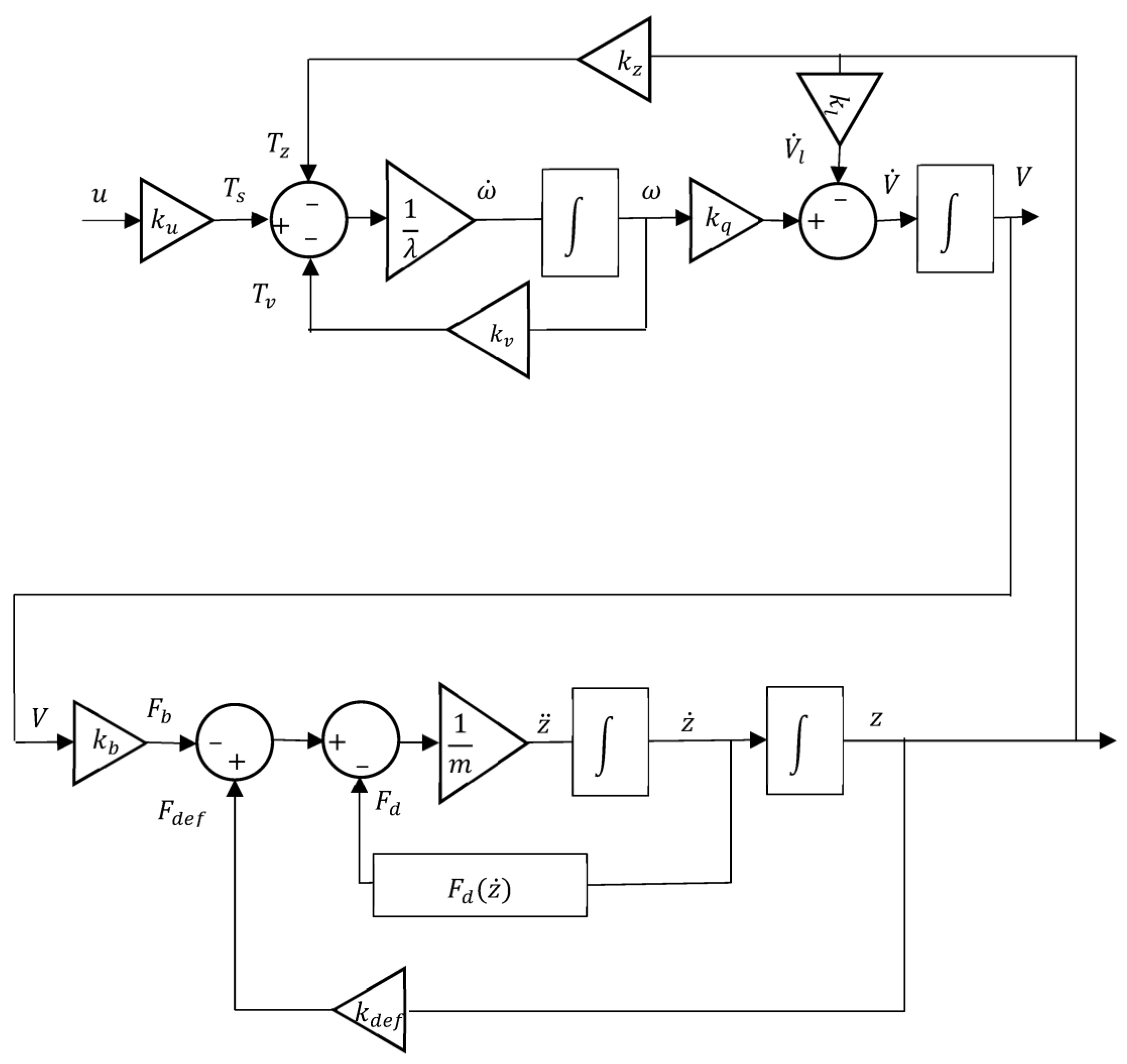



| Constant/Variable | (a) Electrohydraulic Solution | (b) Electromechanical Solution |
|---|---|---|
| Voltage applied to the motor | ||
| Stall torque of the motor | ||
| Torque caused on the motor with the increase in vehicle depth | ||
| Torque losses proportional to motor speed | ||
| Inertia of the motor plus the reflected inertia on the motor of the pump, moving oil, piston and added mass of the displaced water | Inertia of the motor plus the reflected inertia on the motor of mechanical reducer, spindle, piston and added mass of the displaced water | |
| Constant relating the control action and motor stall torque | ||
| Constant relating and the buoyancy force | ||
| Constant relating and | ||
| Volume of the piston | ||
| Motor velocity | ||
| Transfer Function | K (ms−1m−3) | T (s) |
|---|---|---|
| (26) | −7935.54 | 36.3 |
| (27) | −7634.95 | 35.7 |
| CV | CZ | |
|---|---|---|
| kp | 1002 (V × dm−3) | −0.1043 (dm3 × m−1) |
| ki | −7.486 × 10−4 (dm3 × s−1 × m−1) | |
| kd | −2.341 (dm3 × s × m−1) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Falcão Carneiro, J.; Pinto, J.B.; Gomes de Almeida, F.; Cruz, N.A. Electrohydraulic and Electromechanical Buoyancy Change Device Unified Vertical Motion Model. Actuators 2023, 12, 380. https://doi.org/10.3390/act12100380
Falcão Carneiro J, Pinto JB, Gomes de Almeida F, Cruz NA. Electrohydraulic and Electromechanical Buoyancy Change Device Unified Vertical Motion Model. Actuators. 2023; 12(10):380. https://doi.org/10.3390/act12100380
Chicago/Turabian StyleFalcão Carneiro, João, João Bravo Pinto, Fernando Gomes de Almeida, and Nuno A. Cruz. 2023. "Electrohydraulic and Electromechanical Buoyancy Change Device Unified Vertical Motion Model" Actuators 12, no. 10: 380. https://doi.org/10.3390/act12100380
APA StyleFalcão Carneiro, J., Pinto, J. B., Gomes de Almeida, F., & Cruz, N. A. (2023). Electrohydraulic and Electromechanical Buoyancy Change Device Unified Vertical Motion Model. Actuators, 12(10), 380. https://doi.org/10.3390/act12100380








