Abstract
The integration of a passive elastic element in series between a motor and its load is popular in many human–robot interaction scenarios. By virtually imposing elastic behavior on the motor, an impedance control can act as a second stiffness to such an actuator. In this study, we investigated how participants perceived the different stiffness settings in a series elastic actuator by measuring the Just Noticeable Difference (JND) of the real stiffness of the elastic element and the virtual stiffness introduced by impedance control. We conducted a user study during which participants interacted with an impedance-controlled Series Elastic Actuator through a lever. During the user study, we varied the real stiffness of the elastic element and the virtual stiffness. We found that participants seem to perceive both the virtual stiffness and the real stiffness in the same way and in accordance to Weber’s law, which states that the stiffness JND is always equal to a fraction of the initial stiffness. Following these findings, we concluded that the impedance controller can implement an effective virtual stiffness with a behavior comparable to a real torsional spring. Therefore, a system combining real and virtual stiffness can simulate a single combined stiffness for a user interacting with it.
1. Introduction
When asking engineers from different fields about the ideal behavior of an actuator, one might obtain vastly different answers. In the field of wearable robotics, the addition of elastic elements to form elastic actuators has become popular [1,2]. These elastic actuators can decrease energy requirements, improve backdrivability, and absorb mechanical shocks [3,4,5]. Yet, the increased complexity, when compared with direct actuation systems, makes controlling them effectively a challenging task. Variable Stiffness Actuators are even capable of changing the stiffness of their elastic element, allowing an adaption to different conditions and possibly improving energy efficiency [6]. Variable Stiffness Actuator designs generally include mechanisms that alter the physical stiffness characteristics of the actuator or rely on impedance control to add virtual impedance [7].
As indicated above, elastic actuators are widely applied in wearable robotics, e.g., exoskeletons and prostheses. Penzlin et al. [8] used parallel elastic actuation to drive a lower limb exoskeleton. Another lower limb exoskeleton driven by elastic actuators with a variable structure was proposed by Aguirre-Ollinger et al. [9]. A model-based control of an exoskeleton with series elastic actuators was developed by Vantilt et al [10]. Sun et al. [2] designed a nonlinear series elastic actuator for a knee prosthesis, while Carney et al. [11] used the displacement on the elastic element of a series elastic actuator to estimate reaction forces. These studies demonstrate that elastic actuators can provide increased safety and energy efficiency for human–robot applications. Beckerle et al. [12] explored the faults possibly occurring in elastic actuators, the issues resulting from these faults, and possible strategies in dealing with them. Velasco-Guillen et al. [13] evaluated the effectiveness of a control strategy that takes into account faults occurring in the stiffness of an elastic actuator for wearable robotics. In our study, we compare the human perception of the virtual stiffness of an impedance control and the real stiffness of an elastic element to assess the practicality of combining these elements in human–robot interaction.
The stiffness of actuators and their perception by humans is an important part of research in haptics [14] and is significant for human–robot interaction [12]. Psychophysical studies are generally conducted to investigate how physical stimuli are perceived, relying on sensory thresholds [15]. One key figure in the human perception of stiffness is the Just Noticeable Difference (JND), which describes the smallest change in stiffness in a system that a human can perceive. The JND of stiffness has been studied by other researchers as a measure for user perception of stiffness [16,17,18,19]. Kocak et al. [16] explored the JND of stiffness in a virtual environment in different modes of interaction with the stiff object. They found that the JND of stiffness is lowest when interaction with the object is not interrupted during stiffness changes. Fu et al. [17,18] investigated the JND of the stiffness of an impedance-controlled joystick. Initially, they investigated how a visual indicator for participant displacement can help avoid the biases of perceived force on the JND of stiffness [17]. In addition, they found that the JND of the virtual stiffness of the joystick is always equal to the same fraction of the initial value of the stiffness, following Weber’s law [20]. Later, they evaluated the JND of stiffness and damping with different parameters of an impedance control, finding that the mass of an actuator influences the JND of stiffness [18]. Singhala et al. [19] investigated the influence of the velocity of interaction on the JND of stiffness and found that participants choose different velocities to evaluate stiffness. Shepherd et al. [21] investigated the perception of the stiffness of a foot prosthesis across multiple patients. Based on their research, Clites et al. [22] showed that the preference of patients towards a specific stiffness can be explained by a symmetry in gait between the two legs.
Despite ample research on the JND of stiffness, no attempts were made to compare the JND of virtual stiffness as provided by impedance control and real stiffness provided by an elastic element. In this article, we describe the results of a user study evaluating the JND of stiffness in a system that combines both real and virtual stiffness. Our research question in this context is whether humans interacting with a variable stiffness actuator commanded by impedance control perceive changes in the real stiffness of the elastic element in the same way as changes in the virtual stiffness of the impedance control. We formulated two hypotheses along with this research question.
Hypothesis 1 (H1).
The measured values of JND for real and virtual stiffness are the same.
Because the JND of stiffness is used as an expression of human perception, this hypothesis states that the perceptions of real and virtual stiffness are the same.
Hypothesis 2 (H2).
The measured values of JND follow Weber’s law [20].
Weber’s law states that the JND is always equal to a fraction of the initial value that is varied in the measurement. Through this hypothesis, we aim to explore whether the measured JNDs of real and virtual stiffness can be compared to one another, as it confirms that both real and virtual stiffnesses are perceived as such by the user interacting with the system.
2. Materials and Methods
This section details the material and methods utilized to conduct the user study. The hardware setup and the control algorithm of the elastic actuator are presented, followed by user study design.
2.1. Variable Torsional Stiffness Actuator
The actuator used to investigate the JND in stiffness features a torsional rod which can alter its torsional stiffness by modifying its effective length. It is named a Variable Torsional Stiffness (VTS) actuator [23], and it was controlled by a passivity-based impedance controller [24].
A picture of the VTS actuator setup is shown in Figure 1. The Actuation Unit 1, combining a direct current (DC) motor and a gearbox, can be seen in the bottom left. Above it, Actuation Unit 2 combines a smaller DC motor with a gearbox. Actuation Unit 1 is connected to a torsional rod, which is hidden inside the aluminum tube in the picture, via a metal coupling. Actuation Unit 2 is connected to the mechanism that changes the effective length of the torsional rod, also via a metal coupling. The mechanism to change the stiffness of the torsional rod is shown in Figure 2. Actuation Unit 2 moves a counter bearing along the torsional rod, changing its effective length , along with its stiffness . On the right side, the VTS actuator is fitted with a lever for user interaction. Between the lever and the torsional rod, a torque sensor is integrated into the system, measuring the torque acting on the torsional rod. Incremental encoders measure angular positions and . Angular speeds are determined by filtered numerical derivation. The torque of Actuation Unit 1 is commanded using low-level current control. Actuation Unit 2 implements a mid-level position control to control the effective length of the torsional rod, which is measured through a linear potentiometer.

Figure 1.
Picture of the VTS actuator with (1) DC motor with a gearbox (Actuation Unit 1), connected to the torsional rod via a coupling; (2) DC motor with gearbox (Actuation Unit 2), connected to torsional rod mechanism via a coupling; (3) Linear potentiometer measuring ; (4) Torsional rod with a mechanism to change its length ; (5) Torque sensor measuring ; (6) Lever for user interaction.
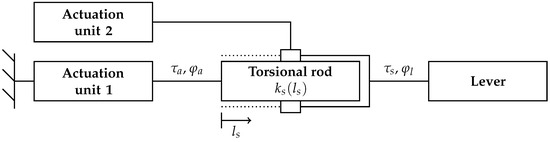
Figure 2.
Mechanism to change effective length of the torsional rod. Actuation Unit 2 moves a counter bearing along the torsional rod that transmits the torque from the torsional rod to the lever, which is used for user interaction. Changing the position of the bearing thus changes the effective length of the torsional rod.
The dynamics of the VTS actuator can be expressed as follows:
using the inertias of the lever and of Actuation Unit 1, the rotations of Actuation Unit 1 and the lever , the interaction torque with the lever , the gravity torque affecting the lever , the torque produced by Actuation Unit 1, and friction torques on actuator side and lever side .
The torque caused by gravity is expressed using the gravitational constant g and the mass and distance to the center of mass of the lever: . The torques caused by friction are adapted from the model used in [25]. The friction on the lever side is assumed to be negligible, while the friction torque on the actuator side is assumed to be a combination of Coulomb friction, with friction coefficient and shaping coefficient S, and viscous friction, with a coefficient . The Coulomb friction is modeled using a hyperbolic tangent function based on the proposition of Mostaghel et al. [26]. This makes the expression of the Coulomb friction continuous, which in turn increases the stability of the control. The expression for the torque resulting from friction in the actuator is the following:
2.2. Impedance Control
While the torsional rod introduced a variable real stiffness to the system, the virtual stiffness is implemented via impedance control. Using the model of the actuator, a passivity-based impedance control is implemented for output trajectory tracking, based on the controller proposed by Ott [24]. The reference of this control is a desired trajectory of lever rotation . This trajectory is transformed into a trajectory for Actuation Unit 1 while accounting for the inertia of the lever and the gravity torque :
This transformed trajectory is then used to compute a new control input u while compensating friction and shaping the impedance of Actuation Unit 1 using a desired virtual inertia , damping and stiffness :
The new input u is then used to calculate the required torque of Actuation Unit 1, while accounting for the deflection of the torsional rod and the friction in Actuation Unit 1:
Computing the torque of Actuation Unit 1 this way leads to the following closed loop dynamics, with the control deviations and :
Based on the control strategy presented by Ott [24], in static or low-frequency applications, the reference trajectories can be defined in position only, i.e., .
The structure of (6) is that of a two-mass torsional oscillator, which is illustrated in Figure 3. For a user interacting with the system, the output stiffness is the relationship between the interaction torque and output deflection , with the following transfer function:
Notice that for the static case, and , which implies that for sufficiently low frequencies the user would perceive the series combination of real and virtual stiffness [24], with the combined interaction stiffness defined as
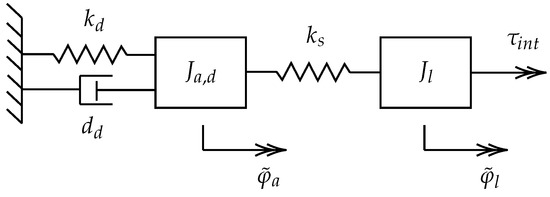
Figure 3.
Structure of an impedance-controlled SEA with real stiffness , load inertia , and virtual impedance parameters: stiffness , damping , and inertia . The system behaves as a two-mass torsional oscillator subject to the interaction torque .
The parameters of the VTS and the lever are obtained from datasheets, direct measurements, and/or by comparing measurements with simulation results. The parameters that are used are shown in Table 1. The relationship between the stiffness , measured in , and the rod length , measured in , is experimentally evaluated by obtaining measurements of torque and deflection at different rod lengths and fitting a curve. The obtained function is the following:
where .

Table 1.
Parameters used in the experiments.
In order to evaluate the applicability of (8) in an interaction scenario, we conducted a series of step responses by interacting with the lever using two stiffness settings:
- Setting A:, ,
- Setting B:, .
The expected interaction stiffness for both settings is . Both settings are also tested without inertia shaping, i.e., , and with inertia shaping, lowering the actuator inertia by a factor or 10, i.e., . For the tests, the lever is commanded to rest at a constant position of 80°, i.e., . Then, it is subsequently deflected by approximately 20° at a slow rate while measuring the interaction torque and deflections. Figure 4 shows the measurements obtained from the interaction steps. From these tests, it is clear that the expected interaction behavior, which corresponds to , is accurately attained when implementing inertia shaping. On the other hand, the expected interaction behavior is not attained without inertia shaping, likely due to unmodeled damping or friction components. The deviation from the expected interaction behavior when inertia shaping is not active is bigger for the lower value of in Setting B, as the unmodeled torque components are likely more significant in the actuator dynamics. This shows the advantage of implementing inertia shaping to make the interaction perception more robust against unmodeled friction behavior.
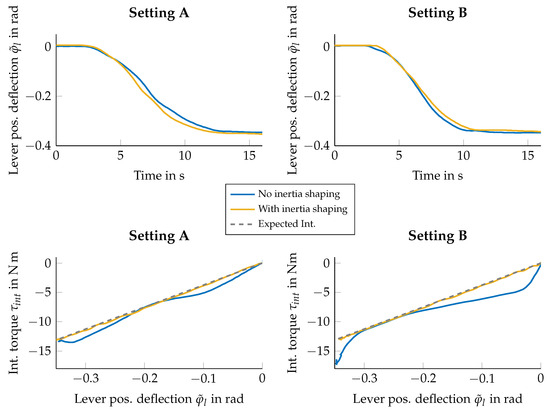
Figure 4.
Interaction step responses. Deflection of from a fixed lever position. Setting A: , ; Setting B: , . Tests show that the expected interaction behavior, i.e., , is obtained when implementing inertia shaping. Without it, unmodeled static friction components are noticeable and deform the interaction curve vs. .
To verify the frequency response of the impedance-controlled lever with settings A and B and inertia shaping, we measure the position deviation and torque when interacting with the lever at different frequencies. A periodic user interaction is approximated by deflecting the position of the lever with an amplitude of approximately and following a visual and auditory metronome at frequencies ranging from to , with uniform increments of . Figure 5 shows the torque and deflection measurements from two interaction examples at and using stiffness setting A. The periodic signals are transformed to the frequency domain using the fast Fourier transform (FFT) and the complex stiffness is determined by dividing the FFT of torque and the FFT of deflection at the fundamental frequency of the interaction. The magnitude and phase of the stiffness frequency response for both settings are shown in Figure 6. It compares the measured and theoretical Bode plots from the transfer function defined in (7), showing that both conditions behave as expected for the lower frequencies, with both settings attaining very similar responses to the expected theoretical behavior for frequencies of up to . The natural frequency of measured response seems to be close to that of the modeled dynamics, but the ideal theoretical response around the natural frequency is not attained possibly due to non-compensated friction components and/or motor speed limits. It is important to mention that the friction compensation terms used in the lever control are selected to allow an effective lever interaction at low frequencies while avoiding aggressive torque compensation terms that cause unwanted lever oscillations at rest. Therefore, for high-frequency applications, friction compensation and motor dimensioning should be adjusted.
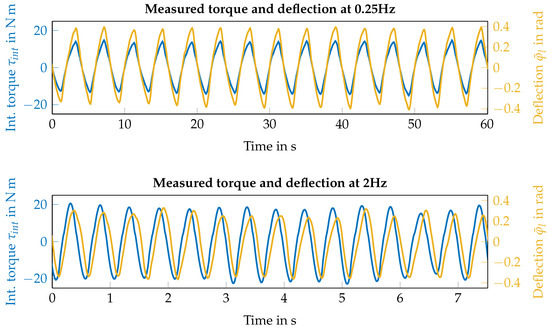
Figure 5.
Periodic interaction examples with setting A: , . The periodic interaction signals are obtained by deflecting the position of the lever following a visual and auditory metronome. The plots show 15 cycles of measured torque and deflection measurements.
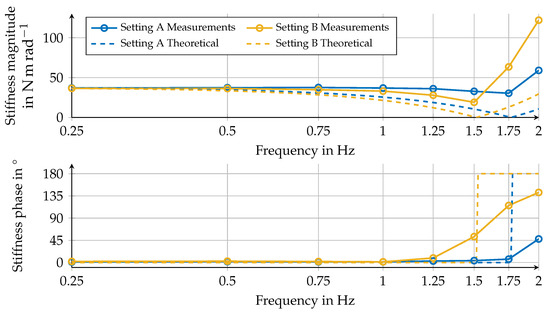
Figure 6.
Measured and theoretical Bode magnitude plot (top) and phase plot (bottom) of stiffness transfer function . Setting A: , , Setting B: , . Natural frequencies of measured response match.
2.3. User Study
The participants were recruited at the chair of Autonomous Systems and Mechatronics of the Friedrich–Alexander University Erlangen–Nürnberg. A total of 15 participants were recruited, 6 of which identified as women and 9 of which identified as men. The mean age of the participants was 27 years with a standard deviation of 5.8 years. Informed consent was obtained from all participants involved in the study. The examinations were conducted in accordance with the Declaration of Helsinki 2008 and a vote from the Ethics Commission at TU Darmstadt (EK 18/2017).
We investigated the JND of stiffness in a quantitative experimental user study, during which participants interacted with the system via the lever, while the system changed either the value of real stiffness or virtual stiffness .
During experiments, the actuator was fully covered using black Plexiglass plates to avoid participants being able to see moving parts. Additionally, participants were asked to wear a noise canceling headset to minimize the influence of sounds of the actuator. The experimental setup is shown in Figure 7.
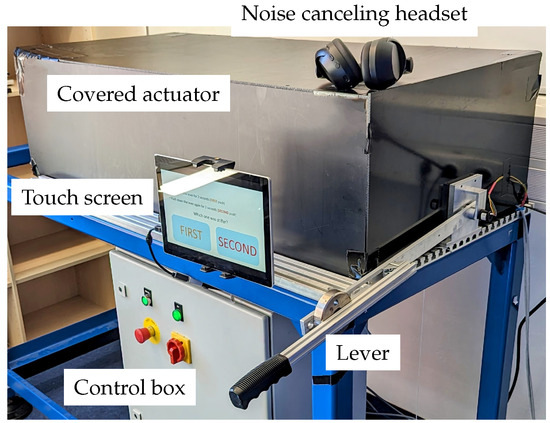
Figure 7.
VTS experimental setup. The actuator is fully covered by black plexiglass and a noise cancelling headset is used during experiments.
In the user study, two independent variables (IV) were defined. The first IV is the stiffness varied during experiments, which is either or . The second IV is the starting value of the varied stiffness, which needed to be changed in between experiments to investigate our second hypothesis. To evaluate both hypotheses with a minimum number of experiments, we decided to conduct the experiments with two separate values of . To investigate the effects of both IVs, we implemented a 2 × 2 repeated measures design, such that a total of four JND experiments were conducted for each participant.
During experiments, the lever was commanded to rest at a constant position of 80°. This proved to be a comfortable position for participants to hold onto the lever. The participant task consisted of moving the lever to the position of 60°, holding it down for 2 s, and then releasing the lever. The target rotation was visually marked in the test bench to avoid biases introduced by the force necessary to move the lever [17].
Each experiment consisted of multiple trials. In each trial, the participant was asked to move the lever twice with different values of the varied stiffness: the initial stiffness and an increased stiffness . The sequence in which both stiffness settings were presented to a participant was randomized to avoid sequencing effects, and a delay of 4 s was left between each movement to allow time for the adjustment of the real stiffness. The same delay was used for all trials in all experiments to avoid introducing biases when varying the virtual stiffness. After the two movements, the participant was asked which movement felt stiffer. If they could identify the movement with the higher stiffness, the response was counted as correct, otherwise it was counted a incorrect. If reached zero, the answer is always taken as incorrect.
Multiple trials were combined into one experiment using a weighted transformed staircase approach [27,28]. The value of was decreased by a magnitude of when the participant answered correctly times in a row. The value of was increased by a magnitude of after incorrect participant response. This so-called 1 up/2 down rule only takes effect after the first incorrect response. The ratio of increase in to decrease in of was , making the expected ratio of correct to incorrect responses
A convergence of against the JND of stiffness was assumed to be achieved after 7 reversals, where a reversal is a change from an increasing to a decreasing stiffness or vice versa. Alternatively, an experiment was stopped after 40 trials to avoid taking too much time per experiment. The JND of stiffness was calculated as the average value of of the last 10 trials. One example run of an experiment is displayed in Figure 8.
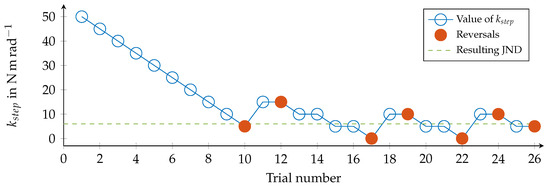
Figure 8.
Example run of one experiment. The varied stiffness is , the initial value is 50 . The value of is 220 for all trials. Reversals are shown as filled red circles. The resulting JND is calculated using the average value of of the last 10 trials.
The JND of stiffness was evaluated at two values of for both real and virtual stiffness per participant, resulting in a total of four experiments per participant. The non-varied stiffness in an experiment was set to a constant value of 220 , which corresponds to the maximum possible stiffness for , to minimize influences of one stiffness on the measurement of JND of the other stiffness. The value of of the first trial was set to 50 when was 50 and set to 100 when was 100 . The conditions of the four experiments are listed in Table 2. The order of these four experiments was also pseudo-randomized.

Table 2.
Conditions of the experiments.
3. Results
To compare the obtained JND, the results are given both in their absolute quantity, measured in , and its normalized quantity, described as a percentage of the initial stiffness . Measurements of the stiffness JND for all conditions are presented in Table 3. Figure 9 shows the boxplot of the normalized JND.

Table 3.
Results of each individual experiment type.
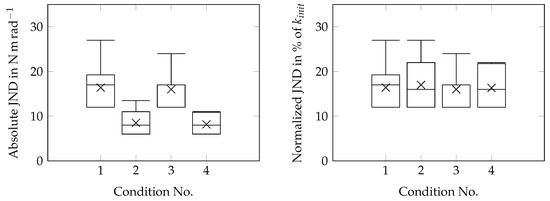
Figure 9.
Boxplot of the obtained absolute JND (left) and normalized JND (right). Condition 1: Varied stiffness (real), initial stiffness . Condition 2: Varied stiffness (real), initial stiffness . Condition 3: Varied stiffness (virtual), initial stiffness . Condition 4: Varied stiffness (virtual), initial stiffness .
For variations of the real stiffness with a higher initial value of 100 , the average number of trials needed to complete the experiment was , the average absolute JND was , and the average normalized JND was . For a lower of 50 , the average number of trials was , the average absolute JND was , and the average normalized JND was .
For variations of the virtual stiffness with a higher value of of 100 , the average number of trials needed to complete the experiment was , the average absolute JND was , and the average normalized JND was . For a lower of 50 , the average number of trials was , the average absolute JND was , and the average normalized JND was .
Initially, it can be observed that the normalized JND values for all conditions were very similar in both mean and standard deviation. This assertion can be further investigated with a two-factor ANOVA [29] analysis, which evaluates how the normalized JND values are affected by the IV. The analysis showed no significant difference () between the mean JND percentages when varying the real stiffness compared with the JND values obtained when varying of the virtual stiffness. The analysis also did not suggest a significant difference () for the comparison of the mean JND percentages resulting for the two starting values of 100 and 50 .
4. Discussion
This study aimed to compare the Just Noticeable Difference (JND) of virtual stiffness as provided by impedance control and real stiffness provided by a torsional spring. The research question was whether humans interacting with a variable stiffness actuator commanded by impedance control perceive changes in the real stiffness in the same way as changes in the virtual stiffness. The user study was conducted using a weighted transformed staircase approach which is widely used in the study of stiffness JND in the literature [16,17,18,19], with participants interacting with a Variable Torsional Stiffness (VTS) actuator through a lever. Kocak et al. [16] found that the stiffness JND lowers when the interaction is not interrupted during stiffness changes. However, this idea was discarded in our study design as it was not possible to replicate the stiffness change from the torsional rod with the virtual spring. Instead, the study was designed such that participants performed two separate interactions with the lever during each trial, both interactions with a different stiffness setting, and they would indicate which interaction felt stiffer.
We analyzed the effectiveness of virtually shaping the actuator inertia within the impedance control scheme and showed that lowering the inertia improves the interaction torque/deflection behavior. This aligns with the findings of Fu et al. [18], who found that stiffness JND is affected by the frequency response of a system with high effective mass in the output impedance during interaction. While the conditions of our experiments would not reach a frequency where the motor inertia might significantly affect the interaction, we did find that inertia shaping improves the robustness of the impedance behavior against uncompensated dynamic components.
The results obtained from the study suggest that there is no significant difference between the JND obtained when altering the real or virtual stiffness. This aligns with Hypothesis 1 and indicates that the perception of real and virtual stiffness is the same. It also indicates that the impedance control strategy can effectively reproduce a virtual torsional spring behavior and that the combined stiffness , as defined in (8), is applicable to describe the interaction behavior in low-frequency tasks.
The results obtained in this study showed no significant difference between the normalized JND measurements obtained with different initial stiffness values . This aligns with Hypothesis 2 and indicates that the results follow Weber’s law, with the JND measurements being fractions of the initial value , as it generally does in the literature [16,17,18]. This also confirms that the spring behavior implemented virtually by the controller is comparable to that of a real torsional spring.
While the results align with our hypotheses, some considerations could be made in future research that could improve the JND results. The staircase method used, which considers the absolute JND as the average of the last 10 trials and which forced a reversal when reached zero, meant that the obtained absolute JND when the participant responded correctly to all the trials was . That means that the minimum normalized JND that could be obtained for all conditions detailed in Table 2 was . It can be seen in Figure 9 that the first quartile and the minimum of all the box plots coincide, which could indicate that lower JND values can be found if smaller values of and are chosen. On the subject of human perception, by asking the participants to perform the same deflection throughout the experiments, it was verified that the stiffness JND is closely related to the force JND [17], as the participant strategy to perceive stiffness is related to the force required to achieve the commanded deflection. Fu et al. [17] showed that the stiffness JND can be improved by adding visual presentation of the task where the participant can clearly see the current and target angular displacement. While this was out of the scope of our study, it could lead to improved JND results in future research.
5. Conclusions
The study presented in this article investigates user perception when interacting with a series elastic actuator through a lever. A real variable torsional stiffness is implemented by altering the effective length of a torsional rod which couples the motor and the lever. At the same time, a passivity-based impedance control method is used to introduce a virtual spring behavior in the motor. The study measures Just Noticeable Difference (JND) when altering the real and virtual stiffness with different initial stiffness values. Results show that the average measured JND values obtained in the experiments, when expressed as percentages of the initial stiffness, did not show a significant difference with respect to the varied stiffness or initial value, which indicates that the virtual and real stiffness are perceived in the same way, and that the results follow Weber’s law. In conclusion, the results indicate that an impedance-controlled elastic actuator can effectively emulate a virtual spring behavior that is comparable to that of a real torsional spring. The findings of this study are important for the continued work on impedance-controlled elastic actuators as it indicates that the physical human–robot interaction behaves as theory suggests, opening up the perspective of such actuators to accurately implement variable compliance or compensate faults in human–robot interaction scenarios.
Future work could expand the research by considering how virtual damping or different interaction conditions, such as lever trajectory and speed, might affect the obtained JND values. At the same time, lowering the stiffness steps and/or adding a visual presentation of the task could improve the stiffness JND results.
Author Contributions
Conceptualization, P.B., R.J.V.-G., A.B. and F.S.; methodology, R.J.V.-G. and F.S.; software, R.J.V.-G. and F.S.; validation, R.J.V.-G. and A.B.; formal analysis, R.J.V.-G., A.B. and F.S.; investigation, R.J.V.-G. and F.S.; resources, P.B.; data curation, R.J.V.-G. and F.S.; writing—original draft preparation, R.J.V.-G. and F.S.; writing—review and editing, P.B., R.J.V.-G., F.S. and A.B.; visualization, R.J.V.-G. and F.S.; supervision, P.B.; project administration, R.J.V.-G.; funding acquisition, P.B. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by a Deutsche Forschungsgemeinschaft (DFG) Research Grant (no. BE 5729/1).
Institutional Review Board Statement
The study was conducted in accordance with the Declaration of Helsinki, and a vote from the ethics commission at Technische Universität Darmstadt (EK 18/2017).
Informed Consent Statement
All subjects provided their informed consent for inclusion before they participated in the study.
Data Availability Statement
The data experimentally acquired with human participants and presented in this paper are stored pseudonymously. They are not publicly available in accordance with the ethics vote but could be shared upon request for research purposes.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| MDPI | Multidisciplinary Digital Publishing Institute |
| JND | Just Noticeable Difference |
| DC | Direct Current |
| VTS | Variable Torsional Stiffness |
| IV | Independent Variable |
| FFT | Fast Fourier Transform |
| DFG | Deutsche Forschungsgemeinschaft |
| Virtual Stiffness (of the impedance control) | |
| Real Stiffness (of the elastic element) | |
| Interaction Stiffness (Combination of virtual and real stiffness) | |
| Initial Value of Stiffness during an experiment | |
| Increase in the Value of Stiffness in between movements of a trial |
References
- Tiboni, M.; Borboni, A.; Vérité, F.; Bregoli, C.; Amici, C. Sensors and Actuation Technologies in Exoskeletons: A Review. Sensors 2022, 22, 884. [Google Scholar] [CrossRef] [PubMed]
- Sun, Y.; Tang, P.; Zheng, J.; Dong, D.; Chen, X.; Bai, L.; Ge, W. Optimal Design of a Nonlinear Series Elastic Actuator for the Prosthetic Knee Joint Based on the Conjugate Cylindrical Cam. IEEE Access 2019, 7, 140846–140859. [Google Scholar] [CrossRef]
- Beckerle, P.; Verstraten, T.; Mathijssen, G.; Furnemont, R.; Vanderborght, B.; Lefeber, D. Series and Parallel Elastic Actuation: Influence of Operating Positions on Design and Control. IEEE/ASME Trans. Mechatronics 2017, 22, 521–529. [Google Scholar] [CrossRef]
- Sensinger, J.; Weir, R.F. Improvements to Series Elastic Actuators. In Proceedings of the 2006 2nd IEEE/ASME International Conference on Mechatronics and Embedded Systems and Applications, Beijing, China, 13–16 August 2006. [Google Scholar] [CrossRef]
- Rouse, E.J.; Mooney, L.M.; Herr, H.M. Clutchable series-elastic actuator: Implications for prosthetic knee design. Int. J. Robot. Res. 2014, 33, 1611–1625. [Google Scholar] [CrossRef]
- Beckerle, P.; Stuhlenmiller, F.; Rinderknecht, S. Stiffness Control of Variable Serial Elastic Actuators: Energy Efficiency through Exploitation of Natural Dynamics. Actuators 2017, 6, 28. [Google Scholar] [CrossRef]
- Vanderborght, B.; Albu-Schaeffer, A.; Bicchi, A.; Burdet, E.; Caldwell, D.; Carloni, R.; Catalano, M.; Eiberger, O.; Friedl, W.; Ganesh, G.; et al. Variable impedance actuators: A review. Robot. Auton. Syst. 2013, 61, 1601–1614. [Google Scholar] [CrossRef]
- Penzlin, B.; Bergmann, L.; Li, Y.; Ji, L.; Leonhardt, S.; Ngo, C. Design and First Operation of an Active Lower Limb Exoskeleton with Parallel Elastic Actuation. Actuators 2021, 10, 75. [Google Scholar] [CrossRef]
- Aguirre-Ollinger, G.; Yu, H. Lower-Limb Exoskeleton with Variable-Structure Series Elastic Actuators: Phase-Synchronized Force Control for Gait Asymmetry Correction. IEEE Trans. Robot. 2021, 37, 763–779. [Google Scholar] [CrossRef]
- Vantilt, J.; Tanghe, K.; Afschrift, M.; Bruijnes, A.K.; Junius, K.; Geeroms, J.; Aertbeliën, E.; Groote, F.D.; Lefeber, D.; Jonkers, I.; et al. Model-based control for exoskeletons with series elastic actuators evaluated on sit-to-stand movements. J. Neuroeng. Rehabil. 2019, 16. [Google Scholar] [CrossRef] [PubMed]
- Carney, M.E.; Shu, T.; Stolyarov, R.; Duval, J.F.; Herr, H.M. Design and Preliminary Results of a Reaction Force Series Elastic Actuator for Bionic Knee and Ankle Prostheses. IEEE Trans. Med. Robot. Bionics 2021, 3, 542–553. [Google Scholar] [CrossRef]
- Beckerle, P. Practical relevance of faults, diagnosis methods, and tolerance measures in elastically actuated robots. Control. Eng. Pract. 2016, 50, 95–100. [Google Scholar] [CrossRef]
- Velasco-Guillen, R.J.; Grosu, V.; Vanderborght, B.; Font-Llagunes, J.M.; Beckerle, P. Experimental Evaluation of a Stiffness-Fault-Tolerant Control Strategy on an Elastic Actuator for Wearable Robotics. In Proceedings of the 2022 9th IEEE RAS/EMBS International Conference for Biomedical Robotics and Biomechatronics (BioRob), Seoul, Republic of Korea, 21–24 August 2022. [Google Scholar] [CrossRef]
- Grunwald, M. Human Haptic Perception Basics And Applications; Birkhauser: Boston, MA, USA, 2008. [Google Scholar]
- Gescheider, G.A. Psychophysics: Method, Theory, and Application; Psychology Press: London, UK, 1985. [Google Scholar]
- Koçak, U.; Palmerius, K.L.; Forsell, C.; Ynnerman, A.; Cooper, M. Analysis of the JND of Stiffness in Three Modes of Comparison. In Haptic and Audio Interaction Design; Springer: Berlin/Heidelberg, Germany, 2011; pp. 22–31. [Google Scholar] [CrossRef]
- Fu, W.; van Paassen, M.M.R.; Mulder, M. On the relationship between the force JND and the stiffness JND in haptic perception. In Proceedings of the ACM Symposium on Applied Perception, Cottbus, Germany, 16–17 September 2017. [Google Scholar] [CrossRef]
- Fu, W.; Landman, A.; van Paassen, M.M.; Mulder, M. Modeling Human Difference Threshold in Perceiving Mechanical Properties From Force. IEEE Trans. -Hum.-Mach. Syst. 2018, 48, 359–368. [Google Scholar] [CrossRef]
- Singhala, M.; Brown, J.D. Prefatory study of the effects of exploration dynamics on stiffness perception. In Proceedings of the 2020 IEEE Haptics Symposium (HAPTICS), Washington, DC, USA, 25 June 2020. [Google Scholar] [CrossRef]
- Norwich, K.H. On the theory of Weber fractions. Percept. Psychophys. 1987, 42, 286–298. [Google Scholar] [CrossRef] [PubMed]
- Shepherd, M.K.; Azocar, A.F.; Major, M.J.; Rouse, E.J. Amputee perception of prosthetic ankle stiffness during locomotion. J. Neuroeng. Rehabil. 2018, 15, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Clites, T.R.; Shepherd, M.K.; Ingraham, K.A.; Wontorcik, L.; Rouse, E.J. Understanding patient preference in prosthetic ankle stiffness. J. Neuroeng. Rehabil. 2021, 18, 1–16. [Google Scholar] [CrossRef] [PubMed]
- Schuy, J.; Beckerle, P.; Wojtusch, J.; Rinderknecht, S.; von Stryk, O. Conception and evaluation of a novel variable torsion stiffness for biomechanical applications. In Proceedings of the 2012 4th IEEE RAS & EMBS International Conference on Biomedical Robotics and Biomechatronics (BioRob), Rome, Italy, 24–27 June 2012. [Google Scholar] [CrossRef]
- Ott, C. Cartesian Impedance Control of Redundant and Flexible-Joint Robots; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar] [CrossRef]
- Stuhlenmiller, F.; Velasco-Guillen, R.J.; Rinderknecht, S.; Beckerle, P. Fault-Tolerant Physical Human-Robot Interaction via Stiffness Adaptation of Elastic Actuators. In Proceedings of the Human-Friendly Robotics 2019; Ferraguti, F., Villani, V., Sabattini, L., Bonfè, M., Eds.; Springer International Publishing: Cham, Switzerland, 2020; pp. 73–87. [Google Scholar] [CrossRef]
- Mostaghel, N. A non-standard analysis approach to systems involving friction. J. Sound Vib. 2005, 284, 583–595. [Google Scholar] [CrossRef]
- Kingdom, F.A.A.; Prins, N. Psychophysics A Practical Introduction, 2nd ed.; Academic Press: London, UK, 2016. [Google Scholar]
- García-Pérez, M.A. Forced-choice staircases with fixed step sizes: Asymptotic and small-sample properties. Vis. Res. 1998, 38, 1861–1881. [Google Scholar] [CrossRef]
- Ståhle, L.; Wold, S. Analysis of variance (ANOVA). Chemom. Intell. Lab. Syst. 1989, 6, 259–272. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).