1. Introduction
Vibration energy harvesting by means of piezoelectric (PE) materials is a promising technology for feeding remote sensor nodes and other microelectronic equipment, especially when weight, space and accessibility constraints are important. In aeronautics, several applications of vibration energy harvesting have been proposed [
1,
2], but the most important application is feeding sensors for structural health monitoring (SHM) [
3,
4,
5]. In the framework of the EU InComEss project [
6], new lead-free piezoelectric materials are under development. A foreseen application is vibration energy harvesting from wing slats. Slats are movable aerodynamic surfaces on the leading edge of the wing that increase the lift force on the wing when they are deployed. In [
7], an analytical model based on the modal superposition approach [
8] was used to simulate PE harvesters mounted on a deployed slat. A comparison was made between the performance of two possible design solutions: cantilever harvesters and PE patches directly bonded to the slat surface. Numerical results showed that both solutions were able to generate relevant voltage and power. The cantilever harvester optimally tuned to the most excited mode of vibration of the slat showed the best performance, since it exploited the resonance phenomenon, but this device required more mass, volume and stress inside the brittle piezoelectric material than the PE patch. Because the mass, volume and reliability of PE devices are very important issues in slat case-studies, the PE patch was selected for further development within the framework of the InComEss project. The deployed slat in [
7] showed the largest vibrations; however, most of the energy could be harvested during the flight when the slat was retracted. The analytical model presented in [
7] was extended in this study to investigate this operating condition. Moreover, to analyze the effect of details such as the three-dimensional geometry of the PE patch and thin adhesive layers used to bind the PE patch to the slat, an integrated approach combining a large-scale analytical model and a small-scale finite element model is proposed.
The large-scale model, implemented in MATLAB®, is fully analytical and is based on the modal expansion approach. It describes a whole slat excited by the broadband acceleration spectrum typical of wings, and it enables the calculation of the bending moment and shear force acting on the portion of the slat where the harvester is mounted. The contact between the slat and the wing edge is simulated by means of a distributed stiffness, and the variation in the value of the contact stiffness makes it possible to simulate both retracted and deployed slats.
The small-scale model, implemented in COMSOL Multiphysics®, is numerical and is based on a multiphysics finite element (FE) method. It describes the sandwich structure of the harvester mounted on an equivalent portion of the slat, which is excited by the loads calculated by means of the large-scale model. This makes it possible to compute the voltage generated by the PE material considering the effects of the adhesive layer and of the other layers that compose the sandwich.
The paper is organized as follows:
Section 2 describes the problem and the structure of the combined analytical–numerical approach.
Section 3 provides the input data: slat dimensions, PE patch dimensions, mechanical properties, and electrical properties.
Section 4 deals with the large-scale analytical model of the whole slat.
Section 5 deals with the small-scale FE model.
Section 6 shows the numerical results and, in particular, the effects of the adhesive thickness on the voltage generated by the harvester. Finally, conclusions are drawn.
2. Integrated Analytical–Numerical Method
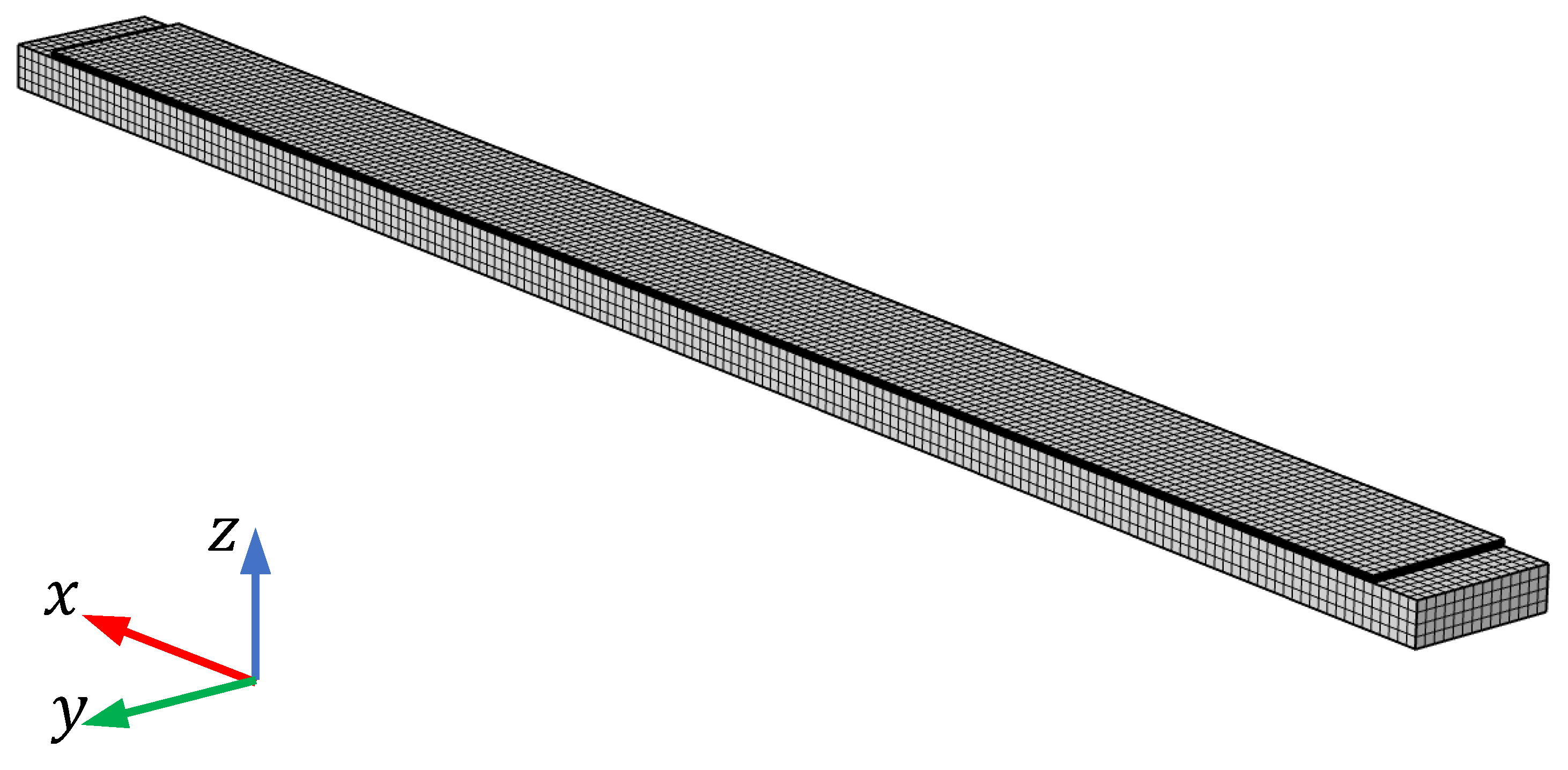
The slat is the mobile leading-edge flap of a wing of an aircraft, which is operated to increase the angle of attack of the wing during low-speed maneuvers, such as take-off and landing. The slats are retracted during flight and are forced by the aerodynamic loads to remain in contact with the leading edge of the wing. The deployment and retraction of the slat is performed by servomechanisms. In the framework of this research, it was assumed that the slat is moved by two servomechanisms, so the whole deployed slat could be schematized as a pinned beam with overhangs, as shown in
Figure 1a. A distributed stiffness was added to allow for the contact force between the wing and the retracted slat.
Figure 1b shows the scheme of the retracted slat. The slat vibrates since it is excited by the wing through the slat supports. The vibration levels of the supports are equal to the vibration levels of the wing’s leading edge corresponding with the connecting points. The slat is not a rigid body; hence, it deforms due to inertia force.
Figure 2 shows that the vibration levels at the supports are different, since vibrations along the wing of the aircraft increase from the root towards the tip of the wing [
7]. In
Figure 2,
represents the displacement of the deformed slat with respect to the undeformed configuration and
is the acceleration level of one of the two supports of the slat.
From a physical point of view, the slat can be modelled as a pinned beam excited by a trapezoidal distribution of forces (as proposed in [
7]) which represents the inertia force due to the vibration of the wing; see
Figure 3.
In aeronautics, acceleration levels are given in the frequency domain according to standard specifications. In this research, the standard specification RTCA-DO-160 CAT S curve E was adopted because it refers to wing components.
Figure 4 shows the PSD of the acceleration of the external support of the slat. Therefore, a frequency domain analysis was needed to calculate the power spectral density (PSD) of the voltage generated by a PE patch mounted on the slat from the acceleration PSD, and then the voltage RMS value could be obtained with Parseval’s Theorem.
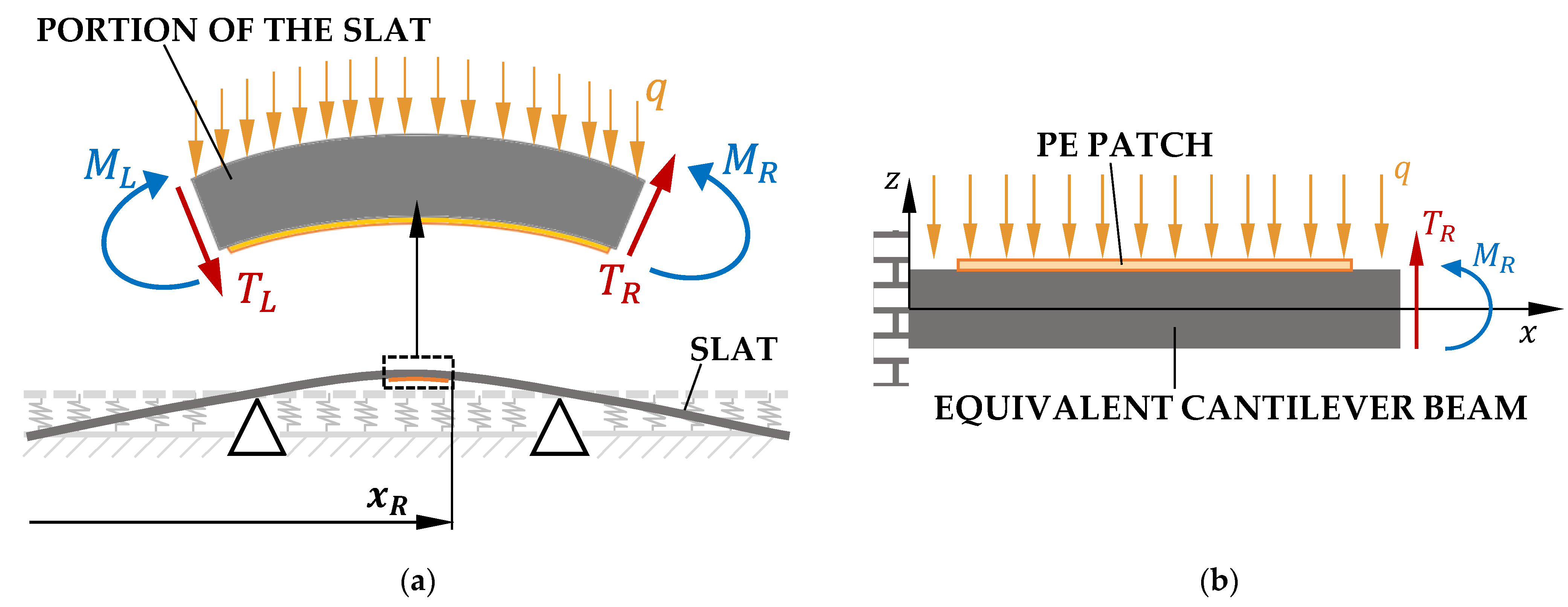
The piezoelectric patch is very thin and flexible and covers a very small part of the whole slat. Therefore, the vibrations of the slat caused by the motion of the supports are not influenced by the presence of the patch. Conversely, the deformation of the portion of the slat skin where the patch is attached determines the strain inside the PE patch and the generated voltage. The adhesive and protective layers that are inserted between the slat skin and the PE patch may also influence the generated voltage. For the above-mentioned reasons, a computational method based on the synergic use of a large-scale model and a small-scale model was developed.
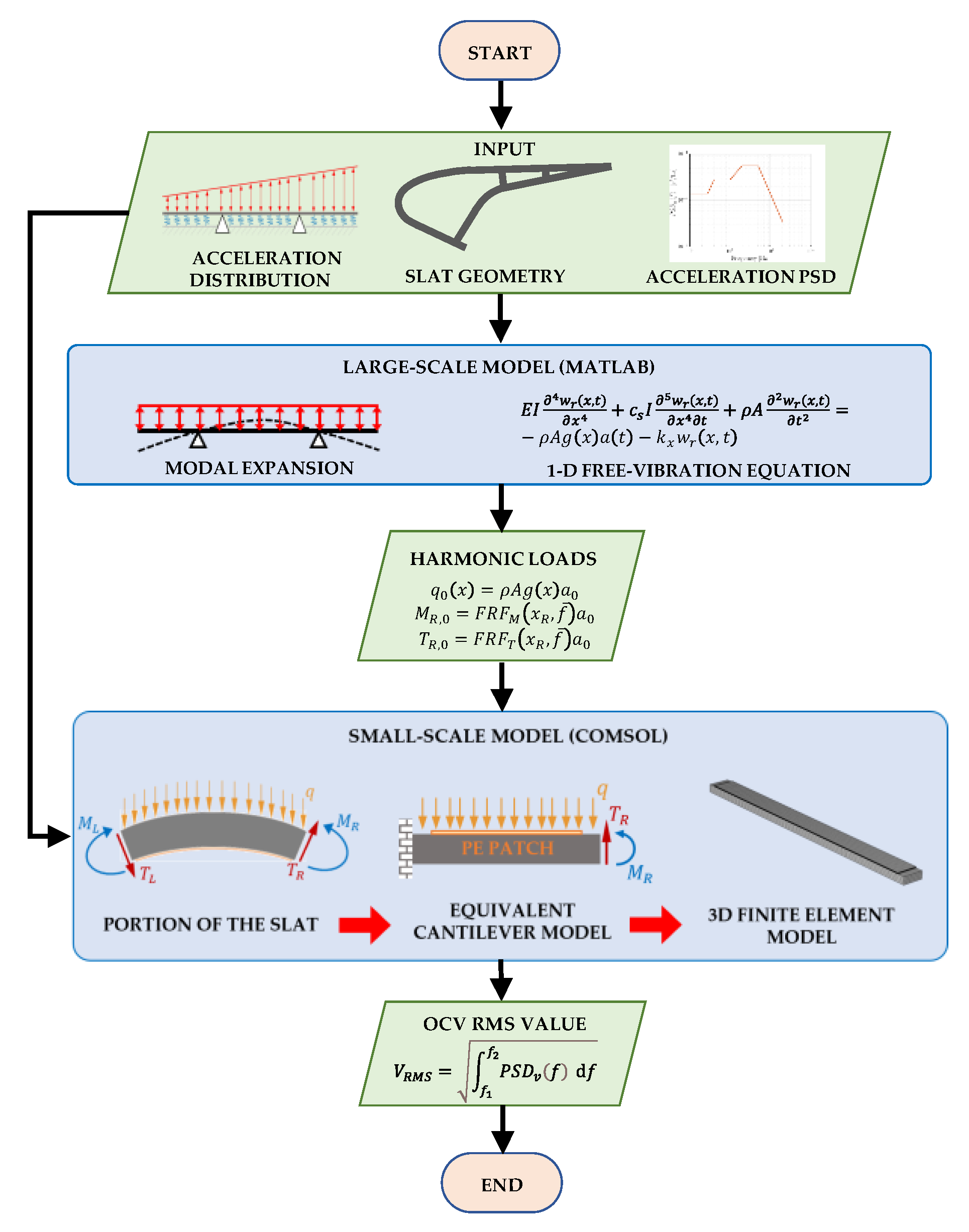
Figure 5 shows a flow chart that describes the steps and the interactions between the large-scale and small-scale models.
The large-scale model refers to the whole slat, is based on the modal expansion approach, and is implemented in MATLAB. The aim of this model is to calculate the frequency response functions (FRFs) of the points along the slat caused by a harmonic distributed inertia force having the shape depicted in
Figure 3. In particular, the FRFs between bending moment, shear force, and slat acceleration are obtained. They enable the calculation of the forces and moments acting on every portion of the slat.
The small-scale model includes the PE patch and the portion of the slat where the patch is attached. It is developed with the FE method and implemented in COMSOL. The actual cross-section of the slat, which is rather complex, is transformed into an equivalent cross-section that generates in the slat skin the same strain pattern as the actual cross-section when the same loads are present. The small-scale FE is used to calculate, for a series of frequencies, the harmonic response of the system stimulated by the inertia distributed force and by the moments and forces deriving from the large-scale model at the assigned frequency. The fitting of the results of these analyses gives the numerical FRF (
between slat acceleration and the open circuit voltage generated by the PE patch. The
relates the
PSD of the OCV to the
PSD of the applied acceleration:
The open circuit voltage
RMS value can be obtained from Parseval’s Theorem as
The OCV is an important merit figures since it allows for the evaluation of the electric performance of the harvester, as discussed in [
9].
3. Input Data: Slat and PE Patch Properties
The slat considered in this paper is built by the aerospace company Sonaca Group. It is made of a composite material and has the cross-section shown in
Figure 6. The properties of the material and the cross-section, provided by Sonaca, are summarized in
Table 1.
A macro fiber composite (MFC) piezoelectric patch manufactured by Smart Material GmbH (patch M8514—P2 in the datasheet of [
10]) and directly bonded to the slat skin was considered here.
Figure 6 shows the slat, the PE patch, and the global reference frame. The y-axis is aligned to the neutral axis of the slat cross-section. The center of the patch is located at
m and
m.
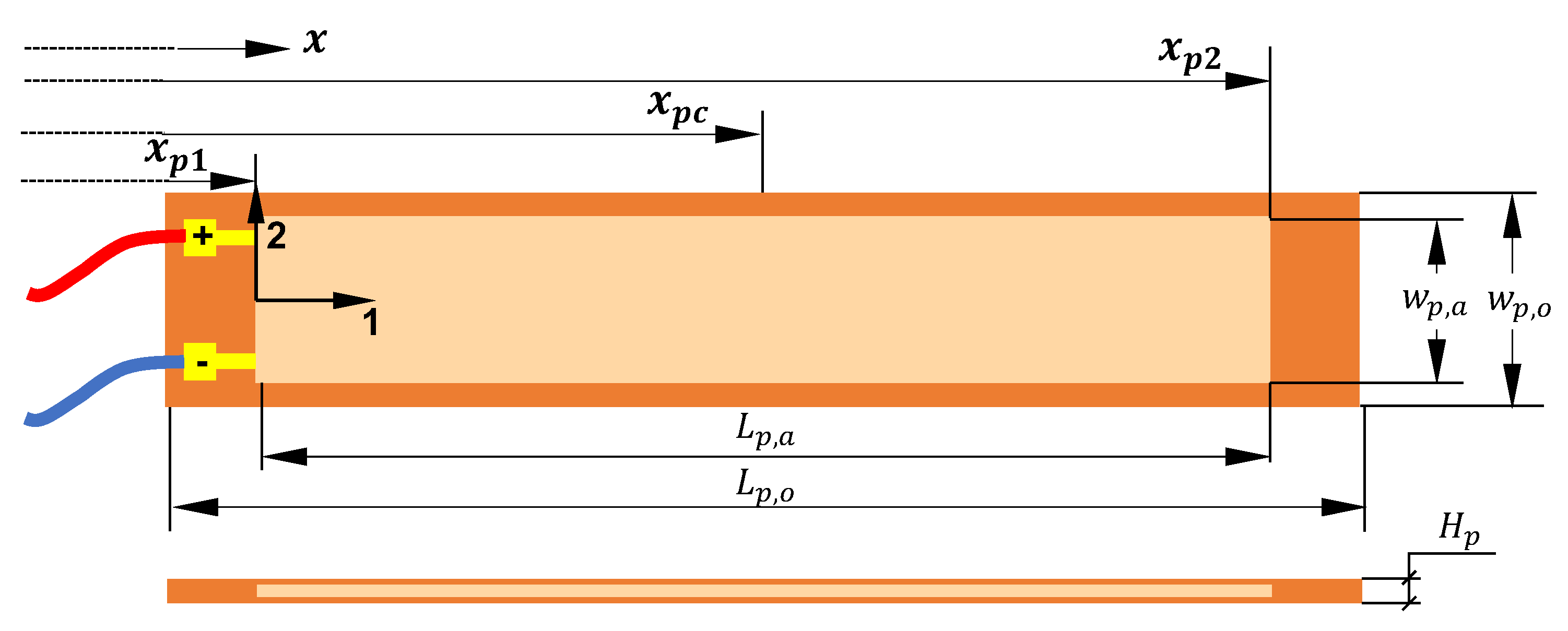
Figure 7 represents the scheme of the M8514—P2 patch and shows the local reference frame and the main dimensions of the patch. The patch is designed to exploit the strain along its longitudinal direction (axis 1), and it is poled along the direction perpendicular to its middle plane (axis 3).
To exploit the largest strain values, the PE patch is oriented to align its 1-axis with the x-axis of the global reference frame of the slat. Indeed, the slat vibrates in the z-direction due to the transverse load distribution; hence, the axial strain caused by the bending moment distribution is the main contribution.
In
Table 3, the electromechanical properties of the considered PE patch are presented.
4. Large-Scale Analytical Model of the Slat
The variable inertia force that excites the slat can be expressed as
where
is a shape function that correlates the acceleration of any point of the slat with the acceleration
of one of its supports (the external in the present study); see
Figure 2. As demonstrated in [
7], the shape function is
where
is a parameter related to the slope of the trapezoidal distribution and
are the length of the spans of the slat; see
Figure 1a. Here, the parameter
was set to 0.05, while
m and
m [
7].
The vibrating slat is considered to be a Euler–Bernoulli beam with constant properties: modulus of elasticity
, cross-section moment of inertia
, mass density
, cross-section area
, and coefficient of strain-rate damping
(a proportional damping is assumed). The equation of the forced vibrations of each of the three spans in
Figure 1a (
) is
where
is the distributed stiffness. The backward electromechanical coupling term [
11] is not considered in Equation (5) since the length of the PE patch is much smaller than the overall slat length and because the PE patch is much thinner than the slat.
The first steps of the modal expansion approach are the calculations of the natural frequencies and modes of vibration of the undamped system.
The free undamped vibrations for the retracted slat are described by the following homogeneous equation of motion:
The relative displacement can be expressed as the product of a spatial function
, which represents the deformed shape of the slat, and a time function
[
8]:
By inserting Equation (7) in Equation (6) and separating the variables, it becomes
The right-hand side of Equation (8) has the dimension of a squared angular frequency:
After some algebraic manipulations, the partial differential equation for the spatial component
of
is obtained:
where
includes the unknown natural angular frequencies. The solution of differential Equation (10) for each of three spans of the slat (
in
Figure 1a takes the form:
where
and
are unknown coefficients. By imposing the boundary conditions on the three spans of the slat and solving the corresponding eigenvalue problem, as discussed in [
7], an infinite discrete set of values
is found and the corresponding values (
) of the unknown coefficients are calculated. From Equation (12), the
ith mode of vibration of the slat becomes
The corresponding natural frequency
of the
ith mode of vibration of the slat can be calculated with Equation (11) as follows:
Equation (13) shows that the slat has the same modes of vibrations when deployed or retracted. On the other hand, Equation (14) shows that the modes are characterized by different natural frequencies due to the dependence on
kx. Therefore, the interaction between the retracted slat and the wing determines an increase in the natural frequency of each mode.
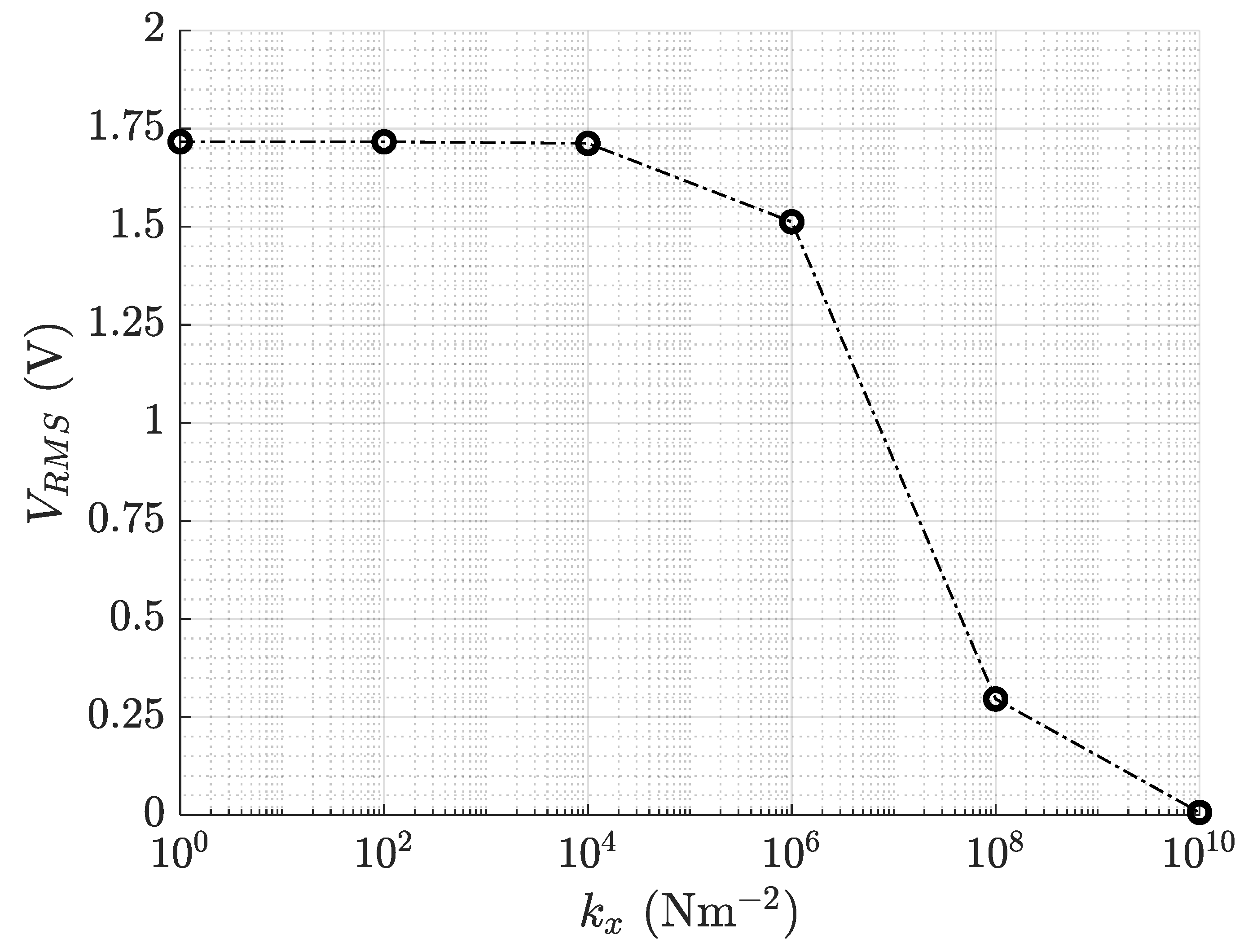
Figure 8 represents the natural frequencies of the first five modes of vibration of the retracted slat as a function of the distributed stiffness
kx considering the mechanical properties of the composite slat shown in
Table 1.
Figure 8 shows that when the distributed stiffness increases, all the natural frequencies of the modes converge to the same value, which means that the dynamics of the slat are close to those of a rigid body mounted on the distributed stiffness
. On the contrary, when the distributed stiffness is much smaller than the flexural stiffness of the slat, it has a negligible effect on the natural frequencies.
The relative displacement
of any point of the slat can be expressed by using the modal expansion approach as a linear combination of the modes of vibration of the slat [
8,
11,
12]:
where
is the
ith mass-normalized mode of vibration (that derives from the non-normalized mode [
7]) and
is the
ith modal coordinate. Hence, the equation of motion of the
ith modal coordinate is obtained by introducing Equation (15) in Equation (5) and applying the orthogonality conditions [
9,
11]:
where
and
are the natural frequency and the damping ratio of the
ith mode of vibration, respectively.
In the frequency domain, the modal coordinates
and the acceleration
are expressed as
The frequency response function (
FRF) between the modal coordinate amplitude
and the amplitude of the acceleration
a0 is
Therefore, only considering
modes of vibration of the slat, if Equation (18) is inserted into Equation (15), the FRF between the amplitude of the relative displacement of any point of the slat and the acceleration
can be calculated as follows:
The bending moment and the shear force along the slat are related to the relative displacement
by the following equations:
With harmonic excitation, the bending moment and shear force can be described in the frequency domain using the displacement
FRF:
Finally, the bending moment and shear force FRFs are defined as
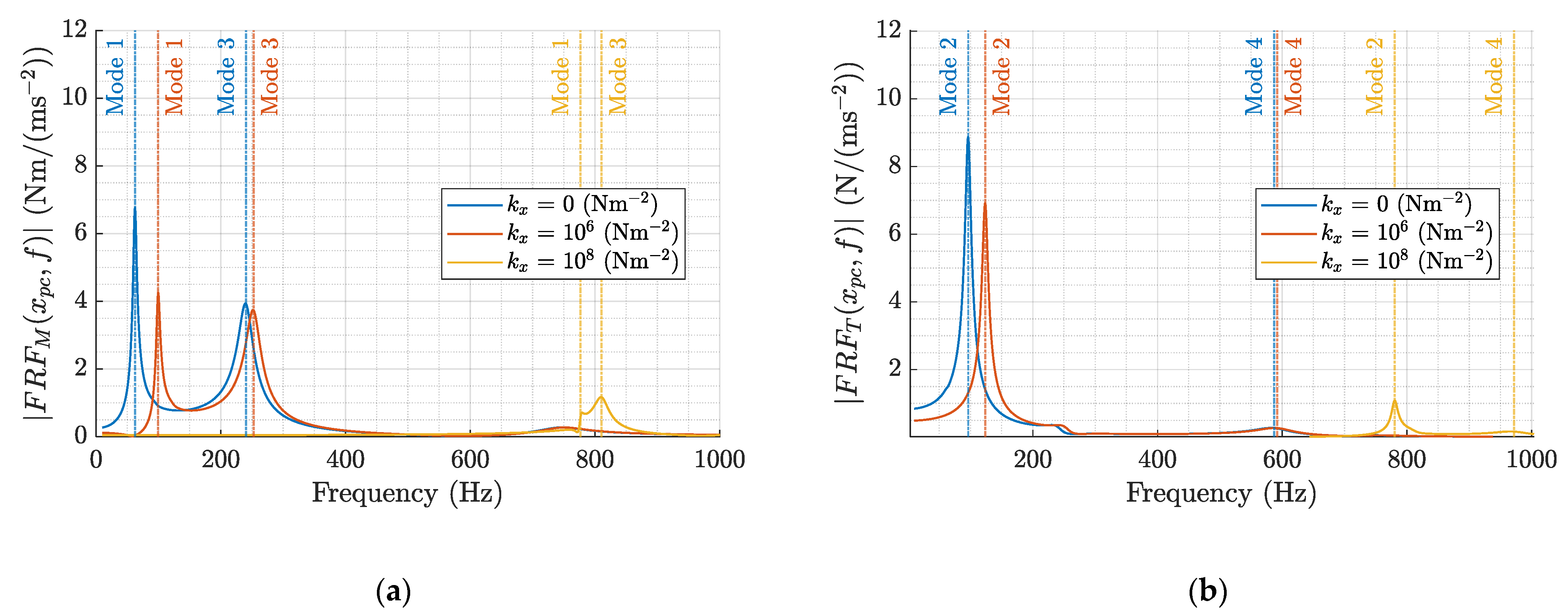
Figure 9 shows the magnitude of the FRFs related to the bending moment and shear force for different values of the distributed stiffness calculated at the center of the PE patch (
). The magnitude of the bending moment FRF in
Figure 9 is characterized by peaks at the natural frequencies of the odd modes, whereas the magnitude of the shear force FRF is characterized by peaks at the natural frequencies of the even modes. Indeed, the bending moment distribution corresponds to symmetric loads acting on a portion of the slat, so it only excites the odd modes, whereas the shear force corresponds to an anti-symmetric load and only excites the even modes.
7. Conclusions
An integrated analytical–numerical model for the prediction of the voltage generated by a small PE patch mounted on a long slender body that vibrates due to random excitation has been presented and applied to a wing slat.
The introduction of a variable contact stiffness between the slat and the wing edge makes it possible to simulate the behavior of the PE patch, both when the slat is retracted and when the slat is deployed. Numerical results showed that the PE patch generated much less voltage when the slat was retracted, because the large contact stiffness reduced the deformability of the slat.
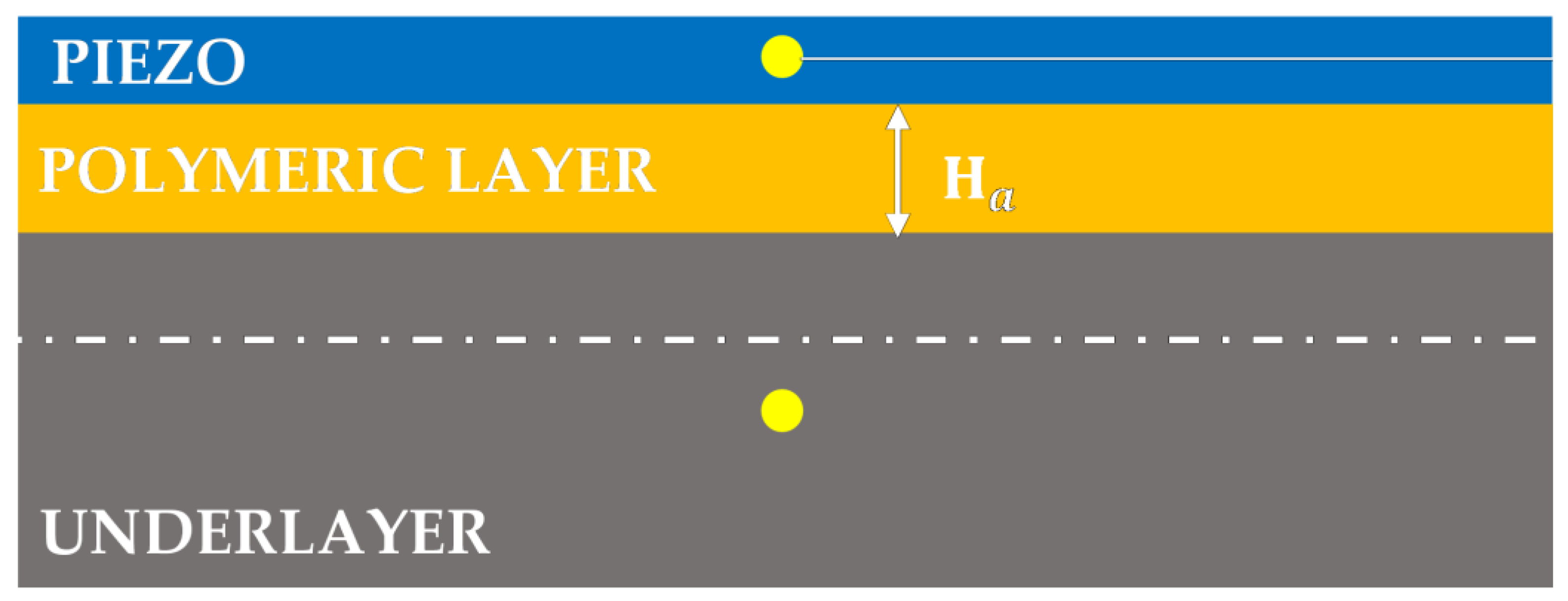
The transmission of the strain from the slat surface to the active PE layer through the intermediate layers (adhesive and protective) is an important issue. To this end, the integrated model was used to simulate the effect of a passive layer of increasing thickness located between the slat and the active PE layer. The results showed that a small increase in the thickness of the intermediate layer had a beneficial effect. This effect was the result of the increase in the distance between the PE layer and the neutral axis of the cross-section caused by the thicker layer. It vanished when the intermediate layer became very thick (some mm with the considered materials).
A further application of the integrated model will be the simulation of more complex sandwich structures such as generators that include both PE harvesters and thermo–electric harvesters based on the Seebeck effect.