Abstract
This paper investigates the problem of finite-time distributed consensus control for non-triangular stochastic nonlinear multi-agent systems (SNMASs) with input constraints. Fuzzy logical systems are used to identify the unknown nonlinear dynamics of non-triangular SNMASs. A finite-time command filter is utilized to eliminate the issue of “explosion of complexity” in the conventional backstepping-based distributed control algorithm, and a fractional power error compensation mechanism is constructed to improve the distributed control performance of SNMASs. It is proved that the proposed distributed controller enables all of the closed-loop system’s signals to be semi-globally finite-time bounded in probability, and the consensus tracking errors will converge to a sufficiently small neighborhood of the origin in a finite time. Finally, the effectiveness of the presented finite-time distributed control scheme is illustrated with a simulated example.
1. Introduction
Cooperative control of multi-agent systems has received considerable attention from many domestic and foreign scholars due to its wide applications in the fields of civil, industry, military, and so on [1,2,3]. For the leader-following consensus, which is an important part of cooperative control, the main objective is to enable all of the followers to achieve a consensus under the topology by designing consensus protocols. In particular, since stochastic disturbances are inevitable in practical systems and may result in system instability, it is significant to consider the distributed consensus control problem of stochastic nonlinear multi-agent systems (SNMASs).
In recent years, many tools and methods for dealing with SNMASs have been developed, and numerous results for SNMASs have been attained [4,5,6,7]. Note that these distributed control algorithms require that the nonlinear dynamics of SNMASs are known or can be linearly parameterized. If the prior information is not available, these distributed control strategies will be invalid. Fuzzy/neural network control methods have become promising ways to handle unknown nonlinear dynamics [8,9]. For first-order or second-order SNMASs with unknown nonlinear dynamics, approximation-based distributed adaptive control algorithms were developed via the fuzzy logical system approximator [10,11]. High-order distributed control algorithms are more precious in practice, and many distributed adaptive intelligent control approaches have been proposed for SNMASs with structured uncertainties [12,13,14,15]. Nevertheless, the aforementioned distributed control strategies are feasible under the assumption that the SNMASs have a strict-feedback structure, and they cannot be applied to the non-triangular case due to the complexity of their system dynamics.
Recently, non-triangular nonlinear multi-agent systems have received extensive attention, and a variety of effective distributed design methods have been reported. In [16], a backstepping-based distributed control algorithm was given for non-triangular multi-agent systems with unmodeled dynamics and quantized input. For non-triangular SNMASs, the distributed state-feedback and output-feedback control schemes were put forward [17,18], respectively. However, the problem of an “explosion of complexity” exists in the classical backstepping-based distributed control methods. With the aid of the dynamic surface control technique, an observer-based distributed fault-tolerant controller for non-triangular SNMASs was designed [19]; a distributed event-trigger control algorithm was presented for non-triangular multi-agent systems [20], which avoided the issue of the “explosion of complexity” but ignores the influence of filtered error. Fortunately, the command-filter-based backstepping design method can simultaneously eliminate the problem of the “explosion of complexity” and remove the influence of filtered error [21]. Soon afterward, by means of the command filter technique, in [22,23], respectively, the distributed prescribed performance control and output-feedback containment control schemes for non-triangular nonlinear multi-agent systems were developed.
It should be pointed out that the aforementioned distributed control strategies merely guarantee asymptotical convergence, i.e., the consensus errors are driven into the origin as the time approaches infinity. Unlike these asymptotic convergence algorithms, finite-time control has obvious merits, faster convergence speed, better tracking accuracy, strong anti-interference performance, etc. In [24], a finite-time bipartite quantized tracking control scheme for high-order pure-feedback SNMASs was proposed via the dynamic surface control technique. The problem of command-filter-based finite-time distributed adaptive control for nonlinear multi-agent systems was considered, where a Levant differentiator was employed to approximate the derivative of a distributed virtual control signal [25,26,27], and a sign function error compensation mechanism was designed to remove the effect of filtered error [25,26]. In spite of great efforts on command-filter-based finite-time distributed control strategies, prior information on the upper bound for the derivative of a distributed virtual control signal is necessary, and the chattering issue may arise.
On the other hand, input constraints are unavoidable for each agent due to the limitations of physical structures, which may destroy system performance or even lead to instability if not disposed of properly. Many researchers have explored various effective methods for dealing with input constraints [28,29,30]. By constructing an auxiliary system to compensate for the effect of input constraints, a command-filter-based distributed control scheme for strict-feedback nonlinear multi-agent systems was proposed in [31]. Considering nonlinear multi-agent systems with sensor faults and input constraints, in [32], a smooth function was introduced to counteract the input constraints. Nevertheless, the distributed consensus control strategies in [31,32] could not guarantee the finite-time stability, and they were invalid for non-triangular SNMASs.
Inspired by the above discussion, we will investigate the problem of finite-time distributed adaptive consensus control for non-triangular SNMASs with input constraints under a directed graph. The main contributions of this paper are summarized in the following three aspects.
- (1)
- In comparison with command-filter-based finite-time distributed control algorithms for SNMASs [26,27], an improved finite-time distributed consensus control scheme is proposed for SNMASs with input constraints, which effectively attenuates the chattering phenomenon, and the consensus tracking errors converge to a sufficiently small neighborhood of the origin in a finite time.
- (2)
- Unlike the existing backstepping [16,17,18] and dynamic surface [19,20] distributed control strategies for non-triangular SNMASs, a finite-time command filter and fractional power error compensation mechanism are constructed to eliminate the problem of the “explosion of complexity” and remove the effect of filtered error in a finite time.
- (3)
- Differently from an error compensation mechanism with asymptotic or finite-time convergence [22,23,25,26], a fractional power error compensation mechanism with finite-time convergence is designed, which further improves the distributed control performance.
The remainder of this paper is organized as follows. The preliminaries and problem formulation are presented in Section 2. The main results, including the finite-time distributed controller design and stability analysis, are described in Section 3. The simulation results in Section 4 illustrate the effectiveness of the proposed finite-time distributed control algorithm. Section 5 draws the conclusions.
2. Preliminaries and Problem Formulation
2.1. Graph Theory
In this paper, a directed graph is used to denote the communication topology for N followers of SNMASs, where stands for a set of directed edges, and represents a non-empty set of nodes. The ordered pair of node is a directed edge, and it implies that node i can access information from node j. is the neighbor set of node i. is a weighted adjacency matrix, where ; if , if . is the Laplacian matrix, in which , . If there is at least one node called a root node that has a directed path to all other nodes, we call this a directed graph, which includes a directed spanning tree. In addition, an extended directed graph is employed to depict the communication topology for the leader 0 and N followers. , where , if , , or else, .
2.2. Stochastic Theory
Consider the following stochastic nonlinear system:
where x is the state vector, and and are nonlinear Lipschitz functions satisfying and . is an s-dimensional independent standard Wiener process defined in a complete probability space , ℘ is a sample space, ℑ is a -field, is a filtration, and P is a probability measure.
Definition 1
([33]). For any given positive definite function , the differential operator of along with (1) is defined as
2.3. Problem Formulation
Consider the following SNMASs consisting of a leader marked 0 and N followers marked , where the i-th follower’s dynamics in a non-triangular structure are given as
in which and ; , is the state vector; is the control input signal, and is the output signal of the i-th follower. and are unknown smooth nonlinear functions; is a known smooth function satisfying , where and are known positive constants. has a similar definition to that in (1). In addition, suppose that the leader 0 is expressed by a time-varying signal .
Assume that the control input with constraint characteristics is in the following form
where and are known constants. We define
Then, can be rewritten as , where .
Control Objective: This paper aims to design finite-time distributed consensus controllers such that all signals of a closed-loop system are semi-globally finite-time bounded in probability, and all of the followers’ outputs synchronize with the leader , that is, the consensus tracking errors converge to a small neighborhood of the origin in a finite time.
To facilitate the control design, the following assumptions and lemmas are required.
Assumption 1.
The leader signal and its first derivative are continuous and bounded, and they are available for the i-th follower satisfying , .
Assumption 2.
The directed graph incorporates a spanning tree whose root node is the leader; then, is invertible.
Lemma 1
([34]). For a continuous function defined on a compact set Ω and any given constant , there exists a fuzzy logical system (FLS) such that the following equation holds:
where is the ideal weight vector; is the basis function vector, , with being the center vector and being the width of the Gaussian function.
Lemma 2
([35]). For , , and , which are real-valued functions, one has
Lemma 3
([36]). For , and , the following inequality holds:
Lemma 4
([37]). For the stochastic nonlinear system (1), if for any , there exists a positive definite function and such that
where , , γ, and Δ are all positive constants, and , , then the system (1) is semi-globally finite-time stable in probability, and the setting time T satisfies
where β is a constant satisfying .
3. Main Results
In this section, the finite-time distributed consensus control algorithm is proposed via the command filter technique and backstepping design method. In each step, a distributed virtual control signal will be structured, and the actual distributed controller will, finally, be designed.
Before starting the command-filtered backstepping design procedure, we define a constant as follows:
where , , , is the weight vector of the FLS. Let denote the estimation of , and is the estimation error.
3.1. Finite-Time Distributed Controller Design
For the i-th follower, the following coordinate transformations are introduced:
where is the output of a finite-time command filter (5) with the distributed virtual signal as the input signal:
with , , and being filter constants, and , .
Remark 1.
Although the finite-time command filter in [25,26,27] was used to approximate the derivative of a distributed virtual control signal, the Lipschitz condition of a distributed virtual control signal is required and the chattering phenomenon may arise. The demand of the distributed virtual control signal in [25,26,27] can be weakened via the adopted finite-time command filter (5), where the distributed virtual control signal is merely continuous and piecewise two-order derivable; meanwhile, the chattering phenomenon is skillfully attenuated.
The compensated tracking errors are defined as
where is the error compensation signal and is the auxiliary signal; these will be further specified later.
We choose the Lyapunov function as . From Definition 1, is obtained:
By using Lemma 2, the following inequality holds:
where is a positive constant. We define . From Lemma 1, one has , . According to Lemma 2, the following inequalities hold:
where is a design parameter. From (8)–(10), one gets
From Assumption 1, the distributed virtual control signal and the error compensation signal are designed as
where , are positive design parameters; , and and are positive odd integers. The initial condition of is set to .
We select the Lyapunov function . Based on Definition 1, one gets
From Lemma 2, the following inequality holds:
with being a positive constant. Let . According to Lemma 1, there exists an FLS such that , . Similarly, using the inequality technique as in (10) yields
where is a design parameter.
We construct the virtual control signal and the error compensation signal as follows:
with and being design parameters, and .
We choose the Lyapunov function . From Definition 1, one gets
By using Lemma 2, one has
where is a positive constant. Let , and this can be approximated by an FLS, that is, , . Furthermore, the following inequality can be obtained:
with being a design parameter.
The distributed virtual control signal and the error compensation signal are designed as
where and are positive design parameters, and .
The Lyapunov function for (29) is selected as . Then, one has
Applying Lemma 2 yields
where is a constant. We define . Similarly, there exists an FLS such that , . Obviously, the following inequality holds:
where is a positive design parameter.
The actual distributed controller and the error compensation signal are designed as
with , being positive design parameters, and .
According to Lemma 2, the following inequality holds:
Based on [[38] and Lemma 4], , together with Lemma 2, the following inequalities can be obtained:
In addition, the adaptive law for the i-th follower is designed as
where and are positive design parameters. From Lemma 2, it can be derived that
Remark 2.
Note that the fractional power error compensation mechanism consisting of (13), (20), (27), and (34) is different from the traditional error compensation mechanism [22,23] and the symbolic function error compensation mechanism [25,26]. An extra fractional power term is added, and the effect of the filtered error is removed in a finite time, which further improves the distributed control performance.
In summary, the finite-time distributed consensus control design procedures are presented in Figure 1.
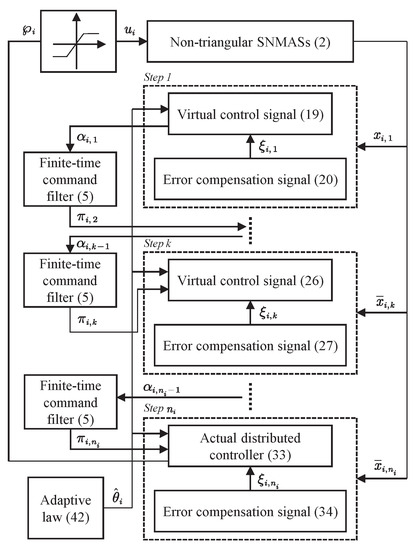
Figure 1.
A block diagram of the finite-time distributed consensus control design procedures.
3.2. Stability Analysis
Theorem 1.
For SNMASs (2) with input constraints under Assumptions 1 and 2, if the distributed virtual control signals (12), (19), and (26), the actual distributed controller (33), the error compensation signals (13), (20), (27), and (34), and the adaptive law (42) are adopted, then the following results can be obtained.
- All signals of the closed-loop system are semi-globally finite-time bounded in probability.
- The consensus tracking errors for the followers and the leader converge to a sufficiently small neighborhood of the origin in a finite time.
Proof.
By using Lemma 3, it follows that
where , , .
Based on Lemma 4, for any , there exists a setting time such that all signals of the closed-loop systems are semi-global finite-time bounded in probability.
We define , and it is easy to prove that
According to (3) and Assumption 2, the consensus tracking error is denoted as . Then, it follows from (46) that
Therefore, for any , one has
Obviously, the consensus tracking errors converge to a sufficiently small neighborhood of the origin in a finite time by appropriately choosing the control design parameters. □
4. Simulation Results
In order to verify the effectiveness and superiority of the proposed finite-time distributed consensus control algorithm, a numerical comparison example is provided. Figure 2 shows the communication topology of the second-order non-triangular SNMASs with one leader and four followers. The follower adjacency matrix A is given as .
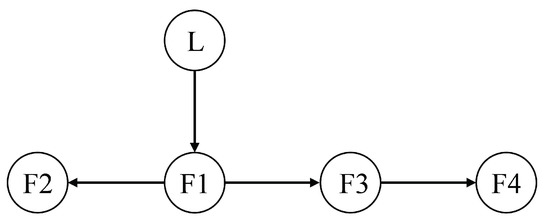
Figure 2.
The communication topology for non-triangular SNMASs.
Consider non-triangular SNMASs as follows:
where , , , , , , , , , , , , , , , , , , , , , , , , , . The input constraint for is chosen as
The leader signal is set to . The initial conditions for followers are taken as , , , and . We choose the FLSs containing seven fuzzy rules, and the Gaussian function with centers evenly spaced in , with the width being 4. The filter constants for finite-time command filters are , and . The control design parameters are selected as , , and .
The simulation results with the proposed finite-time distributed consensus control algorithm are displayed in Figure 3, Figure 4, Figure 5 and Figure 6. Figure 3 shows the trajectories of the follower output signals and leader signal r. The trajectories of the consensus tracking errors are given in Figure 4. The trajectories of the adaptive laws are demonstrated in Figure 5. Figure 6 depicts the trajectories of the control inputs . It can be seen from the simulation results that the proposed finite-time distributed control strategy achieves good consensus tracking performance even though unknown nonlinear dynamics and input constraints are included.
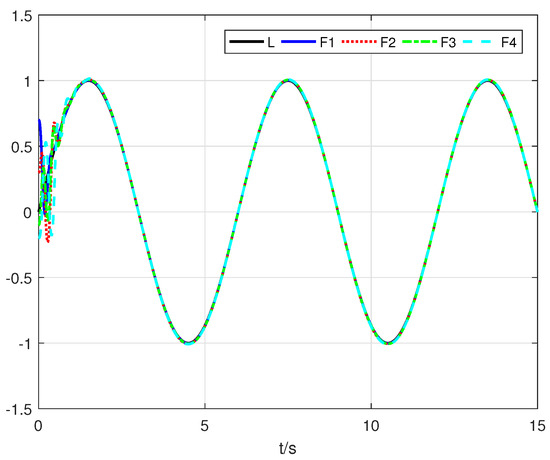
Figure 3.
The trajectories of the follower output signals and leader signal r.
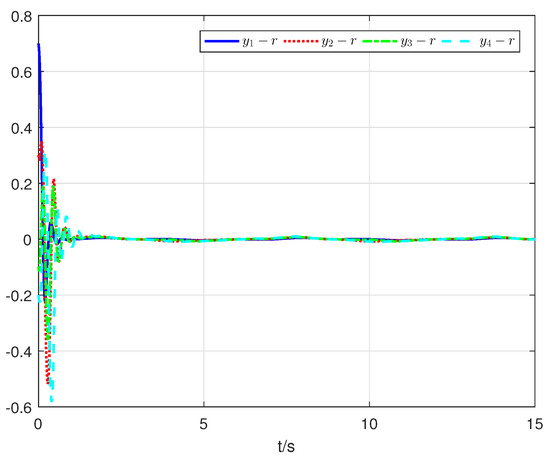
Figure 4.
The trajectories of the consensus tracking errors .
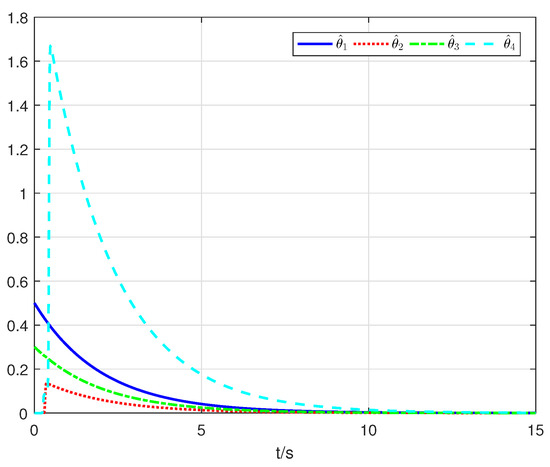
Figure 5.
The trajectories of the adaptive laws .
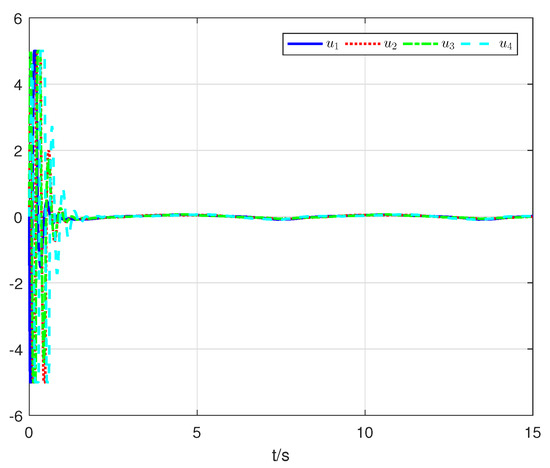
Figure 6.
The trajectories of the control inputs .
To show the superiority of the proposed finite-time distributed consensus control algorithm for non-triangular SNMASs, the command-filtered backstepping (CFB) control scheme in [23] was used to compare the consensus performance with it. The control design parameters for the CFB control scheme were chosen as , , and . The simulations were implemented in MATLAB R2016a/Simulink on a 1.80 GHz Intel(R) Core(TM) i7-8565U computer operating on Windows 11, where the solver was selected as the ode 4 (Runge–Kutta) and the fixed-step size was set to 0.01 s. We defined the overall tracking error and the root-mean-square error to compare the consensus performance, where w was the sample index, and M was the total number of the samples.
The trajectories of the OTE for the proposed control scheme and the CFB control algorithm in [23] are presented in Figure 7. The settling time and the RMSE in the performance comparison between the two control schemes are shown in Table 1, where we suppose that the settling time was the time after which always held. It can be seen from Figure 7 and Table 1 that, benefiting from the finite-time convergence compensation error mechanism, the settling time and RMSE of the proposed control scheme were lower than those of the CFB control algorithm in [23]. Obviously, the proposed finite-time distributed consensus control algorithm not only had a faster convergence rate, but also obtained better tracking performance compared with that of the CFB in [23].
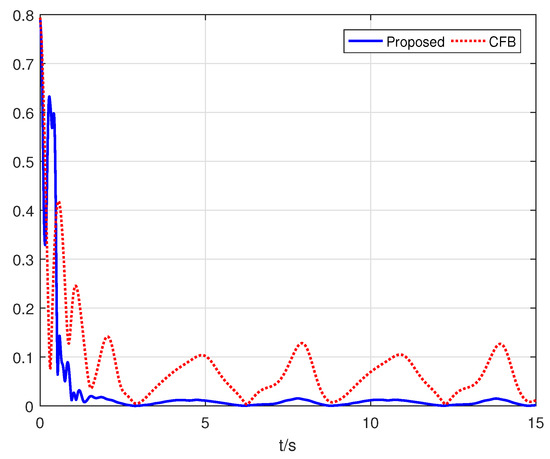
Figure 7.
The trajectories of the OTE with different control algorithms.

Table 1.
Performance comparison.
5. Conclusions
The problem of the finite-time distributed consensus control of non-triangular SNMASs with input constraints was studied. Unlike in traditional distributed control algorithms, the problem of an “explosion of complexity" was solved via a finite-time command filter, and the distributed control performance was improved based on a fractional power error compensation mechanism. The proposed distributed control algorithm could ensure that all signals of the closed-loop system were semi-globally finite-time bounded in probability, while the consensus tracking errors were driven into a sufficiently small neighborhood of the origin in a finite time. Based on the results of this paper, our future research will focus on the problems of the finite-time distributed output-feedback containment control of non-triangular SNMASs and the fixed-time distributed control of non-triangular SNMASs in an event-triggered framework.
Author Contributions
Methodology, Y.Z. and G.C.; Software, Y.L.; Writing—original draft preparation, Y.Z.; Writing—review and editing, Z.L. and W.H.; Supervision, G.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Natural Science Fund for Excellent Young Scholars of Jiangsu Province under Grant BK20211605 and the National Natural Science Foundation of China under Grants 61703059 and 61873144.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Fax, J.A.; Murray, R.M. Information flow and cooperative control of vehicle formations. IEEE Trans. Autom. Control 2004, 49, 1465–1476. [Google Scholar] [CrossRef]
- Ren, W.; Beard, R.W. Distributed Consensus in Multi-Vehicle Cooperative Control; Springer: London, UK, 2008. [Google Scholar]
- Qin, J.; Ma, Q.; Shi, Y.; Wang, L. Recent advances in consensus of multi-agent systems: A brief survey. IEEE Trans. Ind. Electron. 2017, 64, 4972–4983. [Google Scholar] [CrossRef]
- Li, W.; Zhang, J. Distributed practical output tracking of high-order stochastic multi-agent systems with inherent nonlinear drift and diffusion terms. Automatica 2014, 50, 3231–3238. [Google Scholar] [CrossRef]
- Hua, C.; Li, Y.; Guan, X. Leader-following consensus for high-order nonlinear stochastic multiagent systems. IEEE Trans. Cybern. 2017, 47, 1882–1891. [Google Scholar] [CrossRef]
- You, X.; Hua, C.; Yu, H.; Guan, X. Leader-following consensus for high-order stochastic multi-agent systems via dynamic output feedback control. Automatica 2019, 107, 418–424. [Google Scholar] [CrossRef]
- Zou, W.; Ahn, C.K.; Xiang, Z. Event-triggered consensus tracking control of stochastic nonlinear multiagent systems. IEEE Syst. J. 2019, 13, 4051–4059. [Google Scholar] [CrossRef]
- Cui, G.; Yu, J.; Shi, P. Observer-based finite-time adaptive fuzzy control with prescribed performance for nonstrict-feedback nonlinear systems. IEEE Trans. Fuzzy Syst. 2022, 30, 767–778. [Google Scholar] [CrossRef]
- Cui, G.; Yang, W.; Yu, J. Neural network-based finite-time adaptive tracking control of nonstrict-feedback nonlinear systems with actuator failures. Inf. Sci. 2021, 545, 298–311. [Google Scholar] [CrossRef]
- Ren, C.E.; Chen, L.; Chen, C.P. Adaptive fuzzy leader-following consensus control for stochastic multiagent systems with heterogeneous nonlinear dynamics. IEEE Trans. Fuzzy Syst. 2017, 25, 181–190. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, J.; Tong, S. Fuzzy adaptive optimized leader-following formation control for second-order stochastic multi-agent systems. IEEE Trans. Ind. Informat. 2022, 18, 6026–6037. [Google Scholar] [CrossRef]
- Yang, Y.; Miao, S.; Yue, D.; Xu, C.; Ye, D. Adaptive neural containment seeking of stochastic nonlinear strict-feedback multi-agent systems. Neurocomputing 2020, 400, 393–400. [Google Scholar] [CrossRef]
- Guo, X.; Liang, H.; Pan, Y. Observer-based adaptive fuzzy tracking control for stochastic nonlinear multi-agent systems with dead-zone input. Appl. Math. Comput. 2020, 379, 125269. [Google Scholar] [CrossRef]
- Zhao, Y.; Yu, H.; Xia, X. Event-triggered adaptive consensus for stochastic multi-agent systems with saturated input and partial state constraints. Inf. Sci. 2022, 603, 16–41. [Google Scholar] [CrossRef]
- Li, K.; Li, Y. Fuzzy adaptive optimal consensus fault-tolerant control for stochastic nonlinear multi-agent systems. IEEE Trans. Fuzzy Syst. 2022, 30, 2870–2885. [Google Scholar] [CrossRef]
- Qin, Z.; He, X.; Li, G.; Wu, Y. Robust adaptive consensus of nonstrict-feedback multi-agent systems with quantized input and unmodeled dynamics. Inf. Sci. 2019, 498, 117–134. [Google Scholar] [CrossRef]
- Liang, H.; Liu, G.; Huang, T.; Lam, H.K.; Wang, B. Cooperative fault-tolerant control for networks of stochastic nonlinear systems with nondifferential saturation nonlinearity. IEEE Trans. Syst. Man Cybern. 2022, 52, 1362–1372. [Google Scholar] [CrossRef]
- Zhao, G.; Cao, L.; Li, X.; Zhou, Q. Observer-based dynamic event-triggered control for nonstrict-feedback stochastic nonlinear multiagent systems. Appl. Math. Comput. 2022, 430, 127289. [Google Scholar] [CrossRef]
- Wu, Y.; Pan, Y.; Liang, H. Observer-based distributed fault-tolerant containment control for stochastic nonlinear multi-agent systems with asymmetric hysteretic quantization. Int. J. Robust Nonlinear Control 2022, 32, 7408–7430. [Google Scholar] [CrossRef]
- Yan, B.; Niu, B.; Zhao, X.; Wang, H.; Chen, W.; Liu, X. Neural-network-based adaptive event-triggered asymptotically consensus tracking control for nonlinear nonstrict-feedback MASs: An improved dynamic surface approach. IEEE Trans. Neural Netw. Learn. Syst. 2022. [Google Scholar] [CrossRef]
- Farrell, J.A.; Polycarpou, M.; Sharma, M.; Dong, W. Command filtered backstepping. IEEE Trans. Autom. Control 2009, 54, 1391–1395. [Google Scholar] [CrossRef]
- Shi, Z.; Zhou, C.; Guo, J. Observer-based consensus tracking control for a class of nonstrict-feedback nonlinear multi-agent systems with prescribed performance and input quantization. Int. J. Robust Nonlinear Control 2022, 32, 10374–10395. [Google Scholar] [CrossRef]
- Shahvali, M.; Askari, J. Distributed containment output-feedback control for a general class of stochastic nonlinear multi-agent systems. Neurocomputing 2016, 179, 202–210. [Google Scholar] [CrossRef]
- Wu, Y.; Pan, Y.; Chen, M.; Li, H. Quantized adaptive finite-time bipartite NN tracking control for stochastic multiagent systems. IEEE Trans. Cybern. 2021, 51, 2870–2881. [Google Scholar] [CrossRef] [PubMed]
- Zhao, L.; Yu, J.; Lin, C.; Ma, Y. Adaptive neural consensus tracking for nonlinear multiagent systems using finite-time command filtered backstepping. IEEE Trans. Syst. Man Cybern. 2018, 48, 2003–2012. [Google Scholar] [CrossRef]
- Sedghi, F.; Arefi, M.M.; Abooee, A.; Yin, S. Distributed adaptive-neural finite-time consensus control for stochastic nonlinear multiagent systems subject to saturated inputs. IEEE Trans. Neural Netw. Learn. Syst. 2022. [Google Scholar] [CrossRef]
- Song, X.; Zhao, L. Adaptive fuzzy finite-time consensus tracking for high-order stochastic multi-agent systems with input saturation. Int. J. Fuzzy Syst. 2022, 24, 3781–3795. [Google Scholar] [CrossRef]
- Wen, C.; Zhou, J.; Liu, Z.; Su, H. Robust adaptive control of uncertain nonlinear systems in the presence of input saturation and external disturbance. IEEE Trans. Autom. Control 2011, 56, 1672–1678. [Google Scholar] [CrossRef]
- Hosseinzadeh, M.; Yazdanpanah, M.J. Robust adaptive passivity-based control of open-loop unstable affine nonlinear systems subject to actuator saturation. IET Control Theory Appl. 2017, 11, 2731–2742. [Google Scholar] [CrossRef]
- Wu, B.; Wu, J.; Zhang, J.; Tang, G.; Zhao, Z. Adaptive neural control of a 2DOF helicopter with input saturation and time-varying output constraint. Actuators 2022, 11, 336. [Google Scholar] [CrossRef]
- Cui, G.; Xu, S.; Lewis, F.L.; Zhang, B.; Ma, Q. Distributed consensus tracking for non-linear multi-agent systems with input saturation: A command filtered backstepping approach. IET Control Theory Appl. 2016, 10, 509–516. [Google Scholar] [CrossRef]
- Cao, L.; Li, H.; Dong, G.; Lu, R. Event-triggered control for multiagent systems with sensor faults and input saturation. IEEE Trans. Syst. Man Cybern. 2021, 51, 3855–3866. [Google Scholar] [CrossRef]
- Ji, H.; Xi, H. Adaptive output-feedback tracking of stochastic nonlinear systems. IEEE Trans. Autom. Control 2006, 51, 355–360. [Google Scholar] [CrossRef]
- Wang, L. Adaptive Fuzzy Systems and Control, Design and Stability Analysis; Prentice-Hall: Englewood Cliffs, NJ, USA, 1994. [Google Scholar]
- Qian, C.; Lin, W. A continuous feedback approach to global strong stabilization of nonlinear systems. IEEE Trans. Autom. Control 2001, 46, 1061–1079. [Google Scholar] [CrossRef]
- Hardy, G.H.; Littlewood, J.E.; Pólya, G. Inequalities; Cambridge University Press: Cambridge, UK, 1952. [Google Scholar]
- Zhang, H.; Liu, Y.; Dai, J.; Wang, Y. Command filter based adaptive fuzzy finite-time control for a class of uncertain nonlinear systems with hysteresis. IEEE Trans. Fuzzy Syst. 2021, 29, 2553–2564. [Google Scholar] [CrossRef]
- Cui, G.; Yu, J.; Wang, Q. Finite-time adaptive fuzzy control for MIMO nonlinear systems with input saturation via improved command-filtered backstepping. IEEE Trans. Syst. Man Cybern. 2022, 52, 980–989. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).