Dual Synthetic Jets Actuator and Its Applications—Part I: PIV Measurements and Comparison to Synthetic Jet Actuator
Abstract
1. Introduction
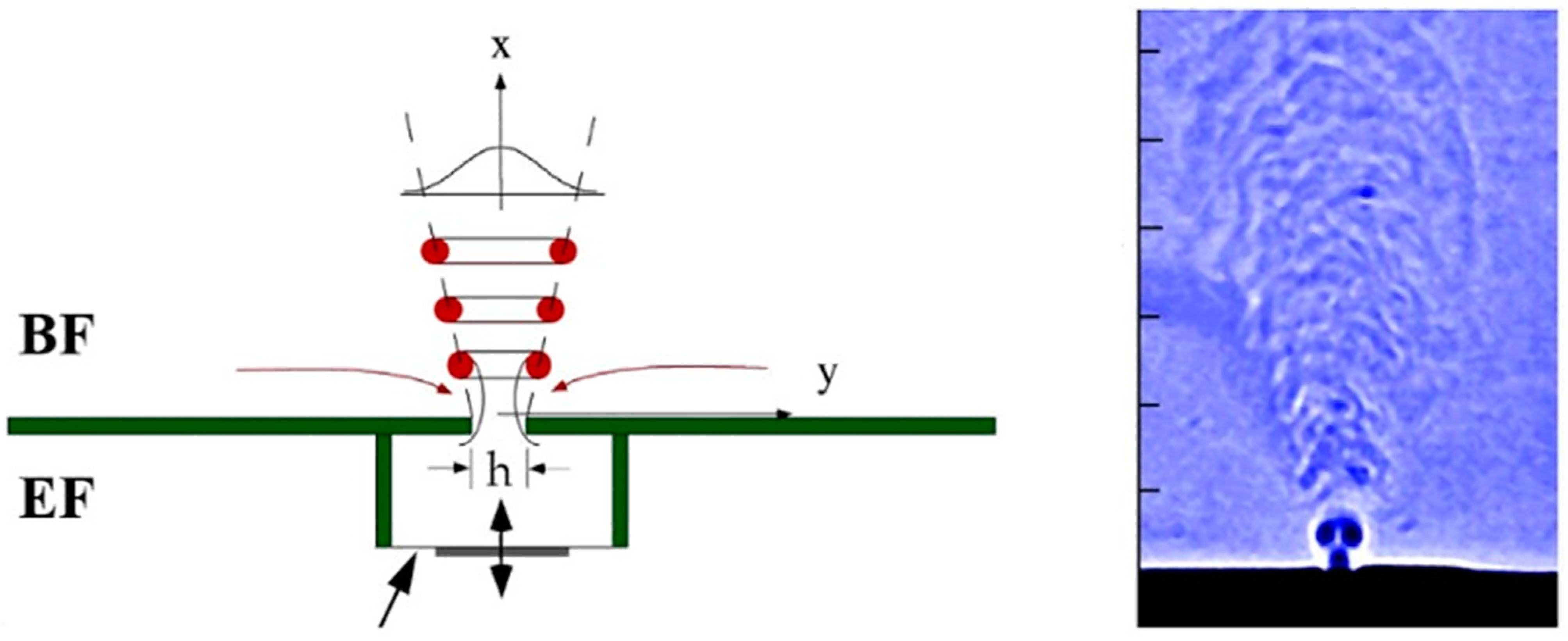
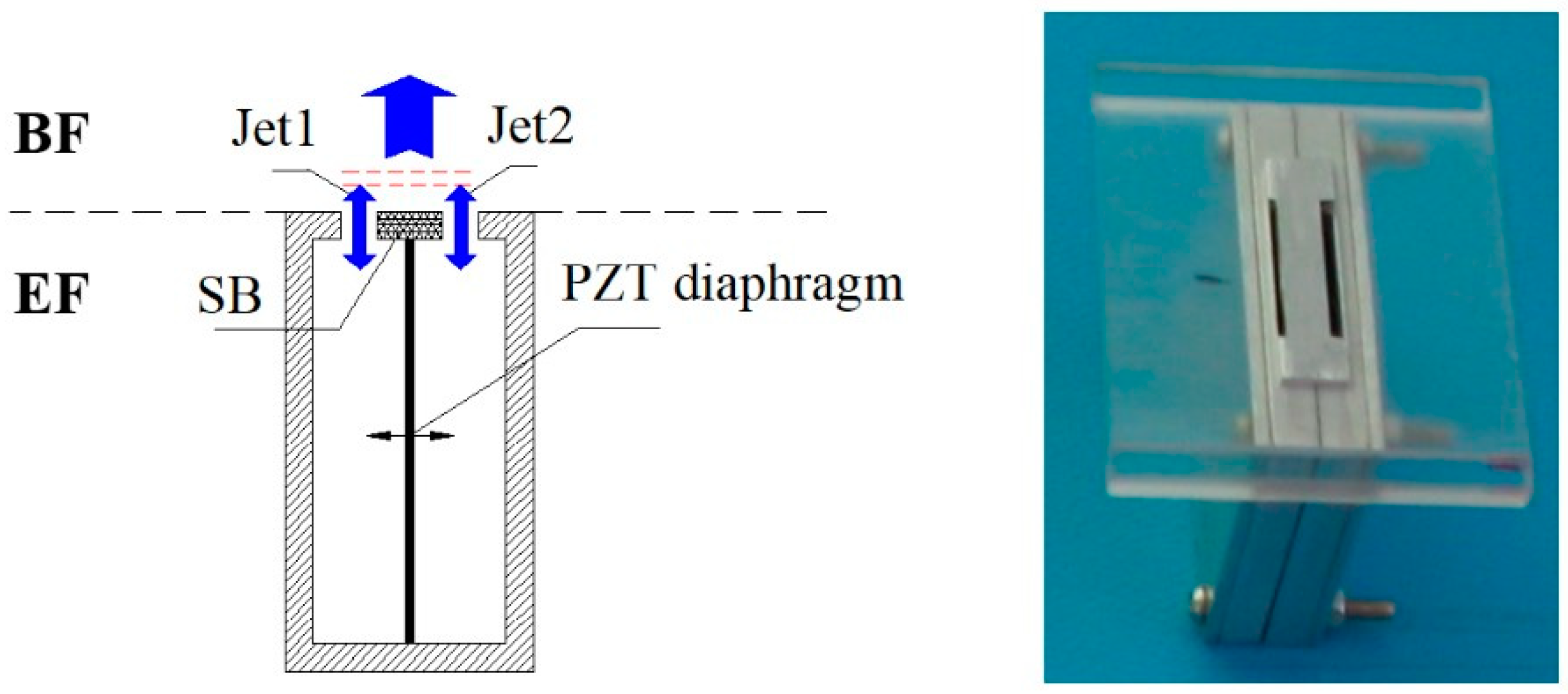
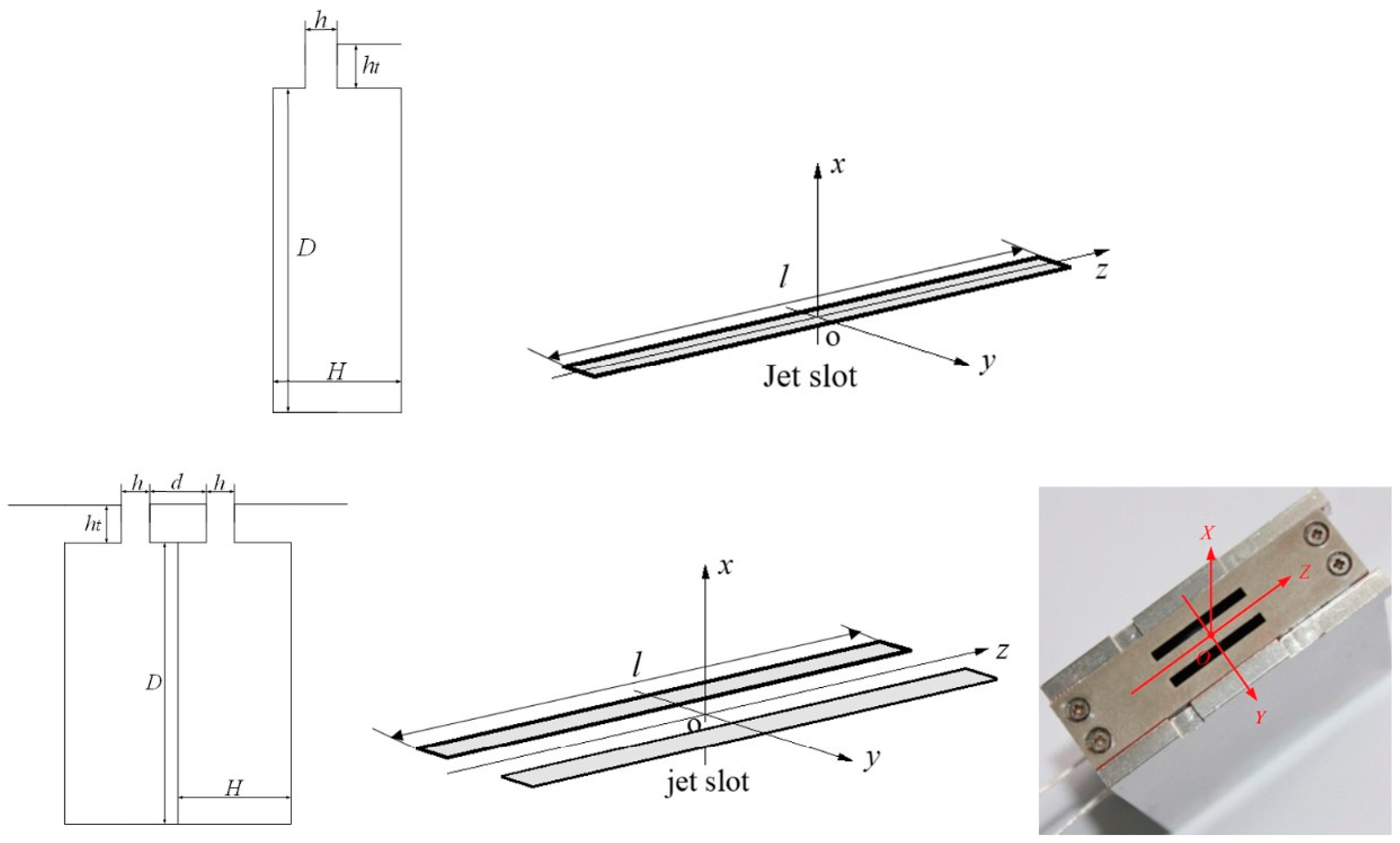
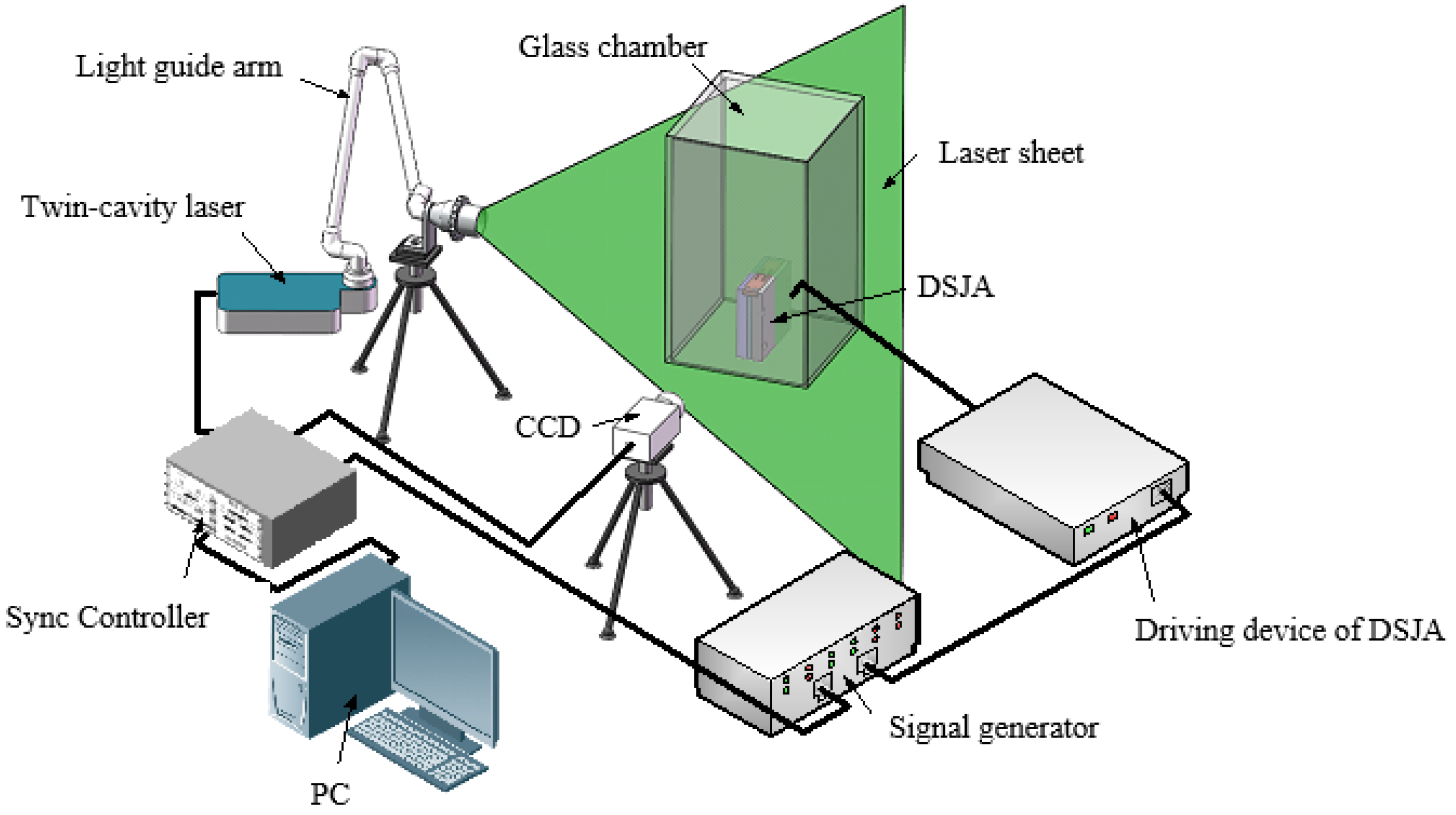
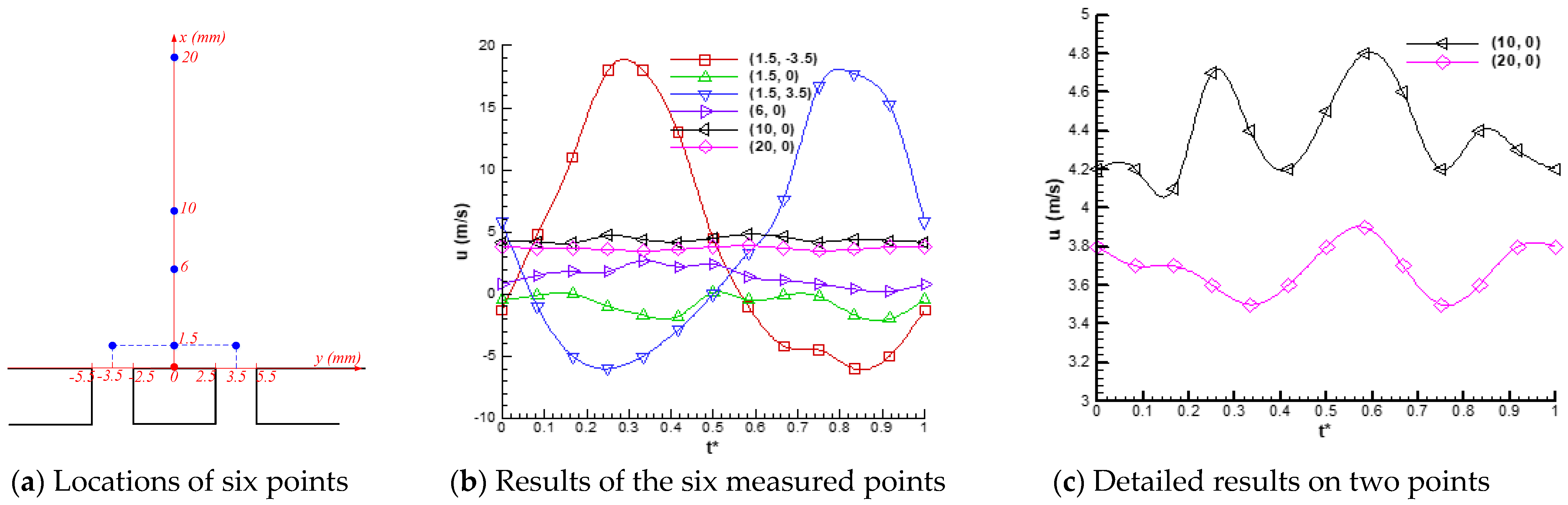
2. Experimental Technique
3. Results and Discussion
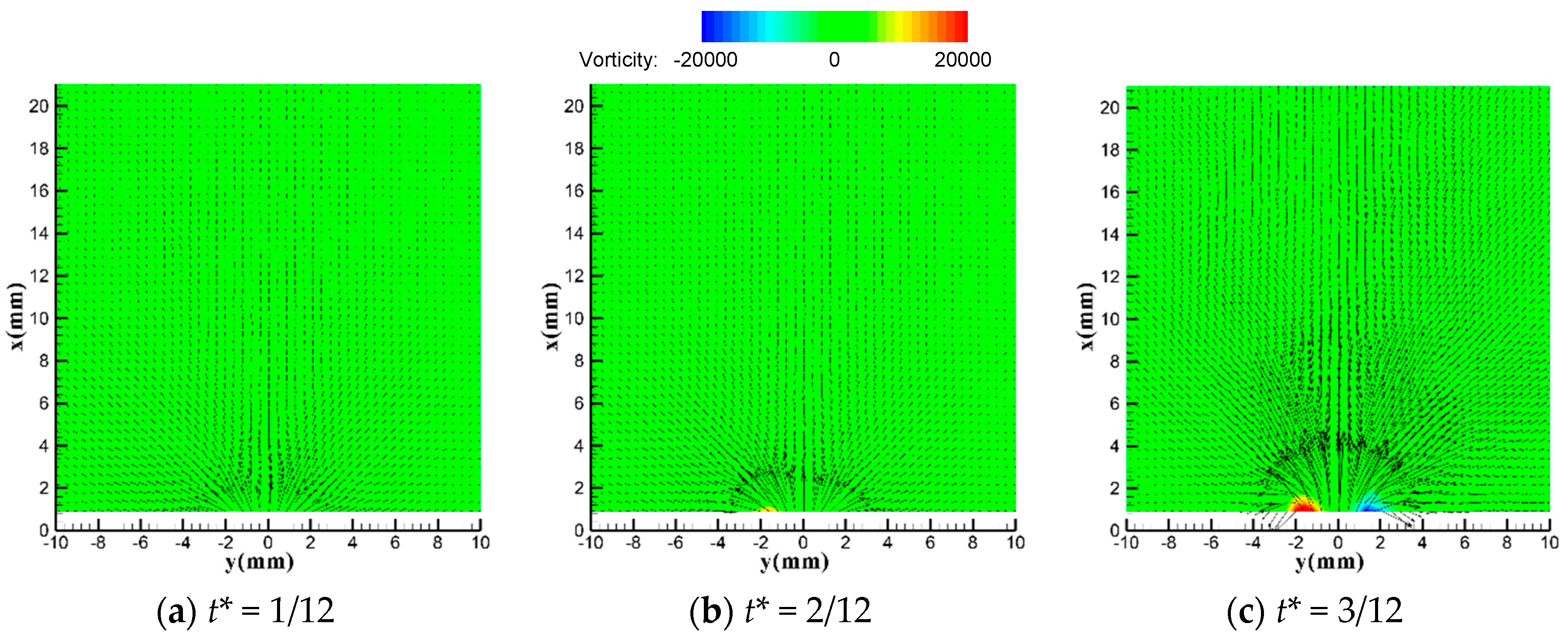
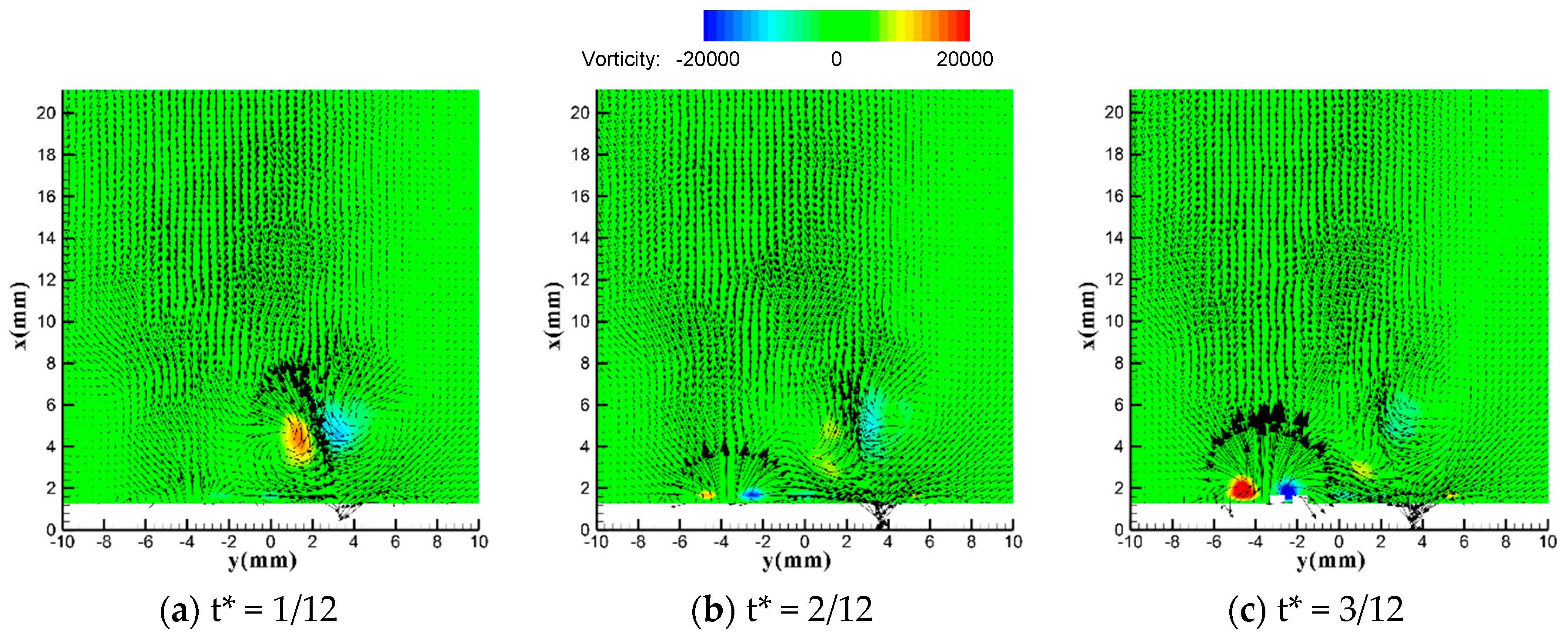
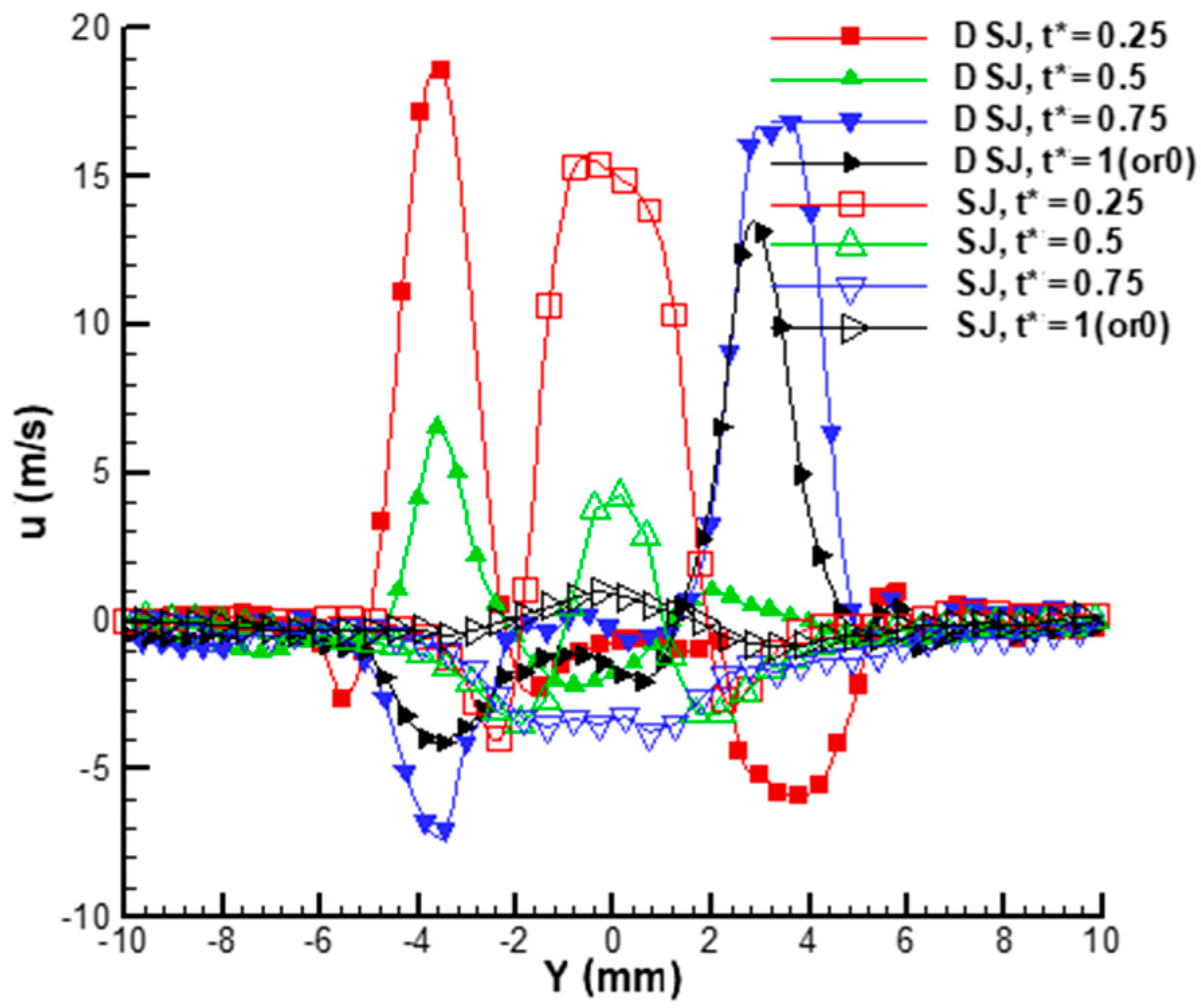
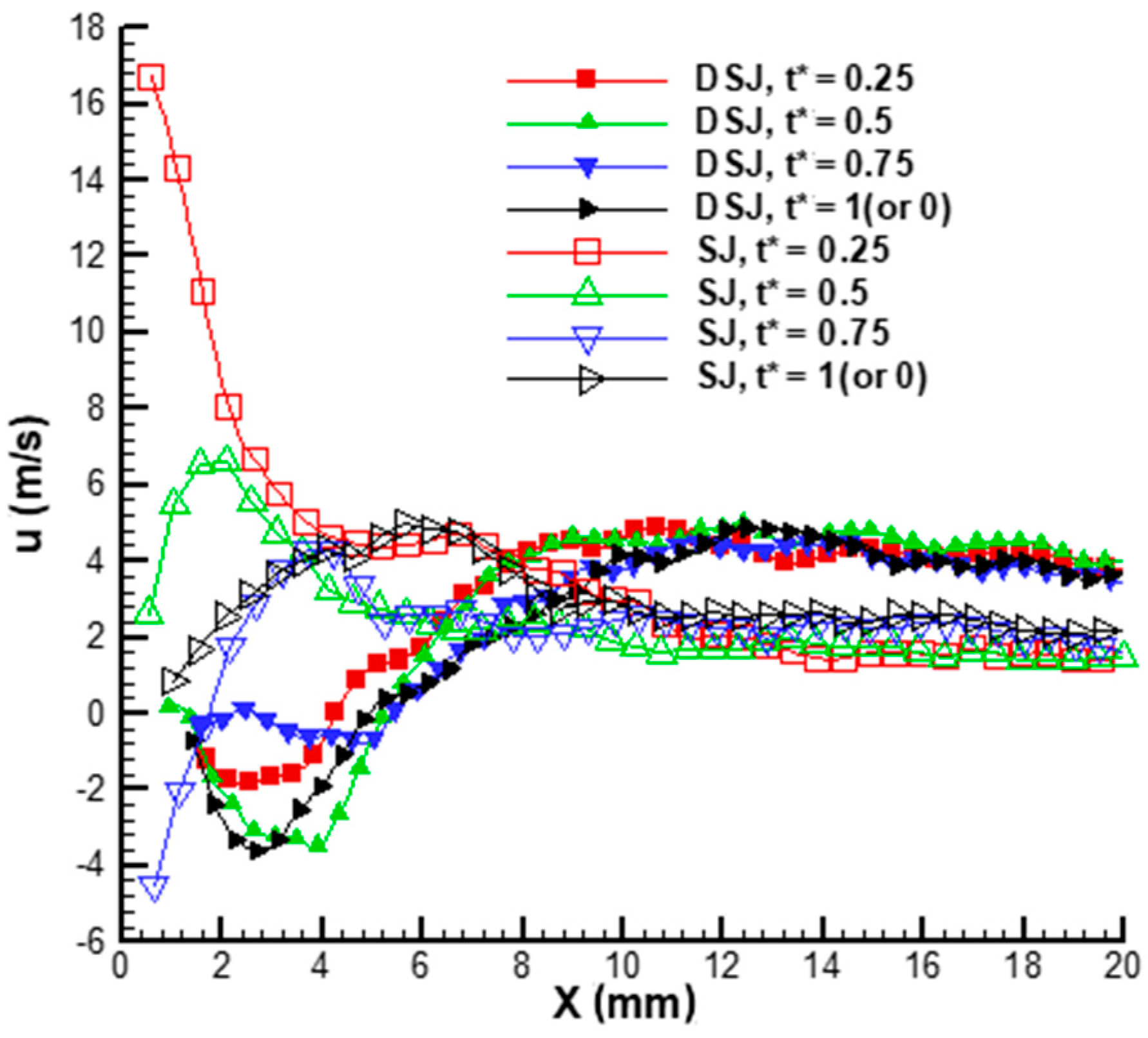
3.1. Comparison between DSJA and SJA
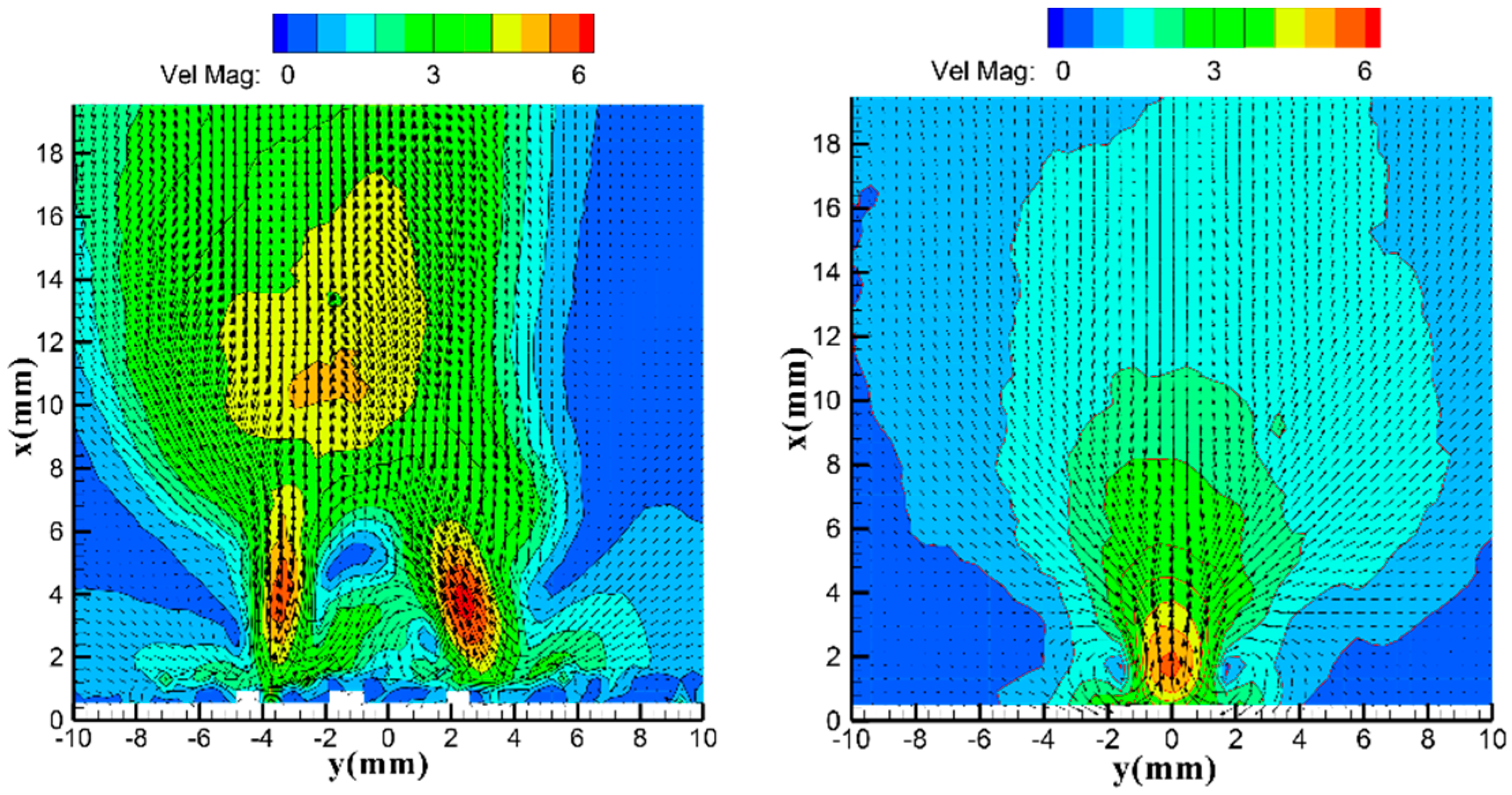
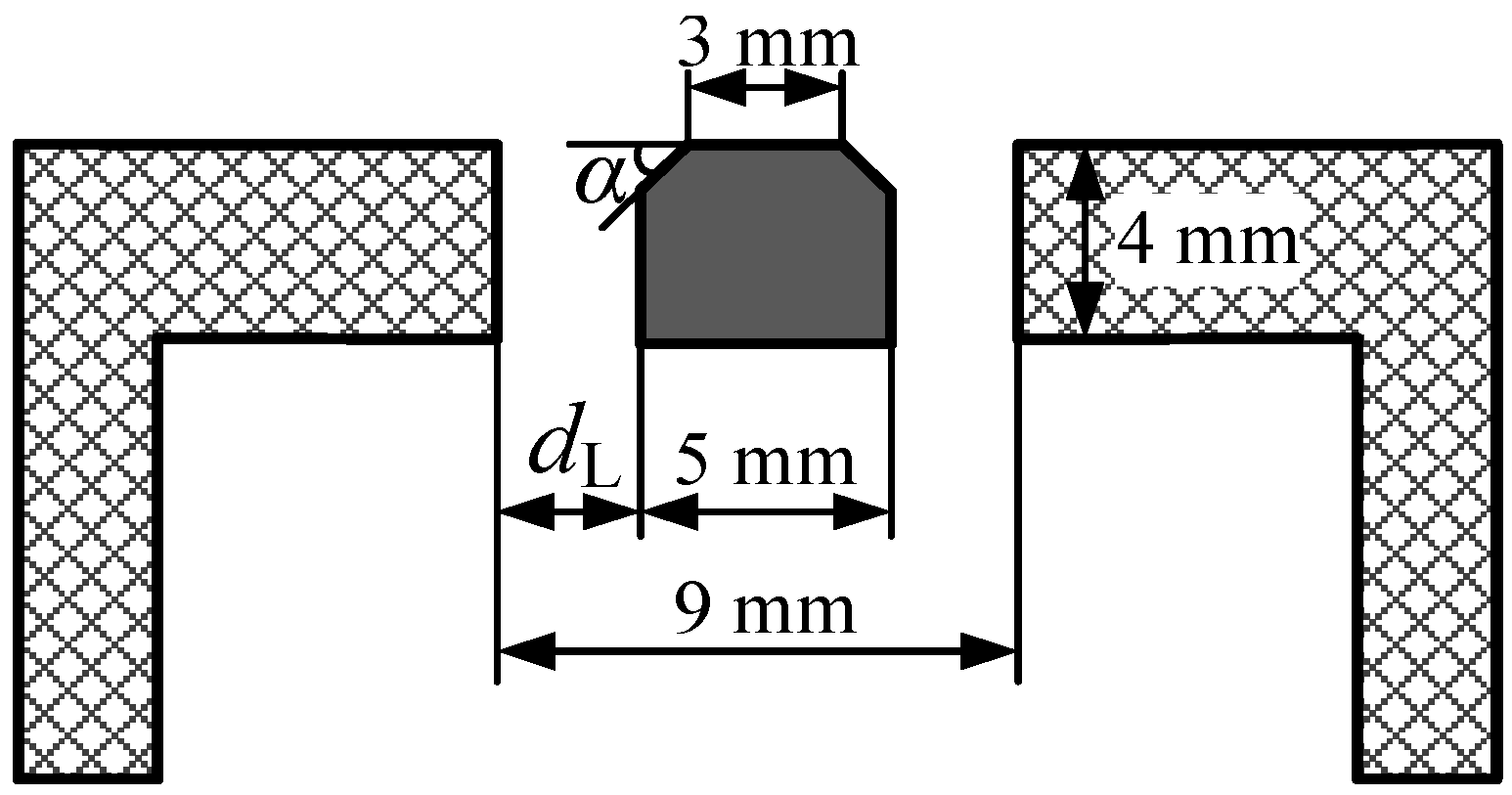
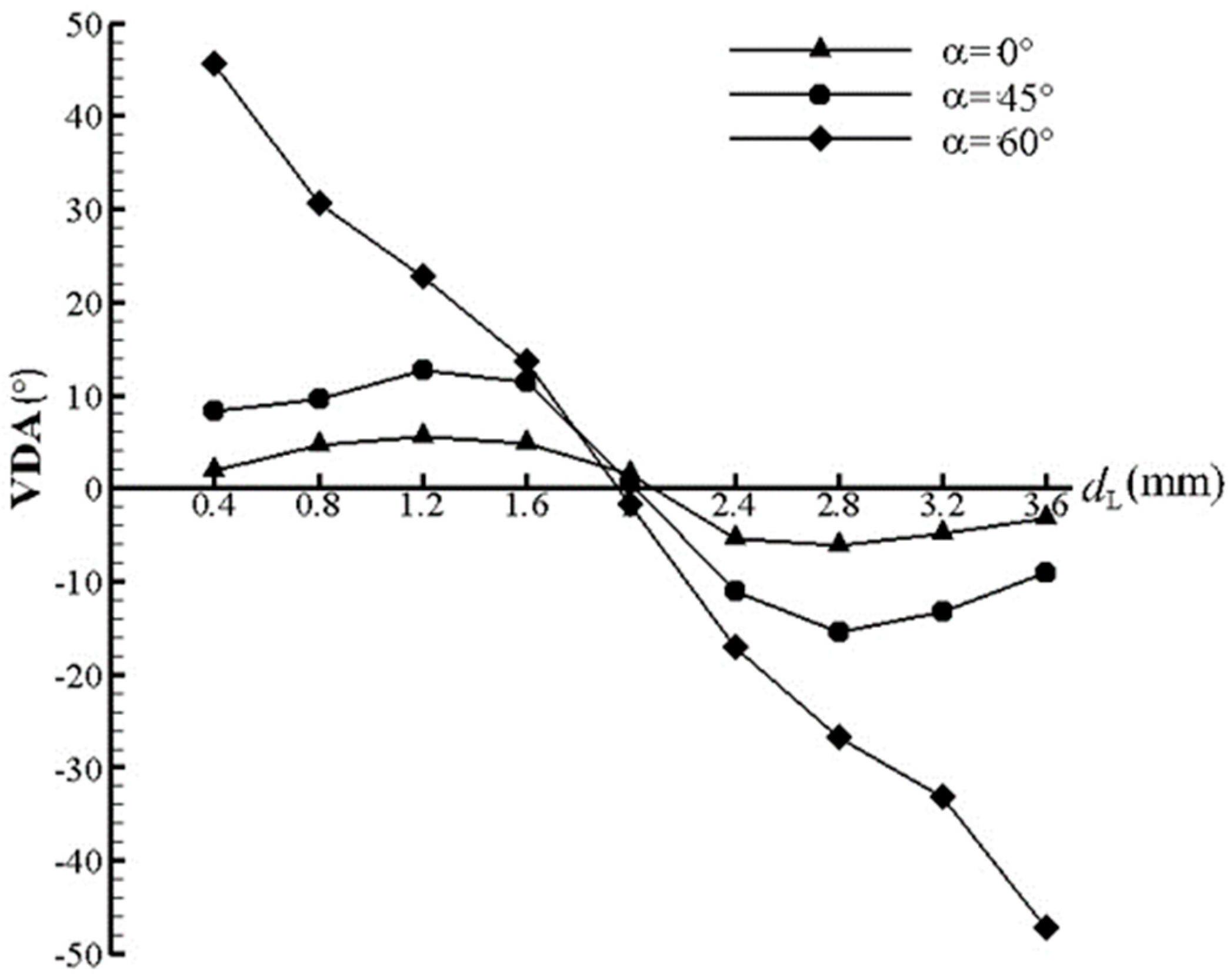
3.2. Special Vectoring Characteristics of DSJA
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| D | Diameter of cylindrical chambers |
| H | Height of cylindrical chambers |
| UA | Driving voltage amplitude |
| f | Driving frequency |
| ht | Thickness of rigid wall |
| l | Length of slots |
| h | Width of slots |
| d | Distance between the two slots |
| Reu | Reynolds number based on jet exit |
| St | Strouhal number |
| w | Vorticity |
| α | Exit chamfer |
| Air density | |
| Air viscosity | |
| uamp | Velocity amplitude of SJ |
| L0 | Stroke length of SJ |
| ReI0 | Re based on the blowing phase per unit width |
| u0(t) | Instantaneous centerline velocity at the actuator slot exit |
| T | Time of a DSJ period |
| t* | Dimensionless time |
| V | “Induced” velocity |
| Circulation | |
| a | Radius of the vortex ring |
| dL | Length of left exit |
References
- Glezer, A.; Amitay, M. Synthetic jets. Annu. Rev. Fluid Mech. 2002, 34, 503–529. [Google Scholar] [CrossRef]
- Luo, Z.B.; Xia, Z.X. Advances in synthetic jet technology and applications in flow control. Adv. Mech. 2005, 35, 221–234. (In Chinese) [Google Scholar]
- Zhang, P.F.; Wang, J.J.; Feng, L.H. Review of zero-net-mass-flux jet and its application in separation flow control. Sci. China Ser. E Technol. Sci. 2008, 51, 1315–1344. [Google Scholar] [CrossRef]
- Wen, X.; Tang, H.; Liu, Y.Z. Interaction of twin synthetic jets in attached and separated boundary layers: Effects of yaw angle and phase difference. J. Vis. 2018, 21, 949–963. [Google Scholar] [CrossRef]
- Wen, X.; Tang, H.; Duan, F. Interaction of in-line twin synthetic jets with a separated flow. Phys. Fluids 2016, 28, 043602. [Google Scholar] [CrossRef]
- Smith, B.L.; Glezer, A. The formation and evolution of synthetic jets. Phys. Fluids 1998, 10, 2281–2297. [Google Scholar] [CrossRef]
- Singh, P.K.; Renganathan, M.; Yadav, H.; Sahu, S.K.; Upadhyay, P.K.; Agrawal, A. An experimental investigation of the flow-field and thermal characteristics of synthetic jet impingement with different waveforms. Int. J. Heat Mass Transf. 2022, 187, 122534. [Google Scholar] [CrossRef]
- Kim, M.; Essel, E.E.; Sullivan, P.E. Effect of varying frequency of a synthetic jet on flow separation over an airfoil. Phys. Fluids 2022, 34, 015122. [Google Scholar] [CrossRef]
- Xu, X.P.; Zhou, Z. Analytical study on the synthetic jet control of asymmetric flow field of flying wing unmanned aerial vehicle. Aerosp. Sci. Technol. 2016, 56, 90–99. [Google Scholar] [CrossRef]
- Trávnícek, Z.; Tesar, V. Annular synthetic jet used for impinging flow mass-transfer. Int. J. Heat Mass Transf. 2003, 46, 3291–3297. [Google Scholar] [CrossRef]
- Pitital, I.; Rajnish, N.S. Large Eddy simulation of a NACA0015 circulation control airfoil using synthetic jets. Aerosp. Sci. Technol. 2018, 82–83, 545–556. [Google Scholar]
- Wen, X.; Tang, H.; Duan, F. Vortex dynamics of in-line twin synthetic jets in a laminar boundary layer. Phys. Fluids 2015, 27, 083601. [Google Scholar] [CrossRef]
- Rice, T.T.; Amitay, M. Forced Flow Reattachment Process and the Effect of Pressure Gradient. AIAA J. 2019, 57, 2795–2807. [Google Scholar] [CrossRef]
- Xia, H.; Qin, N. Detached-eddy simulation for synthetic jets with moving boundaries. Mod. Phys. Lett. B 2005, 28, 1429–1434. [Google Scholar] [CrossRef]
- Hill, D.J.; Saffman, P.G. Counter-rotating vortex patches in shear: A model of the effect of wind shear on aircraft trailing vortices. Proc. R. Soc. Lond. A 2002, 458, 1527–1553. [Google Scholar] [CrossRef]
- Wang, Q.T.; Cheng, K.M.; Gu, Y.S.; Li, Z.Q. Continuous control of asymmetric forebody vortices in a bi-stable state. Phys. Fluids 2018, 30, 024102. [Google Scholar] [CrossRef]
- Zhao, G.Q.; Zhao, Q.J.; Gu, Y.S.; Chen, X. Experimental investigations for parametric effects of dual synthetic jets on delaying stall of a thick airfoil. Chin. J. Aeronaut. 2016, 29, 346–357. [Google Scholar] [CrossRef]
- Luo, Z.B.; Xia, Z.X.; Liu, B. New generation of synthetic jet actuators. AIAA J. 2006, 44, 2418–2420. [Google Scholar] [CrossRef]
- Crispo, C.M.; Greco, C.S.; Cardone, G. Convective heat transfer in circular and chevron impinging synthetic jets. Int. J. Heat Mass Transf. 2018, 126, 969–979. [Google Scholar] [CrossRef]
- Greco, C.S.; Ianiro, A.; Imbriale, M.; Astarita, T.; Cardone, G. PIV Measurements in Twin Synthetic Jets. In Proceedings of the 15th International Symposium on Flow Visualization, Minsk, Belarus, 25–28 June 2012. [Google Scholar]
- Deng, X.; Xia, Z.X.; Luo, Z.B.; Li, Y.J. Vector-adjusting characteristic of dual-synthetic-jet actuator. AIAA J. 2015, 53, 794–797. [Google Scholar] [CrossRef]
- Zhao, Z.J.; Luo, Z.B.; Deng, X.; Liu, Z.; Li, S. Theoretical modeling of vectoring dual synthetic jet based on regression analysis. Chin. J. Aeronaut. 2021, 34, 1–12. [Google Scholar] [CrossRef]
- Luo, Z.B.; Xia, Z.X. Jet vectoring using a novel synthetic jet actuator. Chin. J. Aeronaut. 2007, 20, 193–201. [Google Scholar] [CrossRef]
- Luo, Z.B.; Zhao, Z.J.; Liu, J.F.; Deng, X.; Zheng, M.; Yang, H.; Chen, Q.; Li, S. Novel roll effector based on zero-mass-flux dual synthetic jets and its flight test. Chin. J. Aeronaut. 2022, 35, 1–5. [Google Scholar] [CrossRef]
| Test | Actuator | Slots | Cavies | Electrical Current | |||||
|---|---|---|---|---|---|---|---|---|---|
| l/mm | h/mm | d/mm | D/mm | H/mm | UA/V | f/Hz | Wave Form | ||
| T1 | SJA | 20 | 2 | — | 46 | 7 | 300 | 500 | rectangular |
| T2 | DSJA | 20 | 2 | 5 | 46 | 7 | 300 | 500 | rectangular |
| Test | Actuator | UA/V | f/Hz | uamp/(m/s) | Reu | ReIo | St | L0/mm |
|---|---|---|---|---|---|---|---|---|
| T1 | SJA | 300 | 500 | 16.5 | 2200 | 9500 | 0.19 | 10.5 |
| T2 | DSJA | 300 | 500 | 18.5 | 2500 | 12,000 | 0.17 | 11.8 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, Z.; Zhao, Z.; Deng, X.; Wang, L.; Xia, Z. Dual Synthetic Jets Actuator and Its Applications—Part I: PIV Measurements and Comparison to Synthetic Jet Actuator. Actuators 2022, 11, 205. https://doi.org/10.3390/act11080205
Luo Z, Zhao Z, Deng X, Wang L, Xia Z. Dual Synthetic Jets Actuator and Its Applications—Part I: PIV Measurements and Comparison to Synthetic Jet Actuator. Actuators. 2022; 11(8):205. https://doi.org/10.3390/act11080205
Chicago/Turabian StyleLuo, Zhenbing, Zhijie Zhao, Xiong Deng, Lin Wang, and Zhixun Xia. 2022. "Dual Synthetic Jets Actuator and Its Applications—Part I: PIV Measurements and Comparison to Synthetic Jet Actuator" Actuators 11, no. 8: 205. https://doi.org/10.3390/act11080205
APA StyleLuo, Z., Zhao, Z., Deng, X., Wang, L., & Xia, Z. (2022). Dual Synthetic Jets Actuator and Its Applications—Part I: PIV Measurements and Comparison to Synthetic Jet Actuator. Actuators, 11(8), 205. https://doi.org/10.3390/act11080205







