Influence of Synthetic Jets on Multiscale Features in Wall-Bounded Turbulence
Abstract
1. Introduction
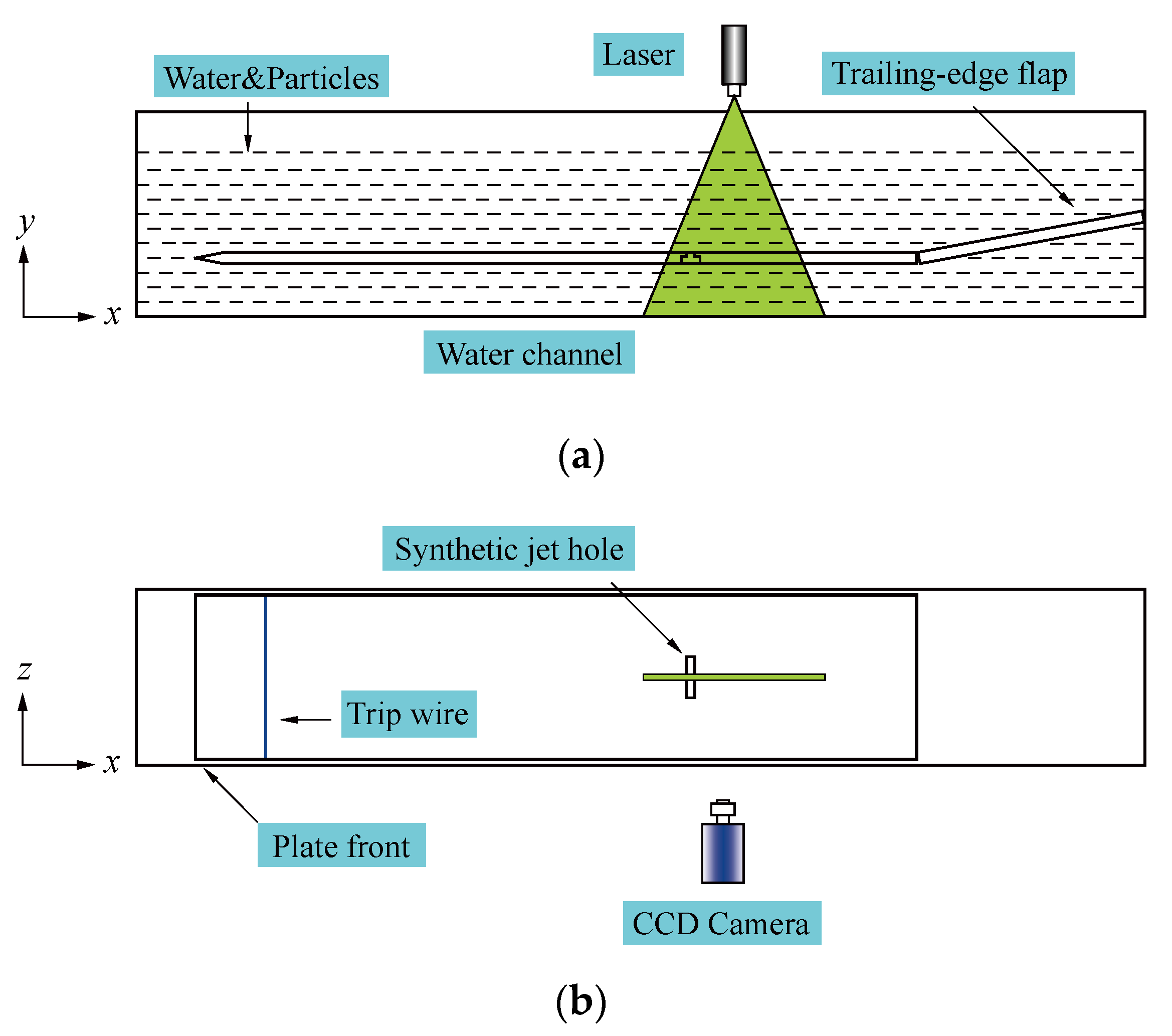
2. Experimental Facilities and Procedure
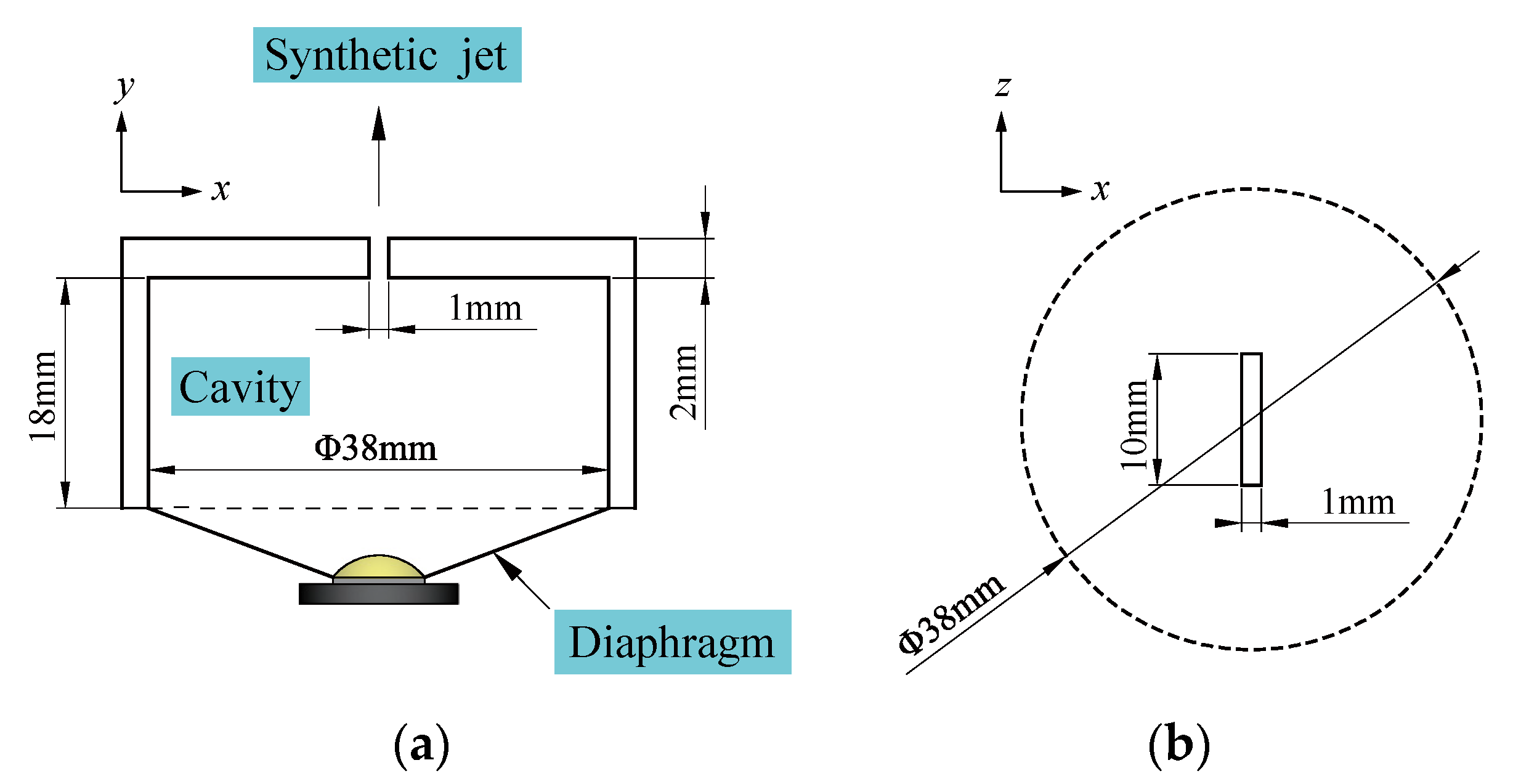
2.1. Laboratory Equipment
2.2. Measurement Process
3. Results and Analyses
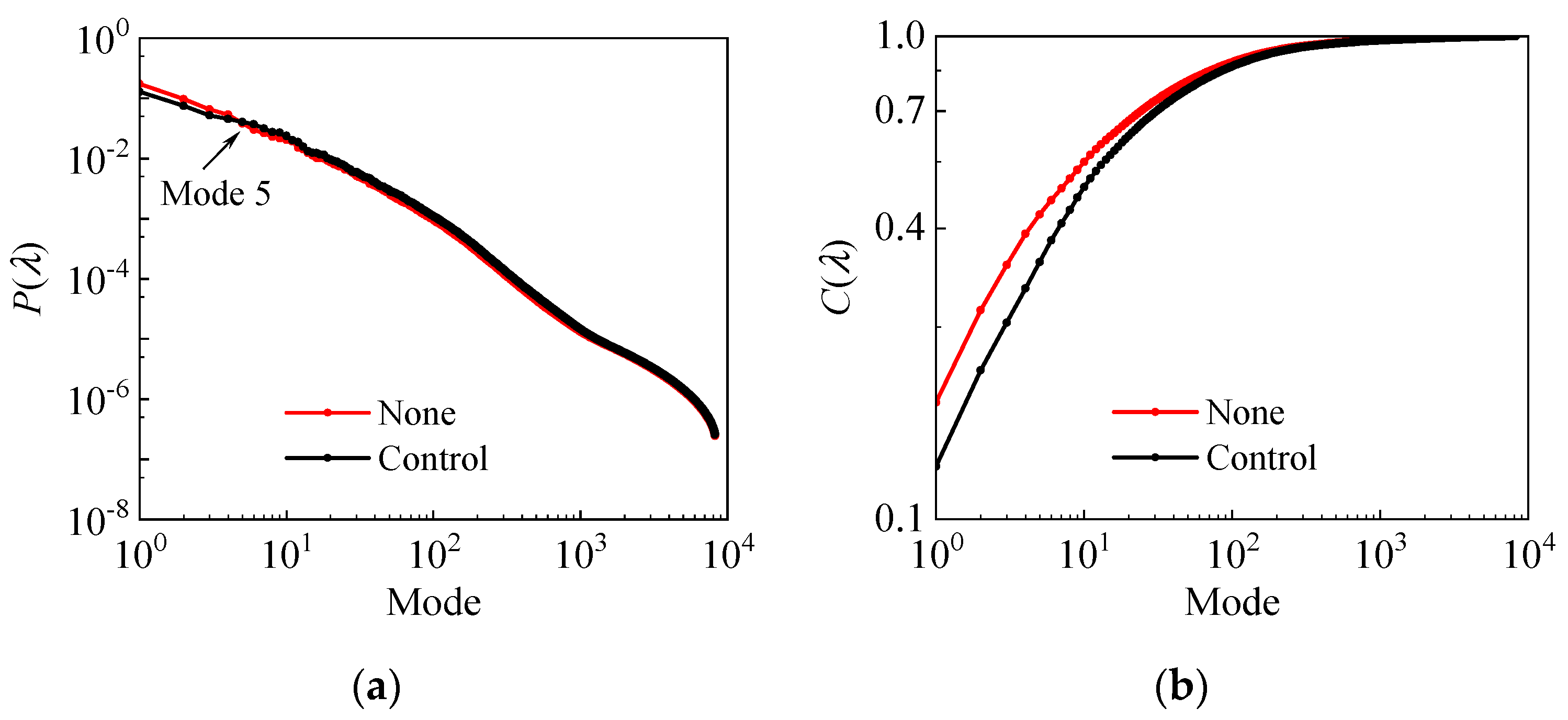
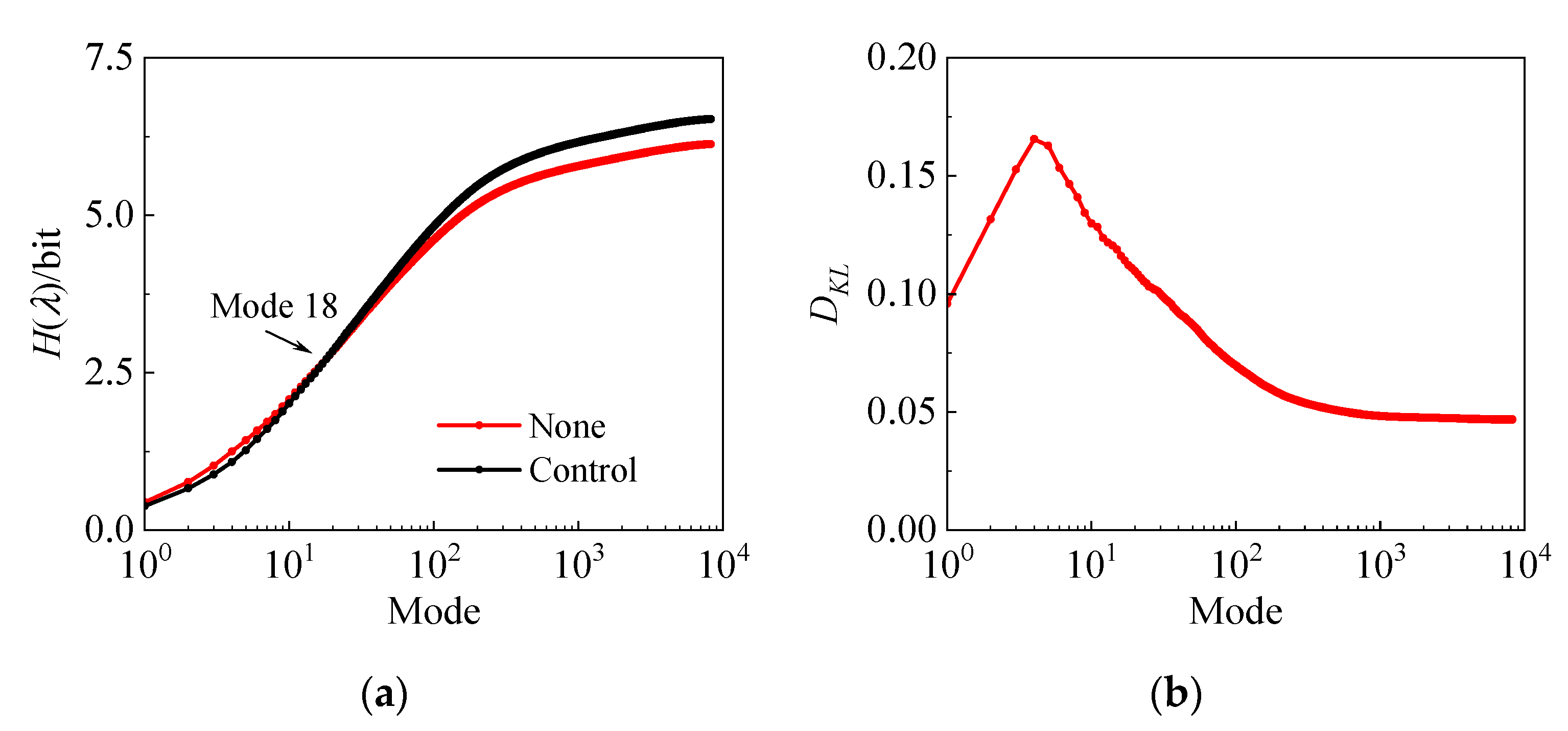
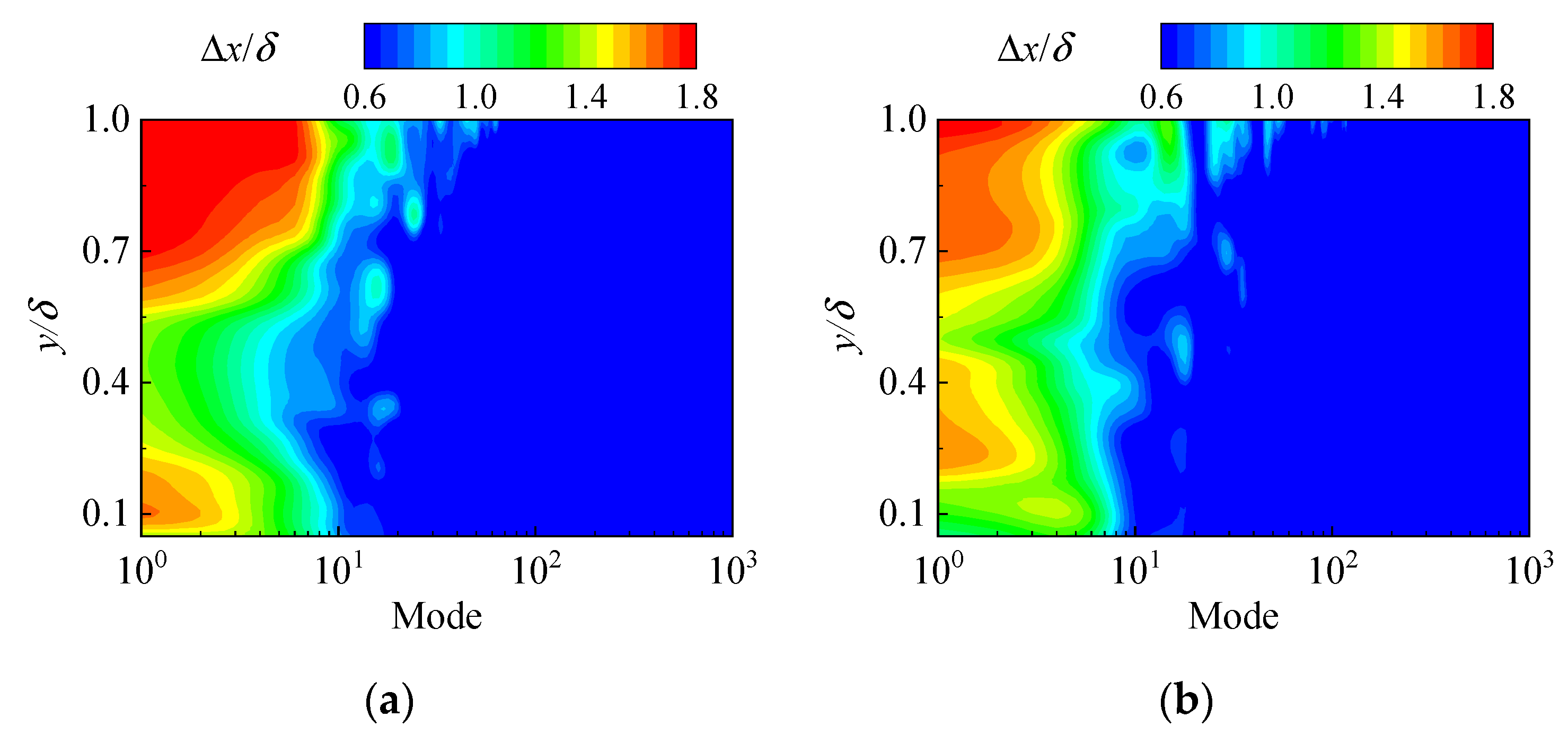
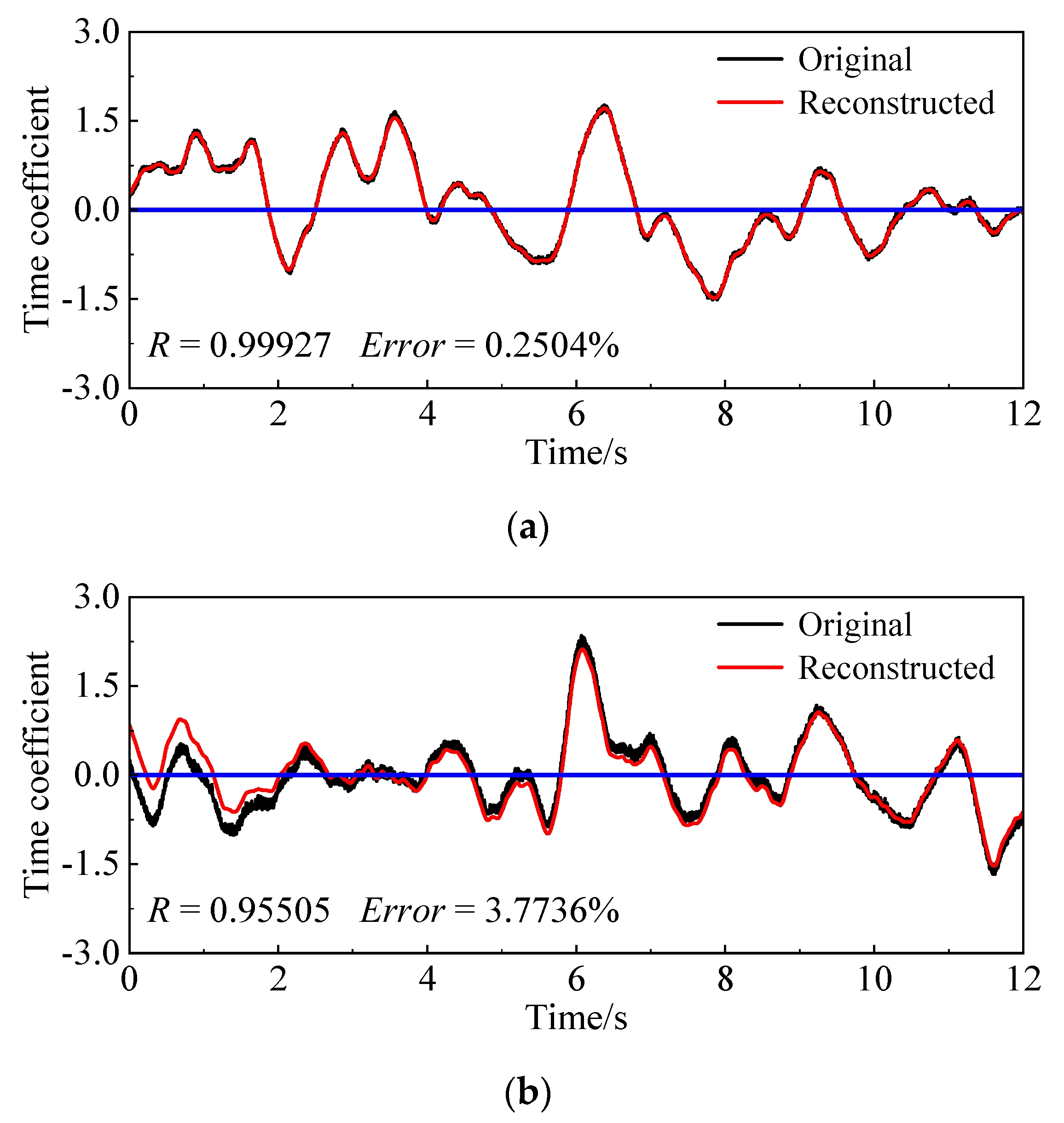
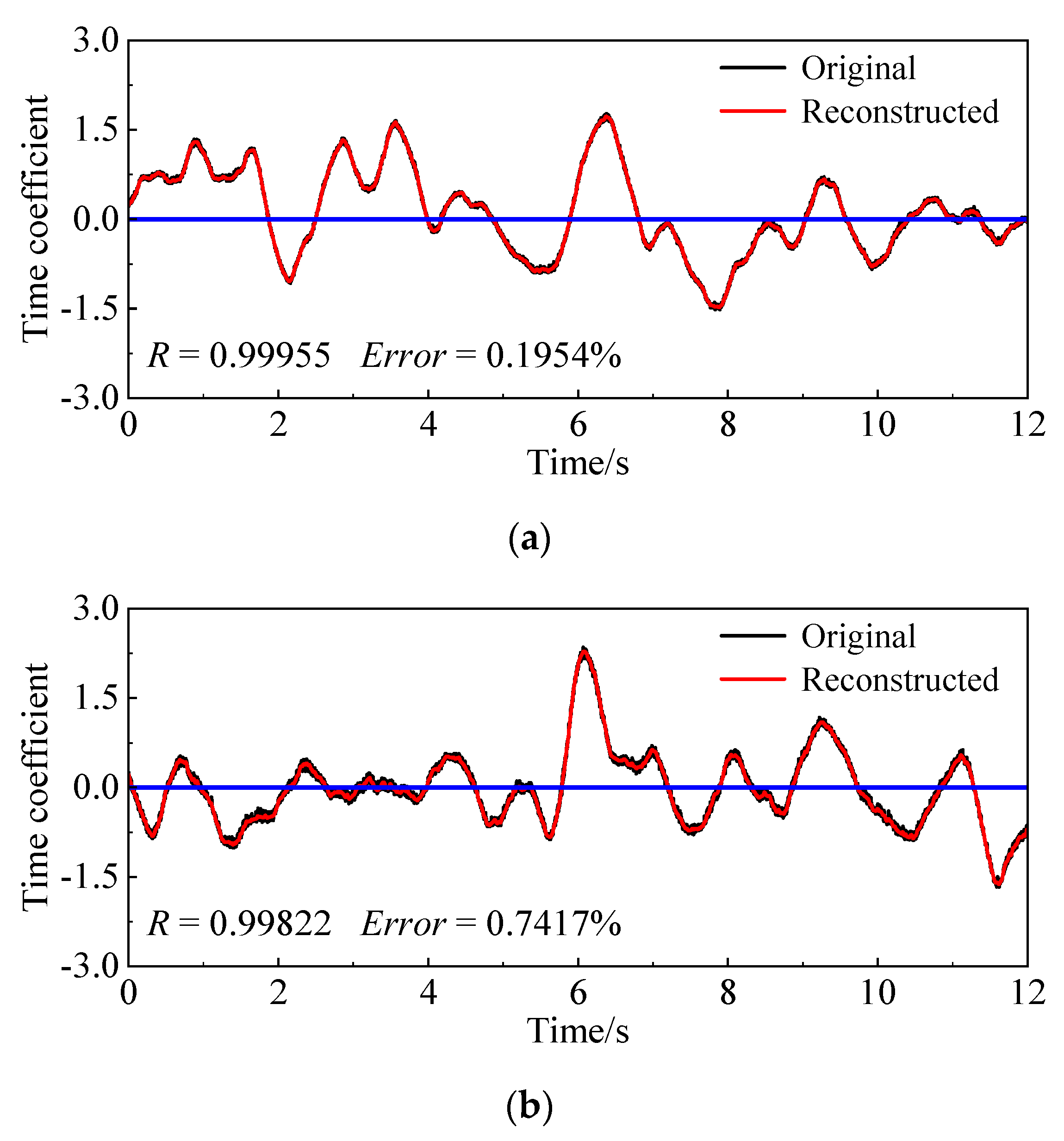
3.1. Proper Orthogonal Decomposition
- (1)
- The time series (fluctuation velocity) matrix is expressed as:
- (2)
- Solving the eigenvectors and eigenvalues of the correlation matrix:
- (3)
- The basis function for POD mode is written as:
- (4)
- The time coefficient (expansion coefficient) of each mode will be realized as:
- (5)
- Reconstructing the fluctuating velocity field:
- (6)
- Single-order mode turbulent kinetic energy ratio:
- (7)
- The proportion of cumulative energy is defined as:
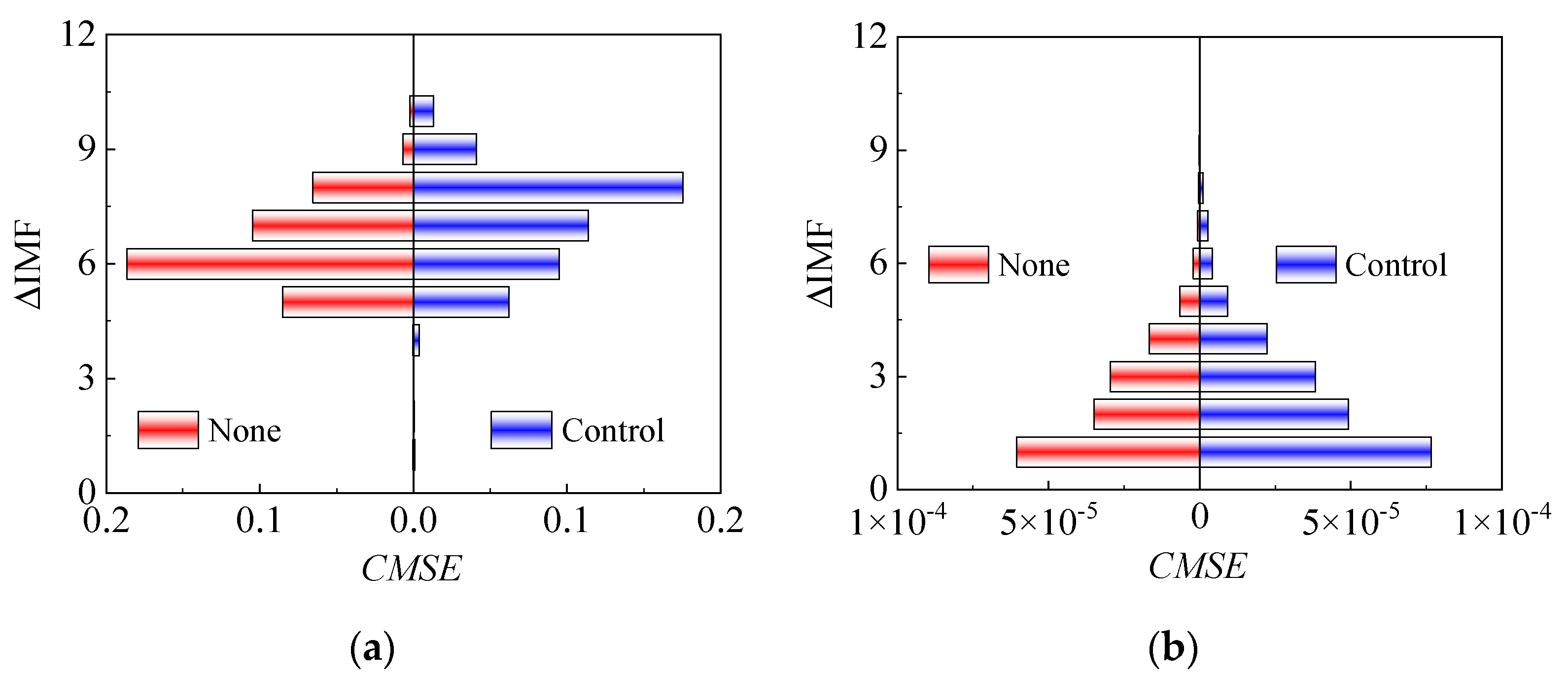
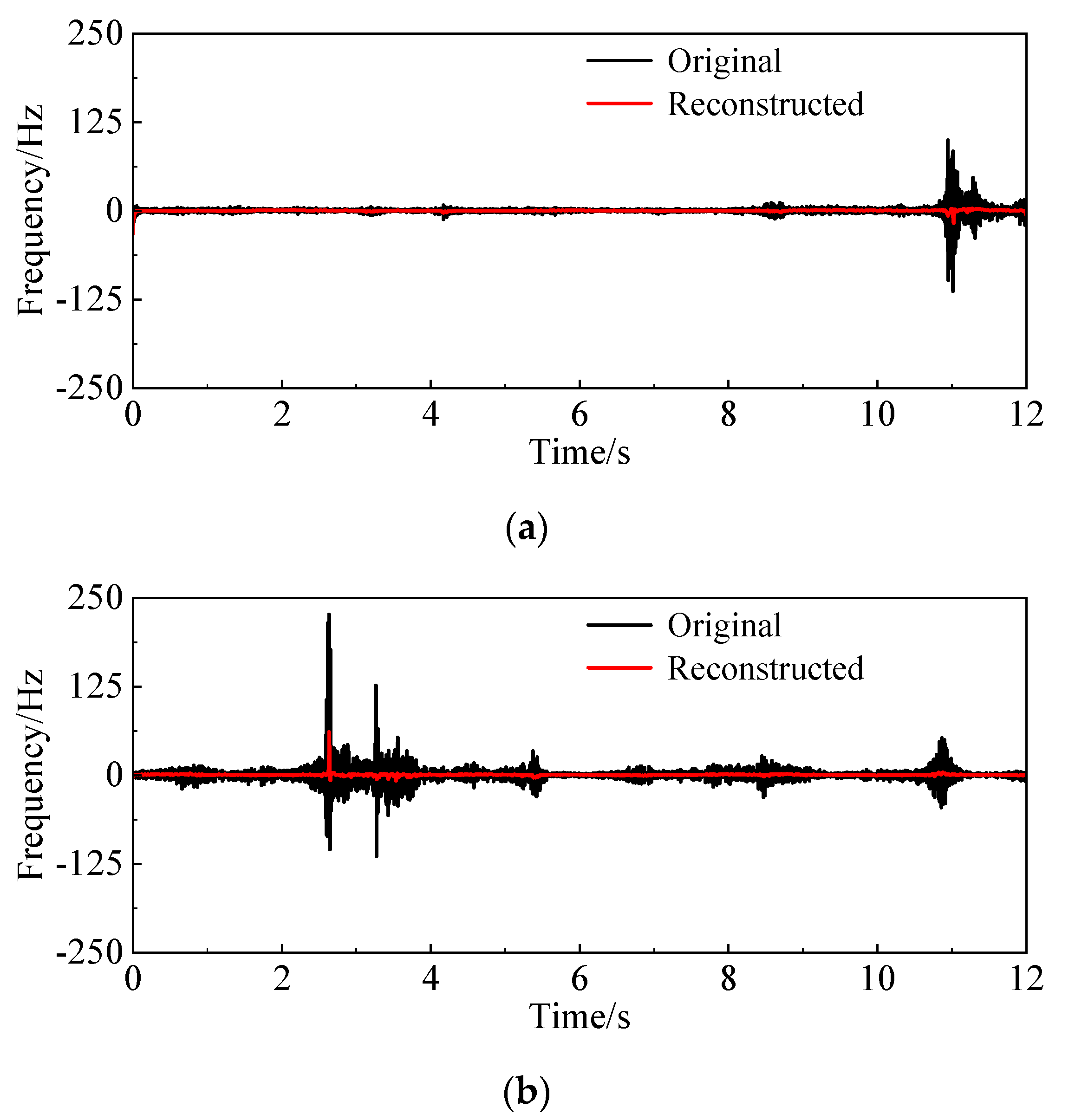
3.2. Complementary Ensemble Empirical Mode Decomposition
- (1)
- Setting the number of processing times h for the original signal;
- (2)
- A pair of positive and negative white noises that are opposite to each other are added to h source signals to form a series of new signals;
- (3)
- Two groups of IMFs will be obtained by performing EMD analysis of the new signals after addition and subtraction of white noise;
- (4)
- The mean value of the h group IMFs of the corresponding mode can be calculated to complete the decomposition.
4. Conclusions
- (1)
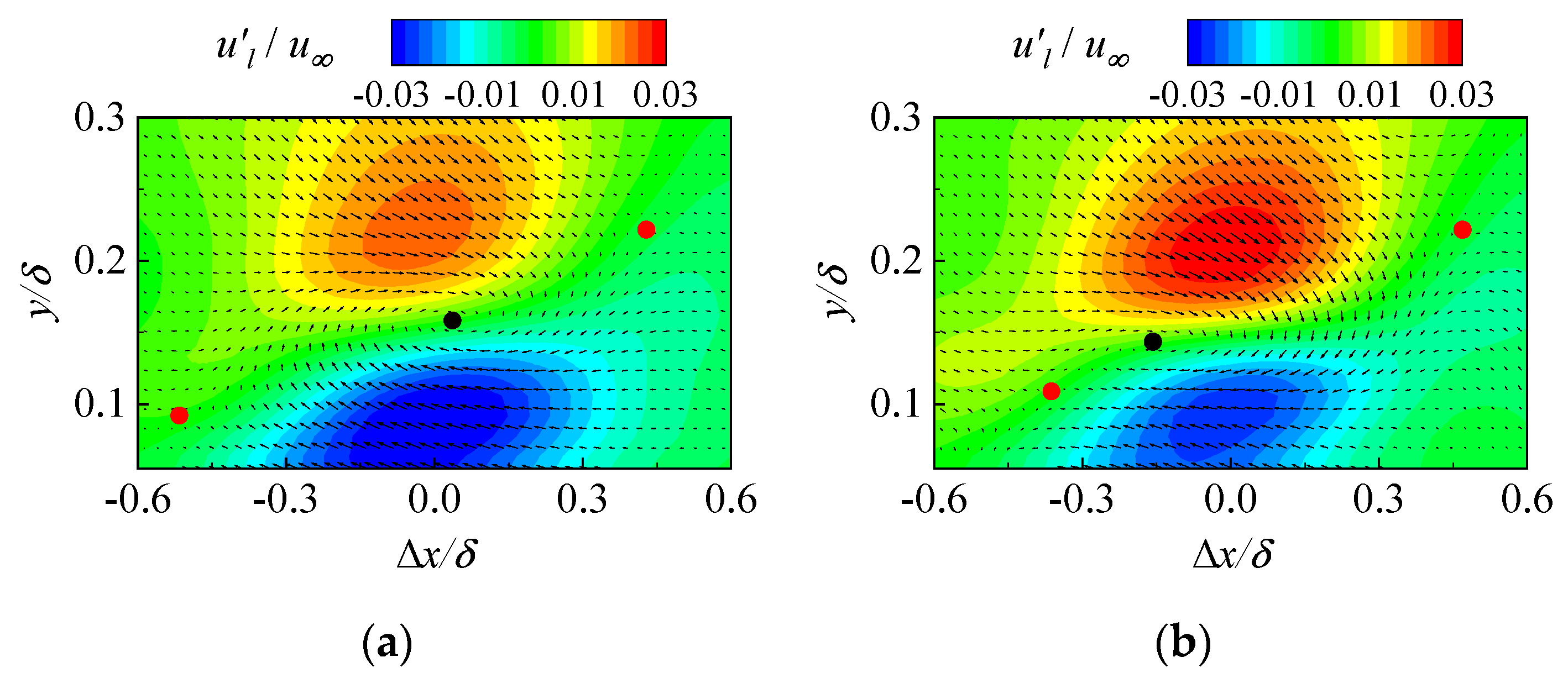
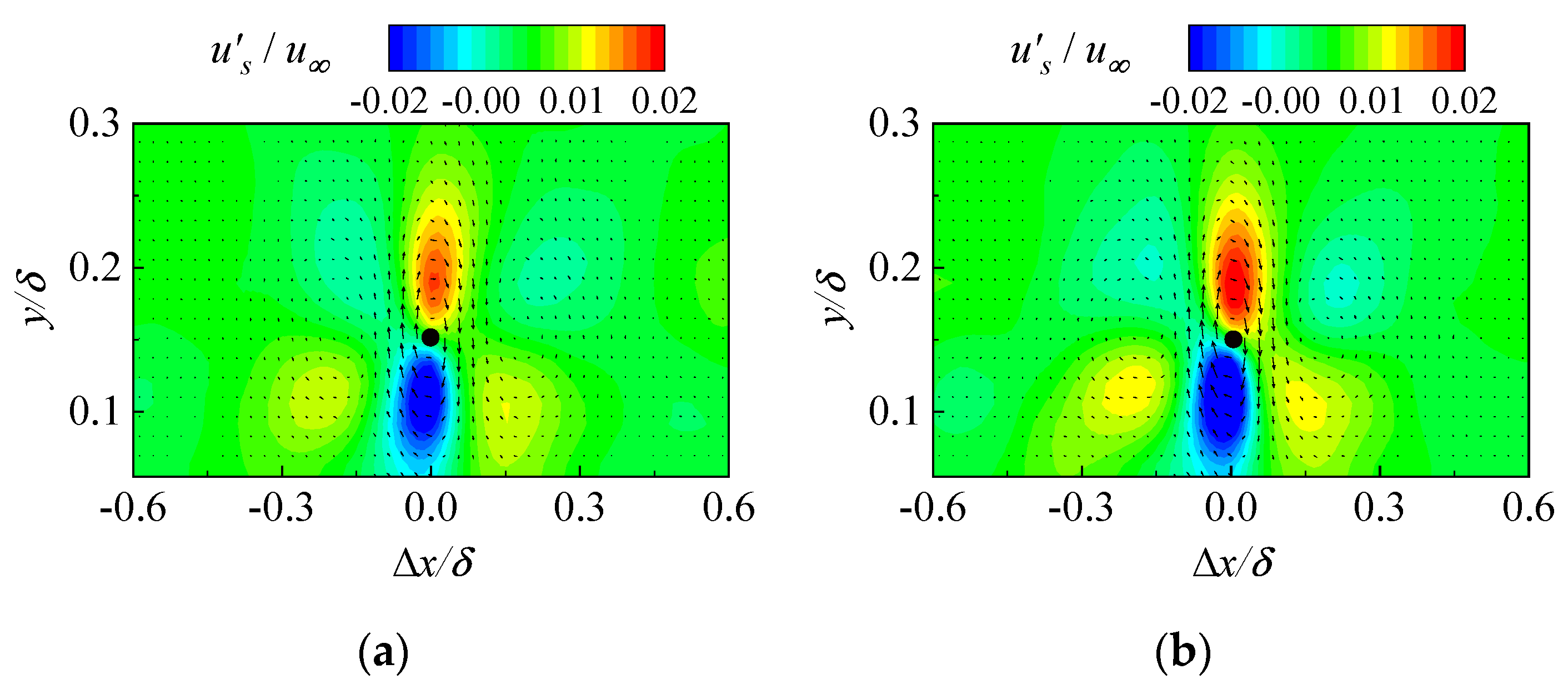
- Due to the action of the wall-normal blowing of the submerged synthetic jet, the large-scale hairpin vortex is far away from the near-wall region, and its ability to induce the low-speed fluid is highly dropped off, and the probability and intensity of near-wall burst events are suppressed.
- (2)
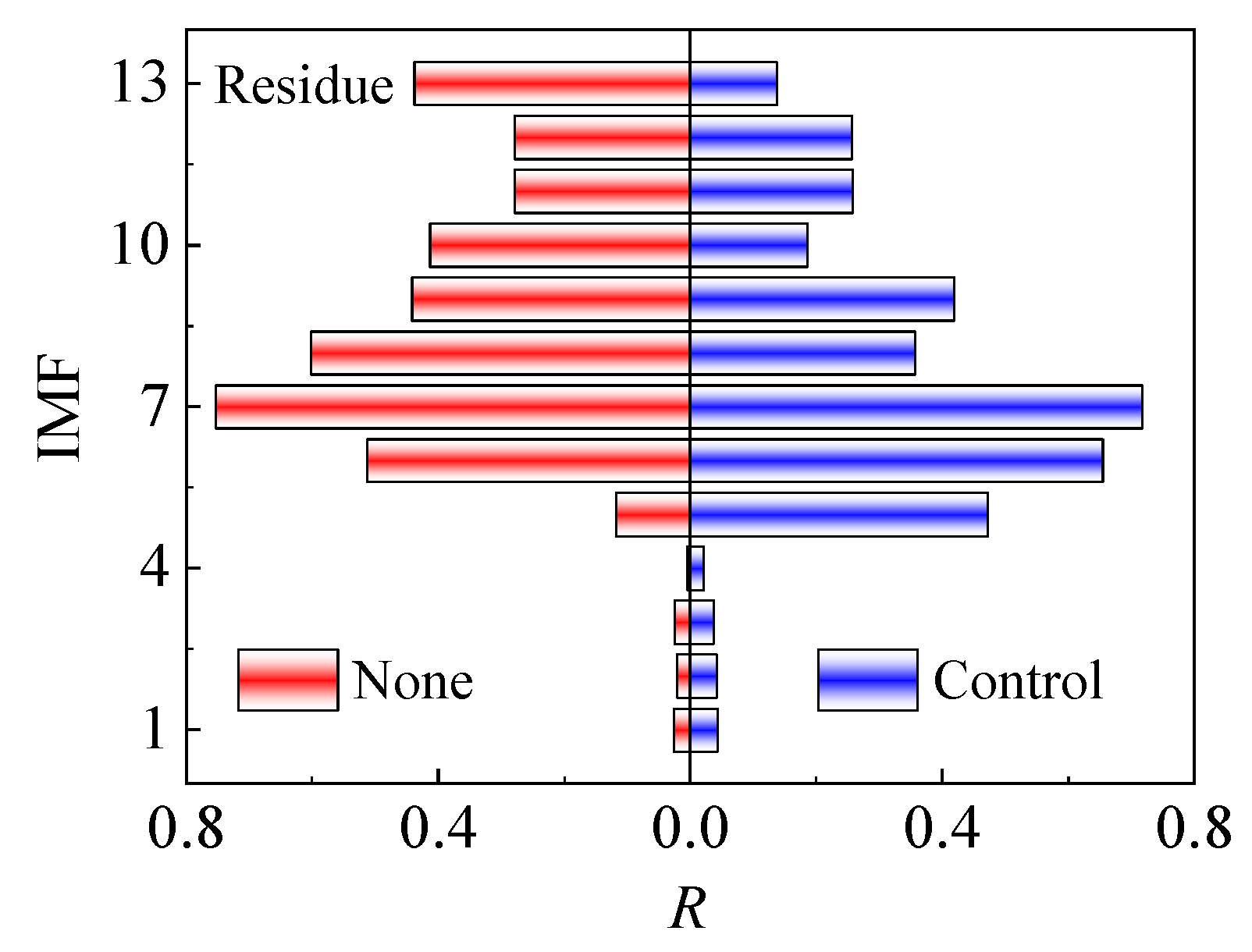
- The large-scale coherent structures in the TBL are dominated by low-frequency signals, while the small-scale coherent structures are related to high-frequency signals. The periodic disturbance generated by the synthetic jet accelerates the migration of low-frequency signals to high-frequency signals.
- (3)
- In the TBL, the probability of low-order modes (large-scale turbulent events) is high, the information entropy is small, and the events are ordered; the probability of high-order modes (small-scale turbulent events) is low, the information entropy is large, and the events are disorderly. The presence of the synthetic jet makes the large-scale turbulent structures become orderly and the small-scale turbulent structures tend to be disordered.
- (4)
- The time coefficients acquired by POD can be analyzed through CEEMD and then combined with the help of CMSE to identify the energy mutation of high- and low frequency signals. Finally, the large-scale flow field will be reconstructed. The advantage of this scale decomposition method is the fact that it can avoid the interference of artificial threshold setting.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, L.; Shan, X.; Xie, T. Active control for wall drag reduction: Methods, mechanisms and performance. IEEE Access 2020, 8, 7039–7057. [Google Scholar] [CrossRef]
- Perlin, M.; Dowling, D.R.; Ceccio, S.L. Freeman Scholar Review: Passive and Active Skin-Friction Drag Reduction in Turbulent Boundary Layers. J. Fluids Eng. 2016, 138, 091104. [Google Scholar] [CrossRef]
- Abbas, A.; Bugeda, G.; Ferrer, E.; Fu, S.; Periaux, J.; Pons-Prats, J.; Valero, E.; Zheng, Y. Drag reduction via turbulent boundary layer flow control. Sci. China Technol. Sci. 2017, 60, 1281–1290. [Google Scholar] [CrossRef]
- Yunqing, G.; Tao, L.; Jiegang, M.; Zhengzan, S.; Peijian, Z. Analysis of drag reduction methods and mechanisms of turbulent. Appl. Bionics Biomech. 2017, 2017, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Corke, T.C.; Thomas, F.O. Active and passive turbulent boundary-layer drag reduction. AIAA J. 2018, 56, 3835–3847. [Google Scholar] [CrossRef]
- Kametani, Y.; Fukagata, K.; Örlü, R.; Schlatter, P. Effect of uniform blowing/suction in a turbulent boundary layer at moderate Reynolds number. Int. J. Heat Fluid Flow. 2015, 55, 132–142. [Google Scholar] [CrossRef]
- Murugan, T.; Deyashi, M.; Dey, S.; Rana, S.C.; Chatterjee, P.K. Recent developments on synthetic jets (Review Paper). Def. Sci. J. 2016, 66, 489–498. [Google Scholar] [CrossRef]
- Ricco, P.; Skote, M.; Leschziner, M.A. A review of turbulent skin-friction drag reduction by near-wall transverse forcing. Prog. Aerosp. Sci. 2021, 123, 100713. [Google Scholar] [CrossRef]
- Iuso, G.; Di Cicca, G.M. Interaction of synthetic jets with a fully developed turbulent channel flow. J. Turbul. 2007, 8, 1–33. [Google Scholar] [CrossRef]
- Yao, J.; Chen, X.; Hussain, F. Drag control in wall-bounded turbulent flows via spanwise opposed wall-jet forcing. J. Fluid Mech. 2018, 852, 678–709. [Google Scholar] [CrossRef]
- Thomas, F.; Corke, T.; Duong, A.; Midya, S.; Yates, K. Turbulent drag reduction using pulsed-DC plasma actuation. J. Phys. D Appl. Phys. 2019, 52, 434001. [Google Scholar] [CrossRef]
- Cannata, M.; Cafiero, G.; Iuso, G. Large-scale forcing of a turbulent channel flow through spanwise synthetic jets. AIAA J. 2020, 58, 2042–2052. [Google Scholar] [CrossRef]
- Xie, F.; Pérez-Muñoz, J.D.; Qin, N.; Ricco, P. Drag reduction in wall-bounded turbulence by synthetic jet sheets. J. Fluid Mech. 2022, 941, A63. [Google Scholar] [CrossRef]
- Tian, G.Z.; Fan, D.L.; Feng, X.M.; Zhou, H.G. Thriving artificial underwater drag-reduction materials inspired from aquatic animals: Progresses and challenges. RSC Adv. 2021, 11, 3399–3428. [Google Scholar] [CrossRef] [PubMed]
- Segawa, T.; Li, F.-C.; Yoshida, H.; Murakami, K.; Mizunuma, H. Spanwise oscillating excitation for turbulence drag reduction using alternative suction and blowing. In Proceedings of the 43rd AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 10–13 January 2005. [Google Scholar] [CrossRef]
- Spinosa, E.; Zhong, S. Reduction of skin friction drag in a turbulent boundary layer using circular synthetic jets. In Proceedings of the 55th AIAA Aerospace Sciences Meeting, Grapevine, Texas, 9–13 January 2017. [Google Scholar]
- Marusic, I.; McKeon, B.J.; Monkewitz, P.A.; Nagib, H.M.; Smits, A.J.; Sreenivasan, K.R. Wall-bounded turbulent flows at high Reynolds numbers: Recent advances and key issues. Phys. Fluids. 2010, 22, 065103. [Google Scholar] [CrossRef]
- Li, B.; Zhang, J.; Tian, H.; Ma, X.; Tang, Z.; Jiang, N. Effects of submerged synthetic jet on the coherent structures in turbulent boundary layer. Acta Mech. Sin. 2022, 38, 321590. [Google Scholar] [CrossRef]
- Taira, K.; Hemati, M.S.; Brunton, S.L.; Sun, Y.Y.; Duraisamy, K.; Bagheri, S.; Dawson, S.T.M.; Yeh, C.A. Modal Analysis of Fluid Flows: Applications and Outlook. AIAA J. 2020, 58, 998–1022. [Google Scholar] [CrossRef]
- Wang, X.; Wang, Y.; Tian, H.; Jiang, N. Effects of the slip wall on the drag and coherent structures of turbulent boundary layer. Acta Mech. Sin. 2021, 37, 1278–1290. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 623–656. [Google Scholar] [CrossRef]
- Kullback, S.; Leibler, R.A. On information and sufficiency. Ann. Math. Stat. 1951, 22, 79–86. [Google Scholar] [CrossRef]
- Wu, Y.; Christensen, K.T. Spatial structure of a turbulent boundary layer with irregular surface roughness. J. Fluid Mech. 2010, 655, 380–418. [Google Scholar] [CrossRef]
- Zhou, J.; Adrian, R.J.; Balachandar, S.; Kendall, T.M. Mechanisms for generating coherent packets of hairpin vortices in channel flow. J. Fluid Mech. 1999, 387, 353–396. [Google Scholar] [CrossRef]
- Fukagata, K.; Iwamoto, K.; Kasagi, N. Contribution of Reynolds stress distribution to the skin friction in wall-bounded flows. Phys. Fluids. 2002, 14, L73–L76. [Google Scholar] [CrossRef]
- Yang, S.Q.; Jiang, N. Tomographic TR-PIV measurement of coherent structure spatial topology utilizing an improved quadrant splitting method. Sci. China Phys. Mech. Astron. 2012, 55, 1863–1872. [Google Scholar] [CrossRef][Green Version]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Huang, N.E.; Wu, M.L.; Qu, W.; Long, S.R.; Shen, S.S.P. Applications of Hilbert-Huang transform to non-stationary financial time series analysis. Appl. Stoch. Models Bus. Ind. 2010, 19, 245–268. [Google Scholar] [CrossRef]
- Yeh, J.R.; Shieh, J.S.; Huang, N.E. Complementary ensemble empirical mode decomposition: A novel noise enhanced data analysis method. Adv. Adapt. Data Anal. 2010, 2, 135–156. [Google Scholar] [CrossRef]
- Wu, H.; Fang, Q.; Peng, Y.; Gong, Z.M.; Kong, X.Z. Hard projectile perforation on the monolithic and segmented RC panels with a rear steel liner. Int. J. Impact Eng. 2015, 76, 232–250. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R. A new view of nonlinear water waves: The Hilbert spectrum. Annu. Rev. Fluid Mech. 1999, 31, 417–457. [Google Scholar] [CrossRef]
- Tang, Z.; Jiang, N.; Schröder, A.; Geisler, R. Tomographic PIV investigation of coherent structures in a turbulent boundary layer flow. Acta Mech. Sin. 2012, 28, 572–582. [Google Scholar] [CrossRef]
- Yang, S.; Li, S.; Tian, H.; Wang, Q.; Jiang, N. Coherent spanwise structures in turbulent boundary layer over drag-reducing riblets. Trans. Tianjin Univ. 2015, 21, 317–323. [Google Scholar] [CrossRef]
- Tian, H.; Zhang, J.; Wang, E.; Yao, Z.; Jiang, N. Experimental investigation on drag reduction in turbulent boundary layer over superhydrophobic surface by TRPIV. Theor. Appl. Mech. Lett. 2015, 5, 45–49. [Google Scholar] [CrossRef]


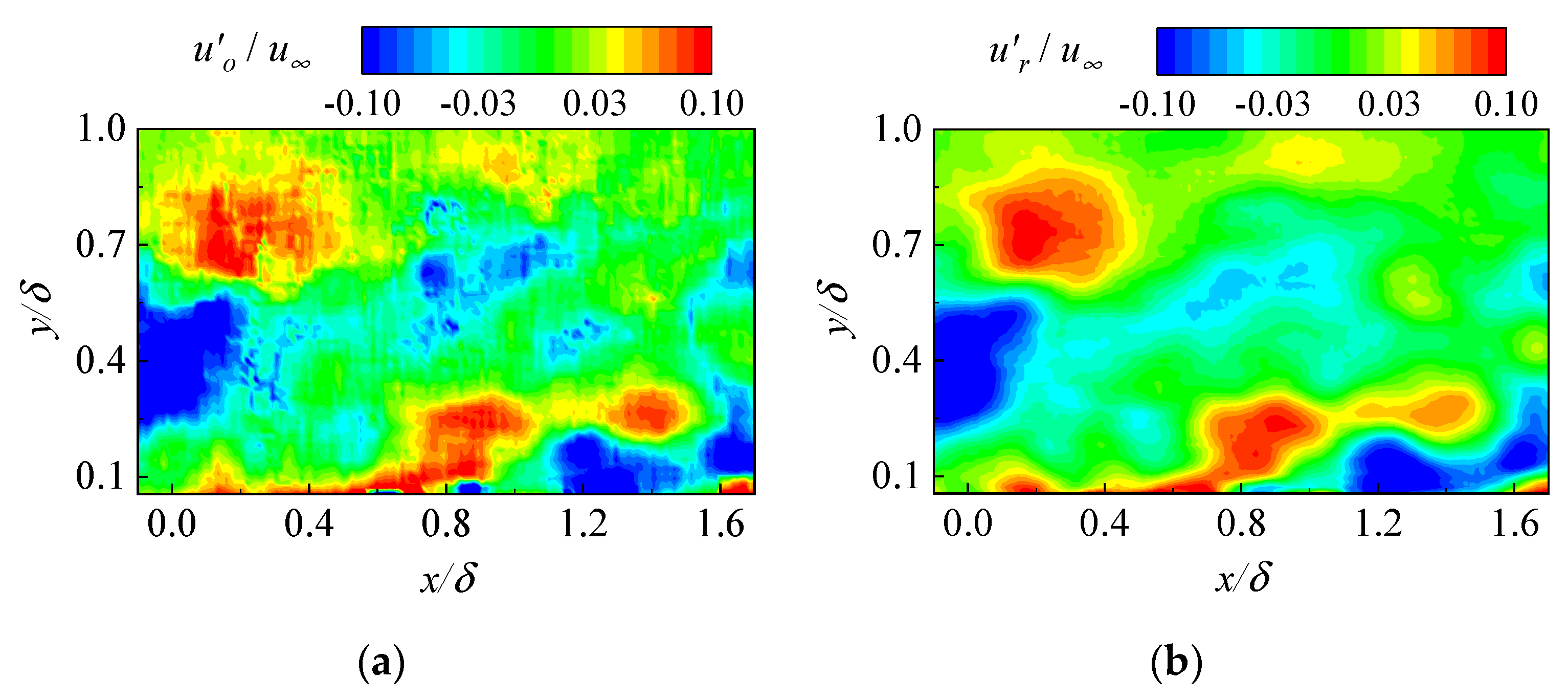
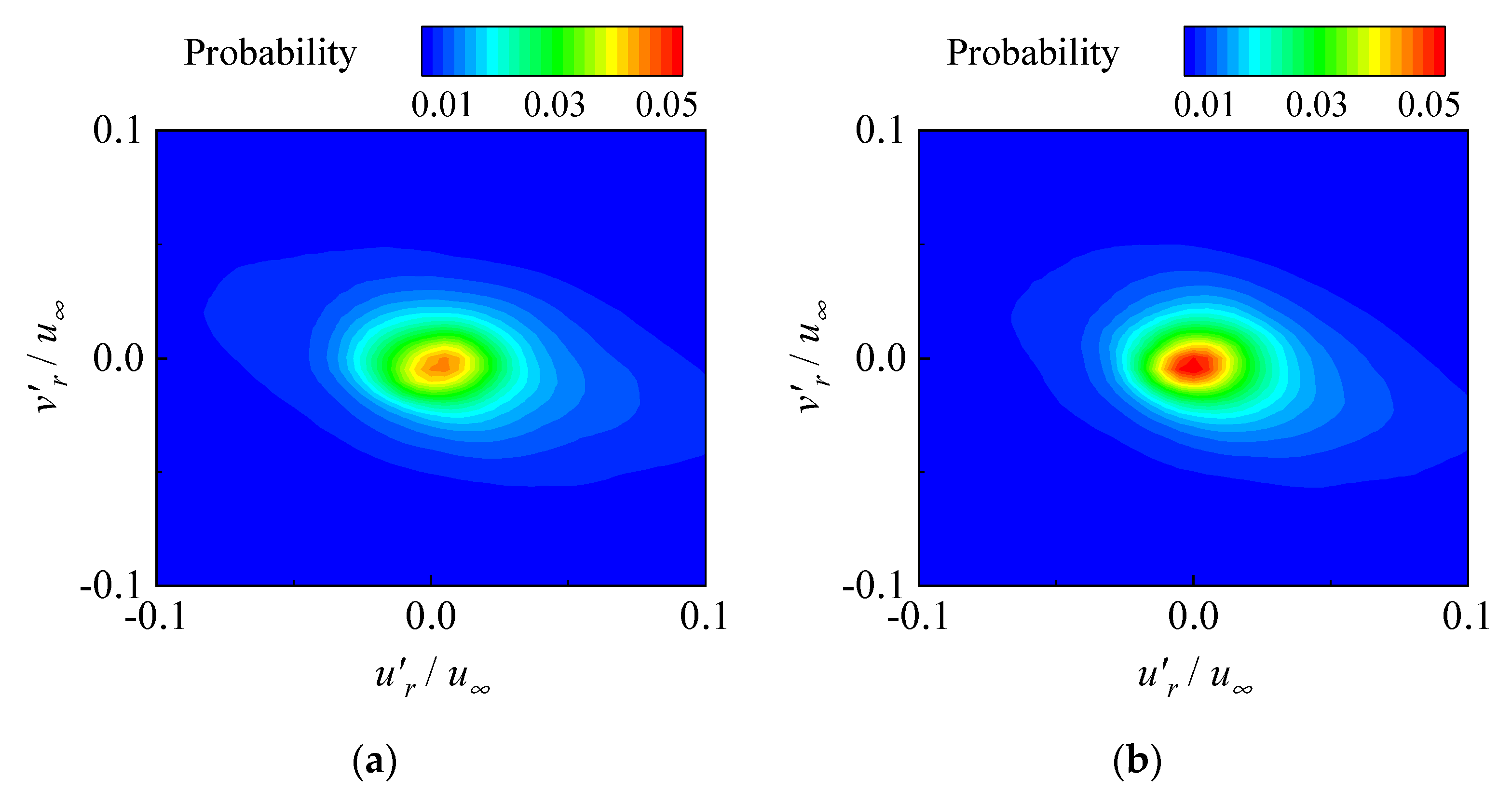
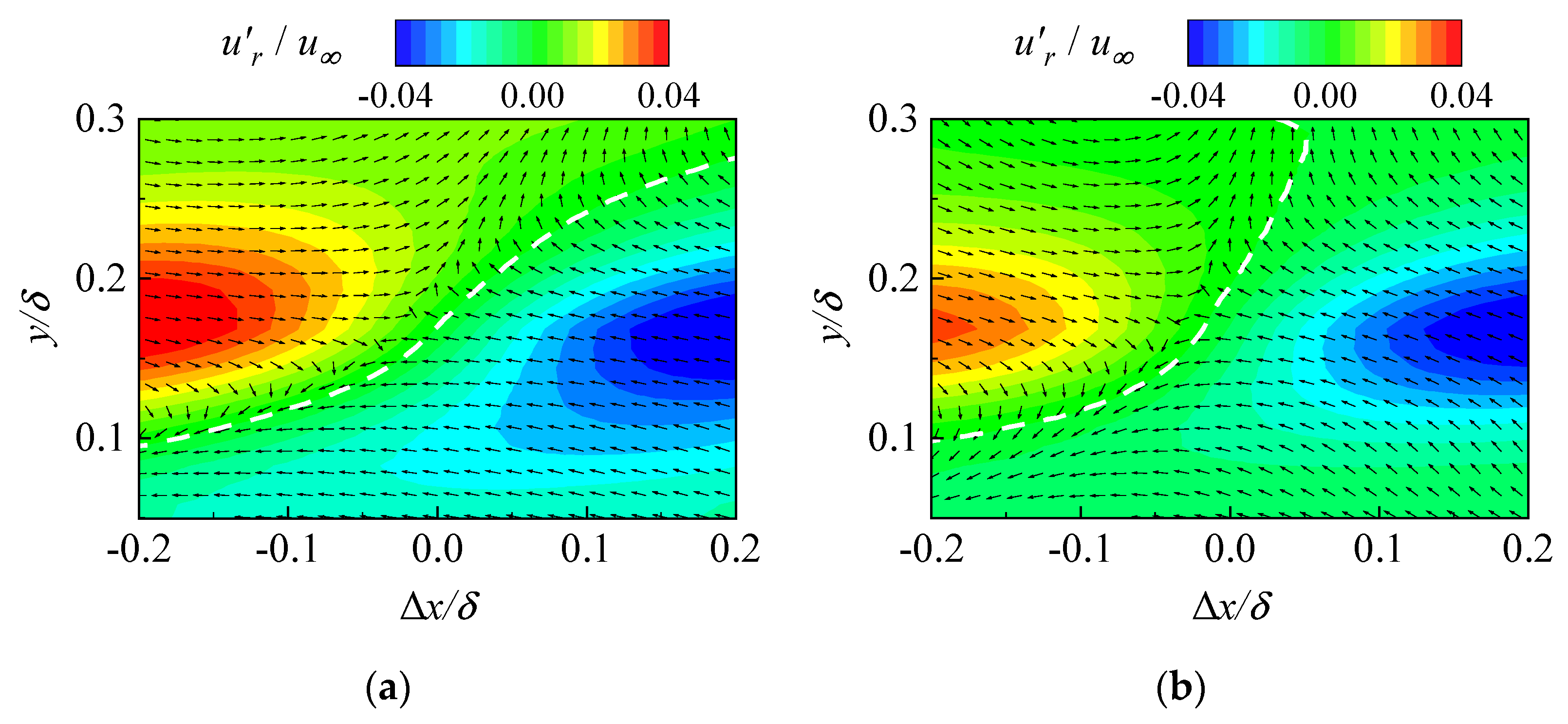
| Parameter | Value |
|---|---|
| Field of view | 99.97 mm × 62.48 mm |
| Sampling frequency | 600 Hz |
| Resolution | 1280 pixels × 800 pixels |
| Number of pictures | 8216 × 5 |
| Scale factor | 0.0781 mm/pix |
| Interrogation window | 32 pixels × 32 pixels, 75% overlap |
| Vector pitch | 0.6248 mm |
| 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | 1.0 | |
|---|---|---|---|---|---|---|
| None | 0 | 0 | 0 | 0 | 28 | 7992 |
| Control | 1 | 2 | 11 | 20 | 59 | 8003 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, B.; Zhang, J.; Jiang, N. Influence of Synthetic Jets on Multiscale Features in Wall-Bounded Turbulence. Actuators 2022, 11, 199. https://doi.org/10.3390/act11070199
Li B, Zhang J, Jiang N. Influence of Synthetic Jets on Multiscale Features in Wall-Bounded Turbulence. Actuators. 2022; 11(7):199. https://doi.org/10.3390/act11070199
Chicago/Turabian StyleLi, Biaohui, Jinhao Zhang, and Nan Jiang. 2022. "Influence of Synthetic Jets on Multiscale Features in Wall-Bounded Turbulence" Actuators 11, no. 7: 199. https://doi.org/10.3390/act11070199
APA StyleLi, B., Zhang, J., & Jiang, N. (2022). Influence of Synthetic Jets on Multiscale Features in Wall-Bounded Turbulence. Actuators, 11(7), 199. https://doi.org/10.3390/act11070199






