Abstract
To maintain the safe operation and acceptable performance of robot manipulators when faults occur inside the system, fault-tolerant control must deal differently uncertainties and disturbances, especially with the occurrence of loss-effective faults. Therefore, in this paper, an active fault-tolerant control for robot manipulators based on the combination of a novel finite-time synchronous fast terminal sliding mode control and extended state observer is proposed. Due to the internal constraints of the synchronization technique, the position error at each actuator simultaneously approaches zero and tends to be equal. Therefore, the proposed controller can suppress the effects of faults and guarantee the acceptable performance of robot manipulators when faults occur. First, an extended state observer is designed to estimate the lumped uncertainties, disturbance and faults. Then, the information from the observer is used to combine with the main novel synchronous fast terminal sliding mode controller as a compensator. By combining the merits of the observer compensation, sliding mode and synchronization technique, the proposed fault-tolerant controller is able to deal with uncertainties and disturbances in normal operation mode and reduce the effects of faults in case faults occur, especially in the occurrence of loss-effective faults. Finally, the enhanced safety, reality and effectiveness of the proposed fault-tolerant control are evaluated through the control of a 3-DOF robot manipulator in both a simulated environment and experiment.
1. Introduction
At present, robot manipulators play an important role in the manufacturing industry and in daily life. In parallel with the development of hardware and advantageous control technology, robot manipulators are required to enhance safety in all situations. Safety is a key role when robots share the workspace with humans or cooperate with humans. Therefore, fault-tolerant control (FTC) was introduced to increase safety and acceptable performance when faults occur in the system. Generally, AFTC can be divided into two main types: (1) active FTC (AFTC) [1,2,3] and (2) passive FTC (PFTC) [4,5,6]. Each FTC strategy has advantages and disadvantages depending on the characteristics of the system, the knowledge about the system, and the types of faults. FTC became very important in the systems with human application systems such as aircraft [2], human robot interaction [7], and wearable systems [8] which require high safety and reliability.
In robot manipulator systems, PFTC has a simple architecture with one controller for both normal and fault conditions. PFTC responds quickly to faults due to the elimination of a fault diagnosis process. Some techniques have been classified into PFTC such as sliding mode control (SMC) [9,10], adaptive control [11,12,13], and so on. For instance, the SMC [10] is widely known due to its robustness and ability to deal with uncertainties and disturbances. In order to guarantee the stability of systems, the design of the SMC required the upper-bound knowledge of faults which is difficult to gain in a real system. Therefore, PFTC with SMC is less flexible and limited to tolerating the fault’s capability in real systems. The second PFTC technique is adaptive control which does not need exact knowledge of faults, but the excessive adaptation rate is a problem with this kind of controller. From the above analyses, it can be seen that PFTC has the advantage in the case of the systems with a good knowledge about the upper bound of uncertainties, disturbances and faults. In contrast, to guarantee the stability and acceptable performance of a system, AFTC uses fault detection and fault diagnosis (FDD) to compensate for the normal controller. In AFTC, the FDD process is a very important process which leads to increasing the ability of tolerating faults. Therefore, FDD [14,15,16,17] has been developed with several techniques. The advantage of the AFTC strategy is it has a strong ability to deal with high-magnitude faults and multiple faults. In addition, the upper bound of faults does not require being exactly known in the same way as PFTC does. However, this strategy slowly responds to faults because the FDD process needs time to feed back the information of faults as well as the time delay problem in a real system. Hence, the performance of AFTC is affected. In a real system, the degradation performance of AFTC can be obtained by the occurrence of the picking phenomenon due to the slow response of AFTC and high magnitude of uncertainties and disturbances. In robot manipulator systems, the FDD has been widely replaced by the fault estimation process (FE) which uses fault detection, fault isolation and fault diagnosis within one step. The structure controller is combined with the estimator and is known as disturbance observer base (DOB). The difference between DOB and AFTC with the estimator is that in AFTC with an estimator, the output value is used to compare the threshold to detect faults and isolation faults. It warns the operator about the occurrence of faults to make the effective action. The AFTC with a structure of DOB control (AFTC-DOB) [18,19,20] may have an effect in the case of bias faults. These kinds of faults can be considered as uncertainties or disturbances so that the AFTC-DOB can show acceptable performance depending on the accuracy of the estimator. However, with the loss-effective fault or the combination of loss-effective and bias faults, using merely AFTC-DOB may not reduce the effect of this kind of fault. Hence, AFTC needs a different way to handle the faults due to the occurrence of loss-effective faults. Most of the research studies on FTC [1,9,21,22] focus on the development of the ability to deal with the uncertainties and disturbances or handle the conventional problems of controllers such as the chattering phenomenon or the fast convergence problem. However, they lack the picking phenomenon of the AFTC strategy which has the most impact in degrading the performance of AFTC. Therefore, in this paper, the synchronization technique is proposed to suppress the picking phenomenon when faults occur, especially with the occurrence of loss-effective for the AFTC strategy.
In the field of control, the synchronization control has been widely known with a closed-loop chain mechanism such as the dual-drive gantry mechanism [23], parallel robot manipulator [24], cable-driver parallel manipulator [25], cooperation robot manipulator [26], and so on. These systems have an internal tensor force during the motion due to the closed-loop mechanism. This kind of force can degrade the performance of systems. By using the synchronization technique, the controller makes the position errors at each joint simultaneously approach zero and reduce the internal tensor force. Therefore, the accuracy of systems can be increased. Unlike a closed-loop mechanism, a serial robot manipulator does not contain an internal tensor force. Due to the open-loop mechanism, this internal uncertainty can be compensated by the consideration of a dynamic model. Therefore, the synchronization technique does not show an advantage compared the model-based controller such as DOB in normal operation. However, the ability to make the position error simultaneously equal to and approach zero still remains in an open-loop mechanism with the synchronization technique. In case faults occur, the internal constraints of the synchronization control to keep the error at each joint equal may suppress the effect of the faults. The synchronization controller increases the ability to quickly respond to the controller before it receives the feedback information of faults from FDD or FE. In [27], the authors first proposed the synchronization technique to reduce the effect of faults. In this study, the experimental results showed the outperformance of the proposed controller. However, it can be seen that the proposed controller in [27] did not consider the finite-time convergence issue. In [28], the finite-time synchronization controller was addressed with two proposed controllers. With the first controller in [28,27], it is unclear whether the ability to reduce the effect of faults comes from the synchronization technique or from the integral term of the cross-coupling technique in the design-sliding surface. In [28], the second proposed controller showed the effectiveness of the synchronization technique without the cross-coupling technique. Motivated by that proposed controller, in this paper, a novel AFTC with a finite-time synchronous fast terminal sliding mode control is proposed. In addition, the analysis of synchronization parameters is presented to show the effect of the synchronization technique in fault-tolerant control. In this paper, the picking phenomenon is the specific problem of the AFTC strategy which is analyzed and considered. Then, it can be tackled by using the synchronization technique to guarantee the acceptable performance of a robot manipulator when faults occur. Due to the internal constraints of position error at each joint of the synchronization technique, the proposed controller can reduce the picking effect before the FE receives the information of faults.
In this paper, AFTC using the combination of an extended state observer and novel finite-time synchronous faster terminal sliding mode control is proposed. Firstly, an extended state observer (ESO) [29] is adopted to estimate the lumped uncertainties, disturbances, and faults. The observer has a role as the FDD includes fault detection, fault isolation, and fault estimation within one step. In addition, by using a high-gain technique, the ESO does not require the upper bound information of faults and simple adjustment of the observer parameter. Therefore, the ESO can easily apply in real robot manipulator systems. Next, an AFTC with a novel synchronous fast terminal sliding mode control is proposed without the cross-coupling technique. The synchronization error in [28] was used to guarantee the finite-time convergence of position error at each joint. Finally, the proposed controller is verified on a 3-DOF robot manipulator in simulations and experiments. The results of the proposed control are compared to AFTC with conventional fast terminal sliding mode control [30]. In addition, the analysis effect of synchronization parameters to the fault-tolerant control is presented in a real implementation system. The contribution of this paper can be summarized as follows:
(1) An active fault-tolerant control based on the combination of novel finite-time synchronous fast terminal sliding mode control and an extended state observer is proposed. The proposed control has the ability to quickly respond to faults, before the controller has the feedback information of faults from fault estimation due to the internal constraints of the synchronization technique. Therefore, the proposed control can reduce the picking phenomenon and suppress the effect of faults to show an acceptable performance when it is compared to AFTC with conventional finite-time fast terminal sliding mode control [30]. The proposed controller has the ability to maintain the accepted performance with the occurrence of faults in the system until the maintenance.
(2) By using a novel finite-time synchronous fast terminal sliding surface without the coupling technique, the proposed controller has fast computation, avoids oscillation due to the integral term, and guarantees the finite-time convergence of the position error at each joint compared [27].
(3) The analysis of synchronization parameters is presented to show the effect and behavior of the synchronization technique in fault-tolerant control. Unlike the conventional AFTC controller, the proposed controller can make the error at each joint simultaneously approach zero. This feature can reduce the effect of fault in the robot systems.
(4) Comparing the proposed controller in this paper with the first controller in [28], it can be seen that without the conventional coupling technique, the proposed AFTC can reduce the time computation, avoid the oscillation due to the integral term, and guarantee the finite-time convergence of position errors and fast convergence. In addition, the proposed control in this paper converges faster than the two synchronous sliding mode surfaces in [28]. Therefore, in this proposed controller, the fault-tolerant controller has the ability to reduce the picking phenomenon due to the synchronous technique, as well as the time convergence, faster than in [28]. The proposed controller in this paper has more advantages than two controllers in [28] in both time convergence and time computation.
(5) The implementation of advantage control in real robot systems faces many challenges such as the noise of sensors and output actuators, time of computation, the drawbacks of the sliding mode technique in real systems, and so on. However, in this paper, the experimental results on a real 3-DOF robot manipulator demonstrated the effectiveness and ability to apply to real systems of the proposed controller.
The rest of this paper is organized as follows. In Section 2, the dynamic model of robot manipulators and faults is presented. The design of fault estimation based on an extended state observer is shown in Section 3. In Section 4, a novel finite-time synchronous fast terminal sliding mode control is proposed. The simulation results and some discussions about the effect of kinds of faults are given in Section 5. In Section 6, the experimental results are shown to verify the effectiveness of synchronization technique and the effect of synchronization parameter selection in fault-tolerant control. Finally, the conclusions are given in Section 7.
2. Dynamics Model of Robot Manipulators and Faults
2.1. Dynamics Model of Robot Manipulators
The dynamics of an n-degrees-of-freedom robot manipulator was defined as
where are the vectors of joint acceleration, velocity and position, respectively. , and represent the inertia matrix, the centripetal and Coriolis matrix, and the vector of gravitation force, respectively. is the vector of torque at the joints.
In practice, the dynamic model of robots is not known exactly, so the system in (1) can be written as
where and are unknown dynamic uncertainties and is external disturbance. are estimation values of . Thus, (2) can be simply rewritten as
where .
2.2. Mathematical Calculation of Joint Actuator Faults
In a robot manipulator, the motions of the robot are generated by a joint actuator which consist of an electronic motor, a motor driver, and a gear. In practice, the occurrence of faults/failure in the electric motor, the gear, the bearing, and the motor driver can degrade the performance of a robot manipulator. For instance, in the electric motor, the increased friction between the stator and the rotor or fault in the driver motor may decrease the motor torque. This can be considered as the loss-effective fault. Generally, the two kinds of faults which commonly occur in a robot manipulator are bias and loss-effective fault, which can be described as
where is the vector of torque at the output joint actuator. is the vector of torque at the output controller. denotes the loss-effective rate. is the vector of the bias faults. is the time of the occurrence of faults. is the identity matrix.
Substituting (4) into (3), the dynamics model of an n-degrees-of-freedom robot manipulator with actuator faults can be written as
Remark 1.
In this paper, only the loss-effective and bias faults are investigated. The loss-effective fault with and lock-in-place fault are not considered because the robot does not have the redundancy actuator, so the robot cannot tolerate those kinds of faults.
3. Fault Estimation with Extended State Observer
In this section, an extended state observer to estimate the lumped uncertainties, disturbances, and faults is presented.
The dynamic model of the robot manipulator of (5) can be rewritten as
where , represents uncertainties, disturbances, and faults or failures.
The dynamic model of (6) can be rewritten in the state space as
where , , , and .
An extended state observer [29] is given as
where and are estimates of and , respectively, and are positive constants, polynomial is Hurwitz, and .
Lemma 1
[31]. Considering a function , is Lipschitz with the respective argument
Theorem 1.
Considering the system (7) with observer (8) and satisfying , , and exist , then , and as .
Proof .
The error dynamics from (7) and (8) can be written as
We define the Lyapunov function as
where
The time derivative of V in Equation (11) is
where
and
Substituting (13) into (12)
where
From Lemma 1, we can obtain
where and we also obtain
so that
Substituting (18) into (14), we obtain
To guarantee the stability of the system, we impose so the convergence is given as
□
Remark 2.
The value of does not need to be exactly known. However, this value always exists to make sure the maximum torque generated at the actuators is able to attenuate .Therefore, robot manipulators can be controllable.
4. Active Fault-Tolerant Control with Finite-Time Synchronous Fast Terminal Sliding Mode Control
In this section, the proposed active fault-tolerant control with finite-time synchronous fast terminal sliding mode control (AFTC S-FTSMC) is presented. Some definitions will be useful in the rest of the paper.
Definition 1.
We define where and . and .
Definition 2.
We define .
Definition 3.
The time derivative of ⌈x⌋Λ is
and where .
The synchronization error [28] was given as:
where is the error at each joint, and is the corresponding positive gains. In matrix form
where , , , and
A novel synchronous fast terminal sliding mode surface is proposed as
where and are positive matrix gain. with .
The proposed active fault-tolerant control with synchronous fast terminal sliding mode (AFTC S-FTSMC) is given as
where , , , and .
Theorem 2.
The system described in (5), using the controller specified in (25), guarantees that is finite time.
Proof.
The Lyapunov function can be selected as
The time derivative of V in (26) is
Substituting (25) into (27), we have
where . When the sliding mode achieves and converges, then and , and we have:
The system in (29) has equilibrium points at . According to the definition of terminal attractors [32], we have
where .
From (5), we have at finite time. Therefore, Theorem 1 is proven. □
Remark 3.
The time convergence shows that
Time convergence :
Time convergence
where , and .
Remark 4.
A singularity may occur at in (25) when the synchronization error approaches or crosses zero. By using saturation function where , the singularity can be avoided and the system retains finite-time stability [33].
5. Simulation Results
This section, the comparison of the proposed AFTC S-FTSMC and an AFTC with the combination of an conventional fast terminal sliding mode and an extended state observer ([30]+ESO) for the 3-DOF manipulator, is presented with different kinds of faults. In this simulation, the geometry parameters from the catalog of a FARA-AT2 robot manipulator were used to establish the 3-DOF robot manipulator. In Table 1, the dynamics parameters of the robot manipulator in Solidworks are shown. From Solidworks, a 3-DOF robot manipulator was imported to Matlab environment through Simmechanics with full information of the dynamics parameters. The robot in the simulation environment was shown in Figure 1.

Table 1.
Dynamics Parameters of 3-DOF Robot Manipulator.
Figure 1.
The simulation of 3-DOF Robot Manipulator in MATLAB/Simulink.
For this trajectory-tracking simulation, the desired position trajectories at each joint are given as
The disturbance at each joint is assumed to be
The related parameters for the ESO were chosen to be , and . The controller [30]+ESO is given as:
where , , and , and . The conventional fast terminal sliding surface [30] was selected as:
The parameters for the [30]+ESO were suitably chosen as and .
The parameters for the AFTC S-FTSMC were chosen as , , , , and .
To avoid a singularity, the terms containing power in (25) and (36) were replaced with the saturation function.
where is a positive constant, and with .
To avoid chattering, the signum function in (25) and (36) was replaced with the saturation function.
where .
5.1. Simulation 1
In this subsection, the comparison of two AFTCs (AFTC S-FTSMC and [30]+ESO) is described with the combination of loss-effective and bias fault at joint 2 at the fifth second. The total torque function at each joint was assumed to be:
where and .
In Figure 2, the estimation of a fault is shown. It can be seen that the FE performance does not have high accuracy, but with that magnitude error in the FE, the sliding mode control technique can handle uncertainties or disturbances. It can be seen in Figure 3. Before the fifth second, both controllers have similar accuracy because in normal operation mode, the synchronization control does not show the effectiveness in an open-loop mechanism that serial robot manipulators do. After the fifth second, the proposed control AFTC S-FTSMC can significantly reduce the effect of the fault when compared with AFTC with [30]+ESO, because in this case, the internal constraints of the synchronization technique can suppress the effect of the fault to make the position error at each joint tend to be equal. However, the accuracy of [30]+ESO is still inside the order radian, so it can be said that [30]+ESO showed acceptable performance in this case. From these results, both controllers have the ability to guarantee an acceptable performance with this kind of fault.
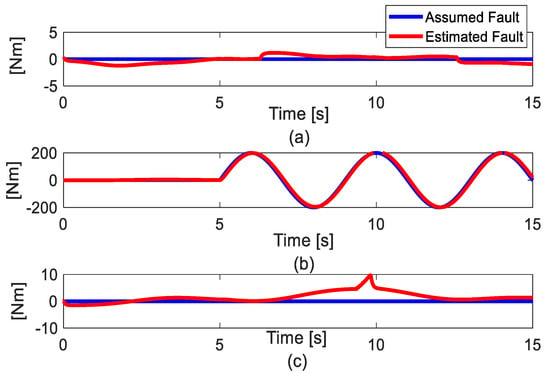
Figure 2.
Fault estimation results. (a) Joint 1; (b) Joint 2; (c) Joint 3.
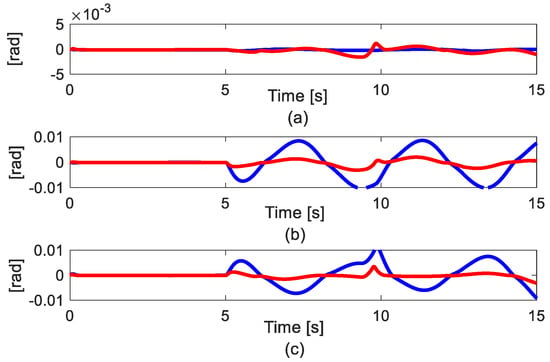
Figure 3.
Tracking error results. Blue line is [30]+ESO controller. Red line is the proposed controller. (a) Joint 1; (b) Joint 2; (c) Joint (3).
5.2. Simulation 2
In this subsection, the total two kinds of actuator fault with a similar magnitude of fault to Simulation 1 are considered. The assumed fault function is shown as
where and .
In Figure 4, the magnitude of fault is similar to the case in Simulation 1, but in this case, the effect of actuator loss-effective fault is considered. In Figure 5, after the fifth second, by using AFTC with [30]+ESO, the picking values occur in joint 2 and joint 3 at 10.42 s and 14.48 s, respectively. The acceptable performance of AFTC with [30]+ESO cannot be guaranteed in this case. In contrast, the proposed AFTC S-FTSMC still maintains the accuracy inside order rad. This causes the effectiveness of synchronization control which can suppress the effect of the fault. However, it can be seen that the tracking error in joint 1 slightly increases due to the synchronization technique which also makes the error at each joint tend to be equal. This characteristic is the disadvantage of the synchronization technique.
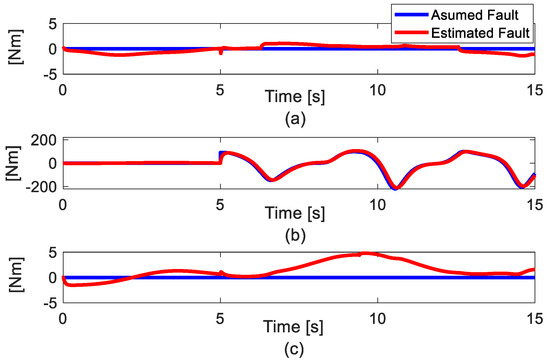
Figure 4.
Fault estimation results. (a) Joint 1; (b) Joint 2; (c) Joint (3).
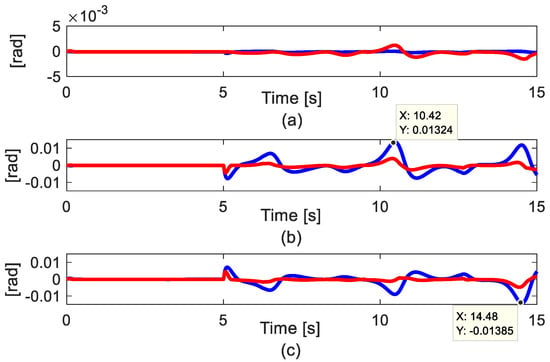
Figure 5.
Tracking error results. Blue line is [30]+ESO controller. Red line is the proposed controller. (a) Joint 1; (b) Joint 2; (c) Joint (3).
Remark 5.
From the results in Simulation 1 and 2, it can be seen that the different kinds of faults can highly affect the performance of the active fault-tolerant control strategy despite having similar magnitude at the actuators. Therefore, to prevent the effect of faults, AFTC needs a different solution for the way it deals with uncertainties and disturbances. AFTC with the conventional controller technique may not be enough to guarantee an acceptable performance in the robot manipulators when faults occur. In contrast, with the synchronization technique, the proposed AFTC showed effectiveness in tolerating faults despite this technique having no effect in the normal operation mode.
6. Experimental Results
6.1. Experiment Setup
The experimental setup is shown in Figure 6 and uses a 3-DOF FARA-AT2 robot manipulator. This robot manipulator has 6 DOF, but for these experiments, joints 4, 5, and 6 were blocked. The 3-DOF FARA-AT2 robot had a CSMP series motor at each joint. The gear box at each joint was 120:1, 120:1, and 100:1 at joints 1, 2, and 3, respectively. The encoder at each joint was a 2048 line count incremental encoder. The controller was run on Labview-FPGA, NI-PXI-8110, and NI-PXI-7842R PXI cards with the frequency control set at 500 Hz. The NI-PXI-8110 was run on a Windows operating system.
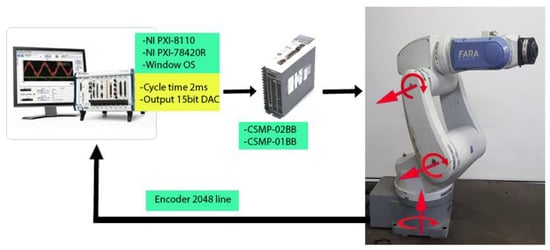
Figure 6.
Experiment setup for 3-DOF FARA-AT2 robot manipulator.
The desired trajectory at each joint is given as:
The related parameters of the fault estimation (8) can be suitably selected as , and .
The parameters of AFTC with [30]+ESO in (36) were suitably selected as , and .
The parameters of the proposed AFTC S-FTSMC (25) were suitably chosen as , , and .
To avoid a singularity, the terms containing power in (25) and (36) were replaced with the saturation function.
where is a positive constant, and with .
To avoid chattering, the signum function in (25) and (36) were replaced with the saturation function.
where .
6.2. Experiment 1
In this experiment, the total two kinds of actuator faults are considered to show the advantage of the proposed AFTC when compared to AFT with [30]+ESO. The assumed fault function is shown as
where and .
In Figure 7, the fault estimation results are shown. Unlike in Simulation 2’s results, the high magnitude of uncertainties occurred in the real implementation estimation results. However, the magnitude of the assumed fault dominated over the uncertainties. Hence, the effect of the total uncertainties and faults is mainly affected by faults. In Figure 8, the tracking error at each joint is presented. Before the 10th second, as mentioned in Section 1, the synchronization technique has no advantage in an open-loop chain mechanism such as the serial robot manipulator in normal operation mode. Therefore, the error at each joint of two controllers has similar accuracy. It is shown that the AFTC with [30]+ESO still maintains the ability to deal with a high magnitude of uncertainties. After the 10th second, in Figure 8b, the difference accuracy of two controllers is shown. The proposed AFTC S-FTSMC outperformed the AFTC with [30]+ESO. It can be seen that the effectiveness of the synchronization technique in the AFTC strategy is verified. In addition, in Figure 8c, the error of the proposed AFTC S-FTSMC is slightly increased due to the synchronization method. However, this increase still guarantees an acceptable performance of the robot manipulator.
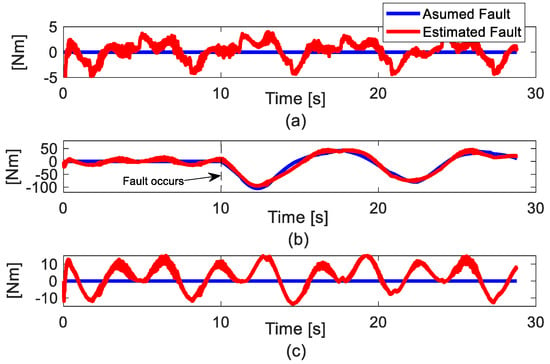
Figure 7.
Fault estimation results. (a) Joint 1; (b) Joint 2; (c) Joint (3).
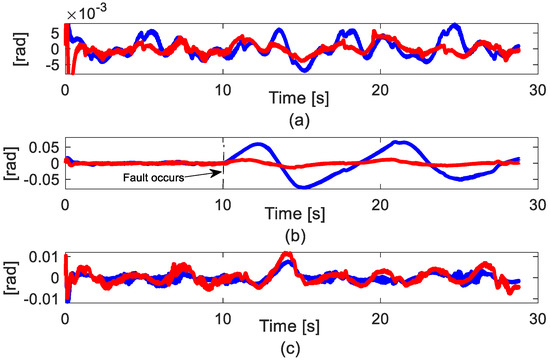
Figure 8.
Tracking error results. Blue line is [30]+ESO controller. Red line is the proposed controller. (a) Joint 1; (b) Joint 2; (c) Joint (3).
6.3. Experiment 2
In this experiment, three different group values of synchronization parameters where and 4.5 were considered to show the effect of these parameters in the proposed controller.
Before the 10th second, in Figure 9a–c, the position errors at each joint tend to be equal so that they have similar behavior due to the synchronization technique. With different values of group , the synchronization occurs during the tracking trajectory of the robot manipulator. However, with a higher value of , the system has better synchronization as shown in Figure 9b,c. It can be seen that from to , the position error at each joint has not much change. In this implementation with a 3-DOF FARA-AT2 robot manipulator, the value of is limited to 4.5. If is selected to be higher, oscillation will occur in the robot manipulator system. In Figure 9d, the error of AFTC with [30]+ESO showed a different characteristic at each joint. However, in Figure 9b–d, the accuracy still maintains. After the 10th second, in Figure 9d without the synchronization technique, the position error at each joint shows dependent characteristics. In contrast, in Figure 9a–c, the synchronization guarantees that the position error at each joint tends to be equal. This characteristic of the synchronization technique is very helpful in tolerating faults because the internal constraints of synchronization can suppress the effect of faults in the system.
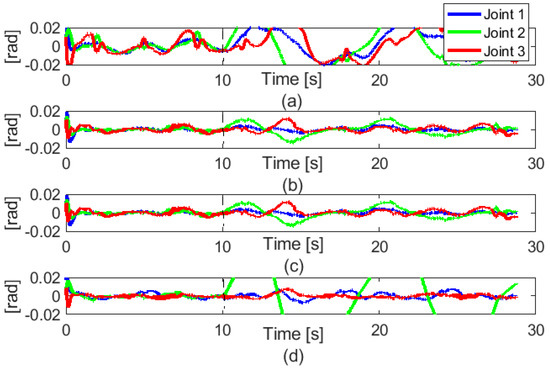
Figure 9.
Tracking error results with difference group value of . (a) ; (b) ; (c) ; (d) Non-synchronization.
7. Conclusions and Future Works
In this paper, active fault-tolerant control with the combination of a novel finite-time synchronous fast terminal sliding mode control and an extended state observer was proposed. Due to the internal constraints of the synchronization technique, the proposed controller has the ability to suppress the effect of faults and reduce the picking phenomenon in systems when faults occur. Without the conventional coupling technique, the proposed active fault-tolerant controller can reduce the computation and fast convergence and avoid the oscillation due to the integral term and guarantees the finite-time convergence of position errors. From the simulation and experimental results, it is shown that the effect of different kinds of faults cannot prevent uncertainties and disturbances like the control technique can. Therefore, the synchronization technique is a suitable technique to tolerate faults. It effectively treats the loss-effective faults at the actuators of robot manipulators.
In future work, selecting the optimal synchronization parameters using an optimal method or intelligent technique such as neural network and fuzzy could be considered to improve the performance of the synchronous technique in fault-tolerant control. In addition, the data-driver technique based on a deep neural network could be useful to detect faults on the system early, which is very important in tolerating the faults and maintaining acceptable performance when the faults occur. The combination of the model and signal base will be applied to a real robot system to detect faults early, then make a decision for the output of the robot actuator to tolerate the faults.
Author Contributions
All authors contributed equally to this article and accepted the final report. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education (NRF-2016R1D1A3B03930496).
Conflicts of Interest
All authors announce that they have no conflict of interest in relation to the publication of this article.
References
- Le, Q.D.; Kang, H.-J. Real Implementation of an Active Fault Tolerant Control Based on Super Twisting Technique for a Robot Manipulator. In Proceedings of the International Conference on Intelligent Computing, Nanchang, China, 3–6 August 2019; Huang, D.S., Huang, Z.K., Hussain, A., Eds.; Springer: Cham, Switzerland, 2019; pp. 294–305. [Google Scholar]
- Shen, Q.; Yue, C.; Goh, C.H.; Wang, D. Active Fault-Tolerant Control System Design for Spacecraft Attitude Maneuvers with Actuator Saturation and Faults. IEEE Trans. Ind. Electron. 2019, 66, 3763–3772. [Google Scholar] [CrossRef]
- Zhang, Q.; Wang, C.; Su, X.; Xu, D. Observer-based terminal sliding mode control of non-affine nonlinear systems: Finite-time approach. J. Franklin Inst. 2018, 355, 7985–8004. [Google Scholar] [CrossRef]
- Wang, R.; Wang, J. Passive actuator fault-tolerant control for a class of overactuated nonlinear systems and applications to electric vehicles. IEEE Trans. Veh. Technol. 2013, 62, 972–985. [Google Scholar] [CrossRef]
- Stefanovski, J.D. Passive fault tolerant perfect tracking with additive faults. Automatica 2018, 87, 432–436. [Google Scholar] [CrossRef]
- Benosman, M.; Lum, K.-Y. Passive actuators’ fault-tolerant control for affine nonlinear systems. IEEE Trans. Control Syst. Technol. 2010, 18, 152–163. [Google Scholar] [CrossRef]
- Le, Q.D.; Kang, H.-J. Implementation of sensorless contact force estimation in collaborative robot based on adaptive third-order sliding mode observer. Syst. Sci. Control Eng. 2022, 10, 507–516. [Google Scholar] [CrossRef]
- Qi, W.; Aliverti, A. A multimodal wearable system for continuous and real-time breathing pattern monitoring during daily activity. IEEE J. Biomed. Health Inform. 2019, 24, 2199–2207. [Google Scholar] [CrossRef]
- Xu, S.S.-D.; Chen, C.-C.; Wu, Z.-L. Study of nonsingular fast terminal sliding-mode fault-tolerant control. IEEE Trans. Ind. Electron. 2015, 62, 3906–3913. [Google Scholar] [CrossRef]
- Shen, Q.; Wang, D.; Zhu, S.; Poh, E.K. Integral-Type Sliding Mode Fault-Tolerant Control for Attitude Stabilization of Spacecraft. IEEE Trans. Control Syst. Technol. 2015, 23, 1131–1138. [Google Scholar] [CrossRef]
- Shen, Q.; Jiang, B.; Cocquempot, V. Fuzzy logic system-based adaptive fault-tolerant control for near-space vehicle attitude dynamics with actuator faults. IEEE Trans. Fuzzy Syst. 2013, 21, 289–300. [Google Scholar] [CrossRef]
- Cao, Y.; Song, Y.D. Adaptive PID-like fault-tolerant control for robot manipulators with given performance specifications. Int. J. Control 2018, 7179, 377–386. [Google Scholar] [CrossRef]
- Zhang, J.X.; Yang, G.H. Robust adaptive fault-tolerant control for a class of unknown nonlinear systems. IEEE Trans. Ind. Electron. 2017, 64, 585–594. [Google Scholar] [CrossRef]
- Jiang, T.; Khorasani, K.; Tafazoli, S. Parameter estimation-based fault detection, isolation and recovery for nonlinear satellite models. IEEE Trans. Control Syst. Technol. 2008, 16, 799–808. [Google Scholar] [CrossRef]
- Edwards, C.; Spurgeon, S.K.; Patton, R.J. Sliding mode observers for fault detection and isolation. Automatica 2000, 36, 541–553. [Google Scholar] [CrossRef]
- Han, J.; Zhang, H.; Wang, Y.; Zhang, K. Fault Estimation and Fault-Tolerant Control for Switched Fuzzy Stochastic Systems. IEEE Trans. Fuzzy Syst. 2018, 26, 2993–3003. [Google Scholar] [CrossRef]
- Bouibed, K.; Seddiki, L.; Guelton, K.; Akdag, H. Actuator and sensor fault detection and isolation of an actuated seat via nonlinear multi-observers. Syst. Sci. Control Eng. 2014, 2, 150–160. [Google Scholar] [CrossRef][Green Version]
- Lin, X.; Yao, X. Improved disturbance-observer-based fault-tolerant control for the linear system subject to unknown actuator faults and multiple disturbances. Int. J. Control 2021, 94, 2730–2740. [Google Scholar] [CrossRef]
- Zhang, X.; Zhu, Z.; Yi, Y. Anti-Disturbance Fault-Tolerant Sliding Mode Control for Systems with Unknown Faults and Disturbances. Electronics 2021, 10, 1487. [Google Scholar] [CrossRef]
- Han, J.; Zhang, H.; Wang, Y.; Liu, Y. Disturbance observer based fault estimation and dynamic output feedback fault tolerant control for fuzzy systems with local nonlinear models. ISA Trans. 2015, 59, 114–124. [Google Scholar] [CrossRef]
- Van, M.; Ge, S.S.; Ren, H. Finite Time Fault Tolerant Control for Robot Manipulators Using Time Delay Estimation and Continuous Nonsingular Fast Terminal Sliding Mode Control. IEEE Trans. Cybern. 2017, 47, 1681–1693. [Google Scholar] [CrossRef]
- Yu, X.; Jiang, J. Hybrid Fault-Tolerant Flight Control System Design. IEEE Trans. Control Syst. Technol. 2011, 20, 871–886. [Google Scholar] [CrossRef]
- Li, C.; Yao, B.; Wang, Q. Modeling and Synchronization Control of a Dual Drive Industrial Gantry Stage. IEEE/ASME Trans. Mechatron. 2018, 23, 2940–2951. [Google Scholar] [CrossRef]
- Ren, L.; Mills, J.K.; Sun, D. Experimental comparison of control approaches on trajectory tracking control of a 3-DOF parallel robot. IEEE Trans. Control Syst. Technol. 2007, 15, 982–988. [Google Scholar] [CrossRef]
- Shang, W.; Zhang, B.; Zhang, B.; Zhang, F.; Cong, S. Synchronization Control in the Cable Space for Cable-Driven Parallel Robots. IEEE Trans. Ind. Electron. 2019, 66, 4544–4554. [Google Scholar] [CrossRef]
- Cui, R.; Yan, W. Mutual synchronization of multiple robot manipulators with unknown dynamics. J. Intell. Robot. Syst. Theory Appl. 2012, 68, 105–119. [Google Scholar] [CrossRef]
- Le, Q.D.; Kang, H.-J. Implementation of Fault-Tolerant Control for a Robot Manipulator Based on Synchronous Sliding Mode Control. Appl. Sci. 2020, 10, 2534. [Google Scholar] [CrossRef]
- Le, Q.D.; Kang, H.-J. Finite-Time Fault-Tolerant Control for a Robot Manipulator Based on Synchronous Terminal Sliding Mode Control. Appl. Sci. 2020, 10, 2998. [Google Scholar] [CrossRef]
- Khalil, H.K.; Praly, L. High-gain observers in nonlinear feedback control. Int. J. Robust Nonlinear Control 2014, 24, 993–1015. [Google Scholar] [CrossRef]
- Yu, X.; Zhihong, M. Fast terminal sliding-mode control design for nonlinear dynamical systems. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 2002, 49, 261–264. [Google Scholar] [CrossRef]
- Zemouche, A.; Boutayeb, M. On LMI conditions to design observers for Lipschitz nonlinear systems. Automatica 2013, 49, 585–591. [Google Scholar] [CrossRef]
- Zak, M. Introduction to terminal dynamics. Complex Syst. 1993, 7, 59. [Google Scholar]
- Feng, Y.; Yu, X.; Han, F. On nonsingular terminal sliding-mode control of nonlinear systems. Automatica 2013, 49, 1715–1722. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).