Energy-Aware Model Predictive Control of Assembly Lines
Abstract
:1. Introduction
1.1. Review of ALBPs and Solution Methods
- SALBPs of type 1 (SALBP-1) deal with minimization of the number of workstations required to execute a given set of tasks.
- SALBPs of type 2 (SALBP-2) aim at minimizing the cycle time, i.e., at maximizing the production rate.
- SALBPs of type E (SALBP-E), where E stands for efficiency, focus on the minimization of the product between the cycle time and the number of workstations, i.e., the objective is to minimize the total idle time.
- SALBPs of type F (SALBP-F), where E stands for feasibility, are aimed at understanding if, for a given number of workstations and a desired cycle time c, it is possible to execute all the tasks.
1.2. Energy-Aware Control Frameworks for Industrial Assembly Lines
1.3. Paper Contributions
1.4. Paper Structure
2. Problem Description
3. Problem Formulation
- , which is a Boolean control variable equal to one if and only if the algorithm commands to execute tasks t on workstation w at time i;
- , a Boolean control variable equal to one if and only if the algorithm commands to assign resource r to task t at time i;
- , a real variable that represents the expected duration of tasks t at time i (that is, the time left to complete tasks t at time i). After the task is completed, it is clearly . We define as the total time to complete task t (it is obviously );
- , a real variable that captures the occupancy level of workstation w at time i. For instance, the occupancy level could be referred to the maximum number of tasks that can simultaneously run on the workstation (as in this paper), or to other metrics as well, depending on the specific case;
- , a real variable that represents the power flowing at the point of connection of the industry with the grid, at time i. It is by convention positive, when the industry absorbs power, and negative instead when the industry injects power into the grid. Thresholds are given for both the maximum allowed power withdrawal () and the maximum power injection ():
- To allow proper computation of the energy bill, we introduce a non-negative real variable, , to capture the power that flows from the grid to the industry, and a second non-negative real variable, , to capture the power that flows in the opposite direction, from the industry to the grid. Given these definitions, can then be defined as:Obviously, at any time, only one of the two components of can be different from zero. To enforce this, we need to introduce two auxiliary Boolean variables, , which should be equal to one if (i.e., when the industry is taking power from the grid), and , which should be equal to one if (i.e., when the industry is injecting power into the grid). This behavior for the auxiliary variables can be enforced by adding the following constraints:andThen, the following constraint ensures that at any time, only one between and can be different (i.e., greater) from zero.
- Next, the real variable is introduced, which represents the charging/discharging power (kW) of the battery at time i, which is limited between a maximum possible charging level and a maximum possible discharging level:
- The real variable represents the energy level (kWh) of energy stored in the battery at time i. At any time, it must be:where and are the minimum and maximum allowed energy levels of the battery, respectively. Furthermore, the dynamics of is:where T is the sampling time of the MPC algorithm, and we consider, for simplicity, a lossless model of the battery;
- , the aggregated power consumption of the tasks running at time i. It is defined as the sum of the power consumed by all the tasks currently executing (i.e., for which ):where is the power consumption of task t when it is at time j of execution (we make the realistic assumption that an estimate of the power consumption of the tasks is available).
- Finally, is the forecast of the power generated by the renewable plant at time i.
3.1. Objective Function
- (1)
- The term is related to the tasks’ control and pushes the minimization of the time left to complete the tasks:
- (2)
- The second term is to the energy cost. It is added in order to minimize, at each instant of time, the cost related to the energy consumption required by the tasks and to maximize the profit when the power is injected into the grid. We consider a scenario with a time-varying time-of-use tariff, where is the cost (EUR/kWh) of energy consumption at time i and is the remuneration (EUR/kWh) of the energy injected into the grid at time i. The term is:where T is the sampling time.
- (3)
- The third term is also energy related. It pushes the minimization of the peaks in the power exchanged between the industry and the grid. To avoid nonlinear formulations, which make the computation time of the algorithms higher, we minimized the H-infinity norm of the injected and absorbed power vectors, i.e., and (we recall that the H-infinity norm of a vector is defined as the largest component of the vector, so that we seek in practice to minimize the greater absorption and injection power peak). To capture the H-infinity norm of and , we introduced two auxiliary variables, and . By definition, the H-infinity norm is greater than or equal to any component of the vector, i.e.:andFinally, we minimized and in the objective function (so that, at the optimum, and are actually the H-infinity norms of the vectors and ).
3.2. Remarks on Practical Implementation and Possible Disadvantages of the Solution
4. Simulation Results
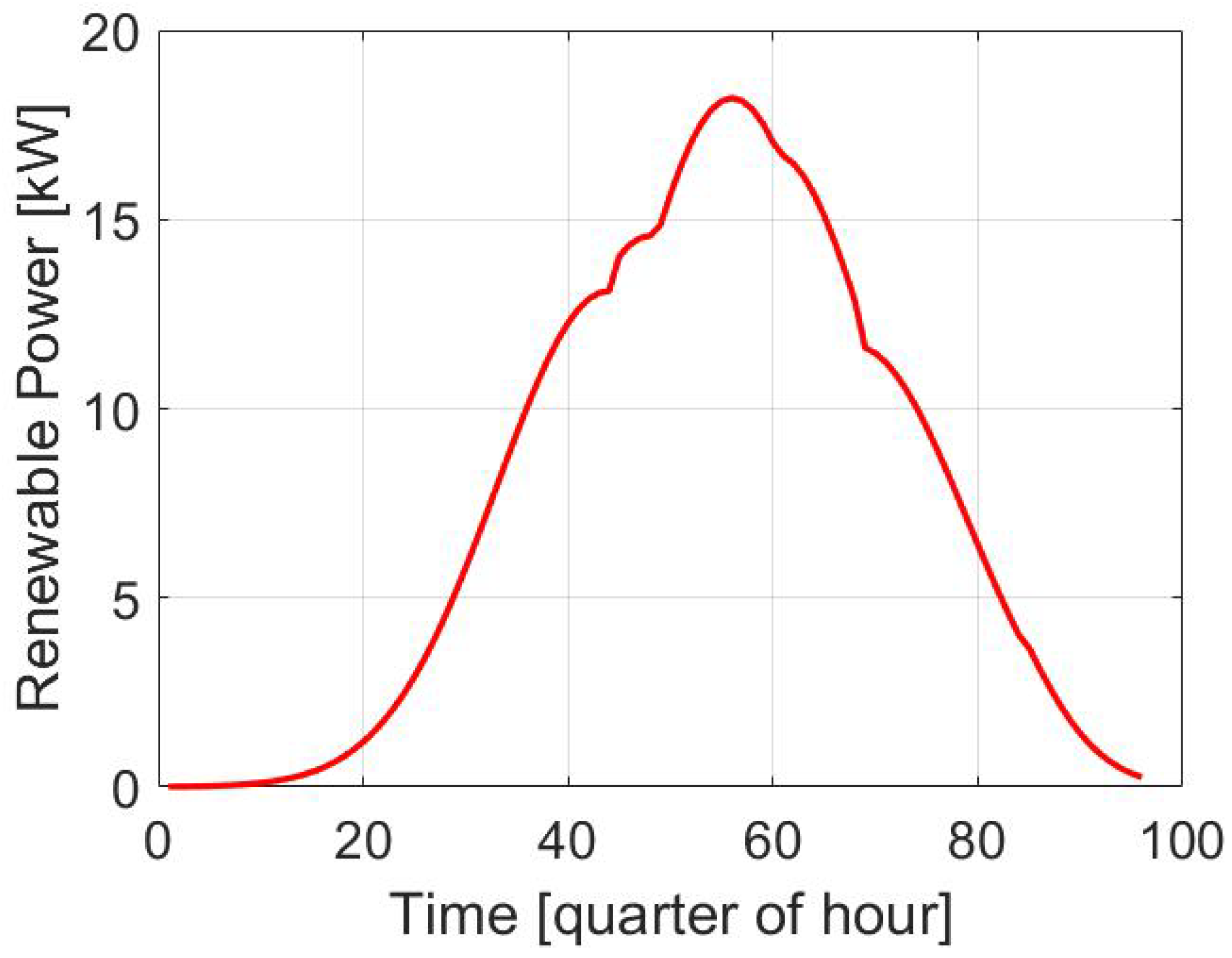
4.1. Simulation Scenario
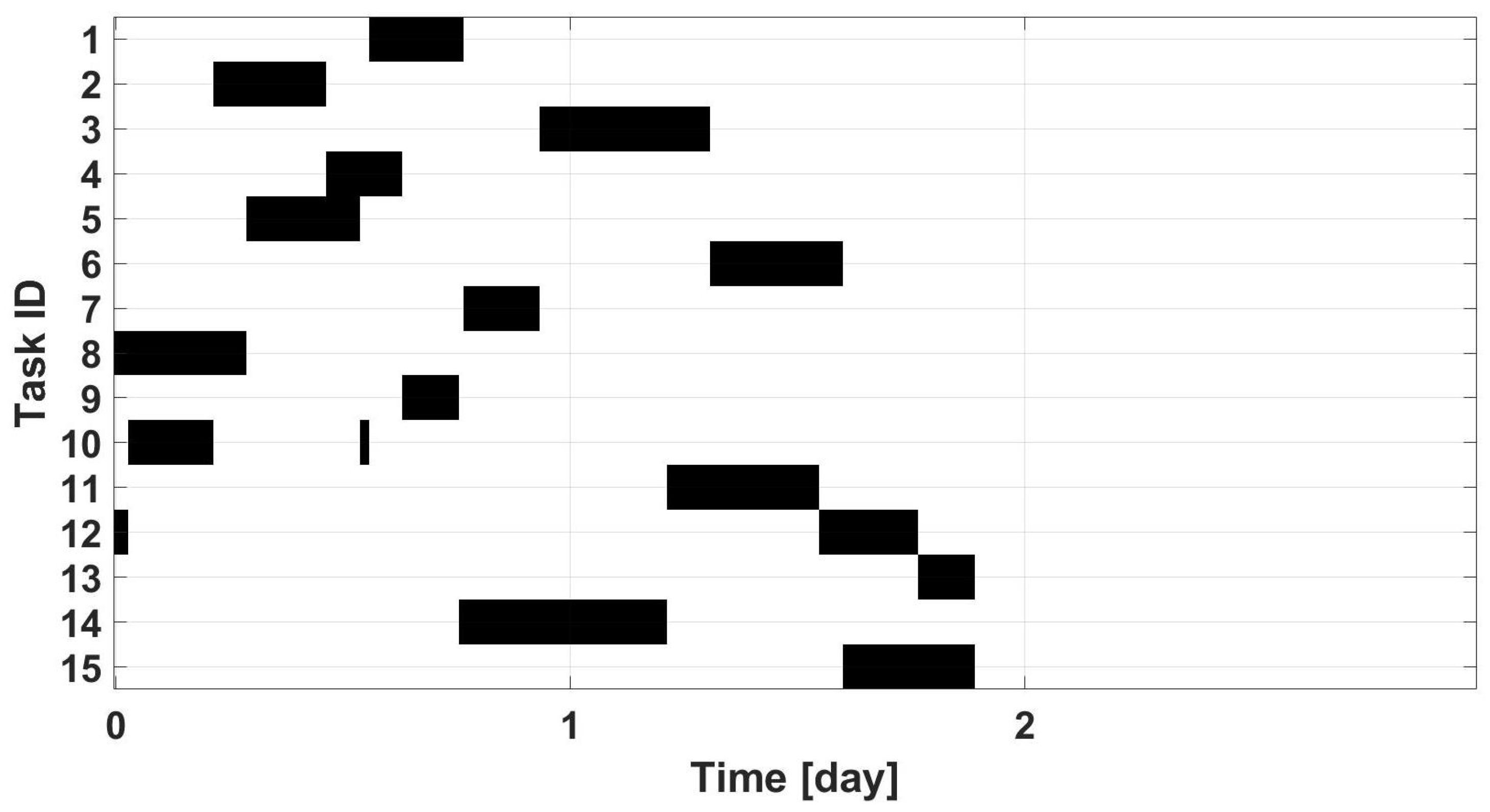
- Minimization of cycle time. In this first simulation, we only sought to optimize the cycle time, while leaving out of the optimization all the energy-related considerations (i.e., we set to and zero in the objective function). This simulation serves as a baseline for the next one;
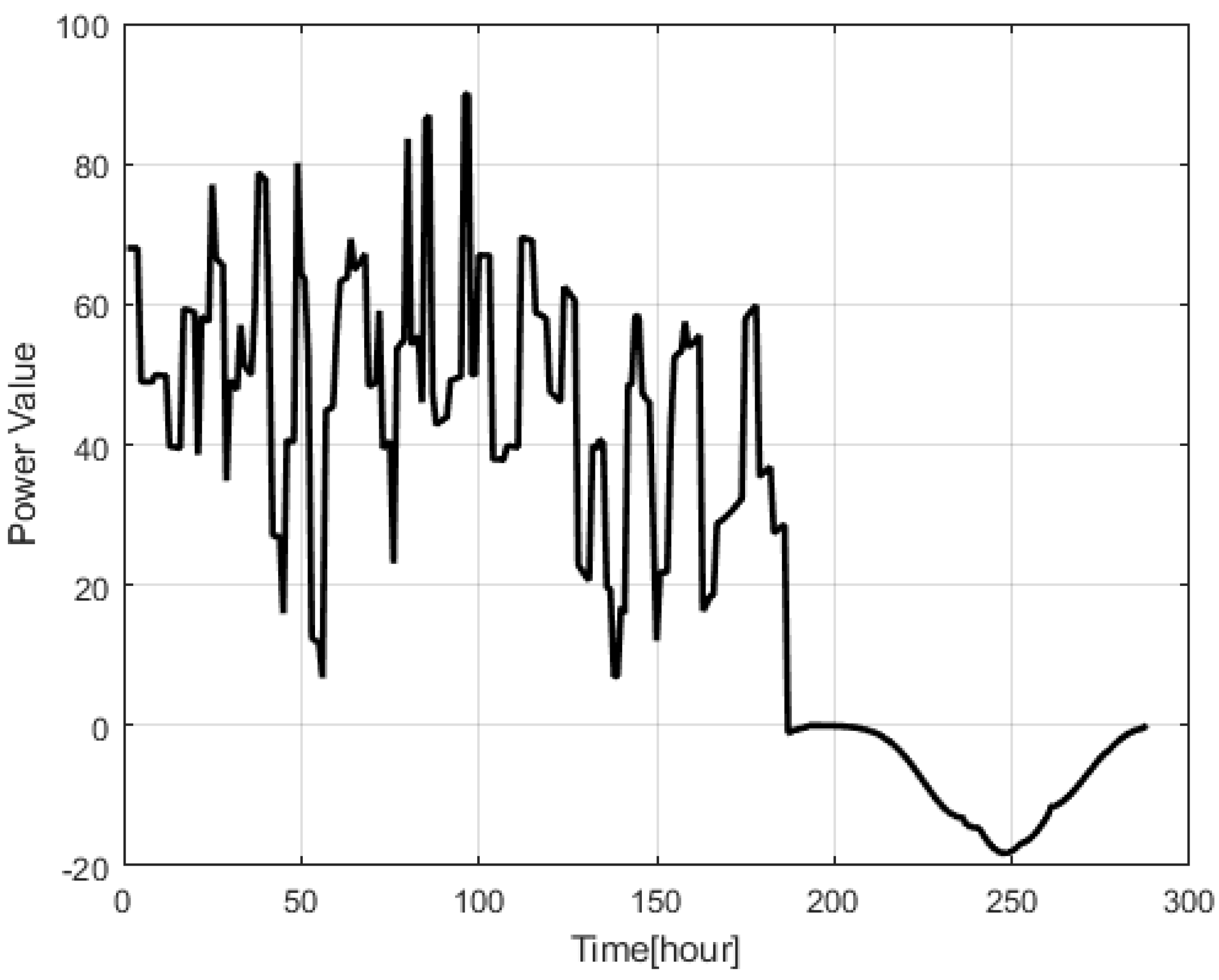
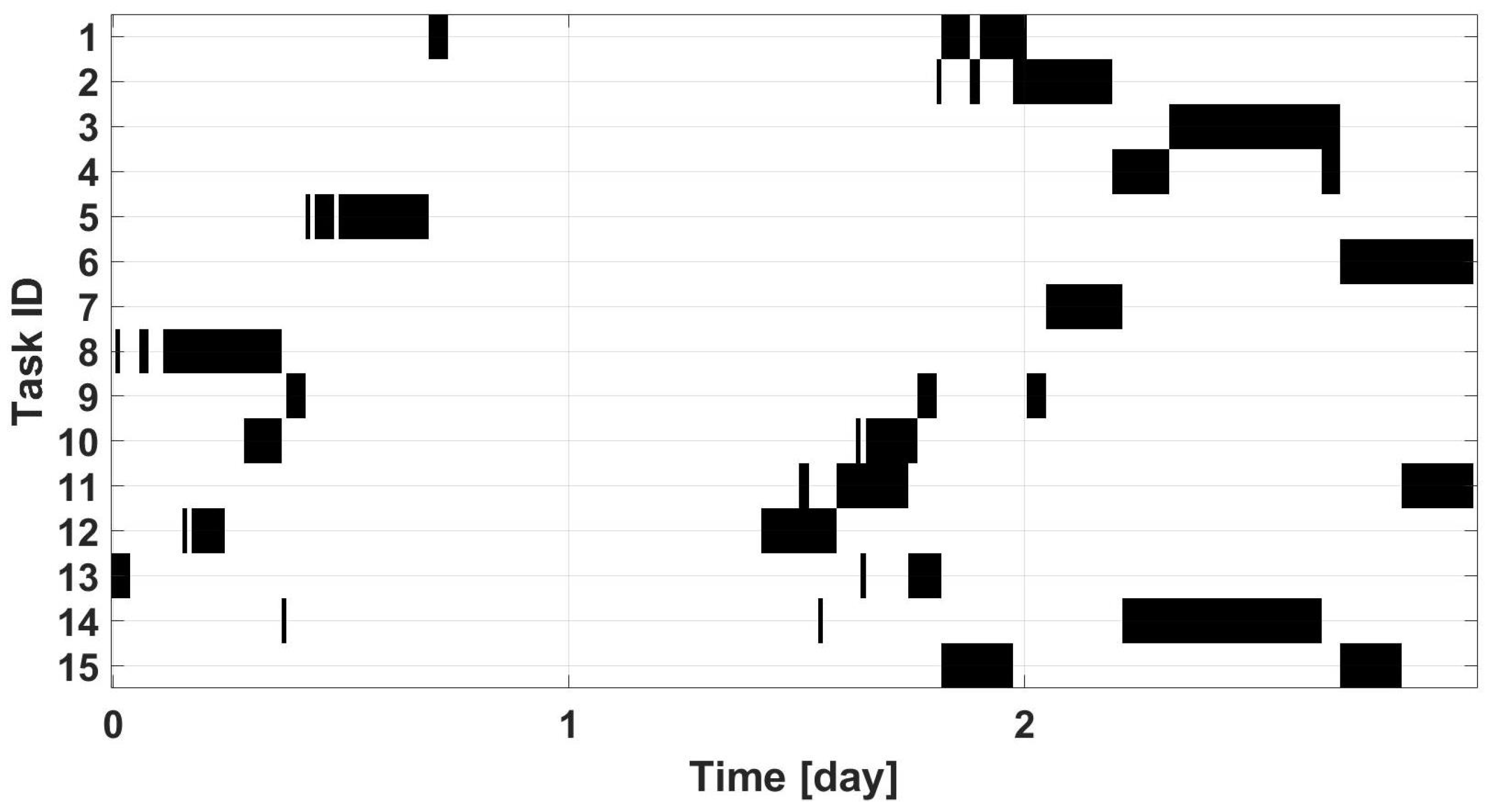
- Energy-aware task control. In this scenario, the proposed algorithm is tested, with all the terms, including also the energy-related ones. The goal is to show that the energy-related performance can be improved (i.e., energy bill savings and reduction of power peaks).
4.2. Minimization of Cycle Time
4.3. Energy-Aware Task Scheduling Optimization
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ALBP | Assembly Line Balancing Problem |
| ESS | Energy Storage System |
| MPC | Model Predictive Control |
References
- Bueno, A.; Filho, M.G.; Frank, A.G. Smart production planning and control in the Industry 4.0 context: A systematic literature review. Comput. Ind. Eng. 2020, 149, 106774. [Google Scholar] [CrossRef]
- Waibel, M.; Steenkamp, L.P.; Moloko, N.; Oosthuizen, G.A. Investigating the Effects of Smart Production Systems on Sustainability Elements. Procedia Manuf. 2017, 8, 731–737. [Google Scholar] [CrossRef]
- Renato, F.; Collotta, M.; Bueno-Delgado, M.V.; Chen, H.C.C. Smart Management Energy Systems in Industry 4.0. Energies 2020, 13, 382. [Google Scholar] [CrossRef] [Green Version]
- Mohamed, N.; Al-Jaroodi, J.; Lazarova-Molnar, S. Leveraging the Capabilities of Industry 4.0 for Improving Energy Efficiency in Smart Factories. IEEE Access 2019, 7, 18008–18020. [Google Scholar] [CrossRef]
- Cohen, Y.; Naseraldin, H.; Chaudhuri, A.; Pilati, F. Assembly systems in Industry 4.0 era: A road map to understand Assembly 4.0. Int. J. Adv. Manuf. Technol. 2019, 105, 4037–4054. [Google Scholar] [CrossRef]
- Ourahou, M.; Ayrir, W.; El Hassouni, B.; Haddi, A. Review on smart grid control and reliability in presence of renewable energies: Challenges and prospects. Math. Comput. Simul. 2020, 167, 19–31. [Google Scholar] [CrossRef]
- Rekiek, B.; Dolgui, A.; Delchambre, A.; Bratcu, A. State of art of optimization methods for assembly line design. Annu. Rev. Control 2002, 26, 163–174. [Google Scholar] [CrossRef]
- Battaïa, O.; Dolgui, A. A taxonomy of line balancing problems and their solutionapproaches. Int. J. Prod. Econ. 2013, 142, 259–277, Anticipation of risks impacts and industrial performance evaluation in distributed organizations life cycles. [Google Scholar] [CrossRef]
- Battaïa, O.; Dolgui, A.; Guschinsky, N.; Levin, G. A decision support system for design of mass production machining lines composed of stations with rotary or mobile table. Robot. Comput.-Integr. Manuf. 2012, 28, 672–680. [Google Scholar] [CrossRef]
- Mourtzis, D. Simulation in the design and operation of manufacturing systems: State of the art and new trends. Int. J. Prod. Res. 2020, 58, 1927–1949. [Google Scholar] [CrossRef]
- Scholl, A. Balancing and Sequencing of Assembly Lines; Springer: Berlin/Heidelberg, Germany, 1999. [Google Scholar]
- Azizoğlu, M.; İmat, S. Workload smoothing in simple assembly line balancing. Comput. Oper. Res. 2018, 89, 51–57. [Google Scholar] [CrossRef]
- Nilakantan, J.M.; Huang, G.Q.; Ponnambalam, S.G. An investigation on minimizing cycle time and total energy consumption in robotic assembly line systems. J. Clean. Prod. 2015, 90, 311–325. [Google Scholar] [CrossRef]
- Gianessi, P.; Delorme, X.M.O. Simple Assembly Line Balancing Problem with Power Peak Minimization. In IFIP International Conference on Advances in Production Management Systems; Springer: Cham, Switzerland, 2019. [Google Scholar] [CrossRef]
- Li, Z.; Kucukkoc, I.; Tang, Q. A comparative study of exact methods for the simple assembly line balancing problem. Soft Comput. 2020, 24, 11459–11475. [Google Scholar] [CrossRef]
- Borba, L.; Ritt, M.; Miralles, C. Exact and heuristic methods for solving the Robotic Assembly Line Balancing Problem. Eur. J. Oper. Res. 2018, 270, 146–156. [Google Scholar] [CrossRef]
- International Energy Agency. Tracking Clean Energy Progress. 2021. Available online: https://www.iea.org/reports/tracking-industry-2021 (accessed on 10 June 2022).
- U.S. International Energy Agency. International Energy Outlook. 2019. Available online: https://tinyurl.com/yc43apkm (accessed on 1 June 2022).
- Gungor, A.; Gupta, S.M. Issues in environmentally conscious manufacturing and product recovery: A survey. Comput. Ind. Eng. 1999, 36, 811–853. [Google Scholar] [CrossRef]
- Ngai, E.W.; Daniel Ng, C.; Huang, G.Q. Energy sustainability for production design and operations. Int. J. Prod. Econ. 2013, 146, 383–385. [Google Scholar] [CrossRef]
- Battaïa, O.; Benyoucef, L.; Delorme, X.; Dolgui, A.; Thevenin, S. Sustainable and energy efficient reconfigurable manufacturing systems. In Reconfigurable Manufacturing Systems: From Design to Implementation; Springer: Berlin/Heidelberg, Germany, 2020; pp. 179–191. [Google Scholar]
- SESAME Consortium. Smart European Space Access through Modern Exploitation of Data Science; SESAME Consortium: Allan, Jordan, 2022. [Google Scholar]
- Liberati, F.; Tortorelli, A.; Mazquiaran, C.; Imran, M.; Panfili, M. Optimal Control of Industrial Assembly Lines. In Proceedings of the 2020 7th International Conference on Control, Decision and Information Technologies (CoDIT), Prague, Czech Republic, 29 June–2 July 2020; IEEE: Piscataway, NJ, USA, 2020; Volume 1, pp. 721–726. [Google Scholar]
- Liu, Z.; Stursberg, O. Efficient solution of distributed MILP in control of networked systems. IFAC-PapersOnLine 2020, 53, 6723–6729. [Google Scholar] [CrossRef]
- Dunning, I.; Huchette, J.; Lubin, M. JuMP: A modeling language for mathematical optimization. SIAM Rev. 2017, 59, 295–320. [Google Scholar] [CrossRef]
- Gurobi Optimization, Inc. Gurobi Optimizer Reference Manual; Gurobi Optimization, Inc.: Houston, TX, USA, 2016. [Google Scholar]
- Perez, E. Vega User Manual, Issue 4-Revision 0. Arianespace Blvd. -l’Eur.-BP 2014, 177, 91006. [Google Scholar]
- Bianchi, S.; Vega Integrated Project Team. Vega, the European small launcher: Development status, future perspectives, and applications. Acta Astronaut. 2008, 63, 416–427. [Google Scholar] [CrossRef]
- Angioli, E.; Chicarella, C.; Ciaccini, M.; Piccione, A. The Electrical Ground Support Equipment (EGSE) and Centre de Contrôle Vega (CCV) for European Space Agency (ESA) Vega launcher. In Proceedings of the 2012 IEEE First AESS European Conference on Satellite Telecommunications, Rome, Italy, 2–5 October 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 1–7. [Google Scholar]
- Nicolini, D.; Roviera, P.M. Vega Launch Operations and Ground Facilities. In Proceedings of the SpaceOps 2014 Conference, Pasadena, CA, USA, 5–9 May 2014; p. 1821. [Google Scholar]
- Nicolini, D. Vega Operations: Transition to Commercial Operations and New Developments. In Proceedings of the 14th International Conference on Space Operations, Daejeon, Korea, 17 May 2016; p. 2528. [Google Scholar]




| Task ID | (h) | (Day) | (Day) | w | Task Precedence Relations | Input Resources |
|---|---|---|---|---|---|---|
| 1 | 6 | 1 | 4 | 2 | 3; 4; 11 | |
| 2 | 3 | 1 | 4 | 2 | 3; 12 | |
| 3 | 4 | 1 | 4 | 2 | 1; 2 | 4; 5 |
| 4 | 8 | 1 | 4 | 1 | 2; 6 | |
| 5 | 0.25 | 1 | 4 | 2 | 1; 2; 3; 4 | 2 |
| 6 | 5 | 1 | 4 | 2 | 5 | 6; 11; 1 |
| 7 | 5 | 1 | 4 | 2 | 5 | 12 |
| 8 | 10 | 1 | 4 | 2 | 5; 6 | 14; 1; 4 |
| 9 | 24 | 3 | 8 | 2 | 6; 7 | 15 |
| 10 | 6 | 3 | 8 | 2 | 6; 7 | 15; 4 |
| 11 | 8 | 3 | 8 | 2 | 6; 7; 8; 9; 10 | 3; 14 |
| 12 | 6 | 7 | 12 | 3 | 6; 7; 8 | 1; 11 |
| 13 | 6 | 7 | 12 | 3 | 6; 7; 8 | 1; 12 |
| 14 | 12 | 7 | 12 | 3 | 6; 7; 8 | 3; 13 |
| 15 | 5 | 7 | 12 | 1 | 4 | 2; 4; 12 |
| 16 | 2 | 7 | 12 | 3 | 12; 13; 14; 15 | 1; 15 |
| 17 | 6 | 7 | 12 | 3 | 16 | 6; 5; 7; 12 |
| 18 | 6 | 7 | 13 | 3 | 16 | 11 |
| 19 | 12 | 7 | 13 | 3 | 16; 17; 18 | 14 |
| 20 | 3 | 10 | 14 | 1 | 15 | 1; 12 |
| 21 | 5 | 10 | 14 | 4 | 17; 18; 19; 20 | 3; 7; 11 |
| 22 | 10 | 10 | 14 | 4 | 17; 18; 19; 20 | 14 |
| 23 | 3 | 10 | 14 | 4 | 17; 18; 19; 20; 21; 22 | 15 |
| 24 | 6 | 12 | 17 | 1 | 20 | 2; 12 |
| 25 | 14 | 12 | 17 | 4 | 24 | 1; 11 |
| 26 | 1 | 12 | 17 | 4 | 21; 22; 23; 25 | 1; 13 |
| 27 | 3 | 12 | 17 | 4 | 21; 22; 23; 25 | 14 |
| 28 | 8 | 12 | 17 | 4 | 21; 22; 23; 25; 26; 27 | 15; 5; 7 |
| 29 | 5 | 15 | 20 | 5 | 28 | 3; 13 |
| 30 | 6 | 15 | 20 | 5 | 28; 29 | 12; 8; 6 |
| 31 | 6 | 15 | 20 | 5 | 28; 29 | 13; 4; 5 |
| 32 | 12 | 15 | 20 | 5 | 28; 29; 30; 31 | 11 |
| 33 | 3 | 15 | 20 | 1 | 24 | 2; 12 |
| 34 | 3 | 15 | 20 | 4 | 33 | 1; 11 |
| 35 | 1 | 15 | 20 | 4 | 34 | 1; 12 |
| 36 | 6 | 15 | 20 | 4 | 34 | 4; 14 |
| 37 | 8 | 15 | 20 | 4 | 35; 36 | 12; 4 |
| 38 | 5 | 15 | 20 | 5 | 37 | 3; 13 |
| 39 | 15 | 15 | 20 | 5 | 37 | 15; 7 |
| 40 | 10 | 15 | 20 | 5 | 37; 38; 39 | 14; 4 |
| 41 | 15 | 15 | 20 | 5 | 40 | 5; 4; 11 |
| 42 | 5 | 15 | 20 | 5 | 41 | 15 |
| 43 | 10 | 15 | 20 | 5 | 42 | 14 |
| 44 | 0.25 | 15 | 20 | 5 | 43 | 11 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liberati, F.; Cirino, C.M.F.; Tortorelli, A. Energy-Aware Model Predictive Control of Assembly Lines. Actuators 2022, 11, 172. https://doi.org/10.3390/act11060172
Liberati F, Cirino CMF, Tortorelli A. Energy-Aware Model Predictive Control of Assembly Lines. Actuators. 2022; 11(6):172. https://doi.org/10.3390/act11060172
Chicago/Turabian StyleLiberati, Francesco, Chiara Maria Francesca Cirino, and Andrea Tortorelli. 2022. "Energy-Aware Model Predictive Control of Assembly Lines" Actuators 11, no. 6: 172. https://doi.org/10.3390/act11060172
APA StyleLiberati, F., Cirino, C. M. F., & Tortorelli, A. (2022). Energy-Aware Model Predictive Control of Assembly Lines. Actuators, 11(6), 172. https://doi.org/10.3390/act11060172








