A Basic Study on Hybrid Systems for Small Race Car to Improve Dynamic Performance Using Lap Time Simulation
Abstract
:1. Introduction
2. Small Racing Car Installed Proposed Hybrid System
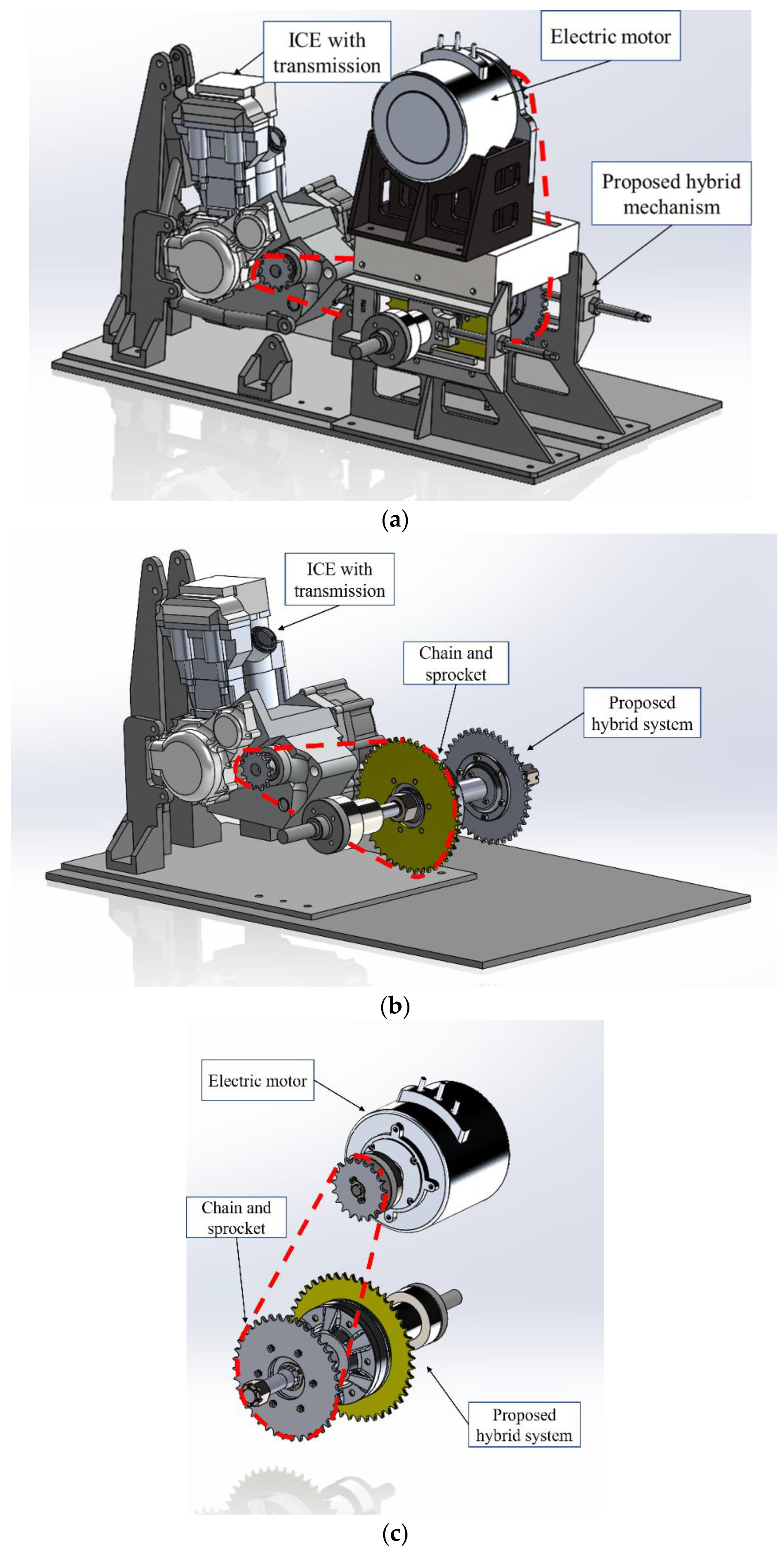
2.1. Outline of Proposed Hybrid Racing Car
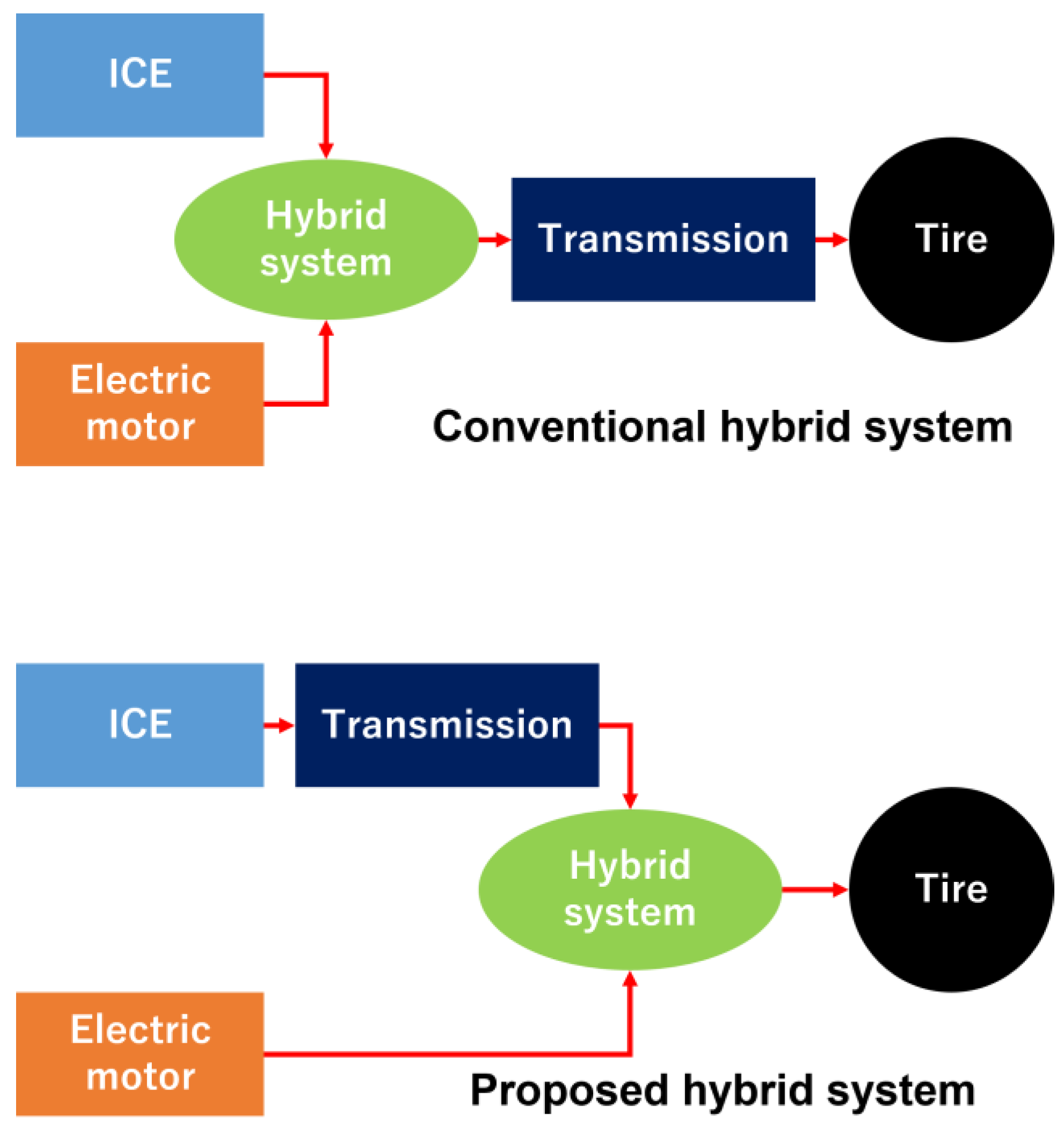
2.2. Structure of the Hybrid System
2.3. Two Power Sources in a Hybrid System
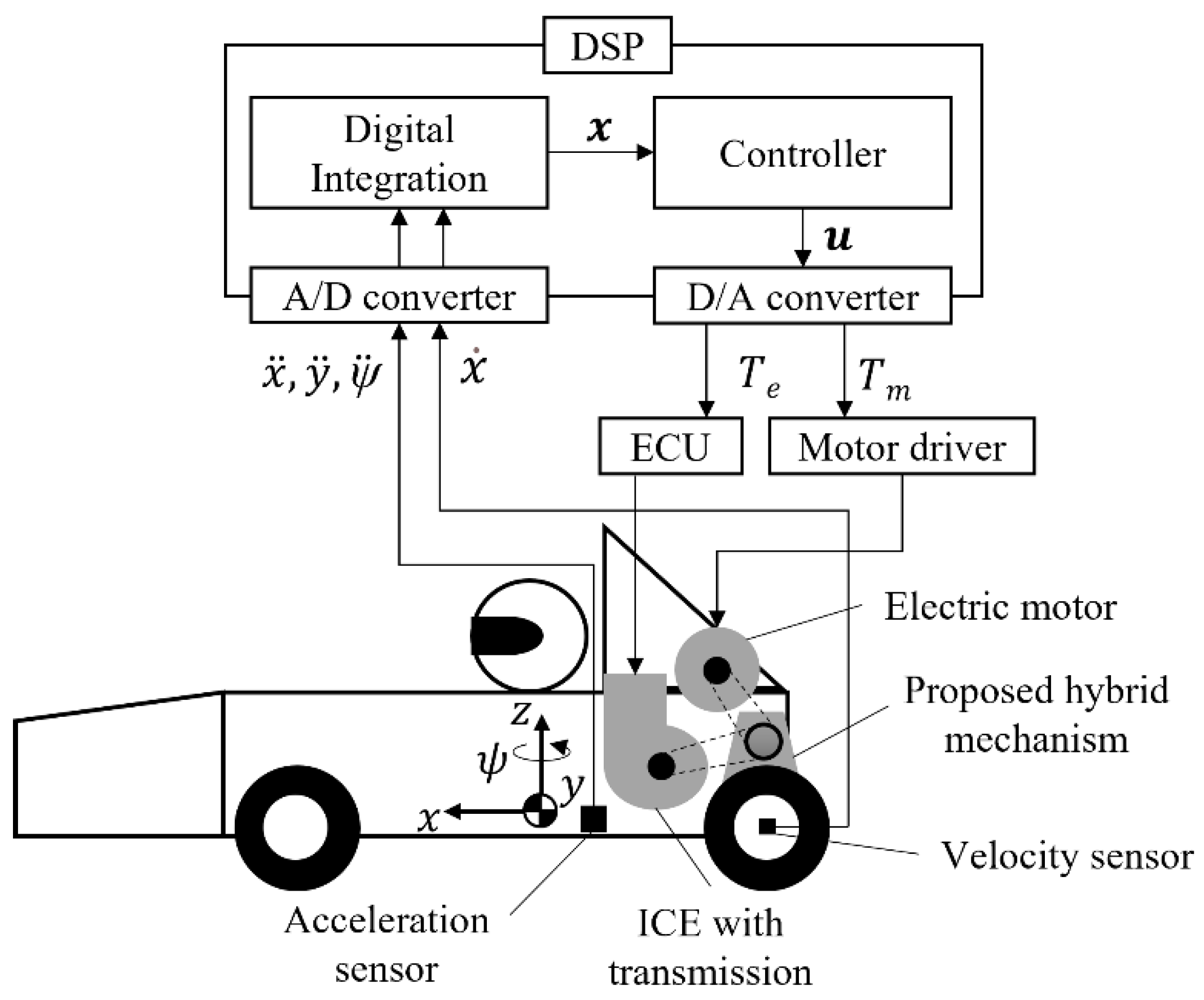
2.4. Control Model of the Hybrid System
3. Calculation Method Using Quasi-Steady-State Lap Time Simulation
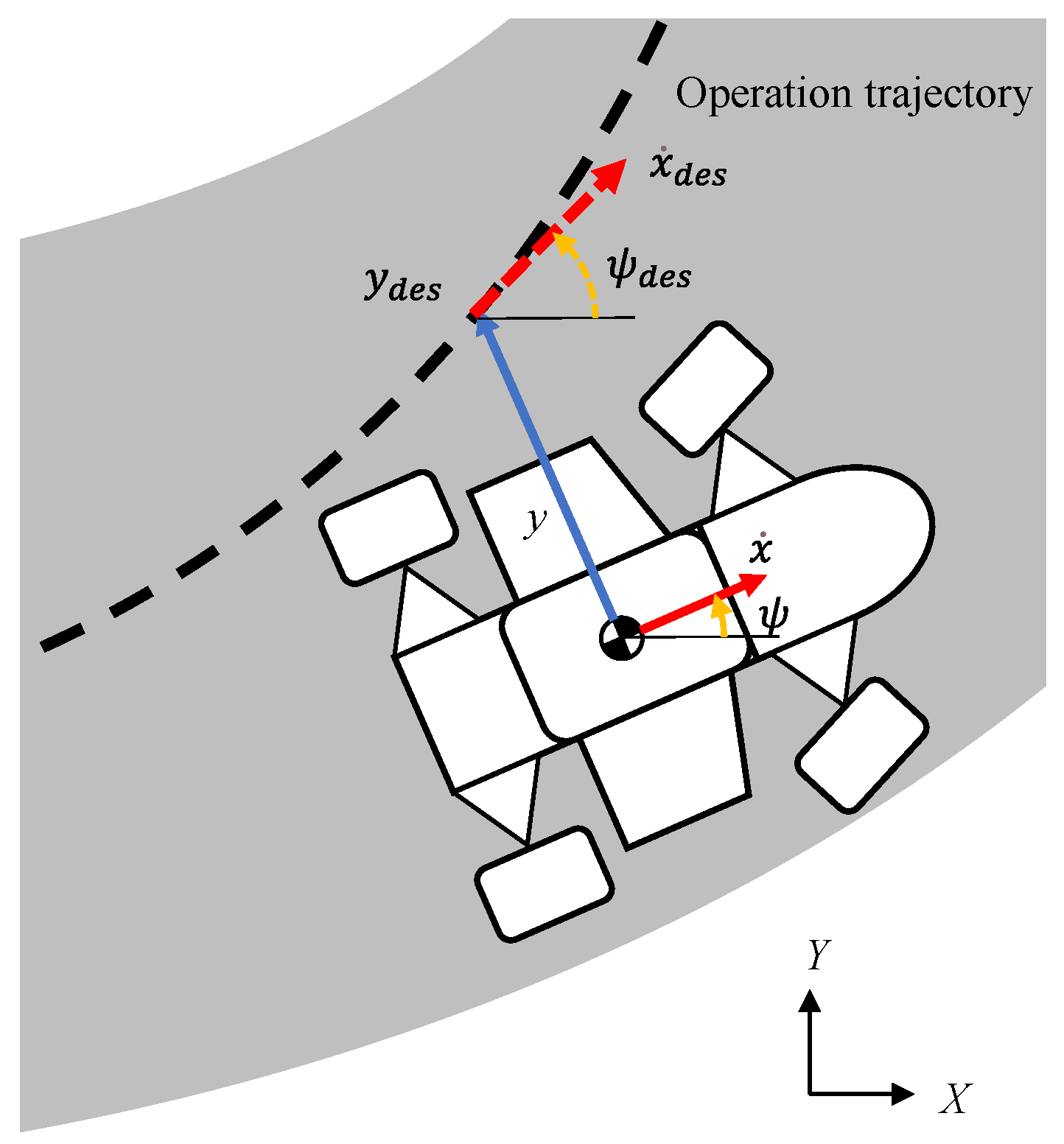
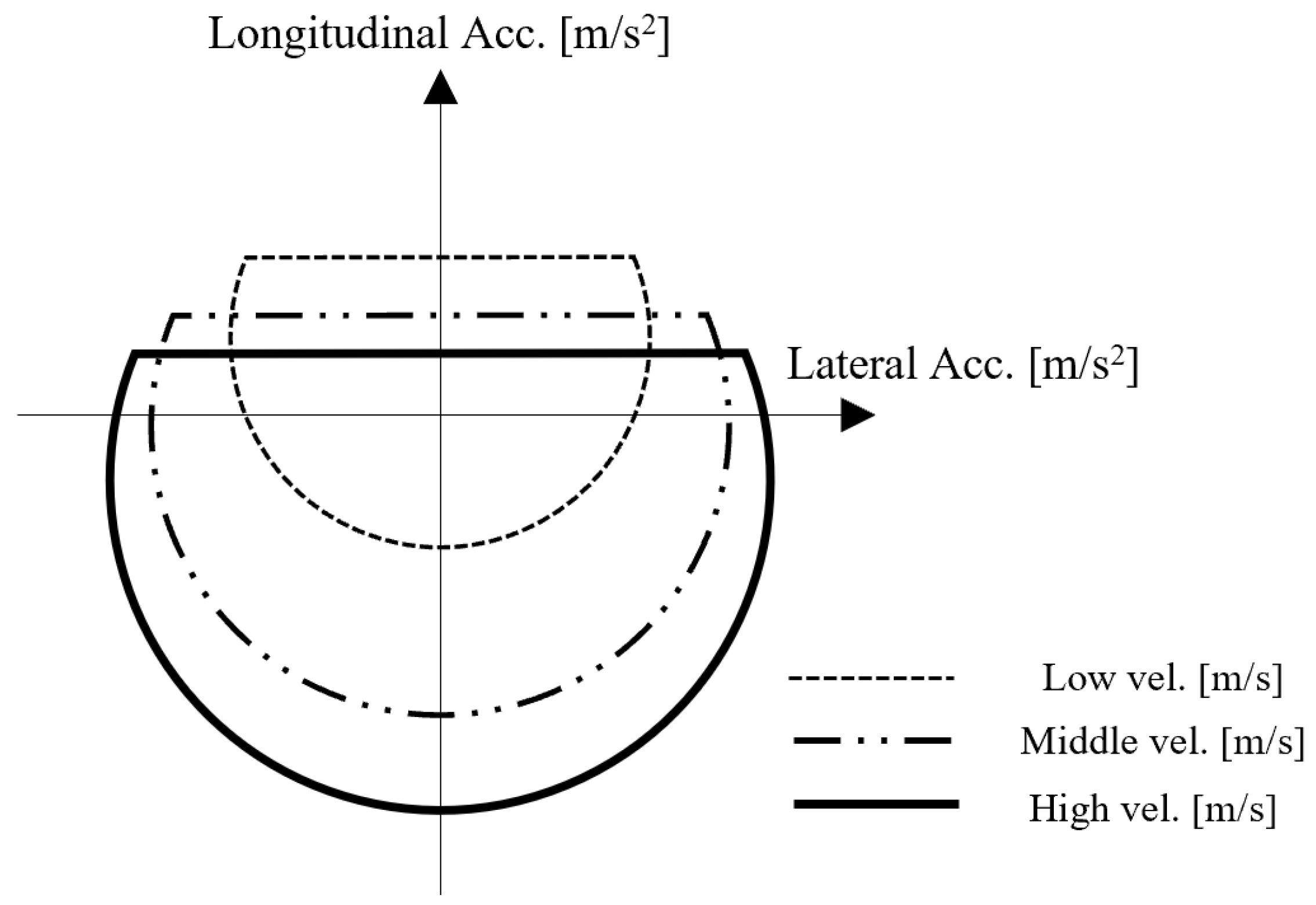
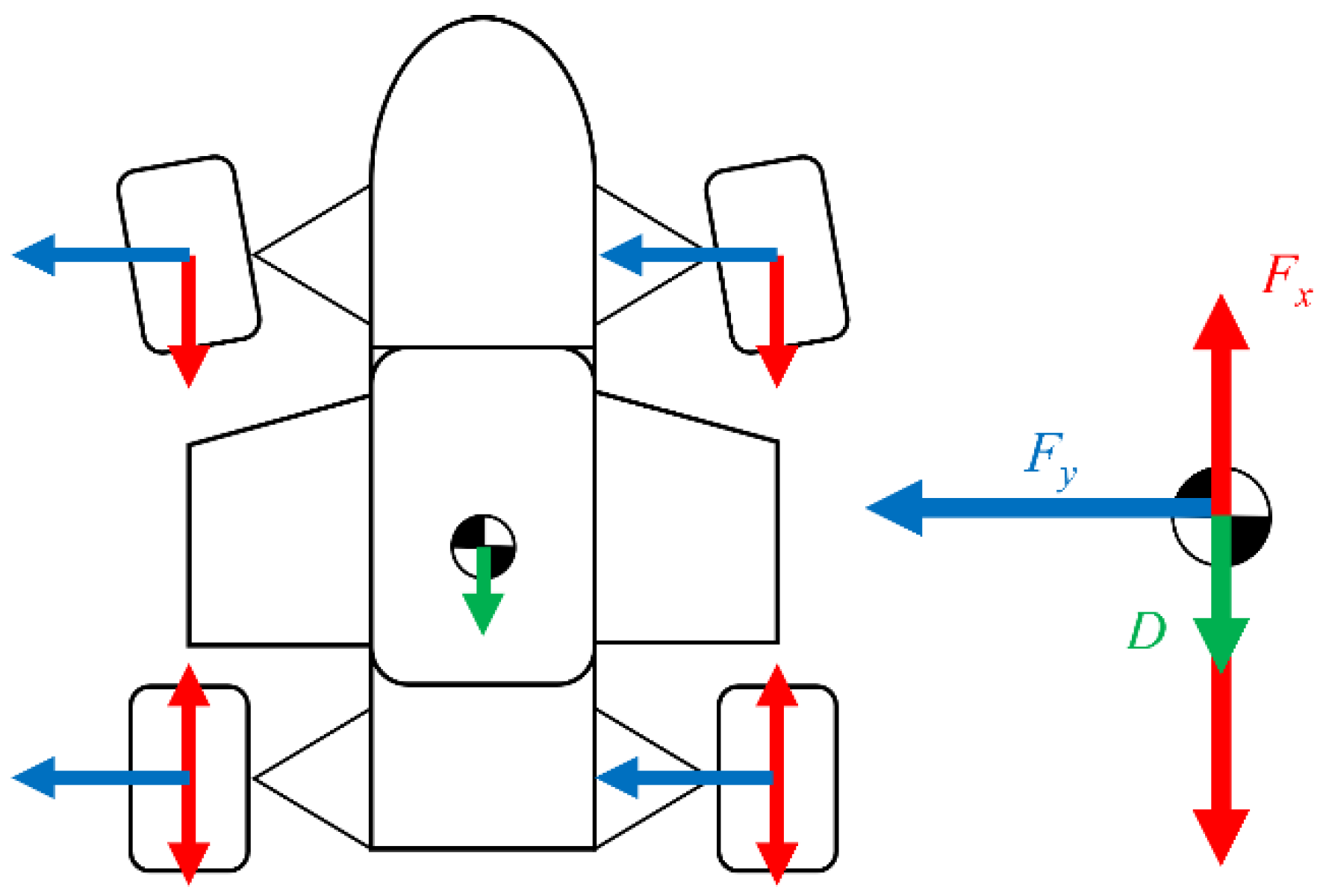
3.1. Simplified Vehicle Model
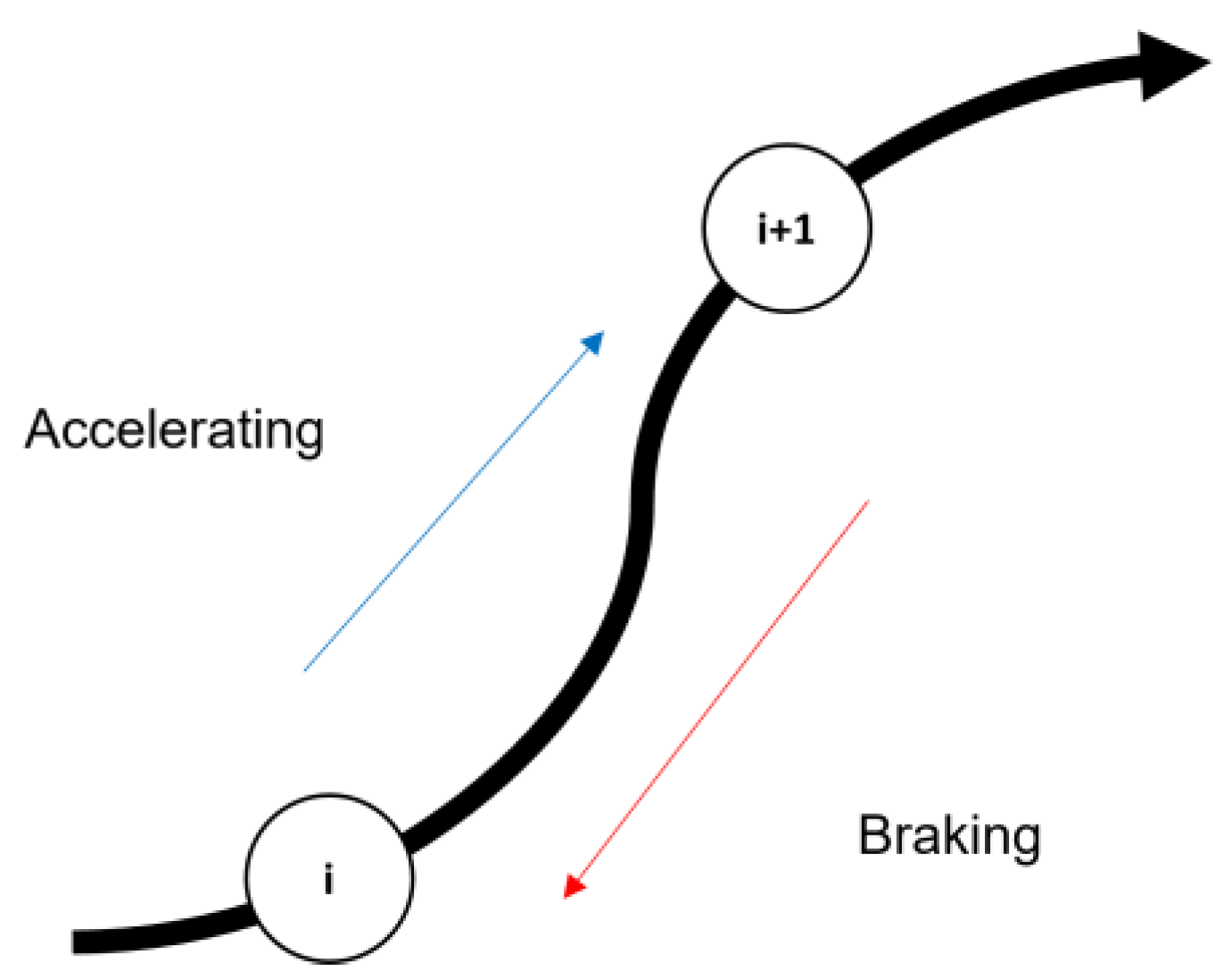
3.2. Calculation Method for Lap Time in Quasi-Steady State
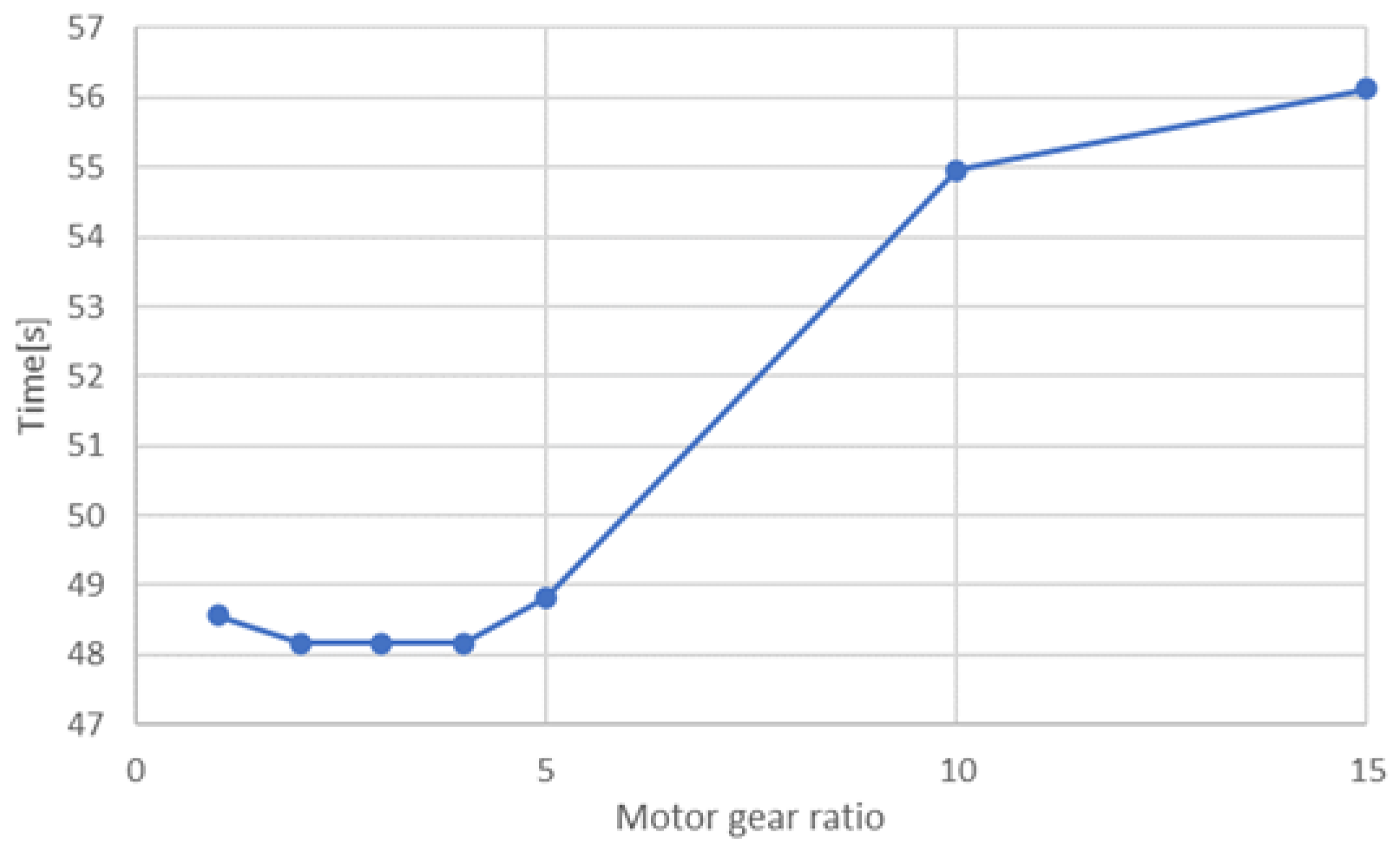
4. Final Gear Ratio and Electric Motor Gear Ratio Study
4.1. Simulation Calculation Conditions
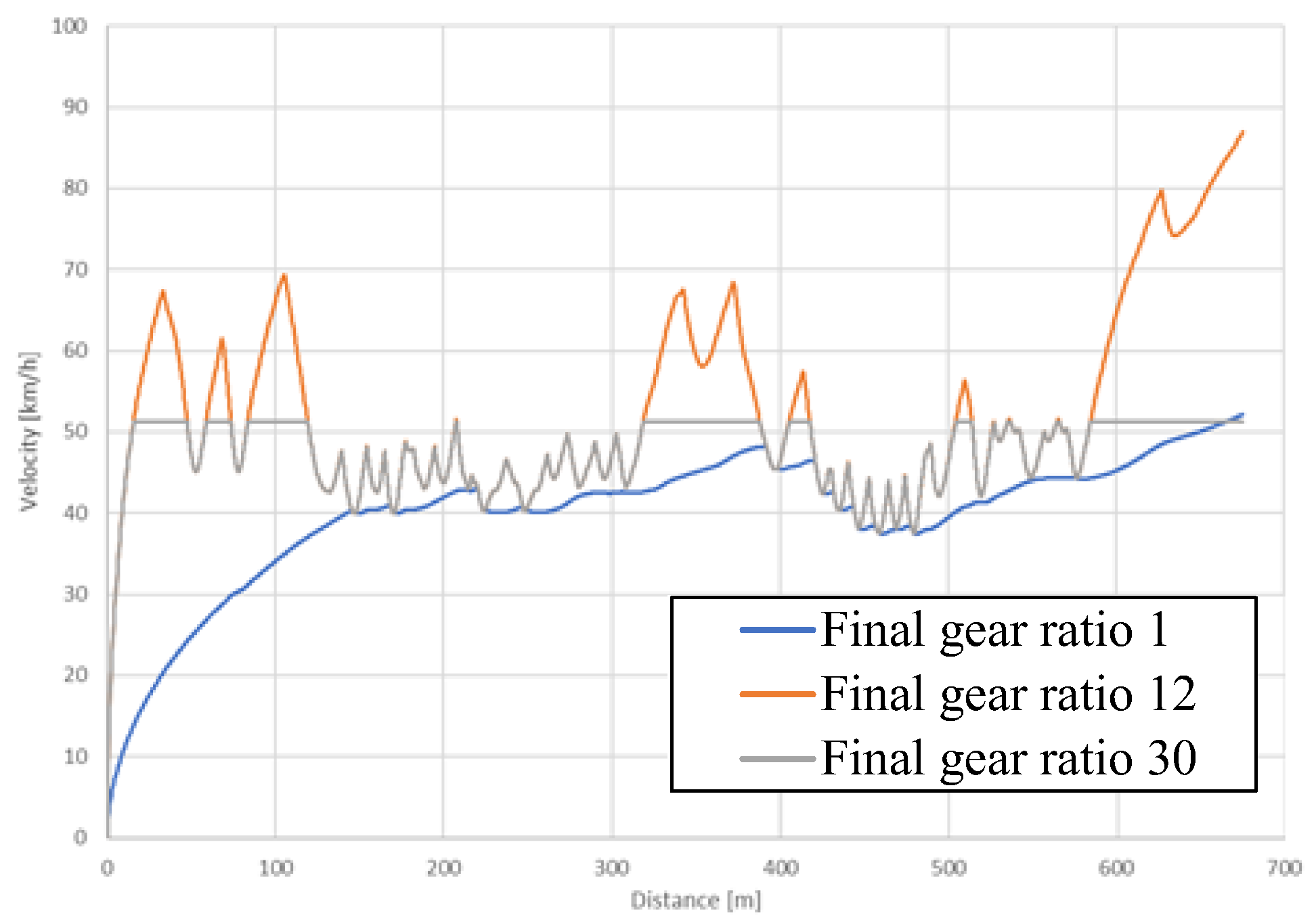
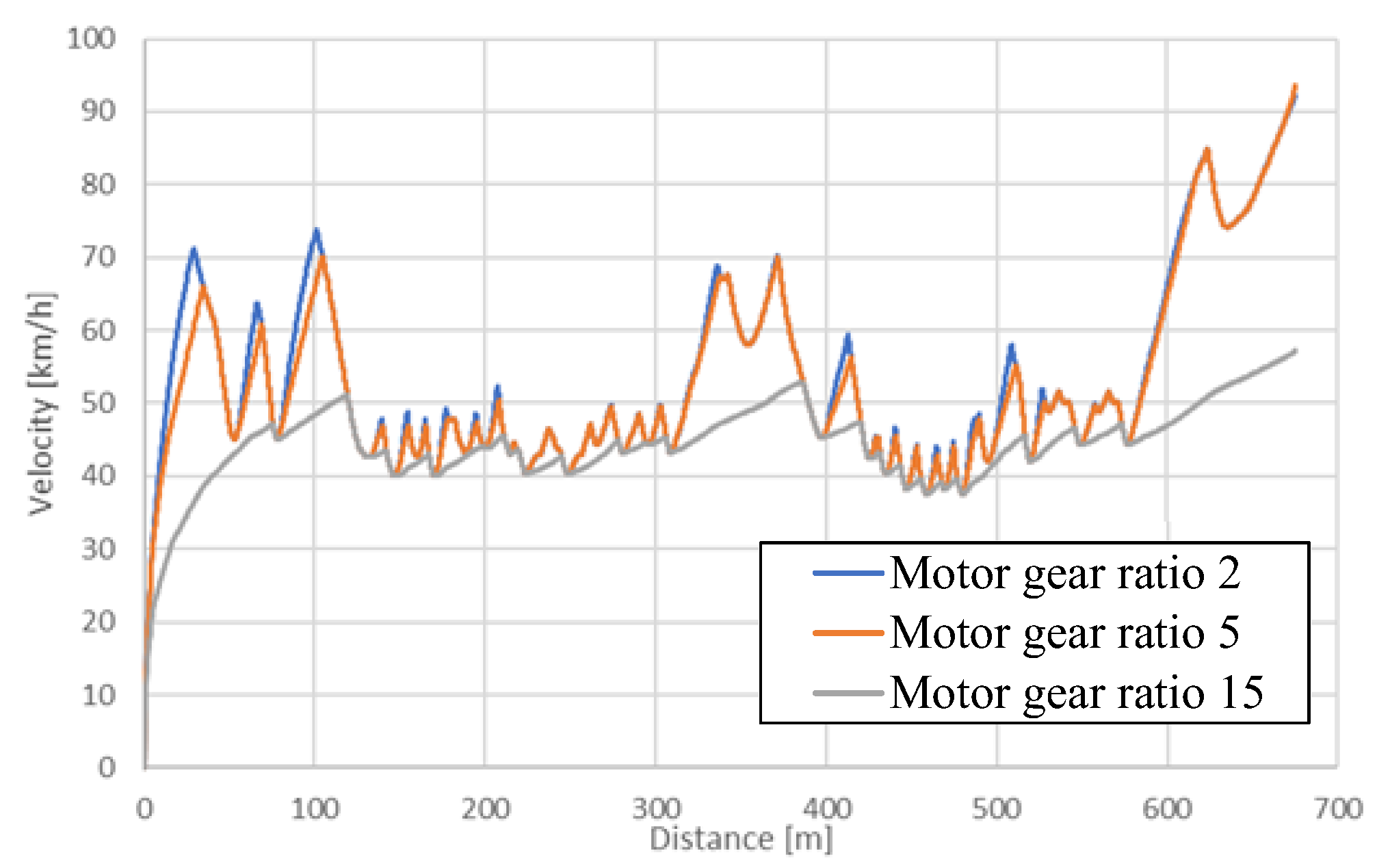
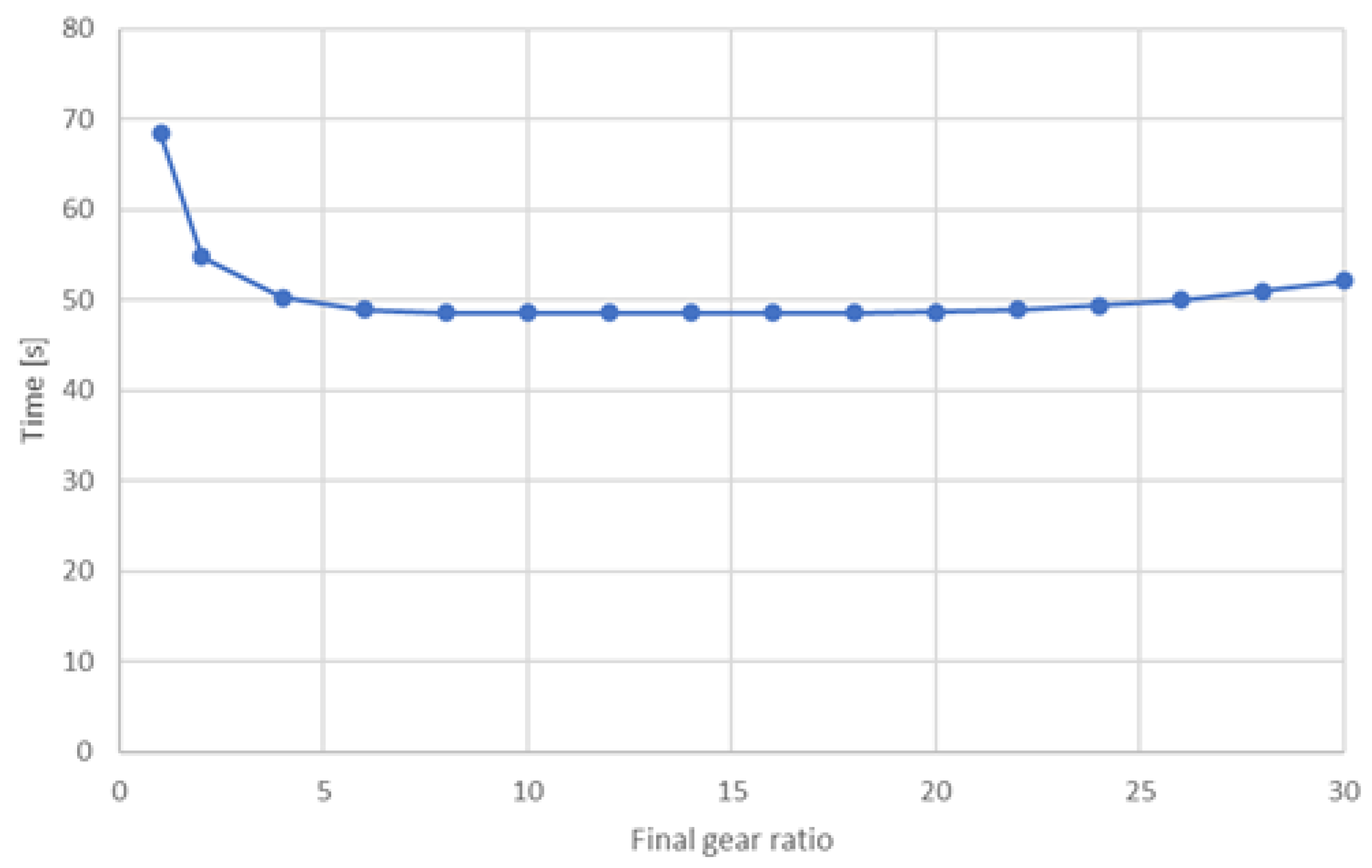
4.2. Analysis Result and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Perez, L.; Pilotta, E. Optimal power split in a hybrid electric vehicle using direct transcription of an optimal control problem. Math. Comput. Simul. Tegucigalpa 2004, 79, 1959–1970. [Google Scholar] [CrossRef]
- Viehmann, A.; Rinderknecht, S. Investigation of the Driving Comfort of the DE-REX Powertrain based on Vehicle Measurements. Int. Fed. Autom. Control. Pap. Online 2019, 52, 103–108. [Google Scholar] [CrossRef]
- Travis, E.; Torrey, J.; John, E.; Denise, M.; Jada, B. Tracked vehicle physics-based energy modelling and series hybrid system optimisation for the Bradley fighting vehicle. Int. J. Electr. Hybrid Veh. 2020, 12, 1–14. [Google Scholar]
- Jing, L.; Xin-ran, W.; Lin-hui, L.; Ya-fu, Z.; Shu-zhou, Y.; Xiu-jie, L. Plug-in HEV energy management strategy based on SOC trajectory. Int. J. Veh. Des. 2021, 82, 1–17. [Google Scholar]
- Zainab, A.; El, A.; Daniela, C.; Luis, M. Energetic macroscopic representation and inversion based control of fuel cell in a series hybrid race vehicle system. Int. J. Electr. Hybrid Veh. 2022, 12, 197–213. [Google Scholar]
- Wu, G.; Zhang, X.; Dong, Z. Powertrain architectures of electrified vehicles: Review, classification and comparison. J. Frankl. Inst. 2015, 352, 425–448. [Google Scholar] [CrossRef]
- Mohammadpour, M.; Rahnejat, H. Dynamics and efficiency of planetary gear sets for hybrid powertrains, Proceedings of the Institution of Mechanical Engineers. Part C: J. Mech. Eng. Sci. 2015, 230, 1359–1368. [Google Scholar]
- Sato, Y.; Narita, T.; Kato, H.; Okamoto, T. Proposal of Power Synthesis Mechanism in Hybrid System for Compact Racing Car: A Fundamental Consideration on Structural Design and Vehicle Movement Performance. Proc. Sch. Eng. Tokai Univ. Ser. E 2018, 43, 31–37. [Google Scholar]
- Lot, R.; Evangelou, S. Lap Time Optimization of a Sports Hybrid Electric. Veh. Proc. World Congr. Eng. 2013, 3, 1711–1716. [Google Scholar]
- Lambert, S.; Maggs, S.; Faithfull, P.; Vinsome, A. Development of A Hybrid Electric Racing Car. In IET HEVC 2008-Hybrid and Eco-Friendly Vehicle Conference; IET: London, UK, 2008. [Google Scholar] [CrossRef]
- Edward, D. The Robust Control of a Servomechanism Problem for Linear Time Invariant Multivariable Systems. IEEE Trans. Autom. Control 1976, 21, 25–34. [Google Scholar]
- Wolter, W. Linear Multivariable Control–A Geometric Approach; Springer: Berlin/Heidelberg, Germany, 1978; pp. 203–210. [Google Scholar]
- Milliken, W.; Milliken, D. Race Car Vehicle Dynamics; Society of Automotive Engineers, Inc.: Warrendale, PA, USA, 1995; p. 343. [Google Scholar]
- Casanova, D.; Sharp, R.; Symons, P. Minimum Time Manoeuvring: The Significance of Yaw Inertia. Veh. Syst. Dyn. 2000, 34, 77–115. [Google Scholar] [CrossRef]
- Bianco, N.; Lot, R.; Gadola, M. Minimum time optimal control simulation of a GP2 race car. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2017, 232, 1180–1195. [Google Scholar] [CrossRef]
- Patton, C. Development of Vehicle Dynamics Tools for Motorsports. Doctor of Philosophy Dissertation, Oregon State University, Corvallis, OR, USA, 2013. [Google Scholar]
- Brayshaw, D.; Harrison, M. A quasi steady state approach to race car lap simulation in order to understand the effects of racing line and centre of gravity location. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2005, 219, 725–739. [Google Scholar] [CrossRef]
- Siegler, B.; Deakin, A.; Crolla, D. Lap Time Simulation: Comparison of Steady State, Quasi- Static and Transient Racing Cornering Strategies. SAE Technical Paper 2000. [Google Scholar] [CrossRef] [Green Version]
- Pacejka, H. Tire and Vehicle Dynamics Third Edition; Elsevier Ltd.: Oxford, UK, 2012; pp. 176–183. [Google Scholar]
- Koutrik, S. Optimal Control for Race Car Minimum Time Maneuvering. Master of Science Thesis, Delft University of Technology, Delft, The Netherlands, 2015. [Google Scholar]




| Engine Model Number | G363E |
|---|---|
| Engine Type | 250 cc liquid-cooled DOHC 4-stroke, 4 valves |
| Bore × Stroke | 77.0 mm × 53.6 mm |
| Compression Ratio | 11.8:1 |
| Fuel Delivery | Fuel injection |
| Ignition | TCI: Transistor Controlled Ignition |
| Transmission | Constant mesh 6-speed, multiplate wet clutch |
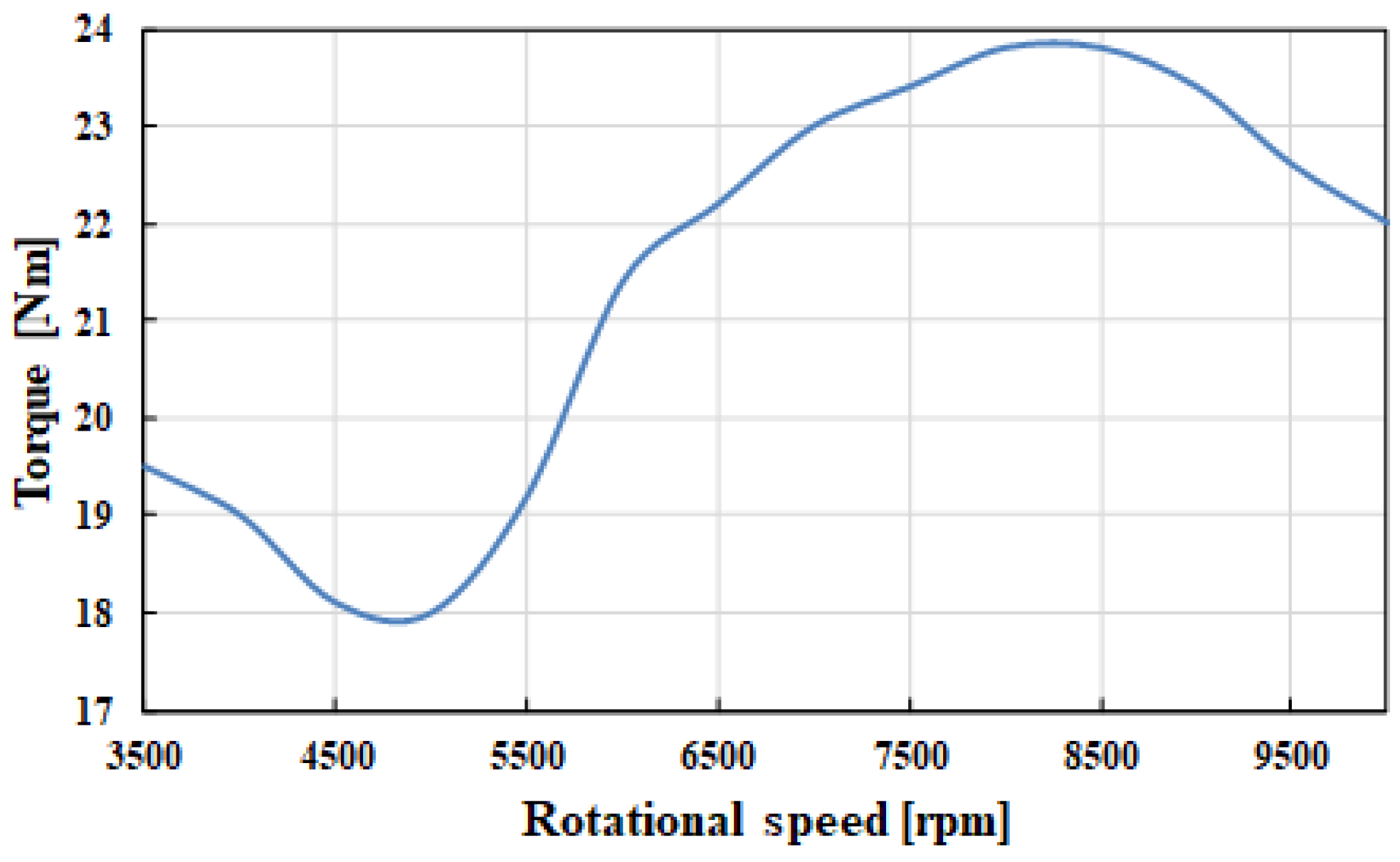
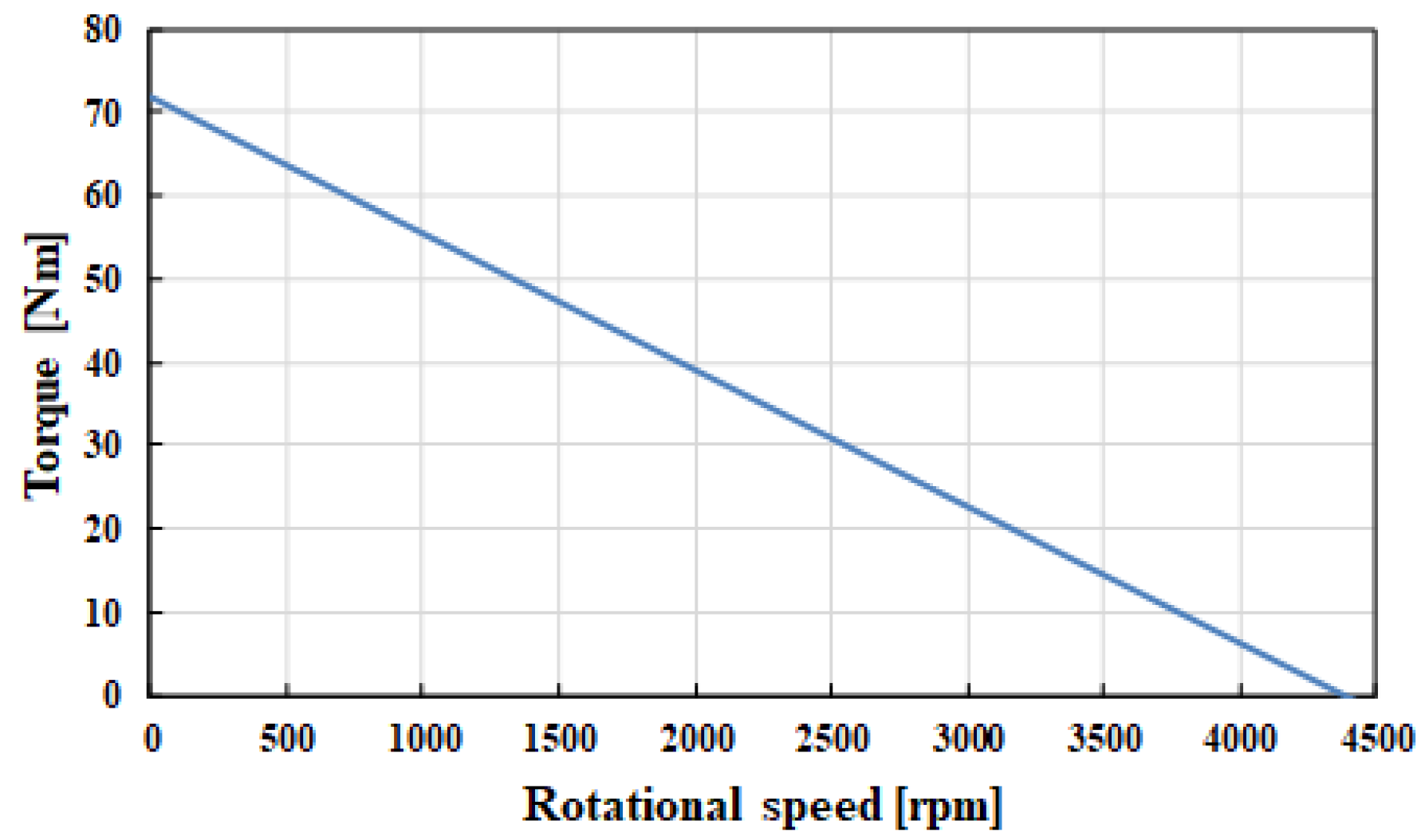
| Max Power | 23 kW/10,000 rpm |
| Max Torque | 24 Nm/8000 rpm |
| Drive voltage | DC 24 V–96 V |
| Maximum current | 550 A |
| Maximum rotation speed | 5000 rpm (No load) |
| Maximum output | 30 kW (DC 96 V) |
| Maximum torque | 90 Nm |
| Continuous output | 12 kW (DC 96 V) |
| Continuous current | 180 A |
| Continuous efficiency | 92 % |
| Continuous rotation speed | 3000 rpm |
| Mass | 15.9 kg |
| Poles | 4 (Magnet 8) |
| Cooling method | Air cooling forced fan system |
| General Data | Engine Data | ||
| Mass [kg] | 369.7 | Thermal Efficiency [%] | 35 |
| Driven Type | 2WD | Transmission | |
| Aerodynamics Data | Gear 1 | 2.642 | |
| Drag Coefficient | 0.8 | Gear 2 | 1.812 |
| Frint Area [m2] | 1.2 | Gear 3 | 1.318 |
| Air Density [kg/m3] | 1.1 | Gear 4 | 1.04 |
| Tire Data | Gear 5 | 0.888 | |
| Tire Radius | 0.128 | Gear 6 | 0.785 |
| Rolling Resistance | 0.03 | Final Drive Ratio | 3.145 |
| Longitudinal Friction | 1.4 | Drive Efficiency | 3.145 |
| Lateral Friction | 1.5 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kobayashi, I.; Ogawa, K.; Uchino, D.; Ikeda, K.; Kato, T.; Endo, A.; Bin Peeie, M.H.; Narita, T.; Kato, H. A Basic Study on Hybrid Systems for Small Race Car to Improve Dynamic Performance Using Lap Time Simulation. Actuators 2022, 11, 173. https://doi.org/10.3390/act11070173
Kobayashi I, Ogawa K, Uchino D, Ikeda K, Kato T, Endo A, Bin Peeie MH, Narita T, Kato H. A Basic Study on Hybrid Systems for Small Race Car to Improve Dynamic Performance Using Lap Time Simulation. Actuators. 2022; 11(7):173. https://doi.org/10.3390/act11070173
Chicago/Turabian StyleKobayashi, Ikkei, Kazuki Ogawa, Daigo Uchino, Keigo Ikeda, Taro Kato, Ayato Endo, Mohamad Heerwan Bin Peeie, Takayoshi Narita, and Hideaki Kato. 2022. "A Basic Study on Hybrid Systems for Small Race Car to Improve Dynamic Performance Using Lap Time Simulation" Actuators 11, no. 7: 173. https://doi.org/10.3390/act11070173
APA StyleKobayashi, I., Ogawa, K., Uchino, D., Ikeda, K., Kato, T., Endo, A., Bin Peeie, M. H., Narita, T., & Kato, H. (2022). A Basic Study on Hybrid Systems for Small Race Car to Improve Dynamic Performance Using Lap Time Simulation. Actuators, 11(7), 173. https://doi.org/10.3390/act11070173






