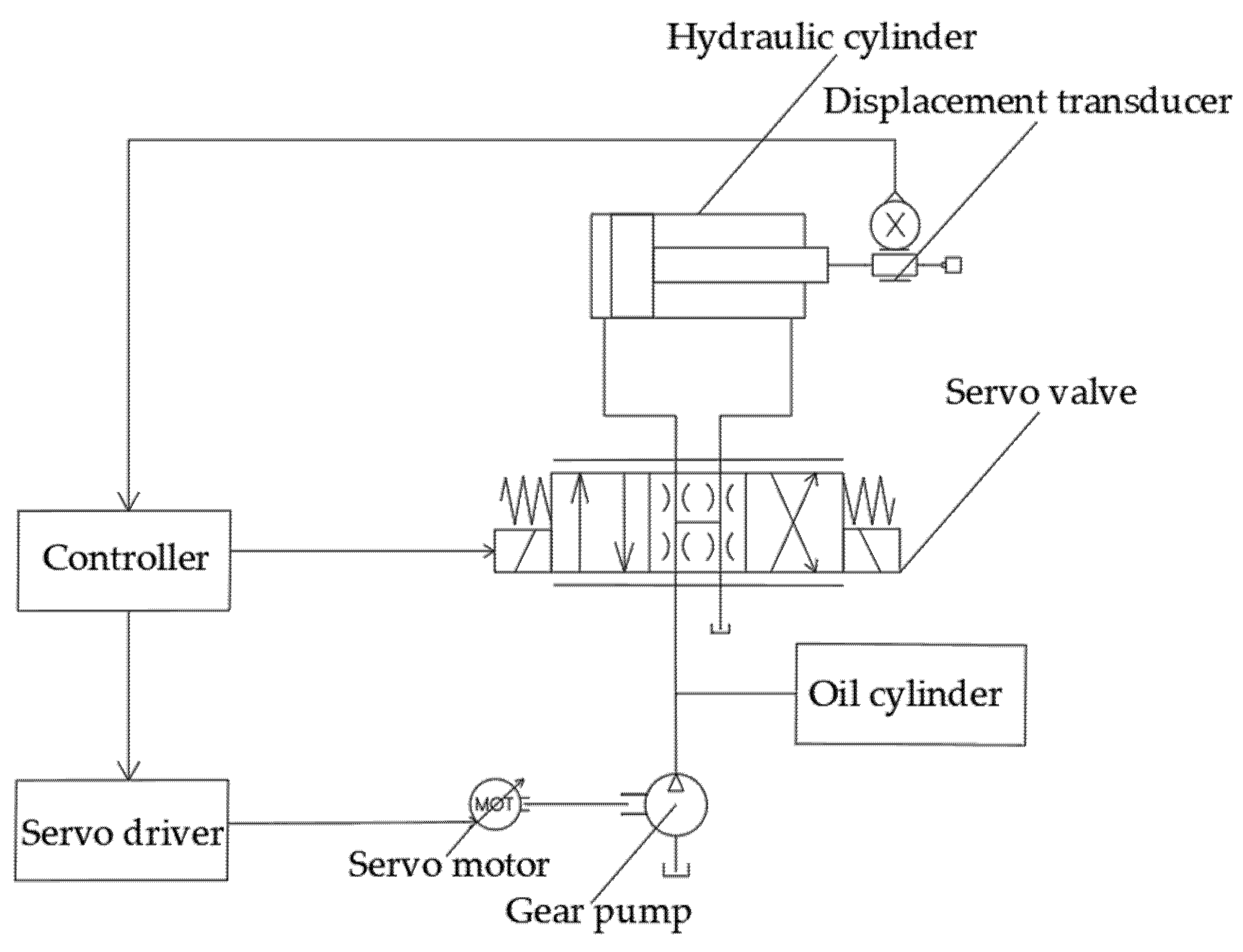
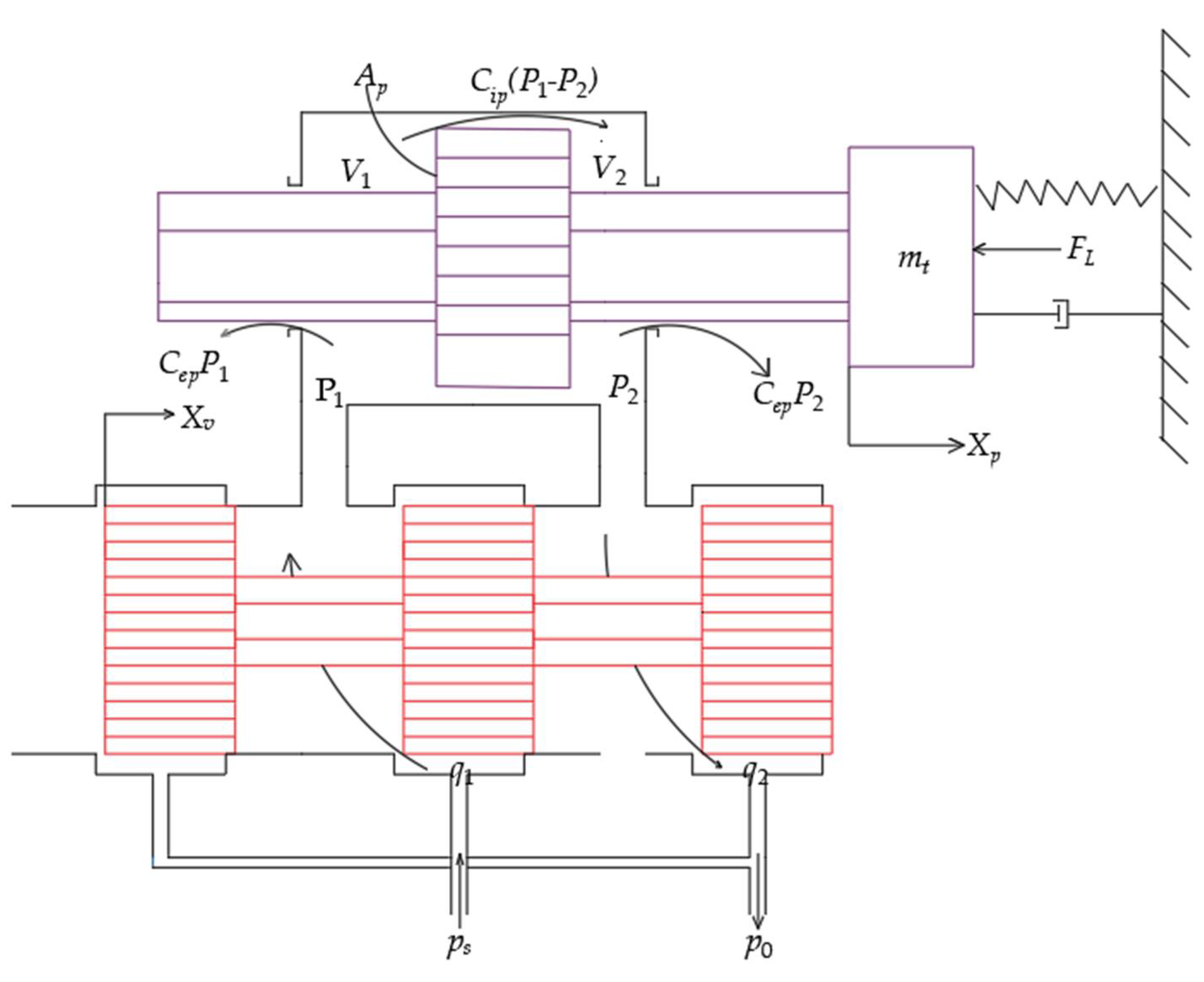
1. Introduction
Hydraulic systems are widely used in industrial and mobile applications due to their high power to mass ratio and reliability. As a closed-loop control hydraulic system, the hydraulic servo system has the advantages of a hydraulic system and has the characteristics of fast response and high servo accuracy. Therefore, a hydraulic servo system is widely used in automation direction. In recent years, research on hydraulic servo systems has focused on trajectory tracking, state estimation, fault diagnosis, and parameter identification to achieve high-performance control [
1]. One of the most desirable requirements is high precision position control with fast response, especially for valve-operated hydraulic cylinders, the actuators of hydraulic servo systems.
The accurate modeling of the controlled object is essential for the position control of the hydraulic servo system. Establishing an accurate mathematical model of the hydraulic servo system is very complicated due to the dead zone in the flow region, the static friction of the fluid, the compressibility and internal leakage of the fluid, the complex flow pressure characteristics of the control valve, and other factors that lead to the problem of a highly nonlinear and largely uncertain hydraulic servo system. In the last few years, some important work has been carried out by related researchers in the modeling of hydraulic servo systems. Xing et al. [
2] analyzed the functions of servo valves and hydraulic cylinders and established the transfer function of an automatic depth-controlled electrohydraulic system using a first-principles approach. Mete et al. [
3] considered the effects of compressibility, friction, servo valve internal leakage, actuator leakage, and inertia on the electro-hydraulic servo system and established a mathematical model of the main components of the internal leakage electro-hydraulic servo system. Zheng et al. [
4] considered the problems of dead zones, saturation nonlinearity, time lag, and time variability in servo-hydraulic presses. Yao et al. [
5] used the known information of the electro-hydraulic servo system to build an adaptive inverse model of the system. For the system’s nonlinear parameters, online estimation was used to adapt the dynamic inverse model in real-time. Ye et al. [
1] considered nonlinear factors such as dead zone, saturation, discharge coefficient, and friction during modeling a valve-controlled cylinder system for a hydraulic excavator. Li et al. [
6] constructed adaptive parts of the hydraulic actuator model with parameter uncertainty to handle it, and considered the residuals of parameter adaptation and the unmodeled dynamics part with a robust part. Shen et al. [
7] analyzed the basic principles of the new hydraulic transformer, established a mathematical model of the system, and simplified the state-space equations of the system by making appropriate assumptions about the system. Knohl and Unbehauen [
8] studied the problem of large dead zones of valves in electro-hydraulic servo systems by linearizing the cylinder and load forces as a second-order system and integrator while connecting the dead zone part and the linear part in a series to describe the hydraulic system. Bao et al. [
9] implemented a multi-pump, multi-actuator hydraulic system modeling based on the dynamic analysis of hydraulic systems. Zhang et al. [
10] trained a BP neural network model to obtain a nonlinear relationship between motor speed and cylinder two-chamber pressure as input and cylinder speed as output and constructed a soft measurement model for the position of the direct-drive hydraulic system by integrating the calculated speed of the network. Nguyen et al. [
11] investigated the motion dynamics of actuators under torque in a mechanical system considering parameter uncertainties, unmodeled uncertainties, and perturbations. They realized the position model of the electro-hydraulic servo system with detailed analysis of servo valve and hydraulic system models. Zhang et al. [
12] considered the clearance problem between spool and sleeve in the construction of the mathematical model of the nonlinear position servo control system of magnetically coupled rodless hydraulic cylinders, established the mass flow relationship of each valve port by analyzing the proportional control valve structure and through experimental tests, and used the friction model after experimental tests for the friction model of the valve-controlled cylinder, so as to realize the establishment of the system dynamics equations. These studies provide some methods for solving nonlinear problems in modeling hydraulic servo systems.
In addition, to achieve good position control, it is necessary to study the control methods used in the hydraulic servo system, such as PID, fuzzy algorithm, neural network optimization, etc. PID control has been commonly used in hydraulic systems with the advantages of simple structure, easy implementation, and mature theoretical analysis. The critical step in PID control is the effective adjustment of three adjustable gains: proportional gain, integral gain, and differential gain. However, PID control has linear characteristics and cannot meet the requirements of nonlinear systems alone. In recent decades, many intelligent optimization techniques have been used to regulate PID gains to solve the control problems of nonlinear and complex systems. Chang [
13] used an artificial bee colony (ABC) algorithm to search for PID control parameters to enhance the control performance of a continuously stirred kettle reactor. He [
14] proposed an improved artificial bee colony algorithm to optimize the gain of the PID controller and improve the control performance of the strip deviation control system. Hao et al. [
15] used the particle swarm optimization (PSO) algorithm to optimize the PID parameters and improved PSO in inertia weights, learning coefficients, and elite variances to improve trajectory tracking accuracy in electro-hydraulic position servo systems. Zheng et al. [
4] introduced a fuzzy PID control method to improve the overall performance of the electro-hydraulic position servo system to establish fuzzy inference rules capable of adaptively adjusting the PID parameters in terms of the error and error variation of the system. Wang et al. [
16] introduced a fuzzy controller based on the particle swarm algorithm to rectify the parameters of the PID. Shutnan et al. [
17] used the clone selection algorithm to rectify the PID parameters for the path tracking problem of a robotic manipulator. Guo et al. [
18] combined PID control and generalized predictive control to exploit the advantages of each and improve the system performance. Odili et al. [
19] applied the African Buffalo Optimization algorithm to rectify the PID controller parameters for effective control of the voltage regulator (AVR). Bingul et al. [
20] used the cuckoo search algorithm to optimize the design of the PID controller parameters in an AVR system. Loucif [
21] used a novel optimization algorithm of the Whale Optimization Algorithm to determine the optimal parameters of the PID controller to achieve better trajectory tracking of the robot operator. Xue et al. [
22] proposed an advanced flaring (AFW) algorithm based on the adaptive principle and bimodal Gaussian function and established a PID parameter rectification model combined with AFW. Gao et al. [
23] proposed an artificial fish swarm algorithm, which has a good optimization effect on the PID of the motion servo control system. Liu et al. [
24] proposed a method for intelligent tuning of PID parameters based on iterative learning control, enabling the PID parameters of the AFM to be self-tuned according to the shape of the sample. Li [
25] proposed a PID control strategy based on bacterial foraging optimization to improve the performance of variable air volume-air conditioning systems. Liu et al. [
26] proposed an improved fruit fly optimization algorithm that combines a PID control strategy with a cloud model algorithm to improve the response performance of a magnetorheological liquid brake proportional-integral differential controller.
Genetic algorithms (GA) are inspired by natural selection and have stochastic optimization properties to optimize any problem without prior knowledge. It also provides faster convergence to near-optimal solutions [
27]. At the same time, compared to traditional optimization algorithms that obtain optimal solutions by a single initial value iteration, genetic algorithms can evolve by searching for multiple solutions in the space simultaneously, thus reducing the risk of falling into a local optimum [
28,
29,
30]. Therefore, the study of the adaptive adjustment of PID parameters using a genetic algorithm has certain reliability and development.
This paper implements modeling of the system by considering nonlinear factors such as internal leakage and oil compressibility of the system. To address the problems of slow response and low accuracy in the position control of valve-controlled hydraulic servo systems, the PID control is used as the basis to improve the performance of the system. In this work, a GA algorithm is used to search the PID parameters to improve the control performance of the system. To solve the amplitude fluctuations caused by the GA algorithm-optimized PID controller in the position response of the hydraulic servo system and to reduce the influence of external disturbances on the system, a Kalman filter is added to the designed GA-optimized PID controller to improve the anti-interference capability of the system.
3. Control Algorithm of Hydraulic Servo System
3.1. PID Control Algorithm
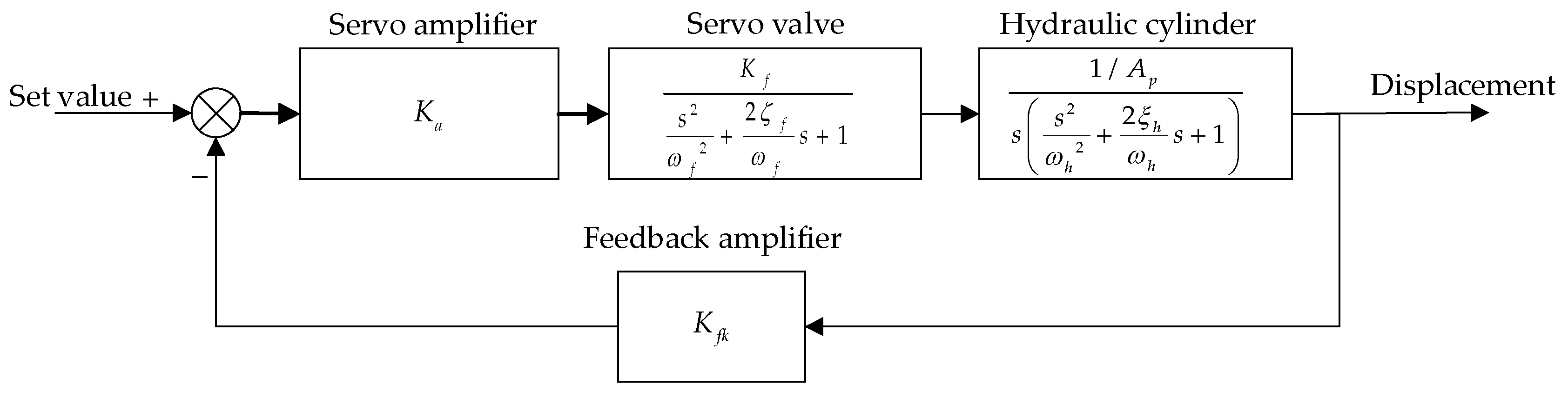
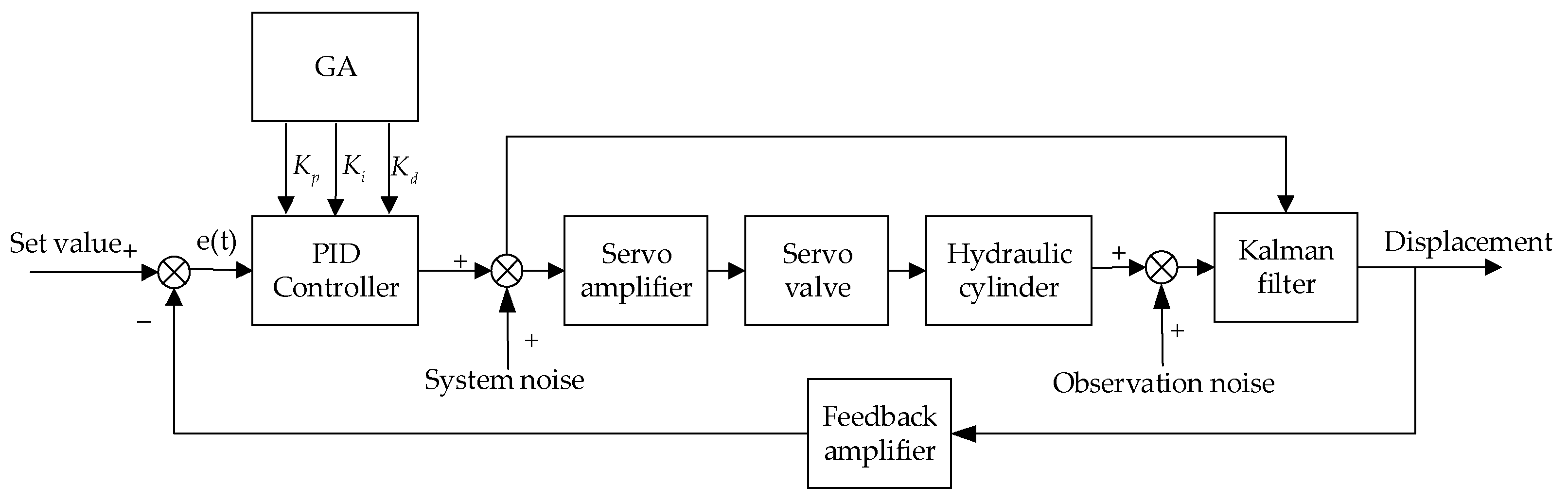
In the closed-loop control system, the PID controller is widely used in the industry. It has the advantages of good stability, convenient adjustment, and high reliability [
6,
7]. Using the PID controller for position control in the hydraulic servo system, as shown in
Figure 4, can increase the accuracy and response speed of the hydraulic servo position control to some extent.
PID control consists of three units: proportional, integral, and differential. PID control adapts to different system requirements by adjusting the gain value of these three units. The PID controller can be expressed as the following mathematical formula [
33]:
where
is defined as the output function of the controller at time
;
is the proportional coefficient;
is the integral coefficient;
is the differential coefficient;
is the error (
equals the set value minus the feedback value);
is the current time; and
is the integral variable. Its expression in the continuous domain
is:
The performance of the PID controller depends on the appropriateness of the selection of the PID gain parameter. Although the gain of the three units of the PID is easy to adjust, different system transfer functions correspond to different PID gain parameters. In the process of gain adjustment, the three units will conflict, resulting in the PID controller not achieving a better performance. Therefore, the gain parameters corresponding to the three units of the PID need to be traded off to obtain the best overall control results. So the key to the PID controller is to adjust the adjustable parameters.
3.2. Optimization of the PID Algorithm by Genetic Algorithm
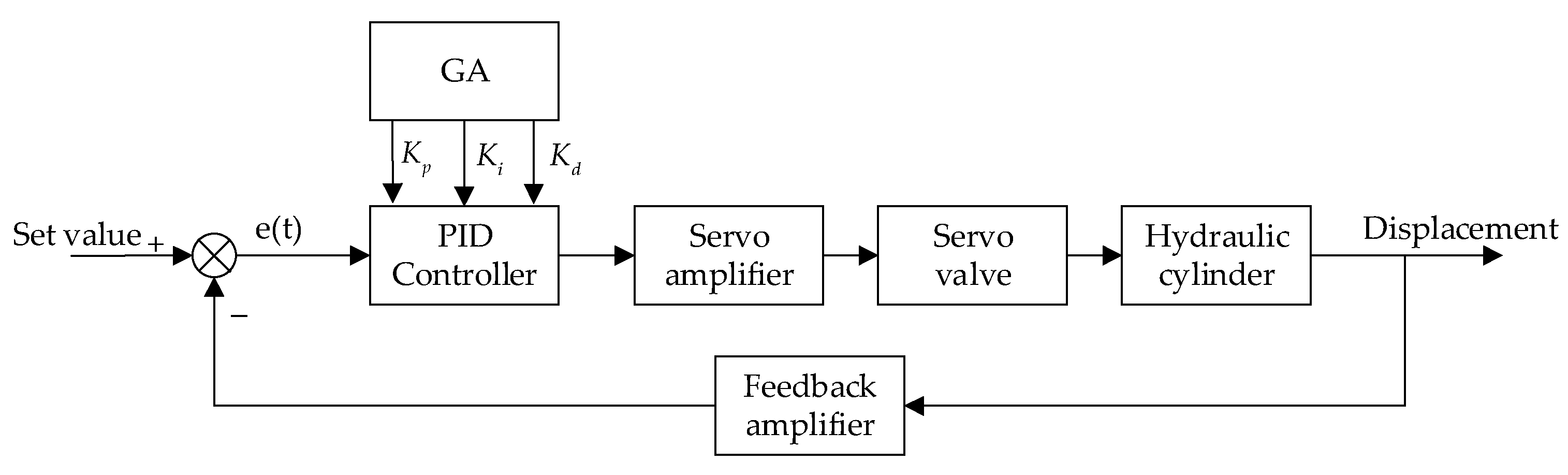
At present, many optimization methods are used to adjust the PID controller parameters, such as PSO, ABC, and so on. ABC can avoid falling into local optimal stagnation in optimization, but it will have the problem of slow convergence; the PSO algorithm converges fast, but easily falls into the local optimal solution and is unstable [
34]. Compared with the above intelligent algorithms, the GA can obtain the global optimal solution according to the principle of natural evolution and converge quickly. The PID controller optimized by GA is used in the hydraulic servo system, as shown in
Figure 5, so that the output response can better track the target.
GA represents an evolutionary process similar to the Darwinian model. This process begins with the creation of an initial random group of individuals. These individuals, the points in the state space, adopt the value of the criterion to be optimized. It goes through the stages of selection, hybridization, and mutation from one generation to another to produce a new population for the next generation. The evaluation of the fitness function makes it possible to provide the optimal solution of the generation under consideration until the unique optimal solution is imposed by the convergence condition of the iterative system [
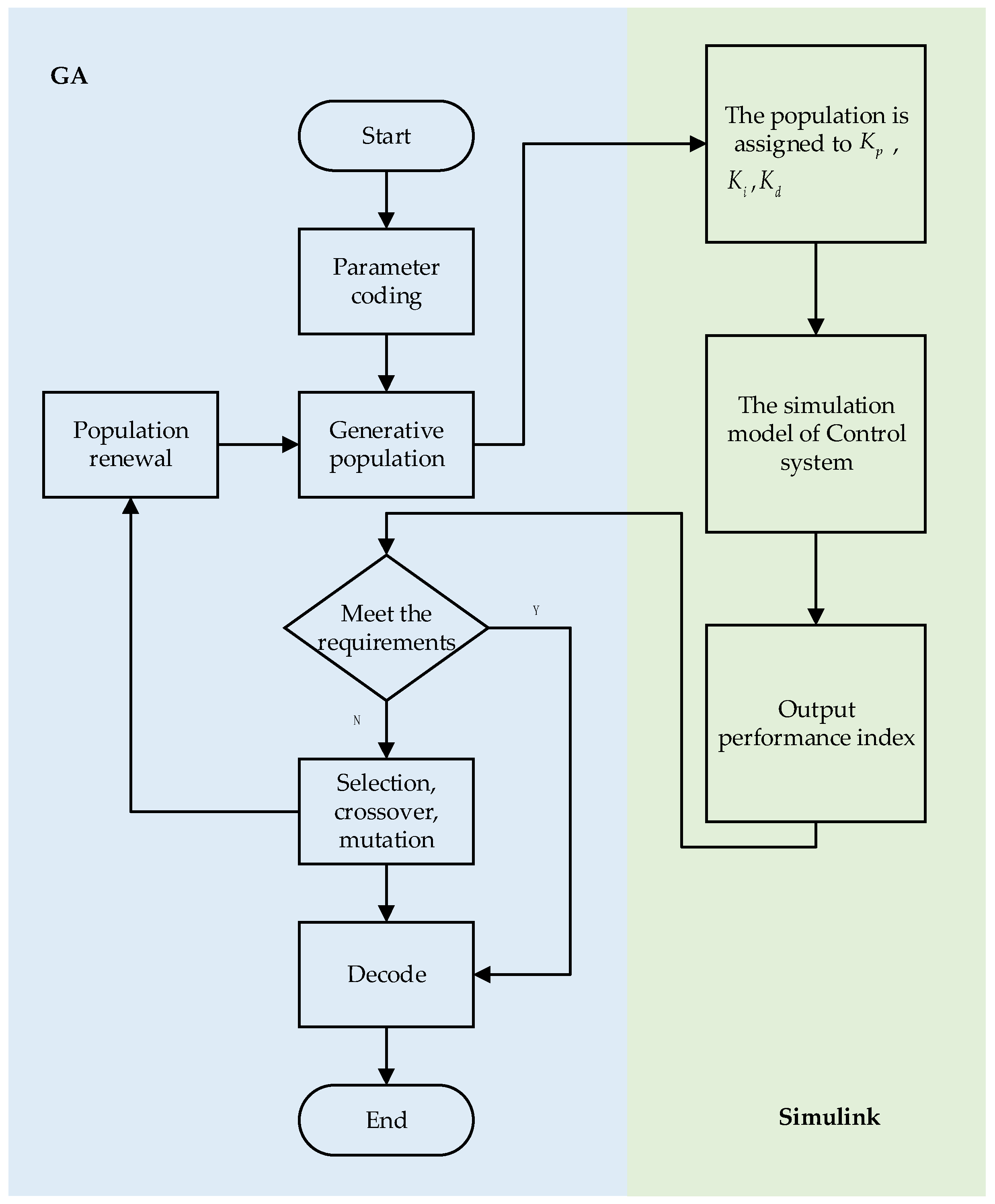
35]. In order to overcome the shortcomings of the PID algorithm, the GA with crossover and mutation operation is used to adjust and optimize the three parameters of PID. GA can flexibly construct a heuristic process and corresponding objective function and can randomly and quickly search the optimal solution and find the global optimal solution in the process of a parameter search. The specific process is as follows:
Coding is the process of converting the three parameters, , , and , in the PID into chromosomes that genetic algorithms can manipulate. The content of the coding is to correspond the genotypes of individuals in biology to potentially feasible solutions. In this paper, the real number coding method is adopted, and the integer in the given range 0 to 9 is used to represent the parameters. The Ziegler-Nichols method is used to determine the optimization interval of PID parameters. The sequence of N, randomly generated [,,], is used as the initial cluster, while the maximum evolutionary generation is set considering the complexity of the calculation.
- 2.
Calculate the value of individual fitness function:
The absolute value time-integrated performance index of the system error is used as the minimum objective function value of the parameter, and the optimal index
for parameter selection is
Among them,
is the optimal index,
is the absolute value of error, and
is the system adjustment time. A penalty factor is added to the optimal index
. In order to avoid the appearance of overshoot and prevent the response time from being slow due to the long rise time, the amount of overshoot is taken as one of the optimal indexes when overshoot occurs, and the rise time is taken as one of the optimal indexes when the response is slow, at which time the optimal index
is
Among them,
is the system overshoot,
is the rise time of the system and
,
,
, and
are the weights corresponding to
,
,
and
. The choice of weights affects the corresponding performance. Adjusting the relative sizes of
,
,
, and
can indicate the importance given to
,
,
, and
. In the program simulation for test debugging,
is set to 0.5, the value of
is set to 0.4,
is set to 0.9, and
is set to 0.4. The fitness function is a tool to determine the genotypic performance of an individual. It can be seen as the driving force for individuals to evolve to salient features. To translate the designed optimal metrics into an adaptation function, the fitness function is designed as
- 3.
Select operation:
The core idea of the selection operation is to calculate each individual’s fitness in the population. Individuals with higher adaptive values have a higher probability of being saved to the next generation, whereas individuals with lower adaptive values are more likely to be eliminated. Using the ranking selection strategy for selection operations, the individuals with larger adaptation values will be selected into the next generation, which can avoid premature convergence to a certain extent.
- 4.
Crossover and variation:
Crossover operation and mutation operation are the main methods for the genetic algorithm to generate new gene individuals. In this paper, the crossover probability is set to 0.8 and the variation probability is set to 0.1. For the variant operation, the random number function is used to determine the location of individual gene mutation. Then, the mutation probability is used to reverse the binary code to produce new individuals for mutation. For crossover operations, the method of uniform crossover is adopted. For two successfully paired individuals and , each gene on their locus can be exchanged with the same probability , thus forming new individuals and .
- 5.
Decode:
Decoding is converting the integer value within 0 to 9 into the actual value of the parameter. When the global optimal value of the parameter selected by the genetic algorithm is the integer value
K, the corresponding actual value after decoding is shown in the Formula (24).
where
is the maximum value in the parameter
optimization interval, and
is the minimum value in the parameter
optimization interval. The decoding mode of the
,
is similar to that of the formula (24).
On this basis, the workflow of optimizing PID parameters based on a genetic algorithm is given, as shown in
Figure 6.
3.3. Kalman Filter
The Kalman filter is an algorithm for estimating unknown variables (states) of linear dynamic systems according to noise and measurements linearly related to the system state. The Kalman filter tracking algorithm mainly consists of two parts: prediction and update [
36,
37,
38,
39,
40]:
The forecast section is shown in (25):
where
is the prior state estimation of the system state
;
is the a posteriori state estimation of the previous system state
;
is the external control quantity of the system;
is the covariance of the prior estimation error (the difference between
and
);
is the covariance of the prior estimation error (the difference between
and
);
is the transition matrix;
is the transpose matrix of
;
is the control matrix; and
is the covariance of the system noise
.
The update section is shown in (26):
where
is the Kalman gain;
is the observation matrix;
is the transpose of
;
is the posterior state estimation of system state
;
is the system observation;
is the covariance of the posterior estimation error (the difference between
and
); and
is the covariance of the observation noise
.
The combination of the Kalman filter and the GA-optimized controller is applied to the position control of the hydraulic servo system. As shown in
Figure 7, it can reduce the impact of external interference (such as periodic vibration of servo valve, etc.) on the system.
4. Simulation and Analysis
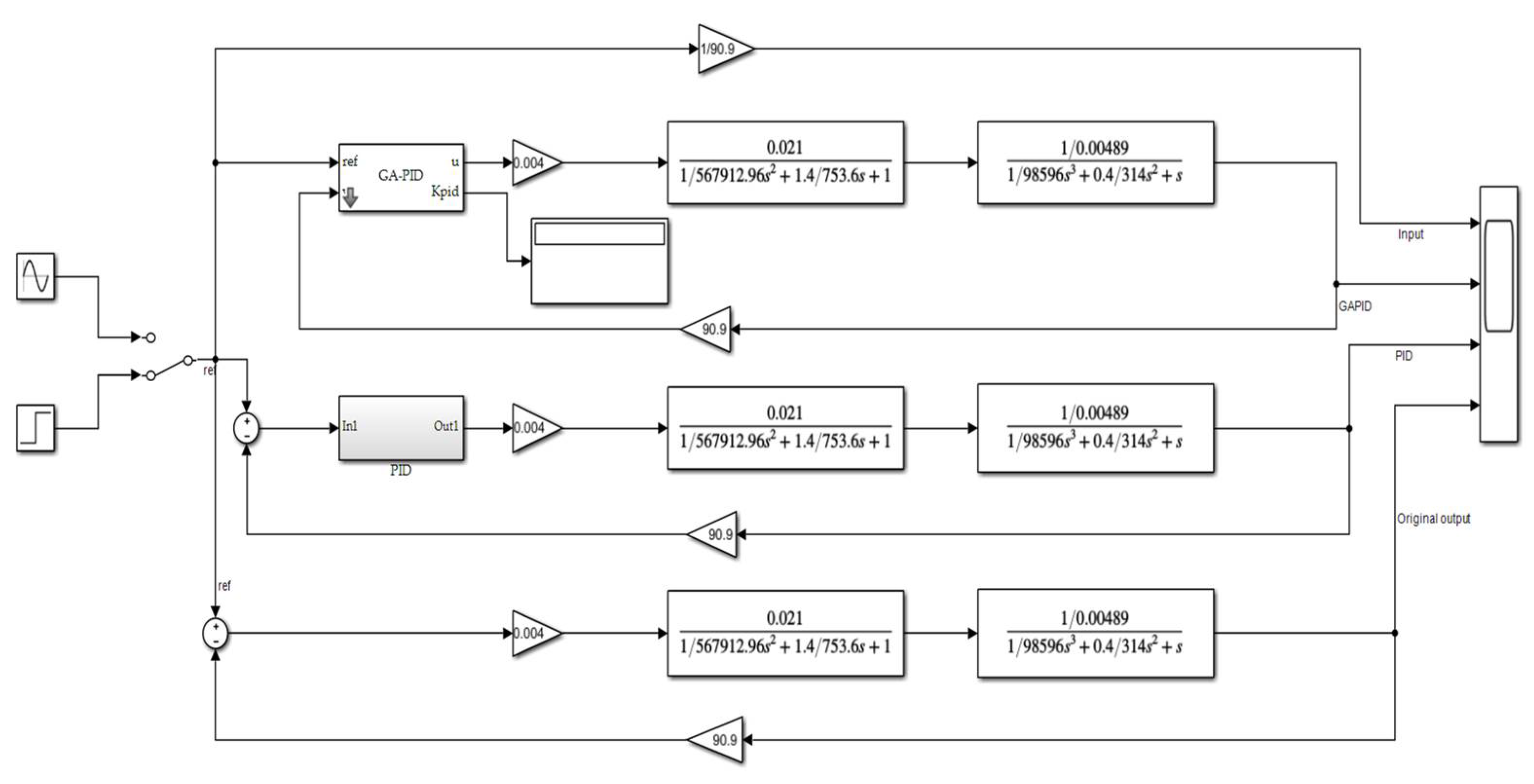
The simulation model of the hydraulic servo system is built in MATLAB/Simulink, and the PID and GA optimized PID control of the system is carried out without interference, as shown in
Figure 8. As shown in
Figure 9a,b, the step signal and sinusoidal signal are used as the input of the system in turn, and the step response and sinusoidal response under PID control and GA-optimized PID control are compared and analyzed. The system simulation results are shown in
Figure 9c,d. The corresponding outputs of the PID control and the GA-optimized PID controller are shown in
Figure 10a,b for the case of step and sinusoidal signal inputs, respectively. The selections of the three parameters
,
, and
of the normal PID and GA-optimized PID are shown in
Table 2.
As can be seen from
Figure 9c, the maximum response of ordinary PID is 0.1132, and the overshoot is 2.9%. The maximum response of PID optimized by GA is 0.1129, and the overshoot is 2.7%. The overshoot of the optimized PID of GA is 0.2% lower than that of ordinary PID. The stable time of the ordinary PID is 1164 s, the adjustment time of PID optimized by GA is 0.063 s, and the adjustment time after optimization is 1101 s better than that before optimization. Taking the time when the output response rises from 10% of the target value to 90% of the target value as the rise time, the rise time of the ordinary PID is 0.0845 s, the rise time of the GA optimized PID is 0.0309 s. The peak time of ordinary PID is 0.248 s. The peak time of PID optimized by GA is 0.061 s. According to the rise time and peak time, under the step signal input, the response speed of the ordinary PID is obviously slower than that of the GA-optimized PID.
As can be seen from
Figure 9d, when the control algorithm does not optimize the input sine signal, there is a large amplitude attenuation and phase lag; under the control of PID optimized by PID and GA, the corresponding output displacement of the valve-controlled hydraulic servo system under the sinusoidal signal input has been improved to a certain extent. From the local magnification diagram of the system sinusoidal signal corresponding to the output displacement in
Figure 9d, it can be clearly seen that the output response of the sinusoidal signal of the system under the PID control optimized by GA is closer to the input signal of the system in terms of phase and amplitude than that of the ordinary PID. Therefore, the tracking performance of the GA optimized PID is better than that of the ordinary PID. That is, the control performance of the GA optimized is better.
As can be seen from
Figure 10a, for the error between the input and output of the system, the PID is close to zero after 0.261 s of regulation, while the system takes 0.227 s with the GA optimized PID regulation, a reduction of 0.034 s over the PID’s regulation time. This shows that the GA-optimized PID has a faster adjustment to error and better tracking performance of the input signal. As can be seen from
Figure 10b, the error between the input and output of the system is corrected after both controllers and the error remains stable, whereas the error is zero when passing the mid-point, preventing the accumulation of errors, but the GA-optimized PID correction is faster than the unoptimized PID.
As can be seen from
Figure 9c,d, although the output response of the hydraulic servo system after the genetic algorithm-optimized PID controller is somewhat better than the normal PID, the genetic algorithm-optimized PID causes large amplitude fluctuations, which are not allowed in the hydraulic servo system. For the fluctuations caused by the genetic algorithm-optimized PID and the possible external disturbances during the operation of the hydraulic servo system, Kalman filtering is introduced in this paper to deal with them. System noise and observation noise are added to the hydraulic servo system to simulate the hydraulic servo system subjected to external disturbance. A simulation model of the hydraulic servo system is built in Simulink, as shown in
Figure 11, to analyze and compare the system immunity under PID, GA-optimized PID control, and GA-optimized PID control after the introduction of the Kalman filter.
The system noise and observation noise are set to 0.002 energy white noise, as shown in
Figure 12. At the same time, the covariance
and
of system noise
and observation noise
are set to 1, and the step signal and sinusoidal signal are taken as the input of the system. The step response and sinusoidal response, as shown in
Figure 9a,b, under PID control, GA-optimized PID control, and Kalman- and GA-optimized PID control are compared and analyzed. The system simulation results are shown in
Figure 13a,b. The corresponding outputs of the PID control and the GA-optimized PID controller are shown in
Figure 13a,b for the case of step and sinusoidal signal inputs, respectively.
From
Figure 13, it can be seen that under the interference of system noise and observation noise with an energy of 0.002, it takes 0.172 s for PID to restore equilibrium and 0.099 s for PID optimized by GA. As can be seen from
Figure 14, the PID takes 0.26 s to eliminate the effect of disturbances on the system error when subjected to external disturbances, compared to 0.22 s after GA optimization. At the same time, GA_PID with the Kalman filter module needs almost no time to adjust. It can be seen that the anti-jamming ability of PID is the worst, the anti-jamming ability of PID optimized by GA is better than that of PID, and the anti-jamming performance of GA_PID after Kalman filter is the best, which not only solves the amplitude disturbance of the system caused by the GA optimized PID, but also largely reduces the effect of external disturbance on the system.